Kim and Lee: Wave Overtopping Formula for Impulsive and Non-Impulsive Wave Conditions against Vertical Wall
Abstract
In this study, two dimensional wave overtopping tests for vertical wall were performed and overtopping formulas were suggested for impulsive and non-impulsive wave conditions. The test results from this study were compared with those from EurOtop(2007). The wave overtopping formulas were derived and suggested considering the recent research trends, while the existing method used the diagram. The wave overtopping formulas have the form of exponential and power functions using non-dimensional variables for wave overtopping and freeboard heights for non-impulsive and impulsive condition, respectively. The wave overtopping formula and effective parameters for inclined superstructure were also suggested. It is analyzed that the locations of inclined superstructure do not have the significant effects on wave overtopping, that is, the wave overtopping rate were almost same for each locations. 핵심용어: vertical structure, inclined superstructure, wave overtopping formula, impulsive condition, non-impulsive condition, 직립식구조물, 경사형 상치콘크리트, 월파량산정식, 충격파 조건, 비충격파 조건
Abstract
본 연구에서는 2차원 수리실험을 통해 충격파 및 비충격파 조건에서의 직립식구조물의 월파량 산정식을 제안하였으며, 연구결과는 EurOtop(2007)의 결과와 비교하였다. 특히, 최근의 월파량 산정기법의 연구동향을 고려하여 도표형태가 아닌 함수형태로 월파량 산정식을 제안하였다. 상대여유고와 무차원 월파량의 관계를 비충격파 조건은 지수함수, 충격파 조건은 거듭제곱 함수 형태로 제시하였다. 또한 경사형 상치콘크리트가 월파량에 미치는 영향계수를 제시하였다. 경사형 상치콘크리트의 설치위치가 월파량에 미치는 영향을 검토한 결과에 의하면 설치위치에 따른 차이는 크지 않은 것으로 나타났다. 핵심용어: vertical structure, inclined superstructure, wave overtopping formula, impulsive condition, non-impulsive condition, 직립식구조물, 경사형 상치콘크리트, 월파량산정식, 충격파 조건, 비충격파 조건
1. 서 론
항만 구조물을 설계함에 있어 월파량은 중요한 설계인자 중 하나이다. 특히 월파량은 구조물의 마루높이를 결정하는 중요한 설계항목으로서 적절한 월파량의 예측은 반드시 필요하다. 월파는 방파제 및 방파호안 배후면의 접안시설 활용 등에 영향을 미칠 수 있으며, 또한 과도한 월파는 전달파를 생성하여 항내정온도에 악영향을 줄 수 있다. 경사식구조물의 경우에는 월파가 항내측 사면에 거치된 피복재의 이탈을 유발함으로서 제체 안정성에 영향을 미칠 수 있다. 이와 같이 월파는 구조물설계 및 항만운영 등의 측면에서 매우 중요한 역할을 한다. 이에 따라 적절한 월파량의 산정 및 예측은 경제적인 측면, 항만구조물의 안정성 확보 및 항만운영 측면에서 중요하다.
우리나라의 설계기준인서인 항만 및 어항 설계기준·해설에서는 Goda 도표( Goda, 1970; Goda et al., 1975; Goda, 1985)가 수록되어 있으며, 단순한 형상의 직립식구조물 및 소파호안에 적용할 것을 제시하고 있다. 미국의 CEM에는 직립식구조물과 경사식구조물에 대한 다양한 월파량 산정식이 수록되어 있으며, 월파량산정식은 여유고와 입사파고의 상관관계를 이용한 지수함수 및 거듭제곱 형태의 식으로 나타내고 있다. EurOtop은 CLASH Project를 통해 상대적으로 가장 최근에 제시된 월파량 산정지침이다. EurOtop에서는 제방과 같은 완만한 구조물, 경사식구조물 및 직립식구조물을 대상으로 확률론적방법(probabilistic design)과 결정론적방법(deterministic design)의 월파량산정식을 제시하고 있다. 직립식구조물의 경우에는 충격파(impulsive)와 비충격파(nonimpulsive) 조건으로 구분하여 각각의 월파량산정식을 제시하고 있으며, CEM과 같이 지수함수와 거듭제곱의 함수로 여유고와 월파량의 관계를 제시하고 있다. 본 연구의 주된 목적 및 내용은 월파량 산정기법의 개선으로서 항만 및 어항설계기준·해설( MOF, 2014)에 적용된 Goda의 월파량 산정도표를 개선하는 것이다. Goda의 월파량 산정도표는 제한된 입력조건에 대한 월파량을 내삽 또는 외삽의 방식으로 산정함에 따라 설계자에 따라 상이한 월파량이 계산될 수 있다. 반면 유럽 및 미국의 설계기준에서는 도표가 아닌 산정식의 형태로 월파량 산정기법을 제시하고 있다. 이에 따라 본 연구에서는 유럽 및 미국의 연구경향에 맞추어 월파량 산정식을 제시하고자 한다. 본 연구에서는 단순한 형상의 직립식구조물을 대상으로 2차원 수리실험을 수행한 후, 충격파와 비충격파 조건으로 구분하여 월파량산정식을 제시하였다. 또한 경사형 상치콘크리트 형상이 월파량에 미치는 영향을 검토하였다.
2. 수리모형실험
2.1 실험시설
수리실험은 한국건설기술연구원의 폭 1.0 m, 높이 2.0 m, 길이 56 m의 수로에서 수행되었으며, 단면수로에는 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다( Fig. 1 참조). 그리고 단면수로의 폭 1.0 m는 폭 0.6 m와 폭 0.4 m로 분할되어 있으며, 분할된 수로에서 실험모형은 폭 0.6 m의 수로에 설치하여 제반 자료를 취득하고, 폭 0.4m의 수로에서는 입사파의 설정 및 보정을 수행하였다. 또한 흡수식 조파를 실시하여 구조물 및 조파기에서 재반사를 최소화 하였다.
Fig. 1.
Schematic sketch of wave flume.
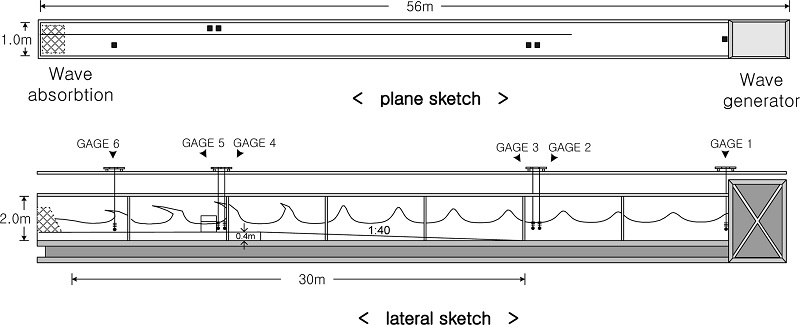
단면수로는 전면 30 m 구간을 강화유리로 처리하여 실험 장면 관찰이 용이하도록 되어있으며, 수로 양쪽 끝 부분에는 여러 겹의 다공성 구조로 형성된 소파장치가 설치되어 있다.
2.2 실험파 조건 및 실험모형
실험파는 Bretschneider-Mitsuyasu 스펙트럼을 적용한 불규칙파 조건을 적용하였으며, 목표 유의파고( H1/3,target)는 H1/3,target= 5.0 cm, 7.5 cm, 10.0 cm, 12.5 cm, 15.0 cm, 17.5 cm, 20.0 cm이고, 목표 유의주기( T1/3,target)는 T1/3,target = 1.4~3.0 sec 범위에서 0.2 sec 간격으로 설정하였다. 실험파는 구조물 설치위치에서 구조물이 설치되지 않은 상태에서 설정하였다. 구조물 설치 후 흡수식 조파를 적용하여 구조물에서의 반사파를 수로내에서 최소화 하더라도 입사파는 변형될 수 있다. 따라서 본 실험에서는 실험시 폭 0.4 m 수로의 구조물 toe 위치에서 입사파( H1/3 및 T1/3)를 상시 분석하여 월파량 분석시의 입사파로 활용하였다. 즉, 실험에서는 Table 1에 제시된 목표 실험파 조건을 완벽히 재현하기는 어렵고 유사한 조건의 실험파가 설정되게 되므로 실험결과 분석시에는 목표 실험파 조건이 아닌 실험시의 입사파 조건을 이용하여 결과를 분석하였다는 의미이다. 그리고 구조물 설치수심( hs)은 hs= 0.3m, 0.4 m 및 0.5 m이며, 여유고(freeboard, Rc)는 Rc= 0.05m, 0.075 m, 0.10 m, 0.125 m, 0.15 m, 0.175 m 및 0.20 m이고, 케이슨 폭( B)은 B = 0.4m이다. Table 1은 본 연구에서 수행한 실험조건을 정리한 것이다. 본 연구에서 수행한 직립식구조물의 표준 단면형상은 Fig. 2와 같으며, 구조물 전면에는 1:40의 경사면이 설치되어 있다.
Table 1.
Test wave and freeboard conditions of experiments
|
parameter |
properties |
|
T1/3,target (sec) |
1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8 |
|
H1/3,target (m) |
0.05, 0.075, 0.10, 0.125, 0.15, 0.175, 0.20 |
|
freeboard (Rc, m) |
0.05, 0.075, 0.10, 0.125, 0.15, 0.175, 0.20 |
|
hs (m) |
0.3, 0.4, 0.5 |
Fig. 2.
Model structure of vertical wall with upright superstructure.
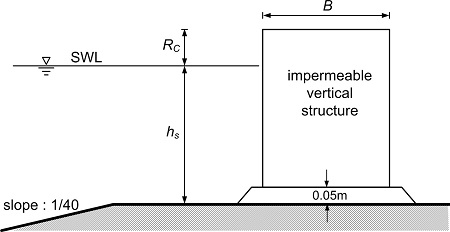
또한 상치콘크리트의 형상이 월파량에 미치는 영향을 검토하기 위하여 Fig. 3과 같은 경사형 상치콘크리트를 대상으로 월파량 계측실험을 수행하였다. 경사형 상치콘크리트의 경사 각( α)은 α = 45°이고, 여유고( Rc)는 Rc= 0.075 m, 0.10 m, 0.15 m이며, CASE 1을 대상으로 하였다. 그리고 경사형 상치콘크리트의 설치 위치가 월파에 미치는 영향을 검토하기 위해 Rc= 0.1m 조건을 대상으로 경사형 상치콘크리트가 전면(CASE 1), 중앙(CASE 2), 끝단(CASE 3)에 설치된 경우에 대해 실험을 실시하였다. 경사형 상치콘크리트의 영향계수 실험에서는 hs= 0.5m를 적용하였다. 경사형 상치콘크리트의 각도가 45° 인 조건을 본 연연구에서 적용하였다. 본 연구에서 적용한 경사각 45°가 경사형 상치콘크리트를 대표하는 단면이라 할 수는 없지만, CEM( USACE, 2005)에서 45° 경사형 상치콘크리트 형상에 대한 Takahashi(2002) 전달파고계수 산정식을 대표 경사각으로 제시함에 따라 본 연구에서도 우선적으로 45°를 적용하였다.
Fig. 3.
Model structure of vertical wall with inclined superstructure.
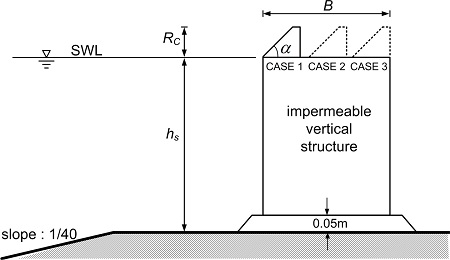
본 연구에서는 직립식구조물의 월파량 산정을 위한 실험식을 도출하기 위해 구조물 후면에서 연속적으로 월파량을 계측하였다. 월파량 계측은 각각의 유의주기 기준 1,000파를 대상으로 하였으며, 유량계를 이용하여 1,000파에 대해 연속적으로 계측하였다. 월파량은 일반적으로 무게 또는 부피를 계측하지만, 연속적으로 1,000파를 계측할 경우에는 월파된 유량을 보관하기 어려우며, 보관시에는 수위변동이 발생될 수 있다. 따라서 본 연구에서는 수중펌프와 터빈형태의 유량계를 조합하여 월파량 계측장비를 개발한 후 수위변동 없이 실시간으로 월파량을 계측하였다( Kim, 2010).
3. 분석 방법
항만구조물을 설계함에 있어 월파량은 평균월파량, 즉 단위폭당 단위시간당 월파량( q, m3/sec/ m)을 일반적으로 활용한다. 월파에 영향을 미치는 변수는 유의파고, 스펙트럼 첨두에 해당하는 주기( Top), 단파봉파(short-crested wave)의 분포형상( σ), 입사파의 내습각도( β), 여유고( Rc), 구조물 전면 수심( hs), 중력가속도( g) 및 구조물 형상 등을 들 수 있으며, 식(1)과 같이 나타낼 수 있다.
식(2)와 식(3)에서 Q는 무차원 월파량이고, 변수 a와 b는 Q와 R의 상관관계를 지수함수 및 거듭제곱함수의 형태로 추세선을 나타낼 경우에 구조물의 형상 및 입사파 조건 등에 의해서 결정되는 계수이다. 특히 식(2)에서 계수 a는 여유고가 0인 조건(zero freeboard)에서의 무차원 월파량을 의미하고, b는 단면형상 및 입사파 조건에 의해 변하는 각계수(angular coefficient)이다.
EurOtop(2007)에서는 수심과 파고, 주기와 수심의 상관관계를 나타내는 식 (4)와 같은 충격지수(impulsiveness parameter, h*)를 도입하여 비충격파 조건( h* >0.3)과 충격파( h* ≤0.3) 조건으로 구분하였다. 식 (4)에서 Hm0와 Tm-1,0는 각각 스펙트럼분석을 통해 산정된 유의파고 및 유의주기이다.
EurOtop(2007)에서 제시한 직립식구조물에 대한 월파량 산정식은 식 (5) 및 식 (6)과 같다. 식 (6)는 비충격파 조건( h* >0.3), 식 (6)은 충격파 조건( h* ≤0.3)의 월파량산정식이다. 식 (5) 및 식 (6)에서 probabilistic design식은 확률론적 월파량산정식을 의미하며, 수리실험으로 계측된 월파량의 평균값이라 할 수 있다. 그리고 deterministic design식은 결정론적 월파량산정식으로서 확률론적 월파량산정식에서 표준편차 만큼 증가시킨 식이다. EurOtop(2007)에서는 항만구조물 설계시 수리모형실험을 수행하는 경우에는 확률론적 월파량산정식을 이용하여 마루높이를 설정하고, 수리모형실험을 수행하지 않는 경우에는 결정론적 월파량산정식을 이용하여 마루높이를 설정할 것을 권하고 있다.
-Probabilistic design (non-impulsive condition, h*>0.3)
-Deterministic design (non-impulsive condition, h*>0.3)
- Probabilistic design (impulsive condition, h*≤0.3)
- Deterministic design (impulsive condition, h*≤0.3)
EurOtop(2007)에서는 유의파고(significant wave height)를 spectral wave height인
Hm0(=4m0)
를 사용하고 있다. 수심이 상대적으로 깊은 경우에는 H1/3과 Hm0는 같지만, 수심의 영향을 받는 지역, 즉 쇄파가 발생하는 경우에는 H1/3과 Hm0가 약 10~15% 정도 차이가 있는 것으로 알려져 있다. 이러한 현상을 고려하고, 주파수 스펙트럼 내의 장주기 성분을 고려하기 위해 spectral wave height인 Hm0를 사용한다고 제시되어 있다.
국내에서는 일반적으로 구조물 설치위치에서의 유의파고(H1/3)를 이용하여 설계를 수행하고 있으므로 본 연구에서는 자유수면자료로부터 영점상향교차법을 이용하여 분석된 유의파고(H1/3)를 이용하여 월파량산정식을 제시하고자 한다.
4. 실험결과 및 분석
4.1 평균 월파량산정식
Fig. 2와 같은 직립식구조물을 대상으로 Table 1의 실험조건을 적용하여 2차원 실험을 수행한 후, 무차원월파량( Q)과 무차원여유고( R)를 이용하여 식 (2) 및 식 (3)의 형태로 분석하였다. 본 연구에서 수행된 실험으로 분석된 Q-R 관계와 EurOtop(2007)의 Q-R 관계를 비교하여 도시한 것이 Fig. 4와 Fig. 5이다. 그리고 본 연구에서는 식 (4)의 충격지수 계산시 Hm0와 Tm-1,0 대신 영점상향교차법(zero-up-crossing method)을 이용하여 분석한 H1/3와 T1/3을 이용하였다.
Fig. 4.
Wave overtopping for vertical wall with upright superstructure (non-impulsive condition).
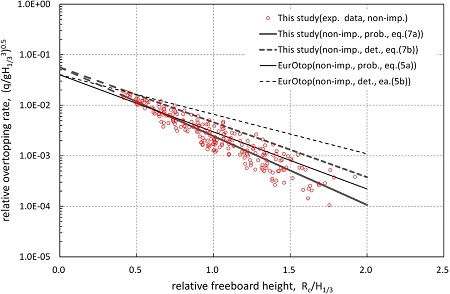
Fig. 5.
Wave overtopping for vertical wall with upright superstructure (impulsive condition).
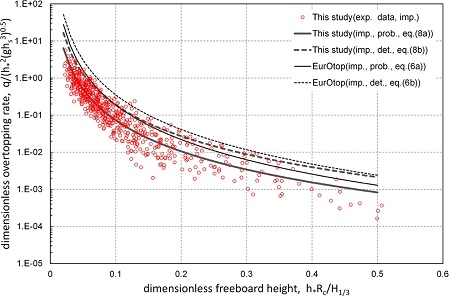
Fig. 4는 비충격파 조건 대한 직립식구조물의 월파량 산정결과이며, 이에 대한 산정식은 식 (7)과 같다.
-Probabilistic design (non-impulsive condition, h*>0.3)
-Deterministic design (non-impulsive condition, h*>0.3)
Fig. 5는 충격파 조건에 대한 직립식구조물의 월파량 산정 결과이며, 이에 대한 산정식은 식 (8)과 같다.
-Probabilistic design (impulsive condition, h*≤0.3)
-Deterministic design (impulsive condition, h*≤0.3)
식 (7)과 식 (8)에서 γs는 직립식구조물의 상치콘크리트 형상에 따른 영향계수로서 표준형인 Fig. 2와 같은 직립형 상치콘크리트의 경우에는 γs= 1.0이다.
비충격파 조건의 경우에 본 연구의 결과와 EurOtop(2007)의 결과를 비교해보면, Kim and Lee(2012)의 결과( Q = 0.14) 와 마찬가지로 Q-R 상관관계식의 기울기가 상이함을 알 수 있다( Fig. 4 참조). 본 연구와 Kim and Lee(2012) 결과의 차이는 분석시 적용한 파고가 상이하기 때문으로 판단된다. 즉, Kim and Lee(2012)는 조파기 전면에서의 유의파고를 사용한 반면, 본 연구에서는 구조물 설치위치에서의 유의파고를 사용함에 따른 것으로 판단된다. EurOtop(2007)과의 결과를 비교해 보면, R<0.7인 경우에는 본 연구결과가 많게, R>0.7인 조건에서는 EurOtop(2007)의 결과가 많게 산정되는 것으로 분석되었다. 이는 실험시 적용된 주파수 스펙트럼의 차이와 적용 유의파고의 차이에 기인되는 것으로 판단된다. 유럽에서는 대부분 JONSWAP 스펙트럼을 적용하며, 국내에서는 Bretschneider-Mitsuyasu(B-M) 스펙트럼을 적용하고 있다. 동일 주파수 영역에서 JONSWAP 스펙트럼은 B-M 스펙트럼에 비해 첨두 에너지밀도 주변의 주파수영역이 상대적으로 좁은 대신 에너지밀도가 높으며, B-M의 경우에는 첨두 에너지밀도 주변의 주파수영역이 넓은 대신 에너지밀도가 낮은 특징이 있다. 이에 따라 상대여유고가 높은 경우, 즉 여유고가 큰 경우에는 에너지밀도가 큰 JONSWAP 스펙트럼인 경우가 보다 많은 월파가 발생하며, 반대의 경우에는 B-M 스펙트럼인 경우에 월파량이 많이 발생하게 된다. 충격파 조건의 경우에는 전반적으로 EurOtop(2007)에 비해 본 연구결과가 적은 월파량을 산정함을 알 수 있다. 본 연구에서도 EurOtop(2007)과 같이 확률론적(probabilistic design) 월파량산정식으로부터 1배의 표준편차 만큼 월파량을 증대시킨 후 결정론적(deterministic design) 월파량산정식을 제시하였다.
4.2 상치콘크리트 형상에 따른 월파량 산정식
Fig. 6.
Wave overtopping for vertical wall with inclined superstructure (non-impulsive condition, probabilistic design).
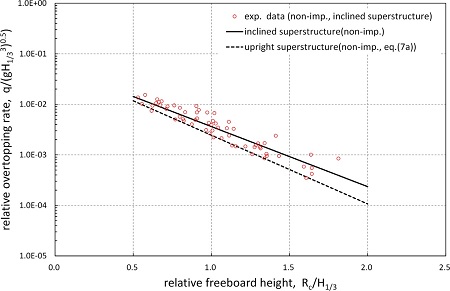
Fig. 7.
Wave overtopping for vertical wall with inclined superstructure (impulsive condition, probabilistic design).
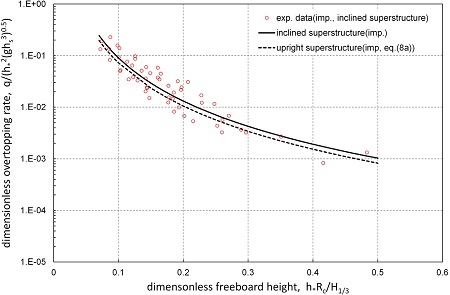
비충격파 조건에서 경사형 상치콘크리트의 월파량 실험결과인 Fig. 6으로부터 평균 월파량산정식은 식 (12)와 같다. 그러므로 식 (7a)와 식 (12)로부터 비충격파 조건의 경사형 상치콘크리트 영향계수는 γs ≒ 1.15이다. 따라서 식 (7)에 γs= 1.15를 대입하면 비충격파 조건에서 경사형 상치콘크리트에 대한 평균 월파량을 산정할 수 있다. 충격파 조건에서 경사형 상치콘크리트의 월파량 실험결과인 Fig. 7로부터 평균 월파량산정식은 식 (13)과 같이 표현할 수 있으며, 식 (13)과 식 (8a)를 이용하면 충격파 조건에서 경사형 상치콘크리트 영향계수는 γs ≒ 1.08이다. 따라서 식 (8)에 γs=1.08을 대입하면 충격파 조건에서 경사형 상치콘크리트에 대한 평균 월파량을 산정할 수 있다.
Fig. 6과 Fig. 7의 결과로부터 직립형 상치콘크리트 단면에 비해 경사형 상치콘크리트 단면의 월파량이 증가함을 확인할 수 있다. 본 연구결과로부터 직립식구조물에 경사형 상치콘크리트를 적용할 경우, 직립형 상치콘크리트인 직립식구조물의 여유고보다 비충격파 조건의 경우에는 약 15%, 충격파 조건의 경우에는 약 8% 높게 설정해야만 유사한 월파량이 산정됨을 의미한다.
Fig. 8은 경사형 상치콘크리트의 설치위치를 변경하면서 월파량을 계측한 실험결과이다( Fig. 3 참조). 경사형 상치콘크리트의 설치위치가 중간(CASE 2) 및 후면(CASE 3)인 경우에 전면(CASE 1)인 경우보다 월파량이 약간 많게 분석되었으며, CASE 2와 CASE 3는 동일하게 나타났다. 즉, 경사형 상치콘크리트가 중간 및 후면에 설치되는 경우에 전면에 설치되는 경우보다 약 4% 정도 월파량이 많게 나타나지만 그 차이는 크지 않기 때문에 설치위치에 따른 차이는 고려하지 않아도 될 것으로 판단된다.
Fig. 8.
Wave overtopping according to the location of inclined superstructure(impulsive condition, probabilistic design).

5. 결 론
항만구조물을 설계함에 있어 월파는 구조물의 마루높이, 배후부지의 활용, 경사식구조물 배후사면의 안정성 등에 영향을 미치는 중요한 설계인자이며, 월파량 예측을 위한 연구는 현재도 활발히 진행중에 있다. 본 연구에서는 국내 항만구조물 설계시 적용되고 있는 Goda의 월파량 산정도표를 최근 연구동향(EurOtop 등)과 같이 월파량산정식의 형태로 개선하고자 하는 것이 목적이다.
본 연구에서는 직립식구조물의 월파량산정식을 제안하기 위하여 2차원 수리실험을 수행하였으며, 연구내용을 요약하면 다음과 같다.
(1) 직립형 상치콘크리트를 가지는 직립식구조물을 표준으로 하여 충격파와 비충격파 조건에서의 월파량산정식을 제안하였다. EurOtop(2007)의 결과와 비교해볼 때 전반적인 경향은 동일하지만 본 연구에 의한 결과가 약간 작게 나타났으며, 이는 적용된 입사파 스펙트럼 등의 차이에 기인하는 것으로 판단된다. (2) 상치콘크리트에 작용하는 파력 등을 저감시키기 위해 직립식구조물에서 경사형 상치콘크리트를 적용하는 설계가 이루어지고 있다. 경사형 상치콘크리트를 적용한 직립식구조물에 대한 월파량 실험을 수행하였으며, 상치콘크리트 형상에 따른 영향계수를 도출하였다. 경사형 상치콘크리트의 경우, 직립형 상치콘크리트를 가지는 직립식구조물과 동일한 월파성능을 확보하기 위해서는 동일 입사파 조건에서 비충격파 조건의 경우에는 상대여유고를 약 1.15배, 충격파 조건의 경우에는 약 1.08배 높게 해야 함을 확인하였다. (3) 경사형 상치콘크리트의 설치위치에 따른 월파량 계측 실험을 수행하였다. 경사형 상치콘크리트가 전면보다 중간 이후에 설치되는 경우에 약간 많은 월파가 계측되었으나, 그 차이는 크지 않았다. 따라서 설치위치에 따른 월파량의 변화는 고려하지 않아도 될 것으로 판단된다.
향후, 유공구조물에 대한 실험 및 입사각이 월파량에 미치는 영향 등에 대한 추가 실험을 진행할 계획이며, 이를 통해 활용범위가 높은 직립식구조물의 월파량 산정기법을 제시할 예정이다.
ACKNOWLEDGEMENTS
본 논문은 한국해양과학기술진흥원의 연구비 지원(과제번호: 20110131) 및 2014년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구(No. 2011-0030040)이며, 연구비 지원에 감사드립니다.
References
1. Anderson, T.L., et al, Burcharth, H.F.. (2009). Three-dimensional investigation of wave overtopping on rubble mound structures, Coastal Engineering, 56, 180-189. 10.1016/j.coastaleng.2008.03.007.  2. British Standard(BS). 2001). British Standards Institution.
3. EurtOtop. 2007). EurOtop-Wave overtopping of sea defences and related structures : Assessment Manual, www.overtopping-manual.com. 4. Franco, C., et al, Franco, L.. (1999). Overtopping formula for caisson breakwaters with nonbreaking 3D Waves, Journal of waterway, port, coastal, and ocean engineering, 125(2):98-108. 10.1061/(ASCE)0733-950X(1999)125:2(98).  5. Goda, Y.. (1970). Estimation of the rate of irregular wave overtopping at seawall, Technical Report of Port and Airport Research Institute, 9(4):3-42.
6. Goda, Y., Kishira, Y., et al, Kamiyama, Y.. (1975). Laboratory investigation on the overtoppping rate of seawalls by irregular waves, Technical Report of Port and Airport Research Institute, 14(4):3-44.
7. Goda, Y.. (1985). Random seas and design of maritime structures (1st edition). World Scientific Publishing.
8. Japanese Port and Harbour Association. 2007). Technical standards and commentaries for port and harbour facilities, (in Japanese).
9. Kim, Y.T.. (2010). Automatic measuring apparatus and device structure for continuous wave overtopping, Korean Patent No. 10-1210651. (in Korean).
10. Kim, Y.T., et al, Lee, J.I.. (2012). Wave overtopping formula for vertical structure including effects of wave period : non-breaking conditions, Journal of Korean Society of Coastal and Ocean Engineers, 24(3):228-234 (in Korean). 10.9765/KSCOE.2012.24.3.228.  11. Lee, W.. (2008). Wave overtopping characteristics of rubble mound revetments. Mater thesis. Hanyang University; (in Korean).
12. Ministry of Oceans and Fisheries. 2014). Design standard for harbor and fishery port, (in Korean).
13. Owen, M.W.. (1980). Design of seawalls allowing for wave overtopping, Report No. EX924. HR Wallingford.
14. Takahashi, S.. (2002). Design of Vertical Breakwaters, Port and Harbor Research Institute. Report No. 34.
16. van der Meer, , et al, Janssen, J.P.F.M.. (1994). Wave run-up and overtopping at dikes, Wave forces on inclined and vertical wall structures, ASCE, 1-27.
17. van der Meer, , et al, Bruce, T.. (2014). New Physical Insights and Design Formulas on Wave Overtopping at Sloping and Vertical Structures, Journal of Waterway, Port, Coastal, and Ocean Engineering, 10.1061/(ASCE)WW.1943-5460.0000221. 
|
|

















