1. 서 론
심해에서 발생하여 천해로 진입하는 파는 다양한 요인들에 의해서 변형되며 이 중에서 파의 진행 방향에 큰 영향을 끼치는 것들이 회절과 굴절이다. 회절은 에너지 차이에 의해 발생하는 현상으로 섬, 부유 구조물 또는 방파제 주변에서만 발생한다. 반면, 굴절이란 파봉선 방향의 위상속도 차이에 의해 파의 진행 방향이 바뀌는 현상으로 전 영역에 걸쳐서 발생한다. 바닥이 불투수층인 경우에 에너지 손실을 무시하면 수심 또는 흐름의 공간적인 변화로 위상속도의 차이가 발생하여 굴절이 발생한다. 파랑이 투수층을 지나는 경우, 흐름의 공간적인 변화뿐만 아니라 항력 저항, 관성 저항 등의 에너지 손실로 위상속도의 변화가 발생하면서 굴절이 발생한다. 이러한 요인들로 인하여 굴절이 발생하여 파가 특정 부분에 집중되면 높은 파 에너지로 인하여 쇄파나 쇄파유도류가 발생하여 연안환경에 영향을 끼치며 또는 연안구조물의 붕괴를 초래하기도 한다.
파의 굴절을 계산하는 방법으로 등수심선이 나란한 경우 Snell의 법칙을 이용할 수 있으며, 수심이 복잡한 경우에는 위상속도를 이용하여 진행 방향을 예측하는 파향선법을 사용할 수 있다(Munk and Arthur, 1952; Wilson, 1966; Noda, 1974). 파향선법은 파의 진행거리 및 방향이 미분식으로 표현되어서 수치차분을 이용하여 파의 이동거리와 방향을 구할 수 있다. 이 방법을 이용하면 주어진 파랑 및 지형조건에서 파랑의 진행상황을 예측할 수 있지만 입사파의 주기, 항력계수 또는 관성계수 등의 조건이 변하였을 경우 굴절이 어떻게 바뀔지는 미리 계산해보기 전에 알 수가 없다.
본 연구에서는 굴절이 파봉선 방향으로의 위상속도 차이에 의해서 발생한다는 사실에 착안하여 다양한 조건에서 발생하는 파의 굴절 정도를 해석적으로 표현하는 방법을 제시하였다. 유도된 식은 불투수층 및 투수층에 대하여 적용하였으며 불투수층의 경우 기존에 알려진 사실과 잘 부합하는 것을 확인할 수 있었다.
2. 해석 기법 유도
파의 굴절은 나란히 진행하는 파와의 진행속도 차이에 의해 발생한다. 따라서 굴절의 정도를 나타내는 굴절수(index of refraction degree)는 다음과 같이 파봉선 방향으로의 위상속도차로 정의할 수 있다.
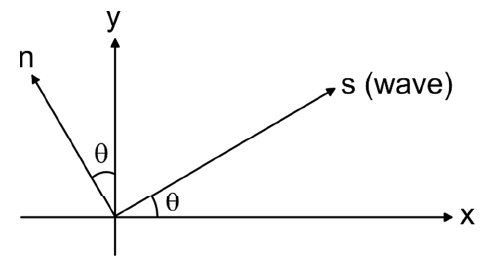
여기서, c는 위상속도, k는 파수, ω는 각 주파수이며 n은 Fig. 1과 같이 파 진행 방향의 법선(즉, 파봉선 방향) 벡터를 의미한다. 맨 앞에 붙은 1/ω는 ∂c/∂n이 [T−1]의 차원을 갖기 때문에 무차원화시키기 위하여 사용되었다.
2.2 불투수층 바닥 위에 물 층 존재하는 경우
식(1)에서 동일한 수심조건에서 진행하는 파의 경우 ∂h/∂n의 값은 동일하게 되며 따라서 실질적으로 굴절의 정도는 다음 값에 의해서 결정이 된다.
식(4)를 계산하기 위해서는 파수에 관한 식을 사용하여야 하며 바닥이 불투수층인 경우에는 다음과 같은 선형분산관계식을 사용할 수 있다.
이 식을 이용하면 다음과 같은 식을 얻을 수 있다.
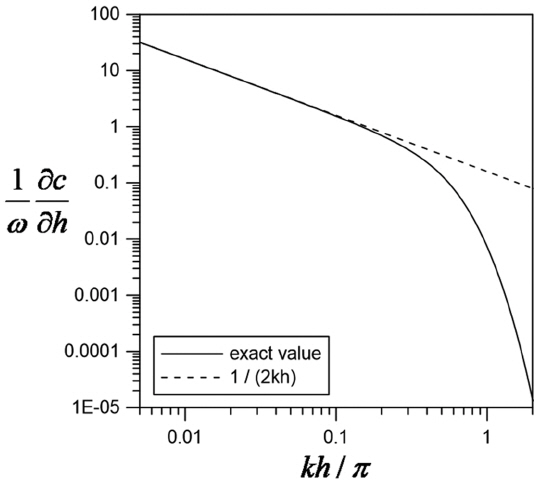
식(6)은 심해에서 0으로 수렴하며 천해에서는 sinh(2kh)/2kh =1이 되므로 다음과 같이 된다.
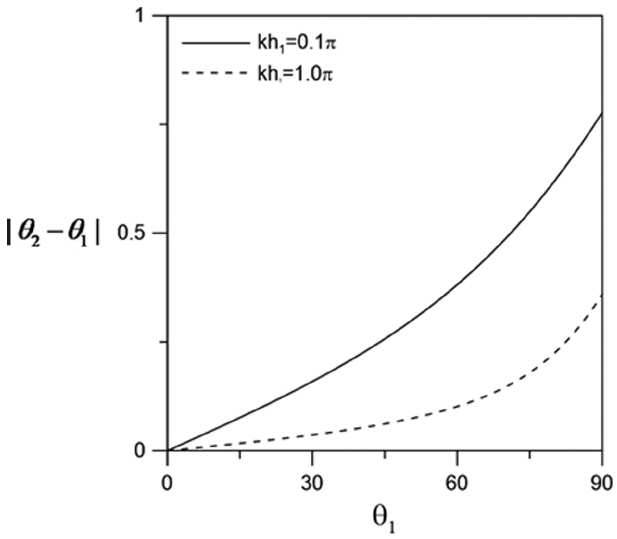
이는 심해에서는 굴절이 거의 발생하지 않고 천해에서는 상대수심이 작을수록 굴절 정도가 크다는 것을 알 수 있다. Lee et al.(2003)은 똑같은 수심 조건에서 주기가 긴 파랑이 짧은 파랑에 비해 굴절이 일찍 발생함을 수치적으로 확인하였다. 그들은 역학적으로 주기가 긴 파랑이 상대수심이 작아서 바닥의 변화를 일찍 감지한다고 하였다. 식(7)이 그들의 주장을 뒷받침하는 이론적인 배경이 된다.
2.3 불투수층 바닥 위에 투수층이 존재하는 경우
파가 투수층 내를 통과하는 경우 투수층의 특성이 파의 굴절에 어떤 영향을 주는지 검토해보았다.
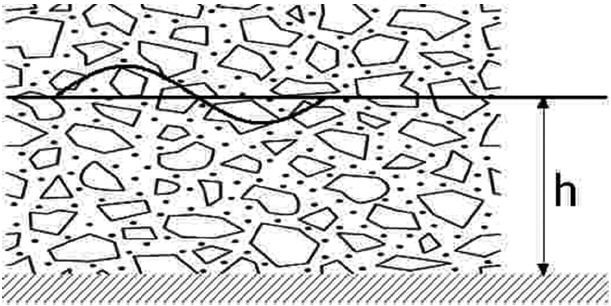
Fig. 3과 같은 투수층 속을 지나가는 파에 적용되는 운동방정식은 다음과 같이 나타낼 수 있다(Sollitt and Cross, 1972; Gu and Wang, 1991; Burcharth and Andersen, 1995; Cruz et al., 1997).
여기서, A는 공극률(λ)과 관련 있는 상수로서 Sollitt and Cross(1972) 및 Gu and Wang(1991)은 1/λ을 사용하였으며 Burcharth and Andersen(1995) 및 Cruz et al.(1997) 등은 1의 값을 사용하였다. 투수층 내를 흐르는 유체의 거동은 매우 복잡하기 때문에 아직까지 A의 값과 관련하여 명확한 기준이 없다. 따라서 본 연구에서는 편의상 Cruz et al.(1997) 등이 사용한 1의 값을 사용하였다. u는 유량속도(discharge velocity)이며 D와 I는 각각 항력저항과 관성저항을 의미한다. Ergun(1955) 및 Cruz et al.(1997)은 항력저항과 관성저항에 대해 각각 다음과 같이 정의하였다.
여기서, α는 항력계수, αl은 층류저항계수, αt은 난류저항계수, λ는 공극률, ν는 동점성계수, d는 자갈(또는 모래)의 입경 그리고 κ는 부가질량계수를 의미한다. 식(9)와 (10)을 식(8)에 대입하고, 자유수면에서의 경계조건을 사용하면 다음과 같은 선형화된 자유수면 경계조건을 얻을 수 있다.
여기서, φ는 속도포텐셜을 의미하며 β는 다음과 같이 정의되는 관성계수이다.
속도포텐셜에 관한 Laplace 방정식을 지배방정식으로 하고
바닥경계조건(w = 0)을 사용하면 다음과 같은 해를 얻을 수 있으며
여기서, γ는 다음과 같이 정의된다.
물 층의 경우에는 λ = 1이 되어 α = 0 및 β = 1이 되며, 따라서 식(15)는 식(5)와 동일하게 된다. 투수층인 경우에는 파수가 복소수(k = kr + iki)로 표현되며 이 중에서 파의 굴절과 관련된 부분은 실수부분이 된다. 따라서 식(6)은 다음과 같이 된다.
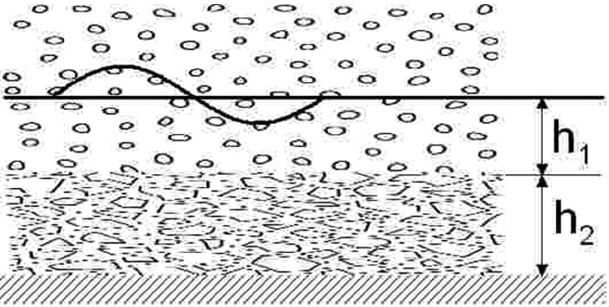
식(17)의 ∂kr/∂h는 해석적으로 구하기 힘든 경우에는 수치적으로 구할 수 있다. 이와 같은 접근법은 투수층이 다수 존재하는 경우에도 가능하며 Fig. 4와 같이 2개층에 대하여 분산관계식을 유도하면 다음과 같이 된다.
이 경우 식(1)은 다음과 같이 표현이 가능하며
여기서, ∂c/∂h1과 ∂c/∂h2는 각각 다음과 같이 나타낼 수 있다.
3. 결과 분석
본 연구에서 제안한 해석적인 방법의 타당성을 검토하기 위하여 먼저 바닥이 불투수층인 지형에 적용해 보았다.
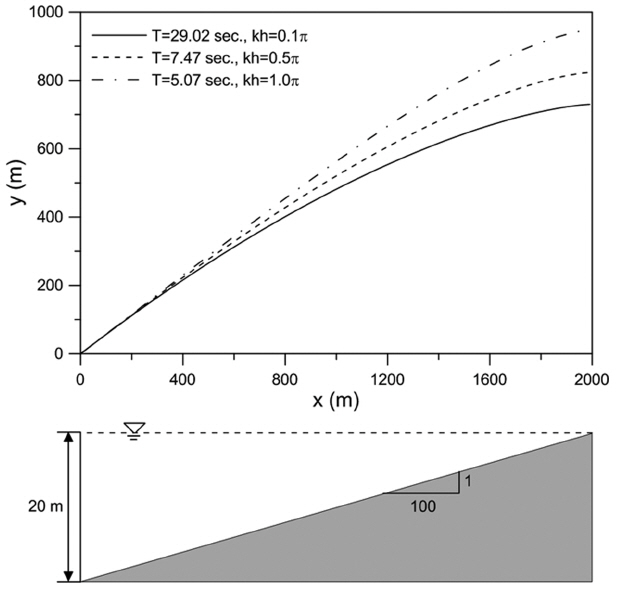
Fig. 5는 수심값에 변화를 주면서 식(6)과 (7)을 계산하여 도시한 결과이다. 식과 그림을 통해 알 수 있듯이 불투수층일 경우에는 굴절의 정도가 오직 상대수심에 의해서만 결정이 되며 상대수심이 작을수록 굴절이 크게 발생하는 것을 예측할 수 있다. 식(7)로 표현되는 근사식은 천해역에서는 정해와 잘 일치하지만 심해역에서는 다소 큰 값을 보인다. 이와 같은 결론은 Snell의 법칙이나 파향선법을 이용하여 파의 진행경로를 계산함으로써 확인할 수 있다. Fig. 6은 서로 다른 상대수심을 가지는 파들이 동일한 지점에서 동일한 입사각 θ = 30°으로 입사하는 경우에 대하여 Snell의 법칙을 이용하여 파의 진행 방향을 그린 것이다. 얕은 수심으로 갈수록 상대수심의 효과로 인하여 파의 굴절이 크게 발생하는 것을 확인할 수 있다. 이는 Lee et al.(2003)이 발견한 것과 동일하다.
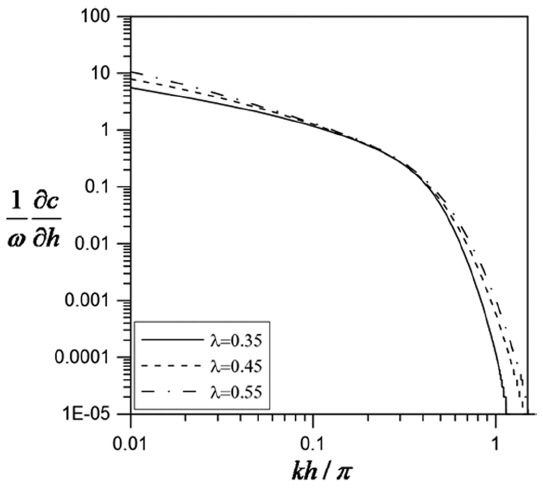
Fig. 7은 서로 다른 공극률(λ)을 갖는 투수층에 대하여 굴절 정도를 계산한 그림이다. 투수층에서의 변수값은 al = 150, ν = 1.15 × 10−6(m2/s), d = 0.01 (m) 및 κ = 0.7으로 고정하고 공극률은 λ = 0.35, 0.45, 0.55의 값을 사용하였다. 투수층에서의 굴절 정도는 전체적으로 물 층인 경우와 비슷한 경향을 보였다. 상대수심이 작은 경우에는 굴절이 크게 발생하였으나 상대수심이 증가할수록 굴절의 정도가 약해지면서 상대 수심이 일정한 값 이상이 되면 굴절이 거의 발생하지 않았다. 공극률이 클수록 굴절이 크게 발생하였으나 그 차이가 크지는 않았다.
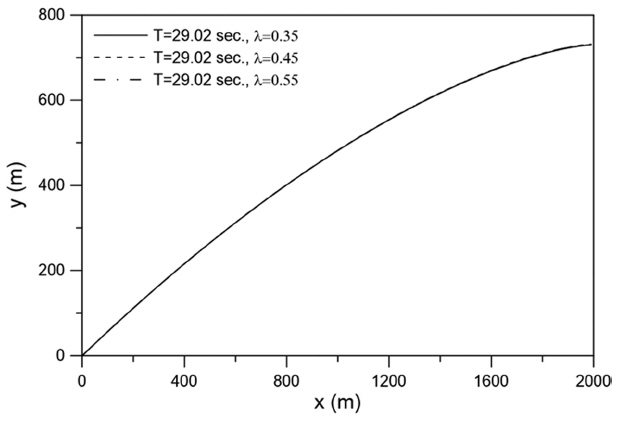
Fig. 8은 Fig. 7과 동일한 수심 조건에서 파의 진행을 계산한 결과이다. 입사파의 각도는 30°이며, 굴절이 크게 발생하도록 장주기(29.02초) 조건을 사용하였다. Fig. 7의 결과에서 보여지듯이 공극률에 따른 굴절 정도의 차이가 미미하기 때문에 실제 파의 진행경로도 거의 동일하게 나타났다.
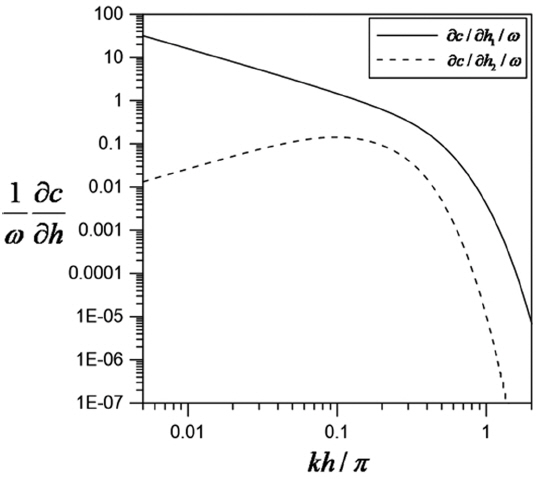
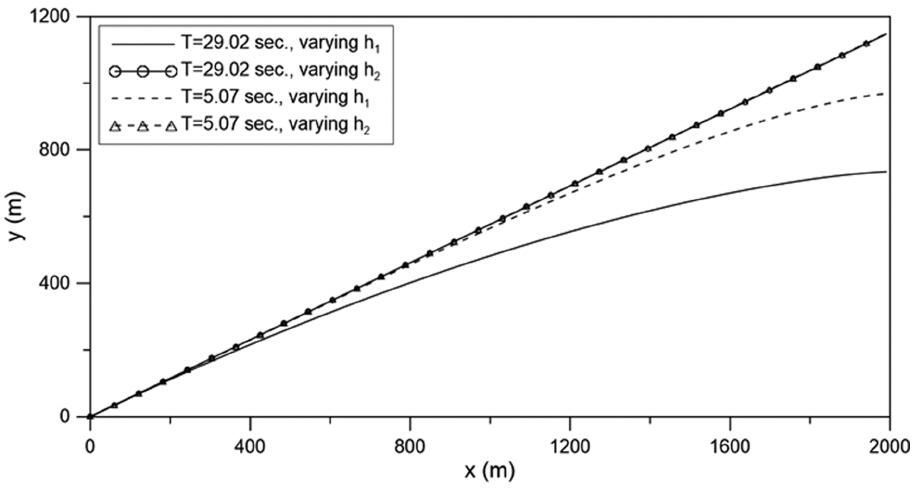
마지막으로 투수층 위에 물 층이 있는 경우에 대하여 굴절 정도를 계산해 보았다. Fig. 9는 식(20) 및 (21)의 ∂c/∂h1/ω과 ∂c/∂h2/ω를 계산한 결과이다. 이는 투수층의 수심을 일정하게 유지하면서 물 층의 수심이 변하는 경우와 그 반대의 경우를 의미하는 것으로써 큰 값을 가질수록 굴절이 크게 발생한다는 것을 의미한다. 투수층에서의 조건은 Fig. 8에서 사용된 조건과 동일하게 사용하였다.
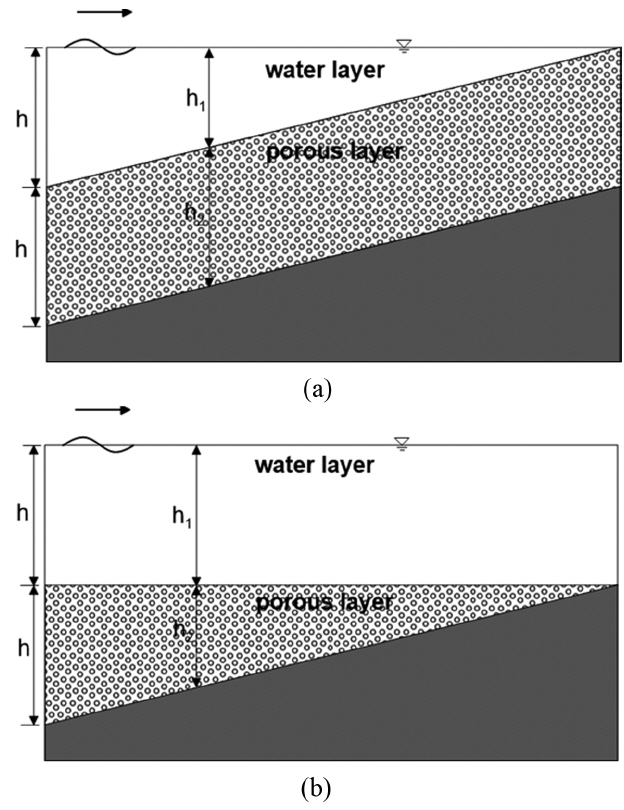
수심 변화가 위의 물 층이나 아래 투수층에서 동일하게 발생할 경우 물 층에서의 수심변화가 굴절에 더 큰 영향을 주었다. 이는 Fig. 10과 같은 지형에 파향선을 그려봄으로써 확인할 수 있다. Fig. 10(a)는 아래 투수층의 두께는 h2으로 고정한 후, 위 물 층의 두께를 h에서 0까지 감소하는 지형이며 Fig. 10(b)는 반대되는 경우에 대한 지형이다.