1. 서 론
황해(Yellow Sea)는 한반도와 중국 사이의 해역으로, 북위 33°17'를 기준으로 동중국해(East China Sea)와 구분된다. 황해의 면적은 380,000 km2으로 동해에 비해 38.9% 정도 된다. 이에 더해 황해역의 평균 수심은 44 m로, 동해 평균 수심의 2.5% 정도에 지나지 않아 동해에 비해 파랑 환경이 온화하다. 이러한 이유로 황해역 파랑 연구는 많지 않은 편이다. 그러나 Hwang et al.(2018)의 연구에 따르면, 2013년부터 2017년까지 한반도 주변 해역에서 발생한 파랑에 의한 해난 사고 중 9.2%가 인천, 충남 보령, 전북 군산 및 부안, 전남 신안 등 서해안 전역에서 발생한 것으로 파악되고 있다.
이처럼 한반도 서해안에서도 파랑에 의한 해난사고가 발생하고 있어, 본 연구에서는 파랑관측자료 분석 및 파랑후측모의 실험을 통해 황해역의 파랑특성을 파악하고자 한다. 본 연구에서는 한반도 서단에서 관측된 파랑자료분석을 통해 황해역 파랑특성을 조사하였다. 이 때 얻은 파랑관측자료 분석 결과를 바탕으로, Chun and Ahn(2017a)의 파랑후측모의 실험의 계산영역을 황해역으로 확장하여 파랑 후측모의 실험을 수행하였다. Chun and Ahn(2017a)의 파랑후측모의 실험이 광역격자에 대해서도 수행되었지만, 천해역 파랑 또한 정확히 계산된 바 있다. 또한 남쪽의 계산 영역이 대한해협에 비교적 가까운 편인데도, 대한해협에 영향을 미친 춘계 S계열 폭풍파랑도 정확히 재현한 바 있다(Chun and Ahn, 2017b). 이러한 이유로 본 연구에서는 효과적인 파랑계산을 위해 광역 격자 파랑 계산을 수행하고 그 결과를 관측결과와 비교하였다. 본 연구의 파랑계산은 2010년부터 2014년까지 5년에 대해서 수행되었다. 본 연구의 파랑 후측모의 실험 기간이 길지는 않지만, 해당 기간 동안 한반도 서해안에 피해를 끼친 태풍들이 포함되어 있다. 태풍파랑 외에 계절풍에 의한 주요 폭풍파랑 또한 해당 기간에 포함되어 있어 본 연구의 파랑후측모의 실험을 통해 황해역의 극치 파랑도 파악할 수 있다.
2. 황해 파랑관측자료 분석
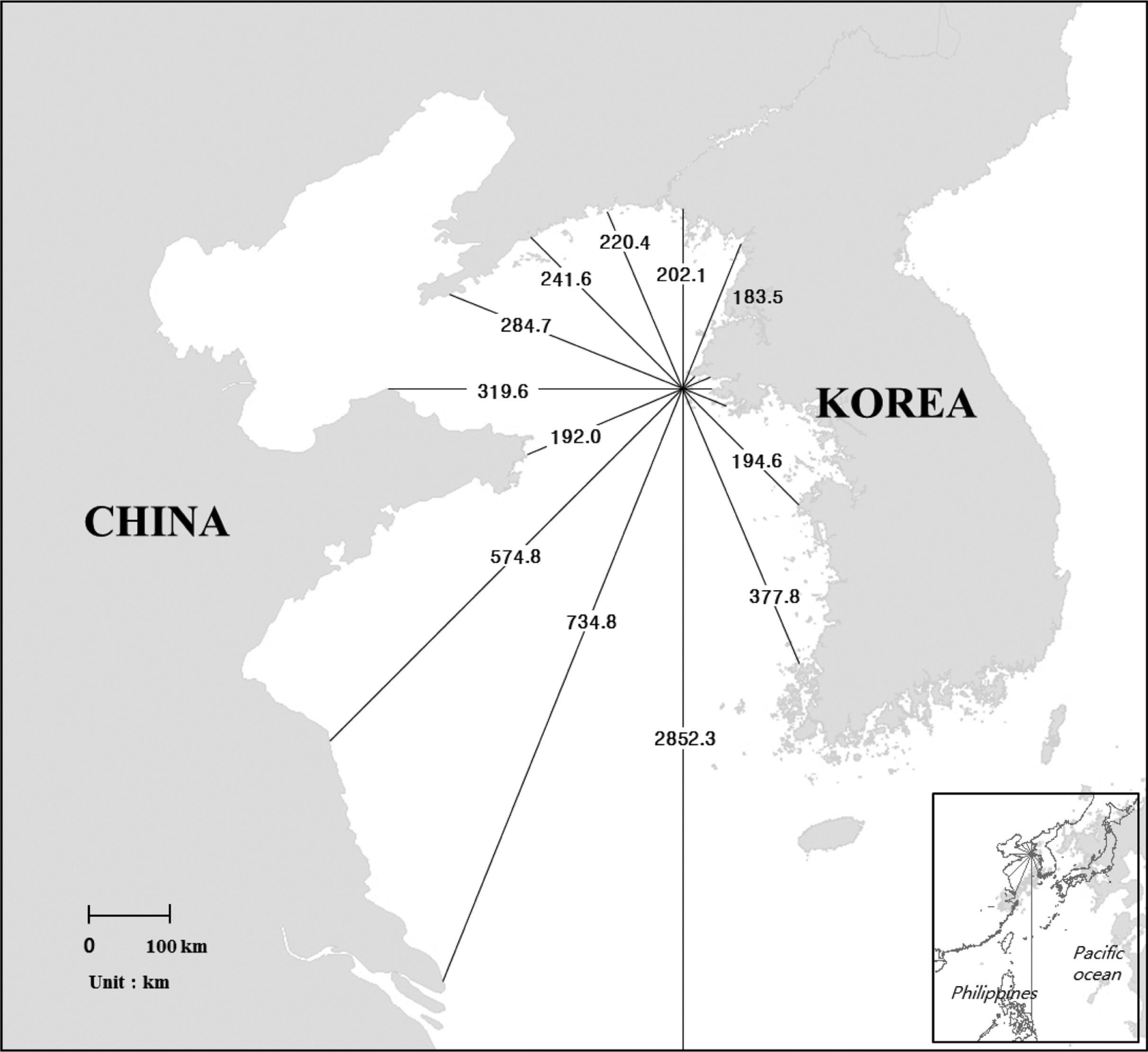
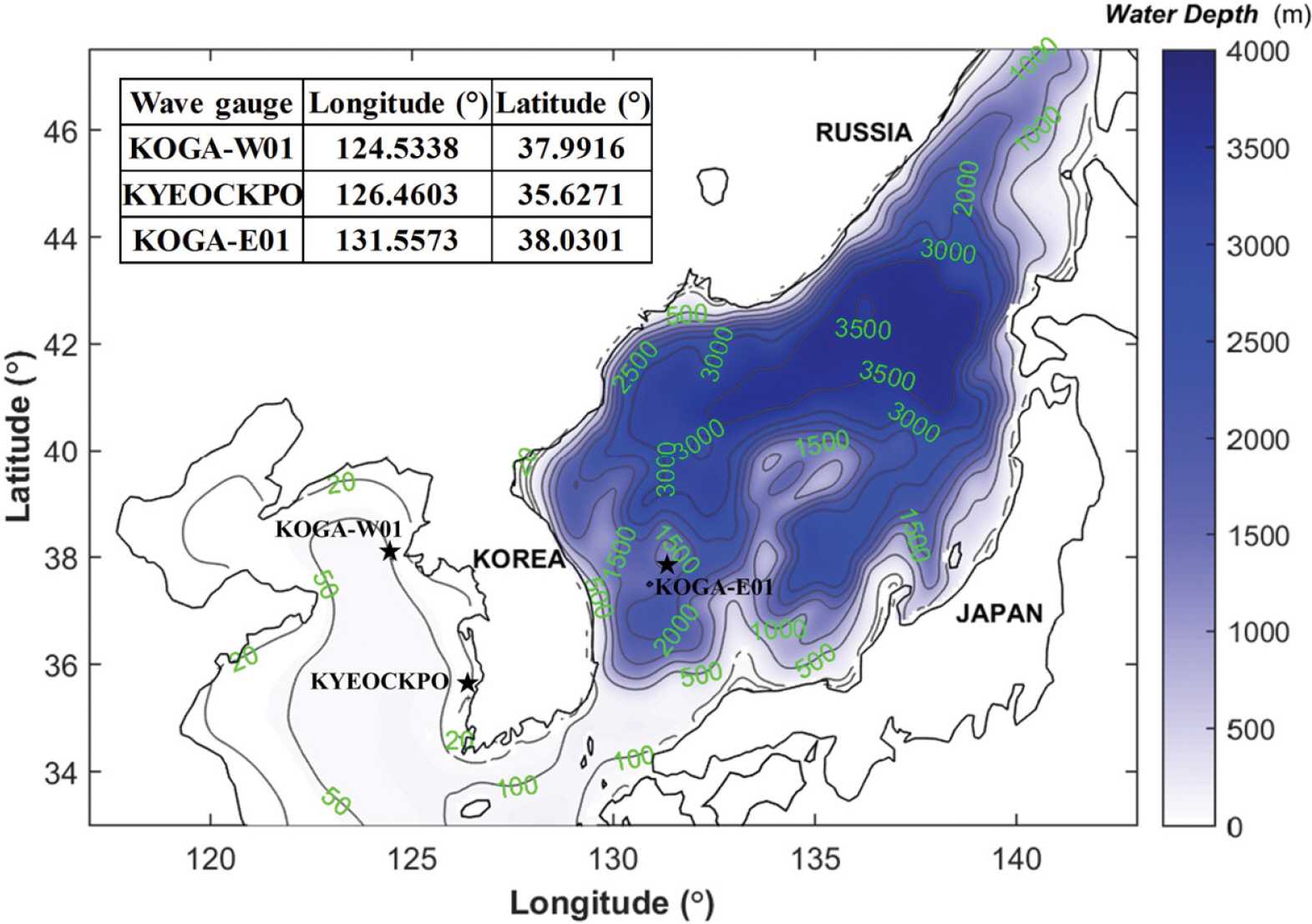
본 연구에서는 황해 파랑 특성 연구의 일환으로, KOGA-W01 파랑관측자료를 분석하였다(Fig. 1). 본 파랑관측자료는 네덜란드 Datawell사의 MOSE-G1000 센서가 탑재된 부이형 파고계로 관측되었다. 이 파랑관측장비는 2 Hz 간격으로 해수면에서의 3차원 해수면 가속도를 측정하는 방법으로 방향성 파랑 관측을 수행한다(Datawell, 2009). 이 후 관측 3차원 가속도 정보는 보정을 거쳐 해수면 변위 자료로 최종 변환되어 제공되는데, 본 연구에서는 이 자료에 개별파랑분석법(zero-crossing analysis)과 스펙트럼분석법(FFT: Fast Fourier Transform)을 적용하여 파랑 정보를 얻었다. 이 때 사용된 부이형 파고계의 파랑 분석과정은 Chun(2012)에 제시되어 있어, 본 논문에서 이에 대한 기술을 생략한다. 본 파랑관측자료의 기간은 2011년 12월 1일부터 2014년 10월 31일까지이지만, 이 중 2012년 5월부터 2012년 11월까지 파랑이 결측되어 실제 파랑관측 기간은 27개월 정도 된다. 해당 파랑관측기간 동안 서해안에 큰 영향을 끼친 태풍 파랑이 관측되지 않았으나, 주요 폭풍파랑은 관측되어 황해역의 파랑 특성을 파악하는데 유용하다.
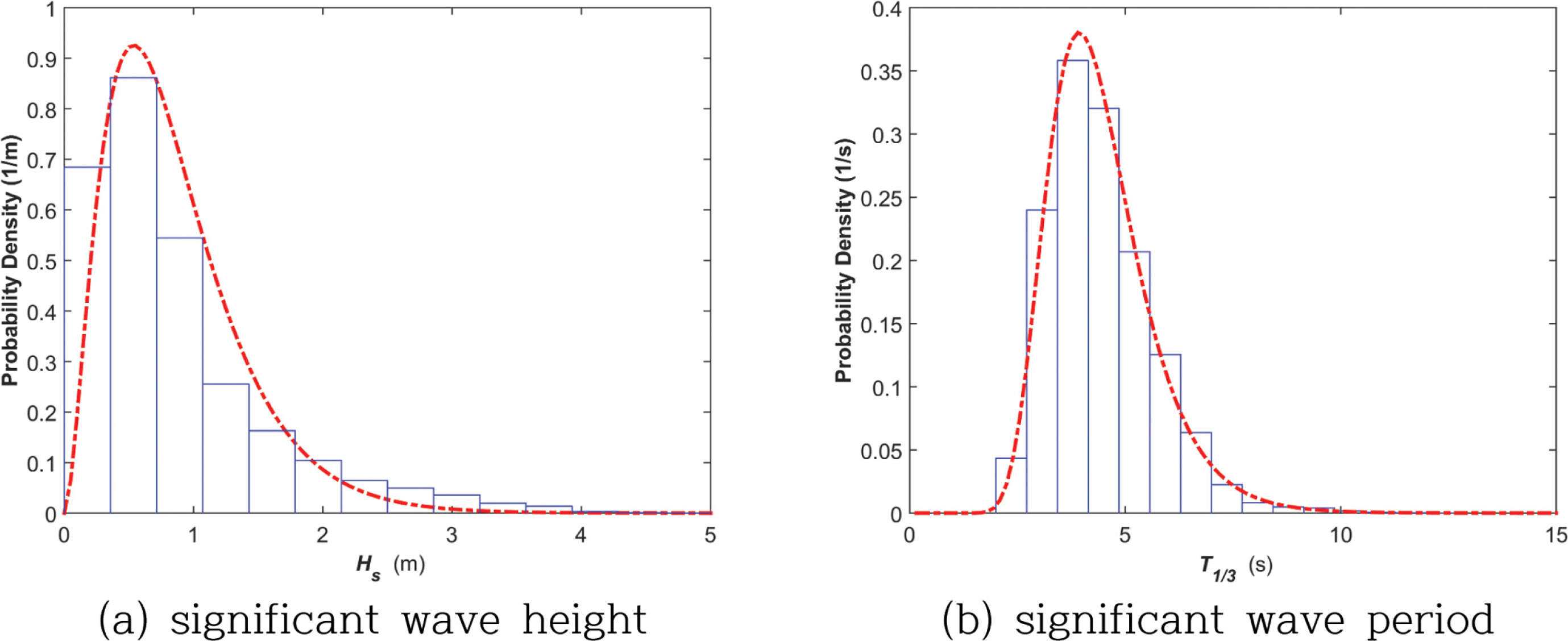
먼저 본 연구에서는 KOGA-W01 지점의 유의파고 Hs 및 유의파주기 T1/3의 분포 특성을 보기 위해 각각을 Generalized Gamma 분포 함수과 Box-Cox 변환 함수에 적용하였다. 이들의 수식은 식(1), (2)에 각각 나타내었다. 각각의 확률밀도함수를 히스토그램과 함께 Fig. 2에 나타내었다.
Generalized Gamma 분포함수의 모수인 λG, m, c의 값은 각각 λG = 3.91, m = 3.07, c = 0.93과 같다. 그리고 Box-Cox 변환함수의 모수인 λB, μB, σB는 λB = −0.23, μB = 1.23, σB = 0.19와 같다. 식(2)에서 T ~ T ~ = ( T 1 / 3 λ - 1 ) / λ B
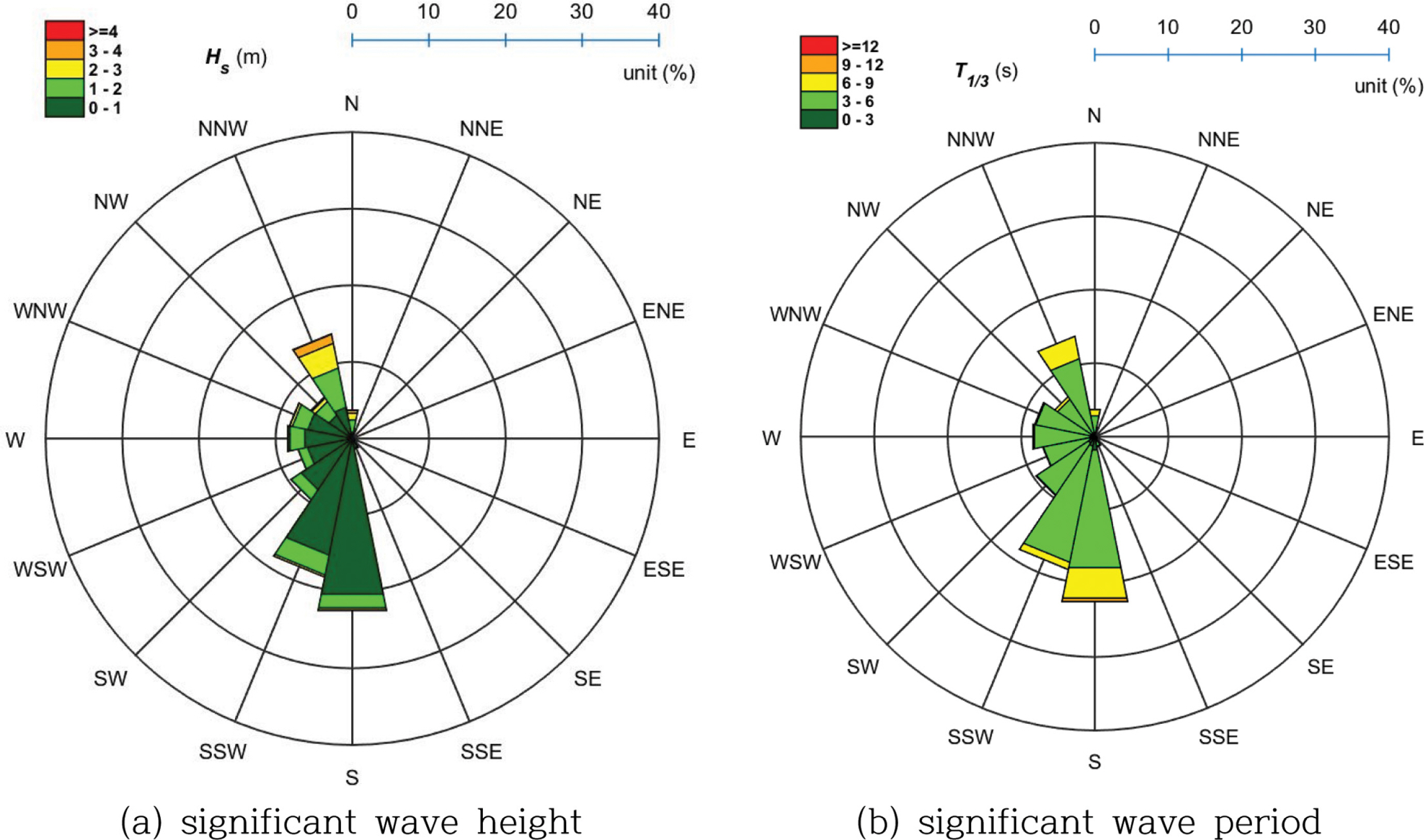
KOGA-W01의 최빈도 유의파고 및 유의파주기의 값은 동해에 위치한 KOGA-E01의 측정자료와 비교하면, 각각 0.42 m, 1.57 s 정도 작게 나타나고 있다. 이는 앞서 언급한 바와 같이 황해역의 크기가 동해보다 작아 나타나는 결과이다. 식(4)의 최빈도 유의파주기의 경우, 심해파 한계 수심은 12 m인데, KOGA-W01 부이설치 인근 해역 수심은 이보다 깊다. 따라서 KOGA-W01이 연안역에 가까이 위치해 있기는 하나, 심해파가 주로 관측되는 것으로 파악된다. 이에 따라 지형과 같은 지역적 특성이 크게 없다고 보고, 파향별 파랑 특성을 조사하였다. KOGA-W01을 중심으로 16개 방위에 대한 바람 취송 거리(wind fetch) F, 각 파향에 따른 파랑 출현율, 유의파고 및 유의파주기의 평균값들을 산정하고, 이들을 Table 1에 제시하였다. Fig. 1을 보면, 남쪽의 fetch length가 필리핀까지 이르는데, 이의 거리는 2,852.3 km와 같다. 하지만 이를 제외한 다른 방향의 fetch length 평균은 246.9 km 정도 된다. 이는 동해안에 위치한 KOGA-E01의 fetch length의 평균, 489.8 km에 비교하면 약 50.4% 정도에 지나지 않아 동해안에 위치한 KOGA-E01의 파고 및 주기가 서해안에 위치한 KOGA-W01보다 긴 것을 알 수 있다.
또한, S 및 SSW의 바람 fetch length가 긴 탓에 이들 방향의 유의파주기는 타방향에 상대적으로 긴 편이다. 특히 9초 이상의 장주기 파랑의 출현율이 타방향에 비해 높다(Fig. 3(b)). 하지만 S 및 SSW 계열의 파랑은 상대적으로 온화한 하계 계절풍의 영향을 받기 때문에 이들 방향의 유의파고 평균값은 각각 0.56 m, 0.6 m에 지나지 않는다. 이러한 특성은 파형경사 Hs/L0에도 반영되는데, KOGA-W01의 파형경사 평균이 0.03인 가운데, S 및 SSW 계열의 파형경사는 0.02 정도 된다. 반면에 북서 계절풍의 영향을 받는 WNW~N 계열 파랑의 파형경사의 평균은 0.04로 풍파(wind wave) 성향의 파랑이 지배적인 특성을 보이고 있다. 이 중 N계열 파랑의 유의파고가 가장 큰데 해당 방향의 유의파고 및 유의파주기의 평균값은 각각 1.77 m, 5.12 s와 같다. 특히 동계 폭풍시, 서해안 관측 파랑의 첨두 파형경사는 0.06~0.07 정도에 이르는 것으로 파악되고 있다(Oh et al., 2015). 한편, Table 1에서 NNW, N의 fetch length가 S, SSW에 비해서 짧지만 유의파주기의 평균값은 오히려 더욱 크다. 이는 하계 계절풍의 평균 풍속이 동계 계절풍의 평균 풍속보다 낮아 나타나는 결과이다. 하지만, S, SSW의 fetch length가 긴 탓에 다른 방향에서는 볼 수 없는 9초 이상의 유의파주기가 이들 방향에서 출현하고 있다(Fig. 3(b)).
이처럼 KOGA-W01 관측자료는 파향에 따라 파랑특성이 뚜렷하게 구분되고 있다. 이에 이의 계절별 특성을 보기 위해 월별 유의파고, 유의파주기, 파형경사를 산정하고 이들을 Table 2에 정리하여 나타내었다. 이에 따르면 하계계절풍의 영향 탓에 5월~10월의 파형경사가 다른 시기에 비해서 작게 나타나고 있다. 이는 당시 유의파주기가 다른 시기의 것보다 0.2 s 긴 반면에 유의파고는 0.41 m가 작아서 나타난 결과이다. 이 중 6월의 유의파고가 작은 탓에 당시의 파형경사 또한 제일 작다. 한편 Table 2에 따르면 7월의 유의파주기가 하계의 다른 시기보다 매우 길다. 이는 하계계절풍 외 동중국해 등지에서의 태풍의 영향으로 보인다.
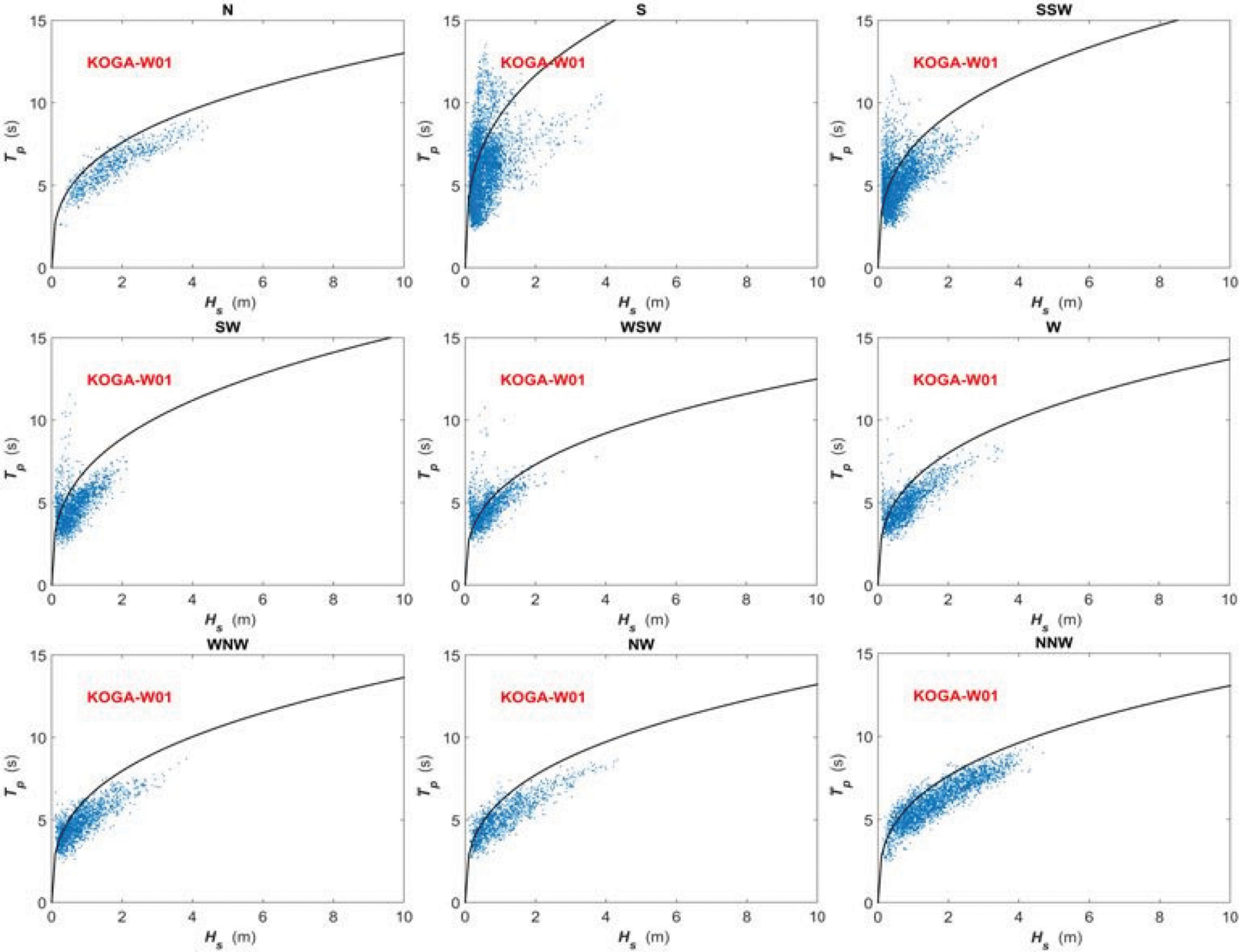
마지막으로 파향별 파랑발달 특성을 보기 위해 유의파고 및 첨두주기의 관계를 JONSWAP 관계식과 함께 비교하였다(Fig. 4). 여기서 JONSWAP 관계식은 Hasselmann et al.(1973)이 북해 파랑 관측자료로 부터 구한 fetch length제한(Fetch-limited) 파랑의 파고 및 주기의 관계를 나타내는 식으로, T p = 0 . 78 F 1 / 6 H s 1 / 3
이에 따르면 WNW~N 계열 파랑의 첨두주기는 JONSWAP 관계식에 의한 것보다 대체로 작게 나타나고 있다. 이는 이들 파향을 중심으로 최송시간 제한(Duration-limited) 파랑의 출현율이 높은 것을 나타내는 것으로, Fig. 3에서 본 것과 같이 이들 파향의 파랑은 풍파 성향이 강함을 의미한다. 한편, S 및 SSW 계열 파랑의 파랑 분석 결과를 보면 유의파고 1 m 이하 구간에서 fetch length 제한 파랑의 첨두주기보다 큰 너울성 파랑이 다수 출현하고 있다. 각 파항에 대해 이들 파랑의 출현율은 각각 28.2%, 25.7% 이며, 이는 Fig. 3에서 분석된 결과와 유사하다. 전체 파랑자료에 대한 이들 파랑의 출현율은 약 10.9%로, 유의파고가 작은 너울성 파랑이 S 및 SSW 방향으로 황해역에 진입하고 있는 것으로 파악된다.
3. 파랑 후측모의 실험
3.1 수치모의 실험 조건
2장의 파랑분석 결과에 의하면 황해역에서는 심해파 출현율이 높은 것으로 나타났다. 이에 본 연구에서는 효과적인 파랑 계산을 위해 Chun and Ahn(2017a)의 수치모의 실험을 황해역으로 확장하여 파랑 계산을 수행하였다. 본 연구의 파랑계산에 사용된 수치모형은 수정 WAM 모형인데, 이에 대한 자세한 내용은 Chun et al.(2008)에 기술되어 있어 본 논문에서는 이에 대한 설명을 생략한다. 본 연구의 계산 영역을 계산 결과 검증을 위한 파고계의 위치와 함께 Fig. 5에 나타내었다. 파고계 KOGA-W01, 부안 격포(Kyeockpo), KOGA-E01에서의 수심은 각각 1036 m, 5 m, 63 m로 해도에 제시어 있다. Fig. 5의 수심자료는 미해양대기국(National Oceanic and Atmospheric Administrator, NOAA)의 ETOPO5의 자료를 이용하여 구성하였다. Fig. 5의 계산영역은 경도 및 위도 방향으로 117°E~145°E, 33°N~47.5°N이며, 위도 및 경도의 공간격자 간격은 5분인데, 이에 의한 공간 격자개수는 313 × 175이다.
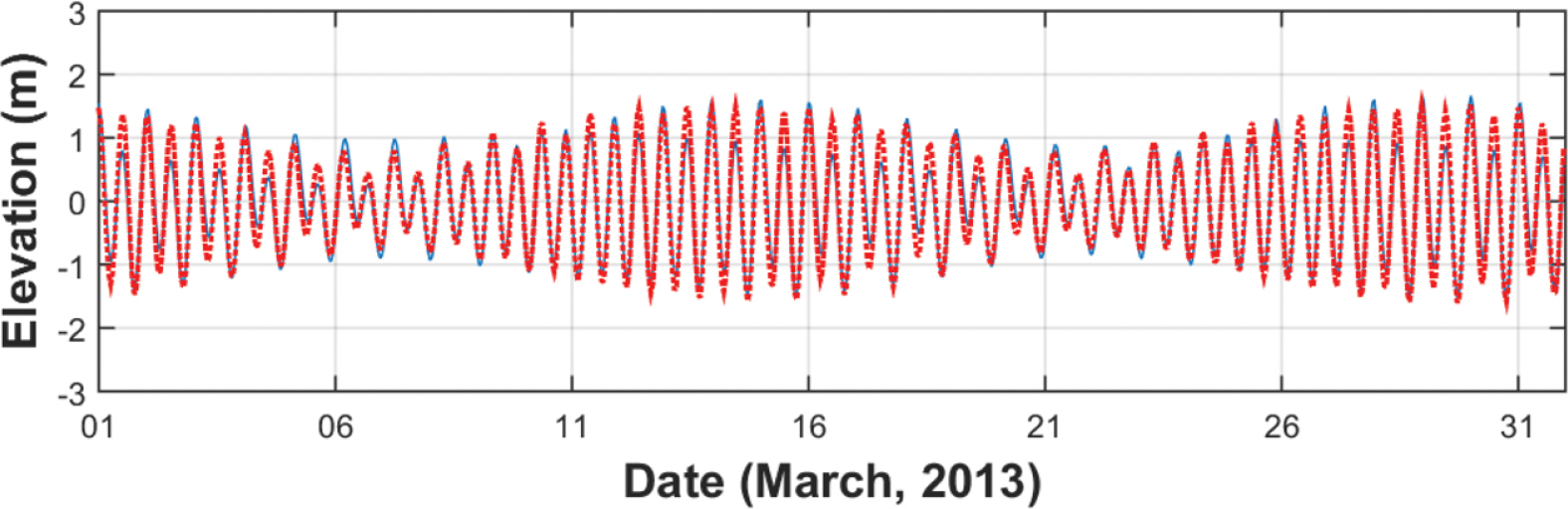
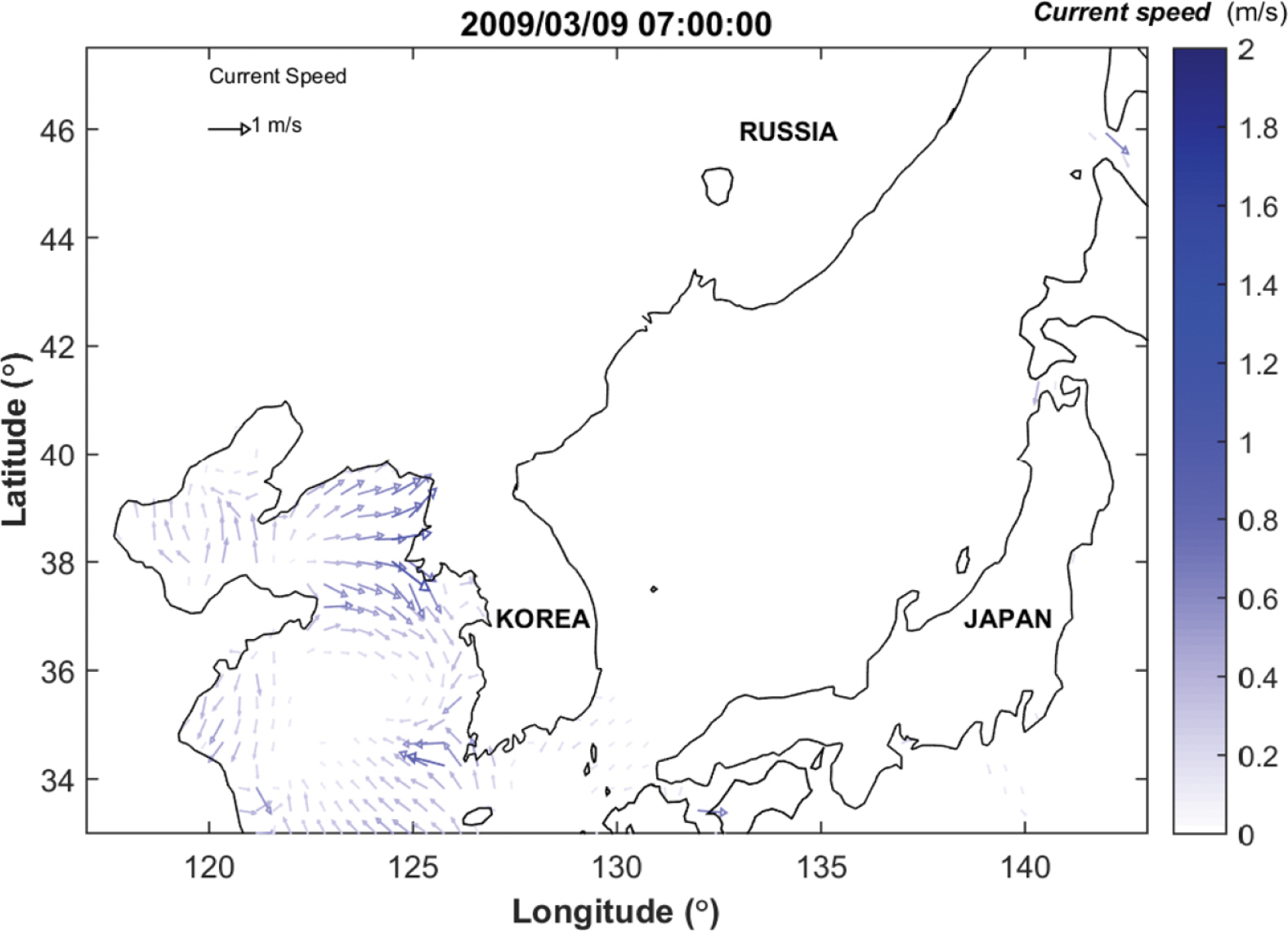
이 외에 본 연구의 계산 영역에 황해역도 포함되어 있어 조석 및 조류의 효과를 파랑계산에 포함하였다. 이를 위해 본 연구에서는 Matsumoto et al.(2000)의 조석 및 조류에 대한 조화상수를 사용하였는데, 효과적인 파랑 계산을 위해 주요 조화상수인 M2, S2, K1, O1의 분조들을 사용하였다. 한편, 본 연구에서는 이에 따른 조위자료를 United Kingdom Hydrographic Office(2003)의 ATT(Admiralty Tide Table)을 이용하여 생성한 조위자료와 비교하여 Fig. 6에 나타내었다. 이에 따르면 생성 조위의 Pearson 상관관계 계수는 0.96으로 서로 잘 일치하는 것으로 나타나고 있다. 그리고 본 연구의 수치모형에서 생성한 조류 벡터도를 Fig. 7에 나타내었다. Fig. 7의 조류는 KOGA-W01에서 최대 폭풍파랑이 관찰된 시점이다.
이 외에 본 연구에서는 파랑 스펙트럼의 주파수 및 해상도와 시간 및 공간격자 간격을 Chun and Ahn(2017a)의 경우와 동일하게 사용하였다. 한편, 조석 및 조류의 영향을 파랑계산에 포함시킨 결과, 이에 의한 도플러 편이(Doppler shift) 효과를 나타내는 상대 주파수(intrinsic frequency)에서의 파랑 에너지의 이동도 파랑 계산에 포함시켰다. 또한 효과적인 파랑계산을 위해 시간 격자 간격으로 20분을 사용하였는데, 이에 따른 Courant number를 식(5)에 나타내었다.
여기서 λ, ϕ, θ, ωr는 경도, 위도, 방향각, 상대주파수를 나타내며, cλ, cϕ, cθ, cωr는 각 방향에 대한 파랑에너지의 전파속도를 가리킨다. 시간에 따라 음해법을 이용하여 계산하기 때문에 1보다 큰 Courant number 에서도 안정적으로 파랑 계산이 수행된다. 파랑 모형을 구동하여 파랑 스펙트럼 S(f)을 얻게 되는데, 이로부터 유의파고 Hs 및 유의파주기 T1/3를 계산한다. 본 연구에서 유의파주기는 Chun and Suh(2018)의 식을 이용하여 계산하는데, 그 식은 다음과 같다.
여기서 Tm−1, 0은 Tm−1, 0 = ∫ 0 ∞ f - 1 S ( f ) d f / ∫ 0 ∞ S ( f ) d f
3.2 수치모의 실험 검증
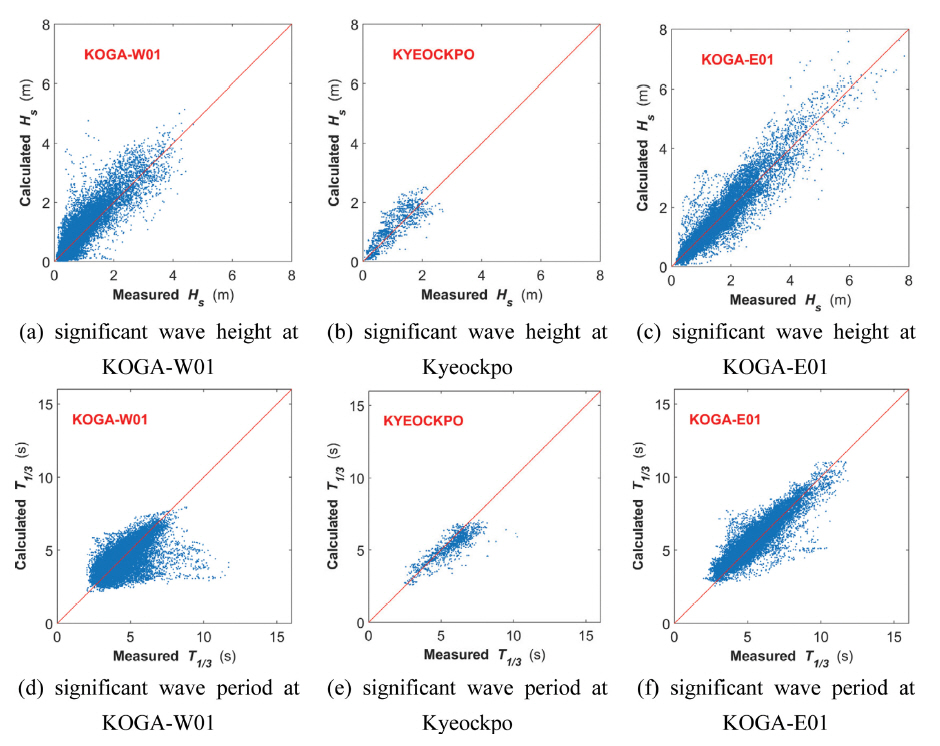
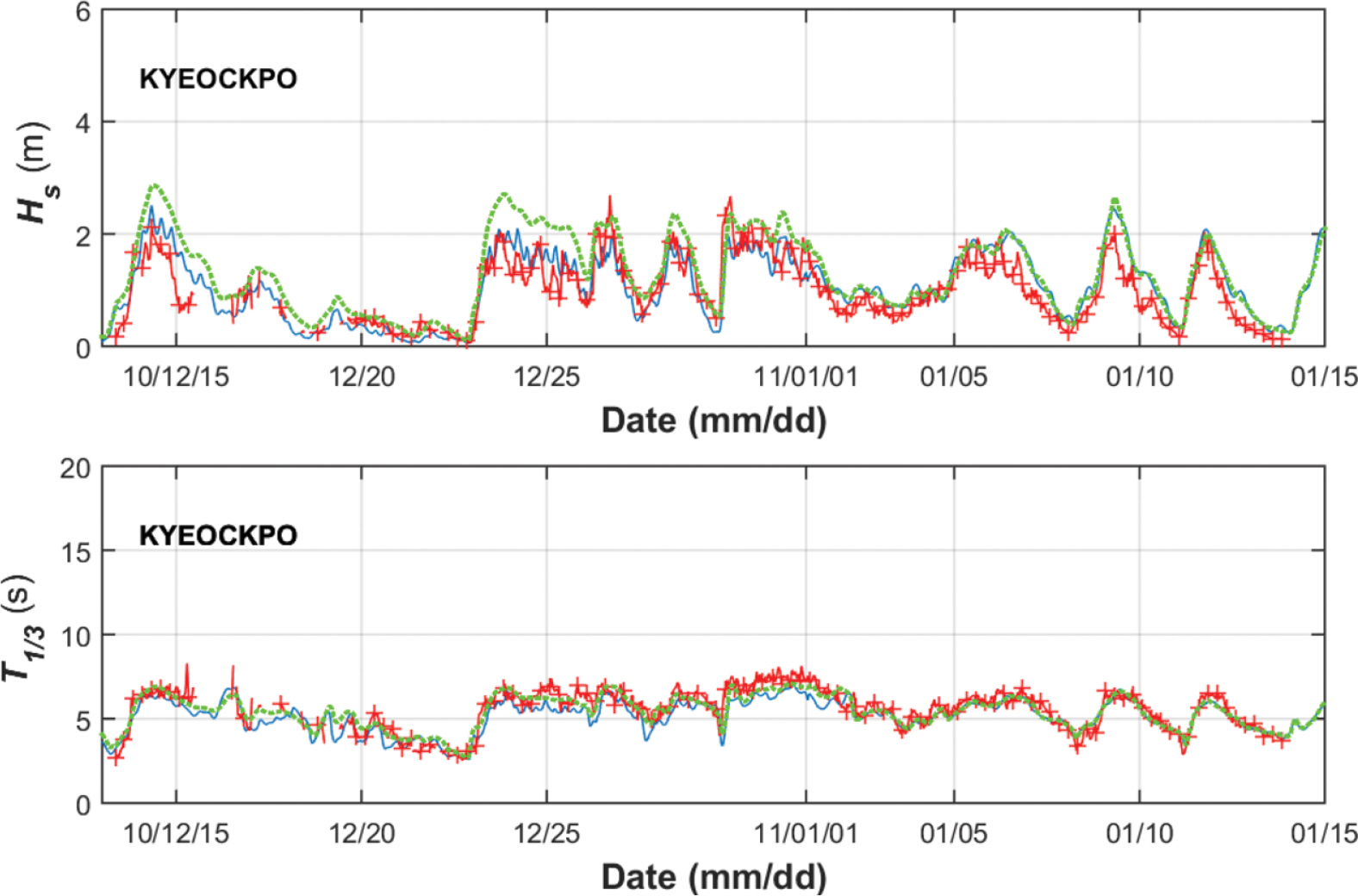
본 연구에서는 수치모의 실험의 검증을 위해 KOGA-W01, 격포, KOGA-E01에서의 계산 유의파고 및 유의파주기를 파랑관측결과와 비교하고 이를 Fig. 8에 나타내었다. 여기에서 실선은 관측결과 및 계산결과의 일대일 비교를 위한 기준선이다. Fig. 8의 계산 유의파고 및 유의파주기의 정확도를 평균편향 bias, 평균제곱근오차 RMSE, 분산지수 SI, Pearson 상관관계 계수 r, skill 등으로 정리하여 Table 3에 나타내었다. Table 3의 통계량 중에서 bias, RMSE, SI, r의 식은 Chun et al.(2014)에 제시되어 있어 본 논문에서 이의 식을 제시하지 않는다. 한편, skill은 Willmott(1981)의 index of agreement을 나타내는 것으로(Warner et al., 2005), 이는 outlier에 민감하게 반응하는 Pearson 상관관계 계수를 개선했다는 장점이 있다. Padilla-Hernandez and Monbaliu(2001)와 Shih et al.(2018)이 이를 이용하여 파랑모형의 정확도를 나타낸 바 있다. 이 중, Shih et al.(2018)에 따르면 skill이 0.65~1.0 사이에 있는 경우 일치도가 탁월하다고 한다.
Fig. 8(a)~Fig. 8(c)을 보면 본 연구의 계산 유의파고가 관측결과와 잘 일치하고 있다. 이는 Table 3에서도 확인되는데, 이의 평균제곱근 오차가 0.5 m보다 작으며, Pearson 상관관계계수가 Pilar et al.(2008)의 것보다 낮지 않다. 이로 볼 때, 본 연구에서 유의파고가 비교적 정확하게 계산된 것으로 보인다. 한편 계산 유의파주기의 평균제곱근오차가 1 s 이하이고, KOGA-W01을 제외한 나머지 지점의 Pearson 상관관계계수는 만족할만한 수준이다. KOGA-W01의 낮은 상관관계계수는 계산영역의 한계로 S 및 SSW계열의 장주기파랑을 정확히 재현하지 못한 결과이다(Fig. 8(d)). 반면에 KOGA-W01 유의파주기의 skill은 0.76으로, 상대적으로 높은 편이다. Pearson 상관관계 계수와 skill의 차이는 앞서 언급한 것처럼 skill이 outlier에 덜 민감해, Pearson 상관관계 계수보다 skill이 더 높은 결과이다. 한편 격포는 KOGA-W01과 동일하게 황해역에 위치해 있지만, 유의파주기의 Pearson 상관관계계수는 낮지 않다. 이는 격포 파랑관측이 S 계열의 장주기파가 나타나지 않는 동계에 수행되어 이의 정확도가 높은 것으로 파악된다.
한편, 본 연구에서는 광역 격자 파랑 모형에서 조석 및 조류의 효과를 보기 위해 조석 및 조류를 포함하지 않고 동일 기간에 대해 파랑 계산을 수행하고, 이 결과를 Table 3에 나타내었다. 격포 지점을 제외하고는 유의파고 및 유의파주기 상에 큰 차이는 없다. 이는 KOGA-W01 및 KOGA-E01 지점의 관측파랑이 심해파 출현 빈도가 높아 나타나는 결과로 보인다. 특히 유의파 주기에 의한 차이는 더 작은 편인데, 심해파에서의 도플러 편이 근사를 부록 1에 정리하여 나타내었다. Table 3을 보면, 격포 지점에서 조석 및 조류의 효과가 가장 큰 것으로 나타나고 있다. 이에 본 연구의 계산결과와 조석 및 조류를 포함하지 않은 계산결과들을 관측결과와 비교하여 Fig. 9에 나타내었다. 격포 파랑관측자료는 KOGA-W01, KOGA-E01과 달리 Nortek사의 Range finder로 관측된 것으로, 이 장비는 육상에서 초음파를 해면에 투사하는 방식으로 수위를 관측한다. 이러한 관측 방식 때문에 다른 파랑관측자료에 비해 비교적 천해에 가까워 조석 및 조류 효과가 상대적으로 크게 나타나고 있다.
마지막으로 Table 3을 보면, 계산 유의파주기의 정확도도 볼 수 있다. 여기에서의 계산 유의파주기는 파랑 스펙트럼 계산 결과를 식(6)에 대입하여 구한 것으로, Table 3의 정확도는 파랑모형의 정확도 외에 식(6)의 정확도도 함께 반영되어 있다. KOGA-W01의 유의파주기의 Pearson 상관관계 계수가 낮은 편인데, 이는 식(6)의 한계라기 보다는 본 연구의 계산영역의 한계로 인해 S 계열의 장주기파를 제대로 재현하지 못한 결과이다. 이로써, 식(6)이 동해의 파랑관측자료를 바탕으로 수립되긴 했으나, 동해와 특성이 다른 황해에 대해서도 적용 가능함을 보여 주고 있다.
3.3 황해역 폭풍파랑 및 태풍파랑
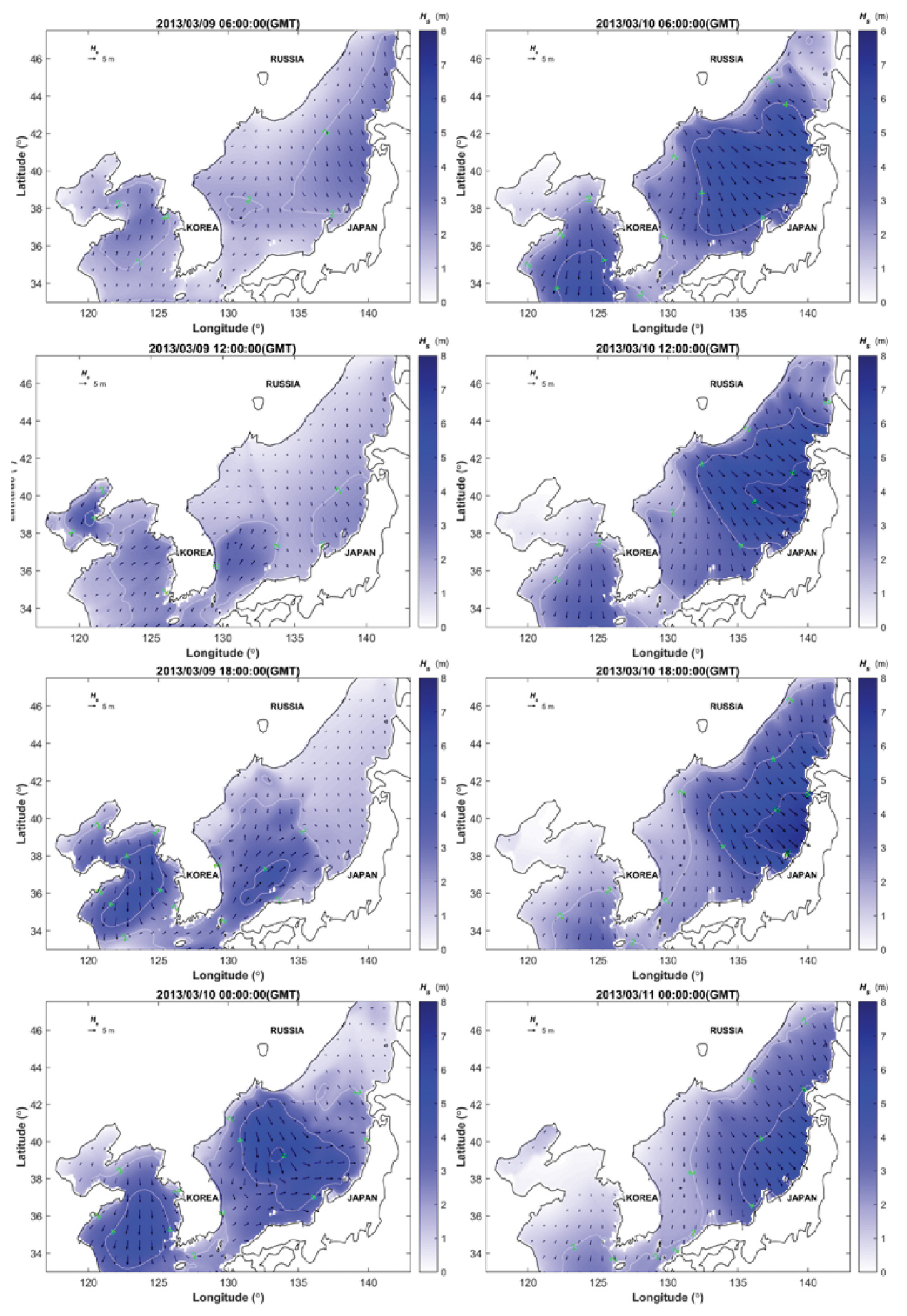
2장에서 언급한 것처럼 KOGA-W01에서 폭풍파랑과 태풍파랑이 관측되었는데, 이들 극한파랑을 중심으로 황해역에서의 폭풍파랑 및 태풍파랑의 발달을 살펴보았다. KOGA-W01에서는 2013년 3워 9일 16시에 4.69 m의 최대 폭풍파랑이 관측되었는데, 당시의 유의파고 크기는 Oh et al.(2015)의 백령도 지점 최대 폭풍파랑의 유의파고보다 4 cm 작다. Fig. 9에 따르면, 해당 시점에 대한 계산 유의파고는 5.14 m와 같은데, Fig. 10의 계산 유의파고의 평균제곱근오차와 Pearson 상관관계 계수는 각각 0.41 m, 0.91과 같다. 이 외에 유의파 주기의 평균제곱근오차와 Pearson 상관관계 계수는 각각 0.7 s, 0.82로 본 연구의 수치모의 실험에서 당시의 폭풍파랑을 잘 재현한 것으로 판단된다. 이에 최대 폭풍파랑 출현 시점 전후의 유의파고 분포도를 Fig. 11에 나타내었다.
Fig. 11에 따르면 2013년 3월 9일 6시에 동해역에서는 NNW 계열의 파랑이 작용하고 있던 반면에, 황해에는 S 계열의 파랑이 형성되어 있다. 이후 계절풍의 작용으로 N 계열의 파랑이 황해역에서 발달하다가 2013년 3월 10일 0시에 황해 전역에 걸쳐 약 4 m 이상의 유의파고가 나타났다가 점차 감소한다. 한편 동해역에서는 한반도 북부에서 발달한 온대성 저기압의 이동에 따라 유의파고가 점차 증가하는 것으로 나타나고 있다.
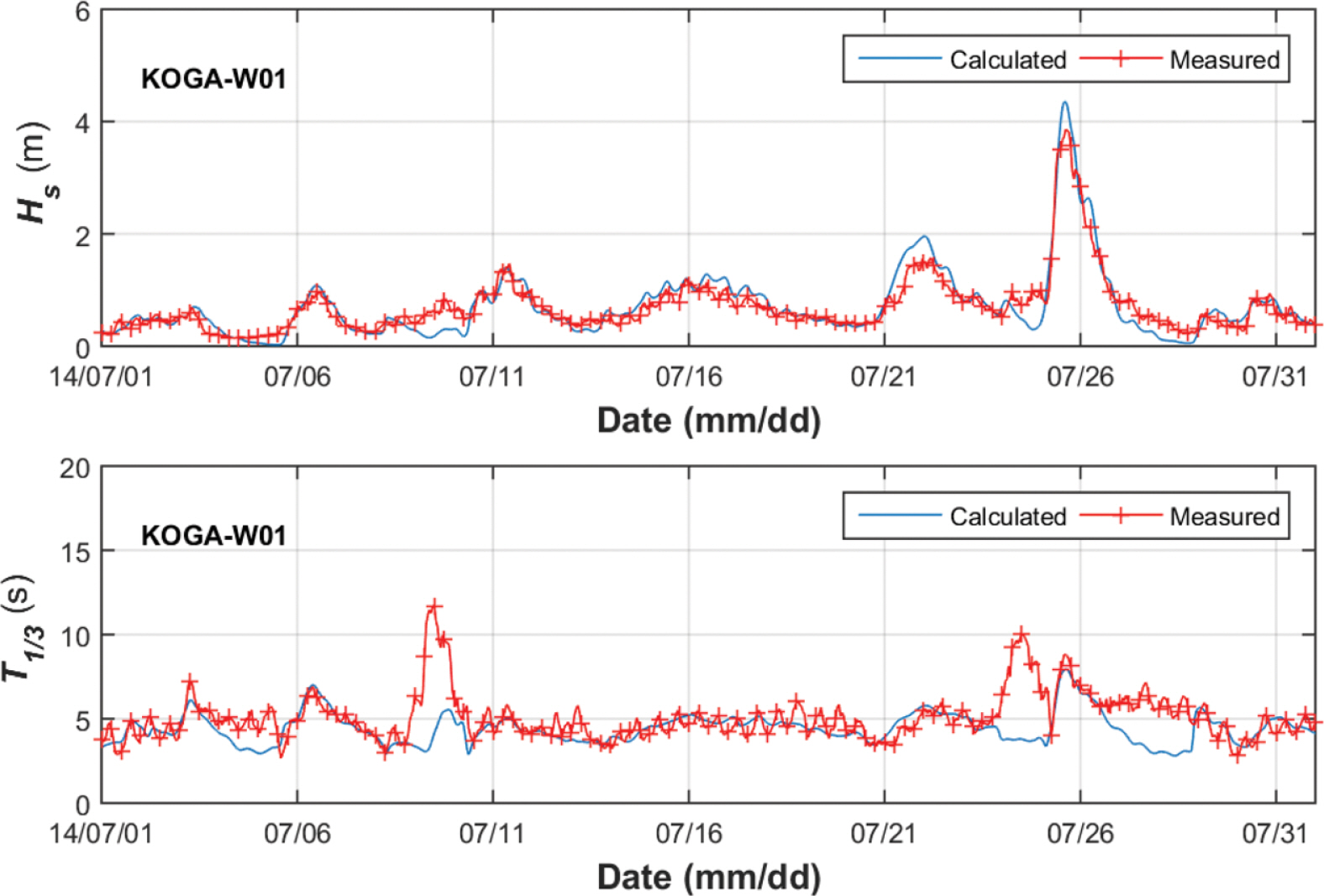
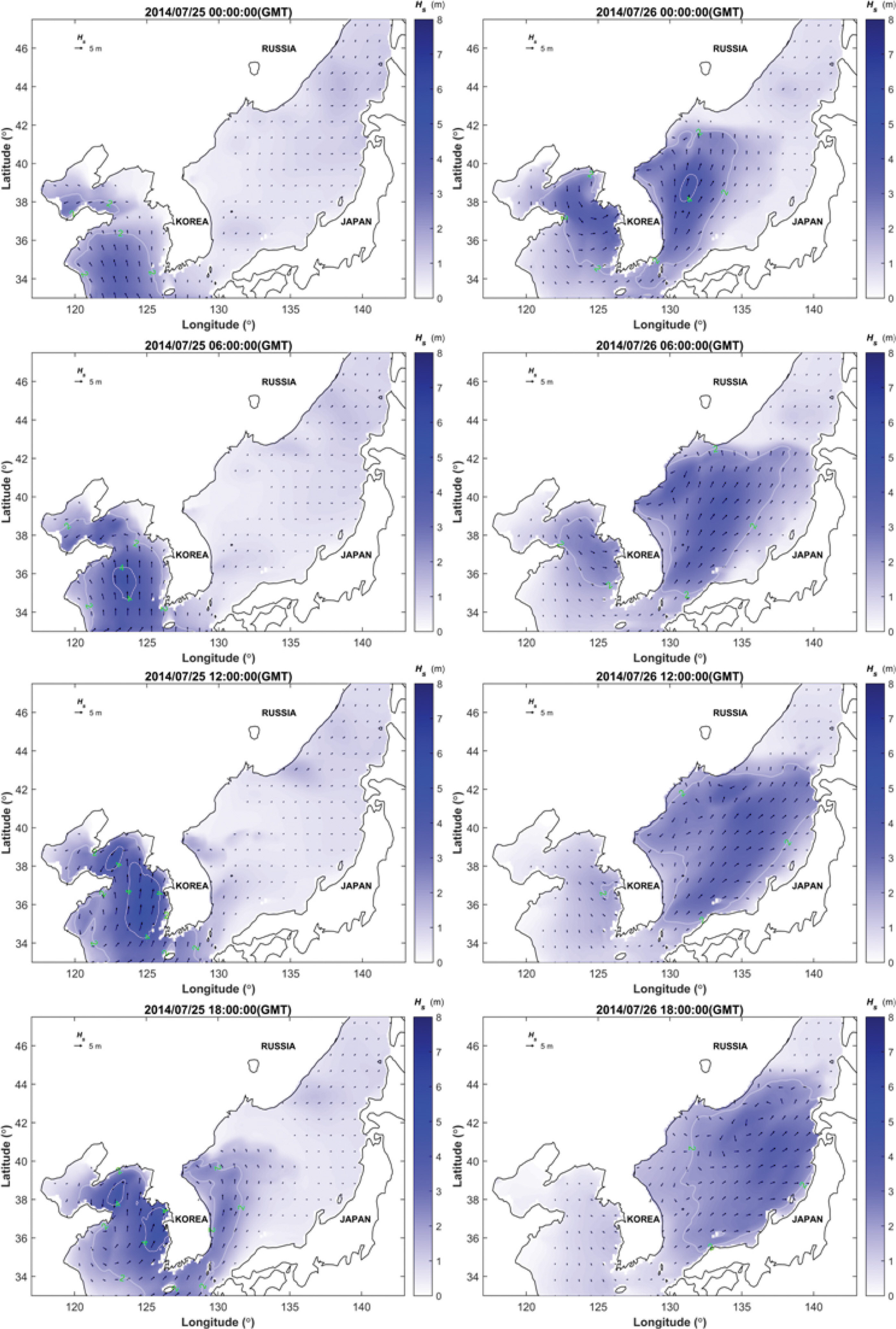
한편, KOGA-W01 파랑관측기간 중 T1410 MATMO에 의한 태풍파랑이 관측되었다. 당시의 파랑 관측결과와 계산결과를 Fig. 12에 제시하였다. 당시 최대 유의파고의 관측값과 계산치는 3.89 m, 4.35 m와 각각 같아, 본 연구의 수치모의 실험에서 당시의 태풍파랑을 잘 재현한 것으로 보인다. 그리고 당시 시점에 대한 유의파주기의 관측값과 계산값은 8.82 s, 7.92 s로, 본 연구의 수치모의 실험에서 0.9 s 정도 과소산정하고 있다. 이는 KOGA-W01 지점의 평균제곱근오차보다 작아 이의 정확도가 낮지 않다고 볼 수 있다. 그러나 2014년 7월 유의파주기의 Pearson 상관관계 계수는 0.25로, 유의파고의 Pearson 상관관계 계수인 0.95보다 작다. 이는 태풍 상륙시점을 전후해서 나타나는 장주기파가 계산영역 밖인 동중국해 및 필리핀해에서 태풍이 발생한 다음, 당시의 너울성 파랑이 황해역으로 진입하였는데, 본 연구 계산 영역의 한계로 이를 재현하지 못하였다. 이와 유사하게 2014년 7월 9일 T1408 NEOGURI에 의한 약 12 s에 이르는 유의파주기도 본 연구의 수치모의 실험에서 이를 잘 재현하지 못한 것이다. 이에 따라 Fig. 12의 유의파주기의 정확도가 낮게 나타나고 있었다.
TY1410 MATMO에 의한 태풍 파랑 발달 양상을 Fig. 13에 나타내었다. 당시 태풍은 중국에 상륙한 다음, 황해역을 거쳐 동해안으로 빠져나갔다. 이에 따라 황해 및 동해역에서 강한 태풍파랑이 형성되었는데, 당시 황해역에서는 약 4 m의 유의파고를 태풍파랑이 나타났고, 이를 본 연구의 수치모의 실험에서 잘 재현하고 있다.
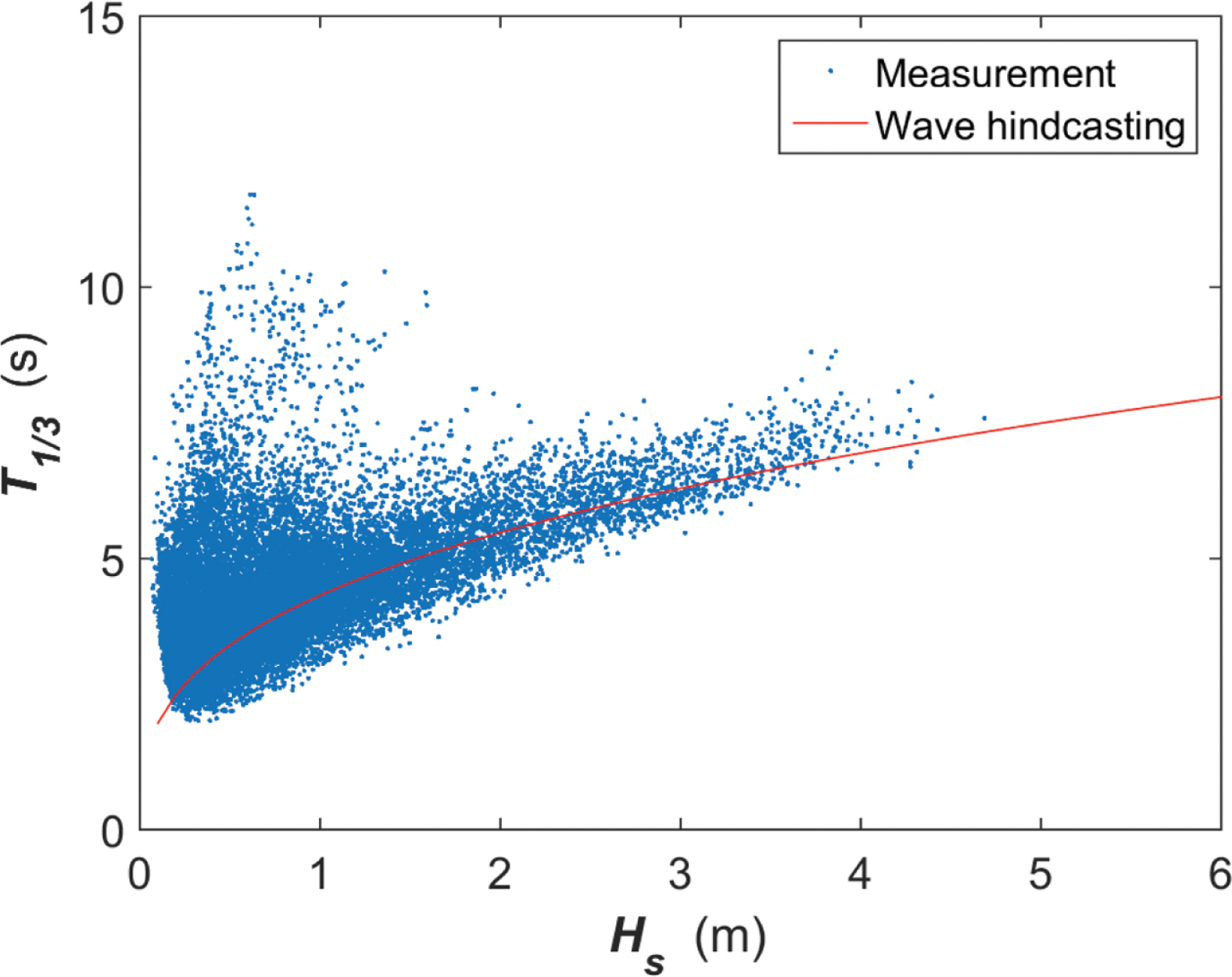
본 연구의 계산 결과에 따르면, 남측의 계산 영역이 제한되어 있음에도 황해역에서의 폭풍 및 태풍에 의한 유의파고를 잘 재현하고 있다. 특히 계산 영역 밖에서 활동하는 태풍에 의한 유의파고도 비교적 정확하게 재현하고 있다. 극한 파랑 환경에서의 유의파주기 역시 어느 정도 정확하게 예측하고 있지만, 계산영역 밖에 생성되어 황해역으로 전달된 태풍 파랑의 유의파주기는 과소 산정하고 있다. 이는 황해역 극치파랑의 주기를 과소 산정하는 가능성이 있음을 의미한다. 이에 본 연구에서는 KOGA-W01에서의 계산 결과를 바탕으로 유의파고 및 유의파주기 관계식을 구하였는데, 이는 T 1 / 3 = 4 . 35 H s 0 . 34
이를 정리하자면, 본 연구의 수치모형이 동중국해에서의 태풍에 의한 태풍 파랑의 유의파 주기를 잘 재현하지 못하고 있으나, 이의 유의파고는 크지 않아서 본 연구의 계산결과로부터 구한 유의파고 및 유의파 주기 관계식을 극치 파랑에 대해서도 적용가능하다고 볼 수 있다.
4. 결론 및 요약
황해역은 한반도 및 중국에 둘러 싸여 있어 파랑이 발달하기 힘들다. 이 때문에 KOGA-W01 파랑관측자료의 최빈도 유의파고 및 유의파주기 값은 0.54 m, 3.93 s와 각각 같다. 이 주기에 대한 심해파 한계 수심은 12 m로, 파고계의 위치가 연안역에 비교적 가깝긴 하지만, 주기가 짧아 심해파 성향이 강한 것으로 판단된다. 이후 파향별로 유의파고 및 유의파주기의 분포를 분석하면, 계절풍의 영향을 크게 받는 것으로 나타났다. 구체적으로 WNW~N 계열 파랑의 출현율은 31.99% 정도 되며, 이의 파형경사는 0.04로 풍파성향이 상대적으로 강하게 나타나고 있다. 특히 N 계열 파랑의 유의파고 및 유의파주기의 평균은 1.77 m, 5.12 s로 나타났다. 반면에 S 및 SSW 계열 파랑의파향 출현율은 40.54% 정도 되는데, 이들 방향의 fetch length가 긴 탓에 유의파주기 역시 상대적으로 긴 편이다. 하지만 유의파고는 작아 이들 방향의 파형경사는 다른 방향에 비해서 작은 편이다. 이러한 특성은 유의파고 및 첨두주기의 관계와 JONSWAP 관계식의 비교에서도 나타나는데, 1 m 이하의 유의파고를 중심으로 너울성파랑이 나타나고 있다.
이러한 이유로 본 연구에서는 Chun and Ahn(2017a)의 계산 영역을 확장하여 파랑 계산을 수행하였다. 황해역은 조석 및 조류의 영향이 크기 때문에 Chun and Ahn(2017a)에 Matsumoto et al.(2000)의 조화상수를 이용하여 조석 및 조류를 생성하여 파랑계산에 반영하였다. 본 연구의 파랑계산은 2010년부터 2014년까지 5년에 대해서 수행하고, 계산결과 얻은 유의파고 및 유의파주기를 KOGA-W01, 격포, KOGA-E01에서의 관측결과와 비교하였다. 여기서 유의파주기는 Chun and Suh(2018)의 식을 이용하여 산정하였다. 이에 따르면 계산 유의파고는 위치에 관계없이 잘 일치하는 것으로 나타나고 있으나, 계산 유의파주기는 계산 유의파고보다 정확도가 다소 낮은 것으로 나타났다. 특히 KOGA-W01의 Pearson 상관관계 계수가 낮은데, 이는 본 연구의 수치모의 실험에서 S 계열의 너울성파랑을 정확히 고려하지 못한 결과이다.
이 외에 본 연구에서는 조석 및 조류가 광역 파랑계산에 미치는 영향을 보기 위해 이를 배제한 경우에 대해서도 수치모의 실험을 수행하였다. 조석 및 조류 효과를 배제한 경우에 대해서도 동일하게 수치모의 실험을 수행하고 이 계산결과를 관측결과와 비교하였다. 본 연구에 따르면 조석 및 조류 조건 포함에 관계없이 유의파고 및 유의파주기는 큰 차이가 나지 않고 있다. 특히 계산 유의파주기는 매우 유사한데, 이는 심해파 출현율이 높은 탓에 도플러 편이가 작게 나타난 결과로 판단된다. 한편 KOGA-W01와 격포 지점의 유의파주기는 Chun and Suh(2018)의 식이 동해 파랑관측자료를 바탕으로 수립되었음에도 잘 일치해, Chun and Suh(2018)의 식이 동해 이외의 해역에 대해서도 적용 가능함을 알 수 있다.
본 연구에서는 황해역의 폭풍파랑 및 태풍파랑의 발달 특성을 보기 위해 2013년 3월 및 2014년 7월의 계산결과를 관측결과와 비교하였다. 이에 따르면, 폭풍파랑 및 태풍파랑의 유의파고를 정확히 계산하고 있는 것으로 나타나고 있다. 그리고 폭풍파랑의 유의파주기 역시 정확히 계산되었는데, 태풍파랑은 최대 유의파고가 나타난 시점을 제외하고 과소 산정하는 것으로 나타나고 있다. 이는 계산영역 밖인 동중국해에서 생성된 태풍파랑을 정확히 재현하지 못한 결과이다. 하지만 이들 파랑의 유의파고가 크지 않아, 본 연구의 계산결과로부터 구한 유의파고 및 유의파주기의 관계식이 실측치와 잘 일치해, 본 연구의 계산결과를 바탕으로 극치파랑의 유의파주기 산정에 무리가 없는 것으로 예상된다.