요약Bound mode의 외중력파와 이로 인한 보강간섭이 이상파 생성 기작이라는 가설을 확인하기 위해 OpenFoam 기반 Tool box인 ihFoam과 Bi-spectrum에 기초한 수치모의를 수행하였다. 수치모의는 건설 과정에서 이상파가 관측된 삼척 LNG 생산기지 전용부두를 대상으로 수행되었으며, Bound mode의 외중력파는 Bi-spectrum에 기반하여 출현빈도가 높은 주기가 7초인 국지 풍성파와 11.4초인 너울의 difference interaction으로 생성하였다. 또한 비교를 위해 비선형 Cnoidal wave, linear wave를 대상으로 한 수치모의도 병행하여 수행하였다. 모의결과 N 계열 bound mode의 외중력파에 의해 삼척 LNG 생산기지 전용부두를 따라 진행되는 연파가 생성되며, 이상파는 전술한 연파와 남측 도류제로부터의 반사파가 더해져 출현하는 것으로 모의되었다.
AbstractWe carry out the numerical simulation to test a hypothesis that freak waves can be triggered by the infragravity waves of bound mode underlying the ever-present swells and its constructive interaction with swells using the Tool Box called the ihFoam that has its roots on the OpenFoam, and Bi-spectrum. Numerical simulation is implemented for the SamChcuk LNG Plant where freak waves have been reported in front of the private wharf during its construction phase due to the uncompleted northern breakwater. Infra-gravity waves of bound mode is generated using the difference wave-wave interaction between the local wind waves of 7 s and a swell of 11.4 s based on the Bi-spectrum. For the sake of comparison, numerical simulation for infra-gravity waves of free mode is also carried out. Numerical results show that stem waves along the private wharf for SamChcuk LNG Plant can be triggered by the infra-gravity waves of bound mode coming from the north, which eventually leads to freak waves when encounters the reflected waves from the south jetty.
1. 서 론먼 바다에서 여러 가지 기작에 의해 생성된 파랑은 인근 연안으로 전파되며, 이 과정에서 해양환경에 내재한 변동성으로 파랑은 불규칙한 모습을 지닌다. 파랑이 진행되는 과정에서 파동계가 바람의 영향권을 벗어나거나, 풍속이 잦아드는 경우, 파랑의 군속도는 풍속을 상회한다. 이 경우 대기의 에너지는 파랑으로 유입될 수 없으며, 단주기의 파랑은 느린 파속으로 파군으로부터 분리되어 후행하며 비로소 너울이 완성된다(Phillips, 1977). 이렇게 너울이 형성되면, 파랑 에너지는 첨두 주파수 인근에 집중 분포하며, 너울의 완만한 진폭변조로 인해 해수위가 동요하는 경우 혹은 성분 파랑간의 subharmonic 공진성 상호작용을 통해 상대적으로 긴 파랑이 출현할 수 있으며 이렇게 생성된 장주기 파랑은 독자적인 속도로 움직이는 것은 아니며, 너울의 운송파(carrier wave)에 연계되어 진행한다. 이렇게 생성된 외중력파는 수심이 깊은 수역에서는 확연하게 드러나진 않으나 연안에서는 얕은 수심과 긴 주기로 인해 큰 처오름으로 이어질 수 있어 최근 우리나라 연안에서 흔히 관측되는 이상파의 생성 기작으로 보는 시각도 존재한다.
천해역에서 진행되는 천수, 굴절, 회절 등과 같은 파랑 변형은 유한 진폭파의 경우 depth averaged approach를 통해 유도된 Boussinesq 방정식(Peregrine, 1967), 미소 진폭파의 경우 mild-slope equation(Berkhoff, 1972: Jung and Ryu, 2012)을 근간으로 수치해석 되어 왔다. 최근 향상된 계산환경을 활용하여 VOF(Volume of Fluid), SPH(Smoothed Particle Hydrodynamics) 등과 같은 정교한 수치기법을 활용하여 Navier-Stokes equation을 직접해석 하려는 노력이 시도되어 surf-zone에서의 plunger 형상, run-up, down-wash, 투과성 방파제에서의 전달파가 상세히 모의되는 등 괄목할 만한 성과를 거둔바 있다(Monaghan, 1994; Monaghan and Kos, 1999, 2000; Shao, 2010; Cho and Kang, 2017).
전술한 비선형 파랑모형에 기초하여 외중력파의 처오름 과정을 수치해석하기 위해서는 선정된 계산영역의 개방경계 혹은 내부에서 조파과정을 거치게 마련이나, 현재 가용한 조파이론의 상당부분은 스펙트럼 조화성분의 화, 즉 선형이론에 기초하여 수행되고 있으며, 이러한 경향은 불규칙 파랑의 경우 더욱 두드러진다. 이 경우 현재 가용한 목표 spectrum의 적용범위를 충족하기 위해서는 개방경계가 심해 쪽에 거치할 수밖에 없으며, 이는 과도한 계산량으로 이어진다. 따라서 과도한 계산을 피하기 위해 수치모의에는 천해역 혹은 유한수심에 해당되는 제한적인 계산영역이 사용되며, 이 경우 상대적으로 얕은 수심으로 인해 파동계 비선형성은 이미 무시할 수 있는 수준을 상회한다. 따라서 너울에 기 생성되어 운송파와 연계되어 진행되는 외중력파의 특성은 반드시 고려되어야하나, 현재 전술한 외중력파의 구속성[bound mode]과 이로 인한 보강간섭은 조파과정에서 적절하게 다루어지고 있는 것으로 보이지 않는다.
파랑 스펙트럼이 협대역에 분포하는 불규칙 파랑의 경우 단지 몇 개의 조화성분만이 존재하며, 이 경우 진폭은 완만하게 변조하며, 이차 조화성분은 bound mode로 해석될 수 있다(Tayfun, 1986). 반면에 스펙트럼의 대역폭이 증가하는 경우, 즉 비선형성이 증가하면 파동계에는 많은 수의 조화성분만이 출현하며, 조화성분간의 wave-wave interaction으로 이차 조화성분들이 증폭되며, 그 중 일부분은 bound mode로 나머지는 free mode로 이동한다(Izadparast and Niedzwecki, 2012). 계측된 파랑 시계열 자료에 bound mode 고차 조화성분의 존재 여부는 고전적인 스펙트럼으로는 해석이 불가하나, Bi-spectrum으로는 가능한 것으로 알려진 바 있다. 이러한 시각에서 Bi-spectrum을 활용하여 비선형 불규칙 파랑 조파기법을 개발하려는 노력이 Ahn(1996)과 Vanhoff와 Elgar(1997)에 의해 수행되었다. Ahn(1996)은 성분 파랑간의 상호작용계수를 Bi-spectrum으로 정의하고 이를 파랑모형에 직접 활용하여 파랑 시계열자료를 수치모의 하였다. 이에 비해, Vanhoff와 Elgar(1997)는 우리에게는 성분파랑의 진폭으로 알려진 Fourier 계수를 먼저 선형 기여 분과 비선형 기여 분으로 분리하고 비선형 기여 분에 선형 조화 성분 사이에 진행되는 상호작용을 Bi-spectrum으로 정의되는 Volterra kernel을 활용하여 설명하였다. Vanhoff와 Elgar(1997)의 모형에서 파랑 시계열자료는 target 스펙트럼과 기 정의된 Fourier 계수를 활용한 Inverse Fourier Transform으로 모의된다.
이상의 논의를 토대로 본고에서는 Bi-spectrum에 기초한 비선형 불규칙 파랑 조파기법을 활용하여 무리지어 내습하는 너울에서 sub-harmonic resonance를 통해 생성된 외중력파를 수치 모의하여 외중력파가 항내 이상파 생성 기작이라는 가설을 확인하고자 한다.
2. Bound Mode의 외중력파가 포함된 비선형 불규칙 파랑 조파2.1 비선형 상호작용비선형성이 상당한 경우, 수면변위 ζ는 다음과 같이 기술될 수 있으며
여기서 두 번째 항은 불규칙 파랑을 구성하는 조화성분간의 summation interaction에 의해 생성된 상대적으로 짧은 고차 조화성분, 세 번째 항은 difference interaction에 의해 야기된 상대적으로 긴 고차 조화성분을 의미하며, χi = kix − ωit + ϕi, ki는 파수, ωi = (gki)1/2는 각 주파수, ϕi는 성분파의 무작위 위상으로 [0, 2π]에 균등분포하며, ai는 각 성분파의 진폭을 나타낸다.
식(1)에서 알 수 있듯 비선형 보정을 의미하는 두 번째, 세번째 항은 첫 번째 선형성분에 phase locked되어 있어 흔히 bound mode로 불리는 조화성분으로 비선형 효과를 설명한다(Tayfun, 1986).
다음과 같은 resonance triad 혹은 quartet[Fig. 1 참조]가 충족되는 경우
출현하는 고차 조화성분은 독자적인 파속으로 진행하는 것은 아니며, 숙주 조화성분에 연계되어 움직인다. 전술한 phase locked, 혹은 phase coherence는 고전적인 스펙트럼으로는 해석이 불가능하나, Bi-spectrum을 활용하는 경우 가능한 것으로 알려진 바 있다(Phillips, 1977). Fig. 1에는 이해를 돕기 위해 [k, ω] 공간에서 식(3)에 기술된 공진조건을 충족하는 네개 성분파랑을 예시하였다. Fig. 1에서는 심해라는 가정을 수행하여 분산관계식을 ω = ± 로 간략화 하였으며, 전술한 분산관계식이 [k, ω] 공간에서 그리는 궤적 상에 위치하는 임의의 두 점 P1, P2을 지나는 네 개 성분파랑 k1, k2, k3, k4는 식(3)에 기술된 공진조건을 충족한다(Phillips, 1977).
2.2 Bound mode의 외중력파로 인해 다수의 첨두를 지니는 파랑스펙트럼의 정식화2.2.1 너울성장 단계의 파랑스펙트럼은 JONSWAP 스펙트럼으로 기술될 수 있으나, 너울의 성격은 생성과정과 이송 이력에 의해 결정된다. 따라서 너울 스펙트럼의 보편적 형태는 특정할 수 없다는 의견이 다수를 이룬다(Phillips, 1977). 그러나 풍속이 잦아들면 너울의 군속도는 풍속을 상회하므로, 대기의 에너지가 해수로 유입될 수 없으며, 또한 단주기 파랑은 느린 파속으로 파군으로부터 분리되어 후행하여, 파랑 에너지는 첨두 주파수 인근에 집중된다.
본고에서는 첨두 주파수 인근 협대역에 파랑에너지가 집중되는 너울의 특성을 고려하여 첨두 증강계수를 통해 대역폭 조절이 가능한 JONSWAP(the Joint North Sea Wave Project) 스펙트럼을 적용하였으며 이를 기술하면 다음과 같다.
여기서 ωpeak는 첨두 각 주파수(radian/s), γ는 첨두 증강계수, α는 Phillips 계수를 나타낸다. 실해역의 경우 γ는 1~6 사이, α는 0.0081~0.1 사이에 분포한다. γ와 α가 각각 1과 0.0081의 값을 지니는 경우는 완전히 발달된 풍성파군에 해당되며 조파수조에서는 이보다 큰 값이 관측된다. σ는 band width parameter를 나타내며 다음과 같이 정의된다.
σ = 0.07 for f ≥ 1/1.296T
σ = 0.09 for f > 1/1.296T
Fig. 2에는 이해를 돕기 위해 첨두 증강계수 γ에 따른 JONSWAP 스펙트럼의 변화 양상을 제시하였다.
2.2.2 Bound mode의 외중력파를 위한 Bi-spectrum너울 성분파랑간의 비선형 difference interaction에 의해 형성된 외중력 파와 너울이 공존하는 파동계의 경우, 파랑스펙트럼은 다음과 같이 기술할 수 있다.
여기서 윗 첨자 I와 S는 외중력파(infra gravity waves)와 너울(swell)을 각각 나타낸다.
전술한 비선형 파동계는 조화성분의 단순중첩으로는 모의가 불가하며 조화성분간에 진행되는 상호작용의 크기를 나타내는 Bi-spectrum이 추가적으로 도입되어야 하며 Bi-spectrum의 유도과정을 정리하면 다음과 같다.
해수면 변위 ζ(t)를 Fourier 급수로 전개하는 경우 다음과 같이 기술할 수 있다.
여기서 f = 1/T[HZ]. 식(6)는 Euler 식을 활용하는 경우 복소수로 기술이 가능하며 이 과정을 정리하면 다음과 같다.
먼저, Euler 식으로부터 얻을 수 있는 다음과 같은 관계식을
식(6)에 대입하고 정리하면 다음과 같은 간결한 파랑모형을 얻을 수 있다.
여기서
조화성분 fk와 fm이 공진 조건[Resonance Triad]을 충족하는 경우(Fig. 1 참조), 조화성분 fk + fm이 출현하며, 이 경우 조화성분 fk + fm의 Fourier 계수
여기서 Q(fk, fm)는 조화성분간의 상호작용의 정도를 나타내는 계수로 다음과 같이 정의된다.
상기 식에서 B*(fk, fm)은 Bi-spectrum을 나타내며, 조화성분 fk의 파랑스펙트럼 크기를 나타내는 P(fk)는 기술하면 다음과 같다.
여기서 E[•]는 괄호 안 물리량의 기댓값을 나타내는 연산자를 나타낸다.
불규칙 파랑의 조파 과정에는 Bi-spectrum을 정규화한 Bicoherence b(fk, fm)가 사용되며 이는 다음과 같이 정의된다.
b2(fk, fm)가 0.5인 경우, 조화성분 fk + fm의 파랑스펙트럼의 50%가 공진성 상호작용의 결과라는 것을 의미하며 이를 정리하면 다음과 같으며
Fig. 3에는 이해를 돕기 위해 성분파랑 fl과 fm 간에 진행되는 공진성 상호작용에 의한 파랑스펙트럼 기여 분 b2(fl, fm)을 예시하였다.
공진 조건(Resonance Triad)이 다수의 조화성분에서 충족되는 경우 Fourier 계수
여기서 Q(fl, fm)는 다음과 같이 기술될 수 있다.
3. 파랑모형수치모의는 OpenFoam 기반 Tool box인 ihFoam에 기초하여 수행되며(Lara et al., 2006, 2008, 2011, 2012; Losada et al., 2008), ihFoam에서 파랑모형은 RANS(Reynolds Averaged Navier-Stokes equation)와 질량 보존식으로 구성되며, 자유수면은 VOF(Volume Of Fraction) 법을 활용하여 추적된다.
ihFoam 파랑모형인 RANS, 질량 보존식, VOF 식을 기술하면 다음과 같다.
여기서 U는 속도 벡터, g는 중력가속도, ρ는 밀도, μeff = μ + ρνturb는 동점성계수, p*는 유사 동적압력, X는 위치벡터, α1는 각각의 단위 Cell에서 해수가 점유하고 있는 부분을 나타내는 VOF 함수를 각각 나타낸다.
4. 수치모의Bound mode의 외중력파와 이로 인한 보강간섭이 이상파 생성 기작이라는 가설을 확인하기 위해 수치모의를 수행하였다. 수치모의는 건설 과정에서 아직 완성되지 못한 동 방파제(breaker2, Fig. 4, 6 참조)로 인해 완전히 차폐되지 못하고 북측으로 외해에 부분 노출되어 취약한 삼척 LNG 생산기지 전용부두를 대상으로 수행되었다. 삼척 LNG 생산기지 전용부두는 전술한 취약부로 인해 전면수역에서 이상파가 관측되었으며, 이로 인해 거치된 케이슨이 이동되는 등 상대한 피해를 입은 바 있다.
수치모의는 과도한 계산량을 피하기 위해 1/5 scale로 축소된 시공간에서 수행하였으며, Fig. 6에 도시된 계산영역은 445 × 297 × 20 = 2,643,330개의 절점을 사용하여 이산화 하였으며 북측 개방경계에서 2절에서 다룬 bound mode의 불규칙 파랑 조파 기법을 활용하여 조파하였다. 또한 비교를 위해 bound mode의 비선형 Cnoidal wave, linear wave를 대상으로 한 수치모의도 병행하여 수행하였으며, Table 1에는 수치모의에 사용된 파랑조건을 정리하였다.
4.1 Bound mode의 외중력파가 포함된 비선형 불규칙 파랑 조파Bound mode의 외중력파가 포함된 비선형 불규칙 파랑은 전술한 복합 첨두를 지니는 파랑스펙트럼을 사용하여 조파할 수 있다. Bound mode의 외중력파는 본 연구의 대상 해역인 삼척 LNG 생산기지 전면 수역에서의 파랑특성을 토대로 출현빈도가 높은 첨두 주기가 Tpeak1 = 7 s초인 국지 풍성파와 첨두 주기 Tpeak2 = 11.4 s인 너울의 difference interaction으로 생성하였다. 이 경우 공진성 difference interaction에 의해 생성될 수 있는 외중력파의 주기 TI는 18.1 s로 다음에 기술된 관계식을 활용하는 경우 산출될 수 있다.
전술한 파랑조건은 파고가 Rayleigh 분포를 추종한다는 가정에 준거하여 유의파고 Hs로 환산하면 각각 Hs = 3.5m, Hs = 3.5 m에 해당하며, 환산 과정에 사용된 관계식을 기술하면 다음과 같다(Goda, 1985).
여기서, mo = ∫Sζ(ω)dω, Sζ(ω), Sζ(ω)는 식(4)에 정의된 파랑 스펙트럼을 나타낸다.
조파판 속도 시계열 자료는 Random phase method를 사용하여 모의하였으며, 이 과정을 정리하면 다음과 같다(Frigaard and Anderson, 2010).
A 복합 첨두를 지니는 파랑스펙트럼을 선택한 성분파랑의 수 N 만큼 등간격 Δf으로 분할한다[Fig. 5 참조].
B 선택된 i번째 성분파랑의 파고 σζ(fi)는 다음과 같이 산출한다.
C Piston 형태 조파판 stroke의 스펙트럼 σx2(fi)은 다음과 같이 정의되는 Biesel(1951)의 전환함수
에 준거하는 경우 다음과 같이 기술될 수 있다.
여기서 H는 파고, So는 조파판 stroke, k는 파수, h는 수심을 각각 나타낸다.
D 이어 Nyquist 주파수 fK 보다 작은 주파수를 지니는 성분파랑에 대해 총 N개의 복 소수 Fourier 계수 G(fi) = A(fi) + iB(fi)를 산출하며 여기서 A(fi)와 B(fi)는 각각 다음과 같이 기술될 수 있다.
여기서 ψ(fi)는 0과 2π 사이에 균일하게 분포하는 무작위 변량으로 i번째 성분파 랑의 위상을 나타낸다. 그러나 주기가 7초인 국지 풍성파와 11.4초인 너울의 difference interaction 으로 Bound mode의 외중력파가 출현한 경우 외중력파와 국지 풍성파는 동일한 위상 ψI을 지닌다.
E Nyquist 주파수 fK 보다 우월한 주파수 성분파랑에 대해서는 전 단계에서 산출한 Fourier 계수의 mirror image를 투영한다.
여기서 윗첨자 *는 complex conjugate을 나타낸다.
F C에 대한 Inverse Fourier transform을 수행하는 경우 wave paddle 위치에 대한 시 계열 자료 X(t)는 다음과 같이 산출한다.
5. 수치결과 및 분석5.1 Bound mode의 외중력파를 포함한 불규칙 파랑
Fig. 7에는 bound mode의 외중력파를 포함한 불규칙 파랑을 대상으로 수행된 수치모의에서 관측된 파동계 snapshots을 순차적으로 도시하였으며, Fig. 7에서 관측되는 수리특성을 단계별로 정리하면 다음과 같다.
A tm = 67.7 s[tp= 151.4 s](Fig. 7(a) 참조)
목표한 불규칙 파랑이 조파되어 삼척생산기지 부두로 진행하는 것을 알 수 있다.
B tm = 70.3 s[tp= 157.3 s](Fig. 7(b) 참조)
도류제[jetty2](Fig. 6 참조) 배후 수역으로 진행되는 회절로 파마루선이 휘어지는 것을 볼 수 있으며, 파마루가 삼척생산기지 부두에 도달하였다.
C tm = 74.1 s[tp= 165.8 s](Fig. 7(c) 참조)
삼척생산기지 부두[wharf]를 따라 진행되는 연파가 형성되기 시작한다.
형성된 연파가 도류제[jetty2]를 향해 진행하며, 상대적으로 큰 파고가 출현하는 영역이 확대되는 연파의 일반적인 특성을 관찰할 수 있다. 이와 더불어 휘어졌던 파마루선이 다시 바르게 배열된 것이 이채롭다.
E tm = 86.62 s[tp= 193.6 s](Fig. 7(f) 참조)
도류제[jetty2]에 도달한 연파의 일부분은 상대적으로 큰 파고로 인해 월파 되며, 일부분은 내항으로 반사되는 것을 알 수 있다.
F tm = 95.83 s[tp= 214.2 s](Fig. 7(g) 참조)
전술한 반사로 후행하는 파랑에 의한 삼척생산기지 부두 전면수역 연파는 한층 강화되는 것을 알 수 있다.
Fig. 8에는 삼척 LNG 생산기지 전용부두 전면수역에 설치된 Gauge 101~Gauge 409에서 관측된 자유수면 변위 시계열 자료를 도시하였다. Fig. 9에는 Gauge 101~109에서 75초~85초 사이, Gauge 201~209에서 77초~87초 사이, Gauge 301~309에서 80초~90초 사이, Gauge 401~ 409에서 83초~93초 사이에 관측된 각 Gauge별 파고를 Ho, rms로 정규화 하여 도시하였으며, Table 2에는 Gauge 101~Gauge 409에서 관측된 증폭비를 정리하여 수록하였다.
5.2 비선형 cnoidal waves비선형성과, 주파수 분산성이 균형을 이루는 경우 uniform한 파형이 가능하며, 이러한 파형으로는 심해역의 경우 2nd order Sokes waves, 유한 수심의 경우 Cnoidal wave 등이 있으며, 이러한 비선형 파랑모형은 조파 과정에 활용될 수 있다. Korteweg-de Vries식의 해석해로 정의되는 Cnoidal wave 모형으로 Bound mode의 외중력파 모사 가능여부와 접근각도가 연파 형성에 미치는 영향을 파악하기 위해 영각을 각각 N0oS, N10oS(Fig. 4 참조)로 조절하여 두 번의 수치모의를 수행하였으며 비교를 위해 파고와 주기는 동일하게 유지하였다.
Cnoidal 파형을 구성하는 각 성분파랑의 진폭 An은 다음과 같이 산정하였다(Cayley, 1895; Frick et al., 1981).
식(30)에서 k는 첫 번째 성분파랑의 파수, q는 다음과 같이 정의되는 방정식의 해를 의미하며
여기서, 변량 m은 파고로부터 다음과 같이 산출될 수 있다.
Fig. 11에는 삼척 LNG 생산기지 전용부두 전면 수역에서 관측된 자유수면 변위를 도시하였다. Fig. 12에는 Gauge 101~409에서 관측된 각 파고를 Ho, rms로 정규화하여 도시하였으며, Table 3, 4에는 Gauge 101~Gauge 409에서 관측된 증폭비를 정리하였다. 최대파고는 Gauge 101, 201, 201, 401에서 각각 3.12, 3.23, 4.23, 2.85으로 관측되었으며, 이는 연파 생성시 구조물을 따라 파고가 점근적으로 증가한다는 연파의 일반적 속성과 일치하며, 이와 더불어 구조물 법선 방향으로 연파 생성영역은 증가하나 파고는 감소한다는 연파의 또 다른 특징도 관측할 수 있다. 또한 최대 파고는 전 Gauge에서 N10 S보다 N0 S에서 크게 관측되어 구조물과 입사파가 이루는 각도가 작을수록 연파 파고가 증가한다는 Wiegel(1964a, b)의 연구결과와 일치한다.
5.4 결과 분석Bound mode의 외중력파가 포함된 N 계열 불규칙 파랑, 영각이 각각 N0°S, N10°S 인 비선형 Cnoidal wave, N 계열 linear wave를 대상으로 수행된 총 네 번의 수치모의에서 linear wave의 경우를 제외하고는 모두 삼척 LNG 생산기지 전용부두를 타고 진행하는 연파가 관측되었다. 최대 연파파고는 N0°S Cnoidal wave에서 발생하였으며, 이어 N10°S Cnoidal wave, N 계열 불규칙 파랑 순으로 이어진다.
비선형 Cnoidal waves는 다수의 조화성분이 phase locked되어 같이 이행하나, 불규칙 파랑의 경우 외중력파와 너울에 해당되는 두 개의 조화성분 만이 phase locked되며, 나머지 조화성분은 free mode로 이행한다. 그 결과 야기되는 상쇄간섭으로 파고는 비선형 Cnoidal waves에 비해 감소한다는 사실을 상기하면 전술한 현상은 충분히 가능해 보인다.
그러나 자연계 특정 수역에서 다수의 조화성분이 phase locked되어 이행될 가능성은 그리 크다고 볼 수 없어 비선형 Cnoidal wave에 준거하여 외중력파를 모의할 경우 상당히 보수적인 설계결과로 이어질 수 있다. 또한 단순히 장주기 선형 파형으로 외중력파를 모의하는 경우 현실과는 상당한 괴리가 있는 결과로 이어질 수 있다.
또한 본고에서 차용한 파랑모형인 RANS는 연파 생성기작인 공진성 상호작용을 설명할 수 있는 기작을 포함하고 있으나, linear wave의 경우 파고가 현저하게 감소하여, 연파를 수치적으로 모의하기 위해서는 두 개 이상의 조화성분으로 seed wave가 구성되어야 함을 알 수 있다.
6. 결 론천수, 굴절, 회절 등과 같은 파랑 변형, 항부진동, 이상파 등을 Navier-Stokes 식에 기초하여 수치해석 하는 경우 과도한 계산량으로 인해 계산영역을 심해역까지 확장하기가 쉽지 않다. 이 경우 유한수심으로 인해 파랑이 지니는 비선형성은 개방경계에서 무시할 수 있을 정도로 작지 않다. 따라서 운송파(carrier wave)에 연계되어 진행하는 고차 혹은 저차 조화성분은 조파과정에서 반드시 고려되어야 하나 현재 적절히 다루어지고 있는 것으로 보이지 않는다. 이러한 예는 축조 중 아직 완성되지 못한 동방파제로 인해 부분적으로 외해에 개방되어 취약한 삼척 LNG 생산기지 전용부두 전면수역에서 발생한 이상파에서 찾아볼 수 있다.
전술한 이상파 생성기작은 N 계열 bound mode의 외중력파로 추정되나 설계과정에서 간과된 듯하다. 본고에서는 이러한 가설을 확인하기 위해 OpenFoam 기반 Tool box인 ihFoam과 Bi-spectrum에 기반한 수치모의를 수행하였다. Bound mode의 외중력파는 Bi-spectrum에 기반하여 출현빈도가 높은 주기가 7초인 국지 풍성파와 11.4초인 너울의 difference interaction 으로 생성하였으며, 또한 비교를 위해 bound mode의 비선형 Cnoidal wave, linear wave를 대상으로 한 수치모의도 병행하여 수행하였다.
모의결과 N 계열 bound mode의 외중력파를 포함한 불규칙 파랑, 비선형 N10 S와 N0 S 계열 Cnoidal waves의 경우에서 삼척 LNG 생산기지 전용부두를 따라 진행되는 연파를 관측할 수 있었다. 최대파고는 N0 S 계열 Cnoidal waves에서 발생하였으며, 이러한 현상은 N0 S 계열 Cnoidal waves는 다수의 조화성분이 phase locked되어 같이 이행하나, 불규칙 파랑의 경우 외중력파와 너울에 해당되는 두 개의 조화 성분 만이 phase locked되며, 나머지 다수의 조화성분은 free mode로 전파되며, 그 결과로 야기되는 상쇄간섭으로 파고는 비선형 Cnoidal waves에 비해 감소한다는 사실을 상기하면 충분히 가능해 보인다. 그러나 자연계 특정한 수역에서 다수의 조화성분이 phase locked되어 이행할 가능성은 그리 크다고 볼 수 없어 비선형 Cnoidal wave에 준거하여 외중력파를 모의할 경우 상당히 보수적인 설계결과로 이어질 수 있다고 판단된다. 또한 단순히 장주기 선형 파형으로 외중력파를 모의하는 경우 현실과는 상당한 괴리가 있는 결과로 이어질 수 있다.
또한 본고에서 차용한 파랑모형인 RANS는 연파 생성기작인 공진성 상호작용을 설명할 수 있으나, linear wave의 경우 파고가 현저하게 감소하여, 연파를 수치적으로 모의하기 위해서는 두 개 이상의 조화성분으로 seed wave가 구성되어야 함을 알 수 있었다.
Fig. 1.A diagram in wave number, frequency space illustrating the four components that satisfy the resonance condition in Eq. (3), where the dispersion relation,
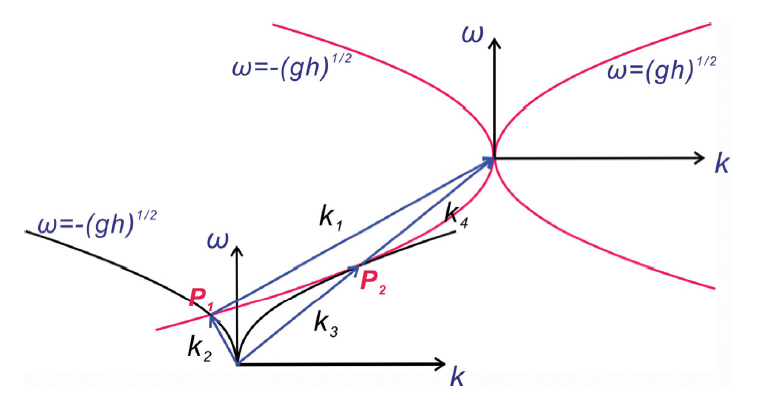
Fig. 3.Double peaked wave spectra and portion of wave spectra to nonlinear difference wave-wave interaction. 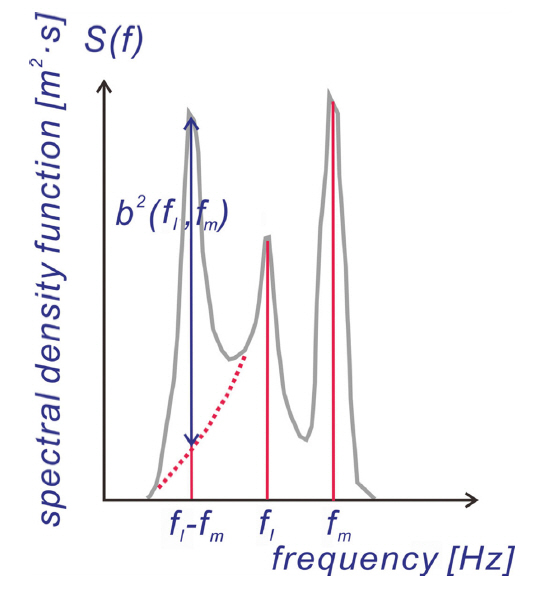
Fig. 7.Sequential snapshots of numerically simulated free water surface displacements using infra-gravity waves of bound mode. 
Fig. 8.Sampled time series of numerically simulated free water surface measured at Gauge 101∼Gauge 409. 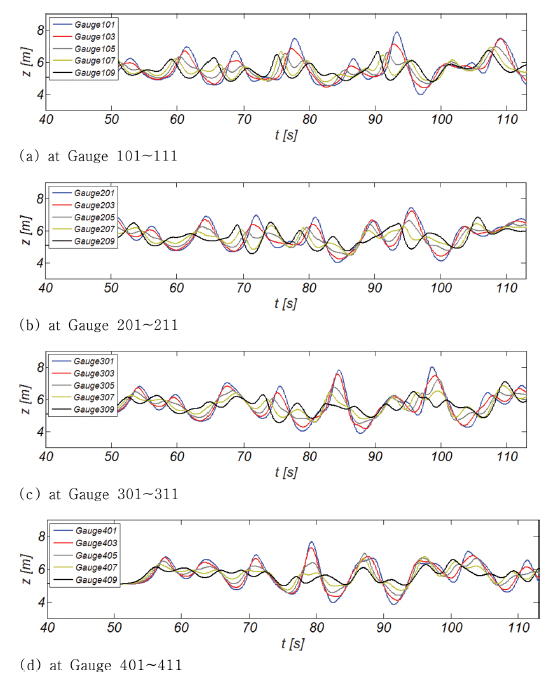
Fig. 10.Snapshots of numerically simulated wave field when over topping occurs between Gauge 101 and Gauge 404. 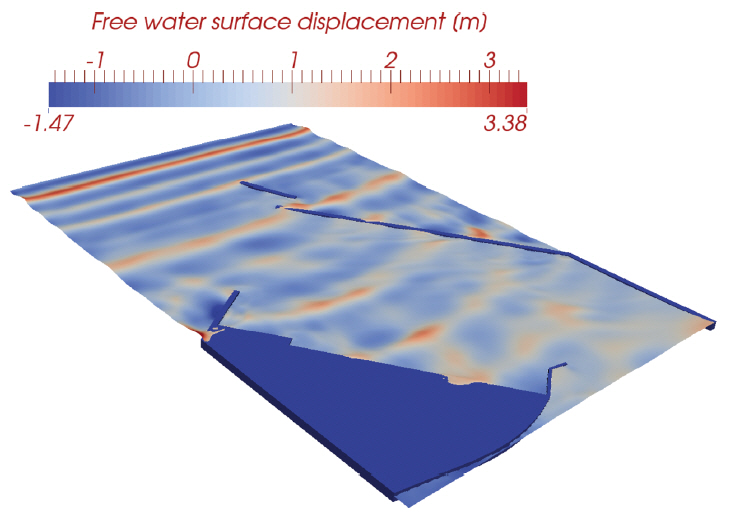
Fig. 11.1.Sampled time series of numerically simulated free water surface measured at Gauge 101∼Gauge 409 for N0 S. 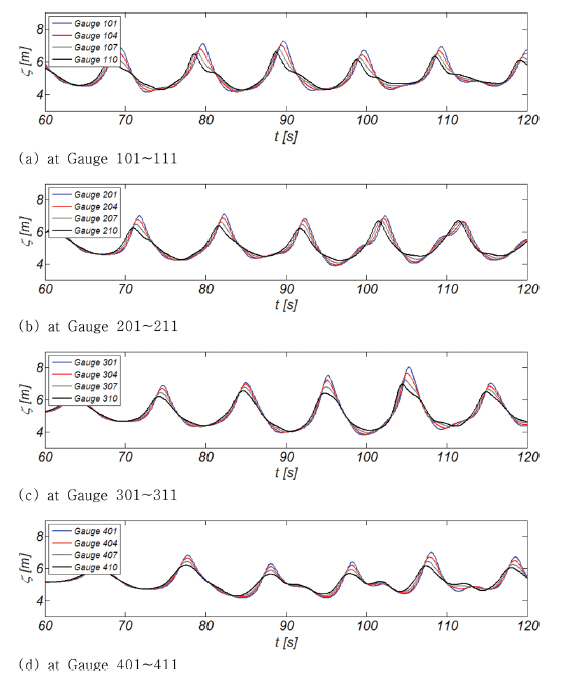
Fig. 13.Sampled time series of numerically simulated free water surface measured at Gauge 101∼Gauge 409 for linar waves. 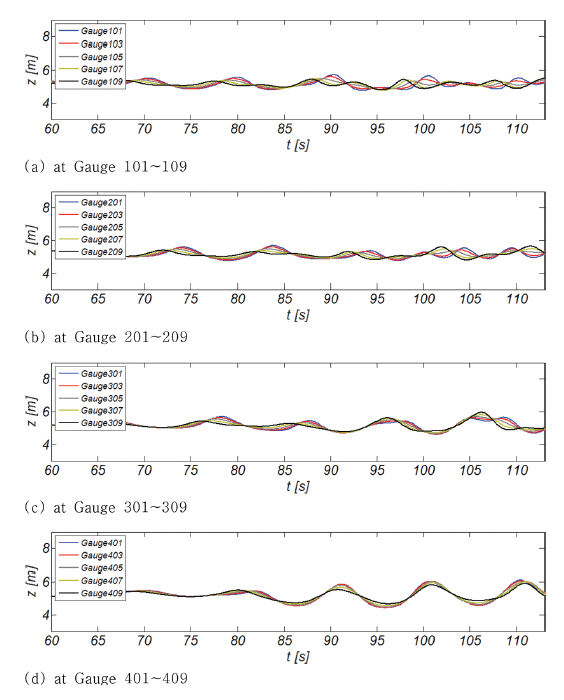
Table 1.List of wave conditions used in the numerical simulation and its corresponding prototype value
Table 2.List of amplifying ratio [H/Ho, rms]
Table 3.List of amplifying ratio [H/Ho] for N
ReferencesAhn, K.M. (1996). The digital simulation of non-linear random waves, Coastal Engineering, 1996, 657-667.
Berkhoff, J.C.W. (1972). Computation of combined refraction—diffraction, Coastal Engineering, 1973, 471-490.
Biesel, F, Suquet, F. (1951). Les apparails generateurs de houle en laboratoire, La Houille Blanche, 6, 2, 4 and 5. Laboratory Wave Generating Apparatus English version Project report 39 St Anthony Falls Hydraulic Laboratory, Minnesota University Minneapolis [1953]..
Cayley, A. (1895). An elementary treatise on elliptic functions. 2nd ed. London: G Bell.
Cho, Y.J., Kang, Y.K. (2017). The Effect of Skewness of Nonlinear Waves on the Transmission Rate through a Porous Wave Breaker, Journal of Korean Society of Coastal and Ocean Engineers, 29(6):1-13.
Flick, R.E., Guza, R.T., Inman, D.L. (1981). Elevation and velocity measurements of laboratory shoaling waves, Journal of Geophysical Research, 86, 4149-4160.
Frigaard, P, Anderson, TL. (2010). Technical Background Material for the Wave Generation Software AwaSys 5, DCE Technical Reports No. 64. Aalborg University.
Goda, Y. (1985). Random seas and design of maritime structures. University of Tokyo Press.
Izadparast, A, Niedzwecki, J. (2012). Application of semi-empirical probability distributions in wave-structure interaction problems. ASME 2012 Fluid Engineering Division Summer Meeting collocated with the ASME 2012 Heat transfer Summer conference and the ASME 2012 10th International Conference, Vol. 1: Symposia, Part A and B..
Jung, T.H., Ryu, Y.U. (2012). Treatment of Inclined Boundaries in a Finite Element Model for the Mild-Slope Equation, Journal of Korean Society of Coastal and Ocean Engineers, 24(2):84-88.
Lara, J.L., Garcia, N., Losada, I.J. (2006). RANS modelling applied to random wave interaction with submerged permeable structures, Coastal Engineering, 53, 395-417.
Lara, J.L., Losada, I.J., Guanche, R. (2008). Wave interaction with low mound breakwaters using a RANS model, Ocean Eng, 35, 1388-1400.
Lara, J.L., Ruju, A., Losada, I.J. (2011). Reynolds Averaged Navier-Stokes modelling of long waves induced by a transient wave group on a beach, Proceedings of the Royal Society A, 467, 1215-1242.
Lara, J.L., Del Jesus, M., Losada, I.J. (2012). Three-dimensional interaction of waves and porous structures. Part II: Model validation, Coast. Eng, 64, 26-46.
Losada, I.J., Gonzalez-Ondina, J.M., Diaz, G., Gonzalez, E.M. (2008). Numerical simulation of transient nonlinear response of semi-enclosed water bodies: model description and experimental validation, Coastal Engineering, 55(1):21-34.
Monaghan, J.J. (1994). Simulating free surface flows with SPH, Journal of Computational Physics, 110(2):399-406.
Monaghan, J.J., Kos, A. (1999). Solitary waves on a Cretan beach, Journal of Waterway, Port, Coastal, and Ocean Engineering, 125(3):145-155.
Phillips, OM. (1977). The dynamics of the upper ocean. 2nd ed. Cambridge University Press.
Shao, S. (2010). Incompressible SPH flow model for wave interactions with porous media, Coast. Eng, 57(3):304-316.
Tayfun, M.A. (1986). On narrow-band representation of ocean waves 1, theory, J. Geophys. Res, 91, 7743-7752.
Vanhoff, B., Elgar, S. (1997). Simulating quadratically nonlinear random processes, International Journal of Bifurcation and Chaos, 7(06):1367-1374.
Wiegel, RL. (1964a). Oceanographical Engineering, Englewood Cliffs. New Jersey: Prentice Hall.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||