1. 서 론
전산유체역학(Computational Fluid Dynamics: CFD)은 컴퓨터를 이용하여 유체의 유동 문제를 해석하는 방법으로서 비선형 편미분 방정식인 Navier-Stokes 방정식을 공간 및 시간에 대해 이산화(discretization)하여 수치기법(numerical methods) 알고리즘으로 풀어낸다. CFD 모델링에는 매우 많은 컴퓨터 자원이 필요하며, 초기에는 주로 슈퍼컴퓨팅 기술을 보유한 기관을 중심으로 사용되었다. 그러나, 최근 컴퓨터 관련 기술의 발달로 PC환경에서도 다수의 계산노드를 이용한 수치해석이 가능해졌으며 CFD 모델이 더욱 활발히 이용되고 있다.
연안 및 해양공학 분야에서는 특별히 파랑 해석을 할 수 있는 다수의 CFD 모델이 개발되어 사용되고 있다. 그 중 국내에서 널리 이용되고 있는 모델 중 하나는 일본 연안개발연구센터에서 개발된 CADMAS-SURF(Super Roller Flume for Computer Aided Design of Maritime Structure)이다(CDIT, 2001). CADMAS-SURF 모델은 계산영역의 내부 또는 경계에서 파랑을 생성하며 VOF(Volume Of Fluid) 방법으로 수면의 위치를 계산한다. 또한, 에너지감쇠대 설정을 통해 구조물에 의한 반사파를 제어할 수 있다. 그러나 유한차분법(Finite Difference Method, FDM) 기반의 모델이기 때문에 구조물 경계면을 정확하게 재현할 수 없는 한계점을 가지고 있다. 또한, 새로운 기능을 추가하기 어렵고 모델 갱신이 지속적으로 이루어지지 않아서 활용성에 제약이 있다는 단점이 있다.
한편, FLOW3D, FLUENT 등의 CFD 상용 모델도 현업에서 사용되고 있다. 이러한 모델들도 FDM 기반 모델이지만 구조물 경계면 형상을 상당히 정확하게 모델링할 수 있는 기능들을 지니고 있다. 또한 사용하기에 편리한 GUI(Graphic User Interface) 환경으로 개발되었다. 그러나 시장 독점화 이후 CPU 코어당 비용 책정 등 라이센스 비용이 급격히 증가하였다. 이로 인해 항공기, 자동차 등 수익이 큰 산업분야에서 주로 이용되고 있으며, 모델 갱신 또한 관련 분야에 집중되어 이루어지고 있는 추세이다.
이러한 이유로 최근 소스가 공개된 CFD 모델에 대한 관심이 높으며, 그 중 가장 대표적인 것이 OpenFOAM이다. OpenFOAM은 소스코드를 일반에 공개하고 누구든지 수정·배포할 수 있도록 하는 GNU-GPL(General Public License) 정책을 채택하고 있다. OpenFOAM에는 Navier-Stokes 방정식을 유한체적법(Finite Volume Method, FVM)으로 해석하는 모듈이 포함되어 있어 구조물 형상을 정확히 재현할 수 있으며, VOF 기법을 이용하여 정밀한 수위 계산도 가능하다. 그렇지만 사용법을 익히기 쉽지 않고 구현되지 않은 기능도 많아서 아직까지는 많은 분야에 적용되고 있지는 못하다.
파랑 CFD 모델에서는 계산영역 내 존재하는 구조물에 의한 반사파의 제어가 매우 중요하게 다루어져야 한다. 만일 반사파가 계산영역 경계에서 적절히 처리되지 못한다면 재반사가 발생하여 계산영역 내부 수면 변위가 교란될 수 있으며 모델링 결과가 부정확해질 수 있다. 현재 가용한 OpenFOAM 기반 파랑 CFD 모델은 대부분 계산영역 경계에서 파랑을 생성하는 외부조파 기법을 이용하고 있다. Jacobsen et al.(2012)은 선형 천수이론에 근거하여 조파 경계에서의 반복 계산을 통해 조파 경계조건을 수정하는 방법을 제안하여 Waves2FOAM 모델을 개발하였다. 이 방법은 비선형성이 약한 파랑조건에서는 반사파를 충분히 제어할 수 있으며, Higuera et al.(2013)로부터 개발된 IHFOAM 및 olaFlow(https://olaFlow.github.io)에서도 사용되고 있다. 그러나 계산영역 내측에서 파랑의 반사로 인해 비선형성이 크게 증가하거나 쇄파가 발생하는 경우에는 반사파 제어가 어려울 수 있다.
구조물로부터의 반사파를 확실하게 제어하기 위해서는 내부조파 및 에너지감쇠대를 적용하는 것이 바람직하다. 이러한 반사파 제어방법은 이미 완경사 방정식, 부스네스크 방정식 등에 적용되어 그 성능이 입증된 바 있다(Lee and Suh, 1998; Lee et al., 2001; Kim et al., 2007). 내부조파 기법은 계산영역 내부의 조파선에서 파랑을 양쪽으로 조파하며, 계산영역 외측에는 에너지감쇠대를 설정하여 파랑을 소멸시킨다. 관심영역 내측의 구조물에서 반사된 파랑은 조파선을 지나 계산영역 외부로 자연스럽게 전파된다. 따라서 반사파가 조파선에서 발생되는 파랑에 영향을 미치지 않으며, 다중반사가 발생하더라도 에너지감쇠대에서 반사파가 소멸되므로 계산이 안정적이고 정확도가 높다. 다만 계산영역이 커져서 모델링 시간이 오래 걸리게 되는 단점이 있다.
이러한 점을 고려하여 내부조파 기법을 OpenFOAM에 도입하여 반사파를 효과적으로 제어할 수 있는 파랑 CFD 모델이 최근에 개발되었다(Oh and Kim, 2017). 이 모델의 조파성능을 검증하기 위해 본 연구에서는 단면 조파수조에서 규칙파를 조파하는 수리모형실험을 수행하고 파랑 CFD 모델 결과와 비교해 보았다. 비교 대상 모델로서는 Oh and Kim(2017)의 개발 모델 및 CADMAS-SURF(CDIT, 2001)와 olaFlow(Higuera et al., 2013) 총 3 가지를 사용하였다.
2. 내부조파 오픈폼 모델
본 연구에서 사용된 CFD 모델에 관해서는 Oh and Kim(2017)에 제시된 바 있지만, 주요 내용을 요약하여 본 논문에 제시하였다. 본 모델은 Waves2FOAM(Jacobsen et al., 2012)을 기반으로 개발되었으며, Waves2FOAM에서 채택하고 있는 조파기법인 이완법(relaxation method) 대신 원천함수(source function)를 이용한 내부조파 기법(Lin and Liu, 1999)을 아래와 같이 구현하여 모델에 적용하였다.
원천함수(source function)를 s(t)라고 할 때 조파영역에서 연속 방정식은 다음과 같이 표시된다.
여기에서 C는 파 속도, η는 수면 높이, W는 조파 영역의 폭이며, lx, ly, lz는 조파 영역의 x, y, z 방향의 길이를 각각 나타낸다. 조파 영역의 크기와 높이는 Chen and Hsiao(2016)의 방법을 따라 선형파의 정규화된 속도분포에 근거하여 정하였다. 이 방법에 따르면 조파 영역의 윗면(zs1)과 아랫면(zs2)의 연직 높이 및 파 진행방향으로의 폭(ws)은 각각 다음과 같이 정의된다.
여기에서 k는 파수, h는 수심, L은 파장을 각각 나타낸다. 조파하려는 파의 파장(주기)이 길어지게 되면 ws도 길어지게 되지만 zs1과 zs2의 값은 큰 차이가 없다. 즉, 파장에 따라 조파 영역의 연직 두께에는 큰 차이가 없고 파 진행 방향으로의 폭만 유의미하게 달라진다.
한편 파 에너지의 소파를 위해서 스폰지층(sponge layer)을 사용하였다. 구체적으로는 Navier-Stokes 운동량 방정식에 각 방향 성분별로 다음과 같은 감쇠항을 적용하여 에너지를 소산시켰다.
여기에서 x0와 y0는 스폰지층의 시작 위치를, N과 θ는 감쇠계수의 크기 및 분포를 결정하는 파라미터이다. 본 연구에서는 N = 2를 사용했고, θ의 값은 예비 해석 결과를 통해 x, y, z 방향에 대해 동일하게 θ = 0.6을 적용하였다.
3. 수리모형실험
3.1 실험 수조
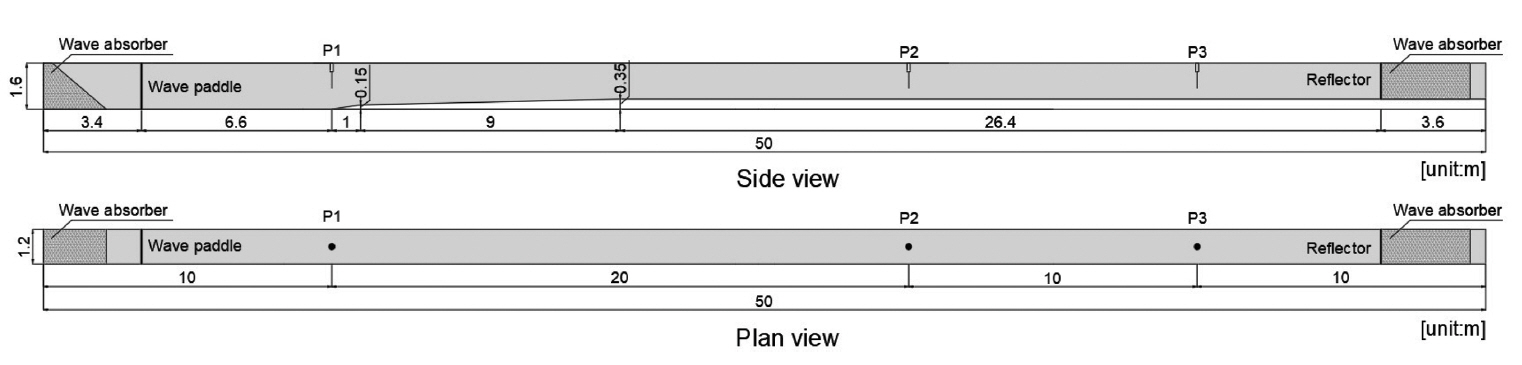
조파 검증을 위한 수리모형실험은 한국해양과학기술원 2차원 조파수조 (Oh and Lee, 2018)에서 수행되었다. 이 조파수조의 길이는 50 m, 폭은 1.2 m이며, 수조의 바닥 높이는 Fig. 1에 보인 것처럼 조파수조의 길이 방향을 따라 다르다. 조파기가 설치된 위치에 가까운 쪽의 수조 한쪽 끝으로부터의 수평 거리를 x라고 정의한다면, 0 m ≤ x < 10 m의 구간은 수조의 전체 높이를 1.6 m로 하였고, 20 m ≤ x ≤ 50 m 구간은 1.25 m로 하였으며, 10 m ≤ x < 20 m 구간은 수조의 높이가 1.6 m에서 1.25 m로 경사가 2단계로 변한다. Fig. 1에 보인 것처럼 수조의 상부높이는 수조 전체 길이에 대하여 동일한 반면, 수조의 하부 높이는 10 m ≤ x < 20 m 구간에서 조파기 위치보다 0.35 m 높아지게 되며, 20 m ≤ x ≤ 50 m에서는 0.35 m 높아진 채로 유지된다. Fig. 1에서 밝은 회색 음영으로 표시된 영역이 수조의 내부 공간에 해당한다. 수조의 바닥 높이를 일정하지 않고 이처럼 달라지게 한 이유는 Oh and Lee(2018)에 자세히 기술되어 있다.
조파판의 위치는 Fig. 1에 보인 것처럼 수조의 왼쪽 끝으로부터 3.4 m에 위치하고 있으며, AwaSys 프로그램에 의해 움직임이 제어된다(Lykke Andersen et al., 2017). 이 프로그램에는 수조 내 구조물로부터 발생하는 반사파의 에너지를 흡수하는 능동형 소파(active reflection compensator) 기능이 탑재되어 있다(Lykke Andersen et al., 2016). 한편, 조파판 바로 뒤쪽과 조파판 맞은 편의 수조 끝쪽에는 고정식 수동형 소파제(passive wave absorber)가 설치되어 있다. Fig. 1에서 수동형 소파제의 위치는 짙은 회색 음영으로 표시되었다.
3.2 실험 조건
본 연구에서는 바닥사면에서의 다중반사 조건에서 수치모델의 성능을 검증하기 위한 실험을 수행하였다. 이를 위해서 조파판 맞은 편에 위치한 소파제 전면에 아크릴판을 수조 상부 높이까지 설치하여 직립 반사판을 설치하였다. Fig. 1에 보인 것처럼 반사판은 수조 왼쪽 끝에서부터 46.4 m, 조파판으로부터는 43.0 m 떨어진 위치에 설치되었다. 따라서 조파판에서 발생되어 전파되는 파랑은 10 m ≤ x < 20 m 구간에서는 바닥사면에서의 파랑변형을 겪으면서 동시에 완만한 반사파를 발생시키게 되며, x = 46.4m에서는 반사판에서 급격한 완전반사를 경험하게 된다. 사면에서의 완만한 반사에 비해 반사판에서의 완전반사가 조파수조 내에서의 파랑 전파에 더 지배적인 영향을 미치게 된다. 완전반사로 인해 입사파와 중복파가 중첩되어 수조 내에서는 중복파가 형성된다. 한편, 조파판으로 되돌아오는 반사파는 AwaSys 프로그램의 능동형 소파 기능에 의해 흡수되게 된다.
실험파는 파고 0.15 m, 주기 2.0 s 인 규칙파를 Table 1에 보인 세 가지 수심 조건에서 60초 동안 조파하였다. Lykke Andersen et al.(2016)에 의하면 이 주기에서 AwaSys 프로그램의 조파판 반사계수는 5% 이하이므로 조파판으로 되돌아오는 파랑 에너지의 거의 대부분이 흡수된다고 할 수 있다. 한편, 파고 계측 위치는 Fig. 1에 보인 것처럼 x = 10m(P1), x = 30 m(P2), x = 40m(P3)의 세 곳이었다. Table 1에서 h0는 P1 지점의 수심에 해당하며, 조파기 위치의 수심과 같다. 한편, h는 P2 및 P3 지점의 수심에 해당하며, h0보다 0.35 m 얕다. h0 = 1.0m인 조건을 Case A, h0 = 0.8m인 조건을 Case B, h0 = 0.6m인 조건을 Case C로 칭하였다. Table 1에서 kh는 P2 및 P3 위치에서의 무차원수심을 의미한다. 육안으로 관찰했을 때 Case A에서는 쇄파가 발생하지 않았으며, Case B에서는 P2 위치에서 중복파의 쇄파가 발생하였다. 한편, Case C에서는 입사파가 P2 위치에 도달하기 전에 이미 쇄파가 발생하였다.
4. 수치모델링
4.1 수치모델링 방법
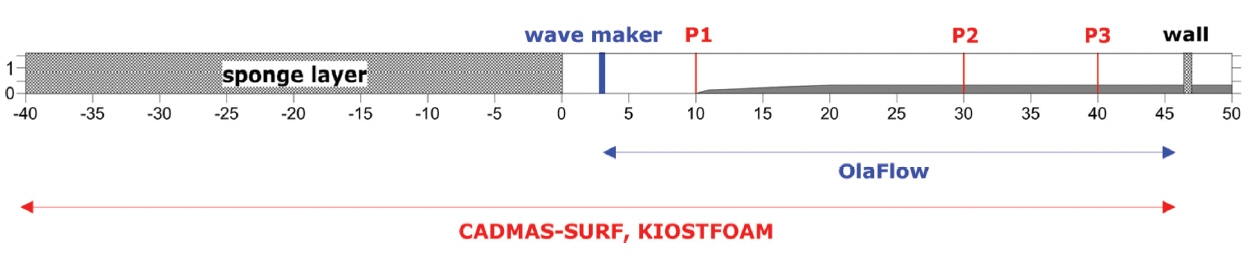
본 연구에서는 CADMAS-SURF(CDIT, 2001), olaFlow(https://olaFlow.github.io, 2018년 10월 22일 공개 버전), 그리고 2장에서 설명된 내부조파 오픈폼 모델(Oh and Kim, 2017) 세 가지를 수치모델링에 이용하였다. Oh and Kim(2007)에 의해 개발된 내부조파 오픈폼 모델은 KIOSTFOAM이라고 명명되었다. Table 2에는 이 세 가지 모델의 주요 특징을 비교하여 제시하였다.
세 가지 모델의 조파 및 파랑 전파 특성을 3장에서 설명된 완전반사 조건의 수리실험 데이터를 이용하여 검증하기 위한 2차원 수치모델링이 수행되었다. CADMAS-SURF와 KIOSTFOAM은 내부조파 기법을, olaFlow는 조파 및 감쇠가 가능한 외부조파 기법(pure active wave absorption)을 사용하였다. 내부조파기법을 이용하는 경우에는 Fig. 2에 보인 것처럼 조파판 뒤쪽으로 40 m 길이의 에너지 감쇠대를 설정하였다. 이에 따라서 해석영역의 길이가 olaFlow는 조파판으로부터 반사판까지 43 m인 반면, CADMAS-SURF와 KIOSTFOAM은 86.4 m로 차이가 났다. olaFlow와 KIOSTFOAM은 FVM 모델이므로 Fig. 3에 보인 것처럼 조파수조 바닥 경사면의 경계를 정확하게 재현하는 것이 가능하였다. 세 모델 모두 바닥 경계에서는 no-slip 조건을, 횡방향으로 양측면의 경계 조건은 slip 조건을 적용하였다. 또한, 세 모델 모두 스폰지 층을 포함한 전체 계산영역의 격자 크기는 수조 길이 방향으로dx = 0.05 m, 연직 방향으로 dz = 0.01m로 동일하게 설정하였다. 총 계산 격자의 수는 CADMAS-SURF 346,000 개, olaFlow 258,000 개, KIOSTFOAM 518,400 개였다. KIOSTFOAM의 격자 수가 더 많은 이유는 오픈폼 모델의 경우 공기에 해당하는 영역도 모델링하므로 연직 방향으로의 계산 영역을 더 크게 설정했기 때문이다.
수치모델링 시간은 실험과 동일하게 60초로 하였으며, 계산 시간 간격(dt)은 각 모델의 내부 계산환경에 따라 자동으로 변동되도록 설정하였다. 또한 난류모델을 비롯한 각 모델의 파라메터 설정은 모두 기본값(default)을 적용하였다. 수치모델링에는 Intel® Core(TM) i7-6800K, 12 core 사양 PC를 사용하였으며, 운영체제는 리눅스 우분투(Ubuntu) 14.04이었다. 이러한 환경에서 개별 실험 조건에 대한 계산 시간은 CADMASSURF가 약 2시간, olaFlow가 약 1.5시간, KIOSTFOAM이 약 3시간 소요되었다. 수치모델링의 결과 검증은 실험 계측이 이루어진 P1, P2 및 P3와 동일한 위치에서 수면변위 시계열을 각각 추출하여 계측된 시계열과 1:1로 비교하여 이루어졌다.
4.2 수치모델링 결과
4.2.1 Case A
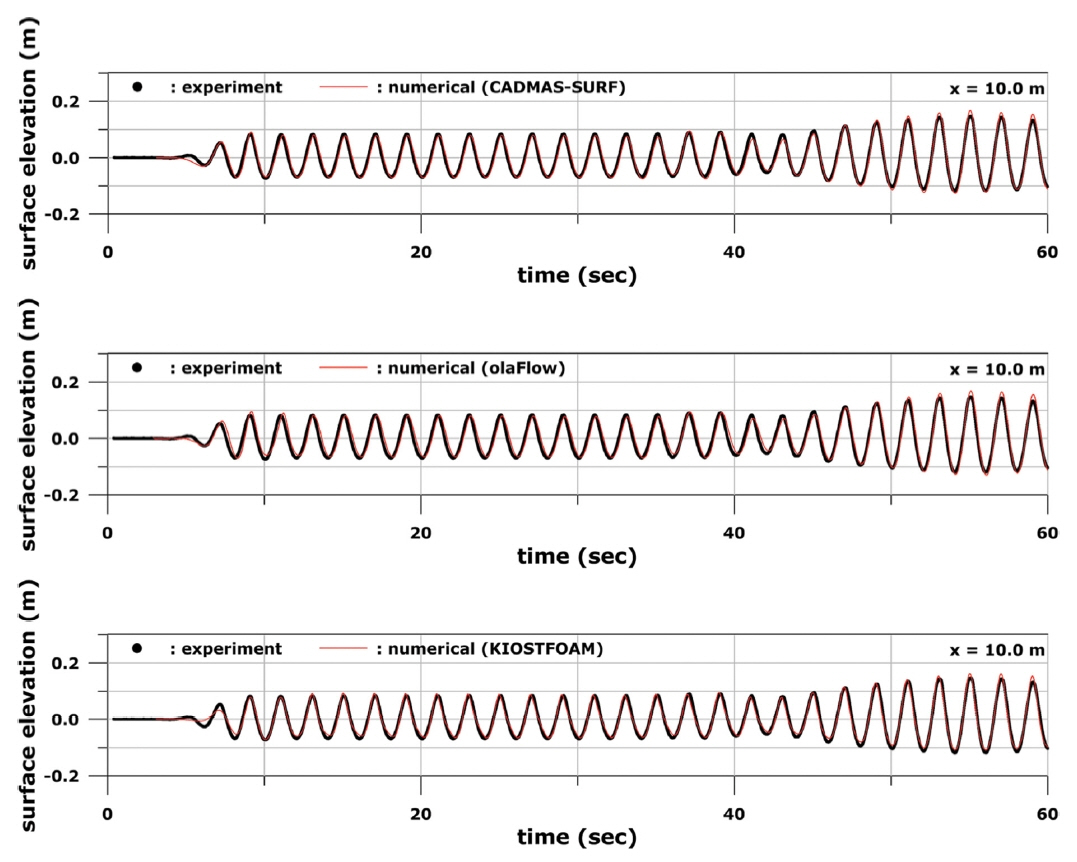
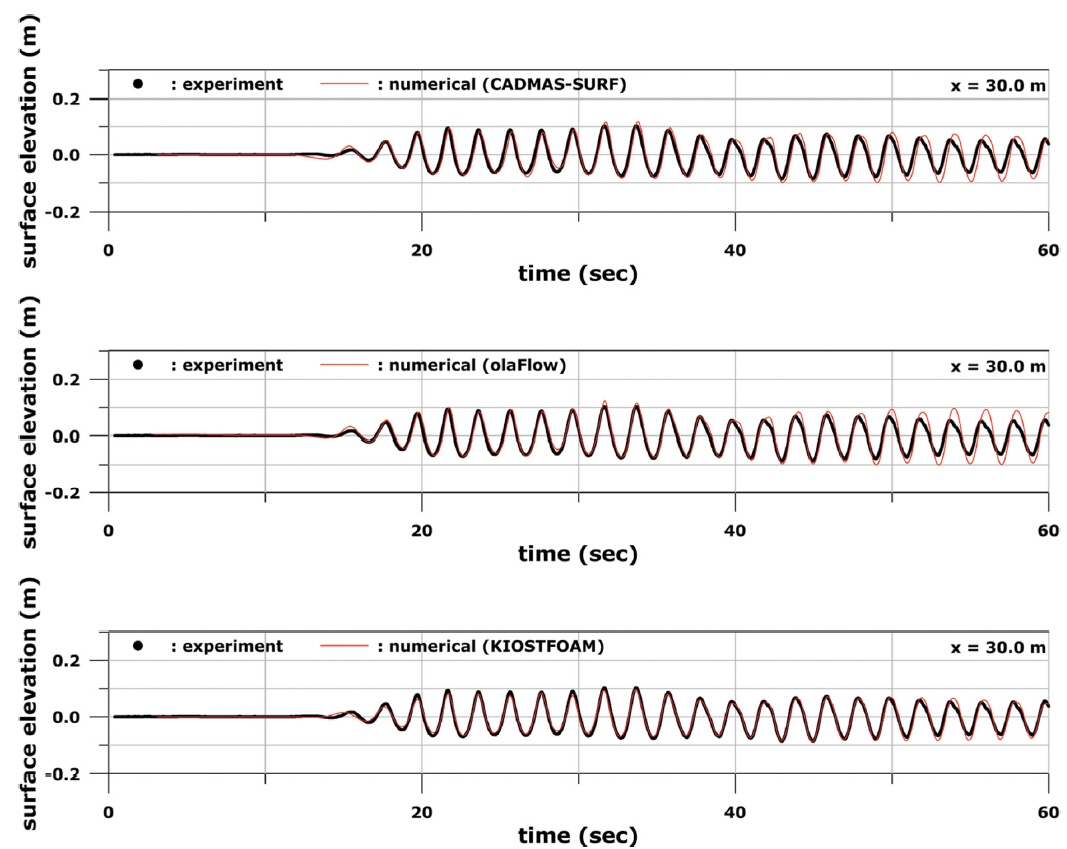
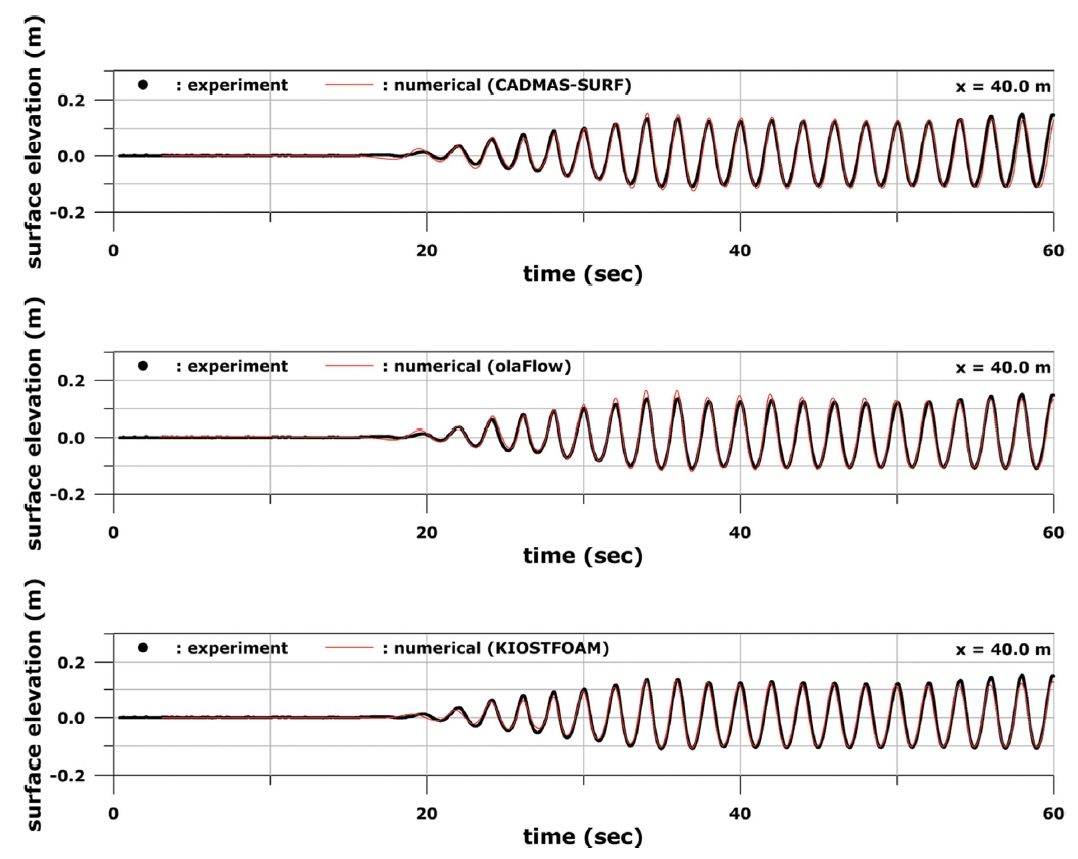
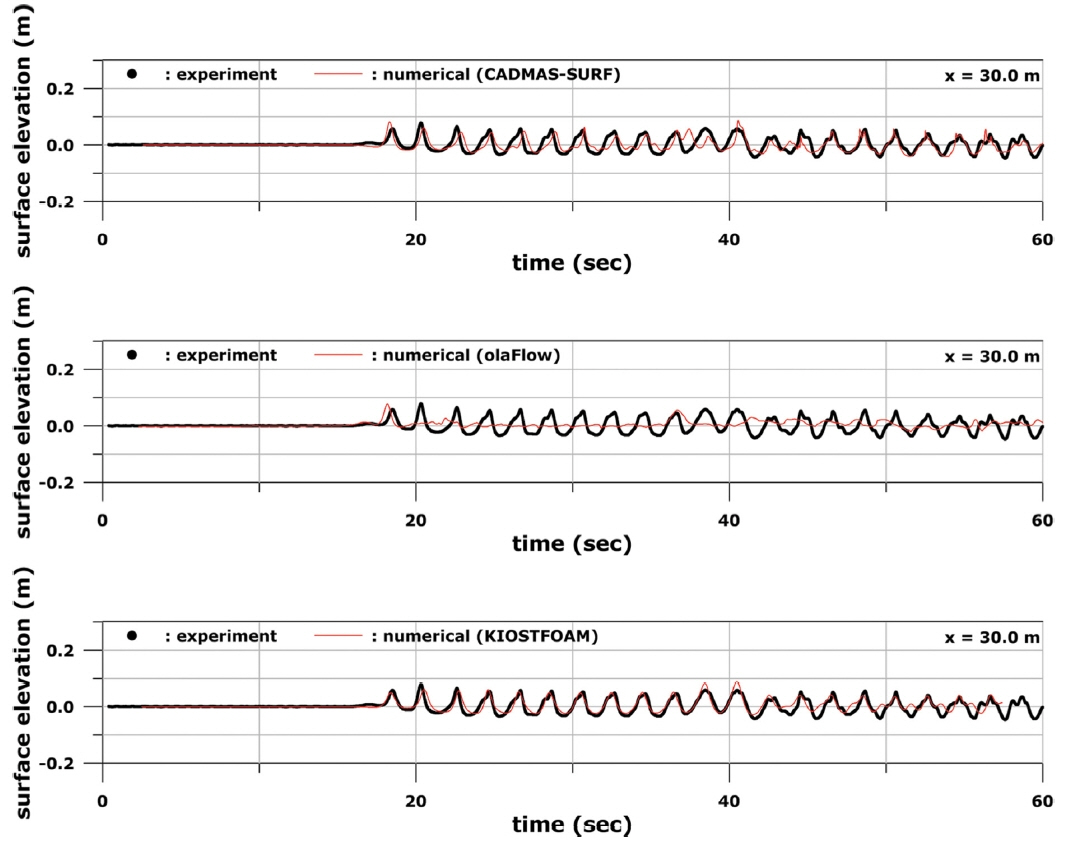
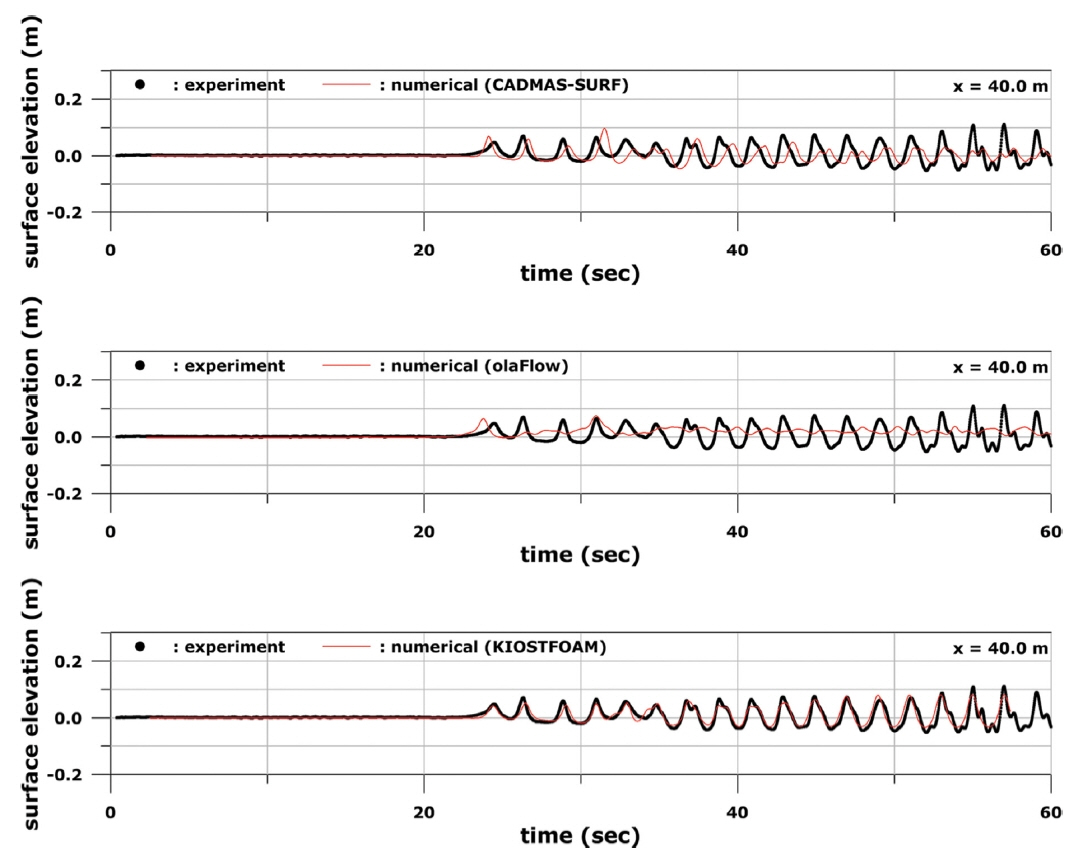
Fig. 4부터 Fig. 6까지는 Case A 조건에서의 수치모델링 및 수리실험 자료로부터 P1, P2, P3 위치에서의 수면변위 시계열을 각각 비교하여 나타내었다. Fig. 4에 보인 것처럼 P1에서는 세 모델에서 계산된 수면변위 시계열이 수리실험 결과와 잘 일치하였다. 다만 조파판에서 재반사된 파가 영향을 미치는 약 50초 이후에는 세 모델 모두 수리실험에 비해 파고가 근소하게 커지는 경향이 나타났다. 한편, P2에 대한 결과인 Fig. 5에서는 약 40초 이전까지의 수면변위 시계열은 세 모델의 계산 결과가 수리실험과 잘 일치하였다. 그러나 입사파와 반사파가 만나서 중복파가 형성되는 약 40초 이후에는 CADMAS-SURF와 olaFlow에 의해 계산된 파고가 실험값에 비해서 더 컸다. KIOSTFOAM은 세 모델 중 가장 수리실험 결과와 유사한 수면변위 시계열을 보였다. P3에 대한 결과인 Fig. 6에서는 CADMAS-SURF와 KIOSTFOAM은 대체로 수리실험과 유사한 결과인 반면, olaFlow는 30초 이후부터 50초 사이에 수리실험에 비해 파고가 더 크게 나타났다.
4.2.2 Case B
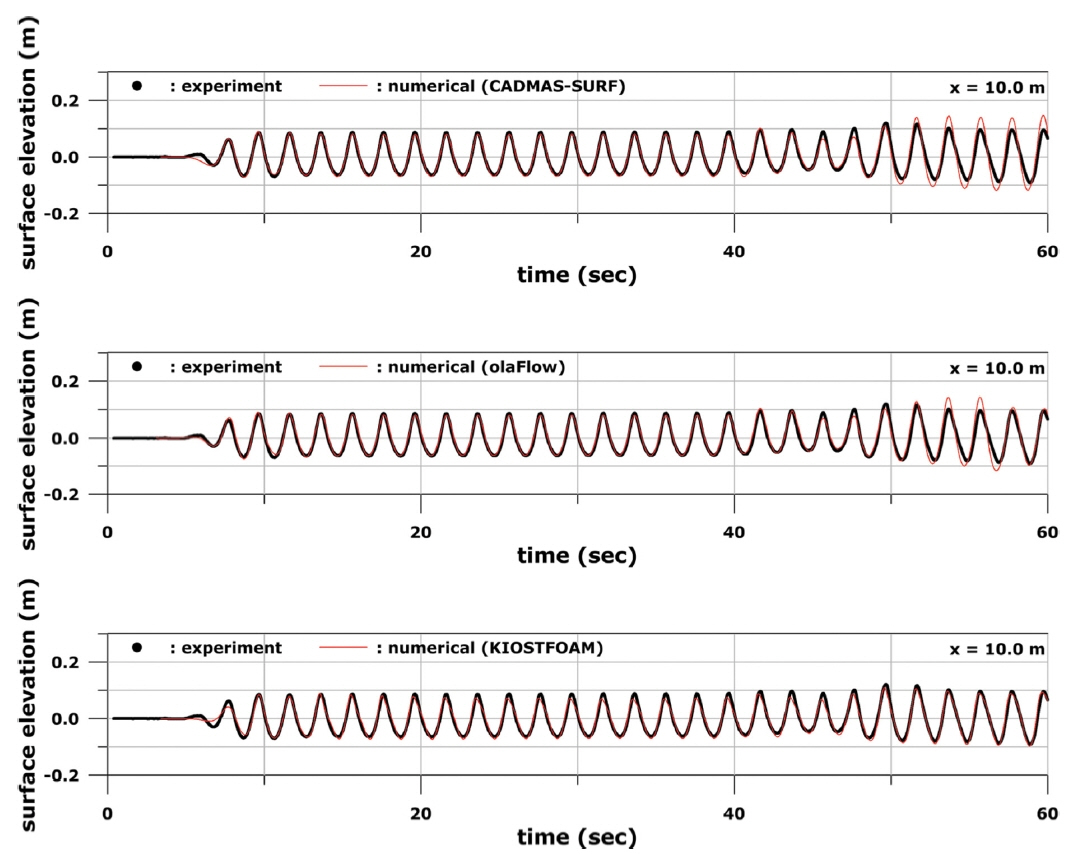
Case A에 비해 수심이 0.2 m 낮은 Case B 조건에 대한 수치모델링 및 수리실험 비교 결과는 Fig. 7에서 Fig. 9까지의 그림에 제시하였다. Fig. 7에 보인 P1위치의 결과에서는 Case A에 대한 결과와 유사한 경향이 나타났다. 즉, 세 모델이 대체로 수리실험 결과를 잘 재현하였으나 조파판에서 재반사된 파가 영향을 미치는 약 50초 이후부터 CADMAS-SURF와 olaFlow 모델에서 계산된 파고가 더 커지는 경향이 나타났다. 한편, Fig. 8에 보인 것처럼 P2에서는 입사파와 반사파가 만나서 중복파가 형성되기 시작하는 약 40초까지는 CADMAS-SURF와 KIOSTFOAM의 결과는 수리실험과 잘 일치한 반면, olaFlow의 경우 약 30초 이후부터 실험값에 비해 모델링 파고가 감소하면서 위상차가 발생하는 경향이 나타났다. 약 40초 이후부터는 중복파에 의한 쇄파가 발생하였는데 세 모델 중에서는 KIOSTFOAM이 수리실험과 가장 비슷한 결과를 보여주었다. 나머지 두 모델은 약 40초 이후부터는 실험값과 모델링 결과의 차이가 상당히 컸다. P3 위치의 결과인 Fig. 9에서는 CADMAS-SURF 모델의 경우 약 35초 이후부터 수리실험 결과와 차이를 나타내기 시작하였다. olaFlow는 파고 및 위상이 실험과 상당한 차이를 나타내었다. 반면에, KIOSTFOAM 모델은 계산된 파고 값이 실험값에 비해 다소 작기는 하지만 전반적으로 수리실험과 잘 일치하는 결과를 보였다.
4.2.3 Case C
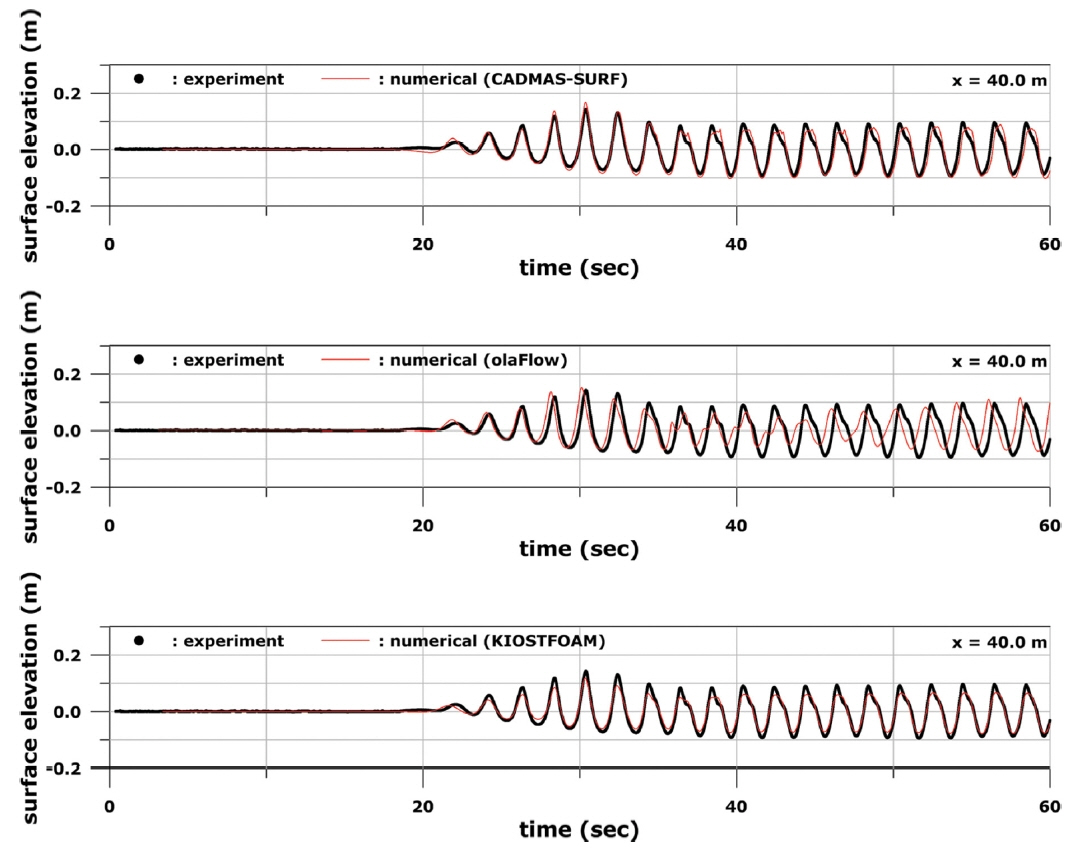
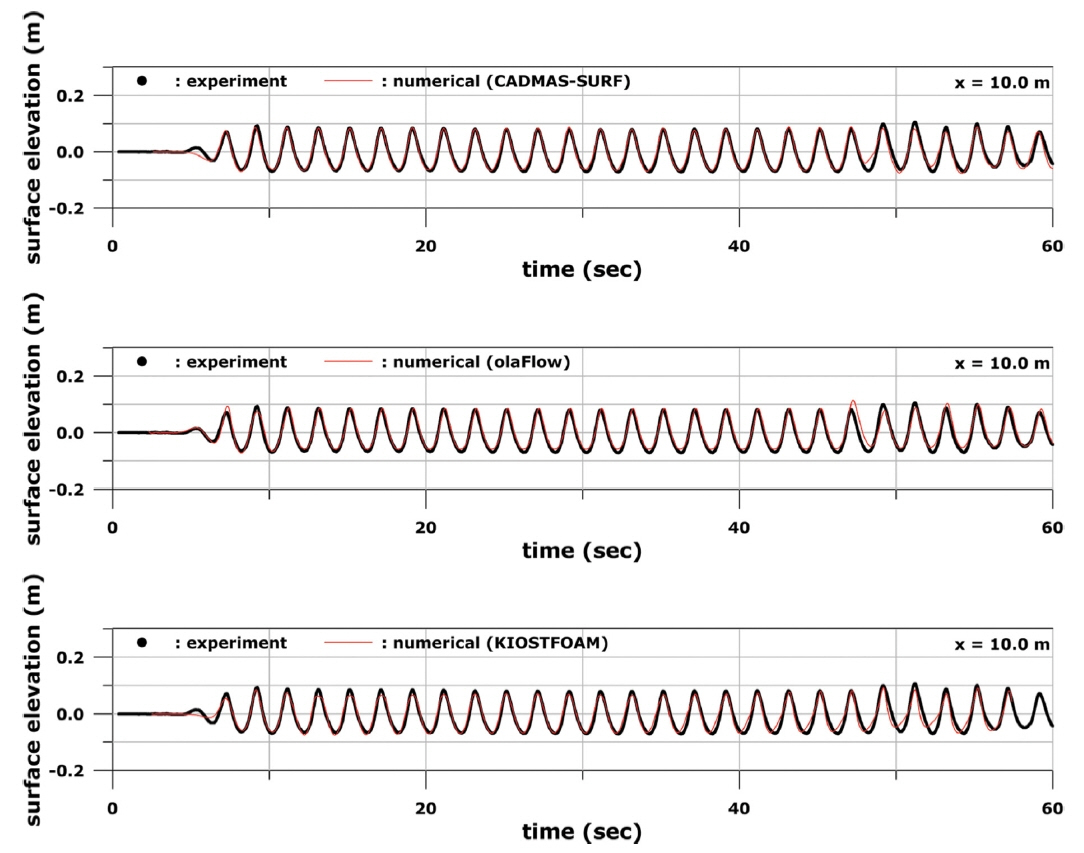
Case A에 비해 수심이 0.4 m 낮은 Case C 조건에 대한 수치모델링 및 수리실험 비교 결과는 Fig. 10에서 Fig. 12까지의 그림에 제시하였다. Fig. 10에 보인 것처럼 P1에서는 세 모델이 대체로 수리실험 결과를 잘 재현하였으나 조파 시간이 경과함에 따라서 서로 다른 특성이 나타났다. CADMASSURF의 경우 약 47초 이후부터 모델링 결과가 실험값과 다소 차이를 보이기 시작하였다. olaFlow는 약 20초 이후부터는 계산된 파고가 실험값에 비해 작게 나타나기 시작하였고, 약 47초 이후부터는 미세한 위상 차이도 발생하였다. KIOSTFOAM은 약 34초 이후부터 미세한 위상 차이가 나타났으며, 약 57초 정도에서 프로그램 실행이 중단되었다.
한편, P2에서의 결과인 Fig. 11에서는 강한 쇄파가 발생한 영향으로 실험자료의 파형이 sine파 형태가 아니라 앞쪽으로 기울어지는 톱니 형태의 파형임을 알 수 있다. 세 모델 중에서는 KIOSTFOAM이 실험자료의 재현성이 조파 후 약 40초까지는 가장 우수한 것으로 나타났다. 그러나 그 이후에는 실험자료와의 일치도가 저하되었다. CADMAS-SURF의 경우 실험자료의 파형을 어느 정도 따라가는 형태의 조파 결과를 보여주지만 KIOSTFOAM에 비해서는 조파 후 약 40초까지는 실험 결과와 일치도가 낮은 편이다. 그러나 오히려 그 이후 구간에서의 일치도는 더 향상되는 경향을 보였다. 한편, olaFlow는 파형이 나타나지 않고 파랑에너지가 거의 소산된 형태의 시계열을 나타내었다.
이러한 경향은 P3에서의 결과인 Fig. 12에서도 다시 한번 확인된다. 즉, CADMAS-SURF는 파형은 어느 정도 유지가 되지만 실험결과와는 상당한 차이를 보이는 결과를 보이며, olaFlow는 파형이 거의 뭉개진 형태의 시계열을 나타내었다. 반면에 KIOSTFOAM은 실험자료와 상당히 잘 일치하는 결과를 보였다. 다만 약 57초 정도에서 프로그램 상의 계산 불안정성으로 인해 실행이 중단되었다.
5. 요약 및 결론
5.1 요약
본 연구에서는 Wave2FOAM 모델에 내부조파 기법을 추가하여 개발된 CFD 모델인 KIOSTFOAM의 조파 및 소파 성능을 규칙파 수리실험 자료를 통해 검증하였다. 성능 비교를 위해 지금까지 국내에서 폭넓게 사용되어 왔던 수치파동수조인 CADMAS-SURF(e.g. Lee et al., 2008; Huynh et al., 2017)와 최근 국내에서 활용도가 증가하고 있는 오픈폼 모델인 olaFlow(e.g. Bae et al., 2018; Lee et al., 2018)에 대한 규칙파 수치모델링을 함께 수행하여 성능을 서로 비교하였다. 그 주요한 결과를 요약하면 다음과 같다.
• 쇄파가 발생하지 않는 조건인 case A의 경우 세 가지 모델이 모두 대체로 수리실험 결과를 잘 재현하였다. 그러나 입사파와 반사파가 중첩되어 형성되는 중복파의 파형을 CADMAS-SURF 및 olaFlow에 비해 KIOSTFOAM이 더 잘 재현하였다. CADMAS-SURF와 olaFlow에 의해 계산된 중복파의 파고는 실험값보다 근소하게 컸다.
• P2 위치에서 중복파의 쇄파가 발생하는 조건인 Case B에서도 KIOSTFOAM이 실험 결과에 가장 가까운 결과를 나타내었다. CADMAS-SURF는 중복파가 발생한 이후의 파의 위상은 실험 결과와 어느 정도 일치하였지만 쇄파가 발생하는 P2 위치에서 계산된 파고는 실험값보다 더 컸다. olaFlow의 경우 중복파가 나타나기 전인 약 30초 정도부터 실험값에 비해 모델링 파고가 감소하면서 위상차가 발생하는 경향이 나타났다. 이러한 현상이 나타나는 이유는 사면에서 반사되어 조파판으로 되돌아 간 파랑에너지가 olaFlow의 조파 경계에서 충분히 흡수되지 못하고 일부 에너지가 다시 되돌아 나오기 때문인 것으로 추정된다. 최근에 Conde(2019) 역시 olaFlow의 조파 경계에서의 반사파 흡수 성능이 문제가 있음을 보고한 바 있다.
• 사면에서 입사파의 쇄파가 강하게 발생하는 조건인 Case C에서도 세 모델 중 KIOSTFOAM이 실험 결과에 가장 가까운 결과를 나타내었다. 특히 쇄파가 발생한 이후에 파랑이 도달하게 되는 P2와 P3 위치에서의 파형을 상당히 잘 재현함을 확인할 수 있었다. CADMAS-SURF도 실험값과 어느 정도 유사한 패턴의 파형을 계산해 내었지만 계산된 파고값 및 파의 위상은 실험값과 꽤 차이를 보였다. olaFlow는 P1 위치에서의 파형은 잘 재현해 내었지만 P2 및 P3 위치에서의 계산 결과는 파랑 정보를 찾을 수 없을 정도로 파의 에너지가 완전히 소산되는 경향을 나타내어 실험 결과와 매우 큰 차이를 나타내었다.
5.2 결론
규칙파 수리실험 및 수치모델링을 통해 본 연구에서 사용된 세 가지 CFD 모델에 대해 다음과 같은 결론을 얻을 수 있었다.
• 세 가지 모델 중 KIOSTFOAM이 모든 실험파 조건에 대해서 실험결과를 가장 잘 재현하는 우수한 성능을 나타내었다. 다만 계산 격자의 수가 더 많이 필요하며 그로 인해 세 모델 중에서 계산 시간이 가장 오래 소요되는 단점이 있다. 또한 입사파의 쇄파가 발생한 Case C에서는 계산 도중에 프로그램 실행이 중단되었는데 수치계산의 불안정성을 해소하기 위한 개선이 필요할 것으로 보인다.
• CADMAS-SURF는 KIOSTFOAM에 비해 계산 격자의 수가 작고 계산 시간도 30% 정도 단축되는 이점이 있다. 그러나 중복파의 파고 및 쇄파 발생 이후의 파고 재현에 있어 KIOSTFOAM에 비해서는 계산 정확도가 낮은 것으로 나타났다.
• olaFlow의 경우 계산 시간 측면에서는 가장 유리하지만 조파 경계에서 반사파가 제대로 처리되지 않는 문제가 있는 것으로 나타났다. 따라서, 반사파 흡수를 위해 사용된 수치해석적 방법(Higuera et al., 2013)의 개선이 필요할 것으로 판단된다. 또한 쇄파 발생 시 파랑에너지가 과도하게 소산되는 문제가 있는 것으로 나타났다.