요약수압식 파고계(WTG)로 관측한 파고가 저파랑 환경에서 저평가되는 문제가 제기되어 왔으며 이 자료를 보정하여 관측오차를 줄이는 것은 WTG 실측자료를 사용해 항만정온도 기준을 개선하는데 매우 중요하다고 할 수 있다. 본 연구에서는 네 지점에서 관측한 AWAC 및 부이식 파고계(Waverider buoy) 자료를 사용하여 동일 지점에서 관측한 WTG 유의파고를 보정하였다. 먼저 저파랑 조건 하에서 WTG 유의파고(Hm0) 값이 저평가되는 경우에도 유의파고와 첨두주기의 곱인 WTG HT는 저평가되지 않고 AWAC 및 부이식 파고계의 HT와 선형관계를 유지함을 발견하였으며, 이 선형성을 적용하여 WTG HT와 Hm0 간의 분포를 대표하는 3차 함수를 각 지점 별로 산정하였다. 이 함수를 사용하여 저파랑 임계파고로 설정한 0.7m 이하의 WTG Hm0를 보정하였으며, 그 결과 보정된 WTG Hm0와 AWAC 및 Waverider buoy Hm0의 선형관계가 향상되었고 저평가되었던 파고도 상당부분 개선되었음을 확인하였다. 본 연구 결과를 적용하면 HT의 선형성이 유지되는 타 지역의 WTG 관측 파고를 보정하는 일과, 나아가 보다 정확한 실측자료를 제공해 해당 항만의 개선된 정온도 기준을 마련하는 일에 기여할 수 있을 것으로 예상된다.
AbstractIt has been reported that the wave heights measured by Wave and Tide gauges (WTG) have been underestimated, and thus it is important to improve its measuring accuracy for enhancing estimation of harbor tranquility. In this study, the significant wave heights from WTG were calibrated using measured data from AWAC and Waverider buoys moored at the same four locations with the WTG. It was observed that the product of significant wave height and peak wave period, HT, was not underestimated but linearly proportional between the measurements by two instruments. This linearity was applied to develop 3rd order polynomial functions that best represented the relationship between HT and significant wave heights measured by WTG. These functions were then applied to calibrate the WTG significant wave heights that were lower than 0.7 m, the critical value established for the low waves in this study. The results showed that the linearity between the AWAC (or Waverider buoy) and calibrated wave heights were improved, and the magnitude of underestimated WTG wave heights were increased to be more realistic. The results of this study are expected to be effectively applied for other data sets obtained by WTG only, to increase the observation accuracy of WTG and to improve the estimation of harbor tranquility.
1. 서 론20세기 중반에 도입된 수압식 파고계(WTG: Wave and Tide Gauge)는 현재까지도 천해의 파랑자료를 측정하는데 널리 쓰이는 관측 장비 중 하나이다. 그러나 해저면에서 측정한 해수압을 선형파 이론(Linear wave theory)을 적용하여 파고로 전환하는 WTG 자료의 정확성은 오랜 기간 논란의 대상이 되어왔다. 대표적인 예로 미육군공병단에서 발간한 보고서(US Army Corps of Engineers, 1984)는 WTG로 관측한 파고가 파랑 주기가 감소함에 따라 함께 감소하는 결과를 제시하여, 특히 단주기 파랑 조건 하에서 WTG로 측정한 파고가 과소평가될 수 있음을 경고하였다.
WTG 자료의 부정확성에 대한 연구는 그 외에도 다수가 있으며 간략하게 소개하면 다음과 같다. 먼저 선형파 이론에서 알 수 있듯이 센서와 수면간의 거리(z)와 수심(d)의 비가 낮을 경우 해수압을 파고로 전환할 때 오차를 유발할 수 있으며(Hom-ma et al., 1966; Simpson, 1969; Esteva and Harris, 1970; Grace, 1978; Cavaleri et al., 1978), 해수입자 궤도운동의 운동에너지에 의해 발생하는 2차 압력항이 선형파 이론에서 적절하게 반영되지 못할 경우 관측수압과 차이가 발생할 수도 있다(Kinsman, 1965; Cavaleri, 1980; Forristall, 1982). Biesel(1982), Lee and Wang(1984)은 비선형파 효과가 불규칙파의 관측값에 오차를 유발할 수 있음을 보였으며, Lee and Wang(1984)은 특히 파랑 외에 흐름이 존재할 경우 단파의 수압이 과소평가되어 결과적으로 계산된 파고를 과소평가할 수 있다는 연구 결과를 발표했다. Forristall(1982)는 불규칙파의 경우 파랑을 주기별로 구분해 내는 것이 쉽지 않기에 스펙트럼 분석을 통해 파고 예측의 정확성을 높일 수 있음을 나타냈다. 그 외 WTG 관측값의 오차 가능성으로 단주기파의 경우 전기신호 오차로 인한 백색 소음(White noise) 및 항만 등에서 발생할 수 있는 파랑 반사(Wave reflection)에 의한 오차가 있다(Lee and Wang, 1984; Miche, 1944).
WTG 이후로 초음파식 파고계인 AWAC(Acoustic WAve and Current profiler)이나 부이식 파고계인 Waverider buoy 등이 개발됨에 따라 정확도가 향상된 파랑 관측이 가능해졌으며 WTG로는 측정이 불가능한 파향도 관측이 가능해졌다(Pedersen et al., 2007). 그럼에도 불구하고 WTG는 현재까지 여러 현장의 파랑 관측에 유용하게 사용되고 있으며 특히 선박을 정박 또는 계류하는 항만에서 많이 사용된다. 항내에서 관측을 통한 실측 파고자료를 제공하는 것은 항만가동율 산정의 정확도를 높이는 데 중요하다(Jeong and Ryu, 2014). 그러나 AWAC 및 Waverider buoy 등은 선박 운항에 방해가 될 가능성이 있어 항내에서 사용이 제한되며 상대적으로 부피가 작은 WTG가 많이 사용된다. 따라서 WTG를 사용하여 측정한 파고가 부정확할 경우 이것을 토대로 산정된 항만가동율의 정확도 역시 저감되어 항만의 효율적 가동에 지장을 초래할 수 있다. 따라서 본 연구에서는 향후 보다 정확한 항만 내 파랑자료를 제공하기 위한 방편으로 WTG 관측 파고를 보정할 수 있는 한 방안을 제시한다. 이를 위해 동해안의 네 지점에서 WTG와 동시에 관측한 AWAC 및 Waverider buoy 자료를 사용하여 보정 기준으로 삼았다.
2. 수압식 파고계 관측 시의 오차 발생 원인여기서는 선형파 이론을 통해 파랑에 의한 압력을 해수면 변화로 전환하는 과정을 소개하고, 이를 토대로 수압식 파고계의 관측 오차 가능성을 살펴본다. 해수면 아래에서 측정되는 압력은 공기압(Air pressure)을 무시하였을 경우 정수압(Hydrostatic pressure)과 동적 압력(Dynamic pressure)의 합으로 구해지며, 다음 식으로 표시될 수 있다.
여기서, P는 센서와 수면 간의 거리 z에서의 압력, ρ는 해수밀도, g는 중력 가속도, k는 파수(Wave number), d는 수심, H는 파고, 그리고 x와 t는 각각 수평 좌표와 시간이다. 선형파 이론에서 해수면의 시공간 변화(η)는 η = H/2*cos[k(x-t)]로 주어지며 따라서 식(1)은 다시
로 표시되며 여기서 압력전달함수(Pressure response factor)인
를 적용하면 다시
와 같이 간략하게 정리되며 여기서 시간에 따라 변하는 해수면 높이 η는
와 같이 파고계에서 측정한 수압의 함수로 나타낼 수 있다. 그러나 US Army Corps of Engineers(1984)는 선형파 이론을 적용해서 구한 식(5)가 항상 정확하지 않으며 이에 따라 실험을 토대로 한 보정계수(Correction factor) N을 도입하여
을 제시하였다. 또한 N은 파랑 주기에 따라 변할 수 있으며 장주기파의 경우 N > 1이 되며 반면에 주기가 감소하면 N < 1이 되는 경향을 보인다고 보고하였으나 이에 대한 자세한 원인은 제시하지 않았다. 그러나 이 결과는 본 연구에서 제기된 문제인 저파랑 조건 하에서 WTG 관측 파고가 저평가되는 것과 비슷한 발견으로, 본 연구 역시 특별히 저파랑 조건하에서 적합한 보정계수를 산출하는 데 그 목적이 있다.
식(6)을 통해서 계산된 WTG 파고는 N 외에 식(3)의 Kz 값에 민감하게 반응한다. 본 연구와 같이 해저면에 센서를 계류한 경우(z ≈ d) Kz는 수심이 증가할수록 0에 근접하며 따라서 식(5)를 사용하여 계산한 파고값의 오차도 증가할 수 있다. 이런 이유로 30 m 이상의 깊은 수심에서는 WTG 파고계의 사용을 가능한 한 억제하며 대신 AWAC 또는 Waverider buoy 파고계를 주로 사용하는 경향이 있다. 본 연구에서 WTG 자료 보정에 사용한 네 곳의 관측 지점 수심은 14.5~24.5 m로 Kz에 의한 오차 범위가 허용 한계를 초과하지 않을 것으로 판단된다. 이에 대한 또 다른 근거는 식(6)에서 나타난 바와 같이 Kz에 의한 오차가 발생한다면, 이는 동일지역에서 관측되는 자료에 대해 파고 및 주기에 무관하게 모든 파랑 영역에서 동일하게 작용할 것이다. 따라서 본 연구에서와 같이 서로 다른 수심의 관측 장비에서 단주기 파랑 조건 하에서만 저평가되는 WTG 관측 오차는 Kz에 기인한 것은 아닌 것으로 판단할 수 있다.
또한 서론에서 제기된 수압식 파고계의 관측오차 원인들 중에서 센서와 수면 간의 거리(z)과 수심(d)의 비가 낮을 경우에 발생할 수 있는 오차가 발생할 가능성은 작다. 본 연구를 포함해 통상적으로 WTG는 철제 설치대에 장착되어 해저면에 설치되며 해저면에서 센서까지의 거리는 0.45~0.60 m의 범위인 경우가 많다. 따라서 본 연구의 관측 지점 수심(14.5~24.5 m)을 고려할 때 z/d 값이 1에 가까워서 이 원인에 의한 오차는 발생하지 않은 것으로 판단할 수 있다.
반면 Lee and Wang(1984) 및 Lee and Oh(2009)에서 주장한 흐름의 효과는 특히 흐름의 영향이 상대적으로 큰 저파랑 조건 하에서 증가할 것이며 따라서 본 연구의 관측 결과에도 영향을 미칠 수 있을 것으로 판단된다. Lee and Wang (1984)의 연구에 의하면 흐름이 수압계의 측정값에 오차를 유발하는 방법은 2가지로 첫째, 파와 흐름의 상호작용에 따라 파수가 변화되고 이는 식(3)에 의해 Kz를 변화시키며 따라서 식(6)의 η가 다르게 측정될 수 있다. 또한 흐름이 존재할 경우 동적 압력에 변화를 가져와 압력계를 통해 측정한 파고에 변화가 발생할 수 있다. 다만 이 두 가지 요인에 의한 변화는 서로 상쇄작용을 발생할 수 있으며 정확한 영향은 보다 면밀한 연구가 필요한 것으로 제기되었다. 그 외 2차 압력항 및 비선형파 효과에 의한 오차는 본 연구의 자료를 통해 구분하기 어려우나 위에서 제기한 보정계수는 실험에 기반한 경험값(Empirical value)으로서 따라서 본 연구에서 시도하고 있는 관측 자료에 기반한 파고 측정값 보정은 이상의 효과들을 포함하는 것으로 판단할 수 있다.
3. 파랑 관측 자료3.1 관측 지점 및 장비본 연구에서 사용한 관측 자료는 후포(A1), 영일만(A2), 포항신항(B1) 및 부산항 신항(B2) 인근의 총 4개 지점에서 측정하였다(Fig. 1). 이 중 A1과 A2에는 WTG와 함께 Nortek 사의 AWAC을 설치하여 수압식 파고계의 자료를 보정하였으며, B1 및 B2 지점에는 WTG와 함께 Datawell사의 Waverider buoy를 설치하여 자료를 보정하였다.
각 장비가 설치된 기간, 관측 위치, 설치수심 등에 대한 정보는 Table 1에 기술하였다. AWAC은 음파를 사용해 해수압과 해수입자 운동 속도, 그리고 해수표면 위치를 측정하여 파고, 주기 및 파향을 높은 정확도로 계산하며, Waverider buoy는 해면에 부유하면서 그 해면의 움직임에 따른 부이의 움직임을 가속도 센서에 의해 계측하는 것으로 파고, 주기 및 파향을 계산한다. 반면 WTG는 해저면에 고정된 압력계의 시계열 자료를 토대로 파고 및 주기를 계산하며 따라서 파향은 측정하지 못한다. 또한 수심이 깊을 경우 측정되는 수압의 정확도가 낮아질 가능성이 있으므로 일반적으로 수심 30 m 이내의 천해에서만 사용하도록 권장되며, 위에서 설명한 대로 단주기 파랑 조건 하에서는 파고를 저평가하는 경향이 있다(US Army Corps of Engineers, 1984).
4개 지점 모두에서 사용한 수압식 파고계 WTG는 매 30분마다 0.5초 간격으로 약 17분간 획득한 2,048개의 시계열 자료를 토대로 스펙트럼 분석법을 통해 유의파고(Hm0)와 첨두주기(Tp)를 계산하였다. A1 및 A2에서 측정한 AWAC과 B1, B2에서 측정한 Waverider buoy 역시 WTG와 동일한 조건으로 시계열 자료를 생성하였으며 이를 토대로 유의파고와 첨두주기 및 평균파향(Dirmn)을 계산하였으며 각 장비별 자료측정에 관한 정보는 Table 2에 나열하였다.
3.2 관측 자료의 유의파고 및 첨두주기 분포
Fig. 2는 네 개의 지점에서 관측한 유의파고 분포를 AWAC (A1과 A2) 및 Waverider buoy와 WTG 자료 간에 비교한 결과를 보여준다. 그래프 상의 각 점은 한 지점에서 두 장비에 의해 동시에 관측된 파고를 나타낸 것으로, 두 장비 간에 측정 오차가 없을 경우 파란 색으로 표시된 y = x 선을 따라 정렬로 분포되어야 한다. 그러나 그림에 나타난 바와 같이 실제 관측된 자료는 두 장비 간에 차이가 발생하게 된다. 특히 네 지점 모두에서 나타난 바와 같이 유의파고 1 m 이하인 저파랑 조건 하에서 WTG 관측값이 AWAC이나 Waverider buoy 관측값에 비해 저평가된 것을 알 수 있다. 예를 들어 A1에서의 비교자료를 보면 AWAC에서 관측한 유의파고가 1.0 m에 근접한 경우라도 동시에 WTG에서 관측된 유의파고는 0.5 m를 넘지 못하는 경우가 대부분이다. 저파랑 조건 시 WTG에 의한 유의파고 저평가는 네 지점 모두에서 동일하게 나타나는 현상이므로, 다른 지역에 설치한 WTG의 자료에서도 이러한 현상이 동일하게 나타날 수 있을 것으로 유추할 수 있다. 따라서 서론에서 언급한 바와 같이 항만 내에서 측정한 WTG 관측값이 실제 유의파고보다 작을 경우가 발생할 가능성이 높으며, 이로 인해 항만정온도 예측 정확성이 낮아질 수 있기 때문에 이런 오차를 보정할 필요가 있다. 단, 그림에서 나타난 바와 같이 이런 오차는 유의파고가 낮을 경우에 주로 발생하며 파고가 증가함에 따라 점점 작아진다. 따라서 본 연구에서는 파고의 오차보정을 0.7 m 이하의 저파랑(Hm0, Cr = 0.7m)에만 국한하였다. 항만 및 어항 설계기준·해설(Ministry of Oceans and Fisheries, 2017)에는 정박지의 초대형선(대형 돌핀 및 Sea berth를 이용하는 50,000톤급 이상의 선박)의 하역한계파고로 0.7~1.5 m를 제시하고 있어 본 연구에서는 저파랑 임계파고를 0.7 m로 적용하였고 이는 항만정온도 개선이라는 연구목적에도 부합한다.
Fig. 3은 Fig. 2와 동일한 조건 하에서 두 장비 간의 첨두주기를 비교한 결과를 보여준다. 첨두주기는 스펙트럼의 에너지가 정점(peak)에 도달하는 주파수에 따라 결정되므로 그림에 나타난 바와 같이 불연속적인 분포를 보인다. 또한 유의파고에 비해 분포 범위가 넓기 때문에 두 장비 간 차이도 더 크게 나타나게 된다. 또한, 주기가 짧은 경우 유의파고와는 반대로 WTG의 관측값이 AWAC이나 Waverider buoy의 관측값보다 고평가된 것으로 나타난다. 예를 들어 AWAC이나 Waverider buoy의 관측 주기가 5초인 경우 WTG의 관측값은 네 지점 모두 5초 이상으로 고평가된 것을 알 수 있다. 따라서 Fig. 2와 Fig. 3에서 발견된 결과를 종합해 보면 파고와 주기가 모두 작은 저파랑 조건 하에서 WTG 관측값은 AWAC이나 Waverider buoy 자료에 비해 유의파고는 저평가되는 반면 첨두주기는 고평가되는 것으로 판단할 수 있다.
4. 수압식 파고계의 오차 보정 방법4.1 가설 및 검증본 연구에서는 저파랑-단주기 조건 하에서 WTG로 측정된 유의파고가 과소평가되고, 반면에 첨두주기는 과대평가된다는 관측 결과를 토대로 다음과 같은 가설을 수립하였다.
① 네 개의 서로 다른 지점에서 동일하게 관측된 결과이므로 WTG의 기기 결함에 의한 계측 오차는 아니다.
② 해저면에 설치된 장비로 측정한 수압을 통해 계산된 유의파고가 특히 저파랑 조건 하에서 저평가되었다는 것은, WTG로 측정하는 수압에 영향을 미치는 요인 중 파랑의 영향이 작아짐에 따라 흐름과 같은 외적 요인의 영향이 상대적으로 커졌으며 따라서 이에 의한 파고 측정 오차가 발생하였을 가능성이 있다.
③ 그러나 동시에 주기가 고평가되었다는 것은 파고와 주기에 각각 발생하는 관측 오차가 서로 상쇄될 수도 있으며 따라서 이를 적용하면 저평가된 파고 관측값을 보정할 수 있을 것이다.
위 가정에 따라 WTG에서 측정한 유의파고와 첨두주기를 결합한 모수(Parameter)인 HT = Hm0 × Tp의 분포 특성을 고찰하였다. Fig. 4는 Figs. 2 및 3과 동일한 방식으로 HT의 분포를 두 장비 간에 비교한 결과를 보여준다. 그림에 나타난 바와 같이 WTG에서 측정된 HT는 유의파고나 첨두주기에 비해 AWAC이나 Waverider buoy의 관측값들과 보다 선형적 관계를 형성하며 그 분포가 y = x 직선에 근접함을 알 수 있다.
Table 3에는 이런 선형성을 수치로 나타내기 위해 사용한 2개의 상관계수 값을 비교하여 제시하였다. 먼저 Dx=y는 두 장비를 통해 측정된 관측값들과 y = x 직선과의 거리의 평균을 무차원화한 것으로
로 표시되며 여기서 disty=x는 각 관측값과 y = x 직선까지의 거리이고 dist0은 관측값과 원점까지의 거리이다. 따라서 Dx=y는 Figs. 2~4에 나타난 각각의 좌표계에서 두 장비에서 관측한 관측값(Hm0, Tp 또는 HT)들로부터 선형 직선인 y = x까지의 평균거리를 나타내며, 이는 곧 관측값과 선형 직선이 얼마나 떨어져 있는지를 알려주는 지표로 볼 수 있다. 따라서 Dx=y이 작을수록 관측값이 y = x 함수에 가깝게 분포한 것이며 선형성이 높은 것으로 판단할 수 있다. Table 3에 표시된 Dx=y 값은 A2를 제외한 모든 지점에서 HT의 값이 Hm0나 Tp에 비해 가장 낮은 것을 알 수 있다.
한편, 또 다른 상관계수인 Rx=y은
로 정의되며, 여기서 xi는 AWAC(또는 Waverider buoy)의 관측값이고 yi는 WTG의 관측값이다. 따라서 Rx=y은 두 장비에서 측정한 관측값 비의 평균값으로 Rx=y이 1에 가까울수록 y = x 직선에 가까우며 선형성이 높아진다고 볼 수 있다. Table 3에 나타난 결과는 Rx=y 값이 HT의 경우 모든 지점에서 오차범위가 10% 이내(1 - Rx=y = -0.06~0.07)로 1에 가장 가깝게 나타났으며, Hm0의 경우에는 오차 범위가 25% 까지 확대되었다(Rx=y = 0.11~0.26). 따라서 Rx=y의 경우 HT의 선형성이 개선된 것이 Dx=y보다 더욱 분명하게 나타난다.
4.2 파고 보정위에서 설정한 가설이 검증됨에 따라 본 절에서는 WTG에서 측정한 HT 관측값을 사용하여 Hm0 관측값을 보정하는 방법 및 결과를 제시한다. 이를 위해 다음과 같이 HT와 Hm0의 관계식을 추정하였다. 먼저 3.2절에서 설명한 것처럼 보정하고자 하는 저파랑의 임계파고(Hm0, Cr = 0.7m)를 적용하여 WTG에서 관측한 파고 중 임계값보다 높은 파랑 이벤트를 선별하였다(Hm0 > Hm0, Cr). 그리고 선별된 Hm0에 해당하는 WTG의 HT 값을 구하고 이 둘의 분포를 계산하였다. Fig. 5는 이렇게 선별된 Hm0와 HT 간의 분포를 HT를 x 축으로 하여 도시하였다. 위에서 나타난 바와 같이 AWAC(또는 Waverider buoy)과 WTG에서 측정한 HT가 높은 상관관계를 가지며 y = x 선형 직선에 부합함에 따라 WTG의 HT를 보정의 기준으로 설정할 수 있으므로 HT를 x 축으로 하여 Hm0와의 분포를 구한 후 이 분포를 대표할 수 있는 회귀곡선(Regression polynomial)을 계산하면 이 함수를 사용하여 저파랑 시의 파고를 보정하는 것이 가능하다.
즉, Hm0 > Hm0, Cr를 충족하는 WTG의 HT를 사용하여 Hm0와의 함수((Hm0)wtg = f[(HT)wtg])를 구할 경우 이를 통해 WTG의 Hm0 값을 추정할 수 있다. Fig. 5에 표시한 파란색 곡선은 각 지점의 WTG 관측값을 토대로 구한 함수를 나타낸다. 이 함수들은 3차 다항식을 적용하였으며 특별히 y 축절편을 0으로 설정하여 HT가 0일 경우에도 보정된 Hm0 값이 0보다 커지는 것을 방지하였다. 즉, 식 (9)와 같이 표시할 수 있으며 여기서 Hcal은 보정된 WTG Hm0을 나타낸다. 식(9)의 다항식 계수는 각 지점마다 다르게 계산되었으며 그 값은 Table 4에 나열하였다.
Fig. 5에서 각 지역마다 회기곡선이 다르게 나타나는데 이것은 지역별로 관측된 HT 자료의 수가 다르고 이에 따른 분포범위가 다르기 때문이다. 또한 각 지역의 관측 수심 및 파랑 환경이 다른 것도 각 지역별 회기 곡선 특성을 결정하는 중요한 요인이 될 수 있다.
식(9)를 적용하면 WTG로 측정한 HTwtg를 사용하여 Hcal를 계산할 수 있다. Fig. 6(b)는 A1 지점에서 계산한 Hcal과 AWAC을 통해 측정한 Hm0와의 분포를 보여준다. 이를 Fig. 6(a)에 나타낸 AWAC Hm0와 WTG로 측정한 Hm0의 분포와 비교하면 기존의 측정값과 비교해 보정된 WTG Hm0가 치우침이 없이 훨씬 폭넓게 분포됨을 알 수 있다. Fig. 6(a)에서는 AWAC Hm0가 1 m일 경우 기존의 관측값인 WTG Hm0는 1 m 이하에 분포하였는데 비해, Fig. 6(b)에 보인 것처럼 보정된 Hcal은 0.5~1.5 m로 그 범위가 확대되었을 뿐만 아니라 y = x 직선을 중심으로 분포의 치우침이 줄어든 것을 확인할 수 있다. 이는 보정의 효과를 확인하는 것으로 WTG Hm0 관측값이 저평가되는 것을 교정하려는 본 연구의 목표가 달성된 것으로 판단할 수 있다.
Fig. 7은 Fig. 6에 표시된 두 분포를 하나로 결합하여 4개의 지점에 대해 표시한 것으로 특별히 보정된 Hcal의 경우 임계파고(Hm0, Cr)인 0.7m보다 작은 파랑만을 선별하여 파란색으로 표시하였다. 그림에 나타난 바와 같이 보정된 파고의 경우 기존의 괸측값에 비해 폭넓게 분포하며 특히 y = x 직선을 중심으로 보다 균일하게 분포됨으로서 기존의 WTG 관측값들이 AWAC(또는 Waverider buoy) 관측값에 비해 저평가되던 것을 상당 부분 교정하는 결과를 보여 준다. 따라서 WTG 관측값만 존재하는 경우라도 저파랑 임계파고(Hm0, Cr) 이상인 파고를 선별하여 Fig. 5와 같이 HTwtg와 (Hm0)wtg의 분포를 구하고, 다시 식(9)를 적용하여 다항식 계수를 결정하면 Hcal을 계산할 수 있다. 그리고 이런 보정을 통해 저파랑 조건에서 과소평가되는 파고를 교정할 수 있을 것으로 판단된다.
Fig. 8은 B2 지점에서 WTG로 관측한 (Hm0)buoy 및 (Hm0)wtg와 보정된 Hcal의 시계열 자료를 2013년 4월 5일부터 2013년 5월 17일까지 약 40일간 비교한 것을 보여준다. 그림에 나타난 바와 같이 유의파고 1 m 이하의 저파랑 환경에서 (Hm0)wtg 관측값이 (Hm0)buoy 관측값에 비해서 유의미하게 작은 경우에 Hcal은 (Hm0)wtg보다 높게 보정되어 (Hm0)buoy에 근접하며, 따라서 저파랑 환경에서 저평가되는 (Hm0)wtg 관측값을 보정한다는 본 연구의 목표에 부합하는 결과를 보여준다.
5. 결 론본 연구에서는 수압식 파고계(WTG)로 관측한 파고자료를 보정하여 그 정확성을 향상시키는 방법을 제시하였다. WTG의 관측파고는 저파랑 조건 하에서 AWAC이나 Waverider buoy로 측정한 파고에 비해 저평가되는 문제점이 제기되어 왔다. 이는 특히 WTG가 설치된 항만 내 정온도 기준을 마련하는 데 오차를 유발할 가능성이 있기에, 이 수압식 파고계의 관측 정확성을 개선하는 것은 중요하다.
본 연구에서는 총 네 지점에서 관측한 AWAC과 Waverider buoy 자료를 WTG 자료와 비교하여, 서로 다른 두 장비에서 측정한 유의파고와 첨두주기가 저파랑 조건에서 각각 저평가되거나 고평가되지만 이 둘의 곱(HT)은 일정함을 발견하였다. 그리고 이 결과를 적용하여 WTG에서 관측한 HT와 유의파고의 분포를 구하고 다시 이 분포를 대표하는 다항식을 계산하여 임계파고(Hm0, Cr)로 설정한 0.7 m 이하의 WTG 파고값을 보정하였다. 그 결과 보정된 WTG 유의파고와 AWAC 및 Waverider buoy의 유의파고의 선형 관계가 향상되었으며 저평가되었던 파고값도 상당부분 개선되었음을 확인하였다. 따라서 본 연구에서 사용한 방법을 적용하면 WTG만을 사용해 측정한 다른 지역의 파고값도 보정할 수 있으며 그 관측 정확도가 유의미하게 향상될 수 있을 것으로 판단된다.
다만 본 연구에서 항만 및 어항 설계기준·해설(해양수산부, 2014)에서 제시된 하역한계파고를 토대로 하여 0.7 m로 적용한 저파랑 임계파고(Hm0, Cr) 값의 기준에 대해서는 향후 추가적인 연구가 필요할 것으로 판단된다. 예를 들어 보정에 필요한 AWAC 자료 없이 WTG 자료만 존재하는 경우라도 HT가 선형으로 증가한다는 가정을 적용하면 저파랑 환경의 파고값을 보정할 수 있으나 이 때 Hm0, Cr을 어떻게 결정하는 지에 따라 다항식의 계수값이 변할 것이고 보정의 정확성도 변할 수 있다. 이러한 점을 고려하여 Hm0, Cr 값을 변수로 하여 여러 차례 분석을 시행한 후 다항식 계수값이 안정화되는 Hm0, Cr 값을 채택한다면 보다 범용적으로 적용 가능한 기준을 제시할 수 있을 것이다.
본 연구는 저파랑 조건의 파고만을 보정 대상으로 하고 유의파고 2 m 이상의 고파랑 자료들은 보정 대상에서 제외하였다. 이는 폭풍파와 같은 고파랑 자료들은 발생 빈도가 적은 관계로 유의미한 통계적 결과를 유출해내기에는 아직까지 축적된 자료의 양이 부족하기 때문이다. 현재 몇 개의 지점에서 WTG와 AWAC을 사용한 동시관측 자료가 측정되고 있으며 가까운 장래에 이 자료들을 토대로 고파랑 조건 하에서도 비슷한 방법으로 WTG 자료의 보정을 시도할 수 있을 것으로 예상된다.
마지막으로, 본 연구에서는 파고가 증가함에 따라 관측된 HT는 선형으로 y = x 직선에 부합하게 증가한다는 가정에 근거하여 자료를 분석하였는데 본 연구결과를 보다 광범위하게 적용하기 위해서는 보다 많은 지역에서 관측한 자료를 통하여 이 가정을 입증하는 것이 요구된다. 또한 향후 연구에서는 보정 오차를 줄일 수 있도록 보정 방법을 보다 정밀화하는 것이 필요하다. 예를 들어 본 연구에서는 두 개의 관측 장비에서 측정한 자료를 모두 사용하여 식(9)의 회기곡선을 산출하였다. 그러나 두 장비 간 오차가 적은 자료를 선별하여 이를 토대로 회기곡선을 계산하고, 그 결과를 오차가 큰 자료의 보정에 적용하는 등 보정 절차를 세밀화하면 그 정확성이 향상될 수 있을 것이다. 또한 Fig. 8에 표시한 시계열 자료는 부산항 신항의 경우로 이 지역의 보정 결과가 타 지역보다 우수하였다. 이에 대한 정확한 원인은 아직 파악되지 않았으나 Table 1에 나와 있듯이 이 지역의 관측 수심이 타 지역보다 얕은 것을 알 수 있다. 따라서 향후 연구에서는 정밀한 분석을 통해 보정에 필요한 모수에 수심 등 다른 요인을 추가하여 절차 및 수식을 보다 세분화시키는 작업도 필요할 것으로 판단된다.
Fig. 1.Map of the locations of Sts. A1, A2, B1 and B2 where WTG was moored at the bottom of seabed together with AWAC (A1 and A2) and Waverider buoy (B1 and B2). 
Fig. 2.Comparison of Hm0 distribution measured at the four stations (A1, A2, B1 and B2). x-axis: Hm0 by AWAC at (a) A1 and (b) A2 or Waverider Buoy at (c) B1 and (d) B2. y-axis: Hm0 by WTG. The blue lines denote y = x. 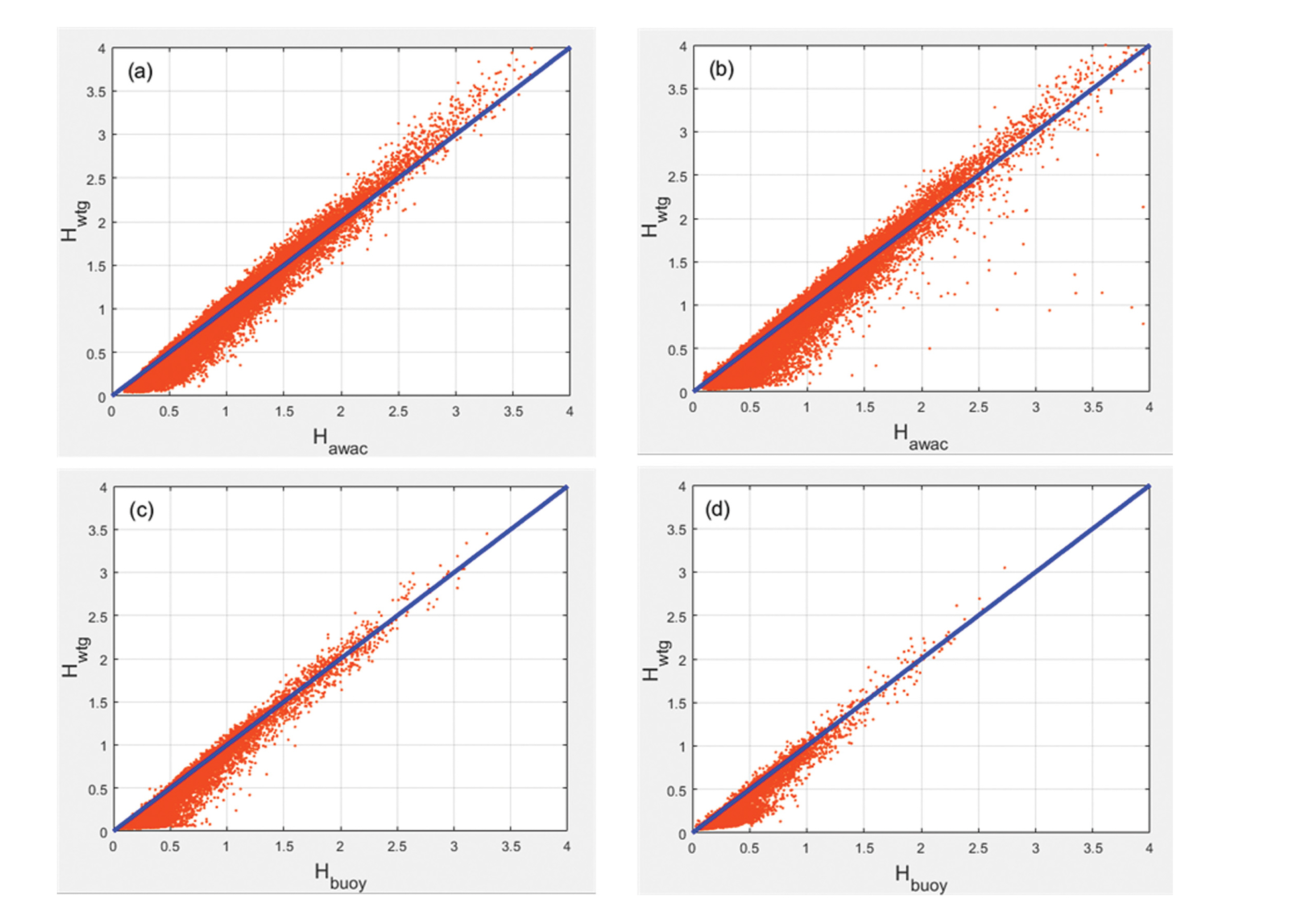
Fig. 3.Comparison of Tp distribution measured at the four stations (A1, A2, B1 and B2). x-axis: Tp by AWAC at (a) A1 and (b) A2 or Wave- rider Buoy at (c) B1 and (d) B2. y-axis: Tp by WTG. The blue lines denote y = x. 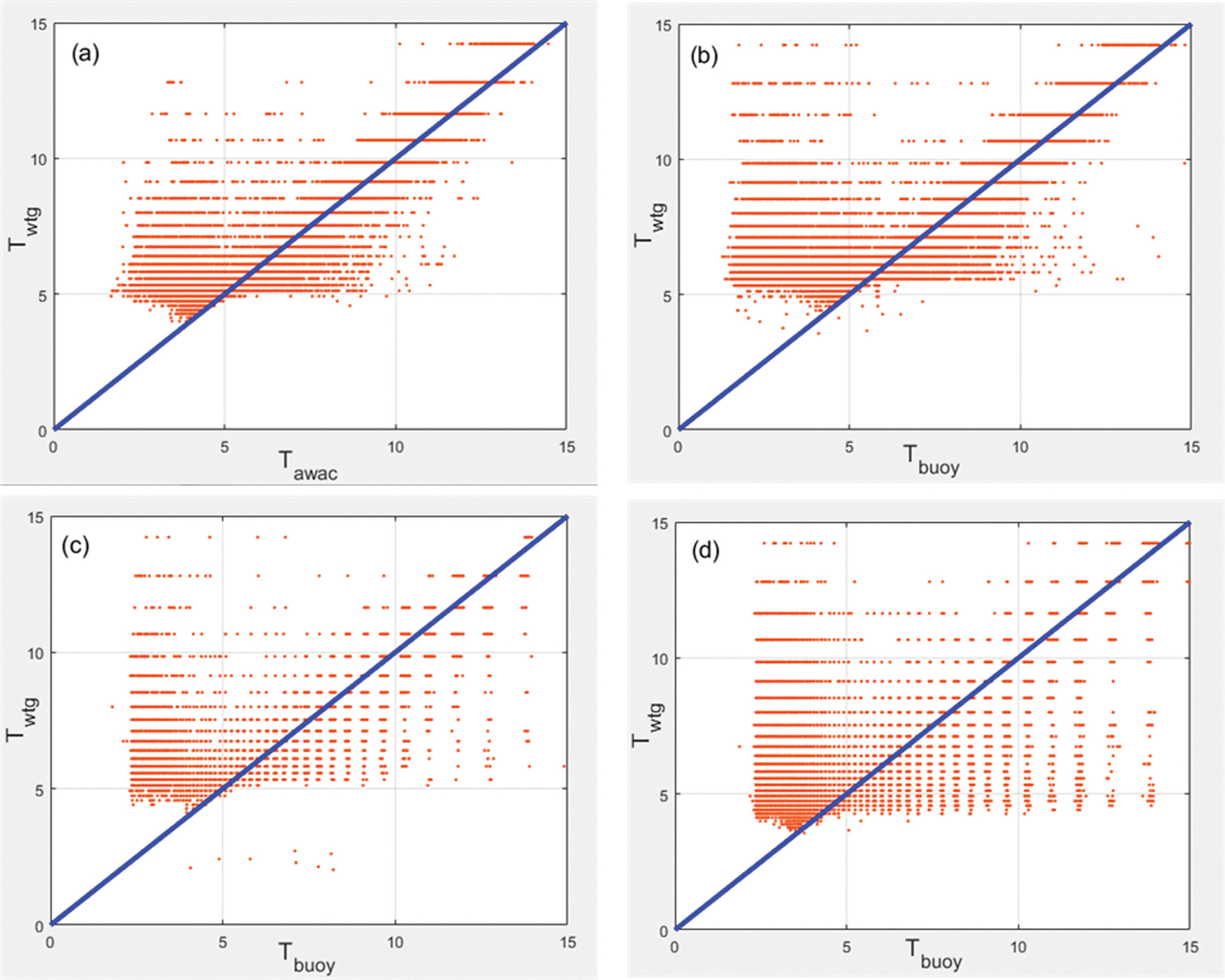
Fig. 4.Comparison of HT distribution measured at the four stations (A1, A2, B1 and B2). x-axis: HT by AWAC at (a) A1 and (b) A2 or Waverider Buoy at (c) B1 and (d) B2. y-axis: HT by WTG. The blue lines denote y = x. 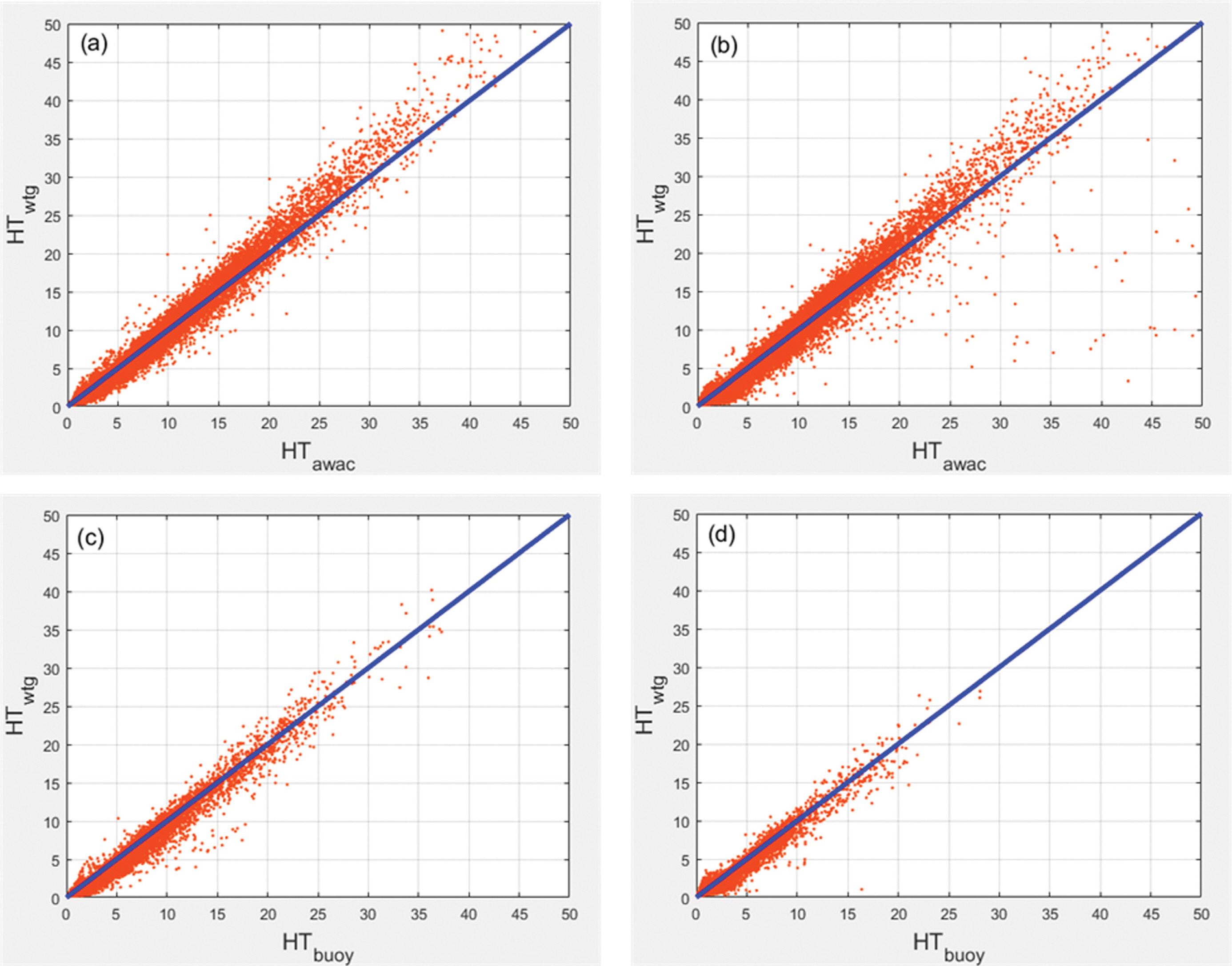
Fig. 5.Distribution Hm0 measured by WTG in terms of HT measured by WTG in the corresponding four stations. The blue lines denote the 3rd order polynomials that fit the distribution with y-intercept to be 0, respectively. 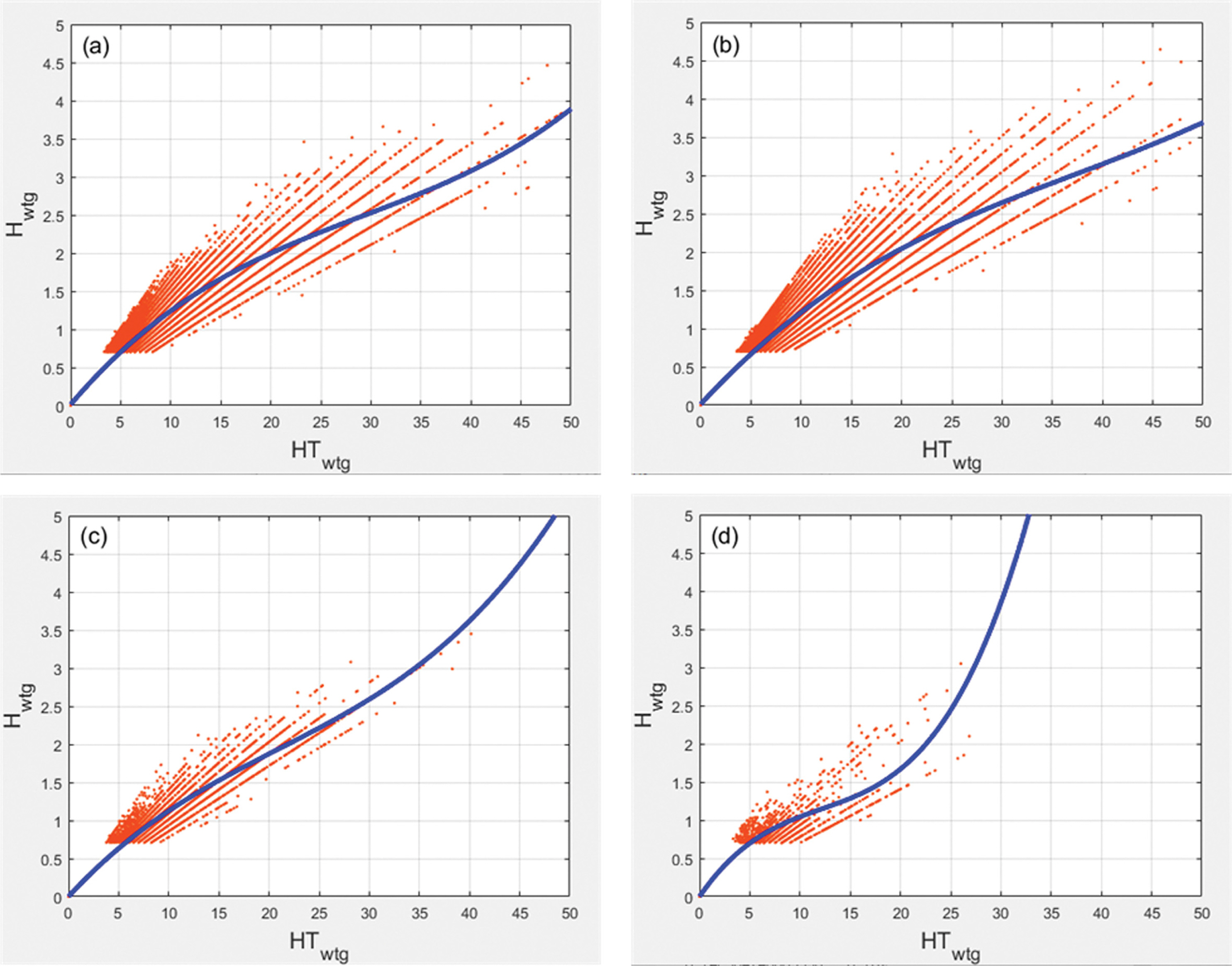
Fig. 6.(a) Distribution Hm0 measured by WTG in terms of Hm0 measured by AWAC in station A1 (this figure is same with Fig. 2(a)). (b) Distribution Hcal in terms of Hm0 measured by AWAC in station A1. 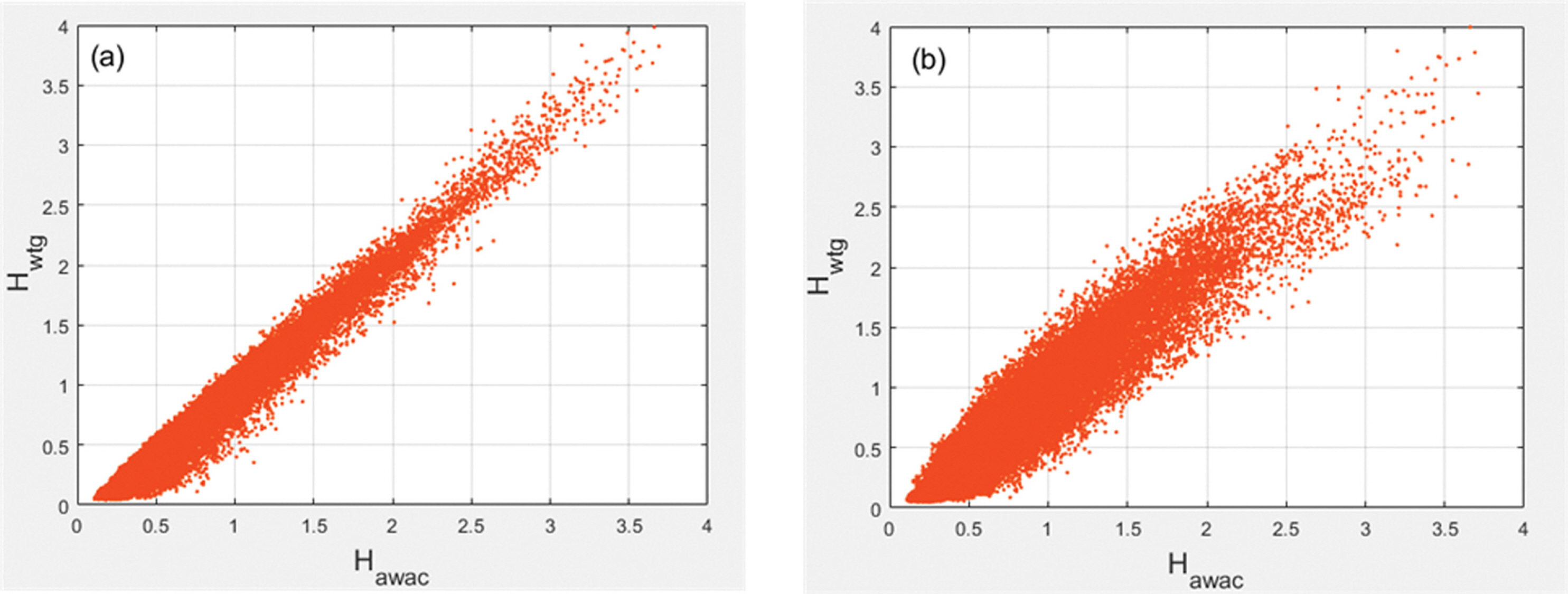
Fig. 7.Distribution of wave heights (measured and calibrated) in WGT in terms of Hm0 measured by AWAC in all four stations ((a)∼(d): A1∼B2, respectively). The red dots represent Hm0 measured by WTG that are higher than Hm0, Cr (= 0.7 m), and the blue dots represents Hcal for the waves less than Hm0, Cr. 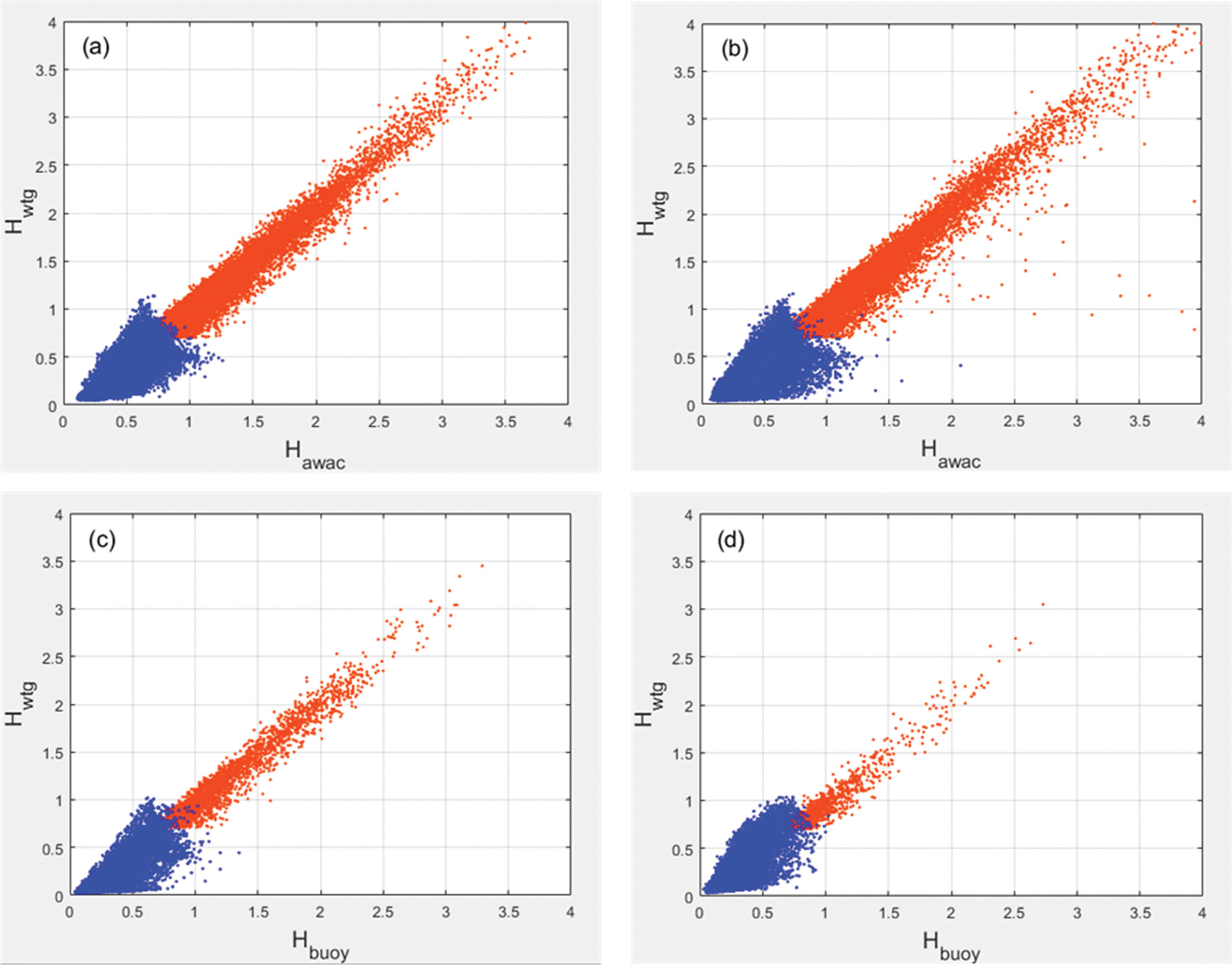
Fig. 8.Time series of observed Hm0 by Waverider buoy (black), WTG (red) and calibrated Hcal (blue) from 2021/12/04 to 2013/01/07 at St. B2. 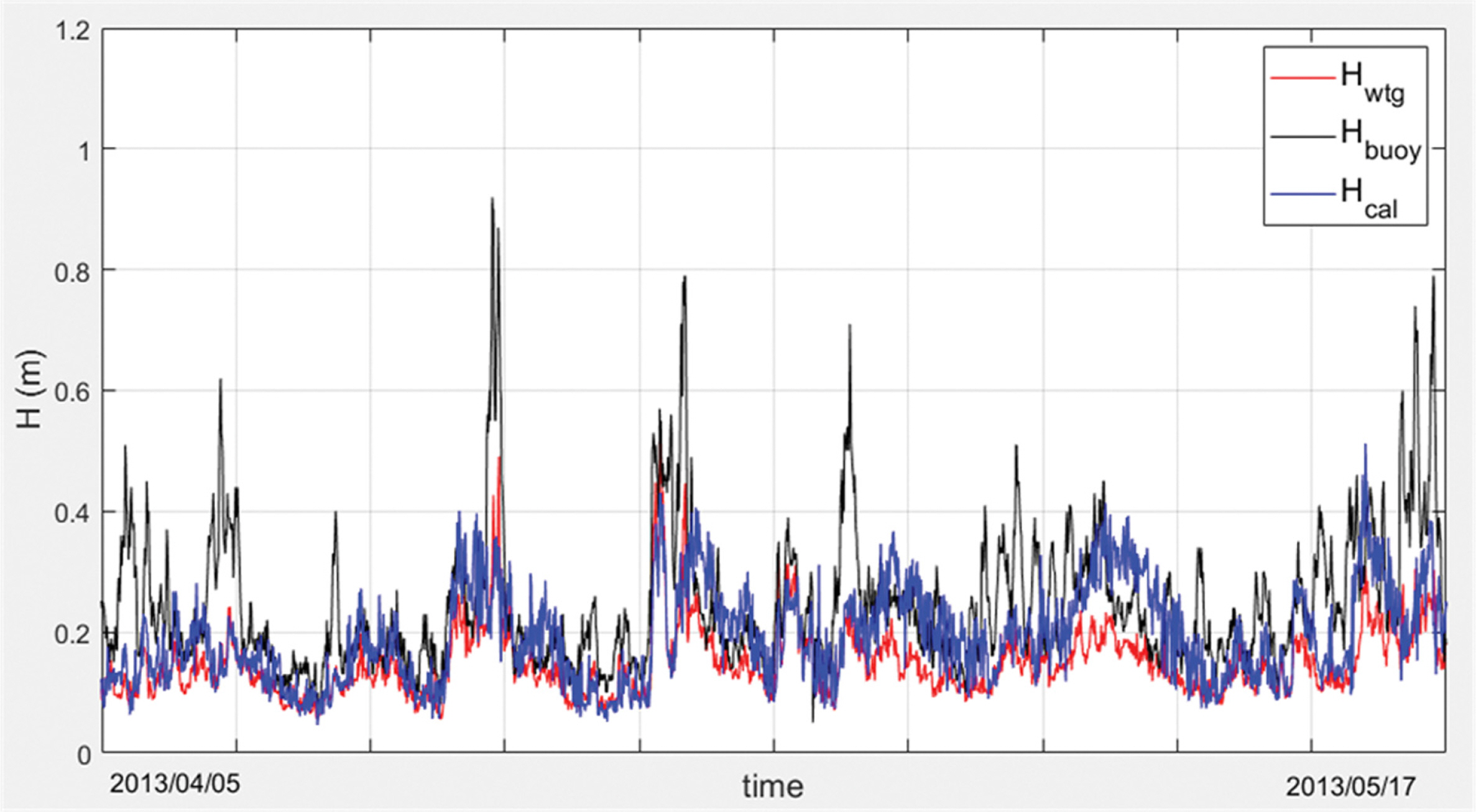
Table 1.List of observation instruments, locations, mooring depth and period Table 2.Summary of data measurements Table 3.Comparison of Dx=y and Rx=y for Hm0, Tp and HT, respectively. The red colored numbers represent the best fit results to the linear line of y = x at each station
ReferencesBiesel, F. (1982). Second order theory of manometer wave measurement, Proc. 18th Coastal Eng. Conf, ASCE, 1, 129-135.
Cavaleri, L, Ewing, JA, Smith, ND. (1978). Measurement of the pressures and velocity field below surface waves, In: Favre A, Hasselmann E, eds. Turbulent Fluxes through the Sea Surface, Wave Dynamics and Prediction. Plenum Press, New York NY: p 257-272.
Cavaleri, L. (1980). Wave measurement using pressure transducer, Oceanol Acta, 3(3):339-345.
Esteva, D, Harris, L. (1970). Comparison of pressure and staff wave gage records, Proc. 12th Coastal Eng. Conf, ASCE, 1, 101-116.
Forristall, GZ. (1982). Subsurface wave-measuring systems In: Measuring Ocean Waves. National Academy Press, Washington, D.C: p 194-209.
Hom-ma, M, Horikawa, K, Komori, S. (1966). Response characteristics of underwater wave gauge, Proc. 10th Coastal Eng. Conf, ASCE, 1, 99-114.
Jeong, WM, Ryu, K.-H. (2014). Review of the improvement of the estimation methods of harbor tranquility, J. Korean Soc. Coast. Ocean Eng, 26(6):397-404 (in Korean).
Kinsman, B. (1965). Wind Waves, their Generation and Propagation on the Ocean Surface. Prentice Hall, Inc, Englewood Cliffs, NJ.
Lee, D.-Y, Wang, H. (1984). Measurement of surface waves from subsurface gauge, Proc. 19th Coastal Eng. Conf, ASCE, 1, 271-286.
Lee, D.-Y, Oh, S.-H. (2009). The significance of current-effect on analysis of wave data obtained from a subsurface pressure gauge, Ocean and Polar Research, 31(4):389-399.
Miche, M. (1944). Mouvements ondulatoiresde lamer en profondeur constante ou decroissante, Ann. Ponts Chausses. France: (in French).
Ministry of Oceans and Fisheries. (2017). Description of standards for design of port and fishing port in the Republic of Korea, (in Korean).
Pedersen, T, Siegel, E, Wood, J. (2007). Directional wave measurements from a subsurface buoy with an acoustic wave and current profiler (AWAC), Oceans, 2007). 10.1109/OCEANS.2007.4449153.
Simpson, JH. (1969). Observations of the directional characteristics of waves, Geophys. J. R. Astron. Soc, 17, 92-120.
US Army Corps of Engineers. (1984). Shore protection manual. 1: 4th edition. Washington D.C: p 1-337.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||