요약부산, 목포 지점의 평균해수면(MSL)과 고극조위, 저극조위 자료의 이상자료 시계열 모델링을 수행하였다. 시계열 모델은 계절성분을 포함하는 SARIMA 모형이며, 일시적인 변화에 해당하는 이상자료(Additive Outlier, AO)와 영구적인 변화를 의미하는 기준고도 변화(Level Shift, LS)를 모델에 포함하였으며, AIC 기준에 의거하여 최적 모델을 선정하였다. 이상자료 모형의 매개변수 추정은 R 프로그램 ‘tsoutliers’ 패키지(‘tso’ 함수)를 이용하였다. 선정 모형을 이용하여 이상자료와 기준고도 변화 진단에 적용한 결과, 부산의 월 단위 고극조위 자료에서 2003, 2012년 발생한 태풍 매미(MAEMI), 산바(SANBA)에 의한 일시적인 수위상승을 65.5, 29.5 cm 정도로 추정하였으며, 목포의 월 단위 평균해수면 자료에서는 1 983년의 영산강 하굿둑 건설 사업에 의한 기준고도 변화를 21.2 cm 정도로 추정하였다. 한편 본 연구에서 구성한 모형은 모형의 편향을 유발하는 이상자료의 영향을 포함하며, 모형에 의한 RMS 오차는 연간 자료를 사용한 경우, 부산은 M SL 1 .95 cm, 고극조위, 저극조위 각각 5.11 cm, 6.50 cm이며, 목포의 경우에는 큰 조차의 영향으로 MSL 2.01 cm, 고극조위, 저극조위 각각 1 1 .80 cm, 9 .1 4 cm로 부산보다 다소 높게 나타났다.
AbstractModeling for outliers in time series was carried out using the MSL and extreme high, low tide levels (EHL, HLL) data set in the Busan and Mokpo stations. The time-series model is seasonal ARIMA model including the components of the AO (additive outliers) and LS (level shift). The optimal model was selected based on the AIC value and the model parameters were estimated using the ‘tso’ function (in ‘tsoutliers’ package of R). The main results by the model application, i.e.. outliers and level shift detections, are as follows. (1) The two AO are detected in the Busan monthly EHL data and the AO magnitudes were estimated to 65.5 cm (by typhoon MAEMI) and 29.5 cm (by typhoon SANBA), respectively. (2) The one level shift in 1983 is detected in Mokpo monthly MSL data, and the LS magnitude was estimated to 21.2 cm by the Youngsan River tidal estuary barrier construction. On the other hand, the RMS errors are computed about 1.95 cm (MSL), 5.11 cm (EHL), and 6.50 cm (ELL) in Busan station, and about 2.10 cm (MSL), 11.80 cm (EHL), and 9.14 cm (ELL) in Mokpo station, respectively.
1. 서 론연안에서 생산되는 장기간의 조위자료는 다양한 자연적 또는 인위적인 환경영향을 받기 때문에 자료 해석에 있어서도 이 영향을 고려하여야 한다. 그러나 그 영향 정도나 원인도 다양하기 때문에 뚜렷한 경우를 제외하고는 자료로 부터 명확하게 원인을 파악하는 것은 한계가 있다. 따라서 자료의 시간적인 변동 양상을 규명하고, 대표적인 변동양상에서 벗어나는 경우와 그 정도를 진단하는 통계적 방법이 유용할 수 있다.
연속적으로 관측되는 조위자료를 이용하여 월 평균 해수면(monthly mean sea level, monthly MSL)을 계산하고, 계산된 월 평균 해수면 자료를 이용하여 연 평균 해수면(annual MSL) 자료가 생산되고 있다. 더불어 월별로 또는 연별로 가장 높거나 가장 낮은 최극조위(extreme tide level, ETL, 고극조위와 저극조위, extreme high and low tide level, 각각 EHL, ELL) 자료를 추출하여 최극조위 자료로 제공하고 있다(KHOA, 2020). 이 자료는 기후변화에 수반되는 장기적인 평균 해수면 및 최극조위 변화 분석에 이용되고 있다. 평균 해수면 변화는 장기적이고, 매우 완만한 변화이며, 고극조위는 일시적인 변화 양상이 반영되는 자료이다. 따라서 평균해수면의 급격한 변화는 연안개발에 의한 조석흐름 변화로 인한 평균해수면 변화 및 다른 다양한 요인에 의한 조위 관측 지점의 기준고도 변화 등과 같은 원인으로 발생할 수 있기 때문에 인위적인 영향을 제거하고 변화양상을 분석할 필요가 있다. 한편 최극조위는 평균 해수면과는 다른 변동특성을 가지기 때문에 빈도분석의 관점에서 검토되어야 한다.
평균해수면(MSL, 이하 월별자료는 mMSL, 연간 자료는 aMSL 기호로 표기) 자료와 최극조위(ETL, 고극조위는 EHL, 저극조위는 ELL, 월별자료와 연간자료는 각각 m, a 기호로 구분; mEHL, aEHL, mELL, aELL) 자료는 장기간의 자료라 할지라도 매년 하나만 생산되어 적은 개수의 자료가 추세분석 및 빈도해석 등에 사용되어 유난히 크거나 작은 이상 자료(outliers)의 영향에 취약하여, 적절한 시계열(TS, time-series) 모형의 매개변수 추정 및 통계적인 측도(measures) 추정 등에 편향(bias)을 유발한다. 따라서 MSL, ETL 자료 분석을 위해서는 통계학적으로 의심되는 다양한 이상자료 진단을 실시하여 그 영향을 배제할 필요가 있다. 어떤 이상한 평균 해수면 변화에 대한 확인 가능한 명확한 원인이 있는 경우에는 분석에서 배제하거나 적절한 처리를 거쳐 사용할 수 있으나, 일반적으로 그 판단이 곤란한 경우가 대부분이기 때문에 평균 해수면 시간변화 자료의 이상자료 진단은 기초적인 자료 품질검정 과정으로 간주되는 통계적인 기법에 의존하여 수행할 필요가 있다. 이 과정을 거쳐 진단되는 이상자료는 과거의 예상되는 영향이력 등을 고려하여 보다 적절한 분석방법을 선택하거나 적절한 자료 조정 등의 과정을 거쳐 사용할 수 있다. 현재 국립해양조사원에서도 월평균 해수면을 추정하는 경우, 결측 정도를 제시하여 추정 결과를 구분하고 있다. 평균 해수면 변화(추세) 분석에 사용되는 자료는 인위적인 영향이나, 일시적인 영향이 배제되어야 하지만 실질적으로는 이러한 영향이 모두 포함될 수 있는 자료를 통계적인 품질 검정 없이 사용하는 경우가 빈번하다. 최극조위 자료도 유사한 방법으로 관리-제공하고 있다. 한편 조위의 결측으로 월평균 해수면 자료가 결측되는 경우, 연평균 자료도 같이 결측으로 처리되기 때문에 분석에 사용되는 자료 개수가 크게 감소하게 되며, 분석의 신뢰수준을 크게 저감하게 된다.
본 연구에서는 서로 변동특성이 다를 것으로 판단되는 우리나라의 평균해수면과 최극조위 자료에 대한 일시적인 기준 고도변화 및 이상자료 진단을 실시하여, 통계적으로 유의미한 이상자료를 진단-제시하는 것을 목적으로 한다.
Cho et al.(2020)은 MSL 자료의 공간 상관관계 분석과정에서 이상자료가 상관계수 추정에 영향을 미칠 수 있음을 제기한 바 있다. Kang and Moon(2000)은 목포의 평균해수면 변화가 방조제, 하굿둑 건설의 영향을 직접 받고 있음을 보고한 바 있다. 그러나 목포와 같이 평균해수면 변화의 원인이 뚜렷하게 드러나는 경우도 있지만, 평균해수면에서 고도기준 변화 여부를 도식적으로 파악하기도 어렵고, 어떤 원인이 어떤 지점의 평균해수면에 미치는 영향을 분석하는 것은 매우 광범위하고 방대하기 때문에 MSL 자료의 품질 검정 수행에 한계가 있다. 한편 Jung et al.(2018)도 부산의 고극조위 자료의 시간변동 성분을 고려하여 극치해면을 추정 한 바 있다. 이 연구에서도 태풍에 의한 고극조위의 급격한 상승 영향이 보고된 바 있으며, 부산 고극조위 자료의 전체적인 추세 분석은 수행되었으나 이상자료 진단 및 그 영향 분석 등은 수행하지 않았다.
따라서 본 연구에서 수행하는 부산, 목포 MSL 자료 및 최극조위 자료의 변동양상 분석 및 이상자료 진단은 이 자료를 이용한 다양한 추정 연구를 위하여 필수적으로 요구되는 내용이다. 통계적인 관점에서 최신 통계기법을 이용하여 잠재적인 기준고도 변화 및 이상자료 진단을 수행하면, 평균해수면 자료 및 최극조위 자료에서 확률적인 변화 영향이 예상되는 경우에는 특정 시기를 진단할 수 있기 때문에, 그 시기에 집중하여 보다 세부적인 검토를 할 수 있기 때문에 매우 효율적이고 효과적인 분석이 가능하다. 더불어 기후변화에 의한 평균해수면과는 무관한 다른 영향이 개입된 경우에는 그 영향을 배제하고 분석하는 경우 보다 적절하고 편기되지 않은 추정-분석이 가능하다.
2. 평균해수면과 최극조위 자료 및 진단방법2.1 평균해수면과 최극조위 자료평균해수면 자료는 국립해양조사원 홈페이지에서 누구나 다운로드 받을 수 있는 공용자료이다(바다누리해양정보서비스 ->실시간해양관측 --> 조위관측소 -> 관측소선택(상세보기) -> 과거해양관측정보보기 또는 http://www.khoa.go.kr/oceangrid/khoa/koofs.do 실시간해양관측정보시스템 -> 조석예보 및 성과 -> 평균해면성과표/최극조위). 본 연구에서는 평균해수면 변화양상 분석이 기본적으로 장기간의 자료를 이용한 분석이기 때문에 최소 50년 이상의 관측 자료가 가용한 지점을 선정하였다. 선정된 조위관측 지점은 이상자료 진단이 예상되는 부산 및 목포 지점이며, 각각 1960년, 1956년 이후부터 현재까지의 자료이다. 평균해수면 자료는 월별(monthly) 평균 해수면 자료와 그 자료를 평균한 연평균(annual) 해수면 자료에 해당된다. 최극조위 자료도 월별 최극조위와 연간 최극 조위 자료로 구성된다. MSL 자료 및 ETL 자료의 기본적인 통계정보 및 시간적인 변화 양상은 다음과 같다(Figs. 1~2 참조). 그림에서 볼 수 있는 바와 같이, 월별 변동 정도가 매우 크게 나타나며, 부산의 고극조위 자료에서는 2003년 태풍 매미의 영향으로 판단되는 매우 높은 조위가 뚜렷하게 보이며, 목포의 모든 자료에서는 1980년대 영산강 개발사업 등의 영향으로 판단되는 결측 구간이 뚜렷하게 존재한다. 한편 연간 변화 자료에서는 월별 변동 양상이 제거되어 전체적인 추세 파악에 적절하다. 기본적인 도시 분석(visual analysis) 관점에서 보면, 전반적으로 장기 추세 경향이 다양한 양상으로 나타나고 있음을 알 수 있다. 보다 세세한 분석은 자료의 변동구조를 반영한 TS 모형을 구성하고, 그 모형을 이용한 객관적인 분석이 요구된다. 통계분석은 자료기반이기 때문에 이론 기반 물리 모형과의 비교·평가도 요구되나, 본 연구에서는 자료 기반 모형 구성에 중점을 두고 수행하였다.
분석에 사용한 부산 지점의 월별 조위 자료는 총 726개이며 MSL 평균은 약 143 cm, 표준편차는 10 cm 정도로 나타났다. 자료의 분산도를 나타내는 표준편차(SD), 중앙값 절대편차(MAD), 사분범위(IQR)은 9.6~20.0 cm로 저극조위(ELL)에서 약간 크게 나타났다. 목포 지점의 월별 조위 자료는 총 774개이며 MSL 평균은 약 232 cm, 표준편차는 19 cm 정도로 나타났다. 자료의 분산도를 나타내는 표준편차(SD), 중앙값 절대편차(MAD), 사분범위(IQR)은 19.2~66.0 cm로 고극조위(EHL)에서 크게 나타났다(Table 1).
2.2 이상자료(AO, LS) 진단, Time-Series 모형 구성 및 결측자료 보충 방법다른 대부분의 자료와는 달리 유별나게 크거나 작은 자료로 정의되는 이상자료는 다양한 통계적인 진단 방법이 제시-활용되어 왔다(Cho et al., 2016). 그러나 대부분이 경우 시간적인 변동양상과 무관한 자료를 대상으로 제시되는 방법으로 MSL 자료와 시간적인 변화양상이 포함되는 경우에는 Time-series 자료의 이상자료 진단방법이 요구된다. 한편 기준고도 변화 진단방법도 변화시점 진단이라는 측면에서 다양한 방법이 제시되고 있다. 각각의 방법이 MSL 자료에 사용된 사례는 제한되어 있기 때문에 어느 방법의 우월을 판단하기는 곤란한 상황이다. 본 연구에서는 기본적인 Time-Series 모형에 해당하는 계절(seasonal) ARIMA 모형을 기반으로 AO 자료와 LS 진단 기법 적용을 검토했으며(Chen and Liu, 1993), 이 기능을 제공하는 ‘tso’ 함수(R 패키지, ‘tsoutliers’ 제공)를 선정하여 진단에 활용하였다(López-de-Lacalle, 2019). ARIMA 모형은 가장 기본적이고 정형화된 TS(time-series) 모형으로 다음과 같은 표준 구조 기술방법을 따른다(Box et al., 2008).
여기서, zt = TS 모형 구성에 사용하는 자료, (p, d, q) =기본 ARIMA 모형의 AR, 차분(difference), MA 모형 성분의 차수(orders), (P, D, Q) = 계절 ARIMA(SARIMA) 모형의 AR, 차분(difference), MA 모형 성분의 차수이며, s =계절 인자(seasonal index)로, 분기자료 = 4, 월별자료 = 12이다. 본 연구에서 사용하는 자료는 월별 자료이며, s = 12 조건에 해당한다.
식(1)로 표현되는 기본 ARIMA 모형에 다음과 같이 이상 자료 및 기준고도 변화 성분을 추가하여 이상자료를 포함하는 ARIMA 모형(xt)을 구성할 수 있다(Tsay, 1988).
여기서, xt = 관측 TS 자료(t = 1, 2, …, n), zt = 기본 ARIMA 모형으로 구성되는 TS 자료 성분, ωAO =AO 성분의 크기, It =충격(impulse) 함수(It = 1, t = tAO; It = 0, otherwise), ωLS = LS 성분의 크기, Ht =계단함수(Heaviside step function) (Ht = 1, t ≥ tLS; Ht = 0, t < tLS), et = 이상자료를 포함하는 ARIMA 모형의 잔차 성분이다.
TS 자료의 이상자료는 외부요인의 일시적인 영향에 의한 이상자료(additive outlier, AO)와 일정한 정도의 기간을 가지고 자료의 구조변화에 영향을 미치는 이상자료(innovative outlier, IO)로 구분된다. 분산변화(variance change, VC), 기준 변화(level shift, LS), 외부 요인의 일시적인 영향이 일정한 비율로 점진적으로 복구되는 변화(temporal change outliers, TC)도 이상자료로 간주하는 경우도 있지만 본 연구에서는 spike(또는 pulse) 형태의 일시적인 형태를 보여주는 AO 유형 이상자료 만을 대상으로 분석을 수행한다. 외부 요인의 영향이 원상 복귀되는 시간의 관점에서는 AO, TC, LS 유형의 이상자료가 각각 즉시 복귀, 점진 복귀, NO-복귀로 간주할 수 있다. 본 연구에서는 LS 유형의 이상자료를 기준 고도변화시점 진단 측면에서 별도의 이상자료로 분류하여 진단항목에 포함하였다.
이상자료 진단 과정은 TS 자료의 변동구조를 ARIMA 모형으로 가정하고, 식(2), (3), (4)로 표현되는 ARIMA 모형을 각각 구성하고, 이상자료 및 기준고도 변화는 외부 영향에 의한 변동으로 가정한다. TS 모델링은 이상자료를 포함하는 보다 일반적인 ARIMA 모형을 구성하고, 반복적으로 모델 매개변수를 추정하고, 개선하면서 모형구조가 수렴하는 단계까지 계산을 수행하는 과정을 포함한다(Davison and Hinkley , 1997). 이 진단방법은 차분모형(ARIMA, I, integrated, 실질적인 의미로는 difference, 차분)을 포함하고 있기 때문에 자료가 어떤 추세 성분을 가지고 있는 경우에도 적용할 수 있는 장점이 있다.
이 이상자료 진단방법은 뚜렷한 외부영향이 예상되는 시점의 자료를 기준으로 통계적인 방법의 진단 성능을 평가할 수 있으며, 그 결과를 바탕으로 예상되는 자료의 변화 구조를 파악하는 모형으로도 활용할 수 있다. 본 연구에서는 이상자료 탐지와 최적 TS 모형 구성 후, ‘na.kalman’ 함수(R 패키지, ‘imputeTS’ 제공)를 이용하여 최적 ARIMA 모형 기반의 결측 자료 보충을 수행했다(Hyndman and Khandakar, 2008; Moritz and Bartz-Beielstein, 2017).
3. 자료의 상관분석 및 이상자료 진단 결과 및 토론3.1 자료의 상관분석자료의 기본적인 특성분석을 위하여 부산, 목포 지점의 MSL 자료와 ETL 자료의 상관분석을 수행하였다. 상관계수 추정결과, 가능한 조합 EHL-MSL, EHL-ELL, ELL-MSL 조건에서 부산의 경우 0.75, 0.59, 0.83, 목포의 경우 0.78, -0.04, 0.48 정도로 추정되었으며, 목포의 EHL-ELL 상관계수는 유의미한 정도가 아닌 것으로 파악되었다. 연간 자료를 이용하여 동일한 조건에서 동일한 방법으로 상관계수 추정한 결과, 부산의 경우 0.55, 0.18, 0.71, 목포의 경우 0.94, -0.48, -0.30 정도로 추정되었으며, 부산의 EHL-ELL 상관계수는 유의미한 정도는 아닌 것으로 파악되었다. 한편 목포 지점에서는 MSL-EHL 자료가 0.78~0.94 정도의 매우 높은 상관관계를 가지는 것으로 파악되었으며, 부산 지점에서는 목포보다는 다소 작은 수치이나 연간자료 EHL-MSL, 월간자료 ELL-MSL에서 0.55~0.83 정도의 높은 상관관계를 보이는 것으로 파악되었다. 상관계수와 추정 상관계수의 95% 신뢰구간 정보는 Table 2에 제시하였다. 한편, 모든 자료는 Mann-Kendall 검정 방법(Mann, 1945; McLeod, 2011)을 이용하여 95% 신뢰수준에서 추세 검정결과, 모든 자료가 추세 성분을 가지는 비정상성(non-stationary) 자료, 독립조건을 만족하지 못하는 자기상관 성분이 있는 자료로 파악되어 기본 ARIMA 모형 구성이 적절하다고 판단하는 근거가 된다.
3.2 자료의 이상자료 진단 결과TS 자료의 진단 결과는 어떤 물리적인 이론에 근거하는 방법이 아니라, 자료의 수치변화에만 의존하는 통계적인 진단에 근거하고 있으며, 자료의 변동 특성이 진단에 반영된다. MSL 자료는 평균 자료이기 때문에 대부분의 자료 변동양상을 대표하고 추정측도의 오차구간(추정에 사용되는
여기서, n =자료의 개수, k =모형의 (추정) 매개변수 개수, RSS =모형 잔차(residual) 성분의 제곱합(SS, sum of squares)이다.
최적 모형으로 선정된 모형의 차수, AO, LS 진단 정보 등 기본 정보는 Table 3에 제시하였다. 최적 모형으로 선정된 모형은 부산, 목포 2개 지점에서 각각 6가지(2 cases – monthly, annual; 3 types – MSL, EHL, ELL) 자료 유형에 대한 것으로 총 12가지이다. 여기서, 진단된 이상자료가 없는 경우는 부산 mELL, aELL, 목포 aEHL 자료 조건 3가지이다. 본 모형은 AO, LS 진단을 중점으로 수행하였기 때문에, 진단된 이상자료가 없는 위 3가지 경우를 제외한 9가지 경우의 진단 결과를 중심으로 분석을 수행하였으며, 각각의 진단결과는 Fig. 3에 제시하였다.
부산의 월 단위 고극조위(mEHL) 자료의 경우, 2003년, 2012년 돌발적인(일시적인) AO 유형의 이상자료가 진단되고 있다. 이 자료는 진단 시기를 보면 2003년 태풍 매미(MAEMI), 2012년 태풍 산바(SANBA)의 영향으로 판단할 수 있으며, 적절한 이상자료 진단으로 확인된다. 이 진단은 mEHL, aEHL 자료 모두 진단되었으며, aEHL 자료의 변동성분 크기를 감안하더라도 매우 작은 확률의 사건으로 파악된다. 그러나 그 영향 정도(AO 크기)는 mEHL, aEHL 자료조건에서 각각 2003년 65.5 cm, 47.0 cm, 2012년 29.5 cm, 20.0 cm 정도로 대략 10~20 cm 정도의 차이를 보이고 있다. aEHL 자료를 이용한 경우에는 1975년 1 8.0 c m 정도의 AO, 1999년 8.1cm 정도의 LS 영향이 진단되고 있다. 이 진단은 통계적인 진단이기 때문에 명확한 원인규명이 곤란한 경우와 태풍의 영향으로 판단되는 AO 영향 크기는 이론 기반의 수치모형 등을 이용한 정량적인 평가가 요구된다. 그러나 이 진단-추정결과는 수치 모형의 성능 평가를 위한 기준으로도 활용 될 수 있을 것으로 판단된다. 1975년 AO 이상자료 진단 시기에는 영향이 예상되는 1975년 8월 태풍 필리스(PHYLLIS)의 내습시기와 큰 차이가 있다. 한편 자료의 초기에 해당하는 1960년, -139.7 cm 정도의 매우 큰 LS 진단결과는 빈번한 자료결측의 영향으로 판단되며, 이러한 유형의 다소 불합리한 이상자료 진단결과는 결측 자료가 빈번하게 발생하는 시기와 일치하고 있으며, 본 모형의 한계로 판단된다. 본 모형은 자료가 결측을 포함하는 경우에도 작동하는 방식으로 모형이 구성되어 있으나, 초기에 적절한 방법으로 결측 자료를 추정(initial guess)하고, 단계적으로 조정(개선)하는 방법의 적용도 필요할 것으로 판단된다. 부산 지점의 mELL 자료에서는 이상자료가 진단되지 않았다.
반면 목포 지점에서는 mMSL, mEHL, mELL 자료 모두에서 AO, LS 이상자료가 진단되었다. mEHL 자료에서는 1970년 -46.5 cm 정도의 LS, mMSL 자료에서는 1960년 -29.4cm, 1983년 2 1.23 cm 정도의 LS, mELL 자료에서도 1960년 -27.59 cm 정도의 LS 진단시기와 크기가 추정되었다. 이 진단 결과는 1960~70년대 초기 불안정한 장비 운영시기 및 결측 자료의 영향으로 판단할 수 있다. 한편 1983년의 mMSL 자료에서 21.23 cm 정도의 LS 진단은 영산강 하굿둑 건설의 영향으로 판단된다. 목포의 고극조위 자료는 Kang and Moon (2000)이 설계조위 추정을 목적으로 영산강하구, 금호방조제, 영암방조제 건설 등의 영향을 정량적으로 분석하였으나, 본 연구에서 사용한 모형에서는 mEHL, aEHL 자료에 대하여 1983년의 LS 이상자료는 없는 것으로 진단되었다. 두 판단의 근본적인 차이는 Kang and Moon(2000)이 사용한 목포의 고극조위(최대 편차 정보로부터 추정한 자료로 판단) 자료와 KHOA 제공 고극조위(ETL) 자료가 서로 다르기 때문으로 판단된다.
한편, aMSL 자료를 이용한 경우, 1983년 21.26 cm, 1999년 9.76 cm LS 진단 결과와 1992년 8.62 cm AO 진단의 원인 분석에 중점을 두고 수행하여야 할 필요가 있다. 1992년 8 .62 cm 정도의 AO 진단도 이 시기의 빈번한 자료 결측과 영산강 하굿둑 및 방조제 건설사업의 복합적인 영향으로 판단된다. mELL 자료의 경우, 2004년 23.5 cm 정도의 AO 진단도 상세 검토 시기에 포함할 필요가 있다. 분석결과, 목포 지점의 mMSL, aMSL 자료에서 1983년 영산강 하굿둑 건설에 의한 LS 영향을 동일하게 탐지하는 것으로 나타났다.
본 연구에서 구성하고 이상자료 진단 목적으로 사용하는 모형은 자료의 변동구조를 통계적인 관점에서 판단하는 것이기때문에 물리적인 의미를 가지지는 못하지만, 간접적으로 외부 환경영향이 자료에 영향을 미치기 때문에 어떤 영향을 받았을 것으로 판단되는 시기와 정도를 예측하는 그 결과도 의미를 가지게 된다. 전반적으로 자료의 변동양상을 통계적인 관점에서 파악하고, 변동양상이 유별난 시기와 정도를 파악할 수 있다면, 유의미한 자료의 변동 원인을 집중하여 파악하여야 하는 우선순위(priority) 결정에 활용할 수 있다. 어느 진단이 적절한 진단인가는 이 시기의 자료에 대한 세부적인 분석으로 판단하여야 하며, 본 연구의 진단결과는 자료의 세부적인 분석 범위를 크게 제한하여 실질적이고 효율적인 집중분석에 기여한다고 할 수 있다.
3.3 결측 자료 보충(missing imputation)본 연구에서 구성한 모형을 이용하여 AO, LS 자료 진단을 하는 경우, 이러한 이상자료는 TS 모형의 구조에 크게 영향을 미치기 때문에 이상자료의 영향을 배제한 모형을 구성하는 경우, 유별난 자료보다는 대부분의 자료로 대표되는 변동양상을 파악할 수 있으며, 유별난 자료로 정의되는 이상자료(ab-normal data, out-liers)가 정상자료(normal, in-liers)에서 얼마나 벗어나는 자료인가를 정량적으로 파악하는 근거로 사용할 수 있다. 또한 결측 자료를 보충하는 경우, 완전한 자료(complete data)가 구성되기 때문에 완전한 자료조건을 요구하는 통계 기법 등을 이용하여 다양한 측면에서 자료의 변동구조를 분석할 수 있으며, 상호비교 및 상관분석을 통하여 인접지점의 자료를 보충(missing data filling-in)할 수 있다. 자료보충은 추정과정에서의 오차전파 등의 단점이 있으나, 여러 지점에서 동등한 시간규모 조건의 변동 구조 비교를 가능하게 하고, 일반적인 통계 측도의 편향을 제거하는 장점이 있다.
4. 결론 및 제언부산, 목포 지점의 MSL, EHL, ELL 자료를 이용하여 AO, LS 유형의 이상자료를 포함하는 TS 모형을 구성-적용하였으며, AIC 기준에 의거하여 최적 모델을 선정하였다. 이상자료 모형의 매개변수 추정은 R 프로그램 ‘tsoutliers’ 패키지(‘tso’ 함수)를 이용하였다.
최적 추정된 모형을 이용하여 MSL, ETL 자료의 AO, LS 진단에 적용한 결과, 부산의 EHL 자료에서 2003, 2012년 발생한 태풍 매미(MAEMI), 산바(SANBA)에 의한 일시적인 수위상승을 65.5, 29.5 cm 정도로 추정하였으며, 목포의 MSL 자료에서는 1983년의 영산강 하굿둑 건설 사업에 의한 기준고도 변화를 21.2 cm 정도로 추정하였다.
한편 본 연구에서 구성한 모형의 RMS 오차는, (1) 부산은 aMSL 자료조건에서 1.95 cm, aEHL, aELL 자료조건에서 각각 5.11 cm, 6.50 cm 정도이며, (2) 목포의 경우에는 부산보다 큰 조차의 영향으로 aMSL 자료조건에서 2.01 cm, aEHL, aELL 자료조건에서 각각 11.80, 9.14 cm 정도로 부산보다 다소 크게 나타났다.
다양한 유형의 이상자료를 포함하는 TS 모형은 우리나라 연안의 MSL, ETL 자료의 변동 구조 파악에 적절한 모형으로 판단되며 이를 이용하여 평균 해수면 예측이 어느 정도 가능할 것으로 판단된다(Fig. 4). 향후 다른 지점을 추가하여 우리나라 연안 조위관측 시설의 장기적인 자료변동 구조 상관관계를 규명하고, 후측(hind-casting)을 포함한 장기적인 MSL, ETL 변동 예측을 수행하는 연구가 수행되어야 할 것으로 판단된다.
감사의 글본 연구는 2019년 ‘낙동강 하굿둑 운영개선 및 생태복원 방안 연구용역(II)’의 지원을 받아 수행된 연구 성과입니다. 연구 지원에 감사드립니다(PG51490). 평균 해수면 자료를 제공해주신 국립해양조사원에 감사드립니다.
Fig. 1.Time-series plots of the monthly MSL (mMSL), extreme high and low tide level data (mEHL, mELL) in Busan and Mokpo stations. 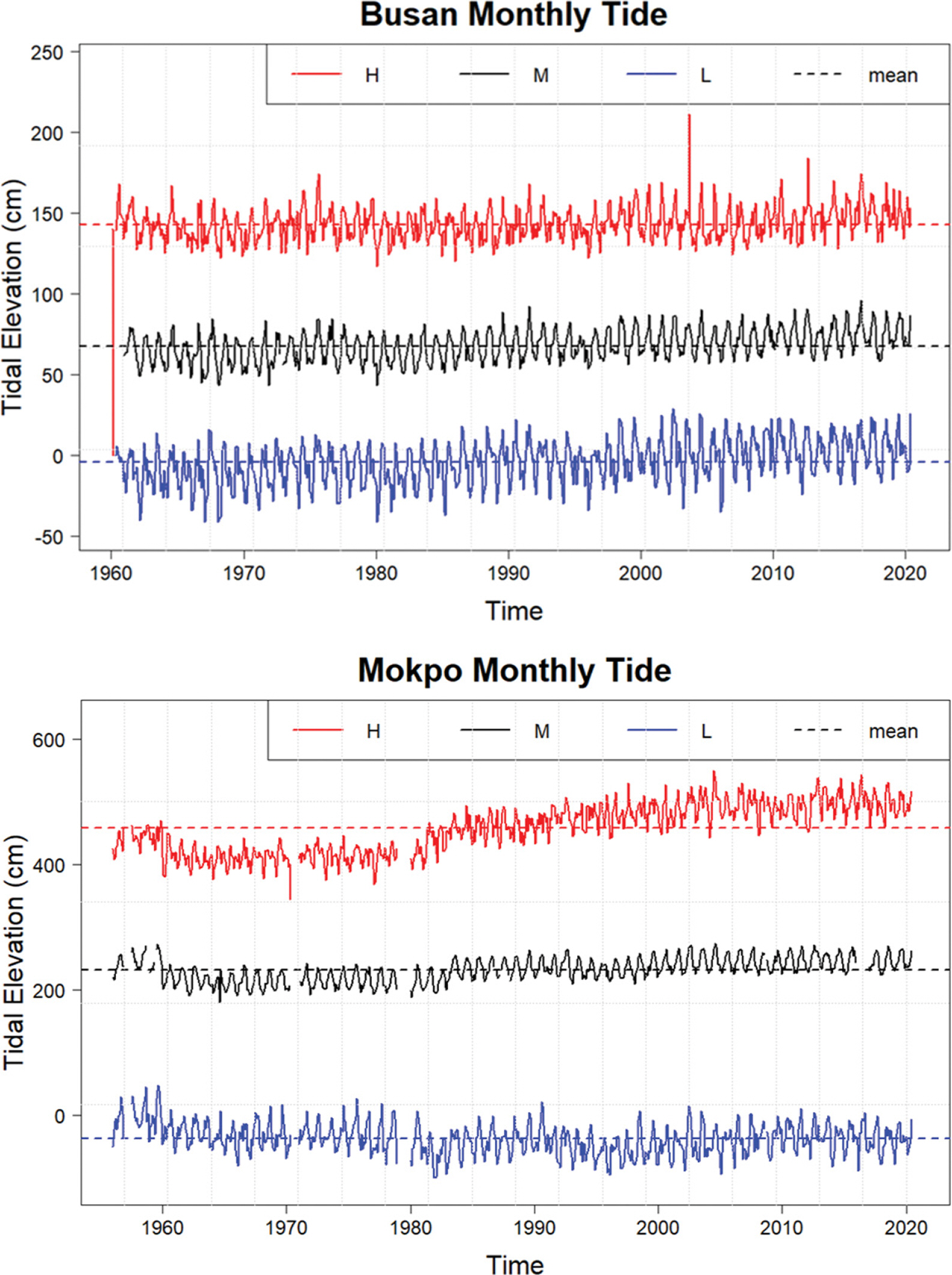
Fig. 2.Time-series plots of the annual MSL (aMSL), extreme high and low tide level (aEHL, aELL) data in Busan and Mokpo stations. 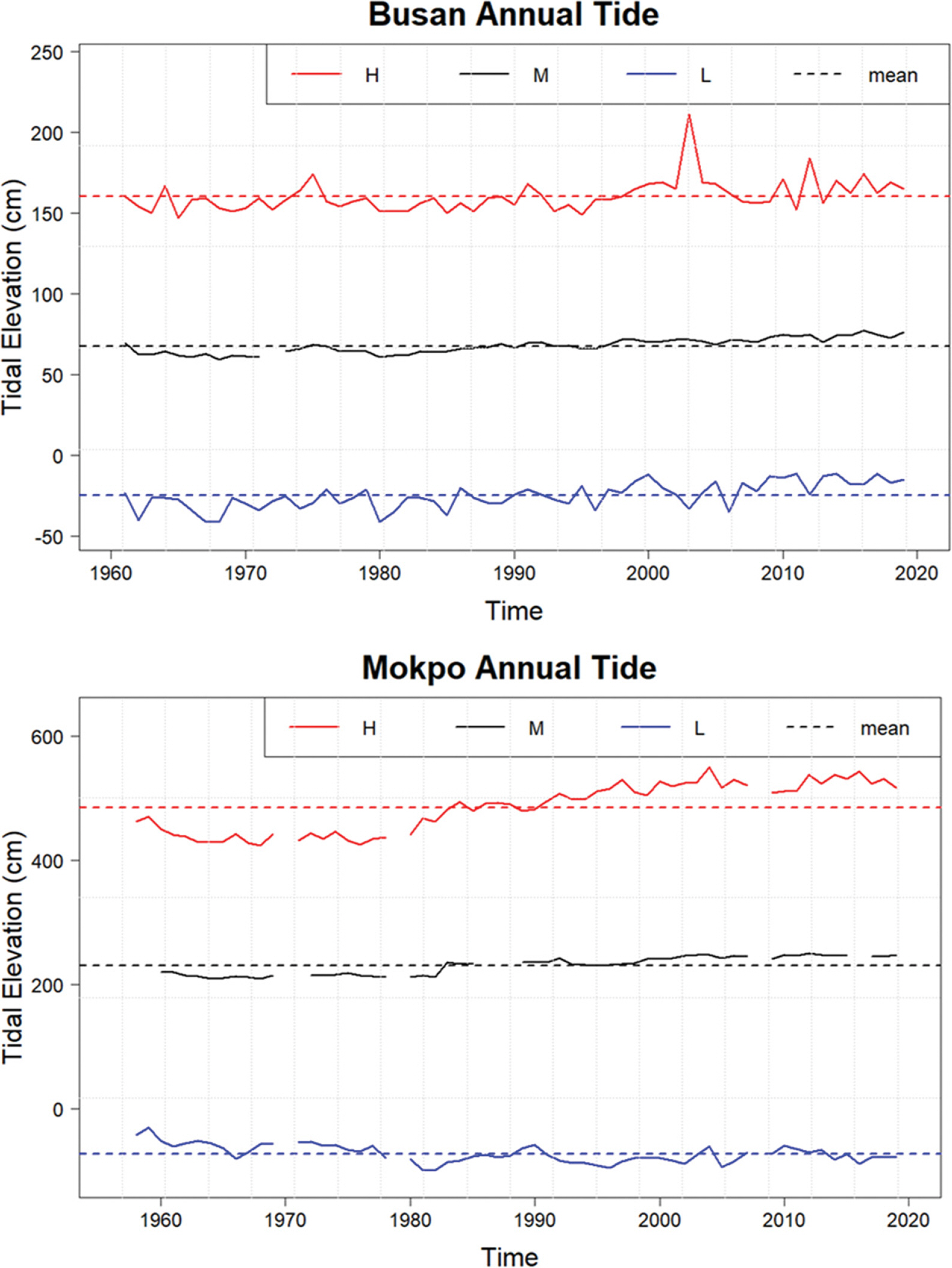
Table 1.Basic statistical measures of the monthly MSL, EHL and ELL data in the Busan and Mokpo Stations. (Mokpo, 1958∼2020; Busan, 1960∼2020) (Unit = cm) Table 2.Correlation coefficient and 95% confidence intervals of the MSL and ETL (EHL, ELL) data in the Busan and Mokpo stations Table 3.Optimal ARIMA model and AO, LS detection information in the the monthly and annual data condition ReferencesBox, GE, Jenkins, GM, Reinsel, GC. (2008). Time Series Analysis Forecasting and Control. Fourth Edition. Chap. 9. John Wiley & Sons.
Chen, C, Liu, LM (1993). Joint estimation of model parameters and outlier effects in time series, J of American Statistical Association (JASA), 88(Issue. 121):284-297.
Cho, HY, Jeong, ST, Lee, UJ (2020). Spatial correlation analysis of the mean sea level data sets in the coastal seas, Korea. J of KSCOE, 32(1):85-93 (in Korean).
Cho, HY, Lee, GS, Ahn, SM (2016). Impact of outliers on the statistical measures of the environmental monitoring data in Busan coastal sea, Ocean and Polar Research, 38(2):149-159 (in Korean).
Davison, AC, Hinkley, DV. (1997). Bootstrap Methods and Their Application. Cambridge University Press.
Hyndman, RJ, Khandakar, Y (2008). Automatic time series forecasting: the forecast package for R, Journal of Statistical Software, 26(3.
López-de-Lacalle, J. (2019). tsoutliers: Detection of Outliers in Time Series. R package version 0.6-8, https://CRAN.R-project.org/package=tsoutliers.
Jung, BS, Lee, OJ, Kim, KM, Kim, SD (2018). Non-stationary frequency analysis of extreme sea level using POT approach, J of Korean Society of Hazard Mitigation, 18(7):631-638 (in Korean).
Kang, JW, Moon, SR (2000). Frequency analysis of extreme high water level at Mokpo Harbor considering tidal environment changes, J of KSCOE, 12(4):203-209 (in Korean).
Korea Hydrographic and Oceanographic Administration; Korea Ocean Observing And Forcecating System. (http://www.khoa.go.kr/oceangrid/koofs/kor/tide/tide.do Accessed 2020-09-22.
McLeod, AI. (2011). Kendall: Kendall rank correlation and Mann-Kendall trend test. R package version 2.2. https://CRAN.R-project.org/package=Kendall.
|
|
|||||||||||||||||||||||||||||||||