1. 서 론
지진해일은 지진으로 인한 해저지형의 갑작스런 변형으로 야기되며 이렇게 생성된 파형은 시속 수백 킬로미터의 빠른 속도로 전파된다. 연안에 도달한 지진해일은 해저지형의 영향으로 굴절, 천수과정을 거치며 상당히 증가된 파고를 지닌다. 연안에 도달한 지진해일은 쇄파과정을 거치나 여전히 세력을 유지한 단파의 형태로 내륙 깊숙이 진행될 수 있어 상당한 파괴력을 지닌다 (Lin, 1985; Lin and Tung, 1986).
유라시아판과 북미판, 태평양판, 필리핀판이 만나는 경계부에 위치하여 비교적 지진이 잦은 일본이나 대만과는 달리 유라시아판 경계에서 수백km 떨어져 있는 한반도는 지진으로부터 비교적 자유롭다는 것이 지금까지의 통설이었다. 그러나 최근 북진하는 인도 대륙과 유라시아판의 동진, 태평양판의 서진, 필리핀판의 북진이 맞물리면서 상당한 응력이 한반도 주변에 부하되고 있는 것으로 판단된다(Lee et al., 2001).
2005년 3월 25일 후쿠오카 북서쪽 약 20 km 해역에서 발생하여 응력 취약부인 대마도 주변 해저의 쓰시마-고토 단층대를 통해 우리나라에도 영향을 미친 후쿠오카 지진은 전술한 응력이 처음으로 그 모습을 드러낸 것으로 인식되고 있다. 전술한 지진은 우리나라 사회에 쓰시마-고토 구조선이라는 큰 활성 단층대의 존재를 처음으로 부각시켰다. 이 단층대는 한반도를 향하고 있으며 필리핀해판이 이 단층을 자극하는 경우 일본과 한반도가 동시에 큰 피해를 받을 가능성도 일각에서 제기되고 있다.
전술한 쓰시마-고토 단층대외에도 일본열도의 남서측에 분포하고 있는 류큐열도 주변은 류큐해구를 사이에 두고 북서쪽에 유라시아판이, 남동쪽에 필리핀해판이 서로 마주하는 판경계 지역으로 지진활동과 화산활동이 매우 활발하여 우리나라 서해안에 직접적인 영향을 미칠 수 있을 것으로 판단된다.
필리핀해판은 수심이 10 km 정도인 류쿠 해구를 따라서 유라시아판 하부로 7 cm/yr로 속도로 섭입되고 있으며 판경계를 따라 큰 규모의 지진이 빈번하게 발생한다. 류큐 열도의 북서 측에는 북동 남서방향의 오키나와 주상해분이 분포하고 있으며, 수심은 1000에서 2000 m사이에 분포한다. 현재 오키나와 주상해분은 중부에서는 북서-남동방향으로 1~2 cm/yr, 남부에서는 남북방향으로 3~5 cm/yr로 확장되고 있다.
이렇듯 한반도는 지진으로부터 비교적 안전하다는 그 동안의 통설과는 달리 한반도도 지진해일에서 자유로울 수 없다는 인식이 바로 우리 눈앞에서 진행된 2011년 일본 후쿠시마 지진과 이로 인한 후쿠시마 원전 파괴를 계기로 빠르게 확산되고 있다.
특히, 냉각수 확보가 용이하다는 지리적 이점으로 인해 그 동안 연안에 집중적으로 건설된 원전 인근 지역사회의 불안감은 최근 비등하여 이의 해소를 위해서라도 지진해일에 대한 내구성이 담보된 연안방재시스템의 개발은 시급한 과제로 보인다.
최근 여러 가지 방재시스템이 검토되고 있으나 상당한 높이의 지진해일 처오름을 제어하기 위해 과도한 첨단고가 불가피한 고전적 차수시스템 위주로 진행되고 있어 개선이 요구된다. 연안이 비교적 잘 보존된 서구의 경우 홍수림(mangrove forest)을 활용한 지진해일로 인한 처오름 제어기법에 관한 연구가 활발히 진행되는 듯하다. 전술한 방법은 수려한 연안환경을 보존할 수 있다는 장점으로 인해 매력적이나 연안개발이 이미 진행된 우리나라의 경우 상당한 면적이 요구되어 차용이 불가능 할 것으로 보여 심미적으로 우수하고 친환경적인 새로운 지진해일 방재시스템 개발이 시급한 과제로 부상하였다.
최근 wave energy vision사는 SSG (Sea Slot Con)라 불리는 파력발전을 목적으로 제체내에 유수실이 거치된 새로운 형태의 경사제를 제안하였다 (Fig.1 참조). SSG는 소규모 파력발전을 위한 것이었으나 구조적 내구성이 담보된다면 처오름 높이를 효과적으로 제어할 수 있어 연안에 집중적으로 배치된 우리나라 원전시설에 적합한 심미적으로 수월한 지진해일 제어시스템으로 차용될 수 있을 것으로 보인다.
이러한 인식에 기초하여 본고에서는 총 세 개의 유수실과 저면에 경사면이 거치된 hybrid breaker가 제시되고 제시된 hybrid breaker의 처오름 저감효과를 강건한 파랑모형인 Navier Stokes 식을 사용하여 수치 해석하였다. 전술한 파랑모형의 수치적분은 VOF 법을 활용하여 수행되며 수치모형의 검증작업은 규칙파와 불규칙파의 처오름 과정에 대한 수치결과와 처오름 높이에 대한 수리모형 결과를 토대로 수행된다.
이와 더불어 본고에서 다루는 지진해일 방재시스템의 규모를 산정하기 위해 우리나라에 내습할 수 있는 지진해일의 전파과정 수치모의도 병행하여 수행된다. 동해안의 경우 일본 서해안에서 발생한 1983년 아키다 현 지진해일, 1993년 훗카이도 오쿠시리 섬 지진해일 등으로 인해 상당한 지진해일 연구결과가 축적된 것으로 보인다 (Lee, 1998; Yoon et al., 2002; Cho et al., 2002; Choi and Lee, 1993). 그러나 서해안의 경우 오키나와 단층대에 직접 노출되어 있음에도 불구하고 상대적으로 소홀히 다루어져 왔다. 이러한 편차를 해소하기 위해 지진해일은 최근 상당한 응력이 누적되어 활동가능성이 큰 오키나와 단층대에서 발생하는 것으로 가정하였다.
SSG의 지진해일 처오름 저감효과에 대한 정량적 분석은 먼저 Solitary Wave를 대상으로 수행된다. Boussineq식의 해석해에 기초한 Solitary wave는 관측치에 비해 처오름 높이가 상대적으로 작은 값을 지닌다 (Zhao et al., 2012). 지진해일 내습 초기 해안선이 일시적으로 전진하나 Solitary wave에는 이러한 수리특성이 결여되어 있다. 이로 인해 발생하는 관성력의 저하로 처오름 높이가 상대적으로 작다는 인식에 준거하여 초기수위 강하를 포함하는 Leading Depression N(LDN) Wave로 확장된다 (Zhao et al., 2012).
2. 오키나와 단층대에서 발생한 지진해일의 전파특성
본고에서 다루는 새로운 개념의 지진해일 방재시스템의 규모를 산정하기 위해 우리나라에 내습할 수 있는 지진해일의 전파특성을 수치모의 하였다. 지진해일은 우리나라 서해안과 마주하는 오키나와 단층대에서 발생하는 것으로 가정하였다.
지진해일은 오키나와 단층대에서 발생하여 한반도에 영향을 미쳤던 지진 중 비교적 생기빈도가 높은 리히터 규모 7.5의 지진에 의해 야기되는 것으로 가정하였다. 오키나와 트러프내에서 한반도에 영향을 크게 미칠 수 있는 지진해일을 유발할 수 있는 해저활성단층은 트러프 중앙부에 위치하는 정단층보다는 한반도에서 연장되는 대륙붕에 연하여 발달하고 있는 단층으로 판단된다.
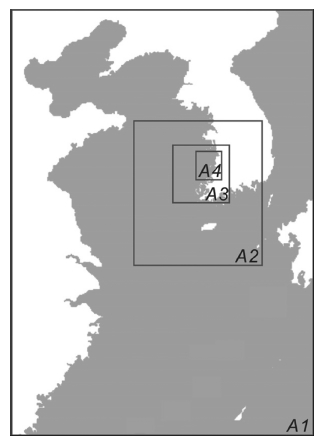
기본방정식으로는 수치적으로 강건한 지진해일모형인 비선형 천수방정식을 사용하였으며 Fig. 3에 도시된 계산영역은 보다 효율적인 수치모의를 위해 총 네 개의 영역 (A1, A2, A3, A4)으로 분할하였으며 각 계산영역은 474×686, 428×464, 610×657, 1000×1039개의 절점을 사용하여 이산화 하였다. 경계조건으로는 개방경계의 경우 에너지 흡수 경계조건, 각 영역사이의 내부경계에서는 동적연계기법을 사용하였다 (Yoon, 2002).
기본방정식은 ADI 기법을 활용하여 차분하였으며, 지진해일의 초기 파형은 Manshinha와 Smylie (1971)의 Green function method에 의해 산출하였다. 진앙 깊이, 융기부의 폭과 길이, 융기고는 지진 규모와 융기부 면적, 융기고간의 경험적 관계식과 Aida (1984) 모형을 원용하여 각각 2 km, 30 km, 90 km, 760 cm로 선정하였으며 주향각 [strike angle], 단층경사각 [slip angle], dip angle은 각각 240o, 40o, 90o로 선정하였다.
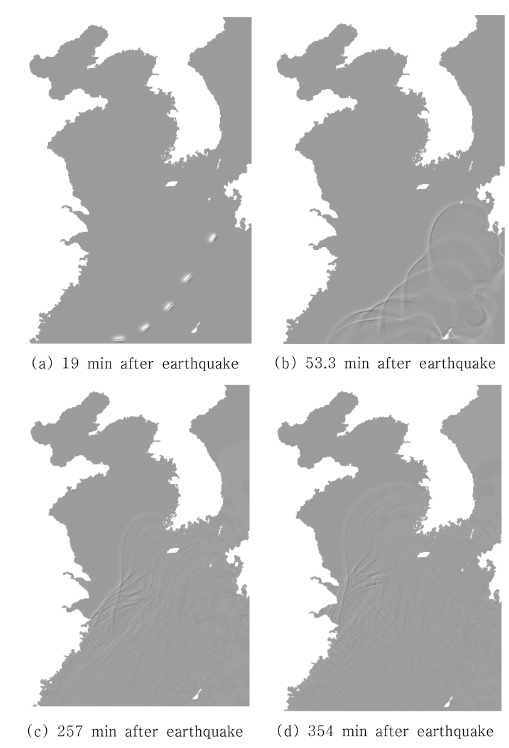
지진발생시 초기 해수면형상은 해저면의 수직변위의 움직임과 같다는 인식에 기초하여 초기 해수면형상을 산출하였으며 (Manshinha and Smylie, 1971) 단층의 면적이 수심에 비하여 넓고, 단층의 파쇄에 의해 해저 지반의 융기가 5초 이내로 순간적으로 진행되면, 해저지반의 상승 및 하강 변위량을 그대로 수면의 초기파형으로 둘 수 있다 (Cho et al., 2002). Fig. 4에는 수치적으로 모의된 지진해일의 전파과정을 도시하였다. 지진해일 발생 후 110여분 경과 후 선도파랑이 제주도 남해안에 도달하며, 약 250분 경과 후 우리나라 남해안에 내습하였다. 257분 경과 후 회절파가 우리나라 서해안에 도달하는 것을 확인할 수 있으나 대륙붕 유입부에서 상당 부분 반사되어 서해안으로 직접 유입되는 파랑에너지는 상대적으로 적으며 원역에서 파고는 2~3 m에 분포하였다.
3. 기본방정식
기본방정식으로는 수치적으로 강건한 파랑모형인 Navier Stokes 식과 질량보존식을 사용하였으며 고정 계산망에서 고형물의 기하학적 특성을 기술하기 위한 부분면적계수, Af와 Vf를 활용하여 이를 기술하면 다음과 같다 (Fig. 5 부분면적 계수와 부분체적 계수 Af와 Vf의 정의도 참조).
Fig. 5.
Schematic sketch showing the calculation of area and volume fraction coefficients, Af and Vf for solid object (shaded area) imbedded in a rectangular grid.

여기서 ρ는 밀도, ũ는 유속 벡터, τ는 점성과 난류에 성분전단응력 벡터, F는 부분 유체 함수로 유체 내에서는 일의 값을 지니며 그렇지 못한 경우 영의 값으로 수렴된다. 자유수면을 지니는 검사체적에서 평균을 취하는 경우 부분 유체함수는 영과 일 사이의 값을 지니며 계산망을 통해 유체가 유동하는 경우 시공을 통해 상이한 값을 지니게 된다. (1), (2), (3)에 기술된 동수역학 모형은 정교한 수치기법인 VOF(volume of fluid) 기법을 사용하여 수치해석 하였다.
4. 수치검증
전술한 수치모형의 검증을 수행하기 위해 규칙파와 불규칙파를 대상으로 일정경사면에서의 처오름 과정을 수치모의 하였다. 수치모형의 검증은 가장 포괄적인 수리모형실험 결과를 토대로 제시된 처오름 높이를 중심으로 수행하였다.
Fig. 6에 도시된 수치수조의 제원은 길이 230 m, 수심 12 m, 폭 20 m이며 수조의 우안에 사면경사가 30o인 구조물을 거치하여 처오름을 유도하였으며 도시된 계산영역은 총 200만여 개의 절점을 사용하여 이산화 하였다. 처오름 과정에서 발생하는 마찰손실을 반영하기 위해 사면 재질의 roughness height는 0.01 m로 조절하였다.
수치모의에 사용된 파랑의 제원은 Table 1에 수록하였으며 파랑은 방파제 전면에서 230 m 이격하여 설치된 wave paddle를 사용하여 조파하였다.
Table 1.
List of wave conditions
| Case | H & Hs [m] | T & Tp [s] |
|---|---|---|
| Run M1 | 3 | 7 |
| Run M2 | 3 | 8 |
| Run M3 | 3 | 9 |
| Run M4 | 3 | 10 |
| Run M5 | 3 | 11 |
| Run M6 | 3 | 12 |
| Run R1 | 3 | 7 |
| Run R2 | 3 | 8 |
| Run R3 | 3 | 9 |
| Run R4 | 3 | 10 |
| Run R5 | 3 | 11 |
| Run R6 | 3 | 12 |
4.1 불규칙 파랑의 조파
불규칙 파랑의 경우 JONSWAP 스펙트럼을 추종한다는 가정을 토대로 조파판 속도 시계열 자료는 Random phase method를 사용하여 모의하였으며 그 과정을 정리하면 다음과 같다 (Frigaard and Anderson, 2010).
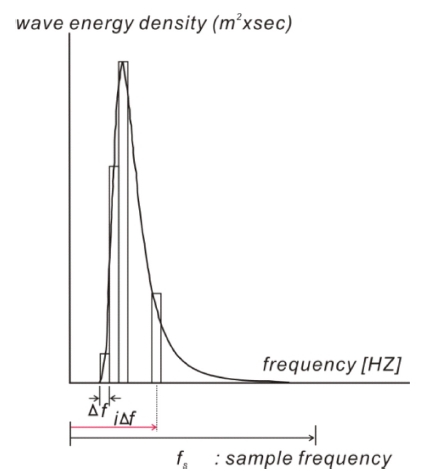
A 먼저 target wave height를 결정하고 이에 해당하는 JONSWAP 스펙트럼을 선택한 성분파랑의 수 N 만큼 등간격, Δf, 으로 분할한다 (Fig. 7 참조). JONSWAP(the Joint North Sea Wave Project) 스펙트럼을 기술하면 다음과 같다.
여기서 ωp는 첨두 주파수, γ는 첨두 증강계수, αp는 Phillips 계수를 나타낸다. 실해역의 경우 γ는 1~6 사이, αp는 0.0081~0.1사이에 분포한다. γ와 αp가 각각 1과 0.0081의 값을 지니는 경우는 완전히 발달된 풍성파군에 해당되며 조파수조의 경우는 이보다 큰 값이 관측된다. 본 연구에서는 사용된 수치수조를 고려하여 γ= 3, αp= 0.025, σ = 0.08의 값을 차용하였다.
B 선택된 i번째 성분파랑의 파고, σζ(fi)를 다음과 같이 산출한다.
C piston 형태 조파판 stroke의 스펙트럼 σχ2(fi)은 다음과 같이 정의되는 Biesel (1951) 의 전환함수
에 준거하는 경우 다음과 같이 기술될 수 있다.
여기서 H는 파고, So는 조파판 stroke, k는 파수, h는 수심을 각각 나타낸다.
D 이어 Nyquist 주파수 보다 작은 주파수를 지니는 성분파랑에 대해 총 N개의 복 소수 Fourier 계수 C (fi) = A (fi) + iB (fi)를 산출하며 이 때 A와 B는 각각 다음과 같이 정의된다.
여기서 ψ (fi)는 0과 2π사이에 2π 균일하게 분포하는 무작위 변량으로 i번째 성분파 랑의 위상을 나타낸다.
E Nyquist 주파수 fN보다 우월한 주파수 성분파랑에 대해서는 전 단계에서 산출한 Fourier 계수의 mirror image를 투영한다.
여기서 윗첨자 *는complex conjugate을 나타낸다.
F C에 대한 Inverse Fourier transform 을 수행하는 경우 Wave paddle 위치에 대한 시 계열 자료 X(t)를 다음과 같이 산출한다.
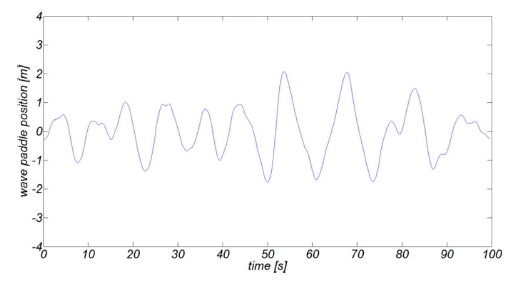
Fig. 8에는 모의된 조파판 시계열 자료를 도시하였다.
4.2 수리모형실험에 기초한 처오름 높이에 대한 경험적 접근
수치모형의 검증에 사용된 수리모형실험 결과를 처오름 높이를 중심으로 정리하면 다음과 같다.
규칙파의 경우 현재 가장 신뢰할 수 있는 처오름 산정식은 Hunt(1959)에 의해 제시되었으며 이를 기술하면 다음과 같다.
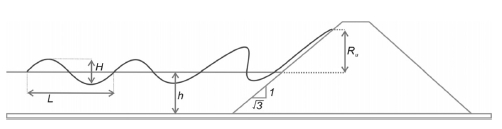
여기서 Ru는 처오름 높이, H는 파고, L은 파장, θ는 방파제 사면경사, ξ′은 Iribarren number 혹은 쇄파 상사 변량을 나타낸다(Fig. 9 참조).
불규칙 파랑의 경우 Van der Meer와 Janssen (1994)등은 Hunt(1959)의 연구결과를 확장하여 다음과 같이 제시한 바 있다.
여기서 γh γf γβ γb는 각각 전빈, 표면 조도, 비스듬한 입사각도, berm 등이 지니는 처오름 감쇄효과를 반영하기 위한 인자를 나타낸다.
반사가 현저한 경우 처오름 산정식은 다음과 같이 수정되며
규칙파의 경우 a는 1.31, 불규칙 파랑 1.17, Cr은 반사계수로 다음과 같이 기술될 수 있다 (Zanuttigh and Van der Meer, 2006).
4.3 수치결과
Fig. 10와 Fig. 11에는 규칙파와 불규칙파를 대상으로 수행된 수치모의에서 관측된 처오름 높이를 각각 도시하였다. 규칙파의 경우 상당히 양호한 결과를 얻을 수 있었으나 불규칙파의 경우에는 다소간의 편차가 관측된다. 또한 규칙파에 비해 처오름 높이가 감소하는 것을 알 수 있으며 이러한 현상은 불규칙 파군에서 흔히 관측되는 성분파랑간의 phase mixing에 기인하는 것으로 판단된다 (Gramstad and Stiassnie, 2013). 불규칙파를 구성하는 성분파랑 사이에 진행되는 상쇄 간섭으로 수면변위는 단순중첩보다 작아질 수 있다. 이 경우 관성력은 감소되며, 이로 인해 처오름 높이가 낮아진 것으로 판단된다.
Fig. 10.
Variation of Run-up Height with period under regular waves (black solid line: Hunt with no reflection, gray solid line: Zanuttigh and Van der Meer with reflection, circle: this study).
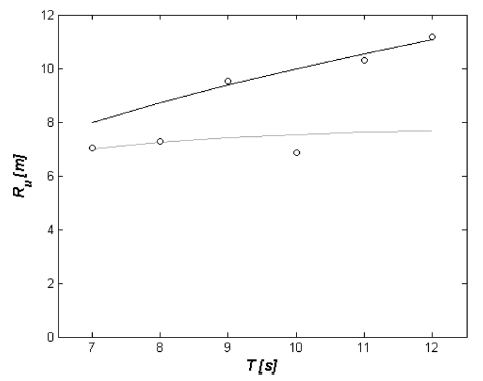
Fig. 11.
Variation of Run-up Height with period under random waves (black solid line: Van der Meer and Janssen with no reflection, gray solid line: Zanuttigh and Van der Meer with reflection, circle: this study).
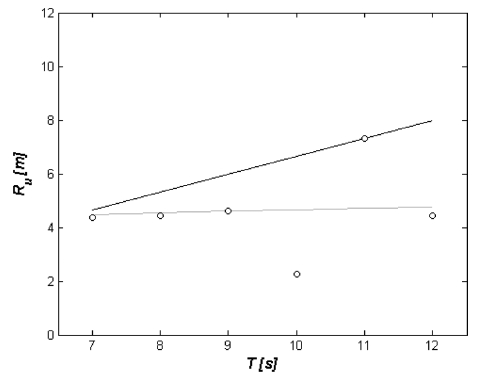
수리모형실험에 기초한 경험식에서는 초과확률이 2%인 처오름 높이 Ru98를 다룬다. 이에 비해 본고에서 수행한 총 모의시간은 120초 내외로 수리모형실험에 비해 sample space가 충분하지 못한 것으로 판단된다.
전술한 문제는 내부조파와 Energy Absorbing Boundary condition을 사용하여 충분한 모의시간을 확보하는 경우 해결될 수 있으나 삼차원 수치수조에서의 내부조파와 Energy Absorbing Boundary condition 구현을 위한 Sponge layer에서의 감쇄계수 연직 분포에 관해서는 아직 더 많은 연구가 필요해 보인다(Cho and Kim, 2004).
전술한 사유로 인해 Ru98대신 총 모의 기간내 관측된 최대 처오름 높이로 취하여 다소간의 편차가 발생한 것으로 보이나 전체적인 일치도는 비교적 양호한 것으로 판단된다.
5. 지진해일로 인한 hybrid breaker의 처오름 높이 저감효과
5.1 지진해일 조파 이론 검토 - Solitary wave와 Leading Depression N (LDN) wave
Solitary wave는 지진해일의 모의를 위해 가장 빈번히 사용되어 왔으며, Piston 형태의 조파판을 사용한 solitary wave의 조파기법이 1979년 Goring에 의해 제시된 이후 지진해일의 전파특성, 처오름, 연안에 미치는 파력 등을 규명하기 위한 많은 연구가 진행된 바 있다 (Synolakis, 1986; Ramsden, 1993). Goring (1979)에 준거하여 조파된 Solitary wave는 생성 후 안정화되기까지 상당한 거리(수심의 80배)가 소요되어 비교적 긴 수조를 필요로 한다. 이러한 현상은 Synolakis(1990)가 지적한 대로 Goring (1979)이 유도과정에서 아직 조파과정에 있는 지진해일의 파속을 최종 목표하는 solitary wave의 그 것과 동일하게 유지한 것에 기인하며 이를 조파 단계별 파고를 반영하는 경우 개선될 수 있다.
순간적 지형변화로 생성되는 지진해일의 특성상, 생성역역 인근에서 관측되는 파형에는 수위 상승뿐만 아니라 수위 하강도 포함된다. 지진해일의 전파과정에서 여러 수위하강은 단일한 성분으로 서서히 융합된다. 수위하강은 유체역학의 시각에서 보는 경우 매우 불안정하나 긴 파장으로 상당히 빠른 속도로 진행되는 지진해일의 특성상 전술한 수위하강 성분은 수위상승 성분과 연하여 진행될 수 있다 (LDN wave). 이러한 수위하강 성분은 지진해일 내습 전 해안선이 일시적으로 전진하는 현상과 관련이 있으며 1995년에 발생한 Mexico 지진해일에서 관측된 바 있다. 전술한 LDN 파형은 Tadepalli와 Synolakis (1994)에 의해 처음 소개된 이후 관측치에 비해 처오름 높이가 작다는 Solitary wave의 한계를 극복할 수 있는 것으로 알려지면서 점차 그 차용 범위가 확산되는 추이로 보인다. 이러한 수월성은 LDN 파형이 Solitary wave전면에 파곡이 배치된 형태로 Solitary wave에 비해 상대적으로 큰 파고를 지니는 것에 기인한다. 그러나 아직까지 LDN 파형에 대한 정확한 이론적 근거는 상승파와 하강파의 여러 결합을 대상으로 비선형 천수방정식에 기초한 Madsen과 Schffer (2010)의 연구에서 알 수 있듯 정립까지는 아직 더 많은 노력이 필요해 보인다.
여기서 논의의 전개를 위해 Goring (1979)의 Solitary wave 조파기법을 정리하면 다음과 같다. Goring (1979)은 Solitary wave가 극장파라는 사실에 준거하여 조파판에서 다음과 같이 정의 되는 경계조건을 사용하였다
여기서 ξ는 piston type 조파판 위치, ũ(ξ,t)는 조파판에 접해있는 수입자의 수평방향 유속성분을 나타낸다. 이어 수입자 수평방향 유속성분이 전 수심대역에서 균일하게 유지 된다는 가정을 수행하고 ũ(ξ,t)를 수심평균 질량 보존식으로부터 취하였다. 이 경우 ũ(ξ,t)는 다음과 같이 기술될 수 있다.
여기서 η는 해수면 변위, c는 파속을 나타낸다. Goring (1979)은 Solitary wave의 조파를 위해 해수면 변위로 Boussinesq 식의 해를 취하여 η를 다음과 같이 기술하였다.
여기서 H는 파고,
k = 3 H / 4 h 3 c = g ( h + H )
조파판의 위치 ξ는 식 (19)와 (20) 으로부터 다음과 같이 산출되며
조파판의 Stroke S는 식 (21)으로부터 2H/kh로 주어진다.
전술한 Goring(1979) 조파법은 아직 조파과정에 있는 지진해일의 파속을 단계별 단파 파고에 기초하여 산출하는 경우 개선될 수 있으며 이 과정을 정리하면 다음과 같다(Mohammadi, 2009).
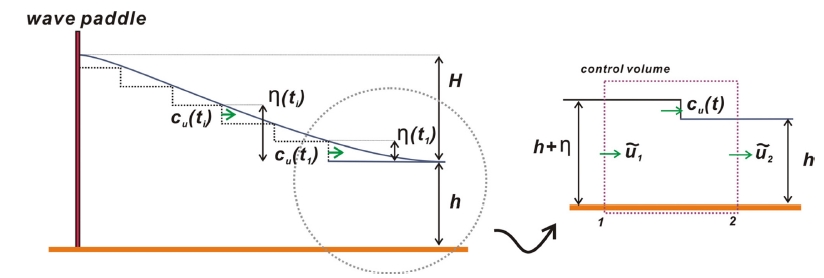
연속한 Solitary waves를 조파가 진행됨에 따라 파고가 단계별로 상승하는 단파의 조합으로 해석하고 Fig. 12에 도시된 통제용적에 질량보존식과 운동량 보존식을 적용하는 경우 다음과 같은 관계식을 얻을 수 있으며
이 과정에서 연직방향 가속도는 미미하여 압력은 정수압분포를 추종한다는 가정을 수행하였다.
또한 ũ1은 depth averaged continuity Eq. 으로부터 다음과 같이 기술될 수 있으며
통제용적 하류단에 아직 파형이 전이되기 전이라 가정하면 ũ2는 영으로 근사할 수 있으므로, 식 (22), (23)으로부터 파속은 다음과 같이 기술될 수 있다.
여기서 η는 시간에 종속하는 조파단계별 단파파고를 나타내며 조파과정에서 파속을 일정하게 유지한 Goring (1979)의 방법과 차별화 된다.
식 (25)을 식 (24)에 대입하고 정리하면 조파판의 속도 ũ는 다음과 같이 기술될 수 있다.
수치적 구현을 위해 식 (26)을 차분화하는 경우 임의의 시간 t = nΔt에서의 조파판의 위치 ξn는 다음과 같이 기술될 수 있다.
본고에서는 지진해일의 초기파형에서 관측되는 하강성분과 상승성분이 진행과정에서 융합되어 생성되는 것으로 추론되는 LDN 파형의 융합과정을 모의하기 위해 파형으로 음양의 solitary를 연이어 조파하였으며
여기서 xp와 xm은 각각 positive hump, depression wave의 위치를 나타낸다.
조파판의 stroke length S와 조파지속시간 T는 Goring(1979)과 동일하게 T = 7.8 ⁄ kc + S ⁄ c와 S = 2H⁄ kh를 사용하였으며 단일 solitary wave의 경우 조파판의 위치는 다음과 같이 기술될 수 있다.
여기서
2장의 수치결과를 토대로 LDN wave의 파고는 토대로 각각, 5 m, 6 m로 선정하였으며, H = 6 m의 경우 식 (30)으로부터 산출된 조파판 속도는 Fig. 13에 도시하였다.
5.2 수치모의
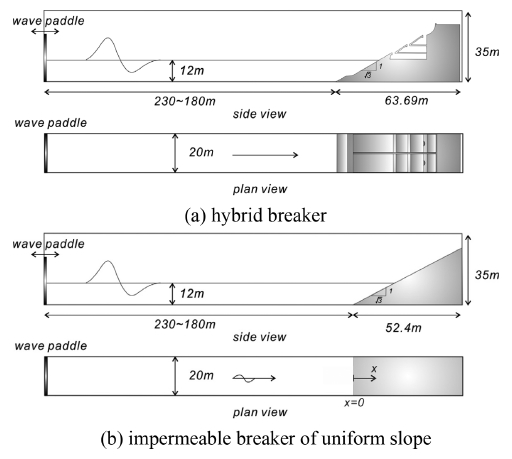
지진해일로 인한 hybrid breaker의 처오름 저감효과를 해석하기 위한 수치모의를 수행하였다. 지진해일 선도파형은 정확한 모의를 위해 5.1절에서 다룬 LDN wave 조파기법을 활용하여 조파하였으며 수치모의에 사용된 수치수조는 Fig. 14a에 도시하였다. 저감되는 처오름량을 산출하기위해 단조사면에서의 처오름과정도 수치모의하였다 (Fig. 14b 참조). 수치수조의 제원은 가로 243.69~293.69 m, 폭 20 m, 높이 35 m 이며 도시된 계산영역은 총 190만 여개의 절점으로 이산화 하였다.
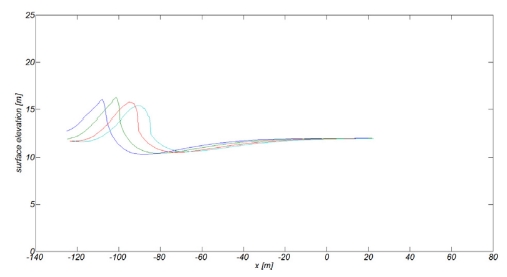
Fig. 15에는 조파판 전면 수역에서 관측되는 LDN 파형의 순차적 snapshot을, Fig. 16에는 일정 수심부 여러 지점에서 관측된 파형의 시계열 자료를 도시하였다. Fig. 17에는 비교를 위해 조파판 전면 수역에서 관측되는 Solitary 파형의 순차적 snapshot을 도시하였다.
Fig. 16.
Time series of water surface elevation at various locations as LDN wave are passing by (H = 6 m).
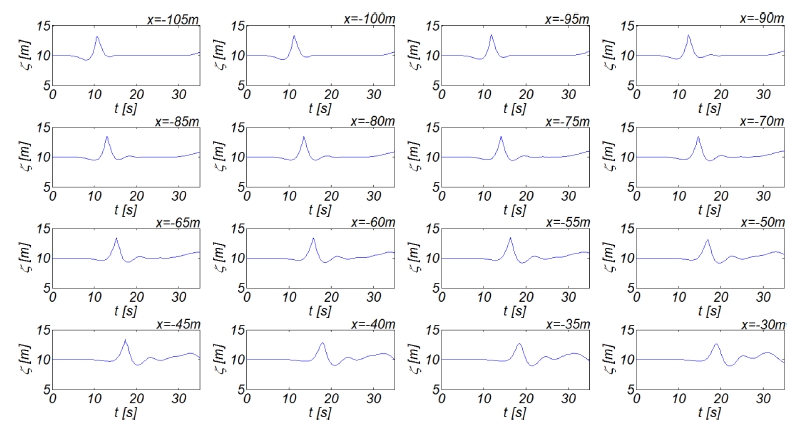
Fig. 17.
Snapshots of numerically simulated Solitary waves as it propagates toward the shore (H = 4 m).
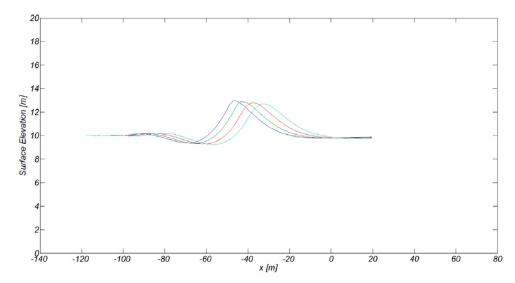
LDN wave의 경우 선행하는 파곡과 후행하는 파봉간의 파속 차이로 파가 진행될수록 파봉과 파곡간의 거리는 점차적으로 감소하며, 파형 전면 경사는 급해지는 것으로 보인다. 또한 파가 진행될수록 파고는 감소하며, 파형은 상대적으로 풍만해지는 것으로 보인다(Fig. 15 참조). 조파판 전면 수역에서는 목표하는 LDN 파형이 조파된 것으로 관측되나 (x = -105 m, -100 m, -95 m, -90 m, -85 m, -80 m), 방파제 전면수역에서는 tail 부분에 여러 scale의 요동이 관측된다 Fig. 16 참조). Soltary wave의 경우 진행과정에서 파형은 비교적 일정하게 유지되는 것으로 보이나 tail 부분에서는 LDN 파형의 경우와 동일하게 작은 요동이 관측되나 크기와 규모는 상대적으로 작다 (Fig. 17 참조).
이러한 현상은 현재 지진해일 수치해석의 주류를 이루는 Boussinesq 모형에서 기보고된 안정된 LDN wave 파형과는 상이한 것으로, 이는 LDN wave를 구성하는 여러 성분파가 상이한 파속으로 서로 나뉘는 분산에 기인하는 것으로 판단된다 (Zhao et al., 2012). Mohammadi (2009)가 언급한 바와 같이 수리모형에서 solitary wave 조파 과정에서 우리가 이제껏 경험했던 어려움과 Boussinesq 계열 파랑모형 유도 과정에서 예외 없이 수행되는 파랑의 비선형성과 분산성이 균형을 이룬다는 가정을 상기하면 우리의 결과가 보다 큰 설득력을 지닌 것으로 판단된다(Mohammadi, 2009).
이상의 논의를 종합하면 파형 tail 부분에서 관측되는 여러 scale의 요동은 파동계가 지니는 고유한 불안정성이라 판단되며, 따라서 이후 수치모의에서는 본고에서 제안된 수정 LDN wave 조파기법을 유지한다.
5.2.1 LDN wave와 Solitary wave에 의한 처오름 높이 비교
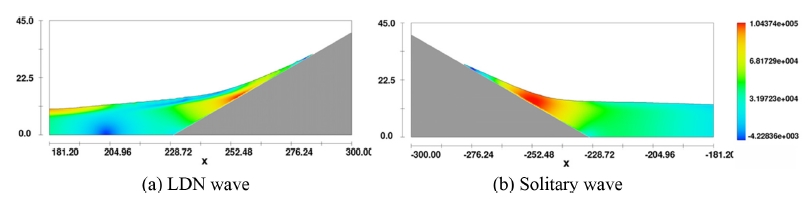
LDN wave와 Solitary wave에 의해 결과되는 처오름 높이를 비교하기 위해 단조사면에서의LDN wave와 Solitary wave의 처오름 과정을 수치모의 하였다. Fig. 18과 Fig. 19에는 처오름 높이가 그 정점에 도달한 순간에서의 자유수면 snap shot을 각각 도시하였다. 수치모의 결과 파고 5 m인 지진해일의 경우 LDN wave에 의한 처오름 높이는 20.01 m, Solitary wave에 의한 처오름 높이는 16.74 m로 각각 관측되었으며, 파고 6 m의 경우 LDN wave의 처오름 높이는 24.27 m, Solitary wave 처오름 높이는 21.84 m로 관측되었다. 이는 Solitary wave에 기초하는 경우 처오름 높이가 과소하게 평가될 수 있다는 기존의 연구결과와 그 맥을 같이 한다 (Tadepalli and Synolakis, 1996).
5.2.2 Hybrid Breaker의 처오름 저감 효과
수치모의에 사용된 Hybrid Breaker는 3개의 유수실과, 전면 거치된 30o의 경사면으로 구성된다. 수치모의 결과 지진해일고 5 m의 경우 복합단면 및 유수실이 있는 경우 처오름 높이가 17.41 m로 계산되었고 지진해일고 6 m의 경우 처오름 높이는 21.86 m로 계산되었다. 복합단면 및 유수실의 지진해일 저감 효과를 비교하기 위해 일반 경사 단면의 경우와 비교하면 H = 5 m의 경우 약 13%, H = 6 m의 경우 10%정도의 처오름 저감 효과를 확인하였다.
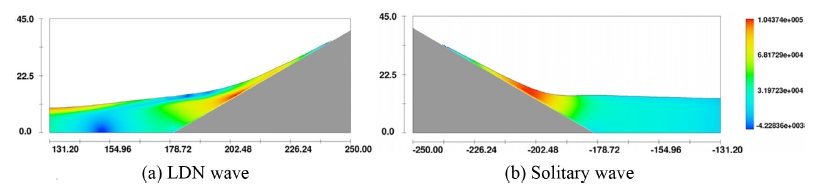
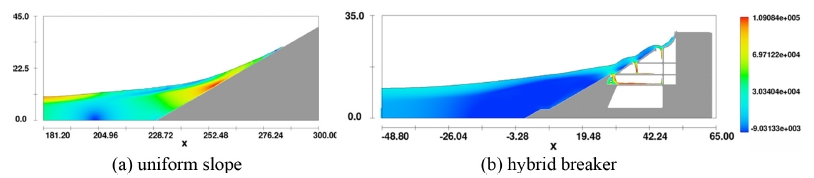
이러한 현상은 모의 전 예상과는 상이한 것으로 지진해일의 강도가 커질수록 높은 파형이 지니는 보다 큰 관성력이 방파제 경사면 처오름 과정에서 그대로 유지되어 유수실로 유입되는 유량이 감소하여 발생하는 것으로 판단된다 (Fig. 20, 21 참조). Table 2에는 수치모의결과를 정리하였다.
Fig. 20.
Snap shots of water surface profile over hybrid breaker when the run up due to LDN wave reaches its maxima (H = 5 m, color contour for water pressure in N/m2).
6. 결 론
유라시아판 경계에서 수백km 떨어져 있는 한반도는 지진으로부터 비교적 자유롭다는 통설과는 달리 우리나라 서해안과 마주하는 오키나와 단층대에는 유라시아판의 동진, 태평양판의 서진, 필리핀판의 북진 등으로 인해 상당한 응력이 누적되어 있다. 유라시아판 하부로 매년 7 cm/yr 의 속도로 섭입되고 있는 필리핀해판으로 오키나와 단층대가 활동하는 경우 우리나라 서해안은 상당한 피해를 받을 것으로 예상된다.
서구의 경우 지진해일로 인한 처오름 제어는 홍수림(mangrove forest)을 활용한 기법을 중심으로 활발히 진행되는 듯하나, 집약적 연안개발이 이미 진행된 우리나라의 경우 홍수림(mangrove forest)을 활용한 제어에는 상당한 면적이 요구되어 차용이 어려운 것으로 보인다. 따라서 심미적으로 우수하고 친환경적인 새로운 지진해일 방재시스템 개발이 시급한 과제로 판단된다. 이러한 시각에서 본고에서는 총 세 개의 유수실과 전면에 경사면이 배치된 hybrid breaker가 지니는 처오름 저감효과를 이용한 지진방재 시스템이 제시되었다.
지진해일에 대한 기존의 연구는 수리모형실험의 경우 광활한 수역의 재현이 필요하다는 점과 이를 해결하기 위해 왜곡모형 차용시 수반되는 scale effect로 인해, 이차원 Boussinesq모형과 Solitary wave에 기초한 수치해석이 그 주류를 형성하여 왔다.
최근 Solitary wave에 의한 처오름 높이가 관측치를 하회한다는 인식에 기초하여 지진해일 내습전 해안선이 전진하는 현상을 재현할 수 있는 Leading Depression N (LDN) Wave가 제시되었으며, 이후 LDN Wave에 기초하는 경우 지진해일에 대한 보다 정확한 모의가 가능하다는 연구결과가 Zhao 등 (2012)에 의해 기 보고된 바 있다.
이러한 성과에도 불구하고 수리모형 실험의 경우 안정적인 Leading Depression N (LDN) Wave 의 구현에 상당한 어려움을 겪는 듯하다. 이러한 이차원 Boussinesq 모형과 삼차원 수리모형 실험에서의 상충된 결과는 이차원 Boussinesq 계열파랑 모형의 유도과정에서 예외 없이 수행되는 파랑 비선형성과 분산성이 균형을 이룬다는 가정과 이로 인해 특히 심해역에서 다소 과소하게 평가될 수밖에 없는 파랑 주파수 분산성에 기인하는 것으로 판단된다.
이러한 시각에서 본고에서는 전술한 Boussinesq 계열 파랑모형의 한계에서 자유로운 삼차원 수치수조에서 자연에서 관측되는 지진해일에 근접한 LDN 파형 조파가 가능한 수정 조파기법이 활용되었다. 이어 수정 LDN wave 조파기법과Navier Stoke 식에 기초하여 제시된 Hybrid Breaker의 지진해일 처오름 저감효과를 수치 해석하였다.
수정 조파기법에 의한 모의 결과 일정수심부에서 안정적 LDN 파형이 유지된다는 Boussinesq 모형에 기초한 Zhao 등(2012)의 결과와는 상이하게 조파 후 down wave 지점에서 관측된 시계열 자료에서는 LDN 파형의 tail 부분에서 여러 scale의 작은 요동이 관측되었다. 이러한 tail 부분의 작은 요동은 Mohammadi (2009)가 수행한 수리모형결과에서도 보고된 바 있으며, LDN wave를 구성하는 여러 성분파가 상이한 파속으로 인해 서로 나뉘는 분산으로 인해 생성되는 것으로 판단된다. 이러한 추론은 Boussinesq 계열 파랑모형 유도 과정에서 예외 없이 수행되는 파랑의 비선선형과 분산성이 균형을 이룬다는 가정에 기초한다. 이상의 논의를 토대로 전술한 tail 부분의 작은 요동은 파동계가 지니는 고유한 불안정성으로 판단하였다.
파랑모형의 검증은 불규칙 파랑을 대상으로 기 수행된 수리모형 실험결과 중 처오름 높이를 중심으로 수행되어 수리모형 실험결과에 상당히 근접한 처오름 높이를 얻었다. 세 개의 유수실과 전면 경사면으로 구성된 Hybrid Breaker의 경우 일반 경사제에 비해 H = 5 m의 경우 약 13%, H = 6 m의 경우 10%정도의 처오름 저감 효과를 지니는 것으로 모의되었다. 이러한 현상은 모의 전 우리의 예상과는 상이한 것으로 지진해일의 강도가 커질수록 높은 파형이 지니는 보다 큰 관성력이 방파제 경사면 처오름 과정에서 그대로 유지되어 유수실로 유입되는 유량이 감소하여 발생하는 것으로 판단된다.