1. 서 론
우리나라의 서해안과 남해안은 크고 작은 내만과 갯벌로 이루어져 있어 영양염류와 먹이 생물이 풍부하고 해양생물의 서식 및 산란장으로서의 가치가 높다. 그러나 1960년 후반부터 경제개발을 위하여 연안역에서의 대단위 매립 및 간척사업이 추진되고 많은 임해 공업단지가 조성됨에 따라 인근지역의 인구가 증가하고 내만으로의 생활하수 유입량이 증가함에 따라 연안의 반폐쇄성 해역들의 수질악화가 시작되었다. 또한 1970년대 초반부터 시작된 4대강 유역 개발 사업으로 인하여 하구둑이 건설되면서 하구 및 만의 생태적 자정기능을 상실하게 되었으며, 1980년대 이후 농업용지 확보를 위하여 추가적인 매립 및 간척을 실시한 결과 많은 면적의 갯벌이 없어지고, 자정기능이 약화되고 연안오염이 가속화되었다(Moon, 2012).
이러한 수질문제로는 대표적으로 적조와 빈산소수괴 현상이 있는데 이 중 빈산소수괴(hypoxia)의 경우 기온이 높은 여름 바닥수심 부근에서 발생하기 때문에 발생 전조에 대하여 적조와 달리 가시적인 확인이 불가능할 뿐 아니라 발생 후 대처에 대해서도 매년 문제점이 제기되어 왔다. 대표적인 빈산소수괴 발생지역의 경우 1980년까지 마산만에 국한되어 나타났으나, 1990년대 들어 진해만의 내역에서도 매년 여름철에 형성되고 있다. 이 외에도 통영의 북만, 여수의 가막만, 천수만, 시화호 등에서 매년 상습적으로 빈산소수괴가 발생하고 있다(NFRDI, 2009).
적조와 빈산소수괴 등 수질 오염은 하천 및 호소의 최고-최저 수온과 직접적인 관계가 있으며 수온은 수중생물의 서식환경을 결정하는 가장 중요한 인자이다. 수온은 수면에서의 열 수지분석과 유입-유출되는 하천수량의 영향을 받으며, 연작방향의 혼합에 의한 영향도 받는다. 일반적으로 수온은 매우 중요한 인자임에도 불구하고 뚜렷한 계절적인 변동 특성을 보이기 때문에 큰 시간규모의 변동양상을 예측하기는 수월하지만, 실질적으로 어떤 수중 생물은 1-2일 정도의 한계수온(고수온 또는 저수온)을 넘어서는 조건에서 생존에 위협을 받기 때문에 하천 및 호소 생태관리를 위해서는 적어도 일 단위(daily)로 최고 또는 최저 수온을 예측하는 모델이 필요하다.
월 단위 정도의 장기 수온 예측은 일사량 변화의 영향으로 개략적인 예측이 가능하지만 직접적으로 생물환경에 영향을 미치는 단기간의 수온변화 예측 연구 성과는 미흡한 수준이다. 또한 대부분의 수온변화 예측은 간단하게 기온과 수온의 상관관계 분석에서 도출된 회귀방정식을 이용하여 추정하고 있으나, 추정오차가 큰 경우에는 4~5oC에 도달하고 있기 때문에 특정 시기에 발생하는 수중 생물의 수온 위협에 대한 대책수립 또는 예측이 곤란하다. 또한 최근에는 기후변화의 영향으로 기온변화에 따른 수온변화가 확실하게 예상되나 기온의 변화에 따른 수온의 변화에 관한 연구는 매우 부족하다.
수온자료의 추계학적(推計學的)인 분석은 1960년대부터 시작되었는데 Morse(1970)는 1차 확정모형에 기상자료와 유체-수리 자료를 적용하여 Columbia강에서의 수온을 예측하였다. Song and Chein(1977)은 기온차의 영향을 받는 수온차를 변수로 하여 자기회귀모형을 만들어 수온차를 예측하였다. Caissie et al.(2001)은 캐나다 New Brunswick의 하천에서 회귀분석 기법을 이용하여 하천온도를 추정하였다. Pedersen and Sand-Jensen(2007)은 덴마크에서 선형 회귀분석 기법을 이용하여 11개 하천의 수온자료를 바탕으로 주변, 식생, 지하수 유입, 하수 처리장 등의 영향을 고려하면서 수온을 예측하였다. 기후 변화에 따른 수온변화를 연구한 경우도 있는데. Lyons et al.(2010)은 미국 위스콘신 50 개주에서 미래 수온 예측모형을 개발하였으며, GCM(General Circulation Model)으로 예측된 기온을 이용하여 수질변화를 분석한 연구가 인도에서 행하여졌다(Rehana and Mujumdar, 2012).
국내에서는 Cho et al.(2007)이 해양수산부에서 제공하는 마산만 연안해역의 기온 및 수온 관측자료를 이용하여 기온과 수온의 관계를 분석하였고, Moon(2012)은 마산만과 시화호를 대상으로 혼합층 역산에 의한 표층수온의 시간적 변화양상을 모의하였으며, Cho and Lee(2012)는 일본의 미카와만(Mikawa Bay)에서 2005~2009년 동안 관측한 자료를 이용하여 대기와 수온관계식을 유도하였다. 최근 An and Lee(2013)는 2009년부터 2011년까지 3년 동안 환경부의 수질자동관측소에서 관측한 최소 873개에서 최대 1,083개의 일 관측 자료를 바탕으로 자기상관관계와 교차상관관계를 조사하고 비선형 기온-수온 상관관계를 구축하였다.
본 연구에서는 만경강과 동진강을 포함한 새만금호 주요지점의 기온자료와 수온자료를 입력자료로 하고 인공신경망 모형을 이용하여 해당 지점의 최고 수온과 최저수온에 대하여 일 단위의 단기 예측을 실시하고자 하였다. 단기 예측의 결과는 수중 생물의 서식환경 위험상태를 미리 예측하고 관리하는 데 이용할 수 있다.
신경망 모형은 입력과 출력의 관계가 복잡한 통계자료의 예측에 많이 이용되며 기상자료, 수문자료 등의 장단기 예측에 많이 적용된 연구가 국내외에 있으나 수온의 예측을 위하여 신경망 모형을 적용한 연구는 국내외에 거의 없다. 신경망 모형은 학습을 위한 많은 입출력 자료가 존재할 경우 스스로 학습을 통하여 연결강도를 조정하면서 예측모형을 구성해가는 장점이 있으며 기존의 알고리즘으로 해석하지 못하는 문제를 해결하는 사례가 있다.
2. 신경망이론
신경망이론은 인간의 생물학적 뉴런을 모방하여 형성되었으며 다수의 뉴런이 서로 결합되어 하나의 신경망을 구성한다. 신경망은 벡터형태의 여러 입력자료를 통하여 학습을 실시하고 반복적인 학습에 의하여 내부의 연결강도를 조정하게 된다. 학습된 연결강도를 이용하여 신경망은 주어지는 입력자료에 따라 결과를 출력할 수 있다. 기존의 컴퓨터 프로그램이 정해진 알고리즘에 따라 수행되는데 반하여, 신경망은 입력값과 출력값을 학습하여 연결강도를 결정하고 그로부터 결과를 출력할 수 있게 된다. 신경망 모형의 입력자료와 출력자료는 이진수의 형태 또는 실수형태의 연속적인 값을 가질 수 있으며 학습의 방법에 따라 지도학습 모형과 비지도학습 모형으로 분류할 수 있다. 본 연구에서는 입력자료와 출력자료가 실수형태로 존재하며 관측된 기온자료와 수온자료를 바탕으로 학습을 실시하는 지도학습 모형을 이용하게 된다. 기상자료와 수문자료의 예측을 위해서는 입력층과 출력층으로 구성된 퍼셉트론 모형을 개선한 다층 신경망 모형이주로 이용된다. 다층 신경망 모형은 입력층과 출력층 사이에 은닉층이 존재하며 학습을 통하여 연결강도를 결정하기 위해서 오차를 최소화해가는 알고리즘으로 역전파 알고리즘을 일반적으로 이용한다.
3. 입력자료
환경부에서는 새만금호의 수질관리를 위하여 새만금호 4개 지점(만경, 동진, 신시, 가력 지점)에서 다양한 환경인자를 센서를 이용하여 5분 간격으로 연속 관측하고 있다. 4개 관측지점의 위치를 Fig. 1에 도시하였으며 각 지점에서의 관측현황을 Table 1에 나타내었다. 본 연구에서는 관측된 환경인자의 하나인 수온자료 가운데 2012년부터 2013년까지 2년 동안의 수온 자료를 이용하였다.
Table 1.
Basic information of water quality measurement stations
2012년과 2013년 2년 동안의 전체 자료 개수는 210,528개(= 12개/시간 × 24시간/일× (365 + 366)일)이며, 이 가운데 나타난 결측 자료의 개수를 Table 2에 나타내었다. 전체적으로 2 - 6% 정도의 결측자료를 가지는 것으로 나타났으며 하천 하구지점에 해당하는 동진과 만경 지점의 결측비율이 새만금호배수갑문 지점에 비하여 2배 이상 높게 나타났다.
Table 2.
Number and percentage of missing data
| No. of missing data | Percentage of missing data | |
|---|---|---|
| Dongjin | 11,250 | 5.2% |
| Mangyeong | 12,074 | 5.7% |
| Shinsi | 5,207 | 2.5% |
| Garyeok | 4,366 | 2.1% |
본 연구에서는 이상자료 감지모형의 적용을 위한 사전단계로 수온 자료가 가질 수 있는 가능한 범위(영하 10oC, 영상 40oC 범위)를 벗어나는 자료와 센서에서 결측을 나타내는 지정수치(본 자료의 경우 정수 -9999, 0) 자료는 결측자료로 제거하였다. 이후 이상자료 감지를 위하여 수온 자료의 시간적인 변동양상을 파악하는 과정과 잔차 성분을 이용한 이상자료 진단과정으로 Cho and Oh(2012) 방법을 보완한 방법을 이용하였다. 본 연구에서는 자료 중 가장 최소가 되는 변동양상을 일단위(day unit)로 간주하여 평균보다는 굳건한(robust) 인자로 제시되는 Median 수치와 표준편차보다는 굳건한 통계적인 수치로 제시되는 IQR(inter-quartile range) 또는 MAD(median absolute deviation) 수치(Agresti & Franklin, 2007)를 이용하였다. 또한 박스도표를 이용하여 기준범위 즉, 3 IQR 이상 크거나 작은 점을 극이상점으로 정의하고 이를 벗어나는 경우 이상자료로 간주하여 제거하였다(Kim et al., 2012).
어림성분의 변화 양상은 Robust Smoothing 기법을 이용하여 수행하였다. Robust Smoothing 기법은 자료의 일정한 연속구간(Span)의 자료만을 대상으로 최적 직선(또는 곡선)을 Robust 기법으로 추출하는 방법으로, 비교적 이상자료에 둔감한 방법이다(Cleveland, 1979). 일단 주어진 Span 조건에서 자료의 어림성분이 추정되면, 어림성분과 관측자료의 차이를 잔차성분으로 간주할 수 있으며, 잔차성분에서 Robust 통계매개 변수에 해당하는 Median 및 IQR 정보를 이용하여 비교적 널리 이용되는 이상자료 판단기준을 적용하여 이상자료를 감지하게 된다. 이상자료를 제거한 후 결측치의 획득은 Complete Spline 내삽기법을 이용하였다. 이상자료 감지모형의 적용에 따른 자료의 변화를 고찰하기 위하여 통계정보의 변화값을 Table 3에 나타내었다. 이상자료 감지모형의 적용에 따라 2-4% 정도의 자료가 제거되는 것을 알 수 있으며 평균 및 표준편차의 변화는 크지 않은 것으로 나타났다. 다만 동진과 신시지점에서의 중간값 변화는 비교적 큰 것으로 나타났다.
Table 3.
Basic statistical information before and after outlier removals
4. 모형의 구성
본 연구에서는 수온의 예측을 위하여 하나 또는 그 이상의 이전 수온이 현재의 수온을 결정하는 비선형 자기회귀 시계열로 간주하였다. 또한 외부 입력인 하나 또는 그 이상의 이전 기온이 입력으로써 수온에 영향을 미치는 것으로 간주하였다. 즉, 외부 입력인 기온을 x(t)라 하고, 예측하려는 출력인 수온을 y(t)라 할 때 이를 그림으로 나타내면 Fig. 2와 같다.
Fig. 2.
Configuration of nonlinear autoregressive with external input model(http://kr.mathworks.com/products/neural-network/).

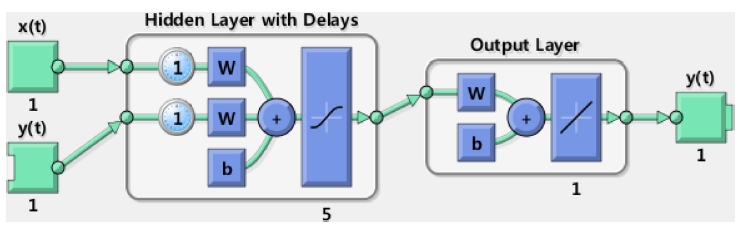
본 연구에서는 Fig. 2의 형태로 가정된 수온-기온 시계열을 해석하기 위한 방법으로 신경망 모형을 적용하였다. 적용한 신경망 모형은 다층 신경망모형으로 이를 그림으로 나타내면 Fig. 3과 같다. 이전의 수온자료와 기온자료를 입력자료로 하여 현재의 수온자료를 예측하는 형태로써 중간에는 은닉층이 존재하고 다수의 입출력자료를 이용하여 학습을 함으로써 입력층과 은닉층의 연결강도, 은닉층과 출력층의 연결강도를 결정하여 가게 된다. 입력층과 은닉층 그리고 은닉층과 출력층은 전달함수를 통하여 연결이 되는데 본 연구에서는 각각의 전달함수로 log-sigmoid 함수와 선형함수를 이용하였다. 이를 수식으로 나타내면 다음과 같다.
Fig. 3과 같이 구성된 신경망의 학습을 위한 알고리즘으로는 역전파 알고리즘을 이용하였다. 역전파 알고리즘은 입력과 출력에 대한 적절한 연결강도의 결정을 위하여 오차함수(error function)를 정의하고 이를 줄여나가게 되는데 경사하강 알고리즘을 이용하게 되며 오차의 값이 출력층에서 입력층으로 역전파되는 방법이다. 본 연구에서는 가공된 자료를 신경망 모형에 적용하기 위하여 Matlab 프로그램을 이용하였으며 학습된 결과를 바탕으로 결과를 도출하였다.
Fig. 3.
Configuration of neural network training (http://kr.mathworks.com/products/neural-network/).
5. 결과 및 분석
본 연구에서는 결과에 영향을 미치는 차수와 은닉층의 개수를 달리하여 모델을 수행하였다. 모형의 수행은 학습을 위하여 전체 자료의 70%를 임의로 이용하였으며 검증을 위하여 15%의 자료를 결과의 예측을 위하여 15%의 자료를 임의로 이용한 후 예측 능력을 판단하였다. 예측의 정도는 실제값과 예측값 사이의 상관계수를 이용하여 판단하였다.
3절에서 기술된 4개 지점에 대하여 최고수온과 최저수온의 예측을 실시하였다. 최고수온의 예측에는 외부입력으로 최고기온과 중간기온, 최저수온의 예측을 위해서는 최저기온과 중간기온을 이용하였다. 각각의 경우에 대하여 은닉층의 개수가 5개일 때 차수를 1, 2, 3으로 달리하며 모델을 수행하였고, 은닉층의 개수가 10개일 때 차수를 2로 하여 계산하였다. 최고수온과 최저수온에 대한 결과를 표로 정리하였으며 그 결과는 Table 5-6과 같다.
Table 5.
Predictions of maximum water temperature
Table 6.
Predictions of minimum water temperature
Table 5와 6에서 보면 모든 결과에서 아주 높은 상관계수를 가지는 것으로 나타났다. 모델링 결과는 은닉층의 개수, 시계열의 차수에 관계없이 높은 상관계수를 가지는 것으로 나타났으며 모형간의 우열은 거의 없는 것으로 나타났다. 최고기온, 중간기온 또는 최저기온을 사용하여도 모델링의 결과는 모두 높은 상관관계를 가지는 것으로 나타났으며 최고수온, 최저수온을 모두 잘 예측하는 것으로 나타났다. 표의 결과에서 기온과 수온의 상관관계가 아주 높은 것을 알 수 있으며, 시계열의 형태 또한 아주 규칙적인 것으로 판단된다.
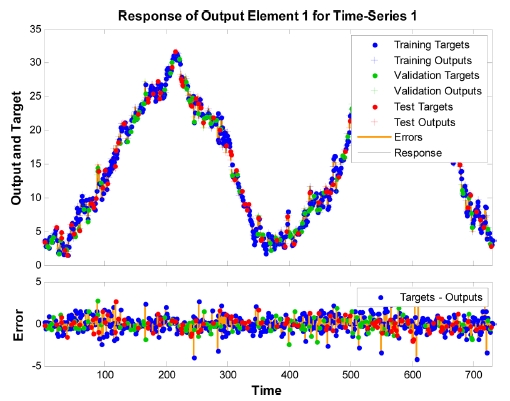
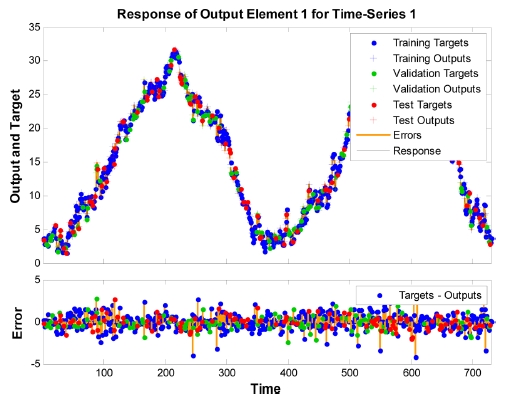
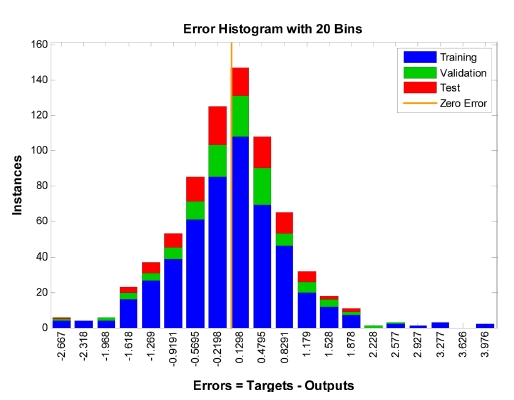
모형의 적용에 따른 결과의 정확도를 파악하기 위하여 학습, 검증, 예측 각각에 대한 오차를 히스토그램으로 Fig. 4-5에 나타내었다. Fig. 4는 부안지점의 최고기온자료를 입력으로 하여 동진지점의 최고수온에 대하여 은닉층의 개수를 5, 이용된 과거자료를 1로 하여 신경망 모형을 적용한 것으로 대부분의 오차는 1oC 이하인 것으로 나타나며 2oC 이상의 오차를 보이는 날은 많지 않은 것으로 나타났다. Fig. 5는 같은 자료에 대하여 입력층의 은닉층 개수를 10, 과거자료를 2로 하여 신경망모형을 적용한 것으로 Fig. 4와 큰 차이를 발견할 수 없었다. Fig. 4와 Fig. 5에 제시된 두 경우에 대하여 실제 값과 모형의 출력 값을 시계열로 나타내어 Fig. 6과 Fig. 7에 비교하였으며 그 오차를 그림으로 나타내었다. 그림에서 보면 은닉층의 개수와 과거자료에 따른 결과의 차이는 크게 보이지 않았으며 특정 지점에서 동일하게 약간 큰 오차를 가지는 것으로 나타났다. 이로 볼 때 특정 지점에서 나타나는 약간 큰 오차는 모형의 부정확성보다는 자료의 부정확성 또는 고려되지 않은 변수에 기인한 것으로 판단된다.
Fig. 4.
Error histogram(predictions of maximum water temperature with maximum air temperature at Dongjin station, hidden layers = 5, used past value = 1).

Fig. 5.
Error histogram(predictions of maximum water temperature with maximum air temperature at Dongjin station, hidden layers = 10, used past value = 2).
6. 결 론
최고수온과 최저수온의 예측을 위하여 기온자료와 수온자료를 이용하였다. 수온의 예측을 위하여 수온을 자기회귀 시계열로 가정하고 외부입력으로 기온이 있는 것으로 가정하였다. 시계열의 해석을 위하여 신경망모형을 이용하였으며 은닉층의 개수, 시계열의 차수, 이용한 기온 등을 달리하여 모델링을 수행하였다.
모델링의 결과 모든 경우에서 아주 높은 상관계수를 나타내었으며 정확성 측면에서 모델간의 뚜렷한 차이를 발견할 수 없었다. 결과에서 판단할 때 수온과 기온은 아주 높은 상관관계를 가지는 것을 알 수 있으며 수온자료는 아주 규칙적인 상관관계를 가지는 것을 알 수 있다. 이와 같이 아주 높은 상관관계를 가지는 것은 외부로부터의 유량의 유입이 상대적으로 작은 것이 큰 원인으로 판단된다. 또한 모델의 적용에 따른 오차를 분석한 결과 대부분의 오차는 1oC 미만으로 나타났으며 일부 특정지점에서 2-3oC 정도의 오차를 보이는 것으로 나타났는데, 이는 모형의 부정확성 보다는 자료의 부정확성 또는 고려되지 않은 입력 변수의 영향으로 보인다.