1. 서 론
해상풍력을 이용한 발전량은 2020년에는 75GW를 넘어설 것으로 예상된다. 이처럼 해상풍력 발전의 성장 가능성은 그 끝을 쉽게 예단할 수 없을 정도로 무한하나, 해상풍력산업은 여전히 과다한 초기투자비용 문제로 어려움을 겪는 듯하다 (Manenti and Petrini, 2010). 이러한 과다한 초기투자비용 문제에는 여러 요소가 작용하나, 그 중 해상풍력 발전체 하부구조물의 보수적 설계로 인해 발생하는 비용은 유체역학의 최근 연구 성과인 Large eddy로 인한 풍력과 파력의 비선형 상쇄간섭을 고려하는 경우 비교적 용이하게 해결할 수 있을 것으로 판단된다(Adrian, 2007).
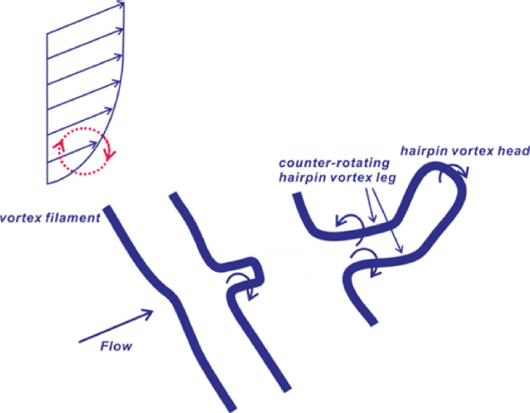
현재 해상 풍력 발전체 하부구조물 설계에는 유체역학의 최근 연구 성과들이 활용되고 있지 않은 듯하다. 그 중 바람으로 해수면이 거칠어지는 경우 해수면 요철로 인해 대기와 해수면의 경계에서 연이어 생성되는 머리띠 모양의 vortex tube (hairpin vortex)와 각 머리띠 모양의 vortex tube의 관상효과가 더해져 출현하는 큰 회오리 (Large eddy)는 해상 풍력 발전체 거동에 상당한 영향을 미칠 수 있다(Adrian, 2007).
전술한 큰 회오리 (Large eddy)는 바람의 진행방향과 반대방향으로 선회한다는 점에서 풍력에 의한 해상 풍력 발전체 변형을 제한하는 역할을 수행할 수 있다. 이처럼 바람으로 해수면이 거칠어진 경우 해수면과 돌풍, 해상 풍력 발전체 사이에는 상당히 복잡한 상호작용이 진행된다. 최근 Cho et al. (2015)는 전술한 상호작용을 풍력과 파력의 비선형 상쇄간섭이라 명하고 수치모의를 통해 비선형 상쇄간섭이 해상 풍력 발전체의 동적 거동에 미치는 영향을 분석하였다. 이 연구에서 Cho et al. (2015)는 Banner와 Melville (1976)이 수행한 풍동실험에서 관측된 vortex tube가 Large eddy와 동일한 성격을 지니는 것으로 판단하였다. Banner와 Melville (1976)의 연구가 지난 칠십년 대에 수행된 것을 감안하면, Banner와 Melville (1976)은 Large eddy의 구조적 특성과 생성과정을 인지하지는 못한 것으로 보인다. 그러나 Banner와 Melville (1976)이 제시한 관측결과에는 평균 풍속계의 진행방향과 반대방향으로의 선회하는 vortex tube가 관측되며 이는 Large eddy의 일반적 특성과 부합한다.
따라서 Banner와 Melville (1976)이 회귀분석을 통해 제시한 풍속분포에는 Large eddy로 인한 진행방향에서의 돌풍 풍속 감소가 기 반영된 것으로 보인다. 이 연구에서 Banner와 Melville (1976)은 황천 시 조도계수를 상향 조정하여 관측결과에 일치하는 평균풍속분포를 얻었다. 이러한 인식을 토대로 Cho et al. (2015)는 수역이 정온한 경우와 황천 시로 구분하여 평균 풍속의 대수 분포 정규화과정에 활용되는 조도계수를 조정하였으며, 이어 수행된 수치모의에서 비선형 상쇄간섭을 고려하는 경우 구조물의 해상 풍력 발전체 변형은 선형중첩모형에 비해 최대 50%까지 감소한다고 제시한 바 있다.
이러한 연구결과는 그 동안의 설계관행 즉, 풍력과 파력을 독립적인 하중으로 간주하고, 각각의 해상풍력발전체 변형을 구한 후 선형 중첩하여 최종 해상풍력발전체의 응답특성을 구하는 경우 매우 보수적인 해상 풍력 발전체 하부구조물이 결과 될 수 있음을 시사한다.
이렇듯 풍력과 파력의 비선형 상쇄간섭은 그 공학적 가치에도 불구하고 이제껏 소홀히 다루어 진 것으로 보이나, 해상풍력산업의 발전을 위해서는 적극적으로 활용되어야 할 것으로 판단된다.
이러한 시각에서 본고에서는 수치모의에 그친 Cho et al. (2015)의 연구결과를 검증하기 위한 수리모형실험이 수행되었다. 파랑의 경우는 5MW급 해상풍력 시범단지가 조성될 예정인 우리나라 서해안 해역에서 관측되는 파황에 가장 근접하는 불규칙 파랑을 얻기 위해 JONSWAP (Joint North Sea Wave Project) 파랑 스펙트럼에 기초하여 Random Phase Method를 사용하여 불규칙 파랑이 조파 되며, 돌풍은 Sirrocco S Blade 편흡입 직렬 사각 송풍기를 사용하여 재현하였다.
2. 해상풍력발전체 하부구조물에 작용하는 외력
해상풍력발전체에 작용하는 풍하중은 공기력 [aerodynamic force]과 해상풍력발전체 거동에 종속하는 motion dependent force로 구성된다. 공기력에 의해 해상풍력발전체의 변형이 발생하는 경우 이 변형은 해상풍력발전체 인근 유동계에 변화를 야기하여 해상풍력발전체에 추가적인 힘과 변형이 유발될 수 있으며 이러한 힘은 self excited force라 불린다.
2.1 풍력
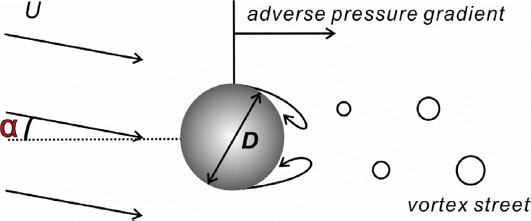
원형모양의 해상풍력발전체 후면에서는 확대되는 흐름단면적과 이로 인한 압력 역구배로 상당히 혼란스러운 흐름이 생성된다. 흐름이 혼란스러워지면 이에 수반되는 에너지 손실로 해상풍력발전체 후면부의 압력은 복원되지 못하고 여전히 전면부에 비해 현저히 작은 값에 머물게 된다. 이러한 압력차로 인해 해상풍력발전체는 흐름방향으로 작용하는 힘에 노출되며, 이러한 힘은 형상항력이라 불리며 다음과 같이 기술될 수 있다.
여기서 CD 는 항력계수로 영각[α, angle of attack]에 종속하며, ρair 는 밀도, A 는 투영단면적을 각각 나타낸다(Fig. 1 참조).
이와 더불어 Von Karman의 vortex street에서 알 수 있듯, 해상풍력발전체 좌단과 우단에서 생성된 소용돌이는 시차를 두고 번갈아가며 down wind 방향으로 휩쓸려간다. 전술한 박리로 인해 생성된 비대칭적인 압력분포는 흐름과 직각방향으로 작용하는 힘으로 이어진다. 따라서 해상풍력발전체는 전술한 형상항력 뿐만 아니라, 주기적으로 방향이 바뀌는 횡력에도 노출되며, 횡력은 다음과 같이 기술할 수 있다
여기서 CL 는 영각 [α, angle of attack]에 종속하는 양력계수, B는 투영단면적을 각각 나타낸다. 횡력 주기 T는 다음과 같이 정의되는 Strouhal 수 S에 종속하며
여기서 n 은 1/T로 정의되는 횡력 주파수, U는 평균풍속, D는 해상풍력발전체 하부구조물의 직경을 각각 나타낸다. T는 해상풍력발전체 하부구조물에서 분리되는 소용돌이의 간격으로도 해석할 수 있으며, 따라서 형상항력의 주파수는 2n으로 정의된다.
주기적인 횡력에 노출되는 경우 해상풍력발전체는 요동하며 이때 진폭은 해상풍력발전체 직경의 절반을 넘지 않으나 Strouhal 주기가 해상풍력발전체의 고유주기에 근접하는 경우 해상풍력발전체 요동은 증폭되어 인근 흐름에 상당한 영향을 미친다. 이 경우 고전적인 풍력 모형은 한계를 지니며 특별한 고려가 필요하다.
2.2 유체역학적 감쇄 [Hydrodynamic damping]
유체 내 해상풍력발전체의 동요는 수입자와 해상풍력발전체 간의 상대속도로 야기하며, 종국에는 해상풍력발전체에 작용하는 형상 항력을 통해 유체역학적 감쇄를 결과할 수 있다. 천해역에 해상풍력발전체가 설치되는 경우, 해상풍력발전체 수중 하부구조물은 강성이 높은 재질로 구성되기 마련이나 이 경우 변위가 상대적으로 작아 유체역학적 감쇄는 미미하다(Adrezin et al., 1996).
2.3 공기역학적 감쇄 [Aerodynamic damping]
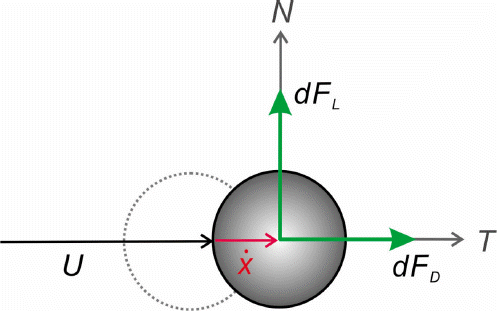
공기력으로 해상풍력발전체가 흐름방향으로 x만큼 이동했다면 (Fig. 2참조) 해상풍력체에 대한 상대풍속 Ur은 다음과 같이 정의되며
, 단위 폭 당 작용하는 항력은 다음과 같이 기술될 수 있다.
, 따라서 C D ρ a i r A U a i r x ˙
2.4 파력
해상 풍력 발전체 하부구조물에 작용하는 파력은 하부구조물의 폭과 파장의 상대적 크기에 따라 small body와 large body로 분류할 수 있으며, small body의 경우 하부구조물로 인한 회절과 파동계 교란을 무시할 수 있으나 large body의 경우 이를 포함하여 해석한다(Kim, 2008).
본고에서 다루는 단파일의 경우 폭[D]는 5 m내외로 설계파 주기를 10초 내외, 수심을 20 m로 가정하면 파장[L]은 121 m로 D/L = 0.04로 small body로 분류되며 이 경우 파력은 Morrison 식에 기초하여 다음과 같이 산출될 수 있다(Morison et al., 1950)
여기서 Cd는 파력에서의 항력계수, Cm는 파력에서의 관성력 계수, A는 투영단면적, V는 하부구조물 단위 길이당 체적을 각각 나타낸다(Sarpkays, 2010).
3. 풍력과 파력의 비선형 상쇄 간섭의 생성기작
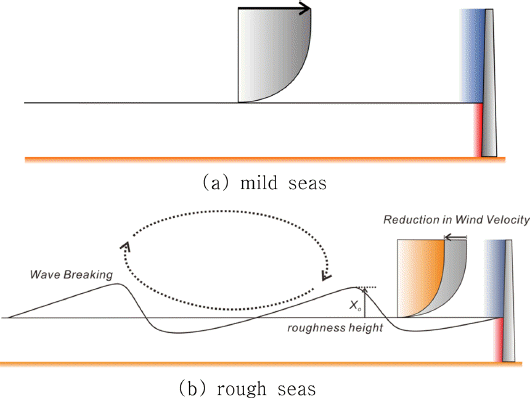
풍력과 파력의 비선형 상쇄 간섭은 바람으로 해수면이 거칠어진 경우 해수면 요철로 인해 대기와 해수면의 경계에서 연이어 생성되는 머리띠 모양의 vortex tube (hairpin vortex)와 각 머리띠 모양의 vortex tube의 관상효과가 더해져 Large eddy가 출현하는 경우 시작된다 (Fig. 3, 4 참조). 전술한 Large eddy는 바람의 진행방향과 반대방향으로 선회하며, 이 경우 대기와 해수면의 경계층 내 평균풍속은 감소하며, 이는 해상 풍력 발전체 변형 감소로 이어질 수 있다 (Fig. 5, 6 참조).
Fig. 5
Vector plot of wind velocity field in the vicinity of the interface between the wind and rough seas clearly showing the development of Large eddy (Adrian, 2007).
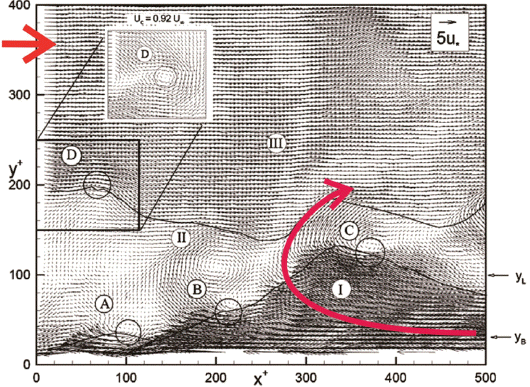
Fig. 6
Schematic sketch of the reduction in wind velocity as mild seas turn into rough seas when wind blows.
Banner와 Melville (1976)에 의하면 황천 시에도 다음과 같이 기술되는 평균풍속 U ¯ a i r ( x )
여기서 xo 는 조도길이를 나타내며, U ¯ r e f
개방해역에서 풍랑이 일고 평균풍속 U ¯ r e f
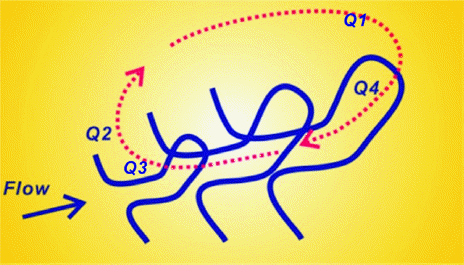
이 밖에도 삼사분면 [Q3, Q4, Fig. 4 참조]에서 내습하는 바람과는 맞서는 모양의 파랑으로 인한 수입자 운동방향, 해양구조물의 대부분을 차지하는 연성구조물(Compliant Structure)의 설계개념의 근간을 이루는 공기역학 감쇄와 유체역학적 감쇄도 풍력과 파력의 비선형 상쇄 간섭에 일정부분 기여하는 것으로 보인다.
풍력과 파력의 비선형 상쇄 과정의 이해를 돕기 위해 운동방정식을 기술하면 다음과 같다 (Chopra, 1995).
여기서 z는 해상풍력발전체 정점에서의 흐름방향 변위, ζζ 는 감쇄계수, ωn 은 고유주파수를 각각 나타내며 기술하면 다음과 같다 (Fig. 7 참조).
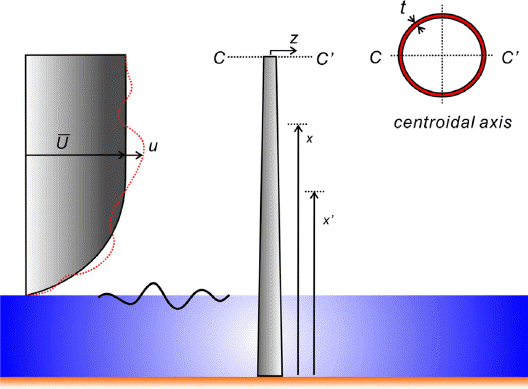
Fig. 7
Definition sketch of coordinate system, centroidal axis, mean wind velocity, and turbulent velocity component.
식 (9), (10)에서 질량 m ˜ c ˜ f ˜ ( t )
식 (13)에서 첫 번째 항은 평균풍속에 의한 감쇄, 두 번째 항은 돌풍에 의한 감쇄, 세 번째 항은 유체역학적 감쇄를 각각 나타낸다.
4. 수리모형실험
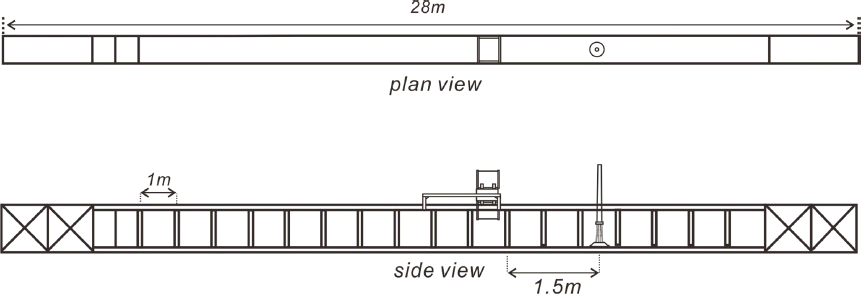
해상 풍력발전체 하부구조물에 작용하는 파력과 풍력의 비선형 상쇄 간섭을 해석하기 위해 5MW급 해상풍력 발전체를 대상으로 한 수리모형실험을 수행하였으며 해상풍력 발전체의 하부구조는 시공이 용이하여 가장 많이 선호되는 mono pile로 취하였다.
4.1 조파수조
4.2 불규칙 파랑의 조파
5MW급 해상풍력 시범단지가 거치될 예정인 우리나라 서해안 해역의 경우 취송 거리가 상대적으로 짧아 파랑의 성장은 취송 거리에 의해 제한된다. 따라서 완전히 성장한 파랑을 대상으로 한 Pierson Moskowitz 스펙트럼보다 성장단계에 있는 파동계를 대상으로 한 JONSWAP 스펙트럼에 기초하는 경우 보다 정확한 기술이 가능하다. JONSWAP 스펙트럼에서는 성장단계에 있는 불규칙 파동계의 특징인 상대적으로 확연히 드러나는 스펙트럼의 첨두 부분은 첨두 증강인자를 통해 재현 가능하다 (Frigaard et al., 2010). 이상의 논의를 토대로 불규칙파랑은 JONSWAP 스펙트럼 Sζζ(ω) 에 기초하여 조파하였으며 이를 기술하면 다음과 같다.
여기서
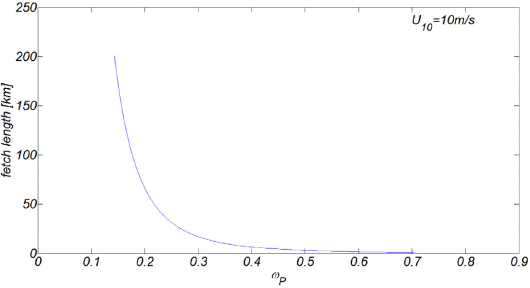
, ω 는 주파수[radian/s], ωp 는 첨두 주파수로 표고 10 m에서의 풍속 U10 과 취송거리 LF 에 의해 다음과 같이 산출될 수 있다.
식 (15)에서 α 는 주파수 스펙트럼 대역폭을 결정하는 인자로 취송거리와 풍속에 의해 결정되며 북해의 경우 0.0081과 0.01 사이에 분포하며, γ는 평균값이 3.3인 첨두 증강인자로 이를 기술하면 각각 다음과 같다.
Fig. 10에는 U10 = 10 m/s인 경우 취송거리에 따른 첨두 주파수 ωp 의 변화를 도시하였다. 취송거리가 증가함에 따라 파랑에너지가 분포하는 대역이 wave-wave interaction에 따라 저주파 대역으로 이동되는 것을 알 수 있다.
목표하는 파랑스펙트럼을 조파하기 위해 먼저 목표 파랑스펙트럼에 해당하는 해수위 시계열자료는 Random phase법을 활용하여 산출하였으며, 이어 조파판의 시계열자료는 다음과 같이 기술되는 Biesel의 전환함수에 기초하여 모의하였다.
여기서 H는 목표파고, So 은 조파판의 stroke, h는 수심, k는 파수를 각각 나타낸다.
구조물 설치위치에서의 통과파 설정시 실험파의 파고 및 주기는 영점교차법 (zero-up crossing)으로 분석하였으며, 평균해면을 상향 통과하는 사상의 평균주기 TZ 는 첨두주기 TP 와 다음과 같은 관계를 추종하며
충분히 숙성된 파동계의 경우[γ = 1], 상기 식은 다음과 같이 전환된다.
4.3 모형제작 및 송풍장치
4.3.1 모형제작
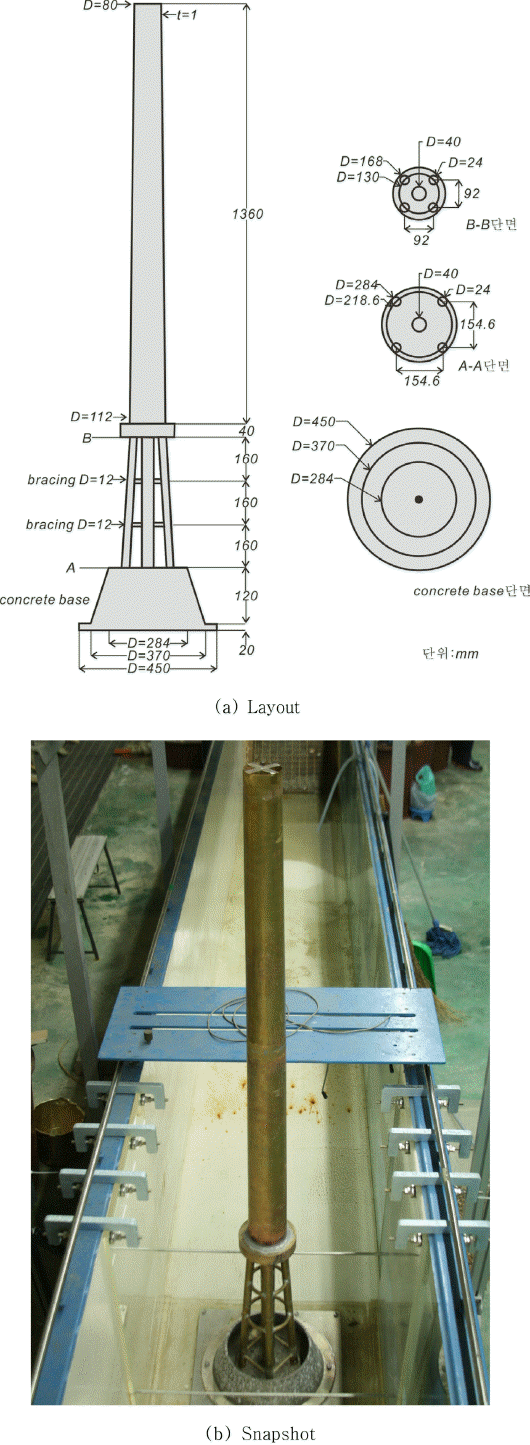
모형의 축척은 수로의 제원, 조파성능, 수심 및 해상풍력발전체의 높이 등을 종합적으로 검토하여 1/50로 결정하였다. 원형에서 해상풍력발전체의 하부구조물 재질은 탄성계수가 200,000MPa인 특수강으로 구성되어 있으며, 50분의 1 축척으로 제작되는 모형의 재질과 탄성계수는 다음과 같이 산출하였다.
A. 동적 상사가 구현된 경우, 모든 외력의 비는 동일하게 유지된다. 또한 해상풍력발전체에 작용하는 주 외력은 바람에 의한 형상항력이므로 다음과 같은 상사 조건이 충족되어야 한다.
여기서 아래첨자 i와 p는 관성력과 압력을 나타내며, 식 (24)로부터 형상항력비율을 결정하는 pR은 다음과 같이 기술될 수 있다.
B. 구조물 동적 거동에 가장 큰 영향을 미치는 인자는 탄성계수로, 동적 상사를 충족하기 위해서는 탄성계수 비율 ER 은 다음과 같은 관계식을 충족하여야 한다.
C. 모형재질을 황동으로 선정하는 경우, 밀도 비율 ρR 은 다음과 같이 산출되며,
D. 이 경우 탄성계수는 다음과 같이 산출되며
E. 전술한 탄성계수는 2,700MPa ~ 3,800MPa에 분포하는 황동의 탄성계수와 부합한다.
이상의 논의를 토대로 해상풍력발전체의 하부구조물의 모형 재질은 밀도가 7850 Kg/m3, 탄성계수가 2,700MPa인 황동으로 제작하였으며 Fig. 11에는 최종 제작된 해상풍력발전체 모형과 제원을 도시하였다.
4.3.2 송풍장치
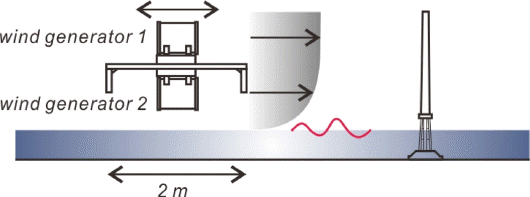
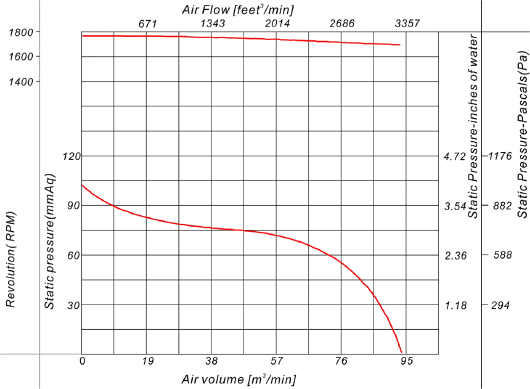
돌풍은 경진 Blower에서 제작한 sirrocco S blade 편흡입 직렬 사각 송풍기를 사용하여 재현하였으며, 대수분포를 추종하는 평균풍속을 재현하기 위해 상이한 풍량을 지니는 두 개의 송풍기를 연직방향으로 직렬 배치하였다 (Fig. 12, 13 참조). Blade의 직경은 400 mm, 풍량은 1785 rpm에서 94±9.4 m3/min까지 조풍가능하다(Fig. 14 참조). Fig. 14에는 송풍기 rpm에 따른 송풍량 변화를 도시하였다.
4.4 Data acquisition system
해상풍력발전체 진동은 초당 1245 frame의 연사가 가능한 초고속카메라(Phantom miro eX2)를 이용하여 촬영한 동영상 자료를 영상 처리하여 분석하였으며, 영상 처리과정을 요약하면 다음과 같다.
1. 먼저 영상 자료를 수치화 하고, 이어 명암으로만 특정할 수 있는 gray 영상으로 변환
2. sobel filter를 사용하여 해상풍력발전체의 윤곽선 추출
3. noise 제거 및 threshold 처리를 통해 중립축의 위치 산출
4. 일련의 영상자료에서 산출한 도심축 위치 (Fig. 7 참조)로부터 변위 시계열 자료 구축
4.5 실험 조건
해상풍력 시범단지가 예정되어있는 우리나라 서해안의 기후조건과 설계하중을 고려하여 기준풍속은 U ¯ x = 10
모형에서의 값으로 환산하면 각각 U ¯ x = 10
순간최대풍속은 돌풍에 내재한 난류성분을 반영하기 위해 Kaimal spectrum과 Cross spectrum을 이용하여 수치모의된 풍속시계열 자료를 토대로 U ¯ x = 80 U ¯ x = 80
Kaimal 스펙트럼 Su은 다음과 같이 정의되며(Kaimal et al., 1972)
여기서 σu 는 난류 유속성분 표준편차, xo 은 조도길이, n은 주파수, u*는 마찰속도, U ¯ a i r ( x = 10 )
상기 식에서 Lu(x) 는 난류 특성길이를 나타내며 다음과 같이 산출될 수 있다.
x와 x′ 에서의 난류 변동성분 간의 Cross 스펙트럼 Su(x,x′) 은 다음과 같이 정의되며 (Fig.7 참조)
여기서 Su(x) 는 난류 변동성분 u(x,t) 의 Kaimal 스펙트럼, Cohu(x,x′) 는 간섭함수를 각각 나타내며 간섭함수 Cohu(x,x′) 는 다음과 같이 기술될 수 있다.
식 (37)에서 C는 x와 x′ 에서의 난류 유속성분 사이의 상관정도에 역비례하는 감쇄계수로 통상 10 정도의 값을 취한다 (Deodatis: 1996A, Deodatis: 1996B).
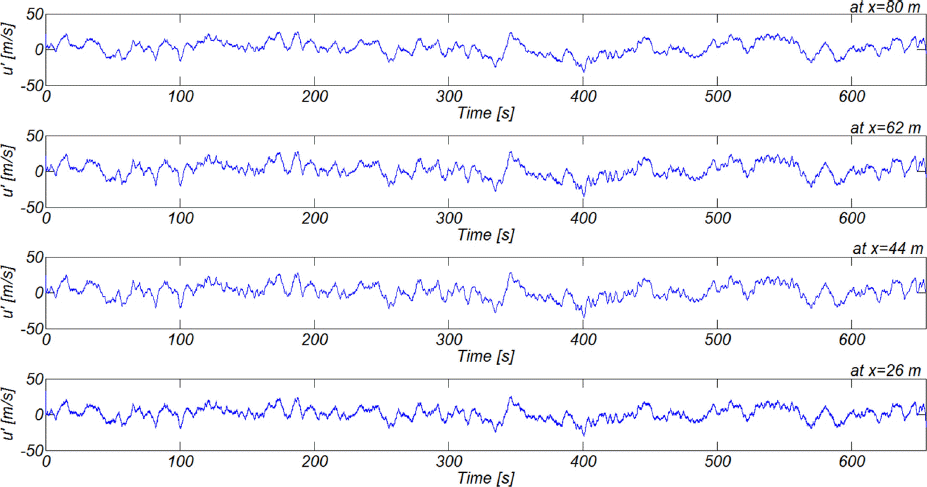
Fig. 15와 16에는 Kaimal spectrum과 Cross spectrum을 이용하여 수치모의된 풍속시계열 자료를 도시하였다. 일반적으로 수백m에 달하는 바람 경계층의 두께보다 단파일의 규모가 작아 모의된 난류 유속 성분은 상당한 상관성을 유지하는 것으로 보이나, 저층인 x = 26 m에서는 고주파 성분을 관측할 수 있다. 이러한 현상은 고주파 성분의 경우 상관성이 현저히 떨어지는 상관함수의 차용에 기인한 것으로 관측결과에서도 흔히 발견된다(Deodatis, 1996A: Deodatis, 1996B).
Fig. 15
Time series of numerically simulated wind velocities at x = 80, 62, 44, 26 m (see Fig. 7) [calm sea].

Fig. 16
Time series of numerically simulated wind velocities at x = 80, 62, 44, 26 m (see Fig. 7) [rough sea].
세 시간 정도 지속되는 파랑에 비해 돌풍 등으로 인한 최대 풍속의 지속시간은 상대적으로 짧다. 이러한 특성으로 인해 풍하중에 대한 해상풍력발전체 설계 시에는 십분 평균 풍속이 차용되며, 파랑하중 고려 시에는 무작위 파랑은 세 시간 동안 모의되는 것이 일반적이다. Fig. 17에는 해상풍력발전체 모형 전면 수역에서 관측된 해수면 변위 시계열 자료와 영점 교차법(zero-up crossing method)로 분석한 파고와 주기의 histogram을 도시하였다. 총 모의시간 동안 5118개의 파랑이 관측되었으며, Fig. 18에는 관측된 해수면 변위 시계열 자료로부터 FFT 변환을 통해 산출한 파랑 스펙트럼을 도시하였다. 상대적으로 짧은 취송거리가 파랑의 성장을 제약하는 우리나라 서해안 파랑특성에 부합하는 협대역 분포의 파랑이 조파된 것을 확인할 수 있다.
Fig. 17
Sampled time series of numerically simulated free water surface and histogram of measured wave heights and its associated period.
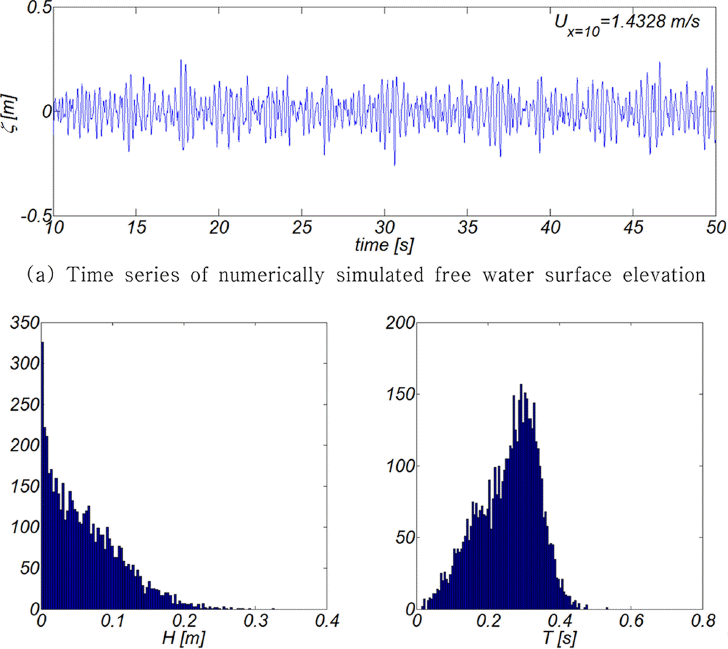
Fig. 18
Estimated wave spectrum from the time series of numerically simulated free water surface elevation.

먼저 풍력과 파력이 동시에 작용하는 경우에 대해 수리모형실험을 수행하였으며 이어 풍력만 작용하는 경우, 파력만 작용하는 경우에 대해서도 수리모형실험을 수행하였다. Table 2에는 수리모형실험에 사용된 파랑조건과 풍속조건을 수록하였다.
Table 2
Summary of wind & wave condition used in the hydraulic model test
4.6 결과 분석
해상풍력 시범단지가 예정되어있는 우리나라 서해안 해역은 수심이 20 m 내외의 천해역이다. 따라서 해상풍력 발전체 하부구조물의 높이 [80 m]를 감안하면 구조체의 상당부분이 풍력에 노출되어 주 외력은 풍력으로 추정된다.
Fig. 19에는 해상풍력발전체 하부구조물 변형 시계열 자료를 도시하였다. 상단 pannel은 풍력만 작용하는 경우, 중간 pannel은 파력만 작용하는 경우, 하단 pannel은 풍력과 파력이 동시에 작용하는 경우에 해당된다. Fig. 20, 21, 22에는 RUN1, RUN4, RUN7에서 최대 변형 발생시 snapshot을 도시하였다. Fig. 23에는 위상공간에서 하부구조물이 그리는 궤적을 도시하였다.
Fig. 19
Measured deflection of the offshore wind energy converter along the wind direction against the different combinations of external forces.
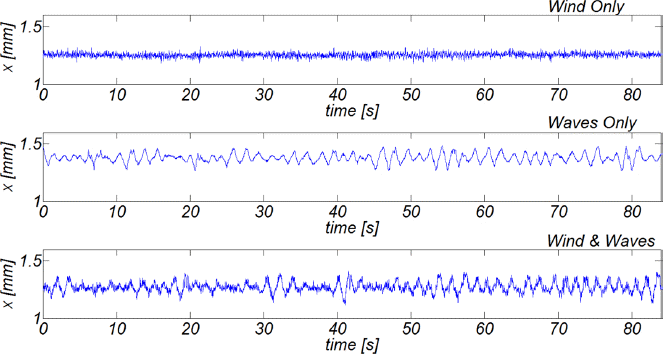
Fig. 20
Snapshot of offshore wind energy converter when the displacement reaches its maxima viewed from the above (green solid line: the reference frame at the rest, gray line: the reference frame subject to vibration) [subject to wind only].

Fig. 21
Snapshot of offshore wind energy converter when the displacement reaches its maxima viewed from the above (green solid line: the reference frame at the rest, gray line: the reference frame subject to vibration) [subject to wave only, Hs =0.2 m].

Fig. 22
Snapshot of offshore wind energy converter when the displacement reaches its maxima viewed from the above (green solid line: the reference frame at the rest, gray line: the reference frame subject to vibration) [subject to wind& wave, Hs =0.2 m].

Fig. 23
Trajectories of the offshore wind energy converter made by its deflection when exposed to different combination of external loads.
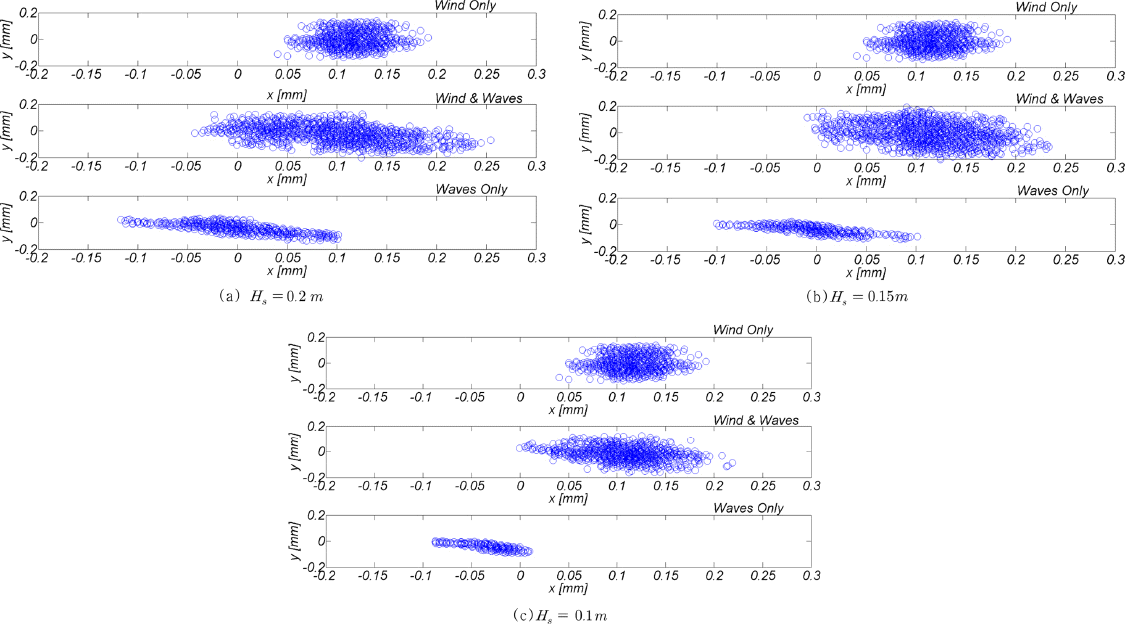
풍력과 파력이 동시에 작용하는 경우, 횡방향 최대변위에는 큰 변화가 없으나 흐름방향 최대변위는 풍력과 파력에 의한 최대변위를 단순히 선형중첩한 경우보다 약 15~20%정도 감소하는 것을 알 수 있다 [Fig. 20, 21, 22 참조]
Fig. 24에는 Hs = 10 cm, 15 cm, 20 cm의 경우, 해상풍력발전체 하부구조물 변형 시계열 자료의 FFT 변환을 통해 산출된 흐름방향, 횡방향 응답 스펙트럼을 도시하였다. Hs = 15 cm에서의 횡방향의 경우를 제외한 모든 경우에서 풍력과 파력의 응답스펙트럼을 선형 중첩한 것보다 풍력과 파력이 동시에 작용할 때의 응답이 확연히 감소한 것을 알 수 있으며, Hs 값이 커질수록 그 차이 또한 증가하는 것을 알 수 있다. 이 결과는 bumpy한 해수면으로 인해 대기와 해수면의 경계에서 출현하는 Large eddy가 비선형 상쇄 간섭의 생성 기작이라는 우리의 추론을 뒷받침한다.
Fig. 24
Response spectra of offshore wind subject to varying environmental load [blue solid line: linear superposition of response spectrum due to wind and waves, green solid line: response spectrum when subject to simultaneously acting wind and waves].
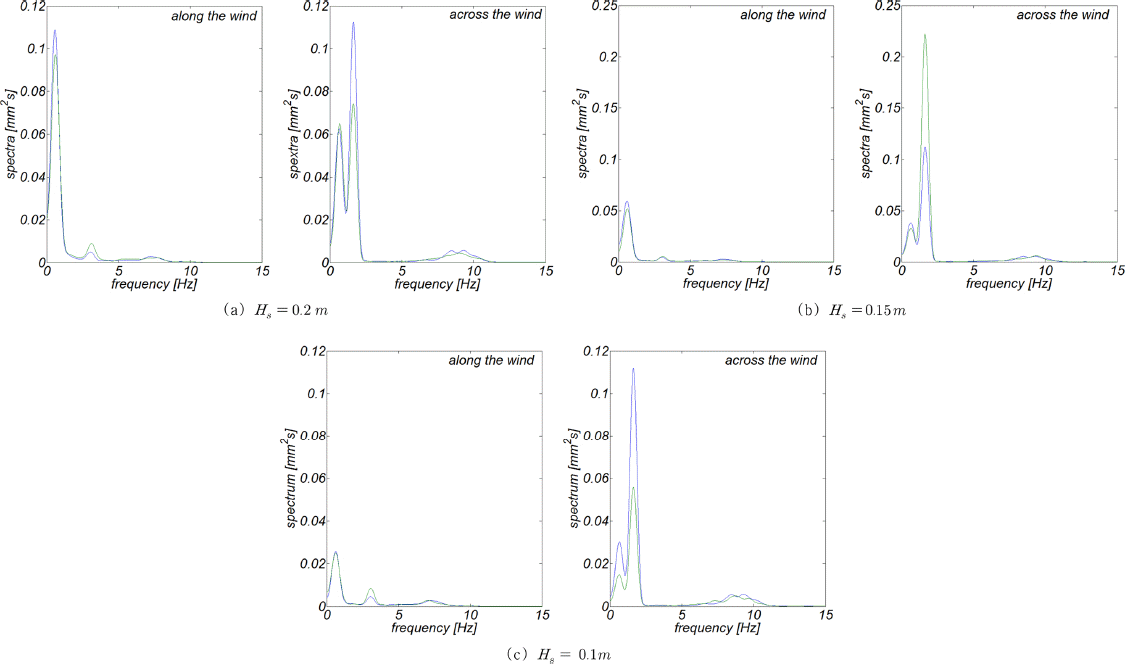
해상풍력발전체 응답스펙트럼은 2.589 Hz와 7.641 Hz에서 정점을 이루며 이를 다음과 같이 정의되는 Froude 상사법칙에 기초하여
원형에서의 주기로 환산하면 각각 2.729s [0.366Hz]와 0.924s [1.081 Hz]에 해당되며, 여기서 LR 은 축척, TR 은 원형과 모형에서의 시간비율을 각각 나타낸다. 이러한 결과는 수치모의에서 밝혀진 하부구조물 고유 주기 0.78 Hz와는 미세한 차이를 보이나 scale effect를 고려하면 받아들일 수 있는 오차라고 판단된다.
5. 결 론
무한한 성장 가능성에도 불구하고, 해상풍력산업은 여전히 과다한 초기투자비용 문제로 어려움을 겪는 것으로 보인다. 이러한 초기투자비용 중 상당부분은 해상풍력 발전체 조립과 거치 과정에서 발생하나, 해상 풍력 발전체와 주 외력인 풍력과 파력의 상호작용에 대한 이해부족으로 현재 상당히 보수적으로 설계되는 관행도 일정부분 기여하고 있는 것으로 판단된다.
따라서 해상풍력 발전체와 풍력과 파력의 상호 작용 중 해상풍력 발전체의 변형을 억제하는 것으로 알려진 풍력과 파력의 비선형 상쇄 간섭을 설계단계에서 활용하는 경우 상당한 비용절감을 꾀할 수 있을 것으로 보인다.
풍력과 파력의 비선형 상쇄 간섭은 세 가지 기작으로 구성되며 이를 요약하면 다음과 같다.
먼저, 바람으로 해수면이 거칠어진 경우 대기와 해수면의 경계에서 연이어 생성되는 머리띠 모양의 vortex tube (hairpin vortex)와 각 머리띠 모양의 vortex tube의 관상효과(solenoidal effect)가 더해져 출현하는 Large eddy는 해상 풍력 발전체 거동에 상당한 영향을 미친다. 전술한 Large eddy는 바람의 진행방향과 반대방향으로 선회한다는 점에서 풍력에 의한 해상 풍력 발전체 변형을 제한하는 역할을 수행할 수 있다 (Adrian, 2007).
둘째, 파랑 내습시 해수면이 하강하는 위상공간 삼·사 분면에서 역전되는 수입자 운동방향에서 찾을 수 있다. 이렇게 역전된 수입자 운동방향은 바람의 진행방향과 맞서게 되며, 풍력으로 인한 해상풍력발전체 변형을 제한하는 역할을 수행한다.
셋째, 해상풍력발전체 변형이 시작되며 발생하는 유체입자와 해상풍력발전체 간의 상대속도를 생각해 볼 수 있다. 전술한 상대속도는 해상풍력발전체에 작용하는 형상 항력을 통해 유체역학적 감쇄를 야기하며, 이러한 공기역학적 감쇄는 파력으로 인한 해상 풍력발전체 변형을 제한하는 저항력으로 작용한다.
따라서 해상 풍력발전체 효율적, 혹은 최적 설계를 위해서는 풍력과 파력의 비선형 상쇄 간섭을 일으키는 공기역학 감쇄를 적극적으로 활용할 필요가 있다. 이를 위해서는 해상풍력발전체 하부구조물 설계에 강성도가 지나치게 높은 재질은 지양하고 적절한 연성도를 확보해야 하며, 전술한 내용이 구현되는 경우, 비용절감과 피로파괴에 대한 내구성도 증가되는 효과를 꾀할 수 있다.
이러한 맥락에서 본고에서는 해상 풍력발전체 최적설계에 필요한 파력과 풍력의 비선형 상쇄 간섭의 정량적 평가를 위해 우리나라 서해안 해역에 예정되어있는 해상풍력 시범단지에 거치예정인 5MW급 해상풍력 발전체를 대상으로 수리모형실험이 서울시립대 조파수조에서 수행되었다.
모형은 1/50 축척으로 제작되었으며 탄성계수가 200,000 MPa인 특수강으로 구성된 해상풍력발전체의 하부구조물의 모형 재질은 Froude 상사법칙을 고려하여 밀도가 7850Kg/m3, 탄성계수가 2,700 MPa~3800MPa에 분포하는 황동으로 선정하였다. 돌풍은 Blade 직경이 400 mm인 Sirrocco S Blade와 Blade 직경이 300 mm인 duct형 송풍기를 직렬로 배열하여 평균풍속의 대수분포를 재현하였으며, 편흡입 직렬 사각 송풍기의 경우 풍량은 1785 rpm에서 94±9.4 m3/min까지, duct형 송풍기의 경우 55±5.5 m3/min까지 조풍가능하다.
모의결과, 우리나라 서해안 해상풍력 시범단지에 거치예정인 해상풍력발전체 하부구조물에 작용하는 주 외력은 풍력으로, 이는 해상풍력 시범단지가 비교적 천해역에 위치하여 해상 풍력 발전체 하부구조물중 25%만이 파랑에 노출되기 때문인 것으로 판단된다.
또한, 황천시 두터워진 대기 경계층과 이에 수반되는 에너지 손실로 평균풍속은 해역이 정온한 경우에 비해 극적으로 감소하였다. 이와 더불어 돌풍의 진행방향은 항상 평균 풍향과 일치하는 것은 아니며 상당기간 평균 풍향과 반대방향으로 발생하며, 돌풍의 크기는 순간적으로 평균풍속을 능가하는 경우도 빈번히 관측되었다.
이러한 현상은 바람의 진행방향과 반대방향으로 선회하는 Large eddy에 기인하는 것으로 판단된다.
따라서 이상의 결과를 종합하면 우리나라 서해안 시범단지 해상풍력 발전체의 경우, 바람으로 해수면이 거칠어진 경우 대기와 해수면의 경계에서 연이어 생성되는 머리띠 모양의 vortex tube (hairpin vortex)와 각 머리띠 모양의 vortex tube의 관상효과(solenoidal effect)가 더해져 출현하는 Large eddy가 비선형 상쇄 간섭을 일으키는 가장 큰 요인으로 판단된다.