Estimation of Probability Distribution Functions for Water Temperature Data in Korean Coasts

Shin Taek Jeong; Hongyeon Cho; Dong Hui Ko; Nam Sun Oh; Kyeong-Pyo Son

doi:10.9765/KSCOE.2013.25.1.11

Abstract

As the temperature data show a distribution pattern with a number of peaks, assumption of normal distribution will result in a serious bias in the analysis. In this study, the Gaussian Mixture Distribution (GMD), a type of bimodal distribution, is presumed as a frequency distribution for the water temperature, in order to estimate the optimal parameter and to carry out the relation analysis between the optimal parameter and the basic statistical information such as mean and variance on the data. By the way, an estimation formulae to compute the frequency distribution of the data is developed by computing the parameters of GMD (i.e. α₁, μ₁, σ₁, α₂, μ₂, σ₂) by means of the major characteristic values, such as mean, standard deviation and skewness of the data. The formulae shows an excellent coincidence with the result from the observation data, in the RMS limit accuracy of 5%.

핵심용어: temperature data, normal distribution, Gaussian Mixture Distribution (GMD), frequency distribution, estimation formulae, 수온자료, 정규분포, 가우스 혼합분포, 빈도분포, 추정공식

Abstract

수온자료는 다수의 첨두를 가진 분포형태를 보이고 있기 때문에 정규분포로 가정하는 경우 분석에 큰 오차가 수반된다. 본 연구에서는 쌍봉 분포함수 형태인 가우스 혼합분포 함수를 수온의 분포함수로 가정하여 최적매개변수를 추정하고, 추정된 최적 매개변수와 자료의 기본적인 통계정보(평균 및 분산 등)의 관계분석을 수행하였다. 또한 자료의 주 특성값인 평균, 표준편차, 왜곡도로부터 가우스 혼합분포 매개변수인, α₁, μ₁, σ₁, α₂, μ₂, σ₂를 산정하여 수온 자료의 빈도분포를 산정하는 추정공식을 개발하였다. 개발된 추정공식은 RMS 오차가 5% 정도로 관측 자료를 이용한 결과와 우수한 일치를 보이고 있다.

1. 서 론

수온은 연안 환경인자의 반응 및 생물의 서식환경에 직접적인 영향을 미치고 있으며, 또한 기후변화에 의한 기온 변화로 인하여 연안의 수온 변화가 예상되고 있다. 장래의 연안 수온변화를 분석하기 위해서는 현재 연안 수온자료에 대한 분석이 수행되어야 한다.

한반도 연안 수온 분포에 대한 연구는 이(1983)가 수온을 포함한 해저지형, 해류, 염분, 파랑, 조석 및 조류 등 한국근해의 海象을 검토한 바 있으며, 수온은 서해, 남해, 그리고 동해로 구분하여 정리하였다. KORDI(1987)에서는 서해안의 수온, 염도, 용존산소 등을 관측하여 분석하였다. 이(1992)는 남해, 동해, 서해의 수온 분포 및 수온의 계절, 장기, 단기 변화를 연구하였다.

최근 해안 및 항만구조물의 설계에 신뢰성 설계기법이 적용되면서 발생확률 추정 및 해석에 관한 연구가 중요한 사안으로 부각되고 있다. 항만구조물의 신뢰성 설계과정에서 고려되는 주요 외력은 심해파고, 조위, 수온, 파랑변형 등을 들 수 있다(해양수산부, 2000; 국토해양부와 한국해양과학기술진흥원, 2011). 신뢰성 설계법은 확률론적 설계법으로도 불리우며, 설계관련 변수의 일부 또는 전부를 확률분포(확률밀도 함수)로 제시하게 된다. 이 경우 확률밀도함수의 종류 및 모수들을 결정하는 것은 매우 중요하다.

조 등(2004)은 국립해양조사원에서 제공하는 조위자료를 통계적으로 분석하여 우리나라 연안 조위자료의 확률밀도함수로 가우스 혼합분포(Gaussian Mixture Distribution, GMD)를 제안하였다. 정 등(2008)은 이 분포함수에 경계조위 상한-하한을 설정하여 분포함수의 범위를 제한하는 이중절단 GMD를 제안하였다. 한편, 정 등(2005)은 국립해양조사원에서 제공하는 인천(율도), 목포, 여수, 부산, 포항, 속초의 조화상수 자료를 사용하여 조위의 발생확률분포를 추정·분석하였고, 조 등(2006)은 서해안 인천, 평택, 군산외항 및 목포 검조소의 1시간 간격 조위자료를 이용하여 조간대의 연속노출시간 특성을 분석하였다. 한편, 조 등(2010)은 가우스 혼합분포 함수 형태를 따르는 조위에 대하여 등가평균 및 등가표준편차를 산정하여 구조물 신뢰성 설계시 활용할 수 있도록 하였으며, 정 등(2012)은 조화상수를 이용한 조간대 노출시간 추정공식을 개발하였다.

본 연구에서는 국립해양조사원에서 제공하는 연안 수온자료를 이용하여 정규분포 가정의 한계를 극복한 새로운 수온분포함수로 쌍봉형 형태를 제안하였다. 제안된 분포함수의 모수를 최소제곱법으로 최적 추정하였으며, 수온자료의 기본적인 통계정보에 해당하는 평균과 분산과의 관계를 분석하여 이들 평균, 분산, 왜곡도를 이용하여 수온 확률분포 함수를 산정하는 식을 제안하였다.

2. 수온 관측자료

우리나라 연안의 수온자료는 해양물리 현상을 규명하기 위해서는 매우 기본적인 자료이기 때문에 다양한 기관 및 학교에서 관측 자료를 보유하고 있다. 그러나 수온자료 분포를 추정하기 위해서는 단기간의 자료보다는 장기간의 자료를 필요로 하기 때문에 본 연구에서는 장기간의 수온자료가 가용한 국립해양조사원, 국립수산과학원 관측 자료를 종합적으로 검토하여 수온 분포함수를 추정하는 데 이용하였다.

국립수산과학원에서는 한반도 연안 34개소의 수온, 기온 등의 자료를 제공하고 있다. 즉 1933년부터 현재까지 일별 전국 연안 수온 및 기상자료를 제공하여 장기간 연안 해황의 변동 조사 및 기후변동과 관련한 연안 수온의 분석 등의 효과를 기대하고 있다.

한편, 국립해양조사원에서는 수온, 염분, 유의파고, 유의파주기, 최대파고, 최대파 주기 등 해양 관측 정보를 제공하고 있다. 이 중 수온자료는 1시간 자료, 월간격 자료, 년 자료 등을 제공하고 있으며, 수온 관측소 유형은 조위관측소, 해양관측소, 해양관측부이, 이어도 종합해양과학기지 등이 있다.

본 연구에서는 국립해양조사원에서 제공하는 조위관측소의 수온자료를 수집하여 분석을 실시하였다. 국립해양조사원 자료를 사용한 이유는 자료의 결측이 적고, 비교적 장기간의 수온자료가 존재하기 때문이다.

연안 수온 관측소의 위치 및 자료수집 기간, 누락 기간 등은 Table 1에 정리하였다. 국립해양조사원 자료는 한반도 연안 31개 정점의 1일 간격 수온 자료이다. 이 자료는 오전 9시에서 10시 사이를 기준으로 일 1회, 즉 특정시간에 측정한 수온자료이다. 일 1회 특정 시간에 측정한 자료이기 때문에 일 평균 자료와의 편기(bias)가 발생할 수 있기 때문에 가용한 시간자료를 이용하여 편기 성분에 대한 정량적인 검토도 필요하다. 그러나 본 연구에서는 연안의 수온 일변화는 육상에서의 기온 일변화에 비하여 그 변화 정도가 절대적으로 작기 때문에 일 1회 관측 자료를 일 평균자료로 간주하여 분석을 수행하였다.

Table 1

Information of the water temperature data around the Korean coasts

Gauging stations	Location		Data download periods	Missing periods
Gauging stations	Latitude	Longitude	Data download periods	Missing periods
Incheon	N 37^o27’ 07'	E 126^o35' 32	1964~2010	1968
Ansan	N 37^o11' 31	E 126^o38' 50	2002~2010
Pyeongtaek	N 36^o58' 01	E 126^o49' 22	1995~2008	1996~1998
Anheung	N 36^o40' 25	E 126^o04' 55	1986~2010	1997
Boryeong	N 3^o24' 24	E 126^o29' 09	1985~2010
Janghang	N 36^o00' 25	E 126^o41' 15	1964~2010	1968, 2003
Gunsan	N 35^o58' 32	E 126^o33' 47	1980~2010
Wido	N 35^o37' 05	E 126^o18' 06	1985~2010
Mokpo	N 34^o46' 47	E 126^o22' 32	1964~2010	1968
Daeheuksando	N 34^o41' 03	E 125^o26' 08	1965~2010	1968
Jindo	N 34^o22' 40	E 126^o18' 31	2006~2010
Chujado	N 33^o57' 43	E 126^o18' 01	1983~2010
Wando	N 34^o18' 57	E 126^o45' 34	1983~2010
Geomundo	N 34^o01' 43	E 127^o18' 27	1982~2010
Goheung	N 34^o28' 51	E 127^o20' 33	2005~2010
Yeosu	N 34^o44' 50	E 127^o45' 57	1965~2010	1968
Tongyeong	N 34^o49' 40	E 128^o26' 05	1976~2010
Masan	N 35^o12' 36	N 35^o12' 36	2003~2009
Geojaedo	N 34^o48' 06	E 128^o41' 57	2006~2010
Gadeokdo	N 35^o01' 27	E 128^o48' 39	1977~2010
Busan	N 35^o05' 46	E 129^o02' 07	1964~2010	1968
Ulsan	N 35^o30' 06	E 129o23' 13	1974~2010
Pohang	N 36^o02' 50	E 129^o23' 02	1971~2010
Hupo	N 36^o40' 39	E 129^o27' 11	2003~2010
Mukho	N 37^o33' 01	E 129^o06' 59	1965~2010	1968
Sokcho	N 38^o12' 25	E 129^o23' 57	1974~2010
Ulleungdo	N 37^o29' 29	E 130^o54' 49	1965~2010	1968, 1973
Jeju	N 33^o31' 39	E 126^o32' 35	1965~2010	1968
Moseulpo	N 33^o12' 52	E 126^o15' 04	2003~2010
Seogwipo	N 33^o14' 24	E 126^o33' 42	1980~2010	1983, 1984
Sungsanpo	N 33^o28' 29	E 126^o55' 39	2003~2010

3. 분석방법

시간이 경과함에 따라서 얻어지는 측정치를 시간의 순서대로 나열한 측정치의 계열(이른바 時系列)을 통계학적으로 분석하려고 하는 경우, 먼저 그 시계열을 확률론적으로 표현할 필요가 있다. 어지럽게 나열되어 있는 자료를 그래프나 도표를 통하여 정리 및 요약하면 자료에 내포된 정보를 보다 쉽고 빠르게 전달할 수 있다.

시계열 자료를 이용하면, 결측 자료, 이상 자료 등의 정보를 쉽게 파악할 수 있고, 시간에 따른 자료의 변화 추이 등을 파악할 수 있다. 그러나, 이 모집단의 상태에 대한 표현(예를 들면 평균, 분산, 정규분포 등)은 추측할 수 없다.

3.1 도수분포

확률변수의 분포 추정은 관측 자료를 이용하여 확률밀도함수를 추정하는 과정으로 정의할 수 있다(Silverman, 1986). 어떤 확률변수의 확률밀도함수 추정에 관한 연구는 통계적으로 모수적(parametric) 방법과 비모수적(non-parametric) 방법으로 구분할 수 있다(Raccine, 2008).

Fig. 1

Histograms of Incheon water temperature data with different bin widths.

본 연구에서는 비모수적 방법인 도수분포도(histogram)를 도시하여 검조소별 수온자료의 빈도분포함수의 개략적인 형태를 분석하고, 빈도분포함수의 빈도자료를 분석에 사용된 자료의 총 갯수로 나눈 밀도 도수분포(density histogram)를 이용하여 확률분포 함수를 계산하였다.

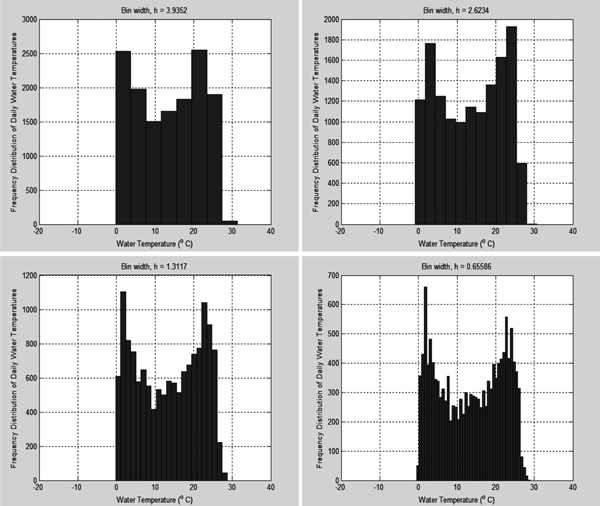
도수분포는 2개의 모수 즉, 계급의 원점인 t_o와 계급 폭(bin width, h)에 의하여 결정된다. 계급 폭은 ‘smoothing parameter’라고도 부르며, 도수분포의 유연도를 결정하게 된다. 즉, 계급 폭이 작으면, 계급의 높이의 변화가 심하고, 계급 폭이 크면, 계급의 높이의 변화가 작다. Fig. 1은 동일한 자료개수를 대상으로 4종류의 계급 폭에 의하여 나타나는 도수분포도의 양상을 보여주고 있다. Fig. 1은 1964년부터 2010년까지 총 47년간 인천 수온 자료 13,981개를 대상으로 도수분포도를 도시한 결과이다. 동일 자료인 경우에도 계급 폭의 크기에 따라 상이한 형태의 도수분포도가 생성되고, 또한 자료의 분포형태를 쉽게 파악할 수 있다.

도수분포를 표현하기 위한 계급 폭(h), 또는 계급 수(number of bins, k)를 구하는 공식은 다음과 같다.

여기서, n은 분석자료 개수, σ 는 표준편차, s는 표본 표준편차, IQR은 interquartile range(Martinez and Martinez, 2005)이다. 본 연구에서는 관계식 (1)을 이용하여 인접한 정수로 결정하였다(Haldar and Mahadevan, 2000).

3.2 분포 함수

히스토그램, 표, 또는 수식 등 어느 것으로 확률변수를 나타내든지, 이들은 곧 확률변수의 움직임을 기술하게 된다. 종종 전혀 다른 자료임에도 불구하고 그 결과가 동일한 형태의 움직임을 나타내는 경우가 있다. 이러한 자료들에 관계된 확률변수들은 본질적으로 동일한 확률분포를 따르게 되고, 동일한 식으로 나타낼 수 있게 된다.

인천 수온 자료의 도수분포도인 Fig. 1은 명확한 쌍봉형 분포를 보이고 있다. 이는 우리나라가 여름과 겨울이 존재하는 4계절이 뚜렷하기 때문이다. 도수분포도가 쌍봉(double peak) 형태임을 고려하여, 수온자료의 빈도분포 함수(p_T(x)로는 평균과 분산이 서로 다른 2종류의 정규분포함수를 선형 결합한 형태, 즉 6개의 매개변수를 가진 가우스 혼합분포 함수 형태를 제안하였다. 이 식은 다음 식 (5)와 같이 표현된다.

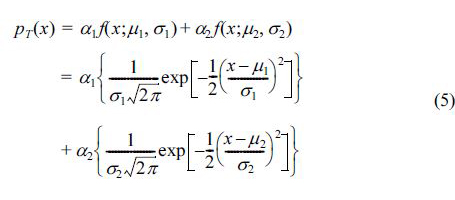
여기서, α₁, α₂는 scale parameter로 α₁ + α₂ = 1의 관계가 있으며, µ₁, µ₂는 각각 평균, σ₁, σ₂는 각각 표준편차에 해당하는 매개변수이다.

3.3 분포 매개변수 추정

전술한 확률변수의 주 특성값들, 즉, 평균 및 표준편차 등은 가장 일반적인 자료로 관측 정점별로 잘 알려져 있거나, 쉽게 산정할 수 있다. 본 연구에서는 MATLAB 프로그램을 이용하여 31개 연안 정점의 관측자료로부터 평균 및 표준편차 등 주 특성값을 산정하였다. 이들 주 특성값과 수온 분포 매개변수의 관계는 다음과 같은 최소자승법을 이용하여 도출하였다. 즉 수온자료가 가용한 정점(본 연구의 경우, 31개 정점)의 주 특성값(본 연구에서는 평균, 표준편차, 왜곡도 사용) 행렬을 H_i,j(i = 정점 인자, j = 주 특성값 인자; known), 수온 분포함수의 매개변수 행렬을 P_i,k(i = 정점 인자, k = 매개변수인자; known)라고 정의하고, 분포함수의 매개변수가 주 특성 값의 선형조합으로 표현된다고 가정하는 경우 다음과 같은 관계 식이 성립된다.

여기서, C_j,k는 선형조합 계수로 구성된 행렬(unknown)이다. 위 식을 정리하면, 식 (7)을 이용하여 최적 선형조합 계수 행렬, C_j,k를 계산할 수 있다.

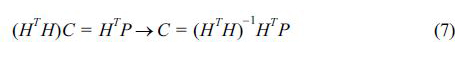
여기서, H^T는 행렬 H의 전치행렬이고, (H^TH)⁻¹는 (H^TH)의 역행렬이다.

4. 자료 분석

국립해양조사원 홈페이지(http://www.khoa.go.kr/)에서 제공 하는 1시간 수온자료는 텍스트 파일형태의 1개월 자료이다. 이 자료를 엑셀파일로 변환하여 전체 관측기간 동안의 자료로 정리하였다. 이 자료는 MATLAB 프로그램을 이용하여 도시한 후, 자료의 결측 및 이상 여부를 확인하였다. 구체적인 순서는 다음과 같다.

Fig. 2

Flowchart of water temperature data alnalysis.

① 국립해양조사원 등 연안 장기 수온 관측 자료 수집

② MATLAB 프로그램을 이용한 자료 도시, 결측 또는 이상 자료 분석

③ MATLAB 프로그램을 이용한 도수분포도 작성

④ 연안 수온 자료의 통계 분석 및 분포함수 비교 분석 MATLAB 프로그램 개발

⑤ 최적 매개변수 추정을 위한 MATLAB 프로그램 개발

⑥ 개발된 프로그램을 이용한 연안 수온 분포함수 추정 및 매개변수 변화 분석

연안 31개 수온 자료를 분석하는 과정 흐름도를 정리하면 Fig. 2와 같다.

4.1 자료의 주 특성값

수온자료의 주 특성값으로는 평균(μ), 표준편차(σ), 그리고 왜곡도(γ)를 산정하였으며, 구체적인 결과는 Table 2와 같다.

4.2 도수분포도

도수분포도를 작성하기 위해서는 먼저, 서로 인접한 자료값을 집단화하여 전체 자료 집합을 몇 개의 그룹으로 나눈다. 이를 위하여 전체 자료의 범위를 몇 개의 계급(class, bin)으로 나누는 것이 필요하다. 본 연구에서는 MATLAB 프로그램의 ‘hist’ 함수를 이용하여 도수분포도를 작성하였으며, 식 (1)을 이용하여 최적 계급 수(number of bins, k)를 산정하였다. 서해, 남해, 동해, 그리고 제주 등 한국 연안 주요 6개정점의 수온 도수분포도는 Fig. 3과 같다.

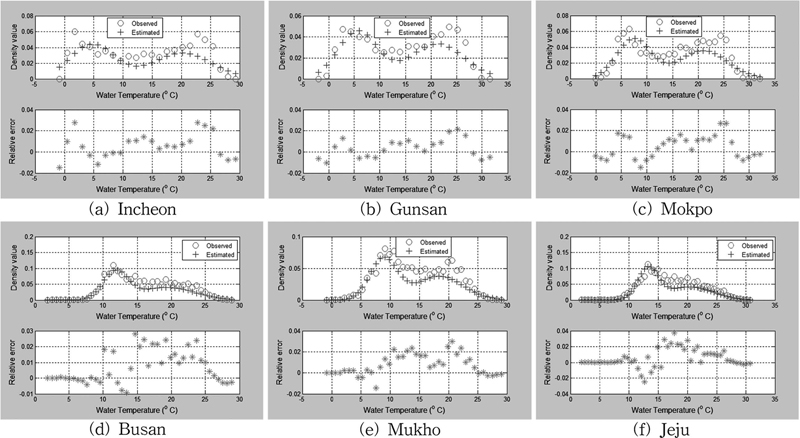
Fig. 3에 도시된 바와 같이, 우리나라는 여름과 겨울을 포함 4계절이 존재하기 때문에 대부분의 정점에서 2개의 첨두 값이 나타난다. 그러나, 부산과 제주의 경우 다른 정점에 비하여 여름철 첨두 값이 뚜렷하지 않다.

4.3 분포 함수

연안 31개 정점의 수온 상대도수분포도를 분석한 결과, Fig. 3에 도시된 바와 같이 대부분 쌍봉(double peak) 형태이다. 따라서 기존의 Single-modal 분포함수를 사용하기에는 한계가 있기 때문에 수온자료의 빈도분포 함수로는 평균과 분산이 서로 다른 2개의 정규분포함수의 합의 형태, 즉 6개의 매개변수를 가진 가우스 혼합분포 함수 형태를 제안하였다 (식 (5) 참조).

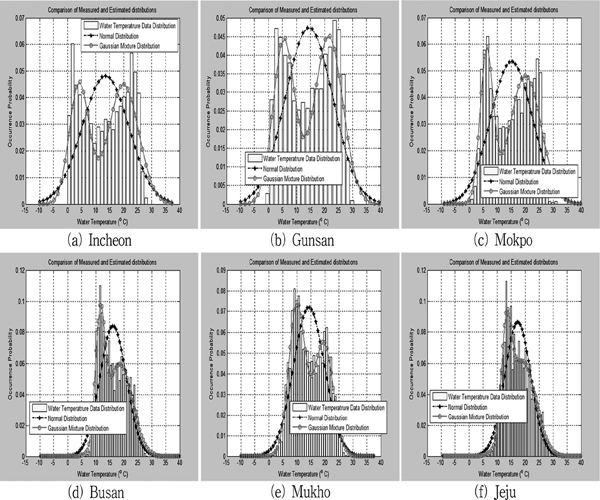
제안된 후보 분포함수의 최적 매개변수는 MATLAB Optimization 도구상자에서 제공하고 있는 함수인 ‘nonlinlsq’ 이용하여 추정하였다. 비선형 최적화 문제는 모수의 초기값 지정이 중요하기 때문에 본 연구에서는 위치모수는 도수분포도 형태에서 보여지는 첨두 영역을 기준으로 다른 영역을 침범하지 않는 범위로 지정하였으며, 분산모수에 해당하는 모수는 간단하게 양수로 지정하였다. 연안 31개 정점의 수온 자료에 대하여 식 (5)를 이용하여 매개변수를 추정한 결과는 Table 3에 제시하였다. 한편, 관측 자료를 이용한 분포함수(밀도 도수분포도, density histogram), 정규분포함수, 추정된 매개변수를 사용하여 산정한 GMD 함수형태 3종류의 곡선을 Fig. 4에 동시에 도시하였다.

Table 2

Characteristic value of water temperature data in Korean coasts

Gauging stations	mean, μ (^oC)	s.d, σ (^oC)	skewness, γ
Incheon	13.52	8.28	−0.08
Ansan	13.77	8.76	−0.14
Pyeongtaek	13.82	8.11	−0.08
Anheung	12.96	6.50	0.14
Boryeong	15.31	7.54	0.03
Janghang	14.69	8.68	−0.06
Gunsan	14.47	8.40	−0.06
Wido	13.93	7.34	0.04
Mokpo	15.08	7.45	−0.06
Daeheuksando	13.47	5.65	0.31
Jindo	14.42	6.93	−0.16
Chujado	15.99	4.49	0.45
Wando	15.49	5.75	0.08
Geomundo	16.77	4.49	0.54
Goheung	15.61	7.61	−0.01
Yeosu	15.38	6.71	−0.11
Tongyeong	16.03	6.03	−0.07
Masan	15.60	6.89	−0.15
Geojaedo	17.06	4.36	0.52
Gadeokdo	16.10	5.52	0.12
Busan	16.17	4.74	0.32
Ulsan	16.16	5.05	−0.01
Pohang	14.99	5.62	0.15
Hupo	15.53	5.16	−0.01
Mukho	14.33	5.54	0.15
Sokcho	13.72	6.36	0.02
Ulleungdo	16.08	4.93	0.07
Jeju	17.35	4.60	0.33
Moseulpo	18.12	3.94	0.30
Seogwipo	18.39	3.84	0.29
Sungsanpo	17.68	4.69	0.29

Fig. 3

Histograms of water temperature data in Korean coasts.

Table 3

Parameters of probability density function for water temperature data

No	Gauging stations	α1	μ1 (^oC)	σ1 (^oC)	α2	μ2 (^oC)	σ2 (^oC)
1	Incheon	0.391	4.10	3.43	0.609	19.97	5.38
2	Ansan	0.539	5.98	6.06	0.461	22.27	3.62
3	Pyeongtaek	0.538	6.70	5.14	0.462	21.83	3.61
4	Anheung	0.331	5.78	2.04	0.669	16.89	5.59
5	Boryeong	0.379	6.99	3.00	0.621	20.69	5.50
6	Janghang	0.388	4.80	3.36	0.612	21.34	5.58
7	Gunsan	0.427	5.53	3.83	0.573	21.44	5.05
8	Wido	0.274	5.12	1.81	0.726	17.95	6.53
9	Mokpo	0.328	6.21	2.29	0.672	20.05	5.55
10	Daeheuksando	0.357	7.79	2.05	0.643	16.67	5.10
11	Jindo	0.396	9.33	2.87	0.604	19.50	5.18
12	Chujado	0.498	12.34	1.99	0.502	19.59	3.61
13	Wando	0.319	8.91	2.02	0.681	18.86	4.82
14	Geomundo	0.455	13.08	1.48	0.545	20.09	4.24
15	Goheung	0.475	8.18	3.82	0.525	22.31	4.22
16	Yeosu	0.430	8.36	3.36	0.570	20.83	3.86
17	Tongyeong	0.374	9.16	2.62	0.626	20.26	4.05
18	Masan	0.303	6.81	2.30	0.697	19.97	5.00
19	Geojaedo	0.414	13.26	1.66	0.586	19.63	4.29
20	Gadeokdo	0.401	10.58	2.25	0.599	20.10	4.18
21	Busan	0.326	11.54	1.63	0.674	18.50	4.52
22	Ulsan	0.319	11.68	1.77	0.681	19.12	4.02
23	Pohang	0.499	10.09	2.81	0.501	19.96	3.61
24	Hupo	0.594	12.08	2.57	0.406	20.96	2.76
25	Mukho	0.535	9.97	2.91	0.465	19.51	3.38
26	Sokcho	0.532	8.54	3.70	0.468	19.69	3.56
27	Ulleungdo	0.364	10.86	2.19	0.636	19.21	3.82
28	Jeju	0.286	13.31	1.76	0.714	19.07	4.64
29	Moseulpo	0.460	14.67	1.54	0.540	21.27	2.94
30	Seogwipo	0.274	14.67	1.00	0.726	19.95	3.74
31	Sungsanpo	0.563	14.18	2.57	0.437	22.19	3.14

Fig. 4

Comparisons of measured and predicted distribution for water temperature data.

Fig. 4에서 볼 수 있는 바와 같이 정규분포 함수 가정은 자료의 중앙 부분과 꼬리 부분에서 매우 큰 차이를 보이고 있음을 알 수 있으며, 본 연구에서 제안한 쌍봉 형태의 분포함수는 뚜렷하게 보이는 대략 2개의 첨두 형태 재현은 우수한것으로 판단된다. 그러나 꼬리 영역의 급격한 감소 형태 재현에는 한계가 있는 것으로 판단된다. 이 문제는 정규분포의 혼합 형태가 아닌 가용한 다른 다양한 분포함수(Log-Normal 분포함수, Rayleigh 분포함수, Weibull 분포함수 등)의 조합을 통하여 최적 분포함수 형태를 도출할 필요가 있을 것으로 판단된다.

4.4 주 특성 값과 GMD 매개변수의 선형조합 계수 추정

식 (7)을 이용하면 평균 및 분산과 GMD 매개변수의 관계를 표현하는 최적 계수를 추정할 수 있다. 여기서, 주 특성 행렬 H_i,j은 (31 × 3) 행렬(여기서, 31 = 정점의 개수, 3 = 주 특성 값, 평균, 표준 편차 그리고 왜곡도)이며, 매개변수 행렬 P_i,k도 (31 × 6) 행렬(여기서, 6 = 매개변수의 개수)이 되기 때문에 최적 선형조합 계수행렬 C_{j, k}은 (3 × 6) 행렬로 다음 식 (8)과 같다.

따라서 GMD 매개변수는 각각 다음과 같은 식 (9)로 계산 할 수 있다.

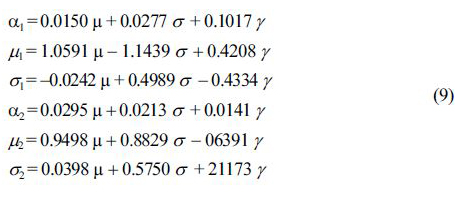
수온 자료는 연안 환경 요소 중 가장 중요한 자료이기 때문에 대부분의 검조소에서 기압, 염도, 파고 등과 함께 측정하고 있다. 따라서, 수온 자료는 획득하기 쉽고, 통계적 특성치 또한 쉽게 계산할 수 있다. 수온의 통계적 특성치인 평균과 표준편차 등을 이용하여 수온 분포 값은 다음과 같은 과정을 통하여 산정할 수 있다.

특정 지역의 평균 및 표준편차를 산정한 후, 인접한 31개 수온 관측정점과 연계하여 GMD 매개변수의 선형조합 계수 관계식 (9)를 이용하여 6개의 매개변수를 산정한다. 이후 식 (5)를 이용하여 수온자료의 확률밀도 값을 산정하게 된다.

추정된 확률밀도 값은 조위관측소의 1일 수온자료를 이용하여 추정한 확률밀도 값과 비교하여 상대오차를 분석하였다 (Fig. 5 참조). 관측 자료를 이용한 확률밀도 값과 본 연구에서 개발한 공식을 이용한 확률밀도 값를 비교한 결과 전반적으로 매우 우수하게 일치하는 양상을 보이고 있다. Fig. 5의 y축은 수온 확률 밀도 값과 상대오차를 의미한다. 밀도 값의 꼬리 부분은 값 자체가 작기 때문에, 절대오차를 산정하는 경우 작은 오차도 증폭되기 때문에 절대오차 대신 상대오차를 비교하였다.

Fig. 5

Comparison plots of the probability density value and relative error.

5. 결론 및 제언

본 연구에서 우리나라 연안의 수온자료 빈도분포 함수로 제안한 가우스 혼합분포(Gaussian Mixture Distribution, GMD) 함수는 정규분포에 비하여 수온자료의 확률밀도함수로 매우 적합한 것으로 파악되었다. 또한 자료의 주 특성값인 평균, 표준편차, 왜곡도로부터 GMD 매개변수인, α₁, μ₁, σ₁, α₂, μ₂, σ₂를 산정하여 수온 자료의 빈도분포를 산정하는 추정공식을 개발하였다. 개발된 추정공식은 RMS 오차가 5% 정도로 관측 자료를 이용한 결과와 우수한 일치를 보이고 있다. 본 공식은 장기간의 수온 자료가 없는 경우, 특정 정점의 수온 자료의 평균, 표준편차 그리고 왜곡도만을 이용하여 수온 분포 함수를 간단하고 정확하게 추정하는 데 활용할 수 있다.

한편, 본 연구에서 제안한 가우스 혼합분포 함수 형태가 수온자료의 빈도분포 함수에서 첨두 형태 재현에는 우수한 결과를 보이고 있으나, 분포의 꼬리에 해당하는 부분에서는 재현성이 떨어지고 있다. 이 부분은 꼬리부분의 표현이 우수한 다양한 함수형태에 대하여 다각적으로 검토하는 연구가 필요가 있을 것으로 사료된다.