1. 서 론
기후변화 중 대두되고 있는 지구온난화는 기후를 구성하는 대기, 해양, 생물, 빙하, 육지 등에 다양한 경로로 영향을 줄 것으로 예상되며 그 영향은 대부분 악영향인 것으로 평가되고 있다(Cho and Maeng, 2007). 지구온난화가 인간 사회에 주는 많은 영향중 장기적으로 가장 큰 영향을 줄 것으로 예상되는 요소는 해수면 상승이다(IPCC WG II, 2001). 해수면 상승은 연안침식, 폭풍 해일 및 연안 범람 증대, 하구 퇴적 변화, 하천 및 지하수 염분 침투 등에 의하여 해안 사빈, 사구, 습지, 수자원과 같은 자연생태계에 대한 영향과 인간의 활동과 관련된 사회·경제적 부분에 영향을 미치고 있다(Cho et al., 2011). 또한, 해수면의 변화는 기후변화에 기여하는 다양한 요인과 함께 광범위한 시간과 공간에서 발생한다(Milne et al., 2009). 삼면이 바다로 둘러싸인 우리나라의 연안지역은 꾸준한 개발이 진행되고 있으며 연안지역 인구증가에 따른 극치해수면에 의한 피해가 가중되고 있다. 우리나라뿐만 아니라 전 세계 곳곳에서 산업화 이후 무분별한 해안지역 개발로 인하여 해안의 생태계가 많이 훼손되어 해수면 상승 시 위험도가 증가하여 이에 대한 대책을 장기적으로 고려하지 않으면 전 지구적으로 심각한 피해가 초래될 전망이다. 해수면 상승은 Intergovernmental Panel on Climate Change(IPCC)을 중심으로 한 연구 결과를 통해 미래에도 계속될 것이 기정사실화 되고있다. IPCC는 Climate Change 2014 Synthesis 5차 보고서에서 이산화탄소 대표적 농도 경로 (representative concentration pathways, RCP)를 고려할 경우 2100년에 평균적으로 약 100 cm이상의 해수면 상승이 발생할 것으로 발표하였다(IPCC, 2014). 이는 제 4차 보고서의 59 cm보다 대폭 상승한 결과이다.
계속된 해수면 상승에 따라, 미래에 발생 가능한 평균해수면 상승의 추정에 관하여 많은 연구가 진행되고 있다(Rahmstorf, 2007; USACE, 2011). 하지만 평균해수면의 미래 값을 추정 할 때 같은 자료를 사용하더라도 시작년도를 다르게 적용하면 추정 값이 다르게 추정된다는 문제점이 있다. 또한, 특정 지점의 현재와 미래 값의 결합에 있어서 평균 해수면의 경년변화(interannual variability)을 고려하지 않아 발생하는 오차와 지점 기준면이 변화됨에 따라 발생되는 오차로 인한 문제가 제기될 수 있다(Flick et al., 2013). 극치자료는 일반적인 변량과는 다른 분포(distribution) 특성을 가지고 있어 단순히 선형 회귀분석과 같은 방법으로는 극치 자료의 경향성을 효과적으로 분석하기 어렵고 이를 빈도개념과 연계시켜 해석하는데 무리가 있다고 지적되고 있다(Lee et al., 2010). 이와 같은 문제점을 개선하기 위해 본 연구에서는 비매개변수적 경향성 검정(nonparametic trend test)을 먼저 시행하여 경향성에 대해서 유의성을 확인한 이후, 극치변량의 분포특성을 고려한 경향성 분석과 이를 빈도분석과 연계할 수 있는 비정상성 빈도분석을 개발하였다. 시계열 자료에서 비정상성이란 통계적 특성이 시간에 따라 변화하는 것으로 일반적으로 기상학적 원인에 의해 나타나는 특성이다. 기존의 활용되는 정상성 빈도해석 방법은 자료의 정상성을 기본 가정으로 해석이 이루어지고 있으나, 해수면자료와 같이 경향성이 존재하는 경우 정상성 해석은 상당한 불확실성을 가져올 수 있다. 본 연구에서는 2단계의 해석모형을 제시하고자 한다. 1단계에서는 평균해수면을 모의할 수 있는 모형을 개발하고 2단계에서는 이를 직접 활용하여 극치해수면을 모의할 수 있는 비정상성 모형으로 확장하였다.
시계열 자료가 내포하고 있는 시간에 따른 변동 특성은 추세, 변동점 및 장단기 주기 등 자료 자체에 대하여 가시적으로 판단할 수 있는 부분이 대다수이며, 이러한 변동특성은 각종 통계기법으로 정량화할 수 있다(Kim, 2006). 경향성 분석 기법으로는 Mann-Kendall(MK) 검정, Hotelling-Pabst검정, Spearman’s Rho 검정, Linear regression 검정, CUSUM 검정, Cumulative Deviation 검정, Worsley likelihood 검정, Rank-Sum 검정 및 Student’s-t 검정이 있으며 다양한 자료를 통해 경향성을 파악하였다(Oh et al., 2005). 이중에서 MK 검정 방법이 가장 일반적인 방법으로 활용되고 있다. Kendall and Gibbons(1990)는 MK 분석은 표본자료의 특성에 영향을 받지 않고 모평균의 분포가 연속적인 모평균을 가진다는 가정아래 검정을 실시한다고 제시하였다.
본 논문에서는 첫째, 우리나라 연안의 20개 지역의 조위 자료를 바탕으로 경향성 및 비정상성 빈도분석에 대한 해석 방법을 설명한다. 둘째, 통계학적 추론 관점에서 분석한 결과에 대한 해석과정을 설명한다. 마지막으로 분석 결과에 따른 국내 연안의 전반적 미래 극치해수면 상승을 분석하며 연안 안정성을 위한 향후 연구방향을 제시하는 단계로 구성된다.
2. 자료특성 분석 및 모의 방법
2.1 MK 검점을 통한 경향성 분석
경향성을 판단하는 통계학적 방법으로는 매개변수에 대한 추론시 모집단 분포에 대한 가정을 포함하는 매개변수적 방법과 모집단 분포에 대한 가정을 하지 않고 분석하는 비매개변수적 방법이 있다. 비매개변수적 방법은 모든 자료간의 관계를 종합적으로 분석할 수 있기 때문에 결측값이나 자료의 계절성을 유동성 있게 고려할 수 있다는 점에서 분석시 매개변수적 방법에 비해 많이 사용된다(Stålnacke et al., 2014). 본 연구에서는 비매개변수적 방법 중 MK 검정법을 사용하여 SLR의 경향성을 분석하였다. MK 검정의 대립가설은 단조경향성이 존재한다고 가정되며, 귀무가설 (null hypothesis)은 단조경향성이 없고 통계적으로 독립으로 가정된다(Lee et al., 2014).
M-K 통계치(St)는
으로 나타낸다. 여기서, sgn(Dj - Di)는 다음과 같다.
정규화된 검정 통계량 Sn은 다음과 같이 정의된다.
Sn값이 양수인 경우 증가 경향성을 나타내며 음수인 경우에는 반대로 경향성의 감소를 나타낸다. 연결 그룹(tied group) G은 동일한 값을 갖는 자료의 집합을 의미한다. 본 연구에서는 분산 산정 시 자료의 특성을 반영하여 연결그룹(G)을 고려하지 않았다.
p는 유의 수준을 나타내며, 일반적으로 5% 내의 자료에 경향성이 존재한다고 판단한다. 여기서, k는 자료의 수를 나타낸다.
2.2 기후정보를 활용한 비정상성 빈도해석 기법
계속된 지구온난화에 의하여 기상이변의 발생 빈도가 증가하고 있다. 이러한 변화에 따라 극치사상에 대한 추정을 하고자하는 연구가 많이 진행되어 왔다. 하지만 기존의 극치사상의 확률분포에서 외부 인자를 고려한 빈도해석 시 매개변수 추정 등 많은 어려움이 존재하였으며, 시계열의 증가 및 감소 경향이 있는 외부인자 고려 시 더욱 어려움을 가중시킨다. 이러한 구조적인 경향성 및 주기(cycle) 특성을 외부인자로서 고려하는 것이 비정상성 빈도해석의 기본 목적이라 할 수 있다. 과거부터 현재까지 이르는 다양한 기후변화 연구들은 온실가스 효과로 인한 지구온난화가 수문기상순환 시스템을 가속화 시킨다고 추정하고 있다. 이러한 시점에서 극치시계열에 대한 경향성을 고려 할 수 있는 모형의 개발은 필수적으로 시행되어야 한다. 본 연구에서는 평균 및 극치 조위 계열의 비정상성 빈도해석을 위해 정규 분포, GEV 분포를 적용하였다.
평균 조위계열 분석 시에는 정규 분포를 적용하였으며, 이 분포의 확률밀도함수와 누가 확률밀도함수는 다음과 같다.
여기서 σ는 규모매개변수(scale parameter), µ는 위치매개변수(location parameter)이다.
평균치계열 자료 Xmean가 앞서 제시한 정규 분포를 따른다고 가정할 때, 정규 분포형의 규모매개변수와 위치매개변수는 다음과 같은 시간에 따라 다른 값을 가지도록 구성할 수 있다.
여기서 σ(t)는 시간에 따른 변수로서의 큰 유의성을 발견할 수 없었다. 따라서 식 (10)과 같이 나타낼 수 있다.
Bayesian 모형에서 식(10)의 모든 매개변수들은 확률분포를 가지게 되며 매개변수들의 불확실성을 확률분포로 나타낼 수 있다. 즉, μmean(t)는 사전분포(prior distribution)를 가지게 되며 μmean(t)는 시간의 함수로서 다음의 식(11)과 같이 비선형관계를 갖는다고 가정한다.
여기서, t는 시간을 의미하며, α0, α1, α2는 시간과 매개변수 µ의 사전분포를 곡선형적으로 연계시키는 회귀분석의 매개변수를 나타낸다.
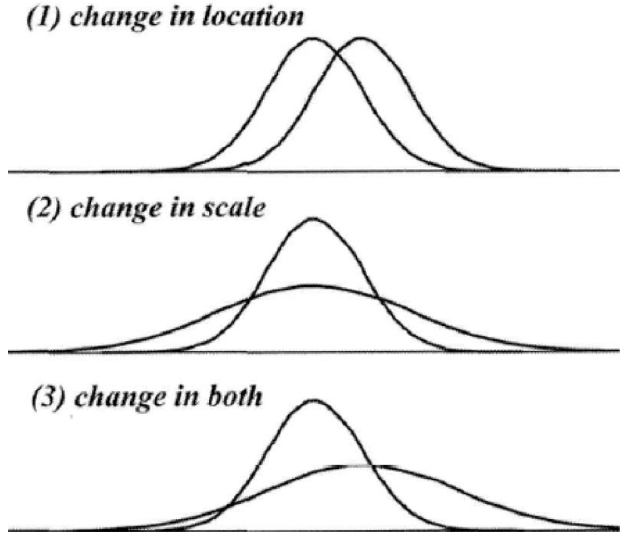
Fig. 1은 확률분포의 위치매개변수와 규모매개변수의 변화 조건에 따른 거동을 나타내고 있으며 본 연구에서는 위치매개변수 µ만 시간에 따라 변화한다고 가정하여 통계적 추론을 실시하였다.
위와 같은 방법으로 극치계열 자료 Xmax도 같은 방법을 적용하였다. 극치 조위계열의 분석 시에는 적합도 검정을 통하여 Xmax를 나타내기 위하여 GEV 분포를 선정하였으며, 이 분포의 확률밀도함수와 누가 확률밀도함수는 다음과 같다.
여기서 σ는 규모매개변수(scale parameter), µ는 위치매개변수(location parameter)이며 ξ는 형상매개변수(shape parameter)이다.
GEV 분포형의 규모매개변수와 위치매개변수 및 형상매개변수는 다음과 같이 시간에 따라 변화하는 비정상성 모형으로 구성할 수 있다.
여기서 σ(t), ξ(t)는 경향성검토를 통하여 시간에 따른 변수로서의 큰 유의성을 발견할 수 없었다. 따라서 다음 식(15)와 같이 나타낼 수 있다.
또한, 본 연구에서는 연극치 조위계열은 연평균치 조위계열의 함수로 가정하여 μmean(t)를 정의하였다.
본 연구에서는 30년 이상의 조위 자료를 대상으로 하며 Markov Chain Monte Carlo (MCMC)기법을 도입하여 매개변수들의 사후분포(posterior distribution)를 추정하였다. 본 연구에서는 MCMC 방법 중 깁스 표본법을 이용하여 회귀매개변수들을 추정하였으며 모형의 수렴(convergence)을 확증하기 위하여 Chain 3개를 독립적으로 시행하여 효과적으로 혼합 되도록 하였다.
깁스 샘플러는 다변량 매개변수 중 한 가지 변수를 제외한 나머지를 고정하여 조건부 분포를 이용한 샘플링을 통하여 고정되지 않는 변수를 추정하는 방법으로 같은 방법을 모든 매개변수에 시행하여 값을 추정해 낸다. MCMC 방법을 사용하는 대부분의 통계 응용 프로그램은 깁스 샘플러를 이용하고 있다. MCMC 방법 및 깁스 샘플러에 대한 자세한 설명은 Gilks et al.(1995)와 Kwon et al.(2009)의 논문을 참고하면 된다.
3. 경향성 및 모의 분석 결과
3.1 국내 조위 자료의 특성
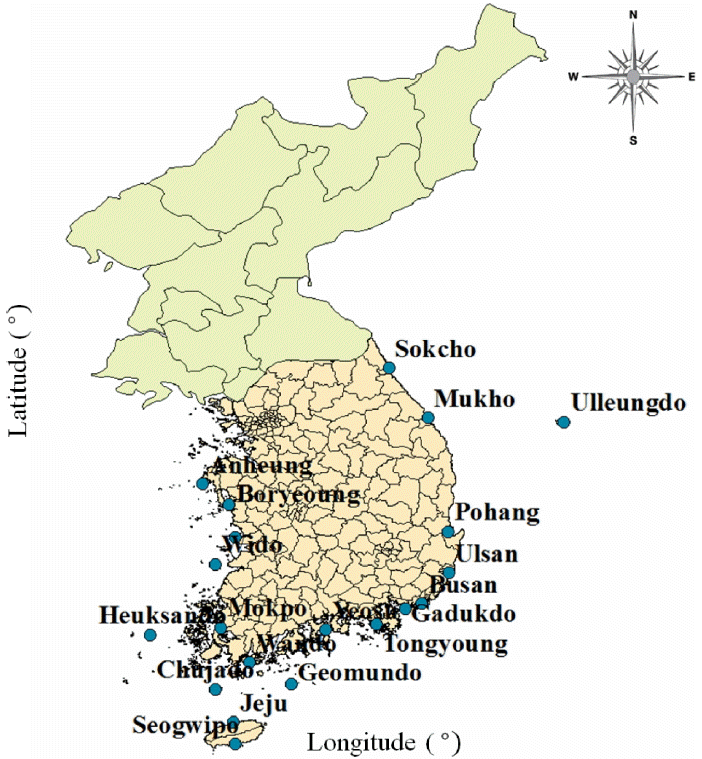
본 연구에서는 해수면 변화에 대한 분석을 위하여 국립해양조사원(Korea Hydrographic and Oceanographic Administration, KHOA)에서 제공하는 예보기준면에 따른 45개 지점의 1시간 조위 자료를 이용하여 평균치 및 극치사상을 추출하였다. 자료의 결측치는 KHOA에서 자체 보간 처리되어 제공되었다. 자료의 특성 및 확률론적 분석을 함에 있어서 짧은 자료 연한은 매우 큰 불확실성을 야기 할 수 있다. 국내 조위 자료는 30년을 기준으로 짧은 지점은 1년~3년 정도의 연한을 나타내고 있었으며 관측기간이 긴 지점은 50년 이상이 구축된 지점이 있었다. 따라서, 통계분석의 신뢰성을 위하여 45개 지점 중 30년 이상의 자료 연한을 가지고 있는 지점 20개를 선정하여 분석을 실시하였다. 분석 시 해수면 변화는 단기간에 변화하는 사상이 아니므로 연평균 해수면 상승(annual mean sea level rise) 및 연극치 해수면 상승(annual maximum sea level rise)의 연 단위 자료를 구축하였다. Fig. 2는 본 연구에서 선정된 20개 지점에 대한 위치를 나타낸다.
3.2 자료의 유의성 검정 결과
조위자료에 대한 변화 양상을 판단하기에 적합한 방법은 자료의 경향성 분석을 실시하는 것이 가장 유용한 방법이다. 가설검증 시 일반적으로 유의 수준을 0.05 또는 0.1로 설정하며 경향성 분석법을 적용하여 추정된 p-value가 앞서 제시한 값보다 적을 경우 귀무가설은 기각된다. 귀무가설은 경향성이 존재하지 않는다고 가정하며, 기각된 경우에는 가정한 것이 틀리기 때문에 경향성이 존재한다고 판단하게 된다. 본 연구에서는 비매개변수적 경향성 분석 방법인 MK 검정법을 유의수준 0.1로 설정하여 경향성 분석을 실시하였다(Uranchimeg et al., 2015).
MK 검정 결과 연평균 조위에 대한 분석에서는 위도 지점에서 감소 경향이 나타났으며, 연극치 조위에 대한 분석시에는 묵호, 완도 및 여수에서 감소 경향을 나타냈다. 본 연구에 사용된 20개 지점의 유의성 분석시에는 연평균조위의 경우 위도, 흑산도및 안흥을 제외한 17개 지점에서 유의수준 0.1에서 유의한 것으로 분석되었으며, 연극치 조위의 경우 부산, 목포, 여수, 보령, 포항, 제주 및 흑산도의 12개 지점에서 유의한 것으로 나타났다. 제주 조위관측소의 경우 연평균자료의 유의 확률 값이 0으로 수렴되고 있어 경향성 존재 유무가 가장 큰 것으로 판단할 수 있다.
3.3 가속도를 고려한 비정상성 빈도분석 결과
기후변화에 관한 많은 연구들에 의하면 지구온난화는 극치사상의 발생을 가속화 시킬 것으로 전망하고 있다. 본 연구에서는 자료의 변동성을 확률론적으로 추론 가능한 비정상성 분석에서 경향성 및 가속화를 고려하여 빈도 분석을 실시하였다. 본 연구에서는 앞서 제시한 방법론에서 설명하였듯이 평균 해수면의 경향성이 극치해수면의 경향성에 영향을 주는 것으로 가정하였다. 따라서, 1차적으로 평균해수면의 경향성을 모의한 후 이를 극치해수면 빈도해석에 외부입력자료로 활용할 수 있도록 모형을 구성하였다(식 16). 가속도를 고려한 미래 연평균 해수면 비정상성 빈도분석을 위하여 전지구적 해수면 상승을 추정하기 위한 추정 식 중 하나인 미국 국립연구회(National Research Council, NRC, 1987)가 제시한 2차식을 구성하여 가속도를 추정하였다. 추정 결과 2차항에 대한 계수인 가속도의 평균적인 범위는 연평균 조위 자료에서 -0.0080 ~ +0.0081가 산정되었다. 따라서 본 연구에서는 미래 연평균 해수면 비정상성 빈도분석 시 식(11)의 회귀분석 매개변수 에 증가 경향성을 나타내는 지점에서는 +0.0081을 선정하여 적용하였으며, 감소를 나타내는 지점에서는 -0.0080을 적용하였다.
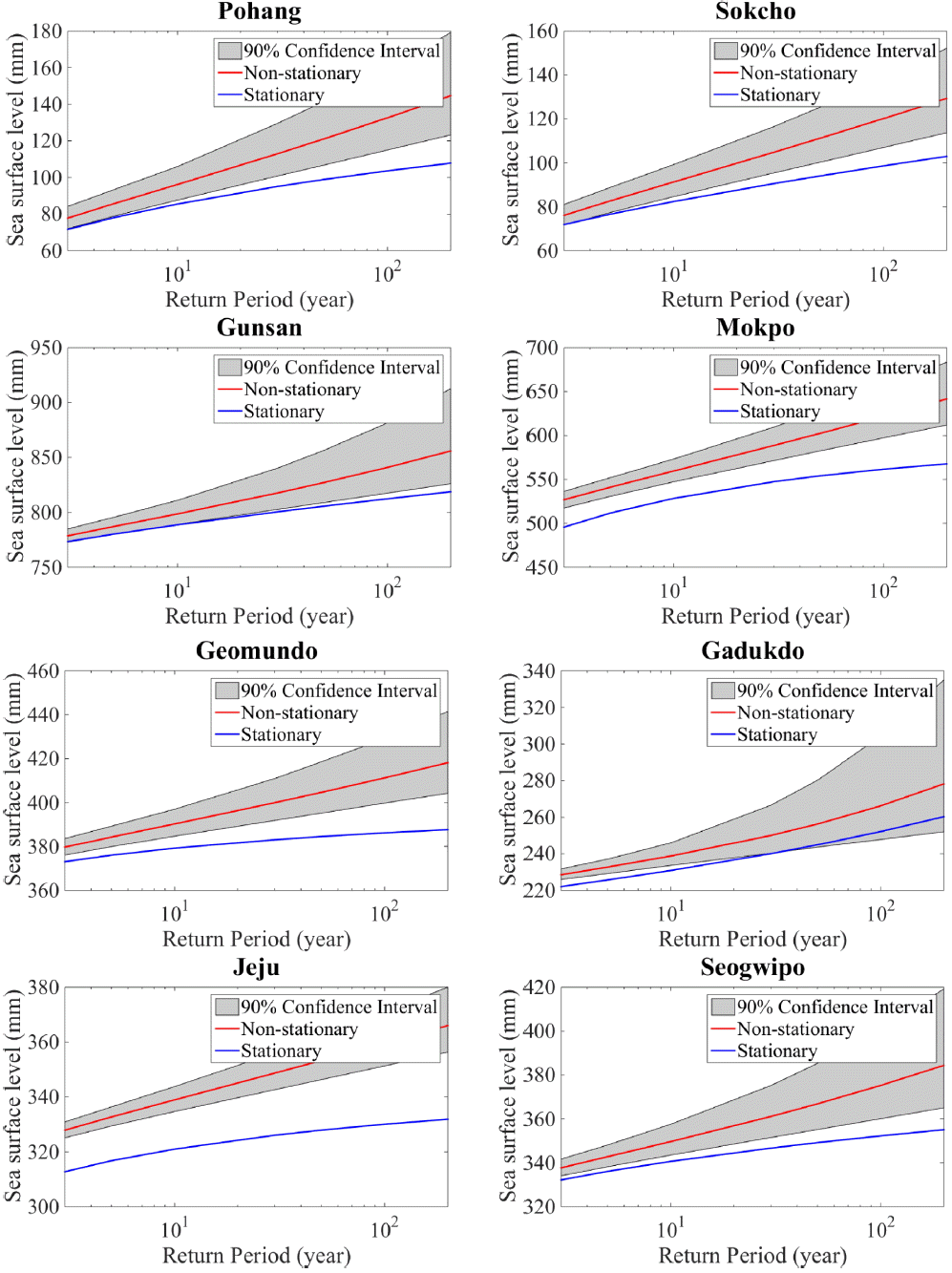
본 연구에서는 정규분포 및 GEV 분포를 이용하여 극치조위 자료에 대한 비정상성 빈도분석을 수행 하였다. 분석 시 국내 연안을 동해안, 서해안, 남해안 및 제주의 4개 권역으로 구분하였으며 Fig. 4에서는 동해안은 포항, 속초, 서해안은 군산, 목포, 남해안은 거문도, 가덕도, 제주는 서귀포, 제주 지점을 선정하여 정상성 및 비정상성 빈도분석 결과를 도시한 것이다.
Fig. 4에 도시된 바와 같이 정상성 빈도분석 시 산정된 결과는 비정상성 빈도분석의 결과보다 다소 작게 추정되는 것을 확인할 수 있다. 특히 제주 지점의 경우에는 정상성 100년 빈도가 비정상성 4년 빈도와 같은 결과를 나타내어 매우 큰 차이를 나타냈다. 목포 및 제주 지점을 제외한 6개 지점은 10년 이하의 빈도에서는 정상성과 비정상성의 차이가 10 mm 내외를 기록하였지만 목포, 제주 지점은 20~30 mm를 기록하여 빈도가 커질수록 정상성 빈도 분석 시 매우 큰 과소 추정된 결과를 나타내고 있다. 일반적으로 사용되는 정상성 빈도해석은 시계열에 경향성이 존재하지 않는 정상시계열에 적용이 가능한 방법으로서 해수면 자료와 같이 경향성이 존재하는 경우 정상성 빈도해석의 기본가정에 위배되며, 해석 결과에 신뢰성의 문제가 발생할 수 있다. 이러한 이유로 자료의 경향성이 있는 경우에는 비정상성 빈도해석이 해석결과의 신뢰성 측면에서 유리한 정보를 제공한다.
Table 4은 비정상성 빈도 분석에 따른 결과를 재현기간에 따라 Quantile를 작성한 것이다. 본 연구에서 활용한 Bayesian 기반의 빈도해석 방법은 매개변수 추정에 있어 불확실성을 정량적으로 평가할 수 있는 장점이 있다. 즉, 동일한 연한을 가지는 자료의 경우에도 자료의 특성에 따라 불확실성의 크기를 정량적으로 평가할 수 있으며, 해석결과에 대한 신뢰성을 평가하는데도 유리하다. 예를 들어 군산의 경우에 빈도가 증가할수록 불확실성 범위가 타 지점에 비해 큰 것을 확인할 수 있다. 이는 군산 지점의 극치자료의 경향성이 통계적 관점에서 유의성이 상대적으로 크지 않기 때문이다. 이에 반해, 제주지점의 경우 불확실성이 타 지점에 비해 작은 것을 확인할 수 있으며, 이는 군산 지점과 상이하게 극치 자료의 경향성이 통계적으로 유의한 것에 기인한 결과이다.
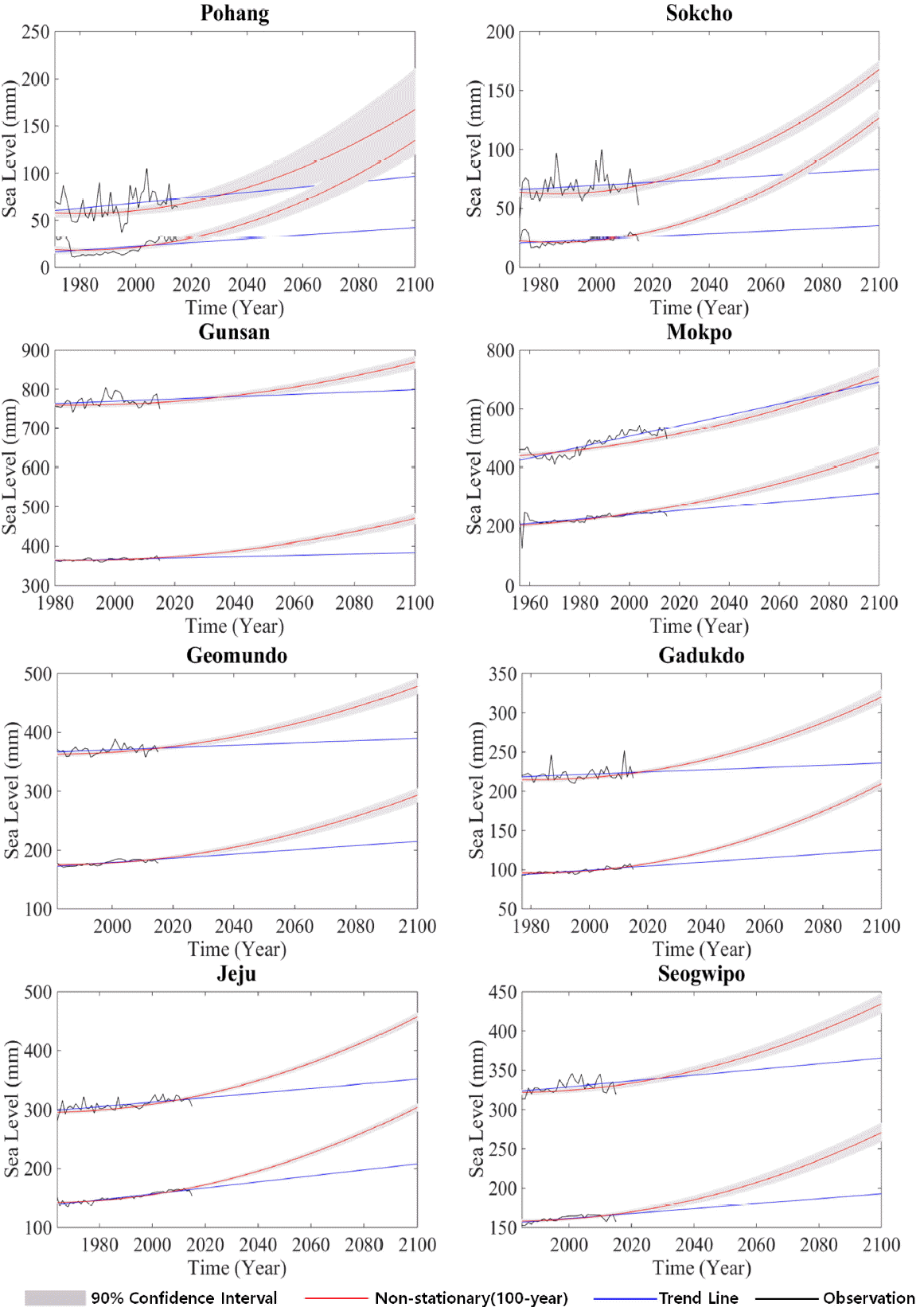
Fig. 5는 해수면의 가속성분과 경향성을 고려하여 추정된 100년 빈도 해수면 상승 시나리오와 기존 정상성을 기반으로 추정된 100년 빈도 해수면 시나리오를 비교한 그림이며, 비정상성 빈도 해석에 추정된 100년 빈도 해수면 증가량의 중앙값 외에 5%, 95%의 불확실성 구간을 사후분포로부터 추정하여 나타내었다.
2100년도 각 지점의 해수위는 2015년 관측 결과에 비해 평균 +125.33 mm를 나타내어 2015년 조위값의 65%에 해당하는 증가를 나타냈다. 각 지점별 증가는 포항 +103.35 mm, 속초 +71.89 mm, 군산 +119.14 mm, 목포 +214.90 mm, 거문도 +111.17 mm, 가덕도 +103.06 mm, 제주 +145.32 mm 및 서귀포 +111.84 mm가 추정되었다. 본 연구에서 제시한 결과는 상대적으로 작은 연한을 가지는 자료를 통하여 추정된 결과로서 100년 후의 기후변화 영향을 평가하는데 한계점이 존재한다 하겠다. 그럼에도 불구하고 현재의 경향성을 토대로 미래의 해수면 상승 시나리오를 구성하고 동시에 불확실성을 평가하는 것은 해수면 상승으로 인한 취약성을 평가하는데 매우 중요한 정보로 활용이 가능할 것으로 판단된다.
4. 결 론
우리나라의 경우 해안 사빈의 배후 지역은 계속된 발달로 인구 및 도시지역이 증가하여 연안의 사회·경제적 활동이 활발해지고 있다. 이러한 점에서 MSLR로 인한 연안재해 취약성이 가중될 것으로 전망되고 있다. 현재 우리나라는 지속되고 있는 기후변화에 대한 국가적응계획의 수립·이행 등 제도적 대응이 활발히 이루어지고 있지만, 여전히 적절한 대응책을 제시하지는 못하고 있는 실정이다. 본 연구에서는 한반도 연안의 해수위 변화에 따른 경향성 분석 및 가속도 상승을 고려한 비정상성 빈도분석을 수행하였다.
연구를 통하여 얻은 결론은 다음과 같다.
첫째, MK 분석 결과 연평균 조위의 경우 위도, 흑산도 및 안흥을 제외한 17개 지점에서 유의한 것으로 분석되었으며, 연극치 조위의 경우 7개 지점에서 유의한 것으로 나타났다. 특히, 제주 조위관측소의 경우 연평균 조위자료의 유의 확률값이 거의 0으로 추정되어 경향성 존재 유무가 가장 큰 것으로 나타났다.
둘째, 빈도분석 결과 20개 조위 관측소에서 정상성 빈도 결과는 비정상성 빈도해석 결과에 비해 과소 추정되었으며, 이는 자료의 비정상성이 크다는 점을 의미한다 하겠다. 특히, 제주지점이 다른 지점에 비해 그 격차가 큰 것으로 나타났다.
전반적으로 우리나라 해수면은 상승 경향을 나타내고 있으며, 가속성분의 유무에 따라 선형분석에 의한 결과와 비선형에 의한 비정상성 빈도분석 결과 2100년 기준 최소 20 mm에서 최대 100 mm까지 나타났으며, 이는 가속성분에 대한 고려가 일부 필요함을 나타낸다 하겠다. 그러나 대상 지점에 따라서 가속성분에 대한 불확실성이 큰 것을 확인할 수 있었다. 가속도를 고려한 비정상성 빈도분석 결과 2100년에는 2015년 해수면 높이에서 최소 +60.33 mm에서 최대 +214.90 mm까지 증가할 것으로 분석되었다.
향후 연구로서 기후변화 영향을 종합적으로 반영하여 산정되는 RCP 시나리오의 가속화 성분을 고려한 비정상성 빈도 분석 시나리오를 개발하여 보다 신뢰성 있는 연평균 해수면을 산정하고 기후변화에 대한 사회·경제적 방안을 수립에 활용하여 안전대책을 마련할 필요가 있다.