1. 서 론
항주파는 선박이 이동할 때 선박의 요동으로 발생하는 파랑으로 선박이 정지해 있다면 이 파랑이 360o 모든 방향으로 전파할 것이다. 그리고 선박의 이동속도가
g h
2. 항주파의 파봉식 유도
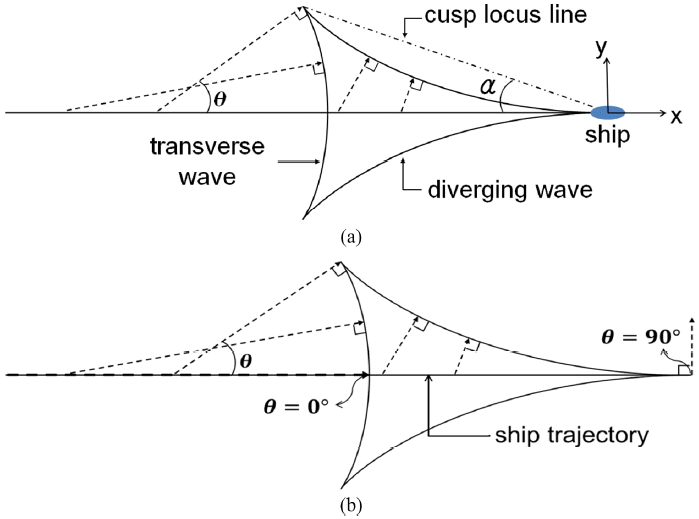
선박이 일정한 속도 U로 항행할 때 항주파는 항적중심선에 있는 원천점에서 θ방향으로 전파한다. 선박이 이동하면서 선박의 이동과 항주파의 전파가 동시에 발생하면서 파봉선이 항적중심선의 좌·우로 전파하는 종파(diverging wave)와 선박의 뒤에서 항적중심선을 가로지르면서 선박쪽으로 전파하는 횡파(transverse wave)로 나타난다. Fig. 1(a)는 파향각(θ)에 따라 다른 속도로 전파하는 항주파의 파봉선을 도시한 것이고, Fig. 1(b)는 항주파의 파향각(θ) 범위를 도시하였다. 항주파의 파향각(θ)은 Froude수가 1보다 작은 경우 항적중심선을 기준으로 왼쪽은 0o~90o의 범위에서 전파하며 오른쪽은 0o~90o의 범위에서 전파한다. 그리고 Froude수가 1보다 큰 경우에는 횡파가 사라지고 종파만이 전파하고 파향각의 범위가 좁아지게 된다. 여기서, 파향각 θ는 항적중심선과 파향선 사이의 각도를 의미하며, α는 최대파향각(cusp locus angle)으로 종파와 횡파가 만나는 점과 선박을 이은 선(cusp locus line)이 항적중심선과 이루는 각도를 의미한다. 항주파는 주기와 방향이 서로 다른 여러 성분으로 구성되어 있다. 따라서, 항주파의 속도포텐셜을 선형파로 표현하면 다음과 같다.
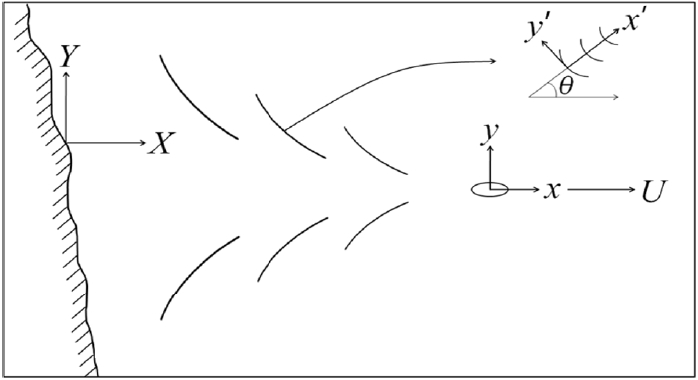
여기서 k는 항주파의 파수, h는 정지수심, g는 중력가속도이다. Fig. 2에서 (X, Y, Z), (x, y, z)는 각각 고정된 지점을 기준으로 한 좌표와 선박을 기준으로 한 좌표로서 X = x+Ut, Y = y, Z = z의 관계가 있다. 식 (1)을 선박을 기준으로 한 좌표로 표현하면 다음과 같은 항주파의 속도포텐셜이 정의된다.
선박을 기준으로 항주파의 파봉을 보면 시간이 지나도 변하지 않으므로(stationary) 식 (2)로부터 다음과 같은 관계식을 얻을 수 있다.
위 식을 파랑의 선형분산관계식에 대입하면 다음과 같은 항주파의 분산관계식을 얻을 수 있다.
Fig. 2에서 항주파를 기준으로 한 좌표계(x′, y′)에서 군속도(즉, Cg = x′⁄t = dω ⁄dk)의 전파를 다음과 같이 표현할 수 있다.
여기서 x′ = Xcosθ + Ysinθ = xcosθ + ysinθ +Utcosθ이고 식 (3)을 식 (5)에 대입하고 k(θ)에 대해 연쇄법칙을 적용하면 다음 식이 유도된다.
위 식을 y/x에 대해 정리하면 다음과 같은 일반화된 식을 얻을 수 있다.
항주파의 분산관계식 (4)를 온전하게 이용하여 식 (7)의 미분항 dk⁄dθ로 유도하면 다음과 같다.
식 (4)와 식 (8)을 식 (7)에 대입하면 본 연구에서 개발한 항주파 파봉식을 얻을 수 있다.
심해(즉, kh≥π)와 천해(즉, kh≤0.1π)에서 식 (9)는 각각 식 (10)과 식 (11)로 유도되며, 식 (10)은 Kelvin(1887)이 제안한 항주파 파봉식이다.
즉, 본 연구에서 개발한 항주파 파봉식 (9)는 심해에서 적용되는 Kelvin(1887)의 식 을 포함하고 모든 수심에서 적용된다는 것을 알 수 있다. 여기서 Fr은 Froude수이고, 선박의 이동속도 U와 장파의 전파속도의 비로서 다음과 같이 표현된다.
식 (6)을 에 대하여 적분하면 다음과 같은 식을 얻을 수 있다.
여기서, 적분 상수 C는 무차원 값으로 0보다 크고 항주파의 위치를 결정하는 상수이다. 종파와 횡파가 전파하는 파봉선을 정확히 표현하기 위해서 x와 y의 좌표를 알아야 한다. 식 (9)를 y에 대한 함수로 표현하여 식 (13)에 대입하면 x에 대한 식을 얻을 수 있고, 이 식을 다시 식 (13)에 대입하면 y에 대한 식을 다음과 같이 얻을 수 있다.
식 (14), (15)는 심해(즉, kh≥π)에서 다음과 같이 표현된다.
식 (16), (17)의 두 번째 항에서 세 번째 항으로 유도할 때 삼각함수의 3배각공식을사용하였다. Lamb(1945)은 a(=–CU2/g)라는 상수를 사용하여 식 (16), (17)의 세 번째 항을 유도하였고, 그는 배가 –x방향으로 항행하는 경우에 유도하여 본 연구의 +x방향으로 항행하는 경우와 반대방향이다. Lamb이 사용한 상수 a는 항주파의 위치를 나타내는 길이 차원의 값이고, 본 연구에서 사용하는 상수 C는 항주파의 위치를 나타내고 파수 k로 무차원화 한 값이다. 그리고 식 (14). (15)는 천해(즉, kh≤ 0.1π)에서 다음과 같이 표현되며, 식 (14), (15)는 심해에서 적용되는 Lamb(1945)의 식을 포함하고 모든 수심에서 적용되는 항주파 파봉식이란 것을 알 수 있다.
식 (18), (19)는 식 (16), (17)과는 달리 항주파의 수심, 선속에 의해 결정된다. 항주파 파봉식의 상수 C는 θ = 0o(항적 중심선에서 횡파성분)에서 항주파의 분산관계식 (4)와 식 (13)으로부터 다음 식으로 표현할 수 있다.
파향각이 θ = 0o인 경우 선박에부터 멀어져가는 방향으로 인접한 n-1번째 항주파와 n번째 항주파 간의 거리 Δdn은 파봉과 파봉 사이의 거리인 파장 λ0이다(즉, Δdn = λ0). 따라서 항주파간의 거리를 결정하는 ΔCn을 다음 식으로 표현할 수 있다.
식 (20), (21)에서 아래 첨자 0는 θ = 0o에서의 값을 의미한다. 상수 C의 차이는 2π로 일정하며, Lamb(1945)도 이와 같은 내용을 언급하였다. 식 (21)로부터 N번째 항주파에 대응하는 상수 CN은 아래와 같이 다시 쓸 수 있다.
C1은 선박 가까이 있는 첫 번째 항주파에 대응하는 C값을 의미한다. 첫 번째 항주파는 선박과 가까이 있어서 선박의 제원, 선속에 따라 민감하게 변할 수 있다. 선박에서 멀리 떨어질수록 이러한 조건에 민감하지 않을 것으로 판단된다. 제 4장에서 식 (9), (22)를 사용하여 이론해와 FLOW-3D의 수치해를 비교하였다.
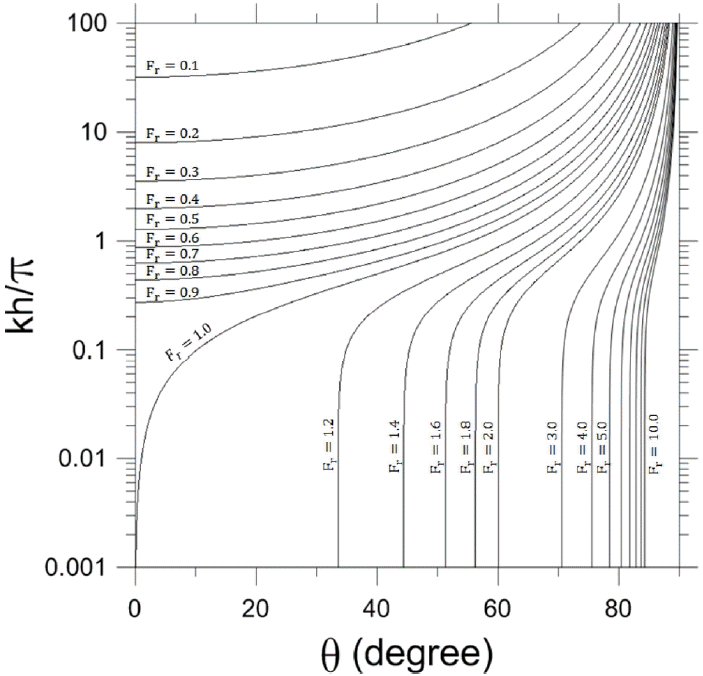
Fig. 3은 Froude수가 주어진 경우 항주파의 파향각에 따른 상대수심의 변화를 도시한 그림이다. 파향각이 작을수록(즉, θ = 0o에 가까울수록) 파장이 길어서 상대수심이 얕아지고, 파향각이 클수록(즉, θ = 90o에 가까울수록) 파장이 짧아서 상대수심이 깊어진다. Froude수가 1보다 작은 경우와 1보다 큰 경우는 서로 다른 경향을 보인다. 예를 들어, Froude수가 0.5인 경우 파향각이 θ = 0o에서 θ = 90o까지 모두 존재하는 반면 상대수심은 심해의 경우만 존재하고 kh = π 이하의 경우(즉, 중간수심과 천해인 경우)가 존재하지 않는다. Froude수가 작을수록 상대수심은 더 깊어지면서 존재 범위가 좁아진다. Froude수가 2.0인 경우 상대수심은 심해부터 천해까지 모두 존재한 반면 파향각은 θ = 60o에서 θ = 90o까지 존재하고 θ = 60o 이하의 경우는 존재하지 않는다. 즉, Fr > 1인 경우 종파는 존재하지만 횡파는 존재하지 않는다. Froude수가 클수록 종파의 파향각은 더 커지면서 존재 범위가 좁아진다.
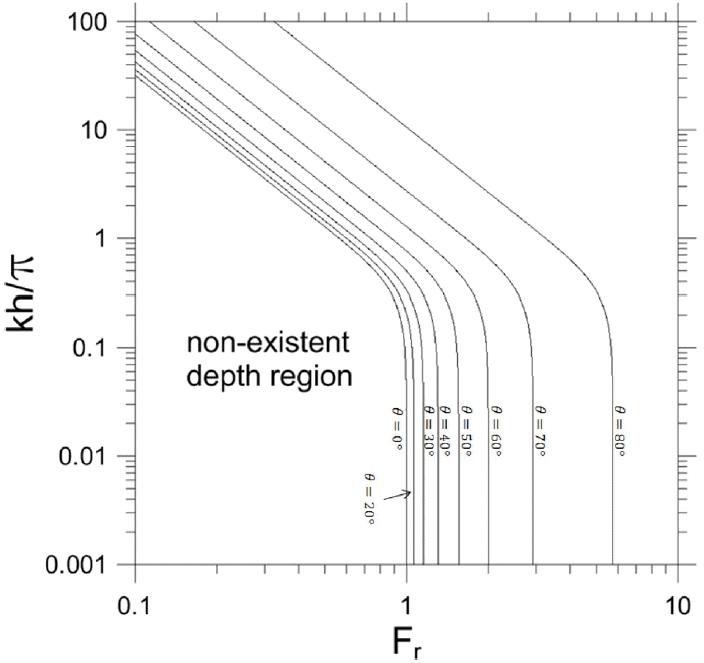
Fig. 4는 파향각이 주어졌을 때 Froude수에 따른 상대수심의 변화를 도시한 그림이다. 파향각 θ = 0o을 기준으로 좌측으로는 존재하지 않는 수심영역이 있음을 보여준다. 예를 들어, Froude수가 0.5이면 상대수심이 π보다 작은 경우는 존재하지 않고, Froude수가 2이면 모든 수심이 존재하고 파향각이 60o보다 큰 경우만 존재한다. 모든 파향각에 대하여 Froude수가 증가하면 그에 대응하는 상대수심이 작아지고 Froude수가 1에 근접하거나 1보다 큰 경우에는 그에 대응하는 천해역의 상대수심이 존재한다.
3. 최대파향각 이론식 유도 및 수치실험
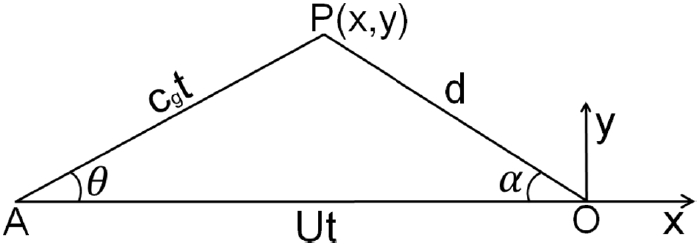
Havelock(1908)은 항주파가 군파(group wave)로 전파하는 것을 이용하고 기하학적으로 Fig. 5와 같은 관계를 이용하여 최대파향각을 제안하였다. 이때 선박의 속도는 일정하다고 가정하였다. Fig. 5에서 U는 선박의 속도, Cg는 군속도, d는 최대파향선(cusp locus line,
O P ¯
여기서, 아래첨자 c는 종파와 횡파가 만나는 점(cusp locus point)을 의미한다. 위 식을 분석해보면 최대파향각은 선속과 수심으로 정의되는 Froude수에 따라 다양하게 나타나는 것을 알 수 있다. Froude수가 0.4이하의 경우 최대파향각이 Kelvin이 제안한 것과 같이 αc = 19.47o로 일정하다. Froude수가 0.4부터 1 사이로 증가하는 경우 최대파향각은 αc = 19.47o에서 αc = 90o로 증가한다. Froude수가 1보다 더 큰 경우 (즉, 천해의 경우) 최대파향각은 αc = 90o보다 더 작아진다.
본 연구에서 구한 항주파의 파봉식 (9)로부터 최대파향각을 구할 수 있다. 즉, 파향각 θ의 변화에 따른 y⁄x의 변화를 관찰하여 y⁄x = (y⁄x)max로 최대가 되는 파향각 θ = θc를 찾고, 이때 αc = tan–1(y⁄x)max를 찾는다. 이를 기울기로 표현하면 다음과 같은 변화를 알 수 있다.
심해의 경우 θc와 αc를 해석적으로 구할 수 있다. 심해의 경우 항주파의 파봉식은 식 (10)으로 표현되고, 다음과 같이 기울기로 표현되는 식을 얻을 수 있다.
최대파향각이 발생하는 d(y⁄x)⁄dθ = 0 조건에서
θ c = sin - 1 1 / 3 = 35 . 26 o
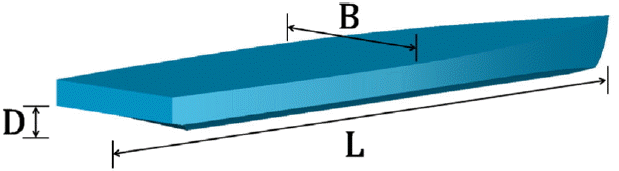
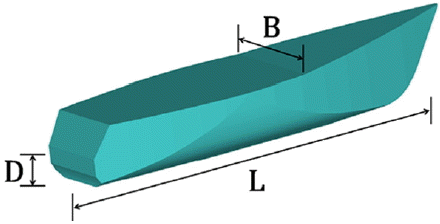
본 연구에서는 Johnson(1958)의 수리실험 조건으로 FLOW-3D를 사용하여 수치실험을 수행한 후 최대파향각을 측정하여 수리모형실험결과와 Havelock의 이론해(즉, 식 (23))와 본 연구에서 제안한 이론해를 비교하였다. 선박의 제원은 Table 1과 같다. x, y, z방향의 계산영역은 42.672 m × 12.192 m × 0.3048 m, 격자간격은 Δx = Δy = Δz = 3.048 cm, 수심은 h = 15.85 cm, 총 계산시간은 t = 100 sec로 두었다. 항적중심선을 기준으로 항주파는 좌·우로 대칭으로 전파하므로 항적중심선(y = 0)에서 대칭경계조건을 사용하여 계산시간을 단축하였다. Froude 수는 Fr= 0.65, 0.75, 0.85, 0.95, 1.0, 1.2, 1.5, 1.8, 2.1, 2.4, 2.7, 3.0에 대하여 실험을 수행하였고, 선박의 속도는 Froude수와 수심에 따라서 다르게 계산된다. 최대파향각은 Froude수가 1보다 작은 경우 연속되는 항주파의 파형에서 최대파고가 발생지점을 선수와 이루는 각도를 각각 계산하여 평균값을 취하였으며, Froude수가 1보다 크면 횡파가 사라지고 종파만 관찰되므로 첫 번째 종파의 파봉선이 항적중심선과 이루는 각으로 정하였다.
Fig. 6은 Froude수에 따른 최대파향각의 변화를 비교한 그림이다. Havelock (1908)의 이론해와 본 연구의 이론해가 Froude수가 0.5보다 작은 경우와 1보다 큰 경우에 거의 같았다. Froude수가 0.5와 1 사이의 경우에 본 연구의 이론해가 Havelock의 이론해에 비해 크게 예측되었다. FLOW-3D의 수치해는 본 연구의 이론해와 더 유사하다. Jonhson(1958)은 항적중심선에서 y방향으로 서로 다른 거리에 5개의 파고계를 두고 5개의 관측지점의 종파의 파고를 측정하여 그 중에서 최대파향각을 찾았다. Fig. 1(a)에서 보는 바와 같이 최대파향각은 종파와 횡파가 만나는 점과 선박을 이은 선(cusp locus line)과 항적중심선 사이의 각도인데, 최대파향각이 이론적인 방법과 차이가 있다. Fr= 0.9보다 작은 경우는 종파와 횡파가 만나는 점보다 관측지점이 바깥쪽에 있어서 이론해보다 더 크게 나오고, Fr= 0.9보다 큰 경우는 종파와 횡파가 만나는 점보다 관측지점이 안쪽에 있어서 이론해보다 더 작게 나온 것으로 보인다. 다르게 해석하면, 수리실험결과는 Froude수가 0에서 1로 증가함에 따라 최대파향각이 증가하는 경향이 이론해에 비해서 더 일찍 나타나서 Froude수가 Fr= 0.9에서 최대가 되고 Froude수가 이보다 더 크면 파향각의 감소 경향이 또한 더 일찍 나타났다.
4. 실해역 제원에서의 수치실험
본 장에서는 실제 해역에서 사용되는 선박의 제원으로 일정 수심에서 FLOW-3D를 사용하여 수치실험을 수행하여 파봉을 관측한 후 수치해와 이론해를 비교하였다. 선박의 제원은 Table 2와 같다. 여기서, 선박의 흘수는 2 m, 수심은 h = 8, 9, 10, 11 m, 선속은 각 수심별로 U = 5.5~15 m/s의 범위에서 총 60가지 경우에 실험을 수행하였다. 그리고 선속은 U = 5.5~10 m/s는 의 단위로 변화를 주었고, U = 10~15 m/s는 1 m/s단위로 변화를 주었다. x, y, z축 방향의 계산영역은 선박의 속도와 수심의 변화에 따라서 최소 700 m × 200 m × 13 m에서 최대 2000 m × 1000 m × 16 m까지 적용하였고, 격자간격은 Δx = Δy = Δz = 1 m로 두었다. 선박은 x축과 평행하게 항행하고 z축은 수심방향으로 자유수면으로부터 위쪽(+z방향)으로 5 m의 여유를 두고 수치실험을 수행하였다. 항주파는 일정수심에서 항적중심선을 기준으로 좌·우로 대칭으로 전파하므로 항적중심선(y = 0)에서 대칭경계조건을 사용하여 수치실험 시간을 줄였고, 총 계산시간은 t = 100 sec로 하였다.
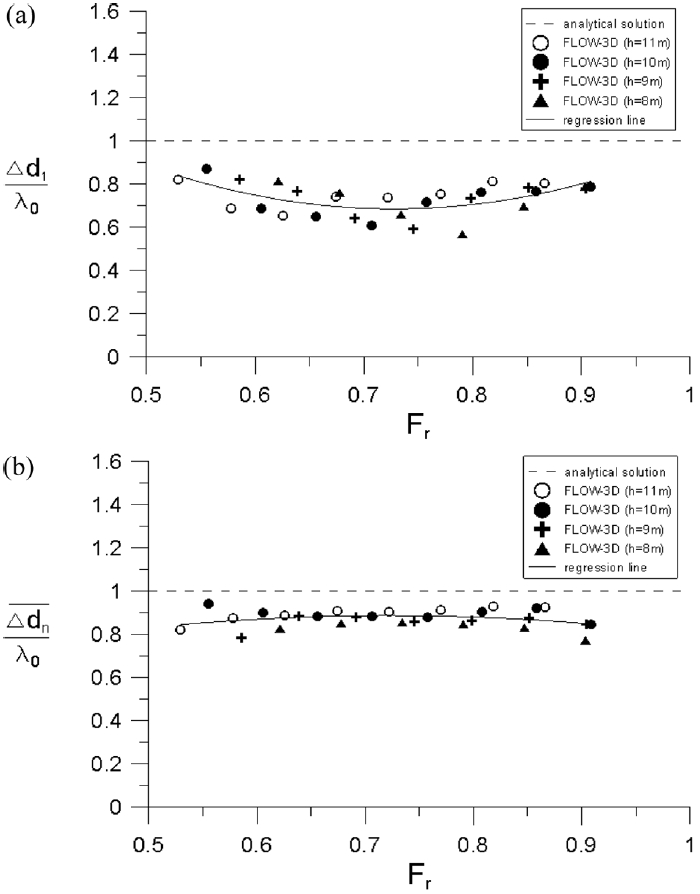
첫 번째로 항주파의 파향각이 θ = 0o일 때 인접한 항주파 간의 거리를 비교하였다. 제2장에서 언급한 바와 같이 인접한 항주파 간의 거리를 알게 되면 식 (21), (22)로부터 항주파의 위치를 결정하는 상수 C값을 결정할 수 있다. 항주파는 선속이 빨라지면서 Froude수가 1에 가까워지면서 횡파가 사라지고 종파만이 존재하게 된다. 이는 천해에서 드러나는 현상으로 θ = 0o일 때의 수치해를 얻을 수가 없게 된다. 그래서 이론해와 수치해를 비교하기 위하여 Froude수의 범위가 0.53~0.91인 결과만 사용하였다. Fig. 7은 파향각 θ = 0o의 조건에서 Froude수의 변화에 따라 인접한 항주파 간의 거리 ∆dn을 항주파의 분산관계식 (4)에서 계산되는 파장으로 무차원 화하여 비교한 그림이다. 항주파의 첫 번째 파형은 다른 파형에 비해 선박의 선수와 횡파의 파봉선간의 거리가 짧아서 Fig. 7(a)에 따로 도시하였다. Fig. 7(b)는 두 번째 항주파부터 인접한 항주파 간의 거리의 평균값을 도시하였다. 수치해에서 재현된 첫 번째 항주파 파봉선간의 거리는 이론값인 파장에 비해 더 작았고, 수치해에서 재현된 첫 번째 항주파를 제외한 파봉선간의 거리는 이론값에 비해 작았지만 조금 더 근접하였다. 두 경우에 Froude수에 따른 Δdn/λ0의 변화를 다항식으로 회귀식을 찾았다. 그 결과 2차 다항식에 의한 회귀식이 측정치를 가장 잘 표현하였고, 제곱평균오차가 첫 번째 항주파의 경우와 첫 번째를 제외한 항주파의 경우에 각각 4.06 × 10–3, 1.63 × 10–3로 나왔다. 식 (26), (27)에서 Δd1은 θ = 0o인 항주파에 대해서 선박과 첫 번째 파봉선 간의 거리를 의미하고, Δdn은 n-1번째 파봉선과 n번째 파봉선 간의 거리를 의미한다.
두 번째로 항주파의 파봉을 정성적으로 비교하였다. FLOW-3D모형의 수치해는 상대수심이 심해인 경우 종파보다 횡파가 전파하는 양상이 두드러지며, 중간수심에서는 종파와 횡파가 함께 전파하는 양상을 확인할 수 있다. 그리고 천해에 가까울수록 횡파는 사라지고 종파만이 존재한다. Froude수가 1보다 작은 경우 이론해를 계산할 때 상수 C1은 회귀식 (26)의 평균값을 사용하여 구했고, 첫 번째 항주파를 제외한 상수 CN은 이론식 (22)를 사용하여 구했다. 이론식 (22)는 θ = 0o의 횡파에 적용되는 식이어서 Froude수가 1보다 큰 경우에는 횡파가 존재하지 않아서 적용할 수 없다. 식 (22)의 Fr > 1 인 조건에서의 적용성을 확인하였다. 그 결과 상수 C1은 10-5보다 작았다. 이는 첫 번째 항주파에 대응하는 C1은 Froude수가 1보다 작은 경우에 이론값 2π에 가깝지만 충격파가 발생하는 Froude수가 1보다 큰 경우에 0 이라는 것을 시사한다. Fr > 1 인 조건에서 첫 번째 항주파를 제외한 나머지 항주파의 경우 파봉선 간의 거리의 수치해가 이론해와 유사하였다. 따라서, 본 연구에서 Fr > 1의 경우 이론식 (22)를 사용하여 첫 번째 항주파를 제외한 상수 CN을 구할 때 C1 = 0을 두었다.
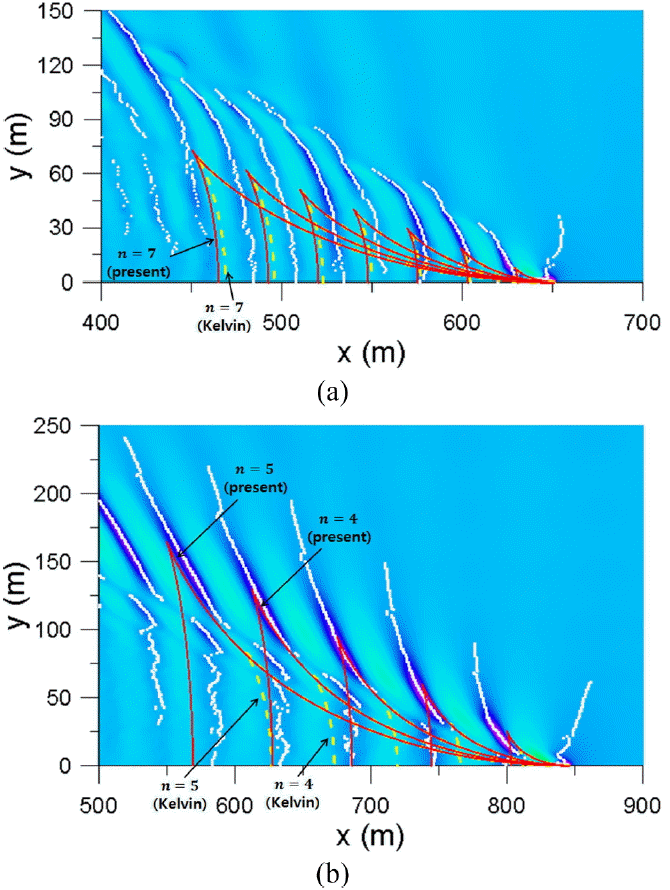
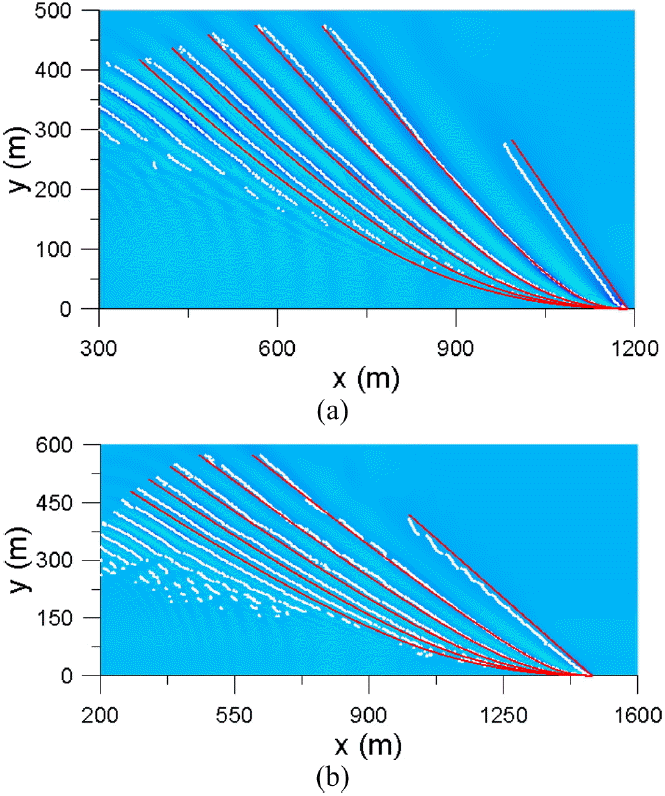
Fig. 8과 Fig. 9는 총 60가지 실험 중에서 차이가 확연한 4가지 경우의 파봉선을 도시한 그림으로 각각 Fr > 1 인 경우와 Fr > 1 인 경우에 도시한 것이다. 수심은 h = 10 m이고, 다른 조건들은 Fig. 8(a)의 경우 Fr = 0.66, U = 6.5 m/s, kh≥0.724π, Fig. 8(b)의 경우 Fr = 0.86, U = 8.5m/s, kh≥0.342π, Fig. 9(a)의 경우 Fr = 1.24, U = 12.0 m/s, kh≥0.003π, Fig. 9(b)의 경우 Fr = 1.51, U = 15.0 m/s, kh≥0.002π 이다. 그림에서 하얀 점은 Flow-3D에서 재현된 파봉(즉, 수면변위가 최대가 되는 점을 이은 선)이고 이 점들을 이은 선이 파봉선이 될 것이다. 그림에서 빨간 실선은 본 연구에서 예측되는 파봉선이고, 노란 파선은 Kelvin의 이론에서 예측되는 파봉선이다. 그림에서 n = 4, 5, 7 등은 파봉선이 선박에서 떨어진 순서로 매겨진 숫자이다.
Fig. 8은 Froude수가 1보다 작은 경우에 항주파의 파봉을 도시한 그림이다. 본 연구와 Lee et al.(2011)의 이론해는 동일한 결과를 얻어서 본 연구의 이론해만 도시하였으며, Kelvin(1887)의 이론해와 FLOW-3D의 수치해를 비교하였다.
Fig. 8(a)는 상대수심이 kh≥0.724π로 심해에 가까운 중간 수심영역으로 본 연구와 Kelvin(1887)의 이론해가 큰 차이를 보이지 않는다. 예를 들어, 7번째 항주파의 파봉선을 보면 본 연구의 예측값과 Kelvin의 예측값에 약간 차이가 있다. 왜냐하면 Froude수가 Fr = 0.66의 조건에서 항주파는 거의 심해파라서 심해의 가정 하에 유도된 Kelvin의 이론값에 오류가 크지 않기 때문이다. 그리고 수치해를 보면 횡파는 잘 재현되지만 종파는 육안으로 확인하기가 어려운데 이는 심해에서 드러나는 현상으로 이론해와 수치해를 비교할 때 횡파의 파형에 중점을 두었다.
Fig. 8(b)는 상대수심이 kh≥0.342π로 중간수심이지만 천해에 가깝다. 본 연구의 해석해와 수치해가 유사하게 나왔다. 수치해를 보면 Fig. 8(a)와는 달리 종파와 횡파가 잘 재현되고 있으며 이는 중간수심에서 드러나는 현상이다. 하지만 본 연구의 이론해가 Kelvin(1887)의 이론해와는 차이가 컸다. 예를 들어, Kelvin에서 예측되는 5번째 파봉선이 본 연구에서 예측되는 4번째 파봉선과 유사하게 나왔다. 다시 말해서 Kelvin의 이론에서는 5번째 파봉선이 한 파장만큼 짧게 예측이 된 것이다. 이때 Froude수는 Fr = 0.86으로 천해에 가까운 해역이 존재한다.
Fig. 9는 Froude수가 1보다 큰 경우에 항주파의 파봉를 도시한 그림이다. Lee et al.(2011)과 Kelvin(1887)은 Froude수가 1보다 큰 경우에 이론해를 계산할 수가 없으므로 결과에 포함하지 않았고, 본 연구와 FLOW-3D의 수치해를 비교하였다. Fig. 9(a), (b)의 상대수심은 각각 kh≥0.003π, kh≥0.002π로 천해이다. 수치해를 보면 두 경우 모두 종파만 전파하고 Froude 수가 커지면 최대파향각이 작아지는 것을 볼 수 있으며 이는 천해에서 드러나는 현상으로 Havelock(1908)이 제안하였던 Froude수가 1보다 크면 횡파는 사라지고 종파만 전파한다는 내용과 일치하였다. 그리고 첫 번째 항주파는 선속이 빨라서 선박의 선수에서 충격파와 같이 전파하는 양상을 볼 수 있다. 정성적으로 비교해 보면 본 연구의 이론해와 수치해가 매우 유사함을 보여준다.
이번에는 항주파의 파형을 정량적으로 비교하였다. 수치실험을 수행한 60가지 경우 중에서 14가지 경우(수심 h = 10 m, 선속 U = 5.5, 6, 6.5, 7, 7.5, 8, 8.5, 9, 10, 11, 12, 13, 14, 15 m/s)에 대하여 오차를 비교해보았다. 선속이 U = 5.5~8 m/s의 범위에서는 상대적으로 수심이 깊어서 관측이 용이한 횡파만 비교하였고, U = 8.5, 9 m/s 는 횡파와 종파의 전파가 뚜렷하여서 횡파와 종파를 각각 비교하였다. 그리고 U = 10~15 m/s의 범위에서는 상대적으로 수심이 얕아서 종파만 관측되므로 종파만 비교하였다. 선박이 속도 U로 항행할 때 항주파는 항적중심선에 있는 원천점에서 방향으로 전파하는 군파이므로 이론해와 수치해는 항적중심선의 원천점으로부터 전파하는 파향선의 거리(r)의 오차를 계산하였다. 항주파의 파향선 거리에 대한 오차를 RMSE(즉, root-mean-squared error)로 다음과 같이 표현하였다.
여기서, 아래첨자 N와 T는 같은 각각 FLOW-3D의 수치해, 본 연구의 이론해의 파향선의 거리를 의미하고, i는 오차 계산 시 적용되는 FLOW-3D 수치해의 총 개수를 의미한다.
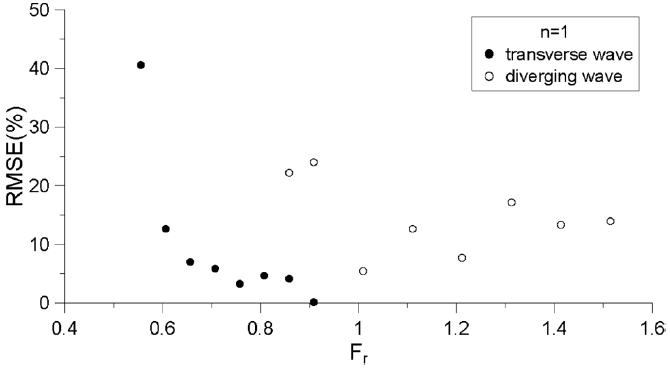
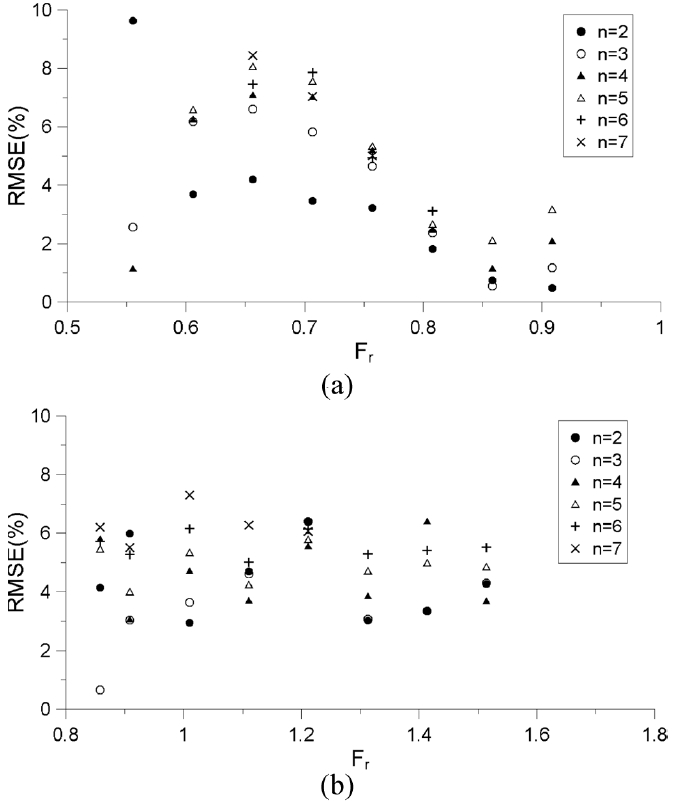
Fig. 10은 첫 번째 항주파(n = 1)의 RMSE이다. 앞서 언급한 바와 같이 첫 번째 항주파는 선박과 가까이 있어서 선박의 제원, 선속에 따라 민감하게 변할 수 있다. 그래서 다른 항주파의 결과와 따로 구분하여 결과를 나타내었다. 결과에서 Froude수가 클수록 대체로 RMSE가 작아지는 경향을 보인다. 그리고 Froude수가 제일 작은 경우(즉, Fr= 0.56)의 RMSE가 약 40%로 다른 경우와 달리 상당히 큰 것을 확인할 수가 있는데, 이는 선박의 속도가 느릴수록 FLOW-3D의 재현성이 떨어지는 것으로 보인다. Fig. 11은 두 번째 항주파부터 재현 가능한 항주파까지 RMSE를 나타낸 결과이다. 첫 번째 항주파와는 달리 전반적으로 RMSE가 10% 이내로 본 연구의 이론해와 FLOW-3D의 수치해가 상당히 유사함을 알 수 있다.
5. 결 론
본 연구에서는 모든 수심(즉, 심해, 중간수심해, 천해)에 적용 가능한 항주파 파봉을 예측하는 이론식을 개발하였고 항주파의 위치를 결정하는 상수 C를 이론적으로 유도하였다. Johnson(1958)의 수리실험 결과와 FLOW-3D의 수치실험 결과를 비교하여 FLOW-3D가 항주파를 잘 재현해 낸다는 것을 검증하였으며, FLOW-3D를 사용하여 일정수심에서 항주파의 파봉의 이론식을 검증하였다. Froude수가 1보다 작은 경우 본 연구의 이론해와 Kelvin(1887)의 이론해와 FLOW-3D의 수치해를 비교하여 본 연구의 이론해가 Kelvin의 이론해보다 더 정확함을 확인하였다. Froude수가 1보다 큰 경우에 본 연구의 이론해가 Havelock(1908)의 이론해와 일치하고, FLOW-3D의 수치해와 상당히 유사함을 확인하였다. 정량적으로 본 연구의 이론해와 FLOW-3D의 수치해로 나온 항주파간의 거리에 대한 오차 제곱 평균의 제곱근 값인 RMSE를 계산하여 첫 번째 항주파를 제외한 나머지 항주파들의 RMSE가 10% 이내로 유사함이 확인되었다. 즉, 심해에서만 적용 가능한 Kelvin(1887)의 항주파 파형 이론식과 Froude수가 1보다 작은 경우에 적용 가능한 순환관계를 이용한 항주파 파형이론식(Lee et al., 2011)보다 본 연구의 이론식의 우수함이 확인되었다. 앞으로는 항주파의 파고에 대한 이론적인 연구를 진행하여 본 연구의 정확성을 높일 필요가 있으며, 해류와 파랑과 항주파를 접목하여 좀 더 진보된 연구를 진행할 계획이다.