요약해상풍력 발전시설은 국제적인 설계기준조위로 최고천문조위(highest astronomical tide, HAT)와 최저천문조위(lowest astronomical tide, LAT) 기준을 요구하고 있다. 우리나라는 설계기준조위로 약최고고조위(AHHW)와 약최저저조위(ALLW) 기준을 사용하여 왔기 때문에 국제적인 설계기준을 만족하기 위해서는 해상풍력 발전시설 후보 해역인 위도에서의 HAT, LAT 추정이 필요하다. 본 연구에서는 위도에서 가용한 31년 조위자료를 이용하여 HAT, LAT 기준조위를 추정하였으며, 추정에 사용한 자료의 신뢰수준을 검토하기 위하여 장기 태음분조에 해당하는 18.61년 주기의 Nodal 변동 특성 분석을 수행하였다. Nodal 보정을 고려하지 않은 연간 M2, O1, K1 분조의 진폭변화는 뚜렷한 18.61년 주기를 보여 조화분석 결과가 적절하게 추정된 것으로 파악되고 있는 것으로 파악되었다. 한편 조위자료를 이용하여 추정한 HAT, LAT 신뢰구간의 상한 및 하한으로 최종 추정한 HAT, LAT 조위는 AHHW, ALLW 기준조위에 비하여 각각 +40 cm, -35 cm 정도로 파악되었다.
AbstractIn designing of the wind power facilities, the highest and lowest astronomical tides (HAT and LAT) are needed in terms of an international design tidal water levels. The AHHW and ALLW, however, have been used as the design tidal levels in Korea. The HAT and LAT in the Wido coastal sea should be estimated to satisfy the standard because the pilot wind power facilities will be located in the adjacent Wido coastal sea. In this study, the HAT and LAT are estimated using the 31-years hourly tidal elevation data of the Wido tidal gauging station and the nodal variation patterns of the major lunar components, such as M2, O1, and K1, are analysed to check the expected long-term lunar cycle, i.e., 18.61-year’s nodal variation patterns. The temporal amplitude variations of the M2, O1, and K1 clearly show the 18.61-years periodic patterns in case of the no-nodal correction condition. In addition, the suggested HAT and LAT elevations, estimated as the upper and lower confidence limits of the yearly HAT and LAT elevations, show 40 cm greater than AHHW and 35 cm lower than ALLW, respectively.
1. 서 론해양학자들은 최근 200년 이상 측량 및 해도 작성 작업을 수행하고 있다. 이 해도에는 특정지역의 수심이 도시되어 있다. 따라서 이러한 수심을 표현하기 위해서는 기준면이 되는 수직기준 체계(Vertical reference system)가 필요하다. 작성된 대부분의 해도는 선박의 항행에 사용되기 때문에 선박의 안전을 위하여 기준면은 특정지역에서 한번은 발생하는 수심으로 정의하고 있다. 이 기준면을 ‘기본 수준면’이라 하며 국제수로기구(IHO, International Hydrographic Organization)에서는 ‘최저극 천문조위’(LAT, Lowest Astronomical Tide)로 정의하고 있다. 최저극 천문조위는 평균적인 기상조건과 천문조건의 결합하에서 예측되는 가장 낮은 조위를 의미한다. 최저극 천문조위 산정을 위해서는 최소 1년이상의 관측자료로부터 산정된 조화상수를 이용하여 최소 19년 이상 산정한 값을 사용하거나 신뢰성 있는 결과를 주는 검증된 방법으로 산정하여야 한다(FIG, 2006).
따라서 최저극 천문조위 값은 특정장소에서 장기간 관측된 조위자료를 분석하여 결정되며, 그 지역에서 예측될 수 있는 가장 낮은 조위값보다 작다. 기본 수준면 값은 육상기준체계와 연결되며, 공간 및 시간적으로 변화한다. 조위자료를 취득하는 과정은 시간이 걸리고, 비용이 많이 소요되기 때문에 낡은 자료가 되기 쉽다. 조위자료가 공간 및 시간적으로 변화하는 것은 사소한 문제가 아니다. 따라서 해안 및 항만공학자들은 전지구 수직기준체계(Global Vertical System)를 구축하여 조석자료를 이들과 연계하여 기본수준면을 검토함으로써 선박의 안전한 항행을 도모하고 있다.
이처럼, 국제수로기구 조석위원회에서는 1997년에 18.6년의 완전한 조석주기동안 조석현상에 의하여 나타날 수 있는 LAT를 IHO회원국들이 기본수준면으로 채택할 것을 권장하였으며, 2010년 현재 영국, 프랑스, 덴마크, 스페인, 호주 등 12개국이 채택하고 있다(KHOA, 2012; ICSM, 2011). 미국의 경우 19년 이상 관측자료를 산술 평균한 MLLW(Mean Lower Low Water)를 기본수준면으로 사용하고 있으나, LAT를 기본수준면으로 사용하는 세계적인 추세를 소개하고 있다(Gill and Schultz, 2001).
한편, IEC 61400-3에서도 해상풍력 발전단지 설계를 위한 설계 기초자료로 수위의 변동을 제시하기 위해 최고극 천문조위(HAT, Highest Astronomical Tide)와 최저극 천문조위(LAT, Lowest Astronomical Tide)란 개념을 적용하도록 제안하고 있다. HAT와 LAT는 태음의 완전한 주기인 18.6년간 발생할 수 있는 최고극 조위와 최저극 조위이며, 수개의 분조에 의해 이론적으로 추정할 수 있다(IEC, 2009).
Slobbe et al.(2013)은 최고극 천문조위를 이용한 천해 흐름모형을 북해에 적용하였으며, Turner et al.(2013)은 최고극 천문조위를 이용한 천해 흐름모형을 전 대양을 대상으로 적용하여 모형의 정밀성을 검토하였다.
Byun and Cho(2009)는 일반적으로 많이 사용하는 6개의 수치모형을 목포해역에 적용하여 조석 예보 모델시 nodal modulation을 고려하여야 오차를 줄일 수 있음을 확인하였다. Haigh et al.(2011)은 18.61년과 8.85년의 태음주기가 고조위에 미치는 영향을 검토하여 조차가 4 m 이상인 해역에서는 18.61년 태음주기가 일주조에, 조차가 6 m 이상인 해역에서는 4.4년 태음주기가 반일주조에 가장 큰 영향을 미치는 것으로 파악하였다.
Houston and Dean (2011)은 60년 이하의 검조기록을 대상으로, 18.6년의 태음주기가 해수면 가속에 미치는 영향을 산정할 수 있는 해석해를 제안하였다. Feng et al.(2015)은 중국연안 17개 검조소에서의 자료를 이용하여 M2, S2, N2, O1, K1 분조의 장주기 변화를 검토하여, 황해에서 M2분조의 진폭이 최대 4~7 mm/yr 증가함을 연구하였다. Hansen et al.(2015)은 18.61년 태음주기의 3배와 4배에 해당하는 55.8, 74.4년의 주기에 커다란 해수면 진동이 북서 유럽해에서 발생함을 주장하였다.
국내의 경우 설계 고조위와 설계 저조위 결정을 위한 조위 기준면으로 약최고고조위(Approximate Highest High Water)와 약최저저조위(Approximate Lowest Low Water)를 적용하였으며, 약최저저조위를 기본수준면으로 사용하고 있으나(MMAF, 2014), IEC(International Electrotechnical Commission) 및 DNV(Det Norske Veritas) 기준에서는 기본수준면으로 LAT를 이용하고 있다. 이처럼 기본수준면(Datum Level, Chart Datum)은 국가마다 다르며 지역적으로 차이가 있기 때문에 지역의 특성을 반영한 관측자료를 이용하여 구할 수 있다.
수위에 대한 기준이 국내와 국외가 다소 차이가 있으며, 국외 해상풍력 터빈 설계 기준을 따르는 국내 현 상황을 감안하였을 때 이에 따른 적절한 검토가 필요하다.
본 연구는 서·남해 2.5GW 해상풍력 실증단지 설계 근거보고서 작성에 필요한 해양조건중 수위를 결정하는 것이 목표이다. 이를 위하여 해상풍력 실증단지 인근 해역에 위치한 조위 관측소를 대상으로 HAT, LAT를 산정하였다. 후보지 인근 해역인 위도의 31년 장기 관측 조위자료를 이용하여 HAT와 LAT를 추정하였으며, 이를 약최고고조위와 약최저저조위와의 차이를 비교하여 구조물 관리시에 위험을 야기할 수 있는 조위에 대하여 검토하였다.
2. 자료 및 방법2.1 조위자료국립해양조사원은 한국 연안 조위관측소에서 조위를 관측하고 있으며, 품질검정을 통해 1시간간격 조위자료를 제공하고 있다. 그러나 장기간 현장 관측 조위자료는 관측 환경과 기상 악화 등의 원인으로 인해 상당한 결측이 발생하고 있으며, 이에 대한 보충은 실질적으로 불가능하다. 이러한 결측 정보는 조화분석 시에 오차를 발생시키는 주요 원인이 되지만, 해상 관측이란 열악한 특성을 이해한다면 완벽한 관측자료를 이용하기란 쉽지 않은 상황이다.
산업통상자원부에서는 2010년 11월 서해안 2.5 GW 해상 풍력 추진로드맵 발표를 통하여 국내 해상풍력 산업의 활성화를 위한 투자계획(2019년까지 약 9.2조)을 공표하였다. 이에 따라 정부와 전력사에서는 전라남도 안마도와 전라북도 위도 해상에 “서해 남부 2.5 GW급 해상풍력 발전단지 개발”의 첫 번째 단계인 ‘100 MW급 실증단지 구축’ 연구사업을 진행중이다.
본 연구에서는 이러한 해상풍력 단지에 가장 근접해 있는 위도 검조소 자료를 활용하여 조위 기준면에 대한 검토를 수행하였다. Cho et al.(2011)에 의하면 1985~2010년까지 26년 동안 위도지점의 조위 관측 자료도 12.5% 결측률을 보이고 있다. 위도 조위관측소 위치 및 정보는 Fig. 1 및 Table 1과 같다.
관측 자료에 대한 결측 정보는 Table 2와 같다.
2.2 분석 프로그램조화분석에 많이 사용되는 프로그램으로는 TASK(Tidal Analysis Software Kit) 2000과 T_Tide가 있다. TASK 2000은 TIRA tidal analysis programs(Murray, 1964)을 바탕으로 POL(Proudman Oceanographic Laboratory)에서 작성하였으며 35개 분조를 이용한다. 한편, T_Tide는 Foreman and Neufeld(1991)과 Godin(1991)이 Fortran 언어로 작성한 조화분석 프로그램을 MATLAB 언어로 변환하여 재작성한 프로그램으로 45개의 분조와 24의 천해 분조를 이용하여 조위를 예측할 수 있다. Pawlowicz et al.(2002)는 T_Tide를 이용하여 조화분석에 대한 오차분석을 수행한 바 있다. 본 연구에서는 MATLAB 언어를 사용하여 개발한 프로그램을 활용하여 145개의 분조를 사용하여 분석을 수행하였다.
2.3 조위 예측기조력은 지구와 천체상의 각 지점과의 상대적 위치에 따라 변화하기 때문에 실제로는 달과 태양대신 천구의 적도상을 일정한 거리를 유지하며 또 일정한 주기로 운행하는 가상천체를 생각하여 이것들에 의해 규칙적인 조석이 지구상에 일어나고 있다고 생각한다. 이와 같이 규칙 바른 많은 조석으로 분해하는 것을 조석의 조화분석이라 하며, 각각의 조석을 분조라 한다.
일반적으로 해수면 변동은 다음과 같은 여현파의 합으로 표현된다.
여기서, Aj는 진폭, ωj는 각속도로 주기 Tj와 Tj = 2π⁄ωj의 관계가 있으며, gi는 지각이다.
분조의 각속도 ωj는 평형조석을 사용하여 다음과 같이 표현할 수 있다.
여기서, ω1~ω6는 천체 매개변수(astronomical parameters)와 관련된 각속도로, 각각, mean lunar day, sidereal month, tropical year, moon’s perigee, regression of moon’s nodes, perihelion으로 이들의 주기는 Table 3과 같다. ia~ic는 -2와 2사이의 작은 정수이다.
모든 태음분조는 18.61년 주기 ω5의 영향을 받으며, 일부 태음분조는 8.85년 주기 ω4의 영향을 받는다. 1년 이하의 관측 자료를 이용하는 경우, 이들 분조는 독립적으로 결정할 수 없기 때문에 다른 형태로 표현하여야 한다. 식(2)에서 이들은 각각 idω4, ieω5, ifω6형태로 표현되며, 이 중 ifω6는 상수로 간주할 수 있다. 따라서 1년 이하의 자료로부터 결정할 수 없는 성분들은 소규모 조정 계수(small adjustment factors) f와 u를 사용하여 다음과 같이 표현한다. 즉,
여기서, fj, uj는 각각 분조 j의 nodal factor와 nodal angle로서 의 함수이며, 태양조의 경우 각각 1.0, 0.0이다.
따라서, 해수면 관측결과를 조화분석을 이용하여 나타내는 경우, 식 (1)과 (3)을 이용하여 다음과 같이 표현한다.
여기서, Z0는 평균 해수면, Vj는 시각 t = 0(기준시각, 본 연구의 경우, 1989년 12월31일 12시 기준)에서 위상각이다.
3. 분석결과조화분석은 nodal factor를 고려한 식 (4)와 nodal factor를 고려하지 않은 식 (1)을 이용하여 2가지 종류로 수행하였다. 일반적으로는 nodal factor를 고려하지 않으나, 최저 및 최고극 천문조위 산정을 위해서는 반드시 고려하여야 할 중요한 요소이다.
모든 태음 성분은 18.61년 주기의 영향을 받는다. Fig. 2는 일일 2회조가 우세한 위도 검조소 31년 조위 자료의 표준편차(Standard Deviation: SD)를 년도별로 도시한 것으로, 조위 기준은 평균해수면을 사용하였다. Fig. 2(a)는 관측자료의 결측 및 품질저하, 위상기록 오차, 기기 이상 등의 원인으로 1999년이후부터 약 18.61년 주기성을 볼 수 있다. Fig. 2(b)는 이론치와 분석치의 표준편차 차이를 도시한 것으로 2007년이후 자료는 타 기간 자료에 비하여 차이가 작다. 이 해역은 1991년부터 2006년까지 33.9 km의 새만금방조제가 건설되어 조석체계가 크게 변화되어, 2007년이후의 자료를 활용하는 것이 적합하다.
주요 4분조중 M2 분조의 진폭 Hm을 Fig. 3에 도시하였다.
Nodal factor를 고려한 결과인 Fig. 3(a)의 경우, 진폭 Hm은 일정한 값을 보여야 하나, 자료의 결측 및 기기이상 등으로 약간의 편차를 보이고 있으나, 1999년 이후에는 비교적 양호한 결과를 얻을 수 있다. 반면에 Nodal factor를 고려하지 않은 결과인 Fig. 3(b)의 경우 18.61년 주기성을 보이고 있다. Fig. 3(b)의 경우 Fig. 3(a)에 비하여 진폭의 연간 편차가 크다는 것을 알 수 있다.
S2 분조의 진폭 Hs를 Fig. 4에 도시하였다. S2 분조의 경우 Nodal factor의 영향을 받지 않으므로 Fig. 4(a)와 Fig. 4(b)가 동일하다. Hs는 일정한 값을 보여야 하나 자료의 결측 및 기기 이상 등으로 약간의 편차를 보이고 있다.
주요 4분조중 O1 분조의 진폭 Ho를 Fig. 5에 도시하였다. Nodal factor를 고려한 결과인 Fig. 5(a)의 경우, 진폭 Ho는 일정한 값을 보여야 하나, 자료의 결측 및 기기이상 등으로 약간의 편차를 보이고 있으나, 1999년 이후에는 비교적 양호한 결과를 얻을 수 있다. 반면에 Nodal factor를 고려하지 않은 결과인 Fig. 5(b)의 경우 18.61년 주기성을 보이고 있다. Fig. 5(b)의 경우 Fig. 5(a)에 비하여 진폭의 연간 편차가 크다는 것을 알 수 있다.
주요 4분조중 K1분조의 진폭 H′를 Fig. 6에 도시하였다. Nodal factor를 고려한 결과인 Fig. 6(a)의 경우, 진폭 H′는 일정한 값을 보여야 하나, 자료의 결측 및 기기이상 등으로 약간의 편차를 보이고 있으나, 1999년 이후에는 비교적 양호한 결과를 얻을 수 있다. 반면에 Nodal factor를 고려하지 않은 결과인 Fig. 6(b)의 경우 18.61년 주기성을 보이고 있다. Fig. 6(b)의 경우 Fig. 6(a)에 비하여 진폭의 연간 편차가 크다는 것을 알 수 있다.
주요 4분조 M2, S2, O1, K1 분조의 위상차 Km, Ks, Ko, K′를 Fig. 7에 도시하였다. S2분조를 제외한 M2, O1, K1 분조의 경우, Nodal factor를 고려한 결과는 Nodal factor를 고려하지 않은 결과에 비하여 위상 차의 연간 편차가 작다는 것을 알수 있다. Nodal factor를 고려한 위상차 Km, Ks, Ko, K′가 년간 편차를 보이는 것은 조석 주파수대의 비조석 성분 에너지 포함에 따른 분석의 한계, 관측 장비의 비일관성, 개발에 따른 실제 조석현상의 변화 등을 원인으로 들 수 있다.
Fig. 8에 도시된 형태수는 Nodal factor를 고려한 경우 비교적 일정한 값을 보이고 있다. 반면 Nodal factor를 고려하지 않은 경우, 형태수의 연간 편차가 크다는 것을 알 수 있다. 특히 1987, 1988, 2007년의 경우 반일주조와 반일주조가 우세한 혼합조의 경계인 형태수 0.25가 나타나 위도의 조석형태를 결정하기 곤란한 경우도 발생한다.
Fig. 9에 약최고고조면(AHHW)과 HAT를, Fig. 10에 약최저저조면(ALLW)과 LAT를 도시하였다. 이러한 경우 조위면 선택기준에 따라 조위 기준면에 큰 차이가 발생한다는 것을 알 수 있다. Fig. 11은 위도 검조소의 31년 자료를 분석하여 HAT와 LAT를 도시한 boxplot이다.
우리나라의 조위 기준면인 AHHW, ALLW 및 유럽 해도의 수심기준면인 HAT, LAT를 Table 4에 정리하였다. Table에서 볼 수 있는 바와 같이 평균치 기준으로 HAT가 AHHW에 비하여 약 40 cm 높고, LAT가 ALLW에 비하여 약 35 cm 낮다.
평균 HAT, LAT 추정자료는 점 추정자료에 해당하며, 확률변수로서 어느 정도의 변화를 가지기 때문에, 안전 측면에서 HAT, LAT 각각에 대하여 95% 신뢰구간을 추정하고, HAT는 95% 신뢰구간의 상한, LAT는 95% 신뢰구간의 하한으로 제안하는 경우 보다 적절하고 안전계수가 포함된 설계 기준조위로 간주될 수 있다.
4. 결 론본 연구에서는 위도 검조소의 31년 조석자료를 사용하여 조화분석을 실시하였다. MATLAB 언어를 사용하여 개발한 프로그램을 활용하여 145개의 분조를 사용하여 1년 단위로 분석을 수행하였다.
Nodal factor를 고려하지 않는 경우, 예상대로 S2 분조를 제외한 M2, O1, K1 분조의 진폭은 18.61년의 주기성이 나타나고 있으며(Fig. 3~6참조), 주요 4분조의 위상 차는 Nodal factor를 고려한 경우에 비하여 연간 편차가 크다는 것을 알 수 있다(Fig. 7 참조). 조석 형태수는 Nodal factor를 고려한 경우 비교적 일정한 값을 보이고 있으나, Nodal factor를 고려하지 않은 경우, 형태수의 연간 편차가 크다는 것을 알 수 있다. 특히 1987, 1988, 2007년의 경우 반일주조와 반일주조가 우세한 혼합조의 경계인 형태수 0.25보다 큰 값이 출현하여 위도의 조석 형태를 결정하기가 힘든 경우도 발생한다(Fig. 8 참조).
또한 우리나라 해도의 수심기준면인 ALLW와 유럽 해도의 수심기준면인 LAT를 비교한 결과 LAT가 ALLW에 비하여 약 35 cm 낮고, HAT가 AHHW에 비하여 약 40 cm 높고(Table 4 참조). 따라서 우리나라가 해상풍력 산업에서 국제적인 인증을 받기 위해서는 유럽기준인 HAT 및 LAT를 기준으로 설계 및 시공하는 것이 필요한 바, 한국 연안해역의 조위자료에 대한 추가 검토가 필요하다.
특히 본 해역은 1970년대에는 군산외항(제1부두) 건설사업, 1980년대에는 금강하구둑 건설사업, 1990년대에는 군산항 및 군장지구 개발 사업적인 사업, 1991년부터 2006년까지 33.9 km의 새만금방조제가 건설되어 조석체계가 크게 변화되었으므로, 조석자료 검토시에는 2007년 이후의 자료를 활용하는 것이 일관성을 유지할 수 있다. 또한 60년이하의 조석자료를 분석하는 경우, 누락되는 56년 혹은 74년 주기의 해수면 상승진동을 검토하는 추가 연구도 필요하다.
Fig. 2.The amplitude of the semidiurnal tides varies over an 18.61 year period, (a) SD(Standard Deciation) and (b) difference of SD. 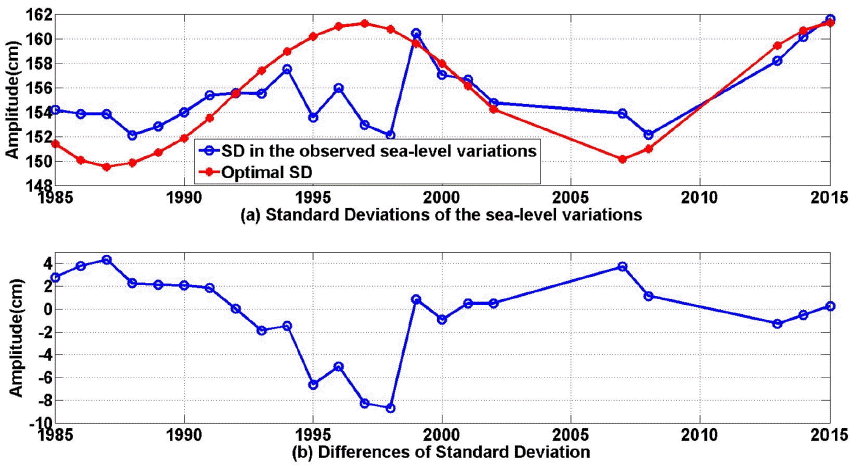
Table 1.Description of tidal gauging station Wido
Table 2.Information of missing period Table 3.The basic speeds and origin of the astronomical arguments(ωn) that gives the frequencies of the harmonic constituents. Note that ω0 = ω1 + ω2 − ω3 (Pugh, 2004; Pugh and Woodworth, 2014) ReferencesByun, D-S, Cho, C-W. (2009). Exploring conventional tidal prediction schemes for improved coastal numerical forecast modeling, Ocean Modelling, 28, 193-202.
Korea Hydrographic and Oceanographic Administration. (2012). Final Report on the re-consideration of the setup of the tidal data treatment system and the reference datum level, (in Korean)..
Cho, HY, Ko, DH, Jeong, ST. (2011). Missing pattern of the tidal elevation data in Korean coasts, Journal of Korean Society of Coastal and Ocean Engineers, 23(6):496-501 (in Korean).
Feng, X, Tsimplis, MN, Woodworth, PL. (2015). Nodal variations and long-term changes in the main tides on the coasts of China, J. Geophys. Res. Oceans, 120, 1215-1232.
FIG (International Federation of Surveyors). (2006). FIG Guide on the Development of a Vertical Reference Surface for Hydrography.
Foreman, MGG, Neufeld, ET. (1991). Harmonic tidal analyses of long time series, International Hydrographic Review, 68(1):85-108.
Gill, SK, Schultz, JR. (2001). Tidal Datums and Their Applications. NOAA Special Publication NOS CO-OPS 1.
Godin, G. (1991). The analysis of tides and currents, In: Parker BB, ed. Tidal Hydrodynamics. Wiley, New York: p 675-709.
Haigh, ID, Eliot, M, Pattiaratchi, C. (2011). Global influences of the 18.61 year nodal cycle and 8.85 year cycle of lunar perigee on high tidal levels, J. Geophys. Res, 116, C06025. 10.1029/2010JC006645.
Hansen, JM, Aagaard, T, Kuijpers, A. (2015). Sea-level forcing by synchronization of 56- and 74-year oscillations with the Moon's nodal tide on the northwest European Shelf (eastern North Sea to central Baltic Sea), Journal of Coastal Research, 31(5):1041-1056.
Houston, JR, Dean, RG. (2011). Accounting for the nodal tide to improve estimates of sea level acceleration, Journal of Coastal Research, 27(5):801-807.
ICSM (Intergovernmental Committee on Surveying and Mapping) Permanent Committee on Tides and Mean Sea Level. (2011). Australian Tides Manual SP9 V4.1.
IEC. (2009). IEC 61400-3: Wind turbines-Part 3: Design requirements for offshore wind turbines.
Ministry of Maritime Affairs and Fisheries. (2014). Harbor and fishery design criteria. (in Korean).
Murray, MT. (1964). A general method for the analysis of hourly heights of the tide, International Hydrographic Review, 41(2):91-101.
Pawlowicz, R, Beardsley, B, Lentz, S. (2002). Classical Tidal Harmonic Analysis Including Error Estimates in MATLAB using T_TIDE, Computers and Geosciences, 28, 929-937.
Pugh, D. (2004). Changing Sea Levels: effects of tides, weather and climate. Cambridge University Press.
Pugh, D, Woodworth, P. (2014). Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes. Cambridge University Press.
|
|
||||||||||||||||||||||||||||||||||||||||||||