1. 서 론
조석에 의한 흐름이 지배적인 해역에서 조석 유입구(tidal entrance)는 해수의 유출입이 이루어지는 주요 통로이며, 연안의 지형학적 평형(regime)을 해석하는데 필수적으로 요구되는 주요 경계조건이다. 이러한 조석 유입구에서는 해수의 유입과 유출이 주기적으로 반복되는데, 이 때 유입되는 유량과 유출되는 유량이 균형을 이루게 되면 해수와 함께 이동되는 퇴적물의 이송량 역시 균형을 이루게 되어 조석 유입구의 흐름단면의 형상, 즉 지형의 변화가 없는 완전한 의미의 동적 평형상태가 유지된다. 그러나 실제로 유입 및 유출량이 균형을 이루는 조석 유입구는 존재하지 않으므로, 해수의 유출입이 반복적으로 이루어지는 조석 유입구에서의 지형의 변화는 필연적이라고 하겠다(Powell et al., 2006).
이러한 지형 변화는 유입구 단면을 통해 유출입되는 물의 체적, 즉 조량에 의해 변화하는데, 해수와 함께 이동되는 퇴적물의 침식 혹은 퇴적작용의 반복으로 인하여 조석 유입구에서의 지형은 지속적으로 변화하게 된다. 지형의 변화는 곧 흐름 단면적의 확대 혹은 축소를 의미하며, 흐름 단면적의 변화는 해수의 유출입량의 변화로 이어지므로 결과적으로 조량 또한 변화하게 된다. 조량의 변화는 다시 지형의 변화를 야기시키게 되는데, 이와 같이 조량과 조석 유입구의 흐름 단면적은 상호간에 영향을 미치며 지속적으로 변화하며 이러한 과정은 계속적으로 반복된다. 결론적으로 지속적으로 변화하는 조량과 조석 유입구에서의 흐름 단면적과의 상관관계는 해수유동과 지형학적 평형사이의 관계를 반영한다고 할 수 있다.
일반적으로 조량은 ‘조석의 창조 혹은 낙조 동안에 조석 유입구를 통해 교환되는 해수의 총량(total volume)’으로 정의되는데, 이는 고조시에 만 내로 유입되거나 저조시에 외해쪽으로 유출되는 해수의 총량을 의미한다(Ippen, 1966). 조량은 해역의 흐름특성 뿐만 아니라 퇴적물의 이송측면에서 매우 중요한 인자인데, 해수와 함께 부유 퇴적물이 이송되므로 조량은 퇴적물의 이송과도 밀접한 관련을 갖는다. 우리나라 서남해안에 널리 분포해있는 세립질 퇴적물은 최소 한계값 이상의 흐름전단응력에서 평형(equilibrium) 부유사농도 값을 가지며 흐름전단응력의 크기가 증가할수록 평형 부유사농도 또한 증가하는 양상을 보이는데(Jung et al., 2012), 이는 세립질 퇴적물이 조석 유입구를 통해 해수와 함께 부유퇴적물의 형태로 이동하여 해역의 침퇴적량(혹은 이송량)에 큰 영향을 미칠 수 있다는 것을 의미한다. 이러한 조석 유입구에서의 조량 및 유입구 단면적 간의 상관관계는 퇴적물의 동적 평형해석 혹은 수로의 안정성 유지에 필요한 유속 혹은 전단응력 등의 산정과 관련된 연구에서 매우 중요하다고 하겠다.
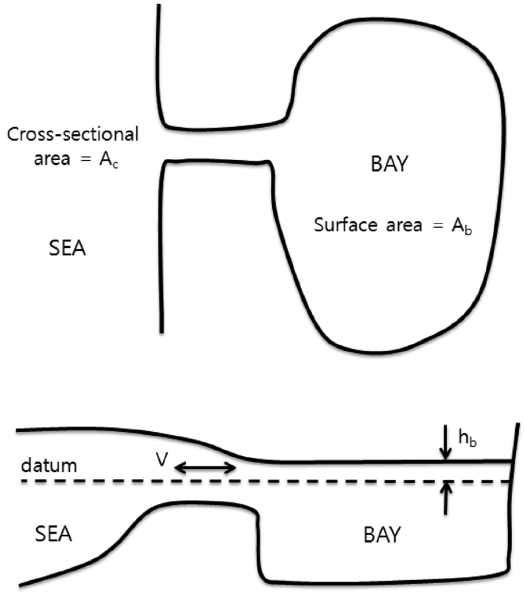
한편, 조량을 산정하기 위한 방법은 크게 두 가지로 구분될 수 있는데, Fig. 1에 제시된 바와 같이 유입구를 통하여 만으로 해수 유출입이 이루어지는 경우, 1) 조석에 의한 만 내부의 조차(hb)에 만의 면적(Ab)을 곱하거나 혹은 2) 만 유입구에서의 흐름단면적(Ac)에 단면평균 유속(V)를 곱하고 창조 혹은 낙조 지속시간 T(보통 약 6시간)에 대하여 시간적분하여 조량이 산정될 수 있다. 각각의 방법에 의해 산정되는 조량은 다음의 식 (1)과 같이 표현된다(USACE, 2006).
이상적인 조건, 즉 하천수의 유입이 없어서 유입량과 유출량이 같은 경우, P1과 P2는 동일하다. 기본적으로, P1보다 P2가 조량의 정의에 더 부합되나, 유입구에서의 Ac와 V의 시간적 변화에 대한 측정보다는 만 내부에서의 hb 및 Ab에 대한 측정의 용이함으로 인하여, 과거에는 주로 통계분석된 조위자료로부터 만 내부의 수위변화를 파악하여 1)의 방법을 적용하여 근사적으로 조량을 산정해왔다. 그러나 최근 측정장비의 발달로 인하여 유입구 단면 전체의 V를 층별로 정밀하게 측정할 수 있을 뿐만 아니라 Ac의 시간적 변화에 대한 측정 또한 가능해져 과거에 비해 더 정확하게 P2를 산정하는 것이 가능하게 되었다.
과거 많은 연구자들은 이론적 혹은 경험적 방법을 통하여 조량을 산정하고, 조량과 유입구 단면적과의 상관관계에 대한 다양한 연구를 수행한 바 있다. 조량 P와 유입구 단면적 A간의 상관관계를 나타내기 위해 일반적으로 가장 널리 사용되고 있는 식은 O'Brien(1969)에 의해 제시된 식 A = aPm인데, 여기서, a 및 m은 모두 각 해역의 특성을 나타내는 매개변수들이다. 많은 연구자들은 다양한 해역에서의 조량을 산정하고 각 해역별 a 및 m값을 제시하였는데, O'Brien(1969)은 모래질 해안에서 유입구 단면적은 조량의 함수임을 제시하였고, 8개의 미국 입구부들에 대하여 최적접합 방법을 통하여 a = 4.69 × 10–4, m = 0.85의 값을 제시한 바 있다. 이후 Powell et al.(2006)은 Florida의 67개 모래질 유입구에 대한 조량-유입구 단면적의 상관관계를 도출하고 창·낙조 삼각주 체적과 연계한 지형학적 상관관계를 검토하였다. 또한, Eysink(1990)은 네덜란드 Wadden Sea의 상관관계를 제시하였으며, Rakhorst(2007)은 Wadden Sea를 Eastern과 Western으로 구분하여 각각의 조량-유입구 단면적 상관관계식을 제시하였다. 그러나 해역별로 다르게 나타나는 매개변수 a 및 m의 직접적인 비교가 어려워짐에 따라, Stive and Rakhorst(2008)은 각각의 해역별 조량과 유입구 단면적간의 상관관계를 m = 1의 조건에 대해 최적접합계수 a를 재산정하여 그 결과를 제시하였다(Table 1 참조).
그러나, 우리나라의 경우 서·남해안의 지형적 특성으로 인하여 조석 유입구가 다수 형성되어 있음에도 불구하고 조량과 유입구 단면적 간의 상관관계에 대한 직접적인 측정 연구는 전혀 수행된 바 없다. 단지 Yi(1972), Seo and Kim(2003) 등에 의해 정량적 조량 산정 값만이 제시된 바 있을 뿐 조량과 관련된 연구는 매우 미미한 실정이다. Yi(1972)는 인천항에서 관측된 창·낙조시 평균유속과 단면적을 곱하여 조량을 산정하였으며, Seo and Kim(2003)은 금강하구 일대의 해수유동 모의를 재현한 수치모형으로부터 임의 통수단면에서의 조량을 산정·제시한 바 있는데, 이들 연구는 단지 특정 단면에서의 조량 값만을 창낙조로 구분하여 제시한 것일 뿐 조량 산정이 수행된 단면의 형상과 관련된 정보는 전혀 제시되지 않으므로 조량과 흐름 단면적 간의 상관관계 해석은 불가능하다.
한편, 조량은 조석의 진폭(tide amplitude)에 따라 변화하는 것으로 알려지고 있는데(Ippen, 1966), 대조, 소조 등의 조석 조건에 따라 조석의 진폭, 즉 조차가 크게 달라지므로 조량의 산정값이 크게 달라질 수 있다. Table 1에 제시되는 과거 연구결과를 살펴보면, 조량 산정시의 조석조건이 연구자들 별로 매우 다양하게 나타나는데, 이는 앞서 설명된 바와 같이 조량을 산정하는 방법에 따라 사용되는 자료가 다르기 때문이다. O'Brien (1969), Powell et al.(2006) 및 Eysink(1990)는 통계분석된 조위자료를 이용하여 1)의 방법에 의해 조량을 산정하였는데, O'Brien(1969)과 Powell et al.(2006)은 평균 대조(Mean spring), 즉 대조기 조차의 평균값과 만의 면적을 곱하여 조량의 근사값을 제시하였고, Eysink(1990)는 평균조위값(mean tide)를 이용하여 조량을 계산하였다. 이들 연구에 제시되는 조석조건이 조금 다르기는 하나 모두 평균(mean) 개념의 자료를 이용하여 조량이 산정되었는데, 이는 과거 연구들이 특정 단면에서 직접 측정한 유속 자료를 토대로 조량을 산정한 것이 아니라 통계분석된 조위관측 자료에 기반하여 조량을 산정하였기 때문이다. 이와는 다르게 Rakhorst (2007)는 2)의 방법을 이용하여 단면의 유속과 단면적을 곱하여 조량을 산정하였는데, 대조기에 창조 및 낙조시 각각의 유입 혹은 유출되는 체적 평균값 중 더 큰 값을 선택하여 조량을 산정하였다. 과거 연구들에서 제시되는 조량의 산정방법 및 산정에 사용되는 자료의 차이로 인하여 엄밀하게 동일한 의미의 조석조건에 대한 조량을 산정하지 못하였는데, 앞서 설명한 바와 같이 조석조건에 따라 조량의 산정결과가 정량적으로 크게 달라질 수 있으므로 분석에 사용되는 조석에 대한 정의를 명확히 명시하는 것이 중요하다고 하겠다.
특히, 단면의 유속측정 수행을 위한 현장관측 수행시에는 O'Brien (1969), Powell et al.(2006) 및 Eysink(1990)의 연구에 적용되었던 평균개념의 조석조건을 적용할 수 없으며, 관측이 수행되는 기간의 조석조건에 따라 조량이 크게 변화할 수 있다. 따라서, 조량산정을 위해 관측이 수행되는 시기의 조석조건에 대한 정의를 명확히 수립하는 것이 필요하다. 과거 O'Brien(1969) 및 Powell et al.(2006)은 조위값을 이용한 조량산정을 수행하긴 하였으나 대조(spring tide) 조석조건에서의 자료를 이용하였고, Rakhorst(2007) 역시 대조기의 창조 혹은 낙조시 평균 유출 체적값을 사용하여 분석을 수행하였다. 대조기에는 가장 큰 조차가 발생하여 해수 및 해수와 함께 이동되는 부유퇴적물의 이송량이 가장 크게 되므로 조량의 최대 극값이 산정될 수 있다.
본 연구에서는 현장관측에 기반한 단면통과 유량 및 조량의 산정이 이루어지는데, 목포해역 내 대표 조석 유입구에서 ADCP를 이용한 단면관측을 통해 층별 유속관측이 대조 및 소조 조석조건에서 수행되며, 관측된 자료로부터 단면통과 유량 및 조량이 정량적으로 산정되어 그 결과가 제시된다. 조량 산정시, 분석에 사용되는 조석조건의 정의를 포함하여 ‘대조기 조석 유입구 단면을 통해 유입 혹은 유출되는 해수의 최대 총량’을 조량으로 정의하였으며, 이러한 정의에 기반한 조량과 조석유입구 단면적이 정량적으로 산정된다. 산정된 결과는 과거 연구결과와 비교·검토되는데, 과거 연구결과의 유효성 및 본 연구결과의 타당성이 검토되어 그 결과가 제시된다.
2. 현장관측
2.1 관측위치
본 연구에서는 조석 유입구의 단면통과 유량 및 조량을 정량적으로 산정하기 위한 목적으로, 목포해역을 관측 대상해역으로 선정하였다. 목포해역은 수심이 복잡하고 많은 섬들로 둘러싸여 있는데, 영산강 하구언, 영암 및 금호방조제 건설 등의 대규모 간척사업이 활발히 수행된 바 있다. 또한 반일주조가 우세한 조석형태를 보이며, 1일 2회의 규칙적인 창·낙조류 흐름이 반복되는 조류특성을 보인다. 특히 목포항 인근해역에는 조간대가 넓게 분포하고 있는데, 이로 인해 천해조의 발달이 두드러져 조석왜곡 현상, 특히 낙조우세 현상이 두드러지게 나타나고 있으며 하구언과 방조제 건설이후 낙조우세는 더 심화된 것으로 알려지고 있다(Kang et al., 1998).
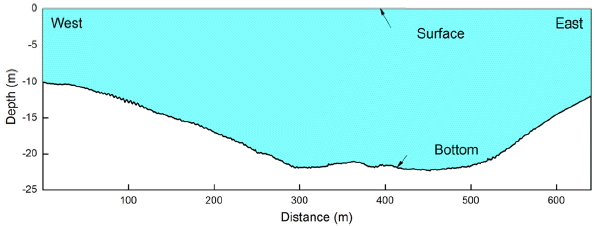
본 연구에서는 목포해역 내 1개 단면에서 ADCP를 이용한 층별 유속관측이 수행되었는데, 관측이 수행된 단면 A-B는 조석에 의한 흐름이 지배적인 단면으로써 압해도와 목포 사이에 위치하고 있다. 본 수로는 청계만으로의 해수 유출입이 이루어지는 주요 통로 중의 하나인데, 이 수로 뿐만 아니라 압해도 북단에 위치한 또 하나의 수로를 통하여 청계만으로의 해수 유출입이 동시에 이루어지고 있다. 본 연구에서는 관측을 위한 선박의 접근이 비교적 용이하고 해수의 유출입량이 상대적으로 더 큰 남측 수로의 단면 A-B에서 관측을 수행하였다. 관측은 정점 A와 정점 B를 왕복하며 수행되었는데, 단면 A-B의 길이는 약 630 m 내외이며, 최대수심은 약 22.3 m이다(Fig. 2 및 Fig. 3 참조).
2.2 관측장비 및 조건
ADCP는 기존 장비에 비해 공간적·시간적 해상도가 향상된 장비로써, 3차원의 유속과 수심 등의 자료를 매우 효율적이고 빠르게 측정할 수 있어 하천 및 해역 등의 흐름측정에 광범위하게 사용되고 있다(Kim and Kang, 2011). 본 연구에서는 ADCP를 선박에 장착하고 단면을 횡단하면서 측정하는 단면 관측(Bottom Tracking) 방법을 통하여 층별 유속관측이 수행되었는데, 단면 관측은 단지 1대의 ADCP만을 이용하여 관측단면 전체에 대한 층별 유속의 산출이 가능하다는 장점을 갖는다. 관측에 사용된 장비는 RD instrument사의 ADCP이며, 사용된 장비에 대한 구체적인 사항은 Kim(2015)에 자세하게 제시된다.
관측은 대조(2013/04/26 07:20~18:40) 및 소조(2013/05/02 06:20~15:20)로 구분되어 수행되었는데, 각각의 관측기간의 조석표가 정리되어 Table 2에 제시된다.
각각의 관측 수행시 약 12시간 동안 40분에 1회씩 단면을 횡단하며 연직방향 25 cm 간격으로 층별 유속이 측정되었다. 단면 A-B를 횡단하는 동안 선박의 이동속도는 약 1.5 m/s로 유지되었으며, 단면횡단에 소요된 시간은 약 6~7분 정도이다. 단면을 횡단하는 동안 각 위치에서의 수위 및 유속 변화는 미미하다고 가정된다.
3. 관측자료 분석방법 및 관측결과
3.1 관측단면에 대한 좌표 회전
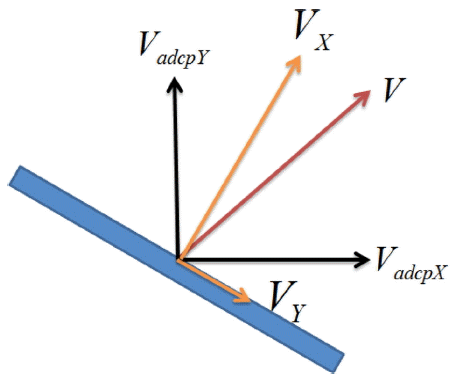
본 연구의 관측단면인 단면 A-B는 동서 기준 시계방향으로 약 45º정도 회전되어 있는데, 단면을 통과하는 유량 및 조량을 산정하기 위해서는 관측단면과 연직한 유속성분이 계산에 사용되어야 한다. ADCP로 측정되어 기록되는 유속 VadcpX 및 VadcpX (Fig. 4 참조)는 자북을 기준으로 하는 유속성분이므로, 관측단면과 연직한 유속성분을 산출하기 위하여 ADCP 유속자료를 새로운 좌표계로 선형변환하여야 하며, 이러한 변환기법으로 단면에서 발생하는 가장 지배적인 유속성분의 분석이 가능하다(Preisendorfer and Mobley, 1988).
본 연구에서는 관측단면 A-B의 연직방향을 X방향, 단면의 폭 방향을 Y방향으로 설정하여 관측단면과 연직 및 평행한 유속성분 VX 및 VY를 산정하였으며, 이후 분석에 사용되는 모든 유속자료는 좌표회전이 수행된 자료이다.
3.2 평균 관측단면 도출
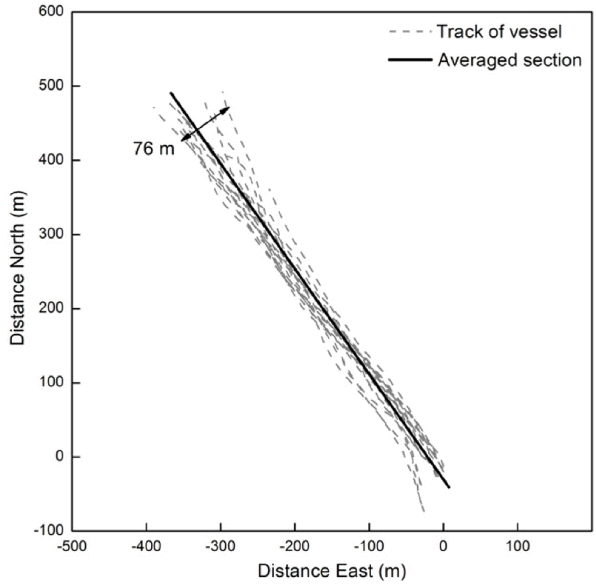
관측단면의 층별 유속 측정은 ADCP가 장착된 선박이 단면 A-B를 따라 왕복하며 반복 측정하게 되는데, 매 관측시 선박의 이동경로는 거의 유사하게 겹쳐지기는 하나 완벽하게 일치하지 못한다. 본 연구에서 관측을 수행하는 동안 매 관측별 선박이동경로는 최대 약 76 m 정도의 차이가 발생하였는데, 선박이동경로가 일치하지 못하므로 관측되는 수심, 즉 단면형상(지형)의 관측값 또한 매 관측마다 달라지게 된다. 따라서 본 연구에서는 모든 선박이동경로를 대표할 수 있는 평균 관측단면을 도출하였으며(Fig. 5 참조), 이후 모든 분석에 평균된 관측단면을 적용하였다.
한편, 매 관측별 선박의 이동경로 차이로 인하여 측정된 유속값 역시 동일한 관측단면에 대한 유속성분이라고 할 수는 없으나, 본 연구에서 측정이 수행된 관측단면은 조석에 의한 흐름이 지배적인 수로에 위치하고 있어 주 흐름방향 유속 VX가 현저하게 크게 나타나는 특징을 갖는다. 따라서 선박이동경로의 차이로 인한 유속 측정결과의 오차는 그다지 크지 않을 것으로 판단되어, 이에 이와 관련된 사항은 무시하고 분석이 수행되었다.
3.3 수평/수직방향 Sigma좌표 변환
단면관측에서 측정된 모든 층의 관측자료를 활용하여 전 구간의 데이터를 일괄적으로 구성하기 위하여, 공간적 관측위치에 따른 수직적 변화(수심) 뿐만 아니라 수평적 변화(거리)까지 일괄적으로 같은 격자로 구성해야 할 필요가 있다(Lee et al., 2012). ADCP 원시자료는 RDI사의 WinADCP ver. 1.12 후처리 프로그램을 이용하여 수치자료로 변환되는데, 이때 자료는 수평적으로는 선박의 이동경로를 따라 측정된 횡단면의 거리값을 가지며, 수직적으로는 표층에서 저층까지 관측된 원시자료의 수심, 즉 Z-level 상의 데이터 형태이다. 단면관측의 특성상 선박이동경로가 매 관측별 동일한 횡단면으로 관측하는 것이 사실상 불가능하므로 수평격자의 간격차이가 발생할 수 밖에 없으며, 우리나라 서해안과 같이 대조차가 크게 나타나는 해역에서는 저조시 표층의 값이 고조시의 표층 하 수 미터의 값과 함께 분석되는 오류가 발생될 수 있으므로, 단면통과 유량 및 조량 산정을 위해서는 정규화를 통하여 수평/수직방향 Sigma 좌표로 변환하는 과정이 반드시 필요하다(Lee et al., 2012). 이에 본 연구에서는 다음의 식 (2)를 이용하여 수평/수직좌표를 Sigma 좌표로 변환하였다.
여기서, σx및 σz는 각각 sigma 좌표로 변환된 수평/수직격자를 나타내며, L은 관측시작점에서 끝점까지의 거리, d는 시작점에서 측정된 임의 ensemble까지의 거리이다. 또한, H는 전체수심, Z는 표층으로부터의 깊이이다.
3.4 Blank zone의 데이터 보정
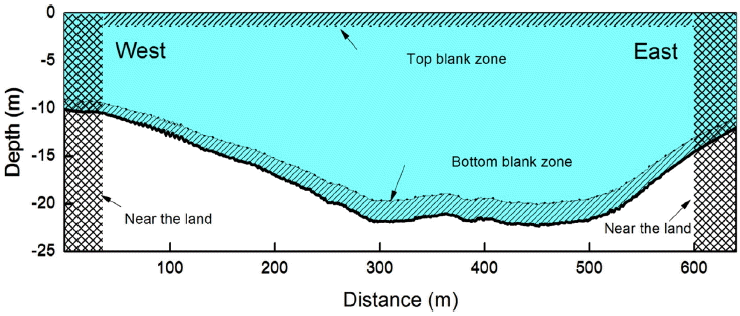
ADCP를 이용한 단면관측의 수행시, 관측장비의 특성 및 대상해역의 지형적 특성으로 인하여 관측이 이루어지지 않는 Blank zone이 발생하게 되는데, 이러한 Blank zone은 크게 3가지로 구분될 수 있다(Fig. 6 참조). 먼저, 저면 및 수면근처에 형성되는 연직방향 Blank zone은 관측 장비의 특성으로 인하여 관측이 이루어지지 않는 영역으로서, 저면근처의 Blank zone은 기본적으로 Layer의 간격설정에 따라, 수면근처의 Blank zone은 ADCP의 장착위치에 따라 그 크기가 변화한다. 단면 관측에서 측정이 이루어지지 않는 또 하나의 Blank zone은 대상해역의 지형적 특성으로 인하여 발생하는데, 육지 근처의 수심이 충분히 확보되지 않아 선박의 접근이 불가능하여 측정이 이루어지지 않는다. 육지 근처의 Blank zone은 선박의 접근가능 여부에 따라 그 크기가 결정되므로, 가능한 Blank zone의 발생영역을 최소화시킬 수 있도록 관측수행 과정시 세심한 주의가 필요하다.
본 연구에서는 수면근처 Blank zone은 약 1.1 m, 저면근처에서는 전체 수심의 약 10% 정도에 해당하는 Blank zone이 발생한 것으로 나타났는데, 이들 연직방향 Blank zone은 전체 수심의 약 15% 정도에 해당되는 영역이다. 단면통과 유량 및 조량 산정시 Blank zone의 영역을 무시하고 계산을 수행하는 경우 그 결과는 실제와 크게 달라질 수 있다.
바닥거치식 방법을 이용하는 경우에도 마찬가지로 연직방향 Blank zone이 발생하는데, 바닥거치식 방법의 경우에는 관측센서를 추가로 설치하는 등의 방법을 통하여 자료를 보완하는 것이 가능하다. 그러나 단면관측 방법을 이용하는 경우, 장비의 추가 설치를 통한 자료보완이 불가능하므로 관측된 자료를 토대로 Blank zone의 데이터를 보간하여 사용하는 것이 최선이다. 따라서 본 연구에서는 ADCP로부터 관측된 원시자료를 보간하고 연직방향 Blank zone의 데이터를 추정하여 분석을 수행하였다.
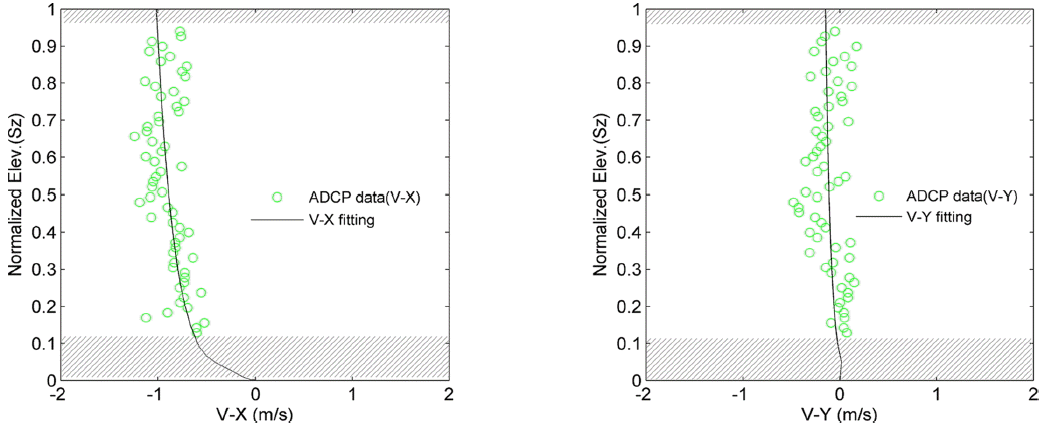
ADCP 관측자료 중 임의 Ensemble에서의 층별 유속 관측자료가 X방향과 Y방향으로 구분되어 Fig. 7에 제시되는데, 저면 및 수면근처에 자료가 획득되지 않는 연직방향 Blank zone이 존재함을 확인할 수 있다. 각각의 Ensemble에서 식(3)에 제시된 von-Karman 유속분포식을 이용하여 층별 유속관측자료의 데이터 보간을 수행하였다.
여기서, V는 각 방향별 유속, A 및 B는 접합곡선 산정을 위한 계수, 그리고 Sz는 무차원화 된 수심을 의미한다.
한편, 단면 폭 방향의 육지부근에서 나타나는 Blank zone은 선박의 접근가능 여부에 따라 결정되므로 매 관측마다 그 크기는 각기 다르게 나타나는데, 이를 최소화하기 위해서 현장관측 수행시 GPS를 이용하여 시작 및 끝점의 위치를 가능한 동일하게 하고자 하였다. 그럼에도 불구하고 육지부근 Blank zone의 크기는 매 관측마다 다소 차이를 보이는 것으로 나타났는데, ADCP로부터 측정된 자료의 배제가 최소화가 될 수 있는 계산영역을 선정하여 매 관측자료의 계산영역의 크기를 동일하게 설정하였다.
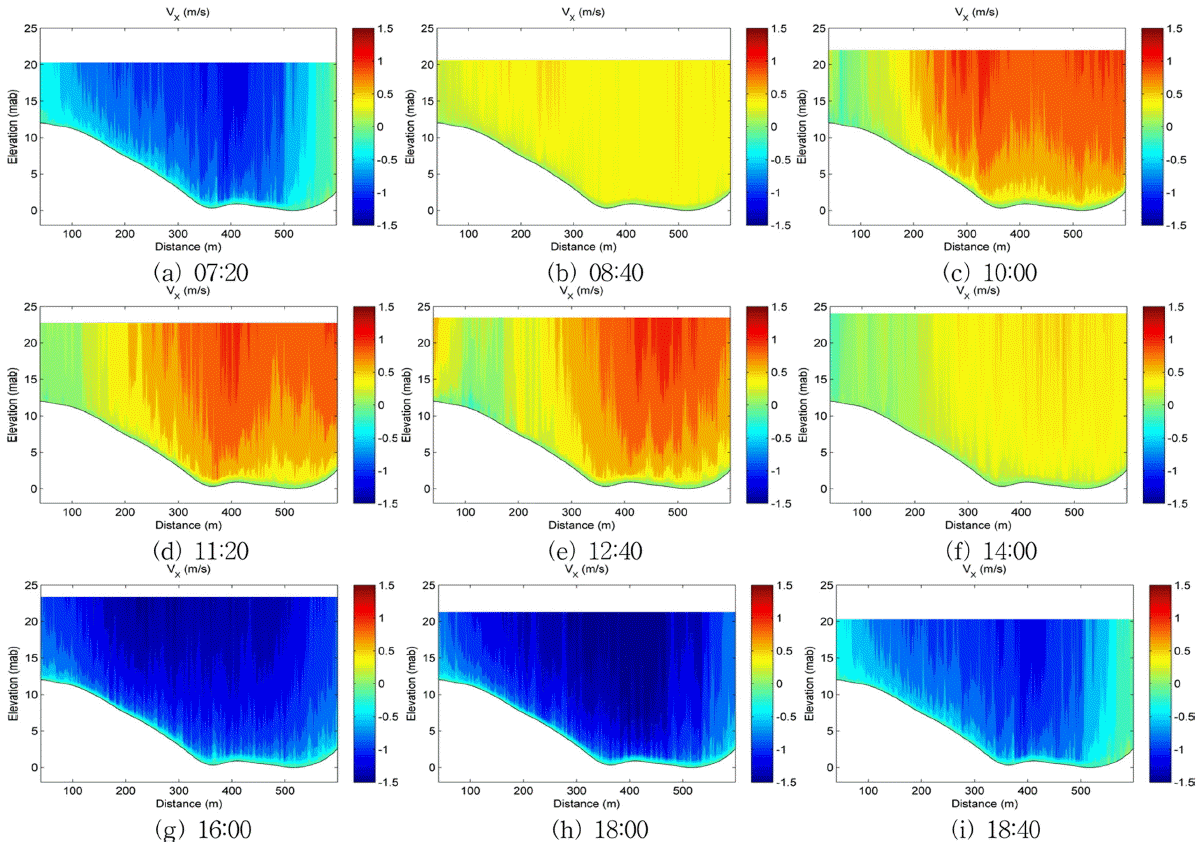
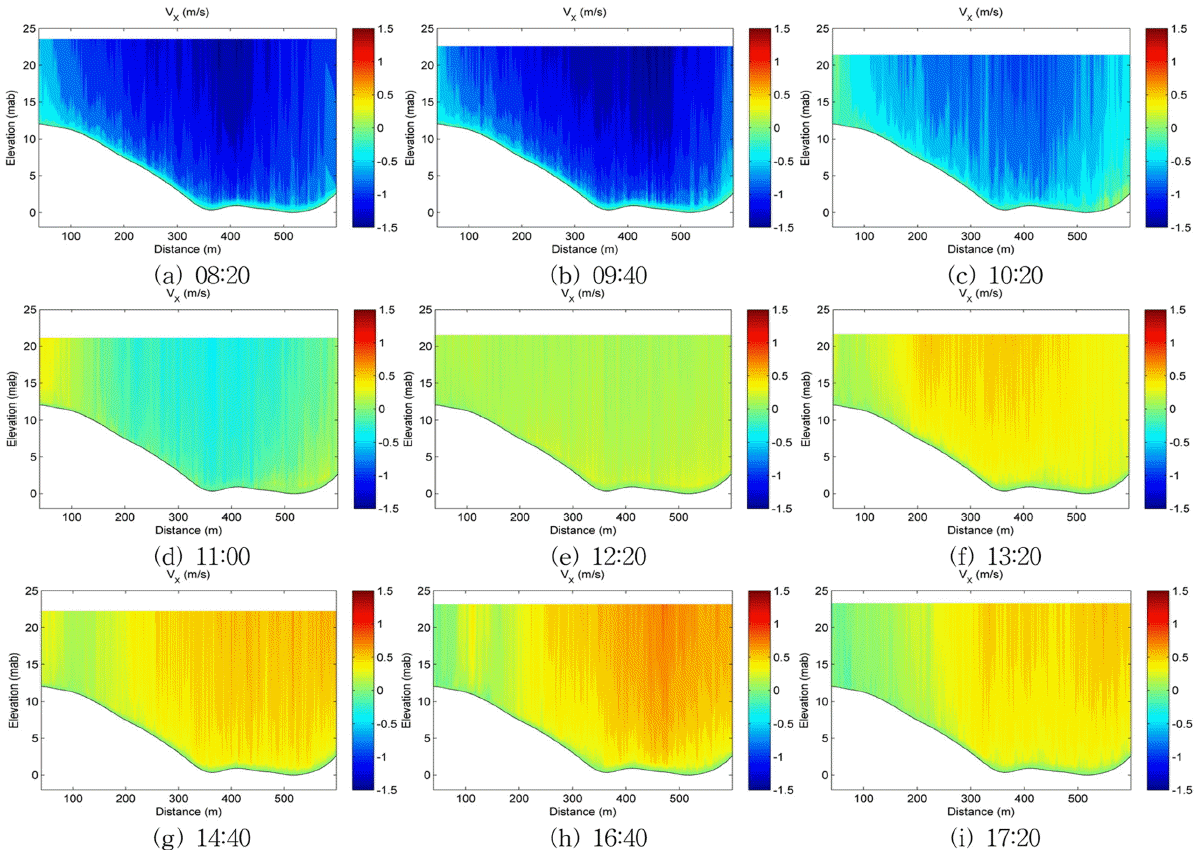
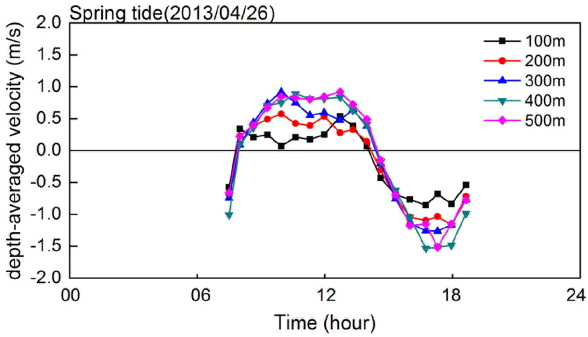
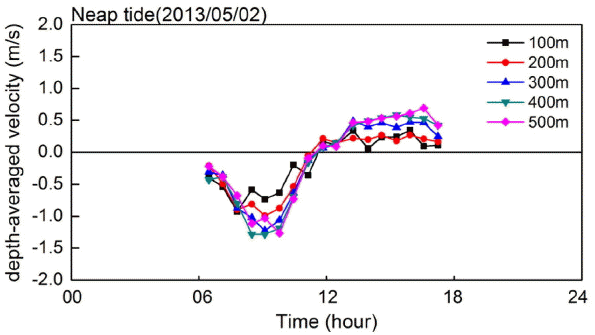
Blank zone의 데이터 보정을 수행한 모든 층별 유속 데이터 중, 대조기 및 소조기에 관측된 층별 유속자료의 분석결과의 일부가 Fig. 8 및 Fig. 9에 제시된다. 수로 폭 방향의 유속 VY은 수로 연직방향의 주 흐름방향 유속 VX에 비해 그 크기가 현저하게 작으므로, Fig. 8 및 Fig. 9에서는 주 흐름 방향 유속 VX만이 제시되었다. 결과를 살펴보면, 관측이 수행된 수로의 폭은 약 550 m 정도이며, 시간에 따라 창조 및 낙조 유속이 명확하게 구분됨을 알 수 있다. 유속은 대체적으로 상층에서 가장 크고 저면으로 갈수록 작아지는 양상을 보이며, 수로 중앙부분에서 유속이 가장 크고 육지와 가까운 영역에서는 작은 유속이 발생하는 것으로 나타났다.
Fig. 8 및 Fig. 9의 단면유속 분포에서, 단면 폭 방향 100 m 간격으로 수심평균 유속이 산정되어 Fig. 10 및 Fig. 11에 제시된다. 관측단면 위치에 따라 수심평균 유속은 정량적으로 큰 차이를 보이는데, 창조시보다 낙조시의 수심평균 유속이 더 큰 것으로 나타났으며 대조기의 수심평균 유속이 소조기에 비해 더 크다. Jung and Choi(2010)는 목포해역의 28개 정점에서의 유속 측정자료로부터 낙조시 유속이 창조시에 비해 평균적으로 1.26배 크다는 결과를 제시한 바 있는데, 이러한 점에 비추어 본 연구에서 측정된 유속결과 역시 목포해역의 낙조우세(ebb predominance) 현상을 제대로 반영하고 있는 것으로 판단된다.
결과를 더 자세히 살펴보면, 단면의 좌측(100 m)에서 우측(500 m)으로 갈수록 수심평균 유속이 증가하는 양상을 보이는데, 단면의 좌측에서 우측으로 갈수록 단면의 수심이 증가(Fig. 3 참조)하므로 수심이 증가함에 따라 수심평균 유속이 증가하는 것으로 볼 수 있다. 이러한 양상은 수심이 낮은 해역에서 바닥마찰의 영향에 의해 유속이 작게 나타나고, 수심이 깊어질수록 이러한 영향이 감소하여 수심평균 유속이 크게 나타난 것으로 해석될 수 있다.
3.5 단면통과 유량 및 조량의 산정
단면 유속 측정결과로부터, 단면 A-B를 통과하는 유량, 즉 단면통과 유량이 정량적으로 산정될 수 있다. 물이 통과하는 단면의 면적, 즉 흐름 단면적의 크기가 일정할 경우 단면통과 유량은 유속에 의해 크게 변화하는데, 유속은 층별, 시간별로 그 크기와 방향이 각기 달라지므로 단면통과 유량 또한 수심과 시간에 따라 크게 변화한다. 전체 단면을 통하여 통과되는 단면통과 유량 는 다음의 식 (4)에 의해 산정될 수 있다.
여기서, VX는 관측단면과 연직방향의 유속성분, B는 단면의 폭, h(t)는 시간에 따른 수위의 변화를 나타낸다.
한편, 단면통과 유량 산정 결과로부터 단면 A-B를 통하여 유출입되는 조량 Pm은 다음의 식 (5)에 의해 산정될 수 있다.
여기서, T는 창조 혹은 낙조 지속시간를 의미한다. 흐름 단면적은 관측시간동안 수위변화로 인해 계속 변화하므로 각 관측 수행시의 단면적을 평균하여 유입구 단면적의 대표값으로 사용하였다.
4. 단면통과 유량 및 조량 산정결과
4.1 단면통과 유량 산정결과
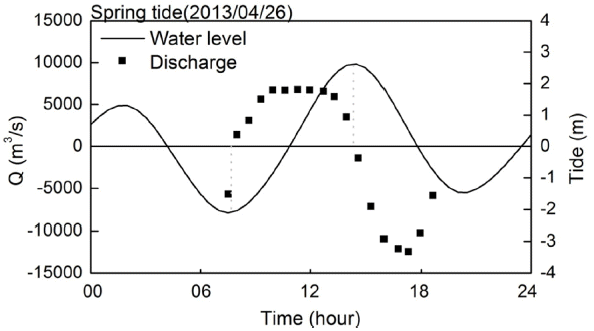
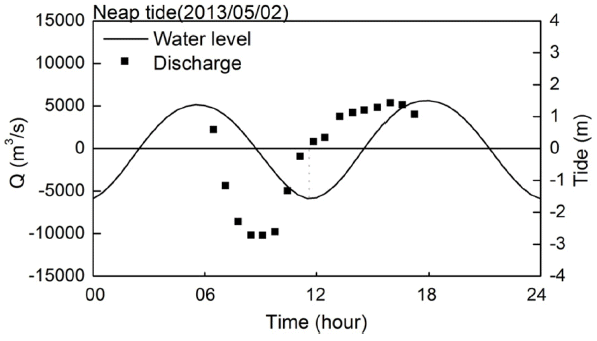
앞서 제시된 식 (4)으로부터 산정된 단면통과 유량 산정결과가 대조 및 소조기로 구분되어 Fig. 12 및 Fig. 13에 제시된다. 그림들에는 관측위치와 가장 근접한 목포 조위관측소의 조위 관측결과가 함께 제시되는데, 조위의 변화에 따른 단면통과 유량의 변화양상이 잘 나타나고 있음을 알 수 있다. 낙조에서 창조, 혹은 창조에서 낙조로 변화하는 시점, 즉 게조시(slack water)에는 유속이 0인 상태가 되는데, Fig. 12 및 Fig. 13에 제시된 결과에서도 이러한 양상이 잘 나타나있다. 또한 창조시에 단면통과 유량이 점점 증가하여 최대값을 갖다가 감소하며, 낙조시 역시 동일한 양상으로 방향만 반대로 나타나는 것을 알 수 있다. 단면통과 유량은 창조시보다 낙조시에 더 큰 값을 갖는 것으로 나타났는데 이는 목포해역의 낙조우세적 조석특성을 잘 반영하는 결과라 할 수 있으며(Kim, 2015), 이러한 결과들에 비추어 단면통과 유량 산정결과는 정성적으로 타당한 값을 갖는다고 판단된다. 정량적인 측면에서 살펴보면, 대조기에는 낙조시에 최대 통과유량이 발생하였는데 약 12,473 m3/s의 유량이 통과하였고, 소조기 역시 낙조시에 최대 통과유량이 발생하였으며 약 10,189 m3/s의 유량이 통과되는 것으로 나타났다. 소조기보다 대조기에 통과유량이 비교적 크게 나타났으며, 대조기의 최대통과 유량은 소조기에 비해 대략 20% 정도 더 큰 것으로 나타났다.
4.2 조량 산정결과
하구 및 연안해역에서 조석(수위) 자료만을 이용하여 창조 혹은 낙조의 우세성을 제시하는 방법은 지형학적 특성 및 수심 등의 영향에 의해 오류를 야기할 수 있으며(Yoon and Woo, 2012), 특히 퇴적물의 이동 분석에 사용되기 어려우므로 유속에 근거한 자료와의 비교분석이 수행되어야 한다(Robin and Davies, 2010). 목포해역은 조석의 비선형성에 의한 전형적인 낙조우세 해역으로 잘 알려져 있기는 하나, 현장에서 측정된 유속자료로부터 창조 혹은 낙조시의 유출입 체적이 정량적으로 산정된 바 없으므로 본 연구에서는 관측단면 A-B에서의 창조시 유입되는 양과 낙조시 유출되는 양을 정량적으로 산정하여 Table 3에 제시하였다. 또한, 단면 A-B에서의 유입구 단면적 산정결과가 Table 3에 함께 제시된다. 결과를 살펴보면 창조시에 1.28 × 108m3이 만 내부로 유입되며, 낙조시에 1.53 × 108m3이 유출되는 것으로 나타났는데, 앞서 제시된 유속 및 단면통과 유량 산정결과와 마찬가지로 낙조시에 유출되는 양이 창조시에 유입되는 양에 비해 더 큰 것으로 나타났다.
한편, 앞서 1장에 제시된 바와 같이 본 연구에서는 대조기의 유입구 단면을 통해 유입 혹은 유출되는 해수의 총량 중 더 큰 값을 조량으로 정의하였으므로, 이에 근거하여 본 연구로부터 산정된 목포해역의 조량은 1.53 × 108m3이다. 조석의 일조부등에 의한 조량의 차이가 발생할 수 있으나, 본 연구에서 수행된 대조기 관측시간동안의 조석은 조차가 가장 큰 시간대, 즉 창낙조의 유량이 큰 시간대에 해당되므로(Table 2 참조), 일조부등으로 인한 조량 산정값의 오차는 무시된다.
4.3 과거 연구결과와의 비교
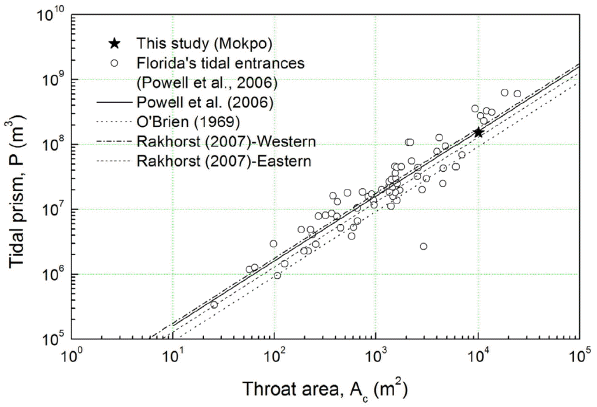
앞서 1장에서 제시된 바와 같이, 과거 많은 연구자들은 조량과 유입구 단면적과의 상관관계에 대한 다수의 연구를 수행한 바 있는데, 대부분의 과거 연구들에서 제시되는 조량은 조석의 통계분석 결과를 이용하여 계산된 근사치이며 연구자 별 각기 다른 조석조건을 사용하여 조량이 산정제시되었다. 과거 연구들에서의 조량에 대한 조석조건의 정의가 동일하지 않을 뿐만 아니라 본 연구의 결과는 현장 관측자료에 기반한 값이므로, 조석조건에 따른 조량의 정량적 차이는 불가피하다. 그러나 각 연구들에서 사용된 자료들의 조석조건을 명시하고 있으므로 조량 및 유입구 단면적 산정결과가 본 연구결과와 함께 Fig. 14에 제시된다. Fig. 14에서, 조량과 유입구 단면적과의 상관관계는 해역별로 크게 다르게 나타나며 대체적으로 유입구 단면적이 증가함에 따라 조량도 증가하는 선형관계를 갖는 것으로 나타났다. 본 연구의 조량 산정결과는 과거 연구들과의 경향성이 대체적으로 잘 일치하는 것으로 나타났는데, 특히 Powell et al.(2006)에 의해 산정된 Florida의 조석 유입구에서의 조량 산정결과와 대체적으로 유사한 범위의 값을 갖는 것으로 나타났다. 이러한 결과에 비추어 본 연구에서 수행된 ADCP 관측결과를 이용한 조량 산정결과는 타당한 범위 내의 값을 갖는 것으로 판단된다.
비록 본 연구는 목포해역 내 1개 조석 유입구에서 관측된 자료만을 이용한 결과이므로, 우리나라 서해를 대표하는 자료로 활용될 수는 없다. 그러나 과거 Jarrett(1976)이 미국의 Atlantic, Gulf 및 Pacific 해안에 위치하는 입구부에 동일한 조량과 흐름 단면적 관계를 적용할 수 있는지에 대한 연구를 수행한 것과 같이, 우리나라의 서·남해안에 발달되어 있는 조석 유입구에서의 조량을 정량적으로 산정함으로써 우리나라의 해안에 적용 가능한 접합계수를 산정하는 것은 매우 의미있을 것으로 판단된다.
한편, 해수는 부유사와 함께 이동하므로 조량은 해역의 퇴적물 이송과 큰 연관성을 갖는다. 해역의 흐름단면에서 조량의 유출입과 함께 동반되는 부유사량을 정량적으로 산정하는 것은 해역 전반에 걸친 침식 혹은 퇴적 여부를 판단할 수 있는 지표가 되는데, 비록 유입구 단면 내외에서의 국부적인 침식 혹은 퇴적을 파악하는 것은 힘들지만 총량적 관점에서의 퇴적물 이송량 산정이 가능하므로 조량과 유입구 단면적의 상관관계를 분석하는 것은 매우 중요한 사항이라 하겠다. 그러나 해역의 흐름특성 및 지형학적 특성에 따라 조량은 크게 달라질 수 있으므로, 반드시 현장관측을 통한 측정자료를 기반으로 하여 정량적 산정이 수행되어야 할 것이다. 또한, 앞서 제시된 조량과 유입구 단면적 간의 상관관계 식 A = aPm의 매개변수 a 및 m은 해역에 따라 크게 변화하는데, Kraus(1998)은 구조물 등의 설치로 인하여 연안이송이 자유롭지 않은 해역의 매개변수 값이 더 작아진다고 제시한 바 있다. 목포해역과 같이 대규모 개발이 활발하게 진행되는 해역의 경우, 다양한 구조물 등의 건설로 인하여 흐름특성은 크게 변화할 수 있으며 이로 인해 단면을 통과하는 조량 또한 크게 변화할 수 있으므로 조량과 유입구 단면적의 변화추세를 지속적으로 파악하는 것 또한 중요한 사항이라고 하겠다. 이러한 자료는 일시적 지형변화로 인한 깨어진 평형상태를 원 상태로 회복시키기 위한 기초자료로 활용될 수 있을 것이다.
5. 결 론
본 연구에서는 조석 유입구에서의 단면통과 유량 및 조량 산정을 위하여, 목포해역 내 대표 조석 유입구에서 ADCP를 이용한 단면관측을 통해 층별 유속 관측이 수행되었다. 관측된 원시자료는 지배적인 유속성분 도출을 위하여 단면의 회전정도를 고려한 좌표회전이 수행되었으며, 정규화를 통하여 수평/수직방향 Sigma 좌표로 변환되었다. 또한, 관측이 이루어지지 않는 저면과 수면 근처의 Blank zone 데이터는 von-Karman 유속분포식을 이용하여 보간이 수행되었다. 보정된 자료를 이용하여 단면통과 유량이 정량적으로 산정되었는데, 단면통과 유량 산정결과 창조시보다 낙조시에 단면통과 유량이 더 크게 나타나는 목포해역의 낙조우세적 조석특성이 잘 나타났다. 또한, 소조기보다 대조기에 단면통과 유량이 더 크게 나타났는데, 대조기의 최대 통과유량은 소조기에 비해 약 20% 정도 더 크게 나타났다.
한편, 과거 연구결과들에서 제시되는 조량 산정결과에 대한 검토가 이루어졌는데, 과거 연구들에서 사용된 조량 산정자료의 조석조건을 보완하여 현장관측자료에 기반한 조량산정 방법의 조건이 재정립되었다. 조량산정 조건의 새로운 정의에 근거하여 조석 유입구에서의 단면 유속관측 자료를 이용한 조량의 정량적 산정이 국내 최초로 수행되었는데, 창조시에 1.28 × 108m3이 만 내부로 유입되고 낙조시에 1.53 × 108m3이 유출되는 것으로 산정되었으며, 이에 목포해역 내 조석 유입구에서의 대조기의 조량은 1.53 × 108m3인 것으로 나타났다. 조량 산정결과는 과거 연구들에서 도출된 조량과 조석 유입구 흐름단면적 상관관계 결과와 비교·분석되었는데, 본 연구에서 산정된 조량 산정 결과는 과거 Powell et al.(2006)의 연구결과와 잘 일치하는 것으로 나타나 타당성 있는 결과가 도출된 것으로 확인되었다.
비록 본 연구에서 수행된 연구 결과는 목포해역의 1개 단면에 국한된 자료이긴 하나, 국내 최초로 현장 관측자료를 이용하여 조량을 정량적으로 산정하고 조량-입구부 단면적의 상관관계와 비교했다는 점에서 큰 의의를 갖는다. 이러한 자료는 우리나라의 서·남해안에 발달되어 있는 조석 유입구에 대한 조량-입구부 단면적의 상관관계 해석을 위한 기초자료로 활용될 수 있을 것이며, 향후 수치해석과의 연계분석을 통하여 수치모델의 예측결과 검증 및 모델의 정확도 향상 등을 위해 사용될 수 있을 것이다. 또한 목포해역에서의 흐름특성 뿐만 아니라 수층 부유사농도 및 이송률 등을 정량적으로 산정·비교함으로써, 목포해역 전반에 걸친 침식/퇴적환경 변화에 대한 체계적이 평가 및 예측이 이루어질 수 있을 것으로 판단된다.