1. 서 론
2011년 3월 11일 14시 46분(KST) 일본 미야기현 센다이 동쪽 산리쿠 앞바다 해저에서 발생한 동일본 대지진(규모 9.0)은 계기지진 관측 역사상 4번째로 큰 규모로 지진해일을 동반하여 전 세계적으로 많은 인적 및 물적 피해를 입혔다. 특히 일본에서는 엄청난 인명 피해(사망 15,894명, 부상 6,152명, 실종 2,562명, 이재민 228,863명)와 건물 피해(완파 121,805동, 반파 278,521동 등)가 발생하였다(일본 경찰청 2016년 3월 발표 기준). 이와 더불어 후쿠시마 원자력발전소에 내습한 지진해일로 인하여 국제원자력평가척도 기준 7단계에 해당하는 심각한 방사성물질 누출 사고가 발생하였다. 또한 지진해일은 태평양을 전파하며 태평양 주변 국가 연안에 위치한 항구, 건물 등에 피해를 주었다(Borrero et al., 2013; Cheung et al., 2013; Hinwood and Mclean, 2013; Lynett et al., 2013). 미국 캘리포니아에서는 최대 2.47 m의 해일고를 보였으며, 주변 20여 개의 항구에 약 5천만 달러의 피해를 준 것으로 보고되었다(Wilson et al., 2013).
동일본 대지진 이후 대규모 지진에 의한 지진해일로부터 피해를 최소화하고 대응하기 위하여 지진해일 예측 정확도 향상을 위한 연구가 전세계적으로 진행되었다. 동일본 대지진은 다양한 관측 기기에 관측되어 지진파뿐만 아니라 GPS 자료, 지진해일 관측 자료를 활용한 단층변위 분포(slip distribution)가 제안되었다(e.g. Satake et al., 2013; Yokota et al., 2011; Yoshida et al., 2011; Yue and Lay, 2011). 그리고 많은 지역에서 지진해일 해일고 및 처오름 높이에 대한 조사가 이루어져 지진해일 수치모의 연구에 활용되었다(Mikami et al., 2012; Mori et al., 2011; Mori and Takahashi, 2012). 우리나라에서도 동일본 지진해일과 같은 한반도 주변해역 이외의 지역에서 발생하는 지진해일에 대응하기 위하여 전지구 지진해일 예측 시스템을 개발하였다(Lee et al., 2015).
대부분의 지진해일 수치모의를 이용한 연구에서는 단층변위 분포에 의한 해저면에서의 수직변위와 지진해일 초기 해수면 변위가 동일하다고 가정한다(Shuto, 1991). 이 가정이 성립하기 위해서는 지진해일이 수심에 비해 파장이 매우 길어 천해파(장파)로 간주될 수 있으며, 단층의 파열 속도(rupture velocity)가 지진해일 전파 속도에 비해 상대적으로 순식간에 발생하고, 평평하거나 경사가 완만한 지형에서 지진이 발생하여 해저면 수평 변위를 무시할 수 있다는 가정이 필요하다(Tanioka and Satake, 1996a). 그러나 경사진 지형에서는 해저면 수평변위에 의해 수직변동이 동반되어 해수면 변위가 발생하고 이는 지진해일 초기파형에 영향을 줄 수 있는데 이를 지형 효과(bathymetry effect)라 한다(Bletery et al., 2015). Tanioka and Satake(1996a)가 지형 효과의 영향력을 처음 제안한 이후 완만한 경사(low dip)의 단층 운동에 의한 지진 및 지진해일에 대하여 지형 효과를 고려한 다양한 사례분석 연구가 진행되었다(Table 1). 2011년 동일본 대지진 또한 완만한 경사에서 큰 변위가 발생한 지진으로 지형효과가 고려됨에 따라 일부 일본 관측소(이와테, 미야기, 후쿠시마 등)에서 최대 해일고가 30% - 60%의 차이를 보였다(Bletery et al., 2014; Satake et al., 2013).
동일본 지진해일 관측 자료 중 일본의 기상청(JMA, Japan Meteorological Agency), 국토지리원(GSI, Geospatial Information Authority of Japan), 해상보안청(JCG, Japan Coast Gaurd) 그리고 러시아의 연방 수문 기상 및 환경국(FSRHEM, Federal Service of Russia for Hydrometeorology and Environmental Monitoring)에서 운영하는 동해 주변의 일부 조위관측소에서 지진해일 수치모의로 예측한 지진해일 도달시각보다 이른 시각에 작은 해수면 변화를 보였다(Murotani et al., 2015). Murotani et al.(2015)은 2011년 동일본 대지진 직후 발생한 단주기의 작은 해수면 변화를 지진해일 선행파(tsunami forerunner)라 정의하였으며, 지형효과를 고려한 지진해일 수치모의를 통해 지진해일 선행파가 지형효과와 관련 있음을 보였다.
우리나라는 일본과 인접해 있음에도 불구하고 동일본 지진해일에 의한 피해 없이 일부 조위관측소에서 0.3 m 이내의 작은 해일고만 관측되었다. 대부분의 조위관측소에서는 지진해일 수치모의(Bae et al., 2012)를 통해 예측한 것과 유사한 시각(지진발생으로부터 약 4 - 7시간 후)에 지진해일이 관측되었다. 그러나 동해에 위치한 일부 조위관측소에서 예측 도달시각보다 이른 동일본 대지진 발생 후 한 시간 이내에 20 cm 내외의 단주기 해수면 변화가 발생하는 지진해일 선행파가 관측되었다. 본 연구에서는 2011년 동일본 대지진에 의해 한반도에서 관측된 지진해일 선행파의 원인을 분석하고자 지형효과를 고려한 지진해일 수치모의를 수행하였으며, 지형효과를 고려하지 않은 결과와 비교하였다. 그리고 본 연구 결과가 기상청(KMA, Korea Meteorological Administration)의 지진해일 통보 시스템에 줄 수 있는 영향력을 분석하였다.
2. 우리나라에 관측된 2011년 동일본 지진해일 선행파
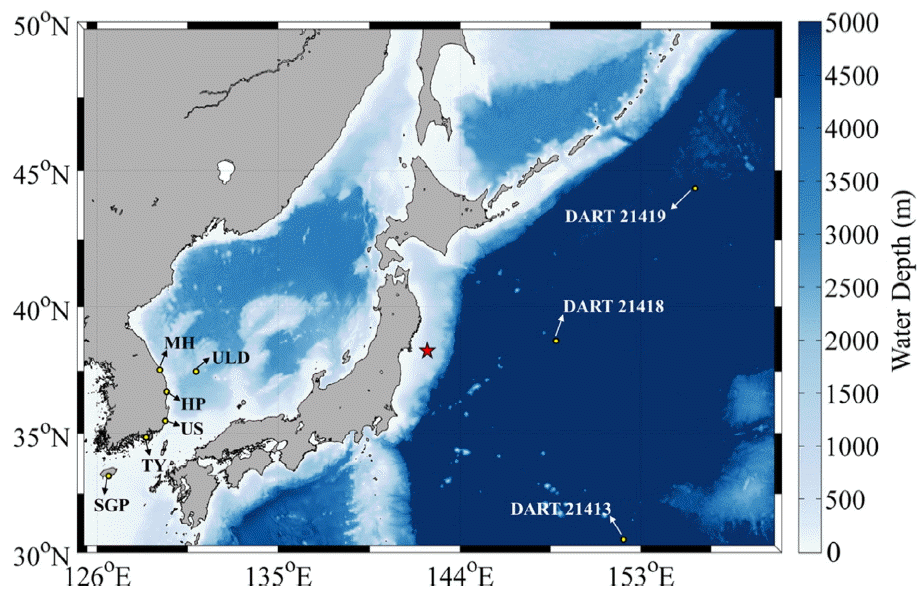
기상청에서는 지진해일 관측을 위하여 울릉도 해일파고계 자료와 국립해양조사원(KHOA, Korea Hydrographic and Oceanographic Agency)의 조위관측소 자료를 활용하고 있다. 본 연구에서는 2011년 동일본 지진해일이 관측된 조위관측소 중 지진해일 선행파가 관측된 울릉도(ULD), 묵호(MH), 후포(HP) 조위관측소와 지진해일 선행파가 관측되지 않은 울산(US), 통영(TY), 서귀포(SGP) 조위관측소를 선정하였다(Fig. 1, Table 2). 조위관측소 자료(1분 간격)에는 자료 송수신 문제, 기기 결함, 악기상 등에 의한 결측 구간이 존재한다. 또한 지진해일뿐만 아니라 조석 성분도 포함되어 있어 관측자료 간 비교뿐만 아니라 조석을 고려하지 않는 지진해일 수치모의와의 비교도 어렵다. 따라서 본 연구에서는 차분법을 이용한 보간 함수로 결측 구간 파고를 예측하고 조화 분석(harmonic analysis) 프로그램인 T_TIDE를 이용하여 조석 성분을 제거한 자료를 사용하였다(D’Errico, 2004; Pawlowicz et al., 2002).
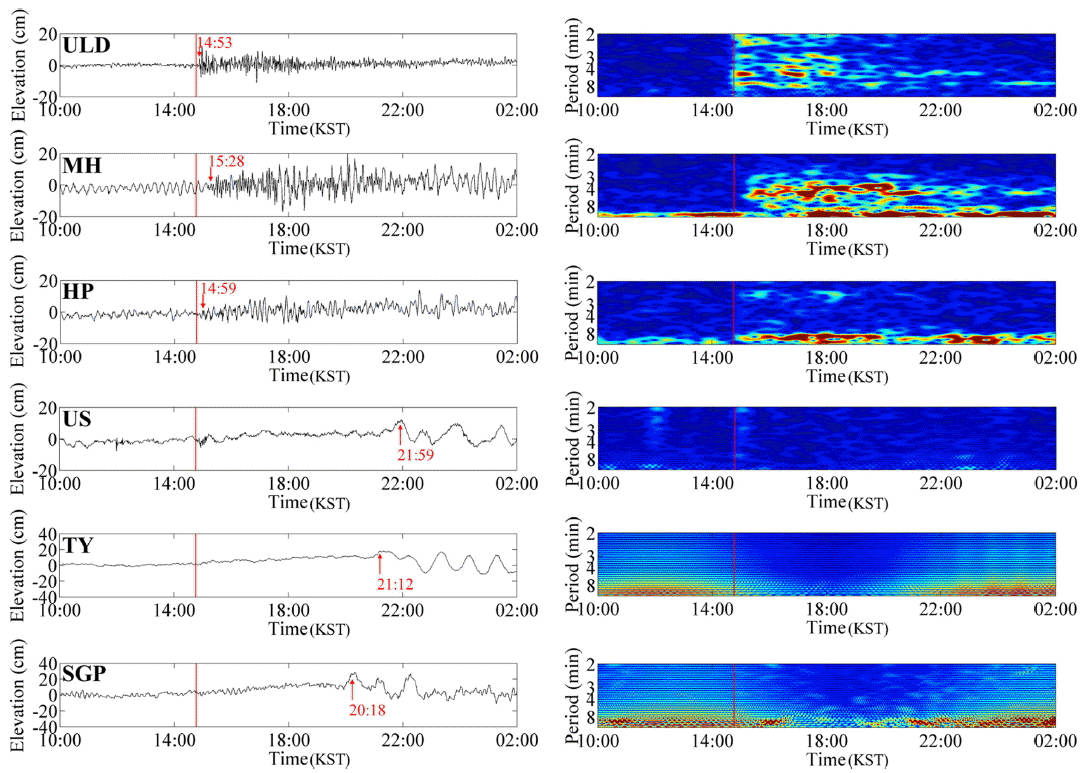
Fig. 2는 결측 구간 파고를 예측하고 조석 성분을 제거한 조위관측소 자료의 시계열과 스펙트로그램이다. 여기서 빨간색 선은 동일본 대지진 발생 시각인 14시 46분이며, 빨간색 화살표는 지진 발생 전과 다른 경향의 해수면 변화가 발생하는 시간을 나타낸다. 진원으로부터 가장 가까운 울릉도에서 동일본 대지진 발생 약 7분 후 20 cm 내외의 해일고가 관측되었으며, 묵호와 후포 조위관측소에서도 동일본 대지진 발생 약 42분, 13분 후 10 cm 내외의 해일고가 관측되었다. 이는 Bae et al.(2012)의 연구에서 지진해일 수치모의를 통해 예측한 지진해일 도달시각보다 이른 시각에 관측된 것이며, 10분 이내의 단주기 성분이 탁월하여 Murotani et al.(2015)이 정의한 지진해일 선행파의 특성과 동일하다. 이에 반하여 울산, 통영, 서귀포 조위관측소에서는 지진해일 선행파 없이 동일본 대지진 발생으로부터 최소 약 5시간 30분 후 해수면 변화가 관측되었다. 이는 Bae et al.(2012)의 연구에서 지진해일 수치모의를 통해 예측한 지진해일 도달시각과 유사하다. 이러한 지진해일 도달시각의 차이는 스펙트로그램을 통해서도 확인할 수 있다. 울산, 통영, 서귀포 조위관측소 스펙트로그램에서는 확인할 수 없는 주기 10분 이내의 단주기 성분을 울릉도, 묵호, 후포 조위관측소 스펙트로그램에서 지진 발생 직후 확인할 수 있으며 울릉도, 묵호, 후포 조위관측소 순으로 지진해일 선행파의 주기가 길어진다.
3. 지형효과를 고려한 지진해일 수치모의
한반도에서 관측된 지진해일 선행파의 원인을 분석하고자 COMCOT(COrnell Multi-grid COupled Tsunami) 모델을 이용하여 2011년 동일본 지진해일 수치모의를 수행하였다. 천수방정식 기반의 유한차분모델인 COMCOT에 대한 보다 자세한 설명은 Liu et al.(1998)을 참조할 수 있다. 지진해일 초기파형은 지형 효과를 고려한 경우와 고려하지 않은 경우를 사용하였으며, 지진해일 수치모의에 사용한 조건은 Table 3과 같다. 구면좌표계 선형 천수방정식을 지배방정식으로 사용하였으며, 미국 국립해양대기청(NOAA, National Oceanic and Atmospheric Administration)의 지구물리 자료센터(NGDC, National Geophysical Data Center)에서 제공하는 위경도 좌표계의 1분 간격 수심자료를 사용하였다. 시간 간격은 CFL 조건(Courant-Friedrichs-Lewy condition)을 만족하는 1 s로 설정하였다.
3.1 유한 단층 모델
COMCOT은 지진 매개변수를 이용하여 단층면에 대하여 동일한 단층 변위량을 가정하는 단층모델을 제공한다. 그러나 동일본 대지진과 같이 단층의 크기가 수백 km인 경우 단층면상의 모든 지점에서 동일한 단층운동을 한다고 가정하는 것은 비현실적이다. 따라서 대규모 지진의 불균일한 단층 운동을 표현하기 위하여 단층을 여러 개의 소단층(subfault)으로 구성하여 단층변위 분포를 결정하는 유한 단층 모델이 널리 사용되고 있다. Lee et al.(2015)은 전지구 지진해일 예측 시스템에 원거리 실체파 역산기법을 이용한 유한 단층 모델을 사용하였다. 원거리 실체파 역산기법은 각 소단층에서 지진 관측소까지 전파하는 실체파(P파, S파)의 이론 합성파형을 계산하여 관측된 파형과 비교함으로써 각 소단층에서의 변위량과 방향을 구하는 기법이다. 이 때 사용되는 실체파의 주에너지는 수 초 - 수십 초로 단층면 상의 세부적인 변위분포에 민감하다. 동일본대지진과 같이 단층의 크기가 수백 km에 이르는 대규모지진의 경우 상대적으로 작은 범위의 세부 변위 분포 뿐 아니라 넓은 범위의 단층변위량을 통해 지진으로 인한 지각변동이나 지진해일 초기 발생지역 등을 이해하는 것도 중요하다. 이를 위해서 주기가 수십 초 - 100초 이상에 이르는 표면파가 주로 사용된다. 본 연구에서는 실체파뿐만 아니라 표면파까지 사용하는 FFI(Finite Fault Inversion)로 명명된 기법을 이용하여 동일본 대지진의 유한 단층 모델을 추정 하였다(National Institute of Meteorological Research, 2013).
본 연구에서는 FFI 기법을 이용한 지진파 역산 수행 시간을 최소화하기 위하여 지진이 발생가능한 지역의 소단층에서 관측소까지 전파되는 이론파형을 미리 계산해두고 지진 발생시 이용하도록 설정하였다. 먼저, 태평양 연안의 11개 주요 섭입대 지역을 대상으로 미국지질조사소(USGS, U.S. Geological Survey)의 3차원 섭입대 수치 모델인 Slab 1.0(Hayes et al., 2012)을 기초로 하여 소단층 조합을 구성하였다. 이 때, 지진해일은 지진에 비해 장주기 성분을 가지므로 국지적 변위에 민감하지 않아 기존 대규모 지진 연구 결과를 참고하여 소단층의 크기를 50 km × 50 km로 설정하였다(Fu and Sun, 2006; Yue et al., 2014). 지진을 발생시킨 단층에 대한 주요 요소인 진원시간함수의 길이와 단층파열 속도는 소단층 크기를 고려하여 각각 20 s와 2.0 km/s로 설정하였다. 일반적으로 섭입대 지역에서 발생하는 대규모지진은 대부분 역단층 운동을 하므로, 각 소단층에서의 단층운동도 역단층 운동을 나타낼 수 있도록 45°와 135°의 기준 면선각(rake)을 설정하였다. 면선각 45°와 135°에 대한 그린함수를 이용하여 역산을 수행하면, 각각의 면선각에 대한 모멘트 비율을 구할 수 있고 이를 이용하여 단층운동 방향을 얻을 수 있다. 각 소단층의 단위 모멘트를 1020 dyne-cm로 설정하였으며, 이를 바탕으로 깊이와 지구조적 요소를 고려하는 3차원 속도모델(S362ANI 모델(Kustowski et al., 2008), CRUST2.0 모델(Bassin et al., 2000))이 적용된 합성파형모델(SPECFEM_3D_Globe(Tromp et al., 2008))로 전지구적으로 전파하는 3성분 전파형(full waveform)을 계산한 후 DB화하였다. DB화되어 있는 전파형의 선형 결합으로 이론 합성파형을 계산하며 (e.g. Hartzell and Heaton, 1983), 이론파형과 관측파형 모두 50 - 500 s의 대역 필터를 적용하여 장주기 특성을 잘 반영하도록 한다. 지진이 발생하면 관측파형과 합성파형에 대한 최소자승법으로 오차를 최소화하도록 역산을 수행하여 단층변위 분포를 얻을 수 있다.
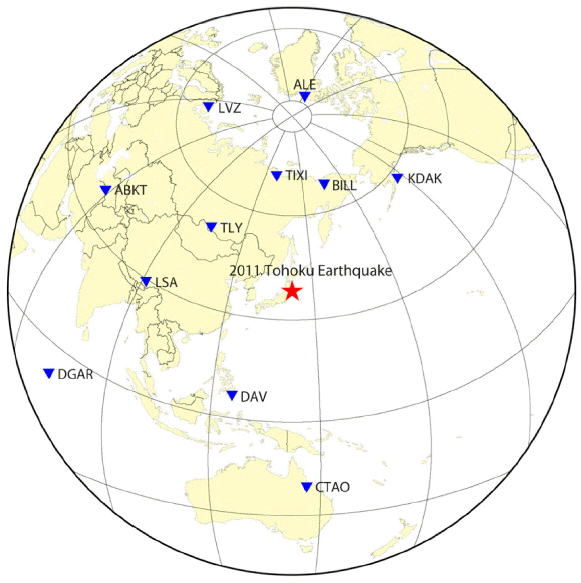
2011년 동일본 대지진의 단층변위 분포 역산에 사용한 11개의 지진 관측소는 Fig. 3과 같다. 방위각과 진앙거리를 골고루 분포시킬수록 다양한 지진파와 전파특성을 반영할 수 있어 분석 결과의 신뢰도를 높일 수 있다. 2011년 동일본 대지진의 경우 남동쪽에 태평양이 위치하고 있어 일부 방위각 범위를 포함하지 못하였으나 3성분 전파형이 기록된 지진 관측소 중 최선의 분포를 선택하였다. FFI 기법을 이용한 유한 단층 모델에 의한 2011년 동일본 대지진의 단층변위 분포는 Fig. 4와 같다. 진앙으로부터 북동쪽으로 약 130 km 떨어진 소단층에서 약 50 m의 최대 변위를 보인다.
3.2 지형 효과
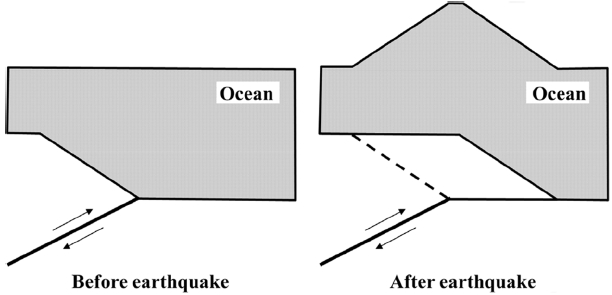
Fig. 5는 지형 효과의 개념도로 경사 지형에서 발생하는 해저면 수평 변위에 의한 상대적인 수직 변위가 해수면 변화를 발생시키는 것을 나타낸다. 단층 운동에 의한 수평 변위와 지형 경사를 이용하여 지형 효과에 의한 수직 변위 uh를 구할 수 있다.
여기서 H는 수심을 나타내며, ux, uy는 단층운동에 의한 수평방향 변위이다. 본 연구에서는 Tanioka and Satake(1996a)에서 제안한 중앙 차분법을 공간에 대한 편미분 항에 적용하였다. 그리고 차분 식 계산에 필요한 위경도 좌표거리는 아래의 대권 거리 공식(great circle distance formula)으로 구하였다.
여기서 D는 위경도 좌표거리(km), R은 지구반지름(6374 km), LAT1, LON1은 지점 1의 위도(rad), 경도(rad), LAT2, LON2는 지점 2의 위도(rad), 경도(rad)를 나타낸다. 단층 운동에 의한 해저면 수평 변위는 유한 단층 모델로 구한 단층변위 분포에 Okada(1992) 모델을 적용하여 구하였다.
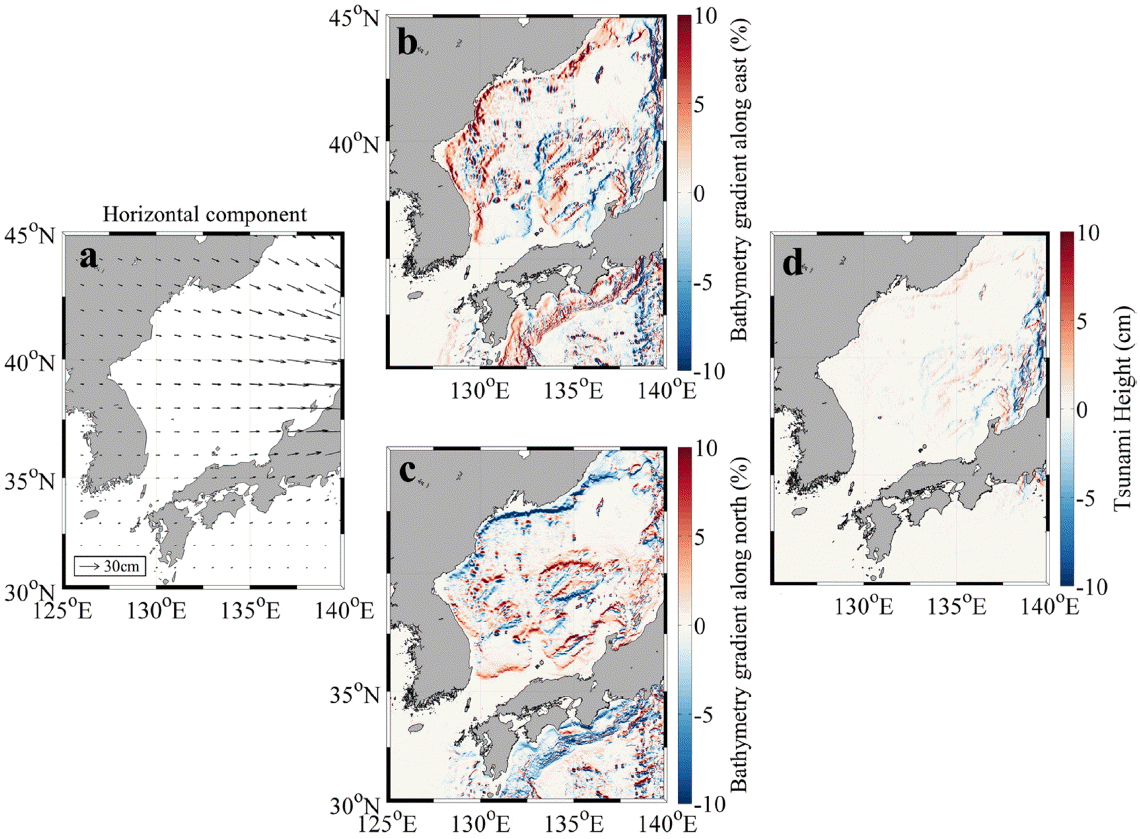
Fig. 6은 2011년 동일본 대지진에 대하여 지형 효과를 적용하는 과정을 나타낸다. Fig. 6(a)는 단층운동에 의한 수평방향 변위 벡터맵이며, Fig. 6(b)와 Fig. 6(c)는 각각 동쪽 방향, 북쪽 방향에 대한 지형 경사도이다. 단층운동에 의한 수평방향 변위는 진원을 향하며 변위량은 진원 주변으로 갈수록 커진다. 지형 경사는 동해안의 대륙사면과 동해의 대화퇴(Yamato rise) 주변에서 급격하게 변한다. Fig. 6(d)는 지형효과에 의한 수직 변위분포도로 지형효과에 의하여 동해에 수 cm의 해수면 변화가 발생한다.
3.3 지진해일 수치모의 결과
Fig. 7은 지형 효과를 고려하지 않은 경우(a)와 고려한 경우(b)에 대하여 2011년 동일본 대지진 발생 시점으로부터 0분, 30분, 60분 경과하였을 때의 지진해일 해일고분포도이다. 지형 효과를 고려하지 않은 지진해일 초기파형에는 단층변위 분포에 Okada(1992) 모델을 적용하여 구한 수직 변위를 사용하였다. 지형 효과를 고려한 지진해일 초기파형에는 지형 효과를 고려하지 않은 지진해일 초기파형과 지형효과에 의한 수직 변위인 Fig. 6(d)를 산술적으로 합한 수직변위를 사용하였다. 지형 효과 고려에 따른 지진해일 초기파형을 비교해보면 동해에서 양의 해수면 변화를 보이고 일본 주변에서 음의 해수면 변화를 보인다는 경향성이 유사하다. 그러나 지형 효과를 고려한 경우 동해에서 수심이 급격하게 변하는 부분을 중심으로 수 cm의 해수면 변위가 추가로 발생한다. 그리고 지형 효과를 고려하지 않은 경우 동해에 장주기의 파만 전파되는 양상을 보이나 지형 효과를 고려한 경우 단주기의 파가 장주기 파와 함께 전파하는 것을 확인할 수 있다.
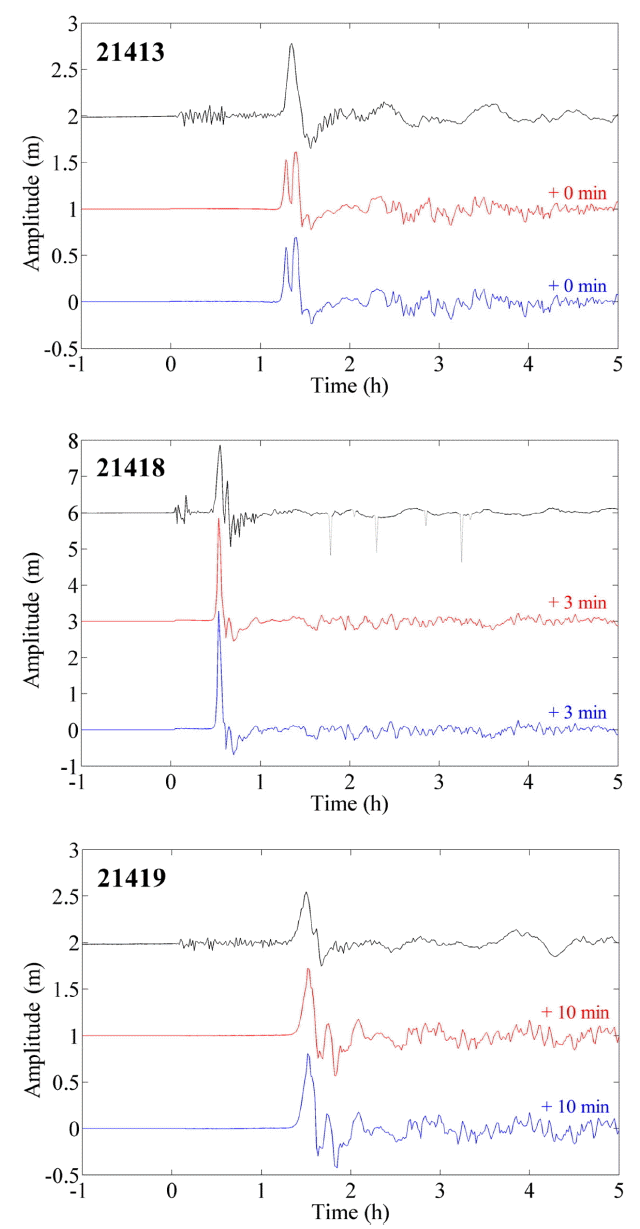
수치모의 결과를 검증하기 위하여 2011년 동일본 대지진의 진원 주변 DART(Deep-ocean Assessment and Reporting of Tsunamis) 부이 3개(21413, 21418, 21419)를 선정하였으며 그 위치는 Fig. 1과 Table 2와 같다. DART 부이 시스템은 주요 섭입대를 따라 설치되어 있는 해저 압력 계측기(BPR, Bottom Pressure Recorder)로 전 세계에서 발생하는 지진해일을 관측한다(Meinig et al., 2005). DART 부이 자료에는 조위관측소 자료와 마찬가지로 지진해일뿐만 아니라 조석 성분이 포함되어 있어 지진 발생 전후의 한 달 자료에 T_TIDE를 적용하여 조석 성분을 제거하였다. Fig. 8은 DART 부이 시계열과 수치모의 결과를 비교한 것이다. 여기서 왼쪽 상단은 DART 부이 번호, 검은색은 조석 성분이 제거된 DART 부이 시계열, 빨간색은 지형효과를 고려하지 않은 시계열, 파란색은 지형효과를 고려한 시계열이다. 그리고 우측 상단의 시간은 지진해일 도달시각을 맞추기 위해 수치모의 결과를 보정한 지연 시간이다. 지진해일 수치모의는 모든 DART 부이에서 지형 효과 고려에 따라 미세하게 증폭되었으나 큰 차이가 발생하지 않았다. DART 21413의 경우 지진해일 도달시각은 잘 모의하였으나 지진해일 첫 파 도달 직후 더 큰 해일고의 파가 도달하는 형상을 보인다. DART 21418과 DART 21419의 경우 관측값보다 큰 최대 해일고를 보이며 지진해일 도달시각을 짧게 예측하였다. 진원으로부터의 거리가 상대적으로 먼 DART 21419에서 지진해일 도달시각을 이르게 예측하였다.
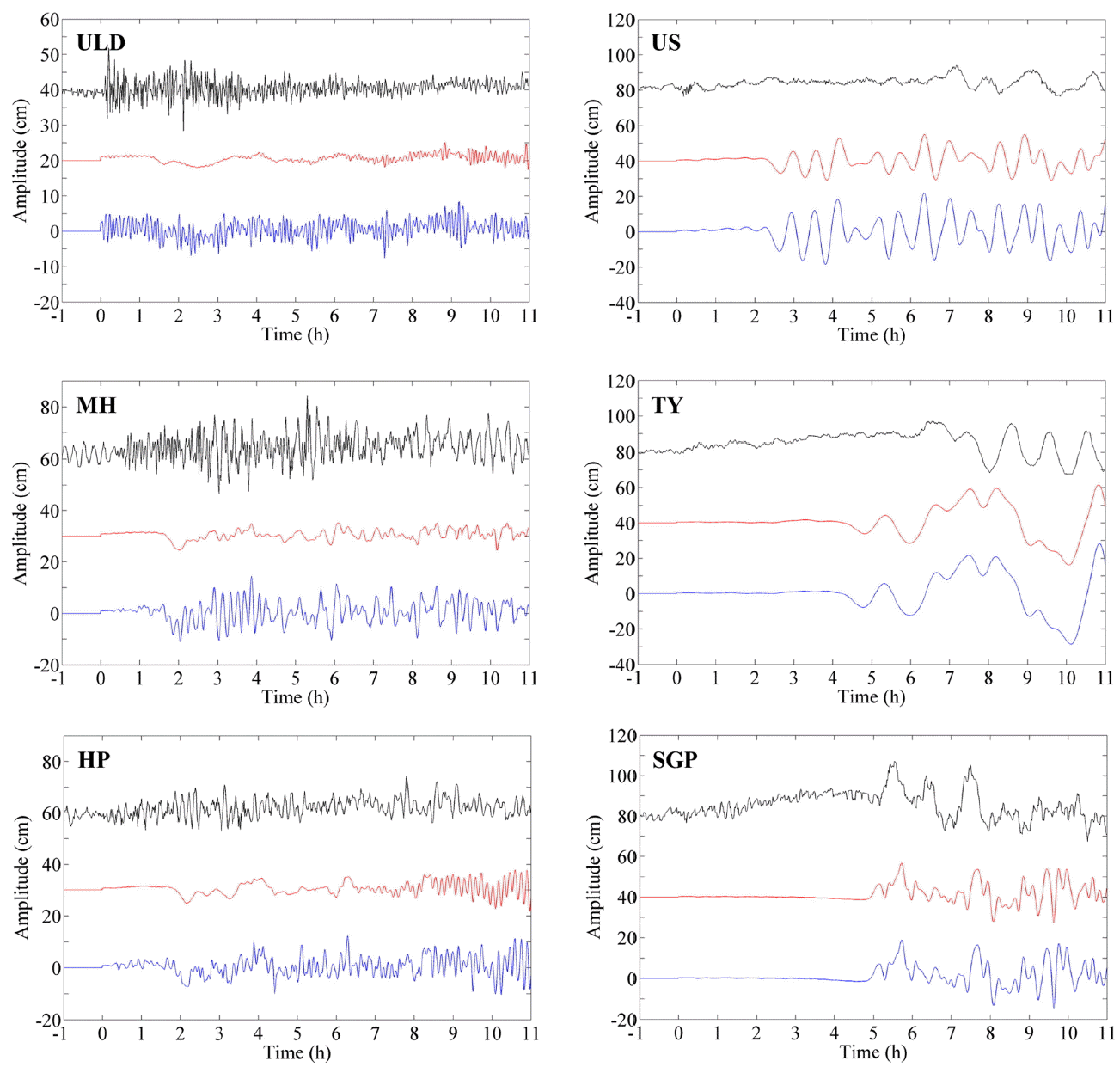
Fig. 9은 조위관측소 시계열과 수치모의 결과를 비교한 것이다. 여기서 왼쪽 상단은 조위관측소 이름, 검은색은 조석 성분이 제거된 조위관측소 시계열, 빨간색은 지형효과를 고려하지 않은 시계열, 파란색은 지형효과를 고려한 시계열이다. 지형효과를 고려함으로써 울릉도, 묵호, 후포 조위관측소에서는 지진 발생 직후 단주기 성분이 발생하였으나 울산, 통영, 서귀포에서는 발생하지 않았다. 이를 통하여 지진해일 수치모의에 지형 효과를 고려함으로써 우리나라에서 관측된 지진해일 선행파를 재현할 수 있음을 알 수 있다. 지형효과를 고려한 경우 울릉도, 묵호, 후포 조위관측소 순으로 길어지는 지진해일 선행파의 주기를 잘 예측하였으나 해일고는 작게 예측하였다. 지형 효과와 관계없이 서귀포 조위관측소에서는 지진해일 도달시각과 해일고를 잘 예측하였지만 울산과 통영 조위관측소에서 관측값보다 큰 해일고를 보이며 지진해일 도달시각을 빠르게 예측하였다.
3.4 지진해일 수치모의 분석
지진해일 수치모의 결과에서 보인 지진해일 해일고와 도달시각 차이는 3.1절에 언급한 바와 같이 FFI 기법을 이용한 유한 단층 모델에 일부 방위각 방향의 지진파 자료를 포함하지 못하였으며, 단층 요소(주향, 경사, 진원시간함수의 길이, 단층파열 속도 등)를 단층대의 대표 값으로 고정한 것으로부터 기인한 것으로 판단된다. 이러한 조건에서 FFI 기법을 사용한 2011년 동일본 대지진의 단층변위 분포는 기존 연구 결과(e.g. Ammon et al., 2011)보다 높은 위도에서 최대 변위를 보이며 37°N, 143°E 부근에서 기존 연구 결과에서 나타나지 않는 큰 변위를 보인다. 즉, 기존 연구 결과보다 DART 21418과 DART 21419에 더 가까운 지역에서 발생한 최대 변위로 인하여 관측값보다 큰 최대 해일고와 짧은 지진해일 도달시각을 보였다. 그리고 최대 변위와 기존 연구 결과에서 나타나지 않는 큰 변위로 인하여 DART 21413에 지진해일 첫 파 도달 직후 더 큰 해일고의 파가 발생하였다.
또한 FFI 기법을 이용한 유한 단층 모델은 일본 서쪽 연안 해역에 해저 방향의 매우 큰 해수면 변화가 있다고 분석하였다(Fig. 7). 이로 인하여 울산과 통영 조위관측소에 관측된 지진해일 도달시각보다 이른 시각에 해수면이 하강하는 첫파가 도달한다고 예측되었다(Fig. 9).
일부 연구자들은 이러한 문제를 개선하기 위하여 단층 요소에 대하여 지진별로 다양한 범위로 테스트를 수행하거나(e.g. Lay et al., 2010), DART 부이, 조위관측소, 위성 자료를 이용한 복합 역산(joint inversion)을 수행하고 있다(e.g. Fujii and Satake, 2007; Percival et al., 2011; Piatanesi et al., 2001). 그러나 분석자의 숙련도에 따라 단층 요소 분석 결과를 얻는데 상당한 시간이 소요될 수 있으며, DART 부이, 조위관측소, 위성 자료는 지진파 자료에 비해 관측 자료를 획득하는데 상당한 시간이 소요될 수 있으므로 신속성을 요구하는 시스템에 적용하기 위해서는 충분한 검토가 필요하다.
지진해일이 실제로 도달하는 시각보다 늦게 도달할 것으로 예측하면 예상하지 못한 시각에 지진해일이 내습하여 더 큰 피해가 발생할 수 있다(Lee et al., 2015). 본 연구에서는 DART 부이와 조위관측소에서 지진해일 도달시각을 유사하거나 더 이르게 예측하였으며, 이는 지진해일 대응 및 방재차원에서 미리 대비할 수 있는 시간을 확보한다는 의미가 있다. 특히 지형 효과를 고려하기 전에는 울릉도, 묵호, 후포 조위관측소에서 지진해일 도달시각을 관측 자료보다 상당 시간 늦게 예측하였으나, 지형 효과를 고려한 후에는 울릉도, 묵호, 후포 조위관측소의 지진해일 도달시각을 관측 자료와 유사하게 예측하여 지진해일 도달시각 예측 정확도를 높인 것을 확인 할 수 있다.
4. 지진해일 통보 시스템
기상청에서는 한반도 주변해역(21°N - 45°N, 110°E -145°E)에서 규모 7.0 이상의 해저지진이 발생하여 우리나라 해안가에 해일파고 0.5 m 이상 1.0 m 미만의 지진해일 내습이 예상될 때 지진해일 주의보, 1.0 m 이상의 지진해일 내습이 예상될 때 지진해일 경보를 발표한다(Park and Lee, 2014). 지진해일 통보 기준인 예상 해일파고는 한반도 주변해역에 대하여 지진해일 수치모의를 통해 구축한 시나리오 지진해일 DB 시스템으로부터 검색하여 사용한다. 시나리오 지진해일 DB 시스템에 사용한 지진해일 초기파형은 지형효과를 고려하지 않고 단층면에 대하여 균일한 변위량을 가정하여 계산되었다. 그리고 국립기상과학원(NIMS, National Institute of Meteorological Sciences)에서는 한반도 주변해역 이외의 지역에서 발생한 지진해일에 대응하기 위한 전지구 지진해일 예측 시스템을 개발하였다(Lee et al., 2015). 전지구 지진해일 예측 시스템에 사용하는 지진해일 초기파형 또한 시나리오 지진해일 DB 시스템과 마찬가지로 지형효과를 고려하지 않고 유한 단층 모델을 통해 분석한 단층변위 분포로 생성한다.
4.1 지형효과 고려의 영향력
2011년 동일본 대지진은 기상청의 지진해일 특보 발표기준인 한반도 주변해역을 벗어난 지역에서 발생하였으며, 해일파고 0.5 m 미만의 작은 지진해일만 관측되어 정량적인 지진해일 통보가 이루어지지 않았다(Yoon et al., 2012). 만약 2011년 동일본 대지진이 한반도 주변해역에서 발생하여 해일파고 0.5 m 이상의 지진해일 선행파가 관측되었다면 즉각 지진해일 통보가 필요한 상황이었다. 그러나 지형효과를 고려하지 않은 현재의 시나리오 지진해일 DB 시스템과 전지구 지진해일 예측 시스템으로는 지진해일 선행파를 예측하지 못하여 0.5 m 이상의 지진해일 선행파가 도달하여도 지진해일 통보가 발령되지 않아 혼란을 초래하였을 것이다. 또한 지형효과는 지진해일 최대 파고 및 최대 파고 도달시각에도 영향을 준다(Fig. 9). 즉, 지진해일 통보 기준 이하의 해일고가 예측되던 지역에서 지형효과를 고려한 후 지진해일 통보 기준 이상의 해일고가 예측되어 전혀 다른 통보문이 발령될 수 있다.
Bletery et al.(2015)은 Slab1.0(Hayes et al., 2012)을 이용하여 전세계 주요 단층대에서 지형효과의 영향력을 분석하였는데 초기파형의 최대해일고가 10% 이상 차이나는 지역이 전체 단층대 중 25%에 달하는 것으로 확인되었다. 향후 우리나라 주변해역에 대하여 구축되어 있는 시나리오 지진해일 DB에도 Bletery et al.(2015)와 유사한 방법으로 지형효과의 영향력을 분석하여, 시나리오 지진해일 DB 시스템을 개선할 필요가 있는지에 대한 검토가 필요하다. 또한 Bletery et al.(2015)에서 제시한 지형효과의 영향력이 큰 단층대에서 대규모 지진 발생 시, 지형효과를 고려한 지진해일 초기파형으로 전지구 지진해일 예측 시스템을 운영하는 것을 검토하여야 한다.
4.2 지형효과 적용의 문제점
지형효과를 고려하기 위하여 수심자료와 단층 운동에 의한 수평방향 변위 자료를 읽고 식 (1)을 적용하는데 추가적인 시간이 소요된다. 수치모의에 사용하는 격자 간격 및 격자망 크기에 따라 다르지만 본 연구의 조건에서는 지형 효과를 고려한 지진해일 초기파형을 생성하는데 PC(CPU: Intel i7 870(2.93 GHz), RAM: 8 GB)에서 1개의 노드를 사용하여 대략 1시간 30분의 시간이 추가로 소요되었다. 한반도 주변 해역에 대해서는 시나리오 지진해일 DB를 구축하므로 이러한 추가적인 연산 시간은 DB 구축 후에는 문제가 되지 않는다. 그러나 한반도 주변해역 이외의 지역에서 발생하는 지진해일의 경우 즉각적인 수치모의가 이루어져야하는데 지형효과 고려에 따른 연산 시간 증대는 신속성이 중요한 지진해일 통보에 커다란 걸림돌이 될 수 있다.
지진해일 수치모의에 있어 수심이 일정하지 않고 단층 운동에 의한 수평 변위가 존재하는 이상 지형효과에 의하여 해수면 변위가 발생한다. 이로 인하여 수심이 복잡하게 변화하는 지역에서는 계산 격자 간격으로 충분히 모사하지 못하는 단주기의 해수면 변위가 생성될 수 있다. 특히 수심에 비해 파장이 짧아 천수 가정이 성립하지 않는 지역에서의 단주기 해수면 변위는 수학적으로 계산될 수는 있으나 물리적으로 타당하지 않을 수 있다. 그러므로 지형효과를 고려한 지진해일 수치모의 결과에서 단주기 해수면 변위에 의해 0.5 m 이상의 지진해일 선행파가 있다면 물리적으로 타당한지 충분한 검토가 필요하다. 만약 충분한 검토 없이 수치모의 결과에 의존하여 지진해일 주의보/경보를 발표한다면 실제 지진해일은 도달하지 않은 시점에 지진해일이 도달할 것으로 오경보를 내보낼 가능성이 있다. 이러한 문제의 원인이 될 수 있는 주기가 매우 짧은 해수면 변위들을 제거하기 위해 Bletery et al.(2015)은 지형효과를 고려한 지진해일 초기파형에 단주기 성분 진동의 감쇠(attenuation of perturbation)를 고려한 공간 필터를 적용하였다. Murotani et al.(2015)은 주기가 매우 짧은 해수면 변위까지 그대로 사용하는 대신 매우 조밀한 격자망(5 s 간격)을 사용하였다. 그러나 공간 필터는 적용 방법에 따라 지진해일 선행파와 같이 의미 있는 단주기 성분을 제거 할 수 있으며, 조밀한 격자는 충분한 수심 자료 없이는 구축하기가 어려울 뿐만 아니라 연산 시간을 증대시킨다는 문제가 있다. 그러므로 공간 필터와 격자 간격에 대한 민감도 분석을 수행하여 재현하고자 하는 적정 수준에 맞는 공간 필터와 격자 간격을 찾는 연구가 필요하다.
5. 결 론
지진해일 수치모의는 목적과 대상에 따라 다양한 가정을 사용한 수치모델을 이용한다. 대부분의 수치모델은 한정된 연산 자원으로 목표 시간 안에 지진해일 정보를 산출하기 위하여 단층 변위량에 의한 해저면 수평변위가 수직변위에 비해 매우 작아 지진해일 초기 해수면 변위에 영향이 없다고 가정한다.
2011년 동일본 지진해일 발생 당시 우리나라 울릉도, 묵호, 후포 조위관측소에서 기존의 수치모델로는 설명할 수 없는 매우 이른 시간에 지진해일 선행파가 관측되었다. 2011년 동일본 대지진은 완만한 경사의 단층에서 발생하여 경사 지형에서 발생하는 해저면 수평 변위가 다른 지진에 비해 상대적으로 크다. 본 연구에서는 한반도에서 관측된 2011년 동일본 지진해일 선행파의 원인을 분석하기 위하여 지형효과를 고려한 지진해일 수치모의를 수행하였다. 관측 자료와 지진해일 수치모의 결과의 비교를 통해 지형 효과를 고려함으로써 지진해일 선행파를 재현할 수 있음을 확인하였다. 지형 효과를 통해 지진해일 도달시각 및 파고 정보의 정확도를 높일 수 있으나 추가적인 연산 시간이 요구되므로 신속성과 정확성을 동시에 요구하는 지진해일 통보 시스템에 적용하기 위해서는 충분한 검토가 필요하다.