1. 서론
물류비용을 절감시키기 위하여 항구에 입항하는 선박의 크기가 대형화함에 따라 이들 선박이 접안하는 항구의 수심 또한 깊어져 접안구조물의 높이가 과거에 비해 매우 높아지는 추세이다. 따라서 접안구조물 배면에 작용하는 매우 큰 토압에 대한 안정성을 확보하기 위해서, 대형 중력식 안벽인 케이슨구조물이 접안구조물로서 각광받고 있다. 최근에는 경제성을 고려하여 케이슨구조물에 뒷굽을 설치함으로써 뒷굽 상부에 놓인 뒷채움 토사의 자중을 이용하여 케이슨구조물의 안정성을 제고하는 시공법을 사용하고 있다. 이 경우 케이슨의 안정성을 조사하는데 결정적인 요소는 토압산정이다. 케이슨 안벽에 작용하는 토압을 계산할 때, 과거에는 관행적으로 뒷굽이 없는 경우에는 벽면마찰각을 고려하여 Coulomb 토압이론을, 그리고 뒷굽이 있는 경우에는 뒷굽 끝의 연직면에 대하여 Rankine 토압이론을 적용하여왔다. 이와 같은 토압계산방법의 적용은 옹벽높이에 비해 뒷굽의 길이가 상대적으로 긴역T형옹벽에서는 문제가 되지 않으나, 케이슨안벽과 같이 뒷굽의 길이가 안벽의 높이에 비해 상대적으로 짧은 경우에 Rankine 토압이론을 적용하는 것은 과다한 토압의 결과를 초래하여 비경제적인 설계방법이 된다. 이러한 문제점을 개선하기 위하여 최근 해양수산부(2014)에서는 뒷굽이 있는 케이슨 안벽에 대한 토압을 산정할 경우에 한계평형법인 Coulomb 토압이론을 적용하도록 하였다. 이 방법에서의 핵심은 뒷굽 상부에서 발생하는 내측 활동면에 작용하는 토압의 산정이다. 이때 내측 활동면의 경사각(θ')을 45º+ ϕ/2로 가정하였으나 이는 벽면마찰력의 영향을 고려하지 않은 가정이다. 본 연구에서는 벽면마찰력을 고려한 한계해석법을 사용하여 지표면이 수평인 케이슨 안벽의 뒷굽 상부에서 발생하는 내측 활동면의 경사각을 구하여 기존 설계방법에 의한 토압과 비교하였다.
2. 옹벽에 작용하는 토압
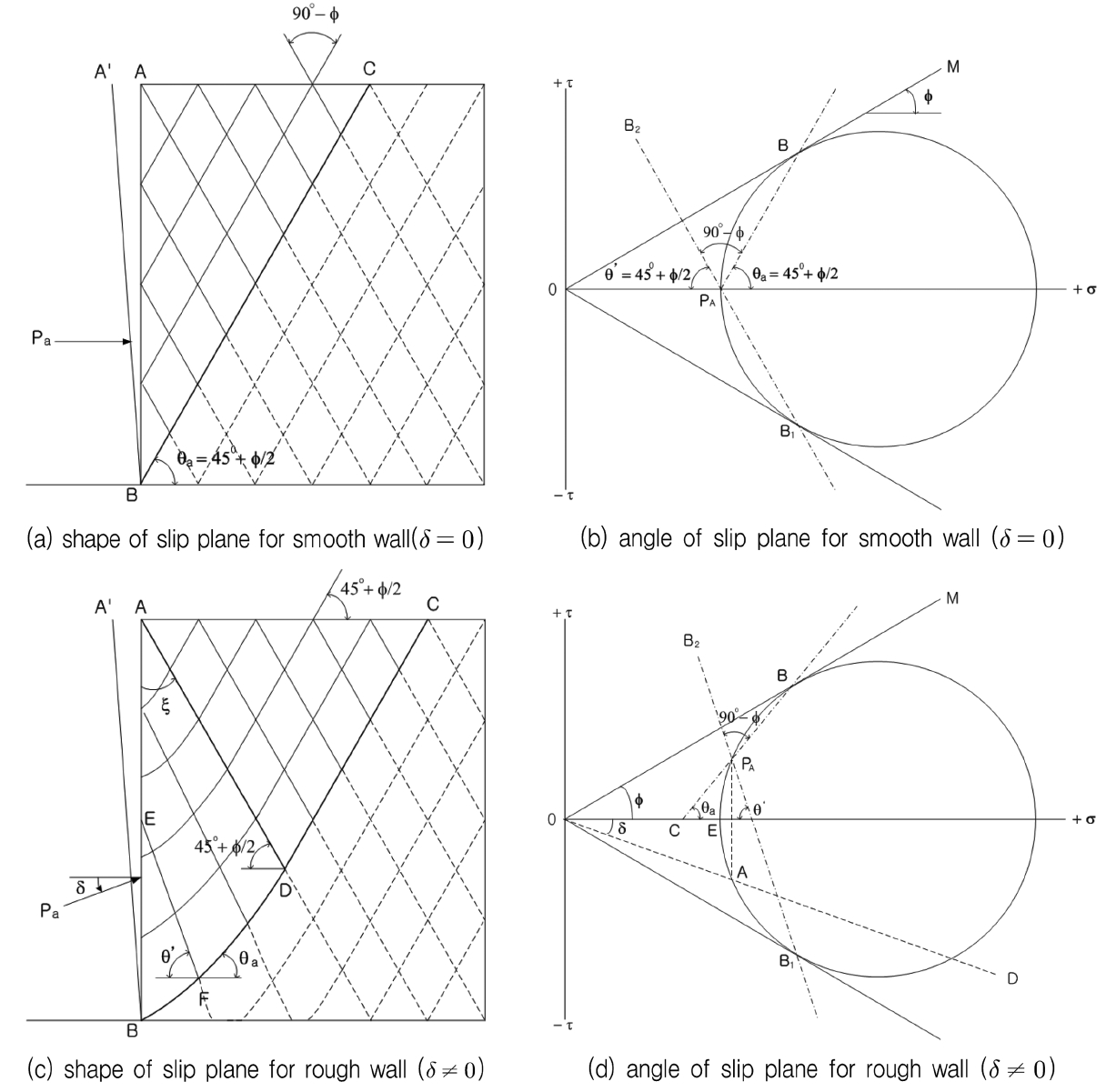
강성옹벽이 뒷채움토사에 의해 기울거나 평행이동하게 됨에 따라, 옹벽에 의해 지지된 토체내에서는 활동면이 발생하게 된다. 이때 활동면의 형상은 벽면마찰각 뿐만 아니라 옹벽의 변형방식에 따라 변한다. 벽체 뒤의 토사내에 생기는 활동면은 벽체가 매끈할 경우(δ = 0), Fig. 1(a), (b)에 나타낸 바와 같이 내외측의 활동면은 평면이며 수평과 이루는 경사각은 식(1)과 같다.
벽체가 거칠다면(δ ≠ 0) 뒷채움 지표면이 주응력면이므로 벽체 상단에서의 활동면은 뒷채움 수평면과 45 + ϕ/2 경사각을 이루는 평면이 된다. 그러나 벽체 하단 근처에서는 벽체와 뒷채움토사 사이에서 발생하는 마찰력으로 인하여 활동면의 경사각(θa)이 감소하면서 곡면이 된다(Fig. 1(c)). 이러한 곡면형상의 활동면을 포함한 주동토압을 매우 정밀하게 구하는 방법을 Kármán(1926), Jáky(1938), Ohde(1938) 등이 제안하였으나, 너무 복잡하여 실무에서는 사용되지 않는다.
Terzaghi(1943)는 Fig. 1(c)의 ABD 영역 내에서 발생하는 활동면의 형상을 r = rof(ξ) 식으로 나타낼 수 있다고 하였다. 여기서 r은 점A로부터 활동면까지의 거리(AD), ξ는 사이각, ro는 ξ =0에서의 r값(AB)이다. Fig. 1(d)의 Mohr원은 벽체 바로 옆에 있는 임의 흙요소에 대한 응력상태를 나타낸다. 벽체 AB에 작용하는 토압이 벽체 AB에 수직면으로부터 반시계방향으로 δ 만큼 회전하기 때문에 이에 상응하는 전단응력은 Mohr원 상에 (−)값으로 표현된다. 이 벽체 AB에 작용하는 응력상태는 Fig. 1(d)의 OD선상에 있으며, 소성평형상태에서는 Mohr원상의 점A로 나타낼 수 있다. 점A를 통과하며 벽체AB에 평행한 직선을 그었을 때 Mohr원과 만나는 점을 PA라고 하면 이 점이 극점(Pole)이 된다. 따라서 극점 PA를 Mohr원과 파괴포락선이 접하는 두 점, 점B와 점B1을 각각 연결하면 PAB와 PAB1이 활동면이 되므로 활동면의 경사각, θ를 구할 수 있다. Fig. 1(d)에서 보는바와 같이 벽면마찰각 δ가 증가할수록 점PA는 점B로 수렴하므로 활동면은 Fig. 1(c)의 BD 구간에서 완만한 곡선을 이룬다. 반면에 벽면마찰각 δ가 감소할수록 점A는 점E로 수렴하여, δ가 영이 되면 활동면 경사각 θa는 45º+ ϕ/2가 되므로 곡선부분은 완전히 직선이 된다. Coulomb(1776)은 흙쐐기의 활동면 형상을 평면으로 가정함으로써 실무에서 사용하기에 충분히 정밀한 토압을 구하는 방법을 제안하였다. Terzaghi(1943)는 내부마찰각 = 벽면마찰각 = 30o인 사질토로 수평하게 뒷채움한 경우, 정밀한 주동토압과 Coulobm 주동토압의 차이는 5% 이내로 이러한 에러는 실무에서 무시할만하다고 하였다. 옹벽은 안식각보다 경사진 사면의 토사를 지지하는 데 사용하는 토류구조물이다. 실무에서는 옹벽에 작용하는 토압을 산정할 경우, 관행적으로 중력식 옹벽에는 Coulomb 토압이론을, 그리고 캔틸레버식 옹벽에는 Rankine 토압이론을 적용하고 있다.
2.1 뒷굽이 긴 캔틸레버식
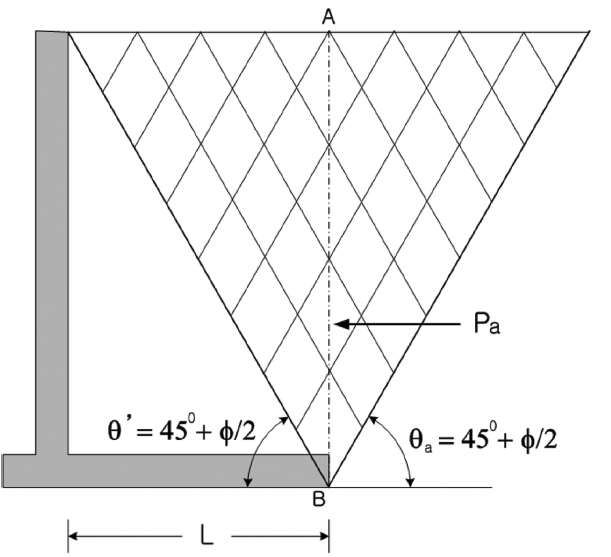
옹벽 뒷채움 사질토의 표면이 수평이고, 옹벽의 벽체가 연직이며 완벽히 매끄럽다면, 벽체에 작용하는 토압은 Rankine 토압과 같다. 그러나 실제 완벽하게 매끄러운 벽체는 존재하지 않는다. 벽면마찰력은 보통 주동토압을 감소시키는 반면 수동토압을 증가시킨다. 따라서 벽면마찰력을 무시하는 가정으로 산정되는 주동토압은 일반적으로 안전측이다. 이러한 가정은 뒷굽의 길이가 옹벽의 높이에 비해 상대적으로 충분히 길다면(L ≥ H/tan(45º+ ϕ/2)) 이론적으로 맞다. 예를 들면, 토압의 영향으로 벽체에 변위가 발생한다면, Fig. 2와 같이 뒷채움 사질토는 옹벽의 뒤굽 끝에서 시작되는 두 세트의 활동면(식(1)과 같이 수평면과 45º+ ϕ/2 경사각을 이룸)을 따라 전단에 의해 파괴가 발생한다. 이 두 평면 사이의 흙쐐기 내에 있는 사질토는 Rankine의 주동상태에 있으므로, 뒷굽 끝의 연직평면 AB를 따라 전단응력이 발생하지 않는다. 따라서 이 연직평면은 주응력면이므로 이 평면에 작용하는 토압은 Rankine 토압과 동일하며(Terzaghi, 1943), 토압의 합력, Pa는 식(2)로 구한다.
여기서, γ: 뒷채움 토사의 단위중량, H: 옹벽의 높이, KaR:Rankine의 주동토압계수
2.2 뒷굽이 짧은 캔틸레버식 옹벽
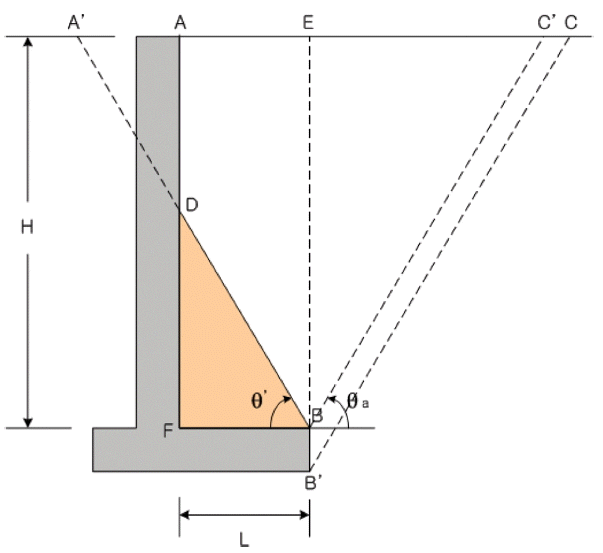
뒷굽의 길이가 옹벽 높이에 비해 상대적으로 짧은 경우(Fig. 3에서 L ≤ H/tan(45º+ ϕ/2)), 토압의 영향으로 벽체에 변위가 발생하여 뒷채움 사질토가 파괴되기 시작한다면, Fig. 3에서 뒷채움 사질토의 일부인 ΔBDF로 표시된 뒷채움 사질토는 실제로 옹벽에 붙어서 마치 옹벽의 일부로서 옹벽과 같이 거동한다. 그 밖의 뒷채움 사질토는 활동면 B'C를 따라서 파괴된다.
이때 활동하는 쐐기내에 모든 흙은 소성평형상태에 이른다. 따라서 활동 쐐기의 왼쪽 경계면 ADBB' 위의 모든 점들은 잠재적 활동면을 나타낸다. 직선 BC'는 B점을 통과하는 활동면을 표시한다. 활동면 BD를 벽체 선단레벨의 A'점까지 연장한다면, 흙쐐기 A'BC'에 대한 응력조건과 변형조건이 Fig. 2의 흙쐐기와 동일하게 되므로, 활동면 BC'와 활동면 BD는 수평면으로부터 각각 식(1)과 같이 θa= θ' = 45º+ ϕ/2 경사각을 이룬다. 그러나 활동면 BA'가 벽체에 의해 차단되면서 벽체 AD를 따라 활동면이 생성되고 이들 경계면에 마찰력이 발생한다. 이 마찰력이 연직평면 BE에 영향을 미침에 따라 연직평면 BE는 더 이상 주응력면이 아니므로, 옹벽에 작용하는 토압은 활동면을 따라 발생하는 마찰력을 고려하여 Rankine 토압이론이 아닌 Coulomb 토압이론을 사용하여 구한다. 뒷굽이 짧은 경우, Teng(1962)은 옹벽 뒷굽 상부에서 발생하는 활동면을 옹벽의 상단과 뒷굽의 끝을 잇는 평면으로 가정하고, 활동면과 뒷굽 사이의 토사를 옹벽의 일부로 포함시켜 중력식 옹벽에 작용하는 토압을 Coulomb 토압이론으로 계산하는 방법을 제안하였다. Barghouthi(1990)는 한계평형법을 사용하여 Fig. 3에서 내측 활동면에 의해 차단된 상부벽체 AD에서 발생하는 마찰력을 고려한 힘의 다각형으로부터 토압을 산정하였다. 김병일 외(2014)는 뒷굽길이와 뒤채움재의 내부마찰각에 따라 개량쐐기법으로 구한 가상의 연직배면에 작용하는 토압 작용각과 내측 활동면의 경사각 등을 기존 토압이론과 비교하였다.
2.3 뒷굽이 짧은 케이슨 안벽
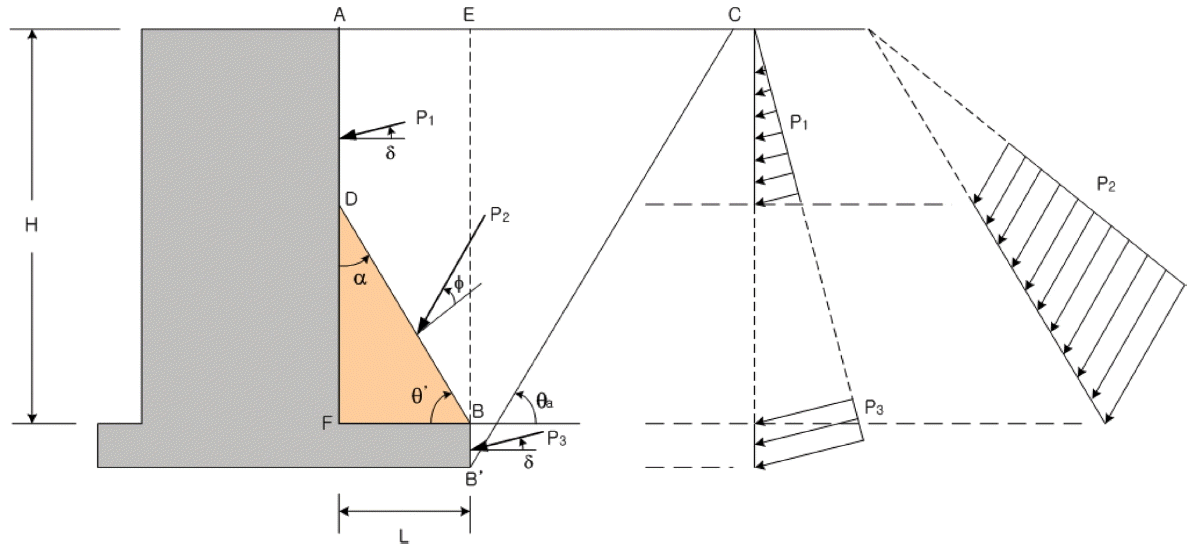
2.2절에서 언급한 Coulomb 토압이론을 사용하며 토압을 산정할 때, Fig. 4에 나타낸 바와 같이 케이슨 안벽을 뒷굽 상부에 놓인 뒤채움토사 ΔBDF를 포함하는 중력식 구조물로 가정한다. 따라서 잠재적 활동면 ADBB'에서 활동면과 접촉하는 물질에 따라 활동면 A D ¯ , D B , B B '
여기서, ϕ: 뒤채움 토사의 내부마찰각, α: 연직면에 대한 안벽 벽체경사각(α = 0) 또는 뒤채움 토사내부 활동면의 경사각(α = 90− θ'), δ: 벽면마찰각(δ) 또는 토사내부 활동면 마찰각(ϕ), β: 뒤채움 지표면 경사각(케이슨 안벽의 경우, β = 0), KaC : Coulomb의 주동토압계수
3. 한계해석법에 의한 내측 활동면 경사각
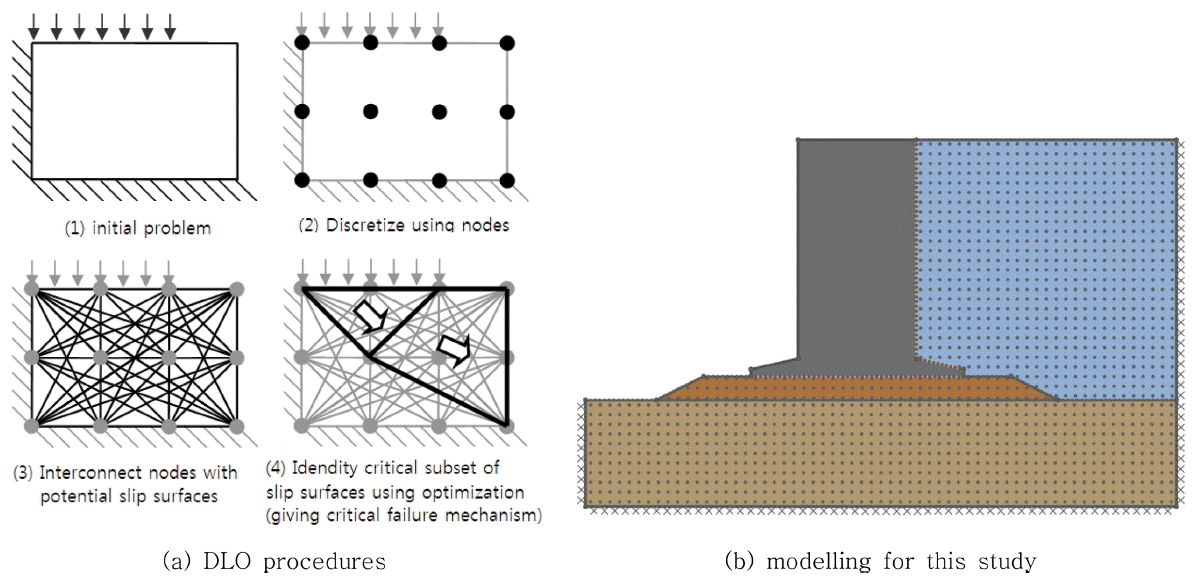
한계평형법(limit equilibrium method, L.E.M.)은 파괴모드를 단순화하여 정역학적으로 문제를 해결하는 방법인 반면에, 한계해석법(limit analysis method, L.A.M.)에서는 한계평형법에서 고려하지 않은 적합조건을 고려한다(Chen, 1975). 종래의 한계해석법에서는 단순한 형태의 문제에 대하여 매우 제한된 갯수의 활동면(slip surfaces)들을 가정함으로써 해석결과를 도출한다. 반면에, 최근에 개발된 DLO(Discontinity Layout Optimization)기법(Smith et al., 2007)을 이용하면 매우 많은(컴퓨터성능에 따라 거의 무한대에 가까운) 활동면들을 생성함으로써 복잡한 형상의 문제들에 대해서도 한계해석법을 적용할 수 있게 되었을 뿐만 아니라 해석결과의 정밀도를 획기적으로 제고할 수 있다. 본 연구에서는 Fig. 5(a)와 같이 임의 활동면들의 방향성을 효율적으로 선택하여 파괴시 최소한의 에너지로 파괴에 이르도록 파괴토체를 여러 개로 나누어 극한하중을 결정하는 DLO기법을 사용하는 한계해석법을 사용하였다. 뒷굽을 갖는 케이슨안벽을 Fig. 5(b)와 같이 모델링하여 뒷굽 상부에서 발생하는 뒤채움토사 내부의 활동면 경사각(θ')을 구하였으며, 구성 모델의 물성값을 Table 1에 요약하였다. 케이슨의 규모는 폭, B = 10 m, 높이, H = 20 m, 케이슨의 단위중량은 콘크리트와 케이슨 내부의 사석 채움을 고려하여 22 kN/m3로 하였으며, 사석마운드와 케이슨 저면 사이의 마찰계수는 0.4로 가정하였다.
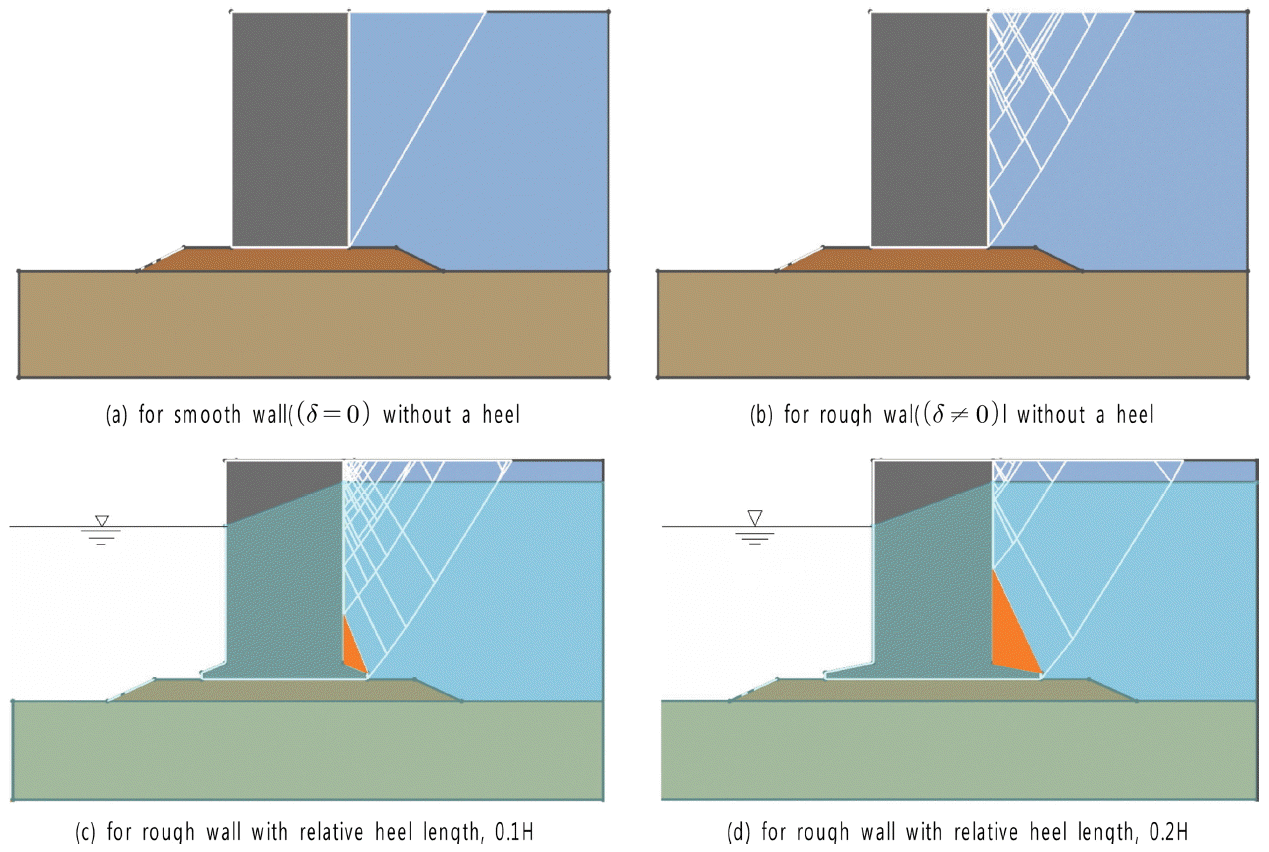
Fig. 6에 뒤채움토사의 내부마찰각 ϕ'=30º, 벽면마찰각 δ=15º인 경우의 활동면에 대한 해석결과예를 그림으로 나타내었다. (a), (b)는 뒷굽이 없는 경우이며, 벽면마찰각이 영인 경우(a)에 비해 마찰력이 존재할 경우(b) 벽면마찰력으로 인하여 케이슨 하부 근처의 활동면의 경사각이 완만하게 나타나는 것을 볼 수 있다. 그리고 뒷굽이 있는 경우, 뒷굽의 길이(L)를 케이슨의 높이(H)에 대한 상대적 길이로 나타내어 해석한 결과를 (c), (d)에 각각 나타내었다. 그림에서 보듯이 뒷굽이 있는 경우, 뒷굽이 짧을수록 벽면마찰력의 영향으로 뒷굽 상부에서 발생하는 내측 활동면의 경사각(θ')은 증가하는 반면에 외측 활동면의 경사각(θa)은 벽면마찰력의 영향을 받지 않아 일정함을 알 수 있다. 또한 케이슨 안벽 앞뒤의 수위차이(4 m 가정)에 따른 잔류수압이 내측파괴면의 각도에 주는 영향을 조사하였다. 해석결과 잔류수위가 내측파괴면의 각도에 영향을 주지 않음을 확인하였으며, 이는 잔류수압이 토압의 합력에는 영향을 미치나, 뒤채움토사에 의한 순토압은 토사의 내부마찰각의 함수이므로 간극수압 자체가 뒤채움토사의 활동면에 영향을 주지 않기 때문이다.
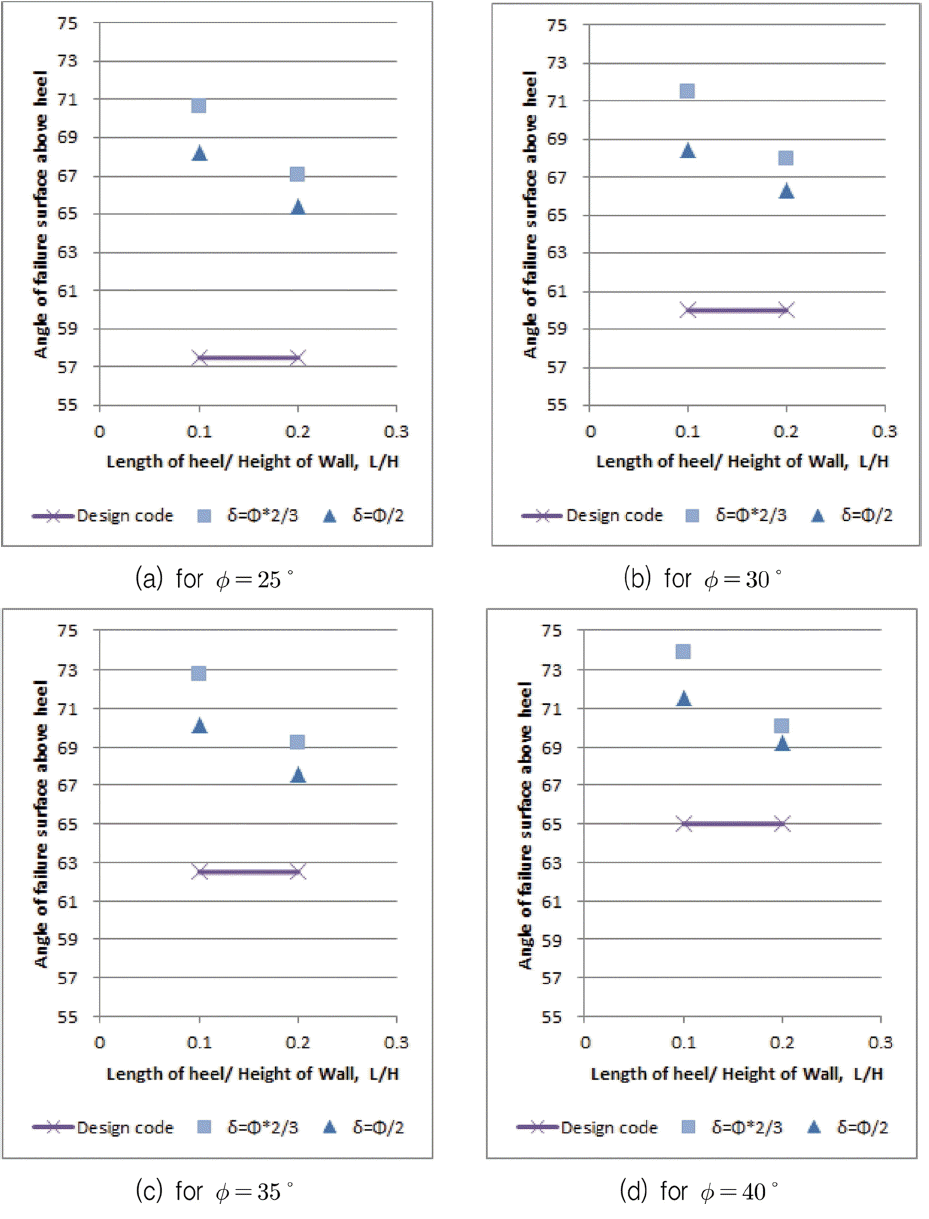
해석결과를 정리하여 뒷굽 상부에서 발생하는 내측 활동면의 경사각(θ')이 케이슨의 뒤채움 토사의 내부마찰각(ϕ)과 벽면마찰각(δ), 뒷굽의 상대길이(L/H) 등에 따라 어떻게 변하는 지를 Table 2와 Fig. 7에 각각 나타내었다.
Fig. 7에 따르면, 뒷굽 상부에서 발생하는 내측 활동면의 경사각(θ')은 뒵굽길이가 상대적으로 짧을수록 그리고 벽면마찰각이 클수록 증가하며, 활동면의 경사각을 구할 때 뒷굽의 상대적인 길이를 고려하지 않는 기존 설계기준(Fig. 7에서 Design code의 경우)에 비해서 훨씬 큼을 알 수 있다. 이러한 현상은 뒷굽길이가 상대적으로 짧을수록, 내측 활동면에 의해 차단되는 벽체 상부(Fig. 4에서 벽체 A D ¯
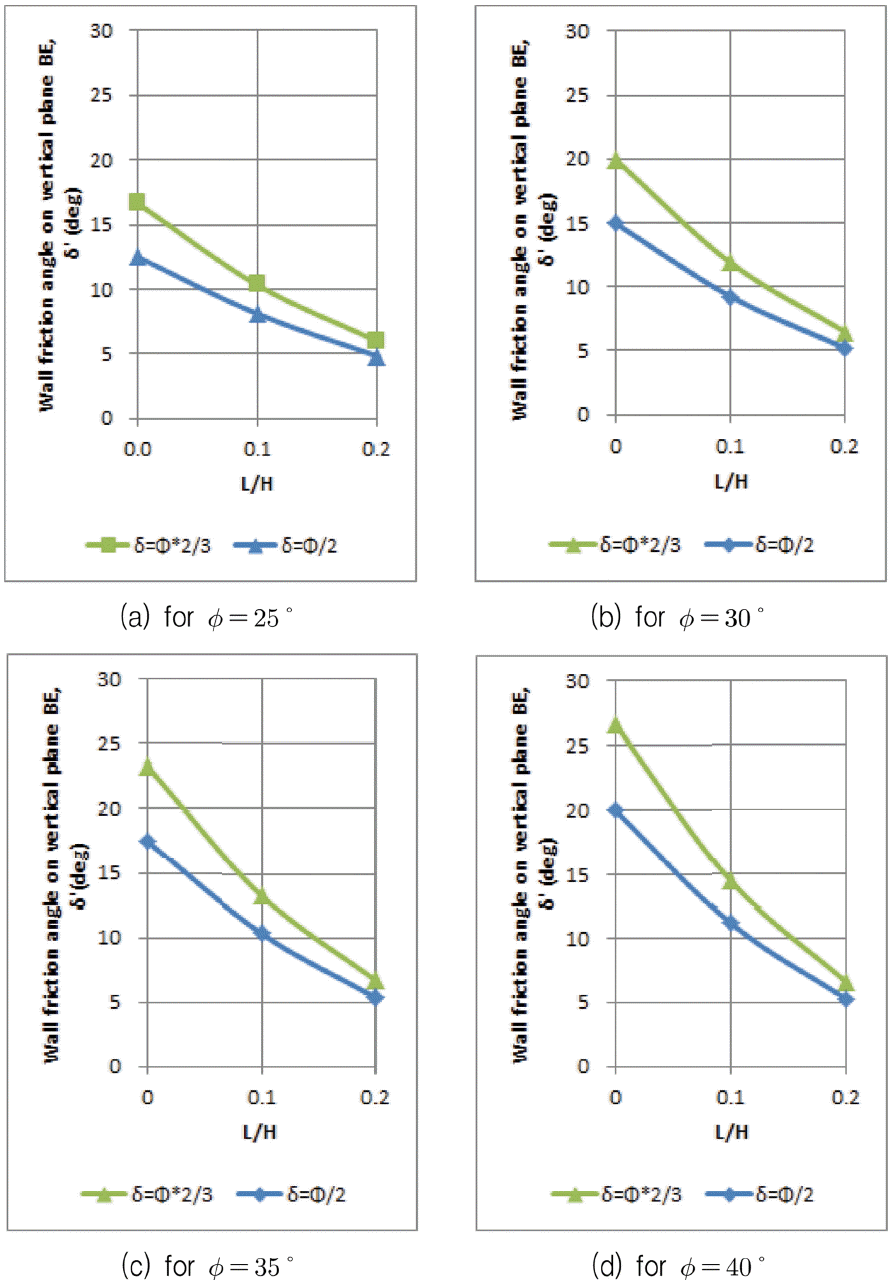
여기서, Pv와 Ph는 가상의 연직배면에 작용하는 토압의 연직분력과 수평분력이며, 연직분력에는 내측 활동면 상부의 토사무게가 포함되지 않는다. 이때 가상의 연직배면 BE에 작용하는 벽면마찰각(δ')을 뒷굽의 상대길이(L/H)에 따라 나타내면 Fig. 8과 같다. 가상의 배면마찰각(δ')은 뒷굽의 길이가 길어짐에 따라 감소하다가 충분히 길이지면 영이 된다. 즉, 더이상 연직배면 BE에 전단력이 존재하지 않는 Rankine 상태가 된다. 즉, 뒷굽이 짧을수록 뒷굽 상부에서 발생하는 내측활동면이 벽체와 만남에 따라 활동면 상부의 흙쐐기는 상부벽체(Fig. 3에서 AD)의 벽면마찰력의 영향을 받게 되어 토압이 Rankine 토압보다는 작아지나 그래도 뒷굽의 길이를 고려하지 않은 Coulomb 토압보다는 항상 큼을 알 수 있다. 따라서 뒷굽이 있는 케이슨안벽에 작용하는 토압을 Coulomb 토압으로 구할 경우, 뒷굽을 무시한다면 불안전측 설계가 된다.
상대길이 0.1H와 0.2H의 뒷굽이 있는 케이슨 안벽의 뒷굽 끝단에서의 연직배면(Fig. 4에서 BE)에 작용하는 토압을 현 설계기준에 의한 토압과 비교하여 Table 7과 8에 각각 나타내었다. 이때 지하수위는 지표면과 일치한다고 가정하였다. 뒷굽이 있는 경우 내측 활동면의 경사(θ')가 항만 및 어항설계기준에서 적용하는 값보다 증가함에 따라, 벽체(Fig. 4에서 A D ¯ D B ¯
4. 결론
본 연구에서는 케이슨 안벽의 뒷굽의 길이가 주동토압에 미치는 영향을 조사하여 다음과 같은 결론을 얻었다.
(1) 케이슨 안벽의 뒷굽 길이가 상대적으로 짧을수록, 내측 파괴면의 경사각(θ')이 설계기준보다 훨씬 크게 나타났으며, 뒤채움토사의 내부마찰각이 클수록 그 차이는 증가하였다. 한편 외측 파괴면의 경사각(θa)은 일정하였다.
(2) 실제 케이슨 안벽에서 발생하는 파괴면을 따라 작용하는 토압과 동일한 토압을 갖는 뒷굽 끝 가상의 연직배면에 작용하는 토압에 대하여 뒷굽의 상대 길이-뒤채움 토사의 내부마찰각-벽면마찰각-가상의 연직배면에 작용하는 배면마찰각 등의 상관관계를 구하였다.
(3) 뒷굽이 짧을수록 케이슨 안벽에 작용하는 토압이 Rankine 토압보다는 작으나 뒷굽의 길이를 고려하지 않는 Coulomb 토압보다는 항상 크게 나타났다.
(4) 따라서 뒷굽이 있는 케이슨 안벽에 작용하는 토압을 Coulomb 토압으로 구할 경우, 뒷굽을 무시한다면 불안전측설계가 된다.
(5) 내측 활동면의 경사각(θ')의 증가로 인하여 가상의 연직배면에 작용하는 수평토압(Ph)은 증가하는 반면 연직토압(Pv)은 감소함에 따라 토압의 합력크기는 설계기준보다 약간 증가하나 차이는 크지 않은 것으로 나타났다. 한편 내측 활동면의 경사(θ')가 증가함에 따라 케이슨 안벽과 일체로 거동하게 되는 내측 활동면 하부(Fig. 4에서 ΔBDF)의 토사중량은 증가하게 된다. 비록 연구결과와 현 설계기준 사이의 토압 합력의 차이는 크지 않으나, 수평토압의 증가와 연직토압의 감소는 케이슨 안벽의 안정성에 부정적으로, 그리고 활동면 하부 토사중량의 증가는 긍정적으로 작용할 것이다.