진도 울돌목의 조류 연직 프로파일 매개변수 분포 특성
요약
일반적으로 멱법칙과 대수함수 프로파일은 유속 연직 프로파일 모델로 많이 사용된다. 그러나 해역특성에따라 모델별 매개변수의 값들이 상이하므로 실제 관측치를 통해 이들 값을 추정할 필요가 있다. 본 연구에서는 울돌목 해역에서 관측한 30분 평균 유속자료를 이용하여 창 ·낙조 시 멱법칙의 고도분포지수(n) 값과 대수함수 프로파일의 마찰속도(u*)와 조도길이(z0)를 추정하였다. 또한, 수심평균유속과 매개변수간의 상관관계를 분석하였으며, 관측치와의 오차분석을 수행하였다. 그 결과, power law의 고도분포지수(n)는 창조 시에는 평균 10.75, 낙조 시에는 평균 9.3의 고도분포지수 값을 가지는 것으로 나타났다. 한편, 대수함수 프로파일의 u*는 창 ·낙조 시, 0.084 m/s와 0.105 m/s로 각각 추정되었으며, z0는 0.004 m, 0.006 m로 각각 추정되었다.
핵심용어: 멱법칙, 대수함수 연직프로파일, 유속 프로파일, 고도분포지수, 마찰속도, 조도길이
Abstract
In general, the power law and logarithmic profile are commonly used as flow vertical velocity profile model. However, since the parameters of profile vary with characteristics of coastal environment, it is necessary to estimate these values from measured data using regression analysis. In this paper, we estimated the power law exponent (n), friction velocity (u*) and roughness length (z0) of logarithmic profile by analyzing measured tidal current data that are averaged at a interval of 30 min. In the results of analysis, power law exponent (n) was estimated to be about 10.75 during flood and about 9.3 during ebb. Meanwhile, u* of logarithmic profile was estimated to be about 0.084 m/s, 0.105 m/s during flood and ebb, respectively. Also, z0 was estimated to be 0.004 m and 0.006 m, respectively.
Keywords: power law, logarithmic profile, current profile, power law exponent, friction velocity, roughness length
1. 서 론
국내 서남해안의 다도해 해역은 조류발전의 최적지로 평가 받고 있으며, 2000년대부터 조류발전터빈 개발 및 성능향상 기술개발이 꾸준히 진행되고 있다( MOF, 2015). 특히 울돌목은 전 세계적으로 손꼽히는 조류발전 후보지로서, 이 해역의 강한 조류 흐름을 이용하여 에너지를 개발하기 위해 다양한 조류발전시스템 개발이 시도되고 있다. 한편, 실제 유속층에서는 점성에 의한 마찰효과로 인해 전단력이 발생하여 수심에 따라 유속의 속도구배가 발생하게 된다. 특히 강, 해협 또는 만입구와 같은 천해역의 수심별 유속과 에너지는 해저지형과 조도계수의 영향으로 수심에 따라 변화하게 되며, 이로 인해 발전 시스템의 파괴, 오염물질의 확산 및 침 · 퇴적 등의 다양한 문제에 직면하게 된다( Lippmann et al., 2013; Prandle, 1982). 2009년 아일랜드 OpenHydro사는 캐나다 펀디만에 10 ton에 달하는 1 MW급 조류발전 터빈을 설치하고 실증시험을 수행하려 하였지만 강한 흐름으로 인해 12개의 블레이드가 파괴되는 일이 발생하였다(CBS, 2011). 따라서 조류에 대한 보다 정교한 분석을 통해 최적 조류발전시스템 설계 기술 및 안정성 확보가 매우 중요하다. 그러나 비교적 수심이 얕고 흐름이 빠르며 시간에 따라 방향이 제각각 변화하는 협수로의 복잡한 조류현상을 정확하게 예측하기란 그리 쉽지 않다. 또한, 수심과 시간에 따라 유속 분포가 변화하기 때문에 대표적인 유속 프로파일 파라미터를 추정하여 수심별 조류속에 대한 특성을 검토하는 것이 합리적인 접근 방법이 될 수 있다. 이론적으로 수심별 유속분포는 멱법칙(power law)과 대수함수 연직프로파일(logarithmic profile)을 따르지만, 더욱 현실적인 유속 프로파일을 작성하기 위해서는 대상 해역의 관측 자료를 기반으로 마찰속도, u*와 조도계수, z0와 같은 해역별 프로파일 파라미터에 대한 연구가 수행되어야한다( Lozovatsky et al., 2008a, 2008b; Taylor and Sarkar, 2008; Ko et al., 2012). Lewis et al.(2017)은 조류터빈 설계와 조류발전 지점의 실제 해양조건을 검토하기 위해 영국의 아일랜드 해역에 조류관측을 수행하여 유속 프로파일 특성을 분석한 바가 있으며, Mofjeld et al.(1984)은 베링해(Bering sea) 두 지점에 유속관측을 수행하여 조류 프로파일 작성 및 특성을 검토한 바 있다. 한편, 대수분포 프로파일에서 마찰속도 u*는 1 × 10 −3~7 × 10 −3m/s의 분포를 보이는 것으로 나타났으며, 비정상적 경계흐름에서 벽법칙(law of the wall)에 따라 u*는 비교적 짧은 시간 동안 상수로 간주되어질 수 있다( Lozovatsky et al., 2012). 이러한 파라미터들은 유속의 크기를 결정짓는 값들로서 조류발전과 같이 유속의 흐름을 이용한 발전방식에서는 발전효율을 더욱 높이기 위해 터빈 성능 곡선에 적합한 유속이 존재하는 수심에 조류발전 터빈을 설치하는 것이 필요하다. 또한 터빈 특성에 따라서는 강한 유속을 회피하여야 할 경우도 생기게 되므로 유속 프로파일에 대한 정보는 매우 중요하다. 따라서 본 연구에서는 울돌목 층별 유속 관측 자료를 활용하여 멱법칙과 대수함수 연직프로 파일의 매개변수를 추정하였다. 분석언어로는 통계 소프트웨어 package R 언어를 이용하였으며 회귀분석을 통해 각 매개변수들의 분포특성 및 추정오차를 분석하였다.
2. 자료 및 방법
2.1 울돌목 지형 및 자료
서남해안은 크고 작은 섬들이 밀집한 다도해로서 수많은 도서와 반도가 자리잡고 있는 리아스식 해안(rias coast)으로 섬 사이로 강한 유속이 발생하고 있다. 특히, 명량수도 내에 위치한 울돌목은 전라남도 해남군 우수영과 진도군 녹진 사이를 연결하는 협수로로, 길이는 약 1,000 m, 폭은 약 500 m에 불과하며 중앙부 수심은 약 20 m 정도로 선박항행이 가능한 수로는 약 400 m에 불과하다. 명량수도 전역에서 대조차는 약 3 m 정도로 크지 않으나, 수도 남단에서 고조 시각이 서단에서 보다 1시간 40분 정도 빨라 창조(漲潮)와 낙조(落潮)시 수도의 양단에서 발생하는 수위차로 인해 울돌목 협수로에서 강한 유속(수심평균 최대 약 5.5 m/s)이 발생한다( MLTMA, 2011). 그래서 울돌목은 전 세계에서 유망한 조류발전 후보지 중 하나로 손꼽히고 있다. 하지만 조류발전 단지개발을 위해서는 대상 해역의 조류 자원평가를 통해 대상해역의 적합성 여부가 결정되어야 하므로 그동안 울돌목에서는 현장관측 및 수치모델링 연구 등이 꾸준히 지속되어왔다( Kang et al., 2005). 본 연구에서는 울돌목 해역의 조류특성을 분석하기 위해 수로에 ADCP(Acoustic Doppler Current Profiler) 수중음향 도플러 유속계를 설치하여 2015년 춘계에 1개월간(2015.04.13.~ 05.15) 관측을 실시하였다. RDI사의 ADCP장비는 해저바닥에 앵커를 이용해 고정하였으며, 0.6 m의 프레임을 이용하여 유속에 의한 장비의 움직임을 최소화하였다. 또한 Transducer에서 첫 번째 bin까지의 거리를 1.92 m, bin 간격은 1 m로 설정하였다.
Fig. 1의 A점은 장비 설치 위치이며, 경위도는 34 o33'56''N, 126 o18'38''E이다. 또한 현장 관측 자료의 시간 간격은 1분 간격이며, 이를 30분 간격으로 재변환하여 사용하였다. Table 1은 본 관측에서 활용한 TELEDYNE RD Instruments 社의 ADCP 장비 성능이며, 관측에 영향을 줄 수 있는 Ping은 2 Hz로 분당 120회의 핑이 사용되었다.
2.2 이론적 배경
경계층 내의 바람과 유속은 마찰과 점성의 영향으로 고도 또는 수심에 따라 다른 유속 분포를 보이고 있다. 이러한 연직 유속 분포를 추정하기 위해 주로 경험적 방법(empirical formulae)인 멱법칙과 이론에 근거한 방법(theory-based formulae)인 대수함수 연직프로파일 이 사용되고 있다.
(1) 대수함수 연직프로파일(logarithmic profile)
조류 연직 유속 분포는 다음 식 (1) 같이 유속 분포의 추정치와 추정오차의 합으로 정의된다. 여기서 zi는 수심(m)이며, z0는 저층의 조도(粗度) 계수(Bottom roughness; m), u*는 마찰속도(shear velocity; m/s), κ는 von Karman 상수(≃ 0.41)이다. 식 (2)는 다음 식 (3)과 같은 형태로 전개되며 식 (4)와 같이 나타내어 선형 회귀계수 a 1과 상수 a 0를 추정할 수 있다. 여기서 추정된 a 1과 a 0는 각각 다음 식 (5)와 (6)과 같다. 이를 u*와 z0에 대해 정리하면 각각은 다음 식 (7), (8)과 같이 계산된다.
(2) 멱법칙
비교적 간단한 함수로 표현되는 멱법칙 함수는 연직 유속 분포를 다음 식 (9)와 같이 기준 수심 zr과 기준 수심의 유속 u( zr)의 관계식으로 가정하고 있다. 멱법칙은 유속 분포로 지수분포를 가정하고 있으며, 층별 조도와 관련된 고도분포지수인 1/n을 포함하고 있다. 일반적으로 유속 프로파일에 대한 고도분포지수는 1/7의 값을 사용하고 있으나, 해역에 따라 1/10의 값도 사용되어지고 있다( Hill, 1991; EMEC, 2009). 식 (9)는 다시 로그를 취해 선형 관계식으로 정리하면 식 (10))과 같다. 식 (10))은 ln( U) = A · ln( Z) 형태의 선형회귀식과 같으며 회귀식의 기울기 A는 1/n이 된다.
3. 분석 결과 및 토의
3.1 조류 특성
울돌목 시험조류발전소 인근 A 지점의 2015년 춘계 조류 관측 자료(30분 간격)를 분석한 결과, 낙조가 창조보다 우세한 경향을 보이고 있었다. 관측기간 동안의 수심평균유속은 창조시, 최대 3.25 m/s, 평균유속은 1.96 m/s로 나타났으며, 평균유향은 325.3 o로 관측되었다. 또한, 낙조 시 평균유속은 2.37 m/s, 최대 3.90 m/s이며, 평균 유향은 138.52o로 나타났으며, 낙조가 창조보다 약 0.4 m/s의 빠른 흐름을 보였다( Table 2 참조).
Fig. 2는 유속과 유향에 대한 시계열 그림이다. 유향은 창조시 북서류(325.3 o)로 흐르며, 낙조 시에는 남동류(138.52 o) 흐름을 보였다.
Fig. 3은 조류자료의 산포도로 뚜렷한 북서류와 남동류 경향을 볼 수 있다.
3.2 조류 프로파일 매개변수 추정
본 연구에서는 가장 낮은 관측 위치인 약 2.5 m 기준 유속의 방향으로 창조와 낙조를 구분하였다. 또한 0.05 m/s 이하의 유속을 정조로 간주 하였으며, 310o~330o의 유향을 갖는 유속은 창조로 유향이 122o~160o인 유속을 낙조로 구분하였다. 그러나 정조로 분류되는 유속의 개수가 매우 작아 본 연구에서는 정조에 대한 분석은 하지 않았다.
분석 결과, 멱법칙의 경우, 창조 시에는 3.14~21.74의 범위에서 평균 10.75의 값을 보였다. 또한, 낙조 시에는 3.3~29.94의 분포를 보였으며, 평균 9.3의 고도분포지수 값을 가지는 것으로 나타나 일반적으로 사용되는 n = 7보다는 큰 값으로 나타났다( Fig. 4 참조).
Fig. 5는 수심 평균된 유속과 n 값과의 상관성 정도를 파악하기 위해 상관분석을 수행한 결과이다. 창 · 낙조 모두 2 m/s 이상의 유속에서는 n 값의 분산정도가 적은 것으로 나타났으나, 2 m/s 미만의 유속이 비교적 느린 지점에서는 n값의 분산이 크게 나타났다. 또한, 수심평균유속과 멱법칙 고도 분포 지수간의 상관계수는 창조 시와 낙조 시 각각 0.312와 −0.227로 나타나 유속과 고도분포지수간의 상관성은 없는 것으로 나타났다.
Fig. 6과 7은 대수함수 프로파일의 매개변수인 마찰속도, u*와 조도길이, z0의 분포도를 나타낸 것이다. Fig. 6에서 보는 바와 같이, 창조 시, u*의 분포 범위는 0.018~0.169 m/s였으며, 평균값은 0.084 m/s로 산정되었다. 낙조 시, u*는 0.001~0.231의 분포를 보였으며, 평균마찰속도는 0.105 m/s로 산정되었다.
Fig. 7은 창조와 낙조 시 조도계수 z0의 발생빈도를 나타낸것이며, 창조 시에는 평균 0.004 m, 낙조 시에는 평균 0.006 m로 추정되었다. 대체로 울돌목 해역의 조도계수 값 분포에서 3사분위수는 창조 시 0.003 m, 낙조 시 0.005 m로 이 값은 Dyer(1986)와 Soulsby(1983)가 추정한 자갈 지반일 경우의 조도계수 값인 0.003 m와 유사하게 나타났다.
마찰속도, u*와 수심평균유속간의 선형관계 정도를 파악하기 위해 두 변수간의 상관성을 검토해보았다( Fig. 8 참조). 그 결과, 신뢰구간 95%에서 신뢰구간 길이는 0.791~0.839로 산정되었으며 두 변수의 상관계수는 0.816로 산정되어 두 변수 간에는 뚜렷한 선형관계를 보이는 것으로 나타났다. 또한 p-value가 0으로 유의수준인 0.05보다 작은 값으로 나타나, 선형관계가 있음을 보이고 있다. 낙조 시에도 상관계수가 0.736으로 두 변수 간에 비교적 높은 상관관계를 보이고 있었다. 반면, 조도길이와 수심평균 유속 간에는 큰 상관성이 보이지 않는 것으로 나타났다.
Fig. 9는 창조와 낙조 시 관측 된 유속 연직분포와 대수함수 프로파일에 의해 추정 된 연직분포 사이의 평균 제곱근 오차(RMSE, Root mean square error)를 나타낸 그림이다. 창조 시 평균 제곱근 오차 범위는 0.00~0.071 m/s였으며, 평균 0.031 m/s의 오차를 보이는 것으로 나타났다. 반면, 낙조 시에는 평균제곱근 오차가 0.004~0.117의 오차범위를 가지며 평균오차는 0.035 m/s로 산정되었다.
한편, Fig. 10에는 창조와 낙조 시 관측 된 유속 연직분포와 멱법칙에 의해 추정 된 연직분포 사이의 평균 제곱근 오차를 나타내었다. 창조 시, 평균제곱근오차범위는 0.004~0.075m/s였으며, 평균오차는 0.033 m/s로 산정되었다. 또한 낙조 시에는 평균제곱근오차범위는 0.004~0.129 m/s로 나타났으며 평균오차는 0.035 m/s로 산정되었다. 결과적으로 대수함수 프로파일과 멱법칙 모델 모두 관측치와의 오차가 약 0.03 m/s 내외로 두 모델 모두 관측치를 잘 재현하는 것으로 판단되었다. 다음 Table 3은 각 프로파일 모델별 매개변수들의 통계량을 정리한 것이다.
4. 결론 및 제언
강한 흐름이 발생하는 수로에서의 조류 관측은 강한 흐름과 작업시간의 제약으로 인해 많은 어려움이 따른다. 본 연구에서는 진도군 울돌목에서 관측한 층별 조류자료를 이용하여 조류 프로파일인 대수함수 프로파일(마찰속도, u*; 조도길이, z0)과 멱법칙(고도분포지수, n)의 매개변수 값을 추정하였다. 본 연구를 통해 분석한 울돌목의 조류 특성을 정리하면 다음과 같다.
(1) 울돌목에서의 수심평균유속은 1.98 m/s로 관측되었으며, 최대유속은 4.22 m/s로 낙조가 창조보다 평균 약 0.4 m/s 빠르게 나타났다. 낙조와 창조 시 평균 유속은 2.21 m/s, 1.77m/s였으며, 유향은 132.71 o와 312.71 o로 각각 관측 되었다( Table 3 참조). (2) 층별 유속 자료로부터 멱법칙의 고도분포지수(n)을 추정한 결과, 창조 시에는 평균 10.75, 낙조 시에는 평균 9.3의 고도분포지수 값을 가지는 것으로 나타났다. 이는 낙조가 창조보다 유속이 더 크기 때문에 고도분포지수 값이 창조시보다 낮게 추정된 것으로 판단된다. 한편, 유속 멱법칙의 고도분포지수 값, n은 주로 7이 사용되지만, EPRI 가이드라인에서는 높은 조류에너지 사이트에서는 n 값으로 10을 사용할 것을 권장하고 있다( Hagerman et al., 2006). (3) 대수함수 프로파일의 매개변수인 마찰속도, u*와 조도 길이, z0를 추정한 결과, 창조 시, u*의 평균값은 0.084 m/s로 산정되었으며, 낙조 시, u* 평균값은 0.105 m/s로 산정되었다. 또한, 조도길이의 경우, 창조와 낙조 시 0.004 m, 0.006 m로 각각 추정되었다.
(4) 본 연구에서는 매개변수간의 관련성을 검토하기 위해 상관분석을 수행하였다. 그 결과, 멱법칙의 고도분포지수와 수심평균유속간의 상관성은 매우 낮은 것으로 분석되었으나, 마찰속도와 수심평균유속 간에는 비교적 높은 선형관계가 있는 것으로 나타났다.
(5) 관측 유속 프로파일과 모델치와의 평균제곱근오차 범위는 0.031~0.04 m/s로 산정되어 유속 프로파일 작성 시 멱법칙 또는 대수함수 프로파일을 사용하여도 큰 무리가 없을 것으로 판단되었다.
감사의 글
본 연구는 해양수산부의 해양청정에너지기술개발사업인 “조류발전 실해역 시험장 구축(과제번호: 20170333)” 과제와 미래해양산업기술개발 해양중소벤처지원사업인 “콘크리트 쉬라우드를 이용한 조류발전시스템 연구(과제번호: 20170122)” 과제의 일환으로 수행되었습니다. 연구지원에 감사드립니다.
Fig. 1.
A location map of observation point. 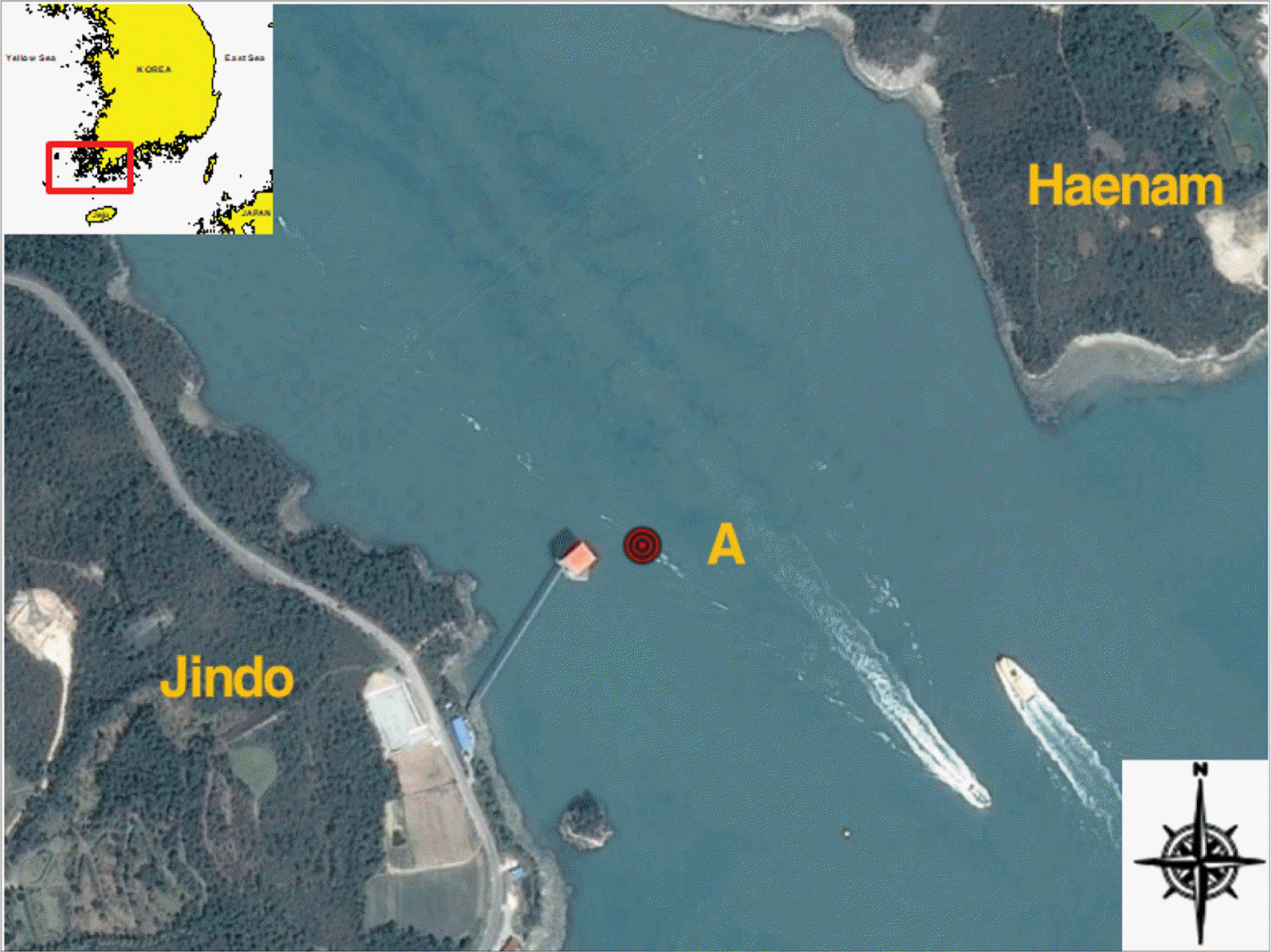
Fig. 2.
Time series of tidal current speed and direction at Uldolmok. 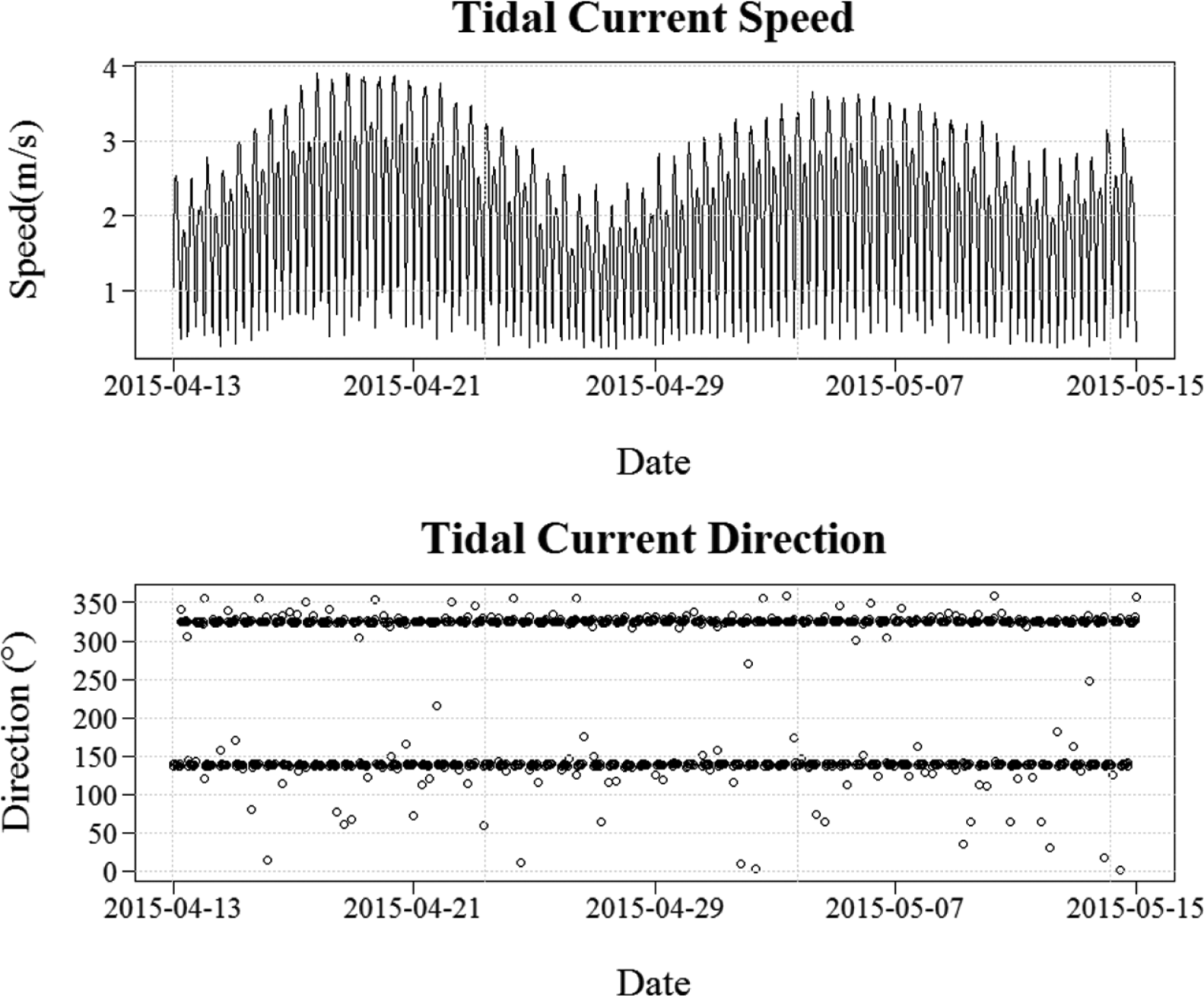
Fig. 3.
Scatter plot of tidal current at Uldolmok. 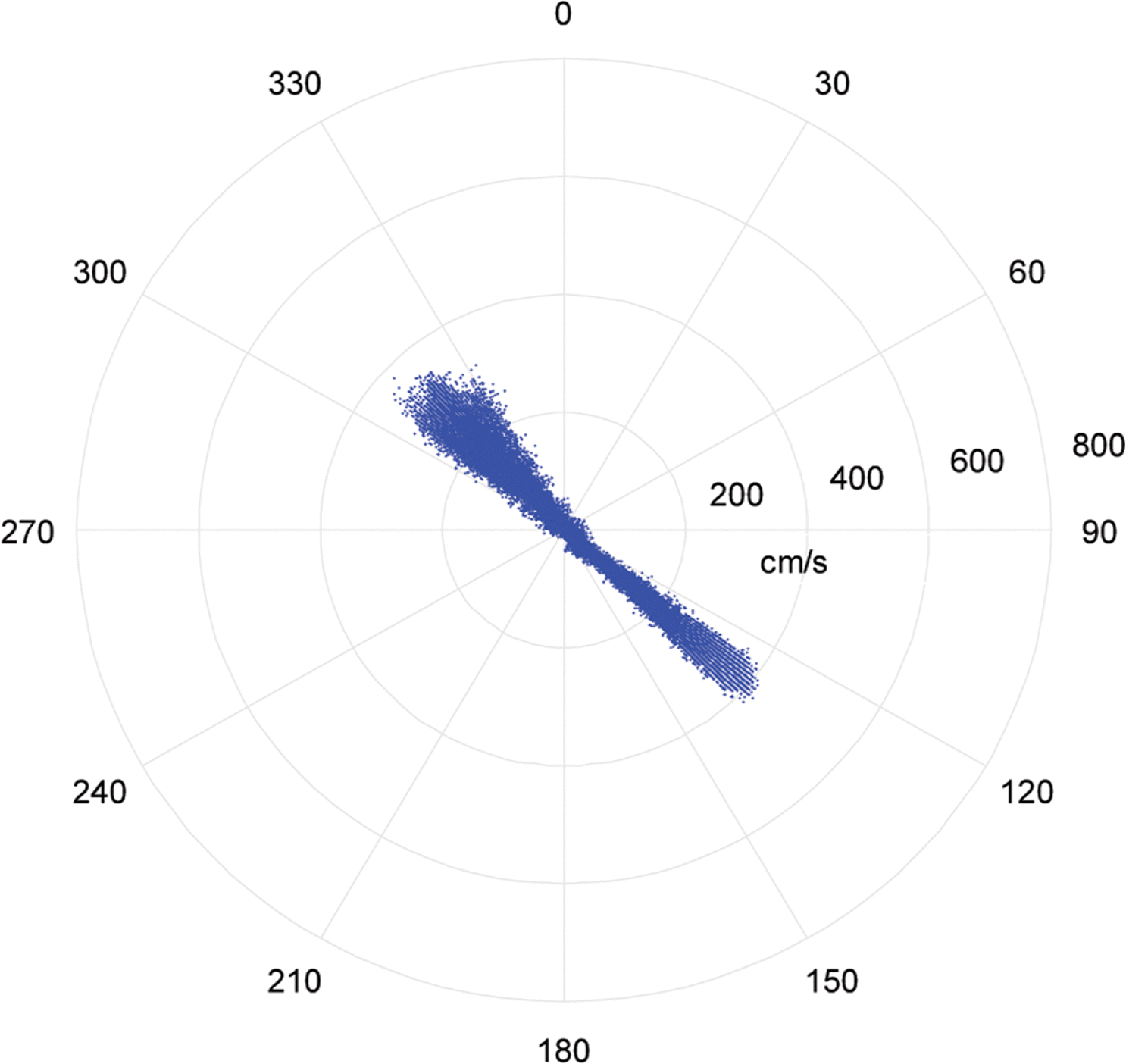
Fig. 4.
Frequency density of power law (n). 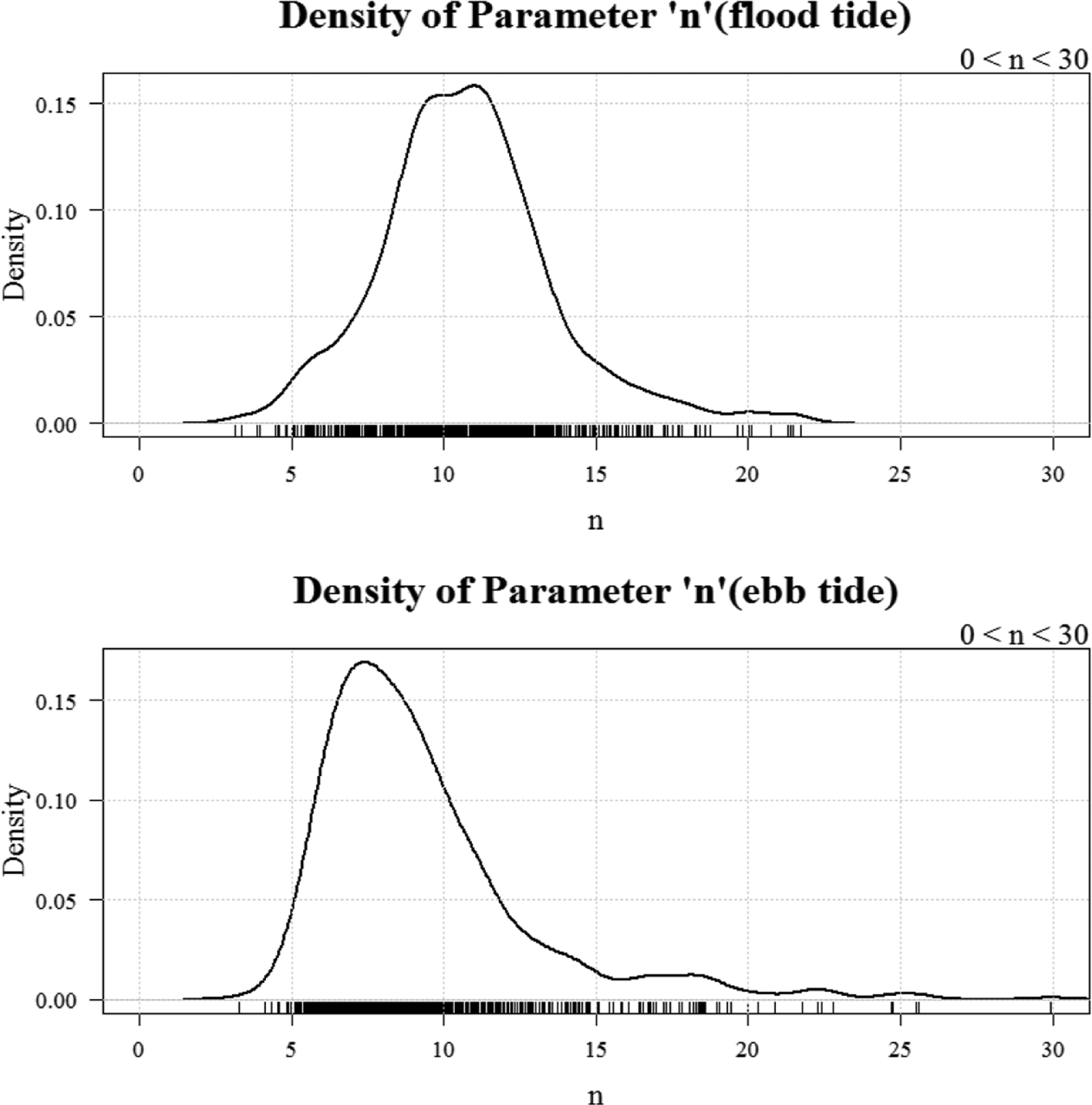
Fig. 5.
The comparison between power law (n) and depth mean velocity. 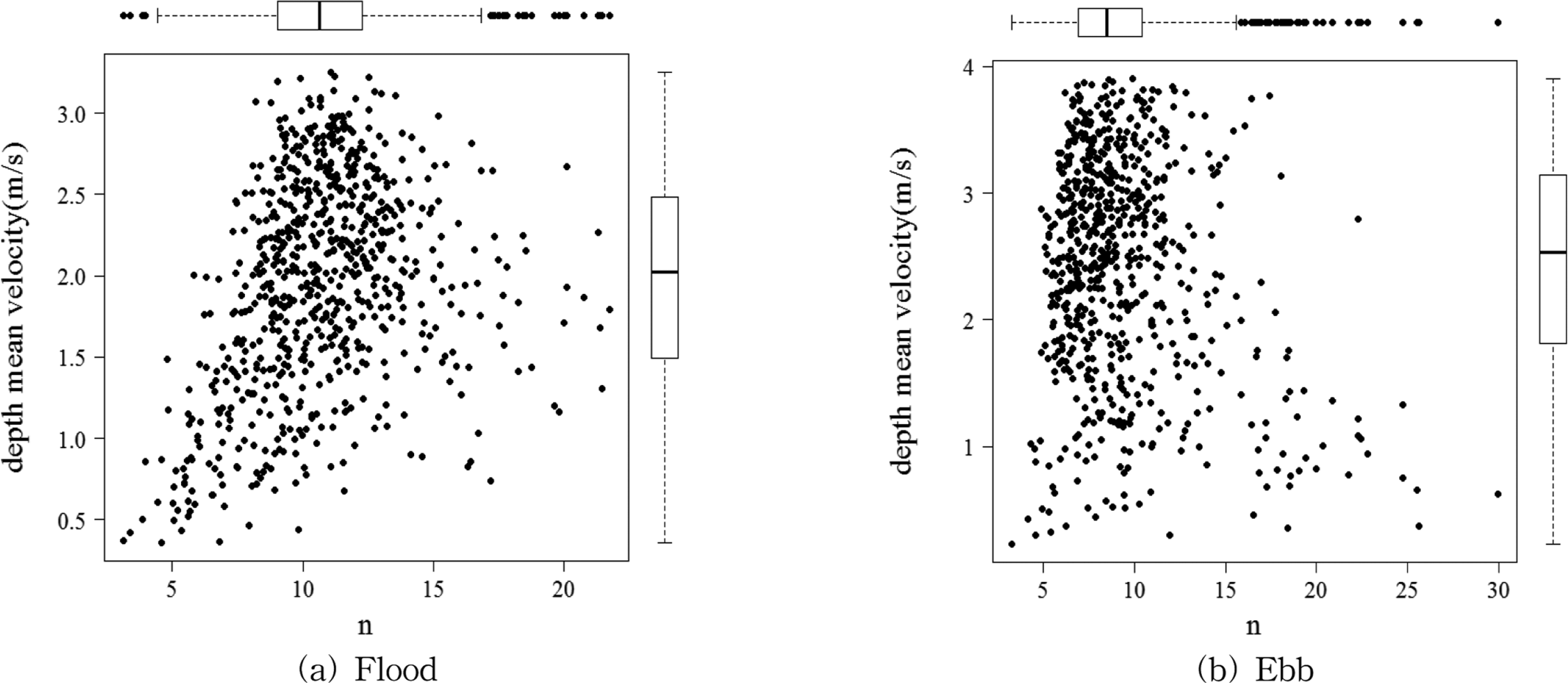
Fig. 6.
Frequency density of shear velocity, u*. 
Fig. 7.
Frequency density of bottom roughness length (z0). 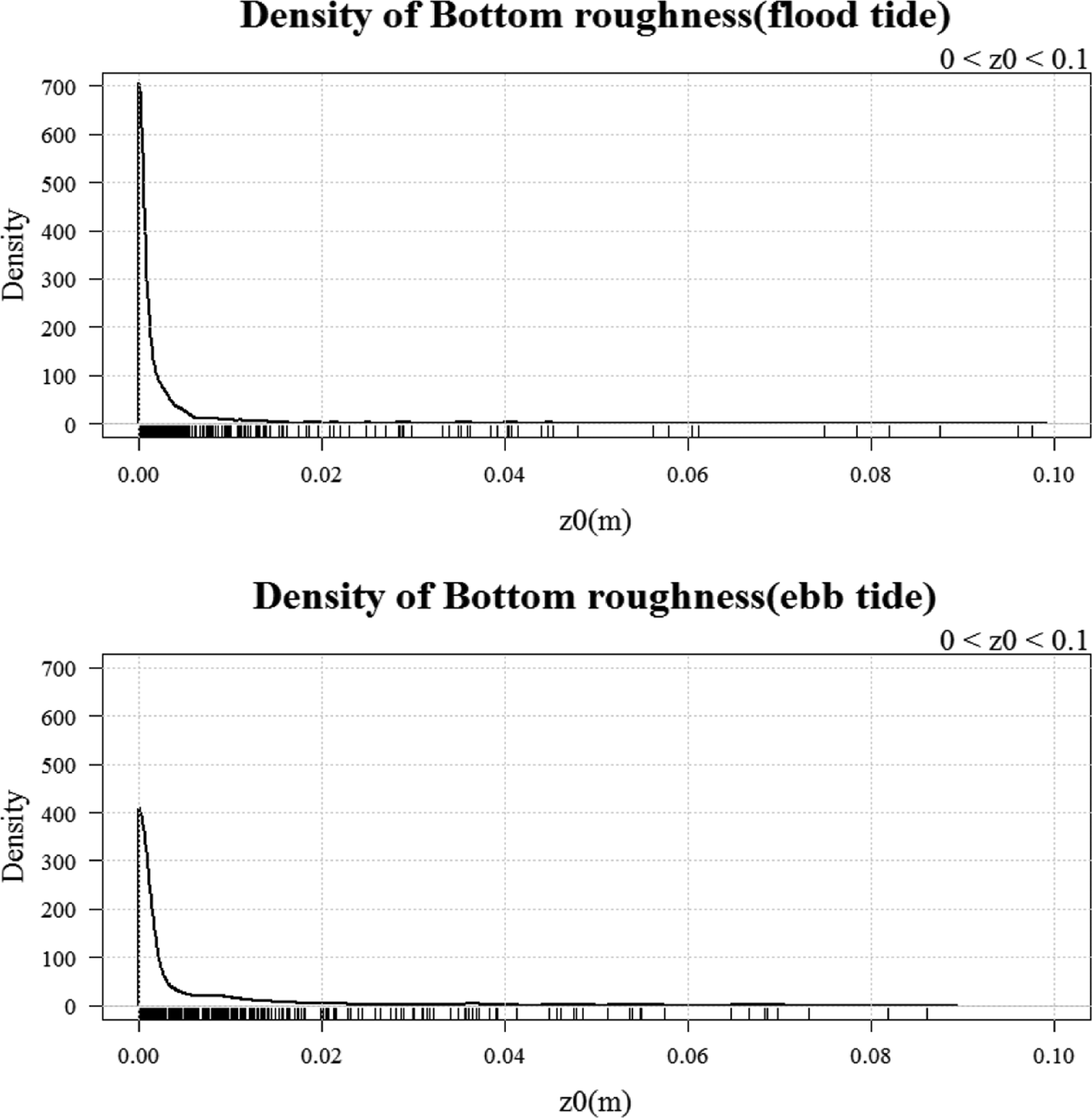
Fig. 8.
The comparison between friction velocity and depth mean velocity. 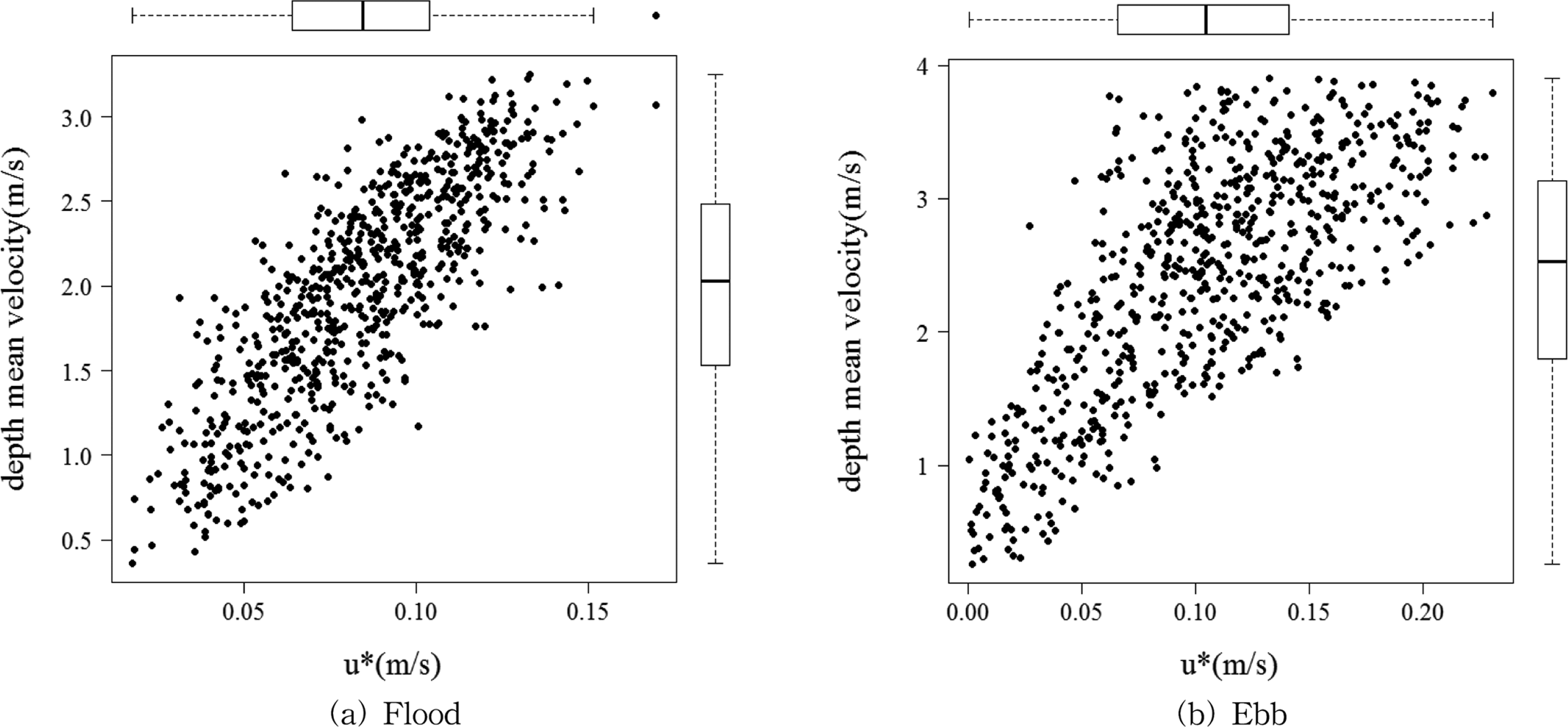
Fig. 9.
RMSE results between measured velocity profiles and estimated velocity profiles by using logarithmic layer profile. 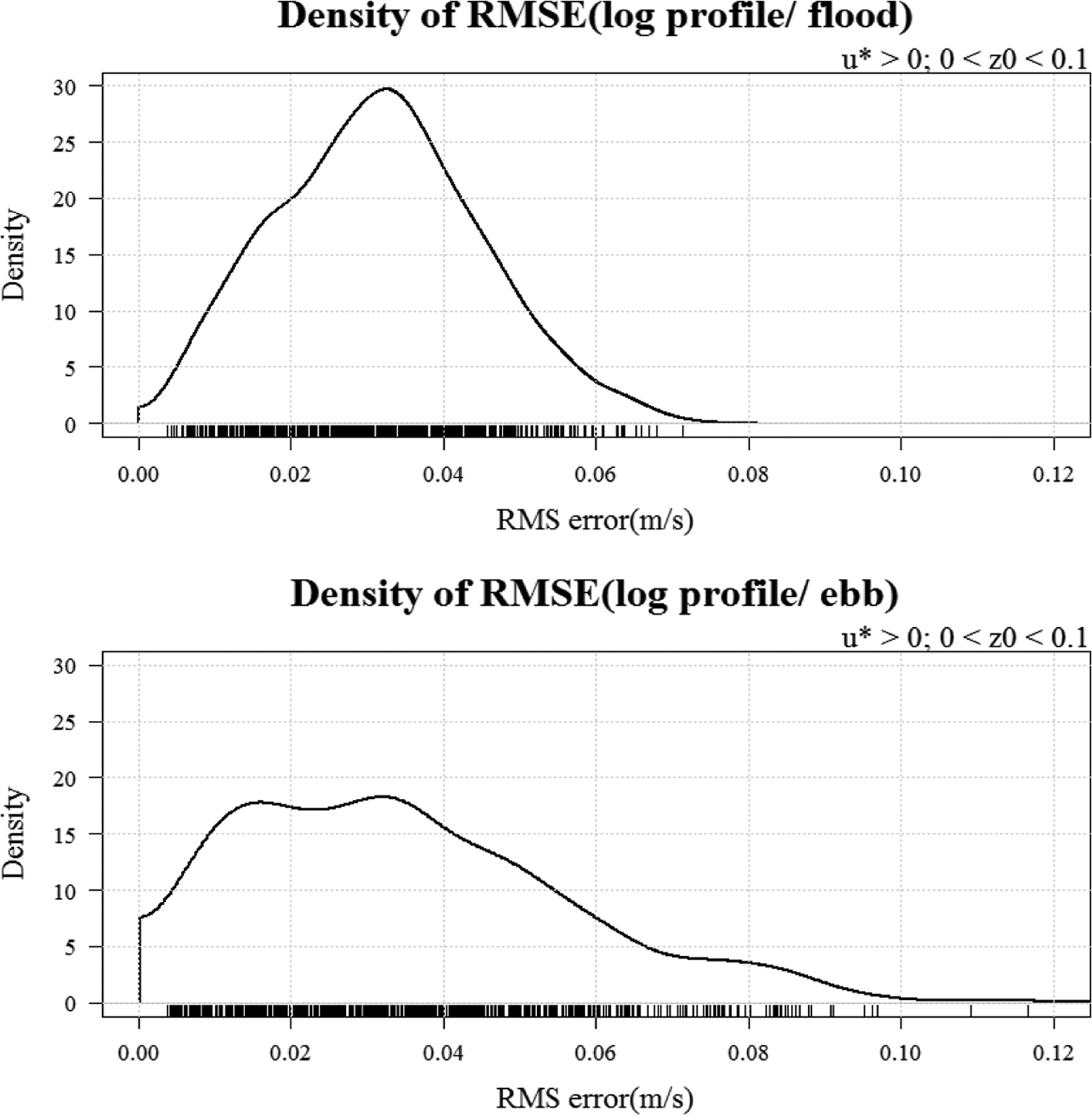
Fig. 10.
RMSE results between measured velocity profiles and estimated velocity profiles by using power law. 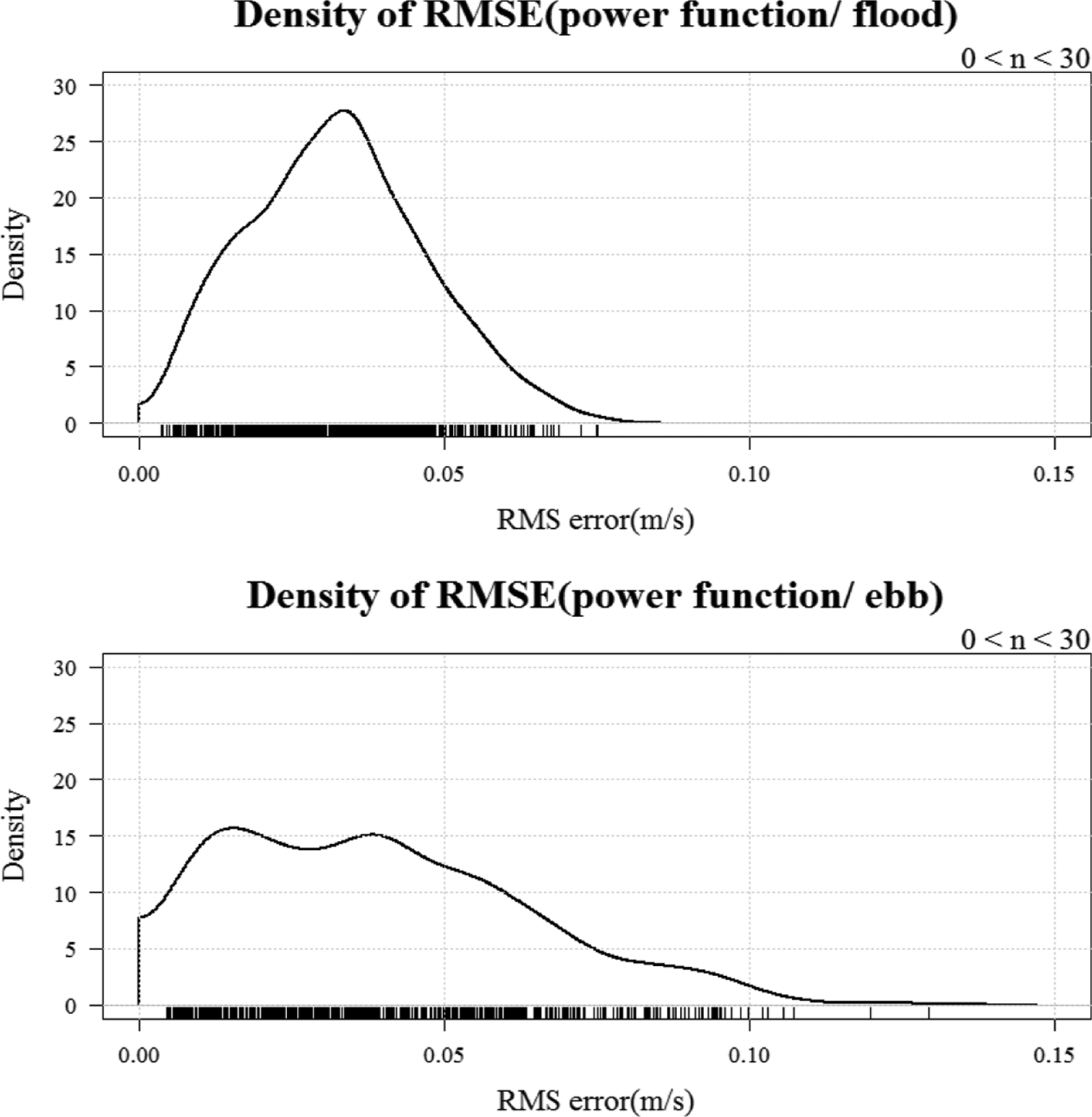
Table 1.
ADCP specification sheets, TELEDYNE RD instruments
|
Contents |
Model: WHWS ADCP 600 kHz |
|
Temperature |
Range |
−5 to 45°C |

|
|
Precision |
± 0.4°C |
|
Resolution |
0.01°C |
|
|
Tilt |
Range |
± 15° |
|
Accuracy |
± 0.5° |
|
Precision |
0.01° |
|
|
Compass |
Accuracy |
± 2° |
|
Precision |
± 0.5° |
|
Resolution |
0.01° |
|
Maximum tilt |
± 15° |
|
|
Velocity |
Accuracy |
± 0.25% (± 0.25 cm/s) |
|
Resolution |
0.1 cm/s |
|
Range |
± 5 m/s (Default) |
|
± 20 m/s (Maximum) |
|
|
Cell |
Depth |
1∼42 (1 m/cell) |
|
|
Ping |
Rate (Hz, typical) |
2 (broadcast) |
Table 2.
Results of measured tidal current data in the spring of 2015
|
Point |
Water depth (m) |
Tidal current speed (m/s) |
Direction (°) |
|
A |
D.L. −20 |
Ebb |
Maximum |
3.90 |
138.79 |
|
Mean |
2.37 |
138.52 |
|
|
Flood |
Maximum |
3.25 |
325.07 |
|
Mean |
1.96 |
325.30 |
Table 3.
Statistics of logarithmic profile and power law parameters, RMSE, the number of data ((1): RMSE between power law and observed velocity, (2): RMSE between logarithmic profile and observed velocity)
|
|
Min |
Q 1 |
Median |
Mean |
Q 3 |
Max |
The no. of data |
|
Flood |
n |
3.135 |
9.038 |
10.615 |
10.746 |
12.274 |
21.740 |
732 |
|
u*
|
0.018 |
0.064 |
0.084 |
0.084 |
0.104 |
0.169 |
725 |
|
z0
|
0.000 |
1.99E-04 |
7.55E-04 |
4.24E-03 |
2.84E-03 |
9.77E-02 |
725 |
|
RMSE (1) |
0.004 |
0.022 |
0.032 |
0.033 |
0.042 |
0.075 |
732 |
|
RMSE (2) |
0.004 |
0.022 |
0.031 |
0.031 |
0.040 |
0.071 |
725 |
|
|
Ebb |
n |
3.295 |
6.947 |
8.490 |
9.303 |
10.455 |
29.939 |
693 |
|
u*
|
0.001 |
0.066 |
0.105 |
0.105 |
0.141 |
0.231 |
698 |
|
z0
|
0.000 |
2.76E-05 |
7.24E-04 |
5.98E-03 |
5.96E-03 |
8.61E-02 |
698 |
|
RMSE (1) |
0.004 |
0.019 |
0.037 |
0.040 |
0.055 |
0.129 |
693 |
|
RMSE (2) |
0.004 |
0.018 |
0.032 |
0.035 |
0.048 |
0.117 |
698 |
References
Bergeron, NE, Abrahams, AD (1992). Estimating shear velocity and roughness length from velocity profiles, Water Resources Research, 28(8):2155-2158.  Dyer, KR. (1986). Coastal and Estuarine Sediment Dynamics. John Wiley & Sons, Ltd, Chichester, UK: p 342.
EMEC (2009). Assessment of tidal energy resource : marine renewable energy guides, EMEC.
Hagerman, G, Polagye, B, Bedard, R, Previsic, M. (2006). Methodology for Estimating Tidal Current Energy Resources and Power Production by Tidal In-stream Energy Conversion (TISEC) Devices, EPRI North American Tidal In Stream Power Feasibility Demonstration Project.
Hill, AE (1991). Vertical migration in tidal currents, Mar. Ecol. Prog. Ser, 75, 39-54.   Hsu, SA. (2013). Coastal meteorology. Academic Press Inc, p 260.
Kang, SK, Yum, KD, Lee, KS, Park, JS (2005). Coastal-physical oceanographic aspects in relation to the tidal current power generation in the Uldolmok, Journal of New and Renewable Energy, 1(2):73-78 (in Korean)..
Ko, DH, Jeong, ST, Cho, H, Kim, JY, Kang, KS (2012). Error analysis on the offshore wind speed estimation using HeMOSU-1 data, Journal of Korean Society of Coastal and Ocean Engineers, 24(5):326-332 (in Korean)..   Lewis, M, Neill, SP, Robins, P, Hashemi, MR, Ward, S (2017). Characteristics of the velocity profile at tidal-stream energy sites, Renewable Energy, 114, 258-272.  Lippmann, TC, Irish, J, Hunt, J (2013). Observations of the vertical structure of tidal cuirrents in two inlets, Journal of Coastal Research, Special Issue, 65, 1-6.  Lozovatsky, I, Liu, Z, Fernando, H, Armengol, J, Roget, E (2012). Shallow water tidal currents in close proximity to the seafloor and boundary-induced turbulence, Ocean dynamics, 62, 177-191.  Lozovatsky, ID, Liu, Z, Wei, H, Fernando, HJS (2008a). Tides and mixing in the northwestern East China Sea part I: rotating and reversing flows, Cont. Shelf. Res, 28, 318-337.  Lozovatsky, ID, Liu, Z, Wei, H, Fernando, HJS (2008b). Tides and mixing in the northwestern East China Sea Part II: near-bottom turbulence, Cont. Shelf. Res, 28, 338-350.  MLTMA. (2011). Development of Utilization Technique for Tidal Current Energy, Ministry of land, transport and maritime affairs, Korea (in Korean)..
Mofjeld, HO, Schumacher, JD, Pashinski, DJ. (1984). Theoretical and observed profiles of tidal currents at tow sites on the southeastern Bering sea shelf, NOAA technical memorandum ERL PMEL-62. NOAA, USA..
MOF. (2015). Midium- and Long-term Development Plan for Marine Energy (′15∼′25), proposal, Ministry of oceans and fish-eries. Korea (in Korean).
Prandle, D (1982). The vertical structure of tidal currents and other oscillatory flows, Cont. Shelf. Res, 1(2):191-207.  Roh, EG (2001). Turbulence, Sigmapress, 131-133 (in Korean)..
Soulsby, RL. (1983). The bottom boundary layer of shelf seas, in Physical Oceanography of Coastal and Shelf Seas. In: Johns B, ed. Elsevier, Amsterdam, The Netherlands: Chapter 5.
Soulsby, R (1997). Dynamics of Marine sands: a manual for practical applications, Thomas Telford, 1997.
Taylor, JR, Sarkar, S (2008). Stratification effects in a bottom ekman layer, American Meteorological Society, 2535-2555. 
|
|




















