1. 서 론
항만도시는 항만과 배후도시로 구성되며 이 두 가지는 과거부터 항만도시의 발달 단계에 따라 서로 상호작용을 통하여 발전되어 왔다. 항만과 도시가 같은 공간에 위치한 초기 항만도시 단계와 급격한 항만도시 확장에 따라서 항만의 확장으로 인하여 도시와 항만공간이 분리되는 단계로 구분될 수 있다(Hoyle, 1989). 또한 1980년대 이후부터 선박의 대형화와 탈산업화에 따라서 항만기능이 상실된 항만이 이전 또는 소멸되면서 그 공간에 친수공간을 적극적으로 개발하기 시작하였다. 이러한 경향으로 항만도시는 점점 바다 주변으로 확장되고 호안 근처에 많은 관광시설물이나 주거 시설물이 건설되고 있다. 이로 인해 태풍이나 폭풍 등이 발생하였을 경우 호안 시설물과 건축물이 직접적으로 피해를 입고 있다. 특히 2016년 제18호 태풍 차바(CHABA)의 발생으로 월파에 의한 침수 등이 발생하여 호안 인근에 위치한 건축물 등에 많은 피해가 발생한 바 있다. 공학적인 설계를 한다면 높은 방벽이 설치되어야 하나 관광 및 거주자들의 요구로 인하여 방벽이 설계 높이 보다 낮게 설치되어 월파에 의한 피해가 유발된 사례이다. 이와 같이 최근에 도시의 개발과 조망권 요구에 의하여 방벽이 설치되지 못하는 지역에 새로운 형식의 방재 구조물이 필요할 것으로 판단된다.
본 연구에서는 호안에 설치되어 평시에는 관광형 데크로 사용하다가 월파 등이 발생하는 이상 시에는 기립 가동하여 월파를 막을 수 있는 가동식 방벽 구조물을 제시하고 이를 분석하였다. 가동식 방벽은 가동방법의 효율성 및 월파를 적절하게 방어할 수 있는 성능을 구비해야 한다. 이러한 성능을 분석하기 위하여 수리수치해석과 가동 및 월파 작용 시 거동 특성을 분석하기 위한 구조수치해석을 수행하였다.
2. 월파방지를 위한 호안 설치형 가동식 방벽의 수리성능 분석
2.1 호안설치형 가동식 방벽의 개요
본 연구에서 제안된 가동식 방벽은 가동 전과 후로 나뉘게 된다. 가동 전은 월파 등이 작용하지 않는 평상시 상태로서 Fig. 1의 좌측 상단과 같이 설치되어 있어 관광형 데크 형태로 일반인들이 운동 및 산책 시 사용할 수 있다. 월파 발생 예보 혹은 월파 시에는 방벽의 후방에 위치하고 있는 윈치에 연결된 케이블을 감게 되면 전면벽이 움직이고 전면벽의 각도가 약 85도가 될 때까지 기립을 위한 가동을 한다. 이 때 롤러가 움직일 때 그 형태를 유지하기 위하여 상하부 가이드레일을 가지며, 육상부는 호안에 해양부는 잔교 파일에 고정되어 전반적으로 격자형태의 프레임(frame)을 형성하게 된다. 만약 월파가 발생할 수 있는 이상시가 종료될 경우 윈치를 회전시켜 케이블 장력을 감소시킬 경우 가동식 방벽은 자중에 의하여 서서히 원래의 형태로 복귀하게 된다. 여기에서 잔교 파일, 프레임은 강구조, 전면 및 후면 벽은 강재와 콘크리트가 합성된 구조이다.
2.2 수치해석을 통한 전면벽의 압력산정
본 연구에서는 폭풍이 발생하였을 경우 파에 따른 전면벽에 발생하는 압력을 합리적으로 도출하기 위하여 CADMASSURF(Coastal Development Institute of Technology, 2001)을 이용하였으며, 본 수치해석 프로그램은 2차원 비압축성 점성유체를 대상으로 하는 Navier-Stokes 방정식을 Porous Model(Sha et al., 1978)에 근거하여 구조물의 형상근사정도를 높인 수치모형으로(Sakakiyama et al., 1990), 복잡한 자유수면을 해석하기 위하여 VOF(Volume of Fluid)법을 사용하였고(Hirt and Nichols, 1981), Sommerfeld 방사경계와 에너지 감쇠대를 사용하여 구조물로부터의 반사파가 조파경계에서 재반사 되는 문제를 제어하였다. CADMAS-SURF v5.1에서는 Dupuit-Forchheimer형 저항칙을 추가되었으며(Coastal Development Institute of Technology, 2010), 기존의 항력산정식과는 달리 투과구조물 구성 재료의 크기와 저항계수의 관계를 표현하는 Engelund(1953)가 제안한 식을 적용하였다.
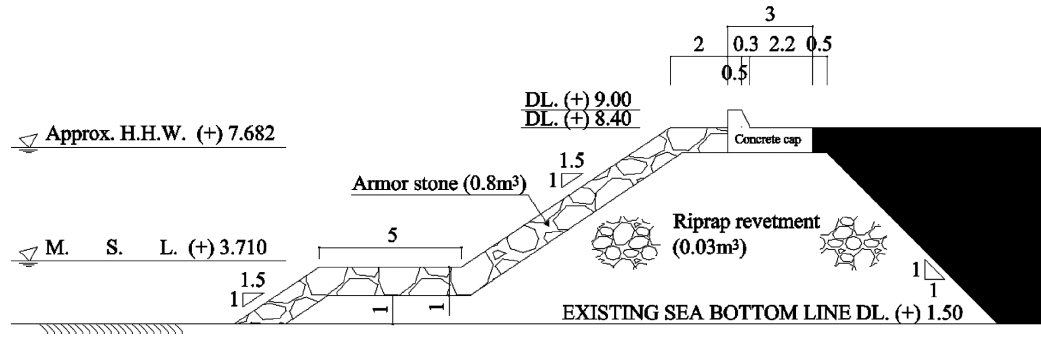
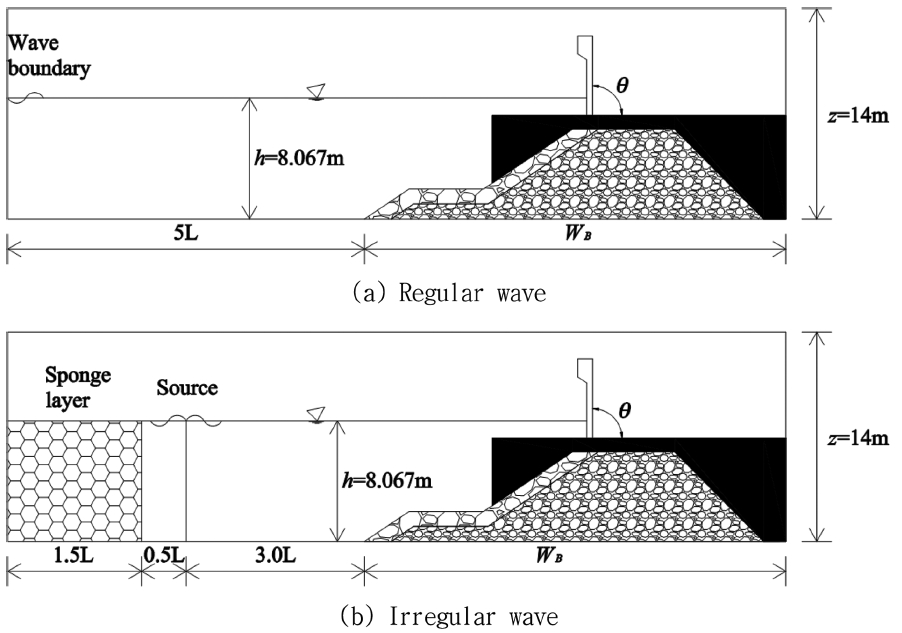
Fig. 2는 서해안의 OO항의 호안으로서 대상지역의 수심은 아라미르 프로젝트의 권역별 설계조위 결정 자료를 참고하여 Fig. 3과 같이 폭풍해일고와 해수면상승고를 적용하였고, 이때의 수심은 8.067 m이다. 본 수치실험에서는 규칙파와 불규칙파를 고려하였으며 이때의 수치실험영역은 Fig. 4와 같다. 검은 색으로 표시한 부분은 잔교부로 계산의 편의상 불투과 구조로 취급하였다.
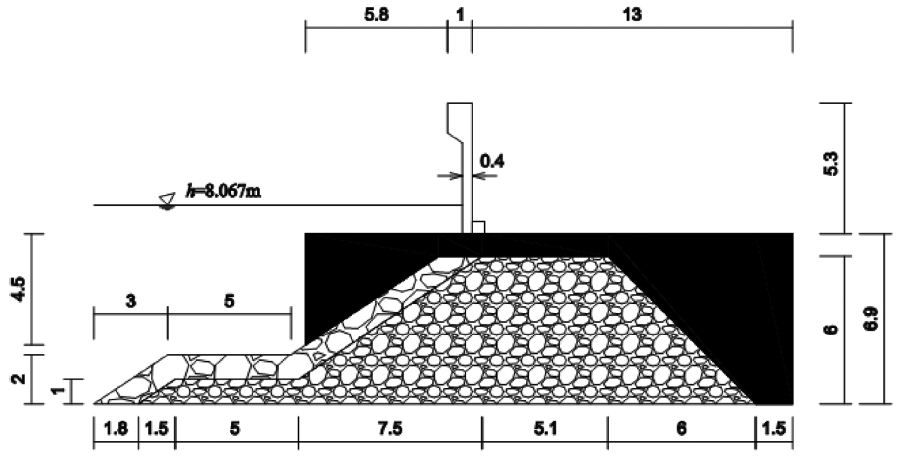
규칙파 실험은 입사파 조건이 내부조파를 하기에 비선형성이 강해서 좌측의 경계에서 조파하였고, 불규칙파 실험은 내부조파를 수행하고 좌측에 에너지 감쇠대를 두었다. 50년 빈도의 설계파를 적용하였고, 설계파고는 2.0 m, 설계파주기는 6.73 sec이다. 그림의 사석을 제외한 부분의 구조물에 대해서는 불투과성 구조물로 간편화하였고, 호안의 폭은 WB = 28.4m, 피복석의 입경은 0.93 m, 호안사석의 입경은 0.31 m로 설정하였으며 porosity는 0.37로 동일하게 가정하였다. 가동식 방벽의 경사는 θ = 60°, 70°, 80°, 90°의 네 가지 경우에 대하여 수치실험을 수행하였다. 자세한 수치실험의 제원은 Table 1과 같다. Table 1에서 stream 22의 숫자는 Stream Function (Dean, 1965)의 차수를 의미한다. 난류 모형의 경험정수들은 default 값을 사용하였고, 유속과 압력의 경계조건은 대수법칙을 적용하였다. 경사진 가동식 방벽을 어느 정도 표현이 가능하도록 격자크기는 Δx = 0.2 m, Δz = 0.1m의 등간격자로 구성하였고, 규칙파와 불규칙파의 해석시간은 각각 100 sec, 130 sec이고, 규칙파 실험은 재반사파가 구조물에 도달하기 전까지의 결과를 분석하였다. 그리고 불규칙파의 성분파의 수는 200개이다. 가동식 방벽의 경사에 따른 상세한 제원은 Fig. 5에 도시하였다.
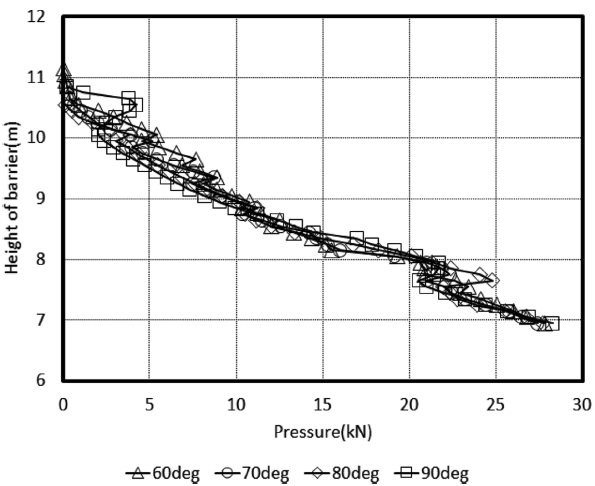
제안된 가동식 방벽의 구조 거동 특성을 분석하기 위해서는 방벽 전면부에 작용하는 압력을 이용해야 한다. 압력은 방벽의 전면에 위치한 모든 셀에서 측정하였고, 수치해가 안정된 이후의 압력을 이용하여 결과를 도출하였다. 수위 상승에 의한 정수압이 가동식 안벽에 영향을 직접적으로 미치므로 이 압력에는 수위 상승에 의한 정수압 성분을 포함시켰다. Fig. 6은 규칙파 실험에서의 방벽 전면의 평균최대압력이고, Fig. 7은 불규칙파 실험에서의 방벽 전면의 최대압력이다. 방벽은 호안의 바닥면(z = 6.9m)에서부터 설치되어 있기 때문에 아래의 그림들은 최하단부에서 가장 압력이 큰 것으로 나타났다. 규칙파와 불규칙파가 작용했을 때의 최대 압력분포는 각각 27 kPa, 30 kPa로 불규칙파가 작용했을 때가 더 큰 것을 볼 수 있다. 또한 방벽의 각도에 따라서 약간의 압력의 차이가 있기는 하지만 각도와 상관없이 거의 유사한 압력분포를 갖는 것으로 나타났다. 본 연구에서는 구조해석을 위하여 아래의 Fig. 8과 Fig. 9와 같이 가동식 방벽의 경사가 80도 일 경우의 시간에 따른 압력 분포를 입력값으로 사용하여 구조적인 거동 특성을 분석하였다.
3. 가동식 방벽의 구조 거동 분석
3.1 구조해석 개요
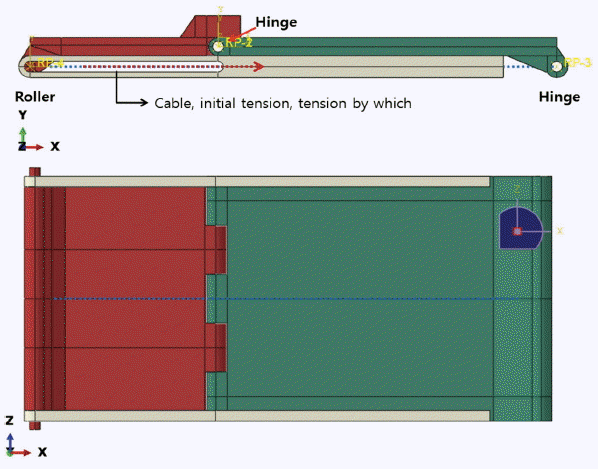
가동식 방벽의 구조거동특성을 분석하기 위해서 범용 구조 해석 프로그램 ABAQUS(Simulia, 2013)를 사용하였으며, Fig. 10과 같이 모델링을 하였다. Fig. 1에서 설명한 내용을 해석적으로 모델링하기 위해서 호안 및 파일 부분을 제외하였다. 이와 같이 해석 모델은 롤러 프레임 2개, 전면방벽, 후면방벽으로 구성된다. 본 연구에서는 방벽의 기립 가동시와, 기립 후 월파에 의한 압력을 받았을 때의 구조적 거동에 대하여 분석하였다.
본 해석모델은 Fig. 10과 같이 2개의 힌지와 롤러의 경계조건으로 구성되어 있다. 롤러 프레임은 고정 상태(6방향 Fix)로 가정하였으며, 호안 부분에 고정되는 힌지(End hibge)는 z 방향의 회전을 제외하고 모두 구속하였다. 전면방벽과 후면방벽은 Connector 옵션을 이용하여 회전을 할 수 있도록 가정하였다. 재료로는 롤러프레임은 강재, 전면방벽과 후면방벽은 강재 콘크리트 합성구조로 가정하였다. 방벽은 상단이 빈 박스 형태로 만들어 빈 공간에 콘크리트로 채워서 모델링을 하였으며 상세 물성치는 Table 2에 정리하였다.
해석모델의 제원은 Fig. 11과 같다. 전면방벽의 길이는 5.6 m, 두께는 0.5 m, 후면방벽의 길이 9 m, 두께는 0.5 m로 하였다. 그리고 힌지와 롤러의 위치는 작은 힘으로도 상승하도록 만들기 위하여 중간힌지에 약 600 mm 정도 아래에 설치하여 모델링을 하였다. 모든 모델은 3차원 요소를 사용하였으며, C3D8R 요소를 사용하였다.
3.2 기립 가동 시 가동식 방벽의 거동 분석
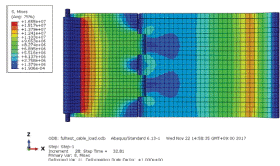
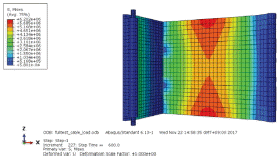
기립 가동 시에 구조적 안정성을 판단하기 위하여 가장 중요한 부분은 롤러프레임 부분과 전 · 후면방벽에 발생하는 응력상태이다. 만약 가동이 효율적으로 진행되지 못할 경우에는 롤러 프레임과 전 · 후면방벽에서 큰 응력이 발생할 가능성이 매우 크기 때문에 이 두 부분에 발생하는 응력을 분석하였다. 먼저 가동 시에 롤러프레임에 작용하는 Von-Mises 응력을 분석였으며, Fig. 12와 같이 응력 확인을 위한 다섯 개의 포인트(A, B, C, D, E)을 선택하였다.
Fig. 13은 롤러 프레임에서의 Von-Mises 응력을 나타낸 것으로서, 기립을 위한 가동이 시작되는 시기(포인트 A를 지나갈 때)와 가동이 종료되는 시기(포인트 E를 지나갈 때)에 응력이 가장 크게 나타났다. 각 포인트 모두 방벽이 롤러프레임을 지나갈 때 응력이 증가하는데, 처음 이동이 시작되는 A를 지나, B, C, D에서는 그 응력이 A에서 보다 50% 가량 감소하는 것으로 나타났다. 정량적으로 살펴보면, 기립 초기 A에서의 최대 응력은 55 MPa이고, 기립 완료 시 E에서의 40 MPa의 최대 응력이 발생하였다. 이는 강재의 항복강도 320 MPa의 17% 수준으로 안전한 것으로 나타났다. 따라서 롤러프레임의 강종을 변경하거나 단면적을 감소시켜도 될 것으로 판단된다.
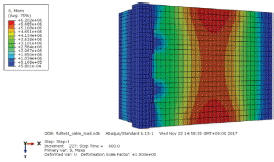
다음으로 전 · 후면방벽에 작용하는 응력에 대하여 분석하였다. 최대 응력 발생 위치를 정성적으로 분석해 보면 Table 3과 같다.
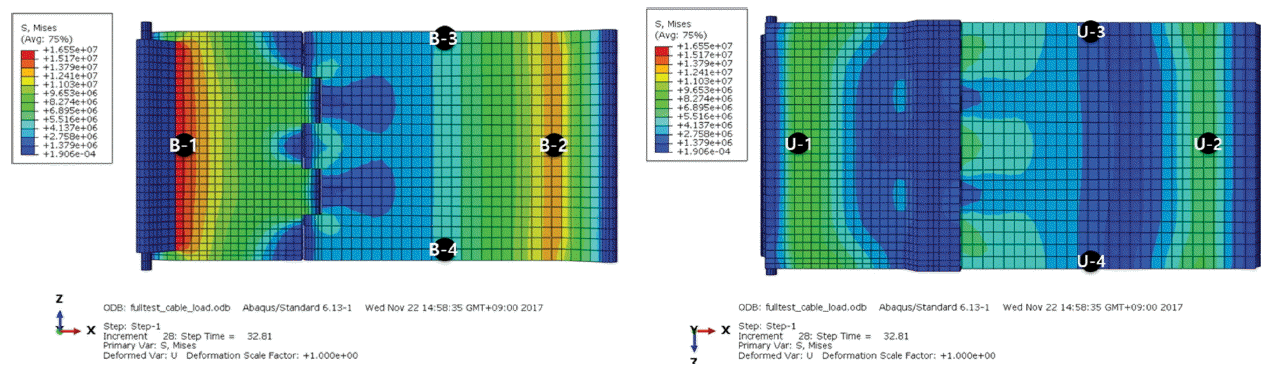
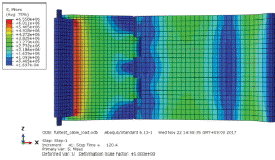
처음 기립을 위한 가동을 시작했을 때는 전면방벽의 힌지부와 가까운 부분에서 압축력을 받게 되어 응력이 가장 크게 발생하는 것으로 나타나며, 방벽이 이동을 한 후에는 후면방벽에서 큰 응력이 발생하는 것으로 나타났다. 발생 응력을 정량적으로 분석하기 위하여 Fig. 14와 같이 방벽 하면(bottom)방벽 하면의 B-1에서 B-4까지, 상면(upper)의 U-1에서 U-4까지 총 8개의 응력 체크 포인트를 설정하였다.
응력분석 결과 Fig. 15와 같이 발생응력이 16 MPa 이하로 작은 것을 볼 수 있었으며, 방벽 하면의 경우, 힌지부와 전 · 후면방벽의 경계부분인 B-1과 B-2가 가장 취약한 것으로 나타나 이 부분의 설계 시 고려가 필요할 것으로 판단된다. 방벽 상면의 경우 가동이 된 이후에 응력이 증가하지만 그 크기가 6 MPa로 작게 나타났다. 이러한 응력 분포는 Table 3의 응력 분포 그림을 보면 쉽게 파악할 수 있을 것으로 판단된다.
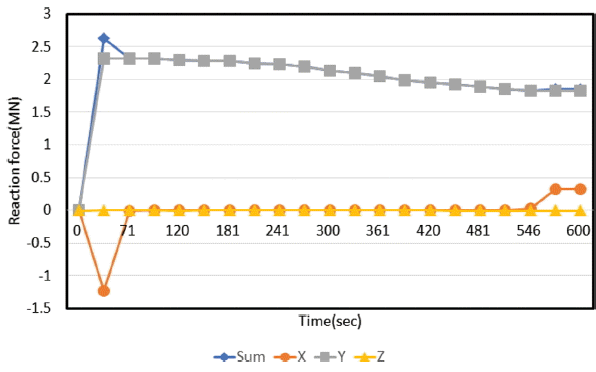
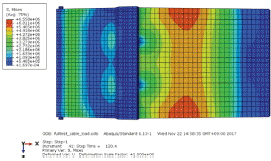
가동 초기에는 힌지와 방벽본체와의 연결부분에서 응력이 집중적으로 발생되었다가 기립이 진행됨에 따라 감소되며, 방벽 상면에서는 후면방벽에서 주로 응력이 발생하는 것으로 나타났다. 이와 같이 초기에 응력이 발생하는 이유는 Fig. 16과 같이 초기에 압축력을 받기 때문인 것으로 판단된다. 방벽이 기립을 시작한 후에는 x 방향의 반력이 0이 되는 것을 확인할 수 있다.
3.3 월파 작용 시 가동식 방벽의 거동 분석
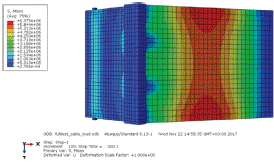
상기 절에서 수행한 방벽의 기립가동 완료 후에 Fig. 9의 불규칙파를 전면방벽에 고르게 가력하였다. Fig. 18은 Von-Mises 응력을 나타낸 것으로, 기립 이후에 응력이 힌지나 롤러 부분의 응력의 크기는 증가하지 않는 것을 확인할 수 있었으며, Fig. 15와 비교해보면 지속적으로 응력이 유지되는 것을 확인할 수 있다. 이를 통해 파력이 지속적으로 작용하는 것이 방벽의 응력변화에 크게 영향을 미치지 않는 것을 볼 수 있었다.
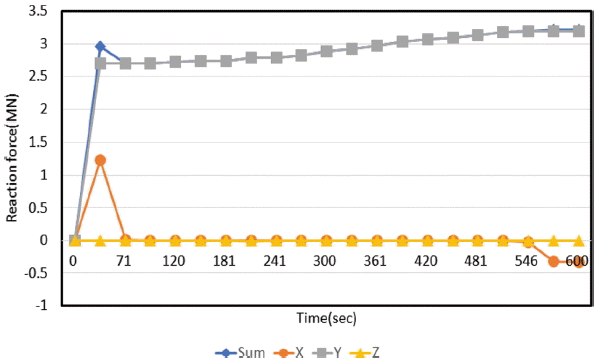
이는 케이블이 지속적으로 방벽을 인장하고 있기 때문에 방벽에 작용하는 응력의 변화가 적은 것으로 판단된다. 이는 Fig. 17과 Fig. 20을 비교해보면 확인할 수 있다. 가동 이후에도 케이블에 인장력이 지속적으로 작용하고 있기 때문에 롤러 프레임에 x 방향의 반력이 지속적으로 작용하고 있는 것을 확인할 수 있다. 이러한 조건으로 인하여 외부 월파에 의하여 Fig. 19와 같이 힌지부에서 x 방향의 반력이 지속적으로 변화되는 것을 확인할 수 있다.
본 구조해석에서 수행한 기립가동 시와 월파작용 시 방벽 구조물의 응력 및 반력 분석결과, 초기 가동 시에 가장 큰 응력이 발생하는 것으로 나타났으나 그 응력의 크기가 작아 구조물이 안전한 것으로 판단된다. 또한 본 삼각형 구조의 가동식 방벽은 월파에 적절하게 대응하는 것으로 나타났으나, 이 때 발생하는 지점 반력을 적절하게 설계해야 할 것으로 판단된다. 가동식 방벽은 롤러프레임과 후측에 위치한 힌지(End hinge)가 거의 모든 반력에 저항하기 때문에 롤러프레임과 힌지를 구조적으로 안전하게 정착시킬 수 있는 지지구조의 설계가 반드시 필요하다.
4. 결 과
본 연구에서는 월파에 대응할 수 있는 호안설치형 가동식 방벽 구조물을 수치해석적 방법을 통하여 분석하였다. 방벽의 수리성능을 확인하고 방벽 전면에 작용하는 압력을 산정하기 위한 수치실험을 수행하였으며, 이를 통하여 도출된 압력시계열을 가동 완료된 방벽에 작용시켜 구조성능을 분석하였다. 구조 해석을 통하여 기립 가동시의 방벽의 응력 분포 및 기립 완료 후 월파 작용 시의 방벽의 거동을 분석한 결과 우수한 성능을 발휘하는 것으로 나타났으며, 추후에 힌지 및 롤러프레임을 지지할 수 있는 적절한 설계 방법이 제안되어야 할 것으로 판단된다.