1. 서 론
해안공학에 있어서 파랑과 흐름의 상호작용에 대한 이해는 연안에서 발생하는 다양한 물리현상을 규명하고 연안구조물에 작용하는 외력을 정도 높게 평가하는데 있어서 매우 중요한 요소이다. 파랑과 흐름의 상호작용에 대한 초기연구는 주로 포텐셜 이론에 기초한 연구(Zaho and Faltinsen, 1988; Baddour and Song, 1990; Isaacson and Cheung, 1993; Lin and Hsiao, 1994)가 대부분 이였으나 최근에는 포텐셜이론의 한계를 극복하기 위해 PIV 혹은 PTV와 같은 영상해석기법을 이용한 실험적인 연구(Umeyama, 2009, 2011)와 Navier-Stokes 방정식에 기반한 수치해석적 연구(Li et al., 2007; Teles et al., 2013; Markus et al., 2013; Zhang et al., 2014)가 활발하게 수행되고 있다. 하지만, 이상의 주요연구들은 주로 파랑과 흐름의 상호작용에만 국한되어 있어 구조물 주변에서 발생하는 파랑과 흐름의 특성에는 직접적인 적용이 곤란하다. 한편, Lee et al.(2016)은 규칙파와 흐름의 공존장에서 불투과성 혹은 투과성을 갖는 배후경사면의 전면에 설치된 투과성잠제를 대상으로 흐름방향 등의 변화(파랑의 진행방향과의 순방향 및 역방향)에 따른 잠제 주변에서의 파동장 특성을 수치적으로 검토하였다. Lee et al.(2016)은 수치해석적 검토를 위해 오픈소스 CFD 코드인 OLAFOAM(Higuera et al., 2015)을 적용하였으며, OLAFLOM의 타당성은 1) 투과성매질에서 단파의 작용에 따른 수위변동을 수리모형실험으로부터 규명한 Liu et al.(1999)의 연구, 2) 잠제 주변에서 규칙파의 수위변동을 고찰한 Ranasinghe et al.(2009)의 연구 및 3) 흐름과 규칙파의 상호작용 조건하에서 수위와 유속의 변화를 실험적으로 검토한 Umeyama(2011)의 연구에서 얻어진 각각의 수치 및 실험결과와의 비교 · 검토로부터 검증하였다.
본 연구는 Lee et al.(2016)의 후속연구로써 실해역의 환경을 고려하여 규칙파를 불규칙파로 확장하여 투과성잠제가 설치된 해역을 대상으로 흐름 및 구조물과의 상호작용에 따른 파동장의 특성을 수치해석적으로 분석하였다. 또한, 투과성잠제 배후사면의 영향을 고려하기 위해 모래 및 자갈로 구성된 사면을 각각 고려하여 수치실험을 실시하였다. 수치해석모델은 Lee et al.(2016)에서 적용한 GNU-GPL 라이선스로 공개된 오픈소스 기반의 CFD 코드인 olaFlow(Higuera et al., 2015; olaFlow는 OLAFOAM의 명칭이 변경된 것임)을 동일하게 적용하였다. 불규칙파랑은 조파소스를 이용한 수치조파기법을 적용하였으며, 목표주파수스펙트럼과 조파파랑의 주파수스펙트럼과의 비교 · 검토로부터 불규칙파랑에 대한 olaFlow 모델의 타당성을 검증하였다. 한편, 불규칙파-흐름-잠제의 상호작용에 대한 수치해석조건은 Lee et al.(2016)에서와 동일한 제원과 조건의 잠제, 수심 및 흐름을 적용하였으며, 입사파랑으로는 규칙파의 파고와 주기에 각각 대응하는 유의파고와 유의주기의 불규칙파랑을 적용하였다. 이로부터 불규칙파와 흐름이 공존하는 유체장에 모래 혹은 자갈로 구성된 배후사면의 전면에 놓인 투과성잠제구조물을 대상으로 흐름방향 등의 변화에 따른 잠제 주변에서 제곱평균제곱근파고변화, 주파수스펙트럼의 변동, 쇄파양상의 차이, 평균 유속 및 평균난류운동에너지의 변화 등과 같은 수리특성을 면밀히 검토하였다.
2. 수치해석이론
본 연구에서 이용한 CFD 수치해석코드인 olaFlow는 비혼합 · 비압축성의 혼상유체(액체 및 기체)의 해석을 위하여 식 (1)의 연속방정식과 식 (2)의 RANS(Reynolds-Averaged Navier-Stokes) 방정식을 유한체적법에 기초하여 이산화한다.
여기서, t는 시간, xi는 공간벡터좌표, ρ는 유체의 밀도, ui(i = x, y, z)는 유체속도의 Cartesian 성분, p*는 Pseudodynamic 압력, Xj는 위치벡터, φ과 D50은 해석영역 내에 위치하는 투과성구조물의 공극률과 중앙입경을 각각 나타내며, μeff는 μ + νturb로 μ는 점성계수, νturb는 난류동점성계수이고, [CT]는 투과성구조물에 의한 저항력으로 다음의 식 (3)과 (4)로 주어진다.
여기서, α, β는 선형 및 비선형마찰계수로 본 연구에서는 층류흐름, 층류와 난류가 혼합된 흐름 및 난류흐름에 대한 수치 및 수리실험결과를 바탕으로 Jensen et al.(2014)이 제시한 α = 500, β = 2.0을 각각 적용하였다. 또한, KC는 Keulegan-Carpenter 수로 TouM/D50φ를 나타내며, To은 진동주기이고, uM은 유체입자의 최대진동속도이다.
혼상류에 있어서 액체와 기체의 경계면 추적에는 계산격자 내에서 유체(액체)가 점유하는 체적을 나타내는 유체율 함수(VOF 함수) F를 이용하는 VOF법을 적용하며, VOF 함수는 액체셀의 경우 F = 1, 기체셀의 경우 F = 0, 그리고 액체와 기체를 모두 포함하고 있는 경계셀의 경우는 0 < F < 1의 값을 갖는다. VOF 함수 F는 식 (1)과 식 (2)로부터 산정된 유체속도에 의해 식 (5)의 이류방정식으로부터 계산된다.
여기서, uic는 인공압축항으로 |uic| =min[cα|ui|, max(|ui|)]과 같이 주어지며, 본 연구에서는 cα = 1을 적용하였다. 또한, 각각의 계산셀에서 유체의 밀도와 점성계수는 VOF 함수를 가중치로 적용하여 다음과 같이 산정될 수 있다.
또한, 전술한 난류동점성계수 νturb는 LES 모델을 적용하여 산정하였으며, 그 밖의 olaFlow에 대한 상세한 수치해석기법은 Lee et al.(2016) 혹은 olaFlow 매뉴얼(http://openfoamwiki.net/index.php/Contrib/olaFlow)을 참조하기 바란다.
불규칙파는 선형파이론으로부터 얻어진 성분파의 주파수에 하나씩 순번을 붙여 무한급수의 합으로 고려된다. 수치조파에서는 조파지점에서 수면파형 η, 수평 및 연직유속 u, w의 시간변동이 필요하며, 이들은 각각 식 (8)~(10)과 같이 주어진다.
여기서, εm은 Random한 위상각, fm은 주파수, am은 진폭, km은 파수, M은 성분파의 수, h는 수심이다. 그리고, 연직좌표 z는 정수면에서 연직상방을 (+)방향으로 취하며, 진폭 am은 다음의 식 (11)로 정의된다.
여기서, Δf는 주파수폭, S(f)는 파랑에너지밀도이며, 본 연구에서는 불규칙파의 스펙트럼은 불규칙파를 모의하는 데에 널리 사용되고 있는 식 (12)의 Modified Bretshneider-Mitsuyasu(Goda, 1988) 스펙트럼을 적용하였다.
여기서, H1/3은 유의파고, T1/3은 유의파주기를 나타낸다. 또한, 주파수 fm의 선택방법에는 주파수스펙트럼을 등구간으로 분할하는 방법과 각각의 성분파의 진폭이 동일하도록 등에너지로 분할하는 방법 등이 있다. 본 연구에서는 Modified Bretshneider-Mitsuyasu(Goda, 1988) 스펙트럼에 대해 등에너지로 스펙트럼을 분할할 수 있는 Goda(2000)에 의해 제안된 다음의 식 (13)을 이용하여 주파수 fm을 선택하였다.
3. 수치해석
3.1 불규칙파의 조파검증
우선, 본 연구에서 적용한 olaFlow 모델에 있어서 조파소스에 의한 불규칙파의 수치조파 성능을 검증하기 위하여 구조물이 설치되지 않은 일정수심(h = 10.1m)의 수치파동수조에서 유의파고 H1/3 = 3.0 m, 유의주기 T1/3 = 11.0 s를 목표로 불규칙파를 조파하였다. 적용한 스펙트럼은 식 (12)에 제시한 Modified Bretshneider-Mitsuyasu 스펙트럼(Goda, 1988)이며, 150개의 성분파를 선형중첩하여 조파하였다. 그리고, 파랑의 반사 및 재반사가 해석영역의 파동장에 미치는 영향을 제거하기 위하여 수조 끝단에는 감쇠경계를 적용하였고, 조파판에는 조파와 감쇠가 동시에 작용하는 Pure active wave absorption 경계를 적용하였다. 이러한 조건으로부터 계산된 불규칙파형과 주파수스펙트럼이 fig 1(a)와 1(b)에 각각 제시되어 있고, 동시에 fig 1(b)에는 목표한 Modified Bretshneider-Mitsuyasu 스펙트럼(Goda, 1988)도 병기되어 있다. 그림을 살펴보면 장시간의 해석에도 평균수위상승과 같은 특이한 사항이 나타나지 않으며, 영점상향교차법에 의한 파별해석으로부터 얻어진 유의파고 H1/3 = 3.067 m, 유의주기 T1/3 = 11.014 s와 입력치가 매우 잘 일치하는 결과를 얻을 수 있었다.
3.2 파랑변형
3.2.1 계산조건
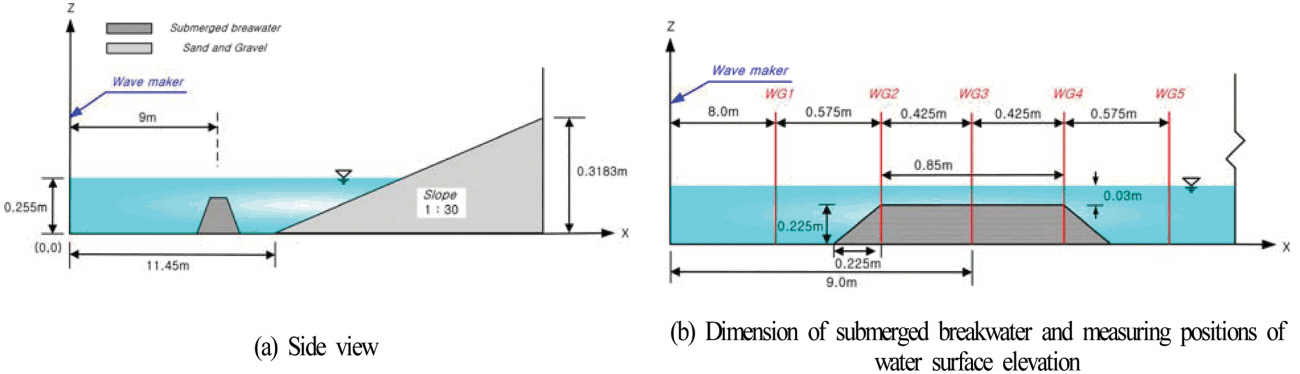
fig 2와 같은 일정 수심 h = 25.5 cm를 갖는 파동장에 설치된 투과성잠제를 대상으로 2차원수치파동수조(길이 21 m, 높이 0.42 m)를 구성하였다. 격자크기는 조파지점에서부터 7.05~10.95 m의 범위에는 Δx = Δz = 0.75 cm의 정방격자를, 그 이외의 영역에는 Δx = 1.5 cm, Δz = 0.75 cm의 가변격자를 구성하였다. 조파판에서 9 m 이격된 지점에 투과성잠제를 설치하였으며, 11.45 m 이격된 지점에서부터 모래 혹은 자갈로 구성되는 1 : 30의 경사면을 설치하였다. 잠제는 높이 22.5 cm, 천단폭 0.85 m를 가지며, 구조물의 천단상에서 강제쇄파를 유도하기 위해 전 · 후의 비탈면경사를 1 : 1로 설정하였다. 잠제의 구성재료는 공극률 φ = 0.44, 중앙입경 D50 = 2 cm를 가지며, 전술한 바와 같이 저항계수로 Jensen et al.(2014)이 제시한 α = 500, β = 2.0을 적용하였다. 배후사면은 모래 혹은 자갈로 구성된 경우를 대상으로 하였으며, 모래의 경우는 공극률 φ = 0.28, 중앙입경 D50 = 0.2 cm, 저항계수 α = 0.0, β = 3.0을, 자갈의 경우는 공극률 φ = 0.49, D50 = 1.59 cm, 저항계수 α = 500, β = 2.0을 각각 적용하였다. 바닥경계조건으로는 Neumann 조건인 ∂f/∂xi = 0을 적용하였다.
Table 1은 불규칙파의 수치실험에서 적용한 조파이론, 입사파의 제원 및 흐름속도의 방향과 크기를 각각 나타낸다. 표에서는 흐름이 없고 오직 파랑만이 존재하는 경우를 WCN으로, 흐름과 파랑의 진행방향이 동일한 순방향인 경우를 WCF로, 흐름과 파랑의 진행방향이 서로 반대인 역방향인 경우를 WCO로 표기 및 정의한다(이하 동일).
3.2.2 수위변동과 주파수스펙트럼
(1) 배후사면이 모래인 경우
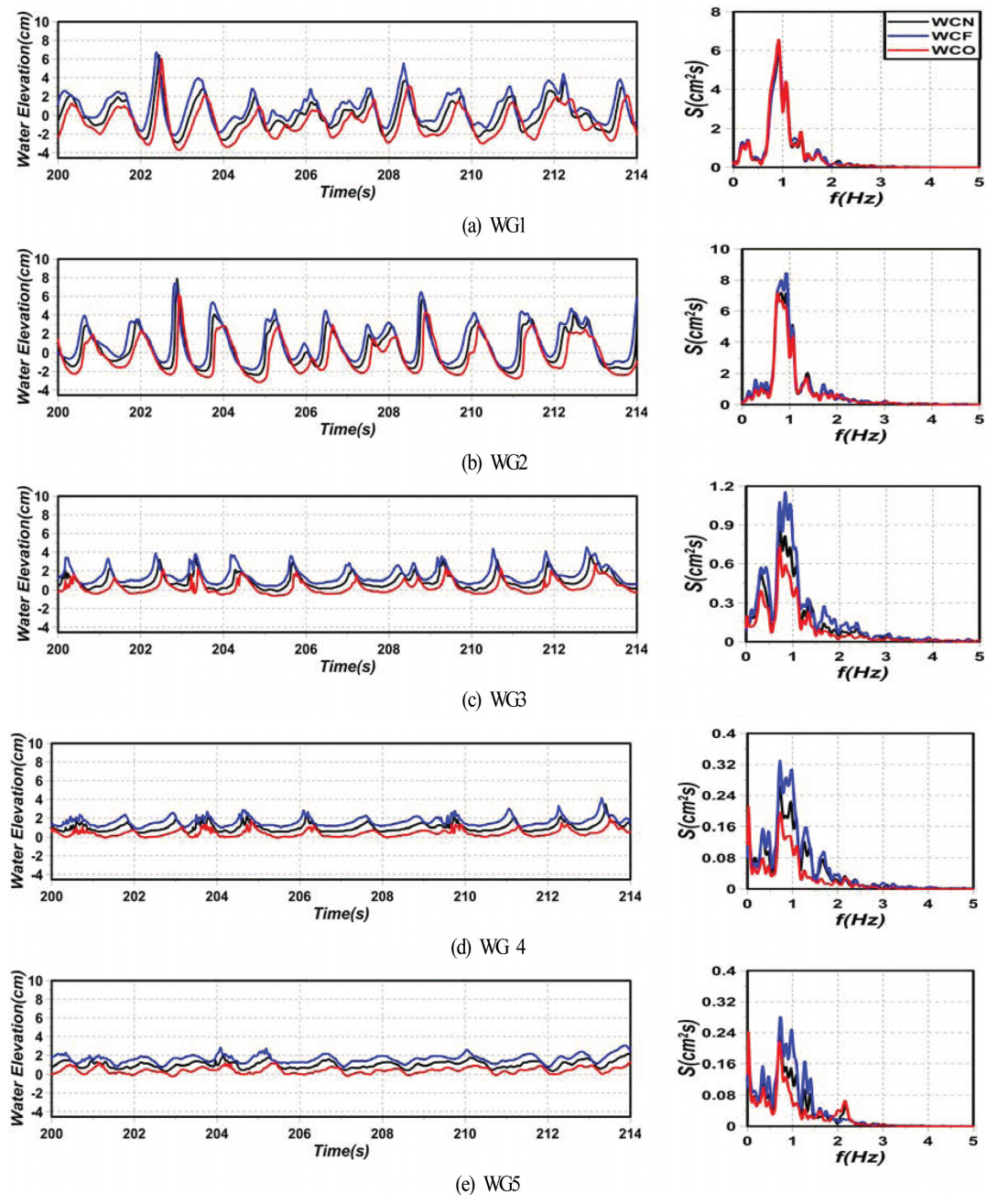
fig 3은 배후사면이 모래인 경우에 잠제 주변에서 수위변동과 주파수스펙트럼의 결과를 나타낸 것이다. 수위변동의 측정위치는 fig 2(b)에 나타내는 바와 같이 잠제의 전면부(WG1, x = 8.0 m), 잠제천단의 시작점(WG2, x = 8.575m), 잠제천단의 중앙(WG3, x = 9.0 m), 잠제천단의 끝부분(WG4, x = 9.425 m) 및 잠제의 후면부(WG5, x = 10.0m)에 각각 해당하며, 수치계산결과는 주파수스펙트럼이 충분히 재현될 수 있도록 지속시간 50 s(200 s~250 s) 동안에 취득된 파랑을 대상으로 해석하였다.
수위변동을 살펴보면 잠제 전면부 WG1에서는 입사파와 잠제에 의한 반사파와 위상간섭의 영향으로 쌍봉형의 수위변동이 일부 발생하며, 잠제천단의 시작점 WG2에서는 급격한 수심의 감소에 따른 천수변형으로 WG1에 비해 보다 큰 수위변동이 나타나고, 전 · 후로 비대칭성이 큰 비선형파가 형성되는 것을 볼 수 있다. 다음으로, 잠제 천단상의 WG3에서는 수위변동의 진폭이 급격히 감소된 것을 확인할 수 있고, 이로부터 WG2와 WG3 사이의 위치에서 쇄파가 발생되었다는 사실을 추정할 수 있다. WG3에서의 수위변동에서 파봉 부분이 솟아있고, 파곡 부분이 평탄하여 상대적으로 파곡의 길이가 길게 나타나므로 상하의 비대칭성(Kurtosis)이 크며, 또한 WG2에서와 같이 파형에서 좌우의 비대칭성(Skewness)이 크게 나타난다. WG4의 경우는 파가 잠제 천단상으로부터 보다 더 전파되었기 때문에 파고감쇠로 인하여 수위변동이 WG3보다 작게 나타나며, 전술한 파형에서 좌우 및 상하의 비대칭성이 유지되고 있다. WG5는 잠제 배후부로 파형에 고주파성분이 포함되어 나타나지만 파의 재형성과정을 통하여 파형에서 좌우의 비대칭성이 개선된 상황을 볼 수 있다.
입사파랑의 진행에 따른 각각의 위치에서의 주파수스펙트럼을 살펴보면 WG1에서 첨두주파수 f ≈ 0.93/s가 유의주파수 f = 1/s보다 저주파수(장주기)영역에 놓이고, 주파수스펙트럼 전체가 저주파수영역으로 약간 이동된 결과를 나타낸다. 이와 같이 첨두주파수가 저주파수영역으로 이동되는 현상은 WG2~WG5에서도 나타나며, 파의 전파에 따라 보다 심화되는 양상을 확인할 수 있다. 흐름방향에 따른 주파수스펙트럼의 변동양상을 살펴보면 잠제 전면부 WG1에서는 WCN의 주파수스펙트럼에 비해 WCO가 크고, WCF가 작은 값을 나타내지만 전체적으로 WCF, WCN, WCO의 순으로 첨두주파수 근방에서 주파수스펙트럼이 큰 값을 나타내며, 특히 잠제 천단상 및 배후부에 걸쳐서 고 · 저주파수영역으로 파랑에너지가 분산되는 것을 볼 수 있다. 여기서, WG4와 WG5의 경우에 f ≈ 0/s에서 급격히 증가되는 긴 장주기의 파랑에너지 성분을 볼 수 있으며, 이는 Lara et al.(2006)에 의해서도 지적된 바와 같이 부진동에 의한 성분이다. 반면에, 규칙파의 해석에서는 하나의 주파수 성분만을 가지므로 이러한 부진동 성분은 나타나지 않는 것으로 알려져 있다(Garcia et al., 2004; Lee et al., 2016).
각 위치에서 주파수스펙트럼의 크기변화를 살펴보면 WG2에서 급격히 상승된 큰 값을, 반면에 WG2에서 WG5로 갈수록 감쇠하는 작은 값을 각각 나타낸다. 특히, WG2와 WG3 사이에 크기변화가 급격히 발생하므로 전술한 바와 같이 이 위치 사이에 쇄파가 발생되었고, 이로 인하여 파랑에너지의 감쇠가 있었다는 사실을 유추할 수 있다. 따라서, 각 위치에서 주파수스펙트럼의 변동양상은 수심이 급격히 얕아짐으로서 발생하는 천수변형, 잠제 천단상에서 쇄파변형, 천단에서 배후역으로 수심의 급격한 증가로 인한 반사 및 모래로 구성된 배후사면에서의 반사, 그리고 흐름의 존재여부와 흐름방향에 따라 크게 변화되는 것으로 판단되며, 많은 파라미터의 작용에 따른 복잡한 과정으로 이해될 수 있다. 여기서, 파의 전파에 따른 파랑에너지의 감쇠는 후술하는 평균난류운동에너지(난류강도), 누적평균난류운동에너지, 쇄파로 인한 파랑에너지의 소산 및 흐름방향에 따른 쇄파양상과도 연관성을 가진다.
(2) 배후사면이 자갈인 경우
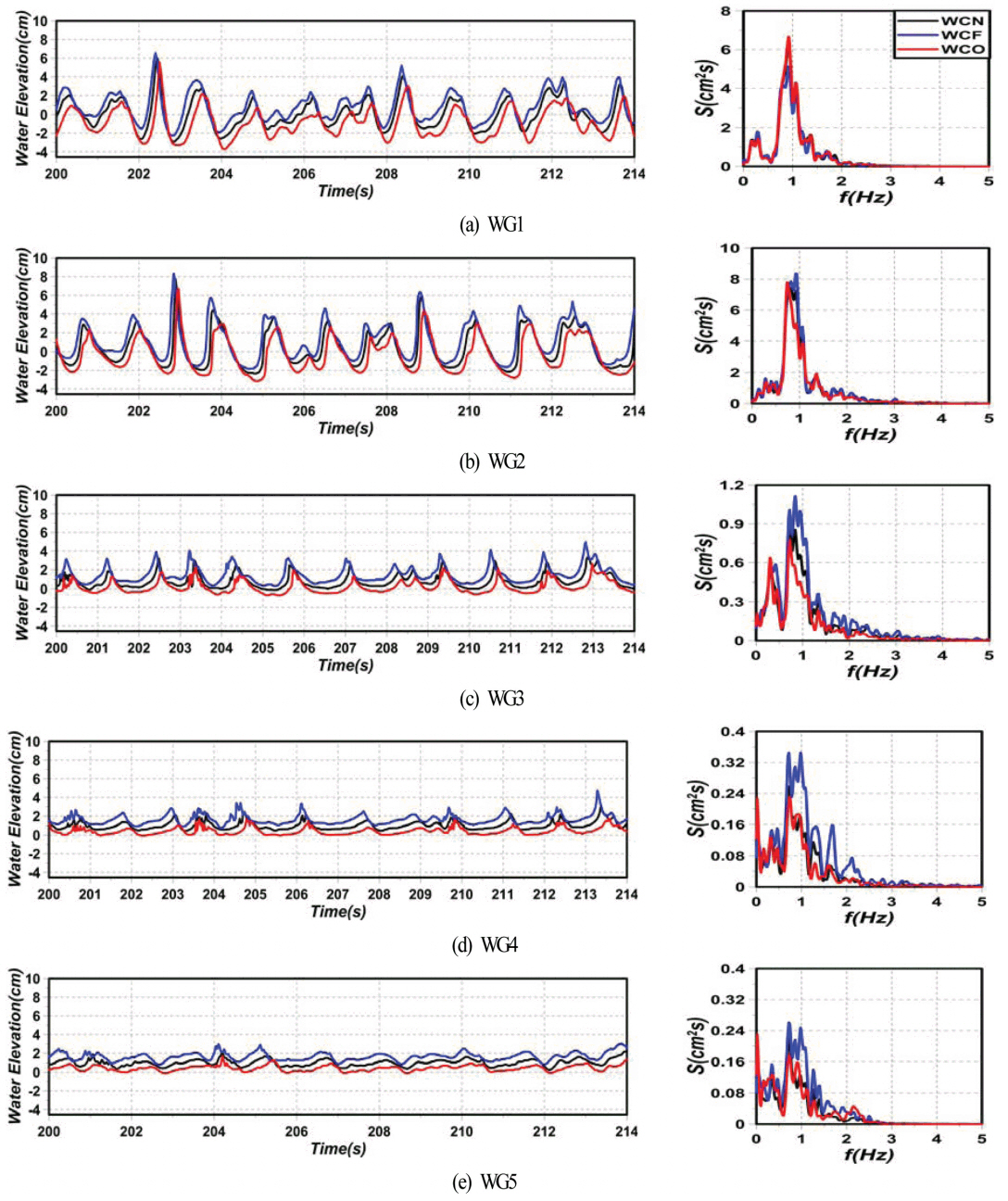
fig 4는 배후사면이 자갈인 경우에 잠제 주변에서 수위변동과 주파수스펙트럼의 결과를 나타낸 것이다. 그림을 살펴보면 전술한 배후사면이 모래일 때와 유사하게 잠제 전면부에서 잠제에 의한 반사파의 영향에 의해 일부에서 쌍봉형의 수위변동이 발생하고, 천단 전면부에서 비선형파의 발달에 따라 비대칭파형이 나타난다. 그리고 파의 전파에 따라 쇄파 발생, 비선형파의 발달 및 감쇠 등이 동반되며, 또한 이러한 수위변동의 현상과 특성을 우측의 해당하는 주파수스펙트럼으로부터도 명확히 확인할 수 있다. 전체적으로 파의 전파 및 흐름방향에 따른 주파수스펙트럼의 변동추이, 잠제 천단상 및 배후부에 걸쳐 고 · 저주파수영역으로 파랑에너지의 분산, WG4와 WG5에서 긴 장주기의 파랑에너지에 해당하는 부진동에 의한 성분의 발생, 각 위치에서 주파수스펙트럼의 크기 변화 등은 전술한 바와 같이 배후사면이 모래인 경우와 유사한 특성을 나타낸다.
하지만, 전술한 배후사면이 모래인 경우와 다소 상이한 결과는 모래의 경우보다 잠제 중앙점인 WG3에서 WCF 및 WCN의 첨두주파수 근방에서 주파수스펙트럼이 상대적으로 작은 값을, 천단의 끝부분인 WG4에서 WCF와 WCO는 큰 값을, 또한 잠제 배후인 WG5에서 WCF, WCO 및 WCN 모두 작은 값을 각각 나타낸다. 이러한 결과는 전술한 바와 같이 많은 파라미터의 영향에 의한 복잡한 변동과정으로 발생되지만 근본적으로 자갈로 구성된 배후사면의 공극률이 모래의 경우보다 크기 때문에 나타나는 낮은 반사율에 기인하는 것으로 판단된다.
3.2.3 쇄파형상
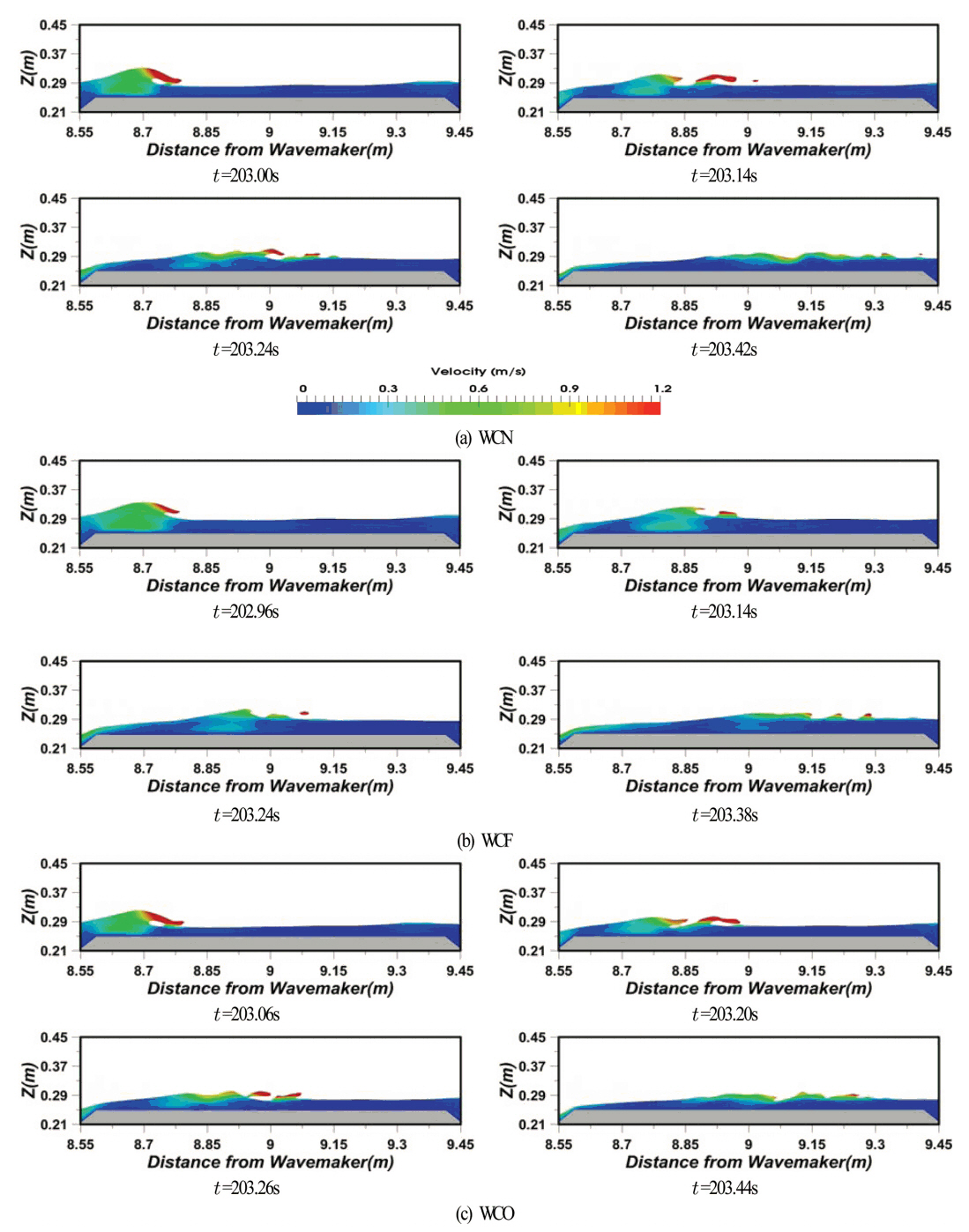
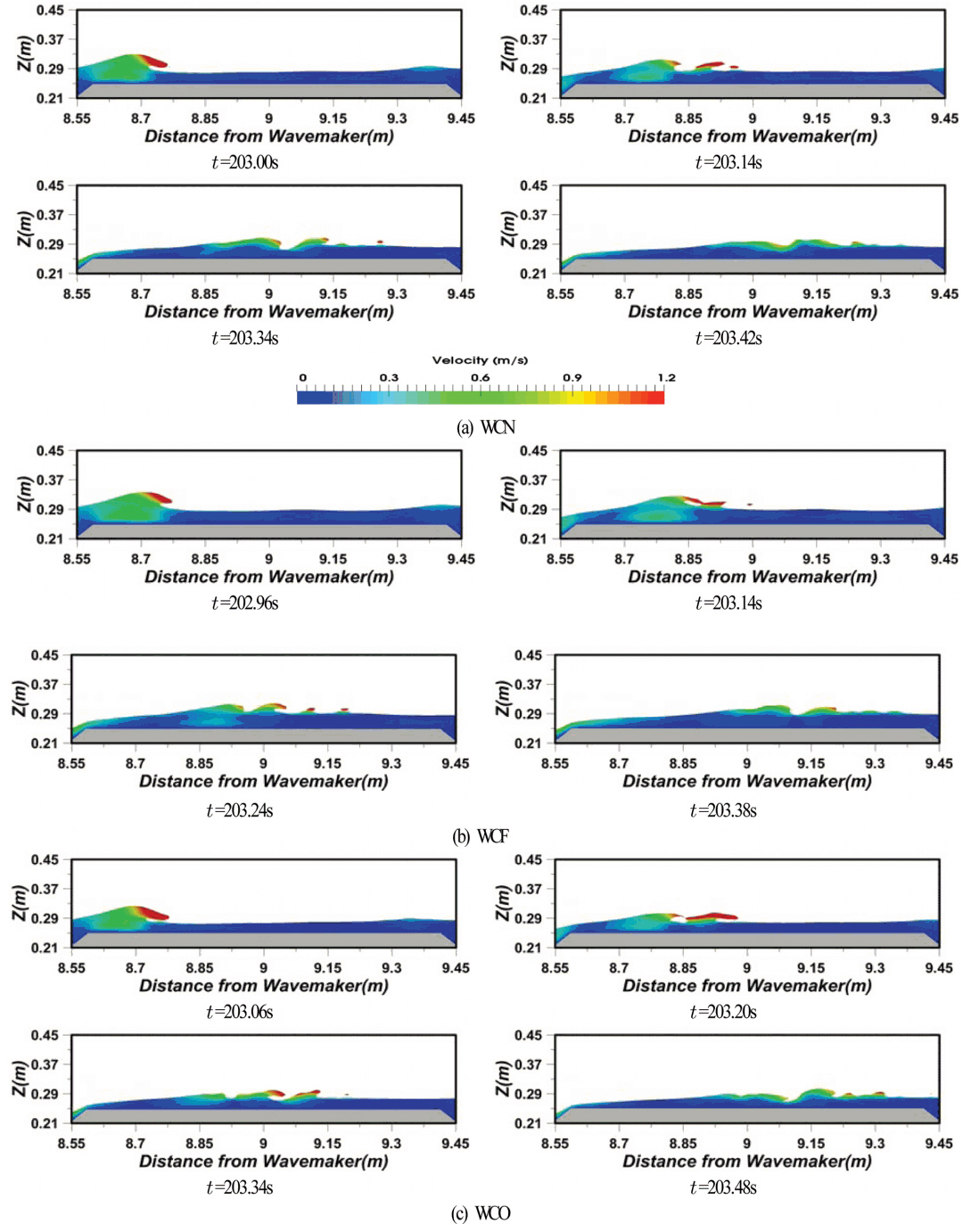
fig 5는 잠제 배후에 모래사면이 위치하는 조건하에서 WCN, WCF 및 WCO의 경우에 잠제 천단상에서 쇄파되는 일련의 과정을 Snapshot으로 나타낸 것이다. 대상파랑은 fig 3(a)와 4(a)의 t = 202~204 s에 나타나는 최대파를 대상으로 하였으며, 흐름의 유무에 따라 쇄파의 발생위치와 및 위상이 다소 상이하지만 상호비교를 위해 쇄파 진행과정의 위상을 가능한 범위내에서 일치시킨 결과이다. 그림으로부터 확인되는 바와 같이 입사파는 잠제 천단상에서 쇄파되고, 더불어 파 전파방향으로 수평유속이 증가하는 것을 알 수 있다. 흐름의 방향에 관계없이 권파형쇄파가 발생하지만 WCO, WCN, WCF의 순으로 보다 뚜렷한 권파형쇄파가 발생한다. 한편, WCF의 경우 초기에는 권파형쇄파를 보이다가 종국에는 파봉이 부서지는 붕괴파형쇄파를 동시에 나타낸다. WCF에서 복합적인 쇄파형이 발생하는 것은 잠수계류부체상에서 발생하는 쇄파형을 실험적으로 검토한 Iwata et al.(1990)에 의하면 잠수계류부체가 진행파와 동일한 위상으로 운동할 때 부체상에서 복합형의 쇄파가 발생된다는 사실에 비춰보면 본 연구의 WCF에서 복합적인 쇄파형을 나타내는 것은 진행파와 흐름이 같은 방향이기 때문으로 판단된다.
fig 6은 잠제 배후에 자갈사면이 위치하는 조건하에서 fig 5와 동일하게 WCN, WCF 및 WCO의 경우에 최대파가 잠제 천단상에서 쇄파되는 일련의 과정을 Snapshot으로 나타낸 것이다. fig 5와 같이 잠제 배후에 모래사면이 위치하는 경우와 동일하게 WCO, WCN, WCF의 순으로 보다 뚜렷한 권파형쇄파가 발생하지만 WCF의 경우는 배후에 모래사면이 위치하는 경우와는 상이하게 종국에 붕괴파형쇄파를 동시에 나타내지는 않는다. 그리고, 권파형쇄파가 발생하는 경우에도 그 규모가 모래사면의 경우보다 약간 약하게 나타난다. 이러한 결과는 잠제 천단상의 파형과 흐름에 영향을 미치는 배후부 경사면에서 반사율이 상이하기 때문이며, 자갈사면의 경우가 모래의 경우보다 공극율이 크기 때문에 반사율이 작게 주어진다.
3.3 파고분포
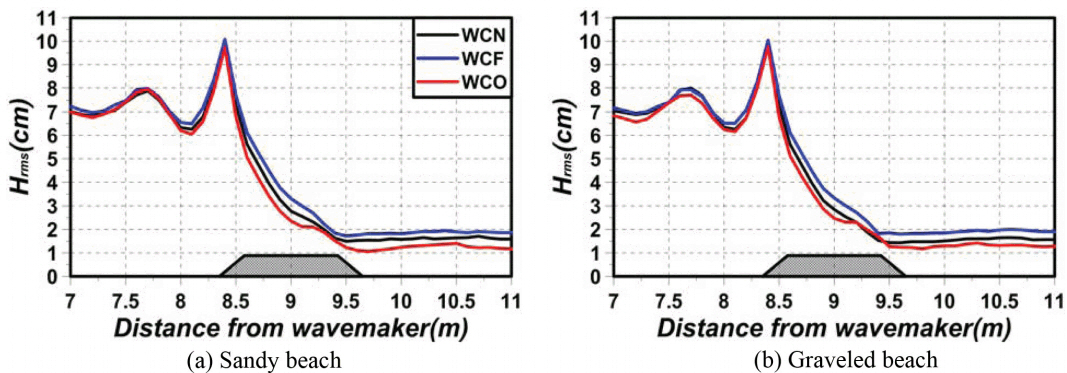
fig 7은 fig 3과 4로부터 도출한 제곱평균제곱근파고(Root mean square wave height) Hrms의 공간분포를 나타낸 것이며, fig 7(a)가 배후사면이 모래인 경우를, fig 7(b)가 자갈인 경우에 각각 해당한다. 전반적으로 잠제로 인한 반사파의 영향 때문에 잠제 전면부에서는 부분중복파의 파동장이 형성되는 것을 알 수 있고, 잠제의 천단상과 후면부에 걸쳐서 배후사면이 모래나 자갈에 관계없이 WCN보다 WCF에서 Hrms 파고가 증가하고, WCO에서 감소하는 경향을 확인할 수 있다. 이로부터 잠제와 같은 구조물이 설치된 흐름-파동장에서는 위치에 따라 흐름의 방향에 따라 Hrms 파고의 변화가 증가하거나 감소하는 일률적인 경향을 나타나는 것이 아니라는 중요한 사실을 알 수 있으며, 이러한 결과는 규칙파의 경우와도 일치한다(Lee et al., 2016).
Table 2는 fig 3과 4에서 나타낸 각 파고계 위치에서의 수위변동으로부터 Hrms 파고를 산정한 것이다. 흐름이 없을 때를 기준으로 파고감쇠율([[WG1에서 Hrms 파고]-[WG5에서 Hrms 파고]]/[WG1에서 Hrms 파고])을 산정하면 배후사면이 모래와 자갈일 때 WCO에서 각각 79.70%와 80.51%의 파고감쇠율이 얻어지고, WCF에서 73.85%와 78.80%의 값이 얻어지며, 이로부터 WCO에서 파고감쇠율이 상대적으로 크다는 것을 알 수 있다. 이러한 결과는 후술하는 흐름방향에 따른 평균난류운동에너지(난류강도)와 누적평균난류운동에너지의 공간적인 차이 및 전술한 쇄파양상의 차이에 따른 파랑에너지 소산양의 차이에 기인하는 것으로 판단된다.
3.4 평균유속 및 평균난류운동에너지의 분포
3.4.1 평균유속
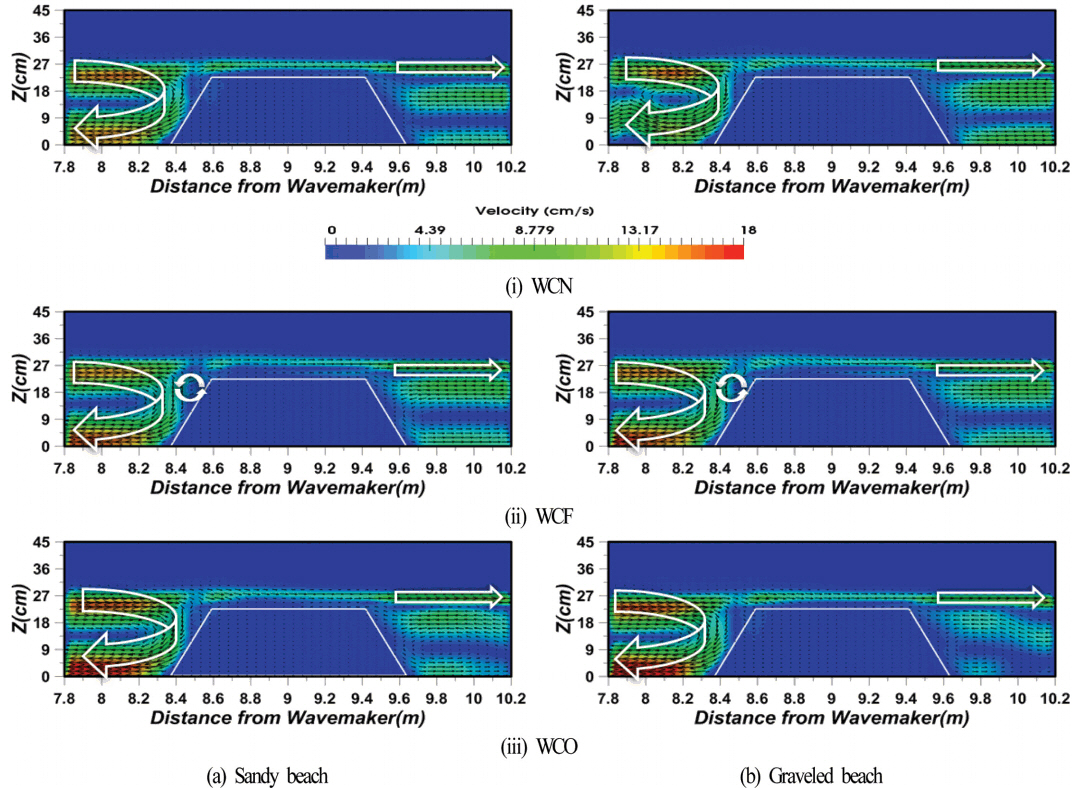
fig 8은 정상상태에 도달한 50 s 동안의 파랑을 대상으로 시간평균한 평균유속을 나타낸 것으로 fig 8(a)와 8(b)는 각각 배후사면이 모래와 자갈인 경우에 해당하며, 각각에서 (i)은 WCN, (ii)는 WCF, (iii)은 WCO의 경우이다. 그림으로부터 배후사면이 모래 혹은 자갈에 관계없이 WCF의 경우에만 잠제 전면에서 반시계방향의 순환셀이 형성되고, 잠제 전면의 해저면에서는 해측으로 강한 유속이 발생한다. 해저면에서 유속의 크기는 WCO, WCF, WCN의 차례로 강하게 발생하며, 배후사면이 자갈인 경우에는 그 차이를 더욱 명확히 확인할 수 있기 때문에 WCO와 공극율이 큰 배후사면의 조건하에서는 잠제 전면에서 세굴의 가능성이 보다 높아진다는 것을 예측할 수 있다.
3.4.2 평균난류운동에너지
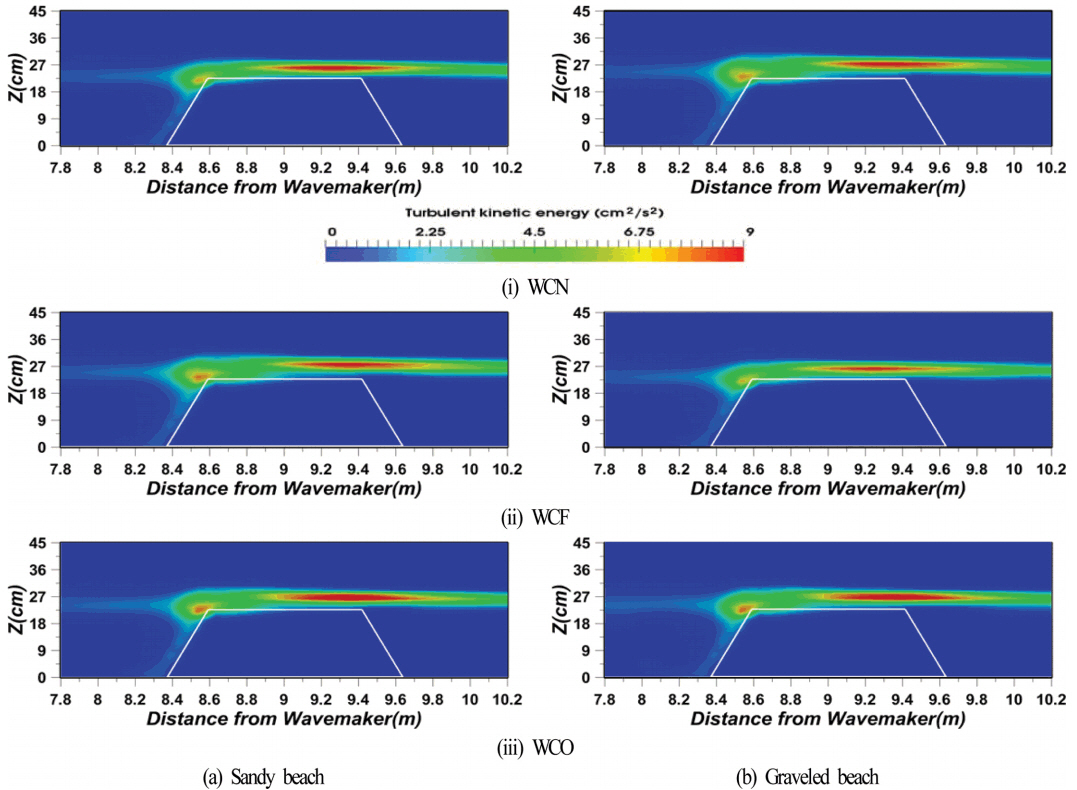
fig 9는 평균난류운동에너지를 나타내며, 이는 ( u ' x 2 + u ' z 2 ) / 2 u ' x 2 + u ' z 2 / 2
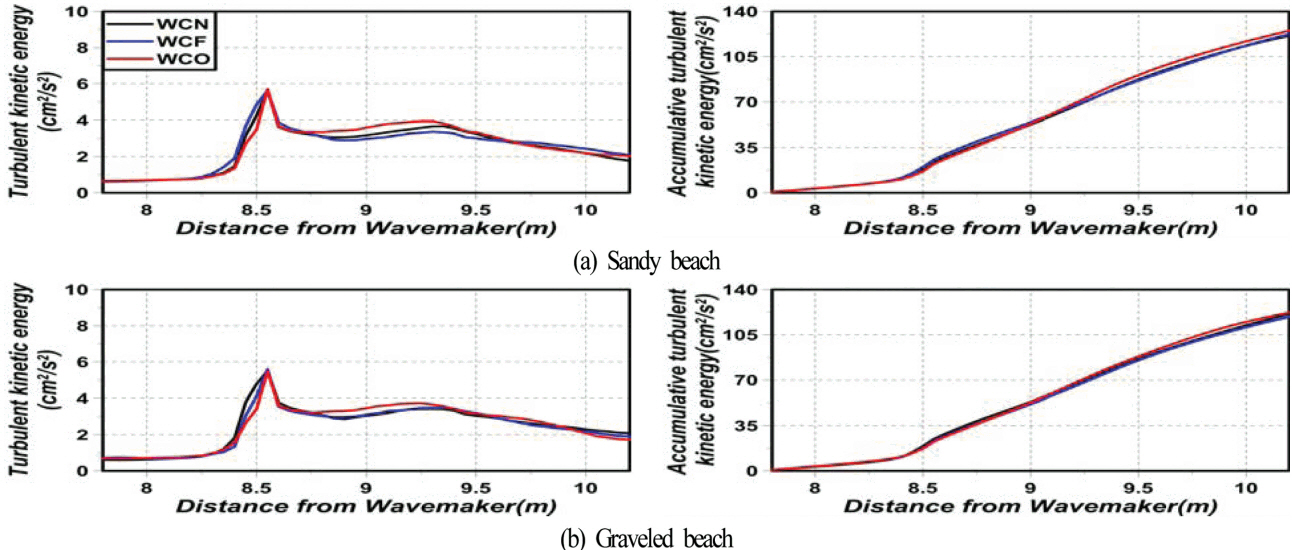
fig 10은 fig 9의 결과를 잠제 천단(z = 0.21m)부터 난류운동에너지의 영향이 미치는 영역(z = 0.285m)까지 수심방향으로 평균한 결과, 즉 시간평균의 연직방향평균난류운동에너지(시 · 공간평균난류에너지로 칭한다)와 그에 대한 누적난류운동에너지(시 · 공간누적평균난류에너지로 칭한다)를 나타낸다. 그림으로부터 시 · 공간평균난류에너지의 공간분포를 살펴보면 배후사면의 모래 혹은 자갈 여부에 관계없이 잠제 전면의 비탈면상에서 크게 나타나고, 천단 중앙의 후반부에서 약간 크게 나타나며, 천단 중앙의 후반부에서 WCO(WCF)의 경우가 WCN보다 큰(작은) 값을 나타내는 것을 확인할 수 있다. 다음으로, 공간파고변화와 직접적인 연관성을 갖는 시 · 공간누적평균난류에너지를 살펴보면 배후사면이 모래 혹은 자갈 여부에 관계없이 잠제 전면부에서 흐름의 유무와 흐름방향에 따른 차이는 거의 나타나지 않지만 잠제 천단 중앙을 지나서부터 차이가 나타나며, 흐름의 여부에 따른 값의 차이는 미미하지만 전반적으로 WCO의 경우가 WCN과 WCF보다 큰 값을 가진다는 것을 알 수 있다.
이러한 사실로부터 구조물과 배후사면이 고려되지 않은 파-흐름장에 대해 Umeyama(2011)도 지적하고 있는 바와 같이 흐름의 방향에 따른 파고감쇠율은 누적난류운동에너지와 크게 연관되어 있는 것을 확인할 수 있고, 누적난류운동에너지가 높을수록(낮을수록) 파고감쇠율이 높게(낮게) 나타나는 것을 알 수 있다. 또한, 이와 더불어 전술한 규칙파-흐름 공존장내의 잠제 주변에서 파랑특성을 연구한 Lee et al.(2016)의 결과와 동일하게 불규칙파-흐름의 공존장내에서도 배후사면에서 반사율의 영향과 흐름의 유무와 흐름방향에 따른 구조물상에서 쇄파형상 및 쇄파고도 동시에 영향을 미치는 것으로 판단된다.
4. 결 론
본 연구에서는 olaFlow 모델에 의한 수치해석으로부터 투과성잠제가 설치된 일정 수심의 수치파동수로에 역방향 혹은 순방향흐름이 있는 상태에서 불규칙파를 조파하여 잠제 주변에서 수위변동과 그의 주파수스펙트럼, 파고분포, 쇄파형상, 평균흐름 및 평균난류운동에너지와 누적평균난류운동에너지 등과 그들의 상호연관성을 면밀히 검토 · 분석하였다. 이로부터 도출된 중요한 사항을 다음에 요약 · 기술한다.
(1) 흐름의 영향에 따른 제곱평균제곱근파고에 대해, 배후 사면의 모래 혹은 자갈의 여부에 관계없이 잠제의 전면부에서는 역방향흐름의 경우가 흐름이 없는 경우보다 제곱평균제곱근파고가 높지만 잠제 천단상의 전반부에서 후면부까지는 순방향흐름의 경우가 흐름이 없는 경우보다 높게 나타난다.
(2) 쇄파형상에 대해, 배후사면이 모래인 경우는 흐름방향에 관계없이 파봉이 휘말리면서 부서지는 권파형쇄파를 나타내며, 순방향흐름의 경우는 초기에는 권파형쇄파를 보이다가 종국에는 파봉이 부서지는 붕괴파형쇄파를 동시에 나타낸다. 배후사면이 자갈인 경우에는 흐름방향에 관계없이 파봉이 휘말리면서 부서지는 권파형쇄파만을 나타내지만 그의 규모는 모래의 경우보다 약하다.
(3) 평균유속에 대해, 배후사면이 모래 혹은 자갈에 관계없이 순방향흐름의 경우에만 잠제 전면의 비탈면 앞에 반시계 방향의 순환셀이 형성되고, 잠제 전면의 해저면에서 해측으로 강한 유속이 발생하며, 역방향흐름의 경우, 순방향흐름의 경우, 흐름이 없는 경우의 순으로 유속이 강해진다. 이로부터 흐름방향에 따라 잠제 전면 해저면에서 쇄굴의 여부 및 정도를 예상할 수 있을 것으로 판단된다.
(4) 평균난류에너지에 대해, 전반적으로 잠제 전면 비탈면상의 수면부근에서 평균난류에너지가 증가하고, 배후사면이 모래 혹은 자갈에 관계없이 모두 순방향흐름의 경우가 상대적으로 잠제 천단부에서 난류에너지가 적게 나타난다.
(5) 시 · 공간누적평균난류에너지에 대해, 잠제 전면부에서는 흐름의 유무와 흐름방향에 따른 차이는 미미하지만 잠제 전면의 천단 중앙을 지나서부터는 차이가 나타난다. 전반적으로 역방향흐름의 경우가 흐름이 없는 경우와 순방향흐름의 경우보다 큰 값을 가지며, 공간파고변화와 직접적인 연관성을 갖는 것으로 판단되고, 이와 함께 배후사면에서 반사율과 흐름의 유무 및 흐름방향에 따른 잠제 천단상에서 쇄파형상 및 쇄파고도 공간파고변화에 영향을 미치는 것으로 판단된다.