1. 서 론
중요한 항 외곽시설 중 하나인 방파제는 그 동안 내습하는 파랑에 대해 내구성과 항내 정온도 확보를 목적으로 설계되어 왔으며, 이 과정에서 지진은 사석경사재 등 지진피해 시 비교적 복구가 용이한 구조형식으로 피해 시에도 항만 이용 등에 현저한 차이를 주지 않는 경우는 내진설계를 수행하지 않을 수 있다는 예외 조항과 적용 내진등급이 II 등급이라는 사실에서 알 수 있듯 비중 있게 다루어진 것으로 보이지 않는다(Korean Ministry of Land, Infrastructure and Transport, 1997). 이러한 관행은 유라시아판과 북미판, 태평양판, 필리핀판이 조우하는 경계에 위치하여 비교적 지진이 잦은 일본이나 대만과는 달리 유라시아판 경계에서 수백km 떨어져 있는 한반도는 지진으로부터 비교적 자유롭다는 인식에서 기인하나, 최근 북진하는 인도 대륙과 유라시아판의 동진, 태평양판의 서진, 필리핀판의 북진이 맞물리며 상당한 응력이 한반도 주변에 부하되고 있는 것으로 판단된다(Cho and Na, 2015).
우리나라의 경우 본격적인 지진관측이 시작된 1978년부터 2000년까지의 23년 간, 총 469회의 지진이 관측되어 연평균 발생빈도는 약 20회 내외로, 이 중 규모 3.0 이상의 지진은 연평균 약 9회, 실제 유감지진은 연평균 약 7회 발생하였다. 지역별 지진 발생분포를 보면 전체 469회 중 해역과 북한지역을 제외한 남한지역에서는 대구를 포함한 경북지역이 57회로 가장 많았고, 다음으로 대전을 포함한 충남지역이 33회이며, 강원도가 26회로 그 다음을 기록하였다. 이렇듯 한반도는 그 동안의 통설과는 달리 지진으로부터 자유로울 수 없다는 인식이 확산되면서 현재 내진 설계가 부분적으로 도입되어 시행되고 있으나, 지난 이십여 년 간 우리나라 연안에 집중적으로 거치된 직립식 방파제는 설계과정에서 내진 성능에 대한 검토가 결여되어 보완이 시급해 보인다(Korean Ministry of Public Safety and Security, 2015).
최근 우리나라에서 선호되던 대형 직립제의 경우 상당한 자중과 이로 인해 확보되는 수평저항력으로 1995년 Kobe 지진의 경우 활동량이 0.3 m에 그쳤으나, 설계 파고가 상대적으로 작은 해역에 거치된 직립제의 경우 활동량이 상당할 수 있어 내진 성능에 대한 검토가 시급해 보인다. 이와 더불어 항만시설은 대부분의 경우 연약지반에 거치되기 마련으로, 기반암과 지표간의 이격거리는 상당하다. 이 경우 지진으로 인한 전단파는 항만시설이 거치된 지표방향으로 증폭되며, 지진에너지의 상당부분은 장주기 대역으로 이동된다. 전술한 전단파 증폭현상은 내습하는 전단파 횟수 누적에 따른 지반 강도 감소에 기인하는 것으로 추정된다(Das, 1993). 본 연구에서 수행된 예비수치모의 결과[2장 예비 수치모의에서 후술]에 따르면 지진에너지의 장주기 대역으로의 이동은 전단파 반주기 동안 항 외곽시설에 외력으로 작용하는 특정방향 지진력이 증가한다는 것을 의미하며 이 경우 상당한 항 외곽시설 활동량이 결과 될 수 있다.
따라서 우리나라 연안 지반특성에 따른 전단파 증폭 현상과 지진에너지가 장주기 대역으로 이동되는 현상을 정량적으로 파악하는 일은 상당한 공학적 의미를 지니나 현재 이에 대한 연구는 상당히 미흡하다. 이와 더불어 현재 내진설계는 등 가정적해석에 상당히 경도되어 진행되어 왔으나, 이 경우 지진에 내재한 불확실성을 안전계수라는 상당히 모호하고, 주관적일 수밖에 없는 개념으로 다루게 되어 보다 우월한 개념인 신뢰성 설계로의 전환과정에 상당한 어려움이 야기될 수 있다. 또한 지진 내습 시 항 외곽시설의 활동량과 같은 구조계의 활동량이 한계치 이하로 제어되는 경우 제시된 항 외곽시설이 허용되도록 하여 보다 다양한 구조 양식과 설계, 시공 방법을 권장하는 성능기반 설계가 최근 그 외연을 확장하고 있다는 사실을 고려하면 전술한 등가정적해석은 지양할 필요가 있다. 따라서 항 외곽시설의 성능기반 내진 설계가 구현되기 위해서는 국지적 지반특성이 반영된 전단파 누적 횟수에 따른 지반 강도 감소와 이로 인한 전단파 증폭 현상을 기술할 수 있는 외곽시설의 시간이력 동적 해석이 선행되어야 할 것이다.
현재 지진 내습으로 인한 지표면 응답 해석 시 가용한 모형은 크게 시간이력과 주파수 영역으로 분류되며, 시간이력 동적해석방법은 U. of Berkely에서 개발한 지반증폭 해석 프로그램인 “SHAKE”(Schnabel et al., 1972)의 근간을 이루고 있으며, 주파수 영역에서는 Miura 등(2001)의 응답스펙트럼법, Xing 등(2012)의 수정 응답스펙트럼 법 등이 가장 빈번하게 차용되고 있다. 전술한 SHAKE는 설계 지진 사상이 기반암에서의 가속도 시계열자료인 경우 효율적이나, 설계 지진 사상이 가속도 응답 스펙트럼으로 정의되는 경우 먼저 감쇠율을 고려한 PSD[Power Spectral Density Function]로 변환하고, 이로부터 기반암 가속도 시계열자료의 Monte Carlo 시뮬레이션, 이어 모의된 가속도 시계열 자료를 대상으로 지반을 통한 전단파 전파과정을 수치 해석하고, 최종적으로 수치 모의된 지표면 가속도 시계열 자료로부터 지표면 응답 스펙트럼을 산출하는 과정을 거치게 된다. 또한 Monte Carlo 시뮬레이션에 내재한 통계적 편차를 최소화하기 위해 필요한 ensemble average를 수행하기 위해서는 전술한 과정은 수십회 이상 반복되어야 한다.
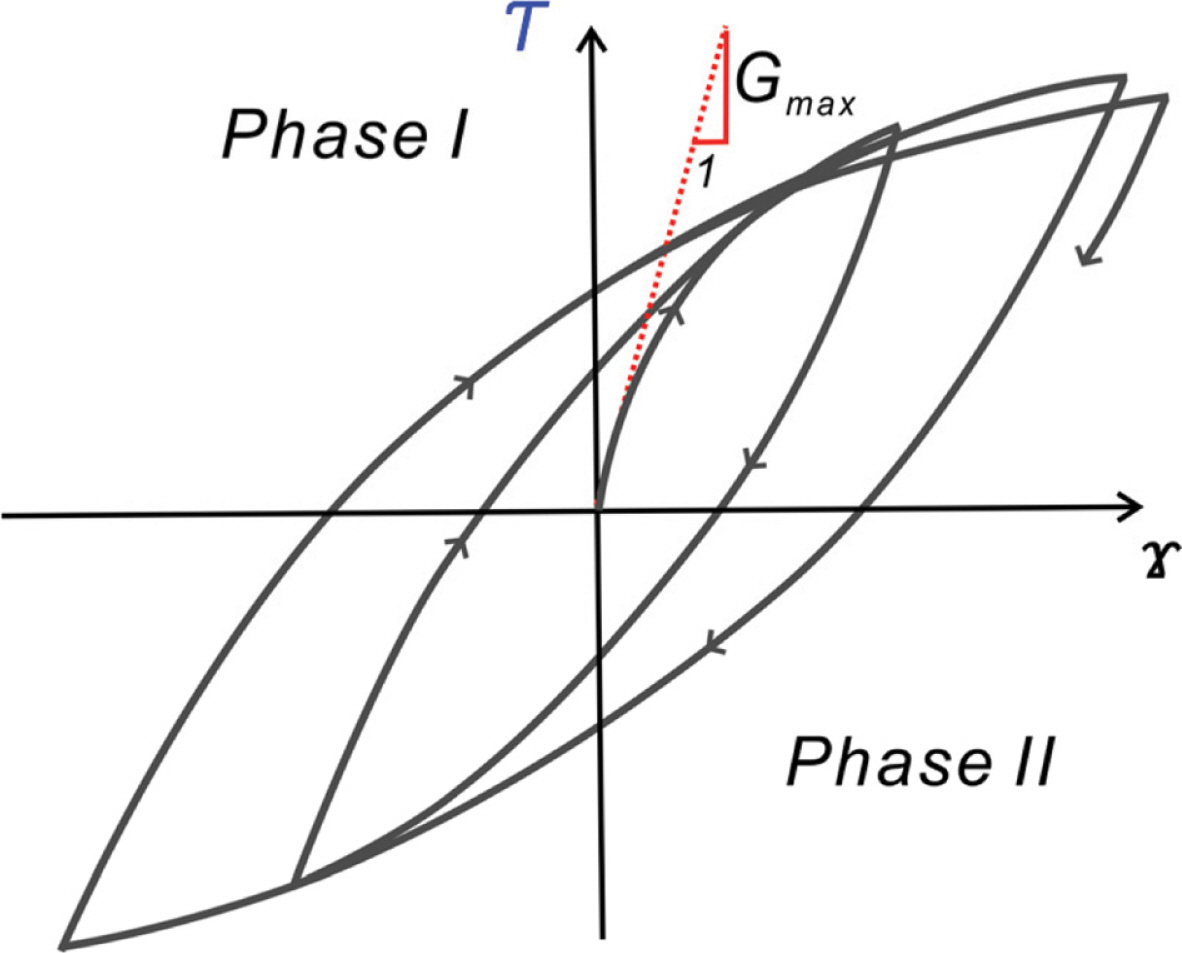
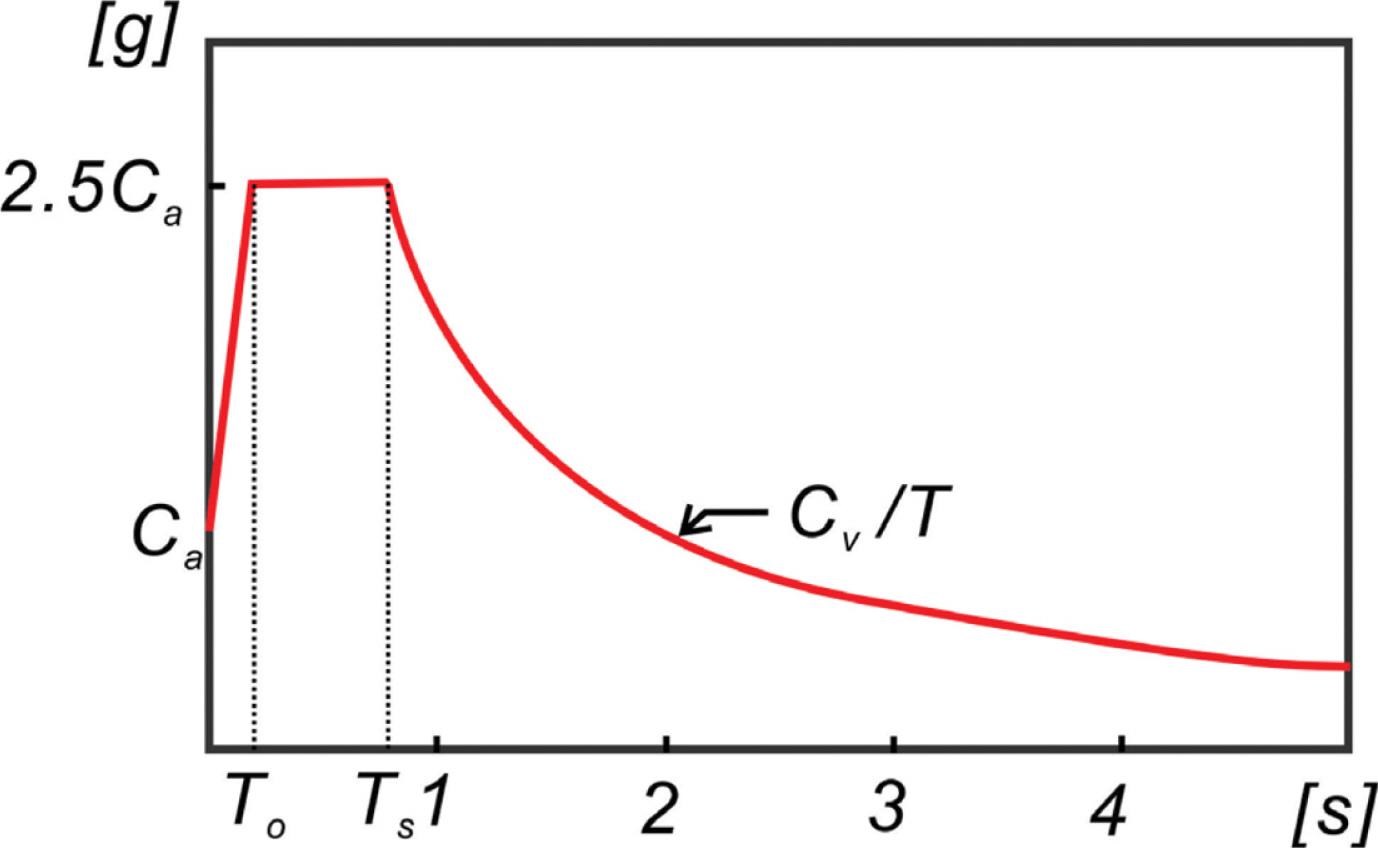
지진으로 인한 전단파의 지반을 통해 전파되는 과정에서 흔히 관측되는 증폭과 장주기 대역으로의 지진에너지 이동을 결정하는 지반 물성치는 구속 응력의 감소로 인한 지표면 방향으로의 전단계수 감소로, 이러한 기반암과 지반 간의 Impedance 차이는 Romberg-Osgood 계열의 비선형 응력-변형률 관계식을 활용하여 설명된다. 그러나 가령 지진으로 인한 전단파가 수백 회 발생했다면 지반강도는 전단파가 누적될수록 약해지나[Fig. 1 참조], 이러한 지반강도 약화는 수백 회에 걸쳐 평균된 전단계수를 활용하여 간접적으로 설명하고 있어 개선이 요구된다.
Miura 등(2001)과 Xing 등(2012)의 주파수 영역 모형에서는 전술한 시간이력 모형에 내재한 복잡한 과정을 피하기 위해 기반암 설계 가속도 응답 스펙트럼으로부터 지표면 응답 스펙트럼이 직접 산출되면 지반은 등가 탄성계수와 감쇠계수를 지니는 하나의 자유도를 지니는 구조계로 모의되며 전단파 파동 방정식의 해로부터 유도된 전환함수를 활용하여 기반암의 첫 번째, 두 번째 고유주기에서의 지반 응답 특성을 반복법을 활용하여 산출하게 된다. 전술한 Miura 등(2001)의 응답스펙트럼 법은 그 편이성으로 인해 일본 Building Standard Law에서는 사용을 권하고 있으나, 전단파 누적에 따른 지반 강도 약화와 같은 천이현상은 설명할 수 없다는 한계를 지닌다.
현재 지반 전단계수의 내습한 전단파 횟수 누적에 따른 지반 강도, 즉 전단계수의 감소를 기술할 수 있는 모형으로 가장 선호되는 것은 Hardin과 Drnevich(1972) 모형으로 보인다. Hardin과 Drnevich(1972)는 먼저 전단 변형률을 기준 전단변형률[Reference shear strain]로 정규화하고, 횟수 누적에 따른 전단계수의 감소는 정규화된 전단 변형률을 누적 횟수에 종속하는 계수를 포함한 쌍곡형 전단 변형률[Hyperbolic shear strain]로 변환하는 경우 전단계수 감소량과 쌍곡형 전단 변형률은 간단한 함수관계를 구성하다는 사실을 정교하게 구성된 실험을 통해 입증 하였으며, 이 후 Hardin과 Drnevich(1972) 모형은 지반을 통한 전단파 전파과정 해석에 큰 흐름을 구성한다.
이러한 시각에서 본 연구에서는 전단파 횟수 누적에 따른 전단계수의 감소에 대한 Hardin과 Drnevich(1972) 모형과 파동방정식으로 수치모형을 구성하고, 수치모의를 수행하였다. 전단파 횟수 누적에 따른 비선형 응력-변형률 관계를 설명하기 위해 수치모의 과정에 Newmark-β 방법과 수정 Newton-Raphson 방법을 차용하였다.
2. 예비 수치모의
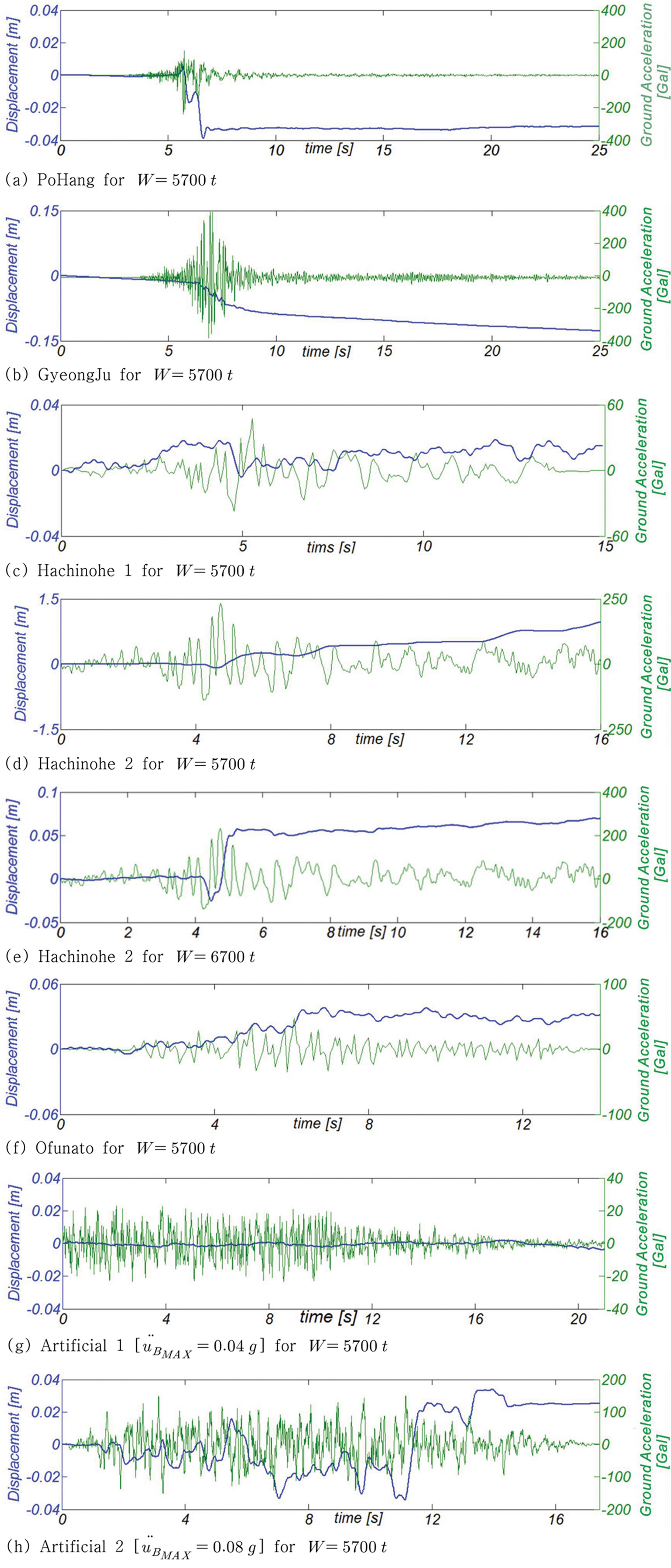
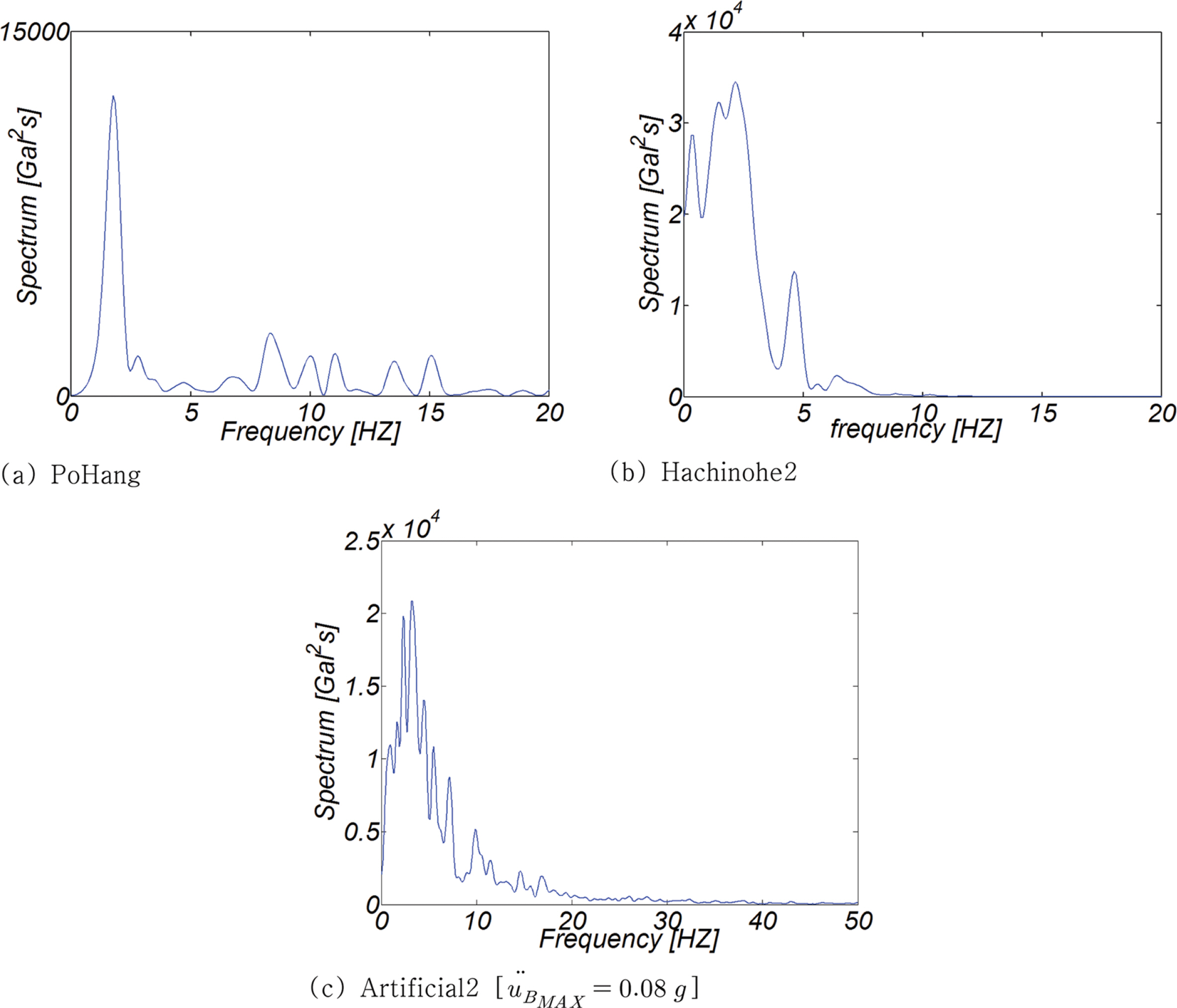
전단파 특성이 항 외곽시설 활동량이 미치는 영향을 파악하기 위해 포항, 경주, Hachinohe1, Hachinohe2, Ofunato, 인공지진파를 대상으로 수치모의를 수행하였다. 이 중 Hachinohe1, 2와 Ofunato는 Tokachi-Oki[1968]와 Miyagi-Ken-Oki[1978] 지진 발생 시 관측된 가속도 시계열 자료로 항에서 관측되어 일본에서 항만구조물의 내진설계에 가장 빈번히 차용되고 있으며, 포항과 경주의 경우는 최근에 발생한 지진 중 강도가 가장 큰 것으로 우리나라의 지반 특성을 반영하고 있다고 판단되어 선정하였다. 포항[ML = 5.4]의 경우 2017년 11월 15일에 진앙으로부터 25 km 이격된 청송관측소[36.18113E, 129.08811N]에서 관측된 것으로 기반암의 종류는 일반암(SB)이며, 경주[ML = 5.8]의 경우 2016년 9월 12일에 진앙으로부터 8.23 km 이격된 울산관측소[35.7024E, 129.1231N]에서 관측된 것으로 기반암의 종류는 연암(SC)이다. 인공지진파는 우리나라처럼 지진 관측 자료가 일천한 경우 가용한 대안인 설계응답스펙트럼과의 비교를 위해 선정한 설계응답 스펙트럼으로부터 Random Phase Method에 준거하여 모의하였다.
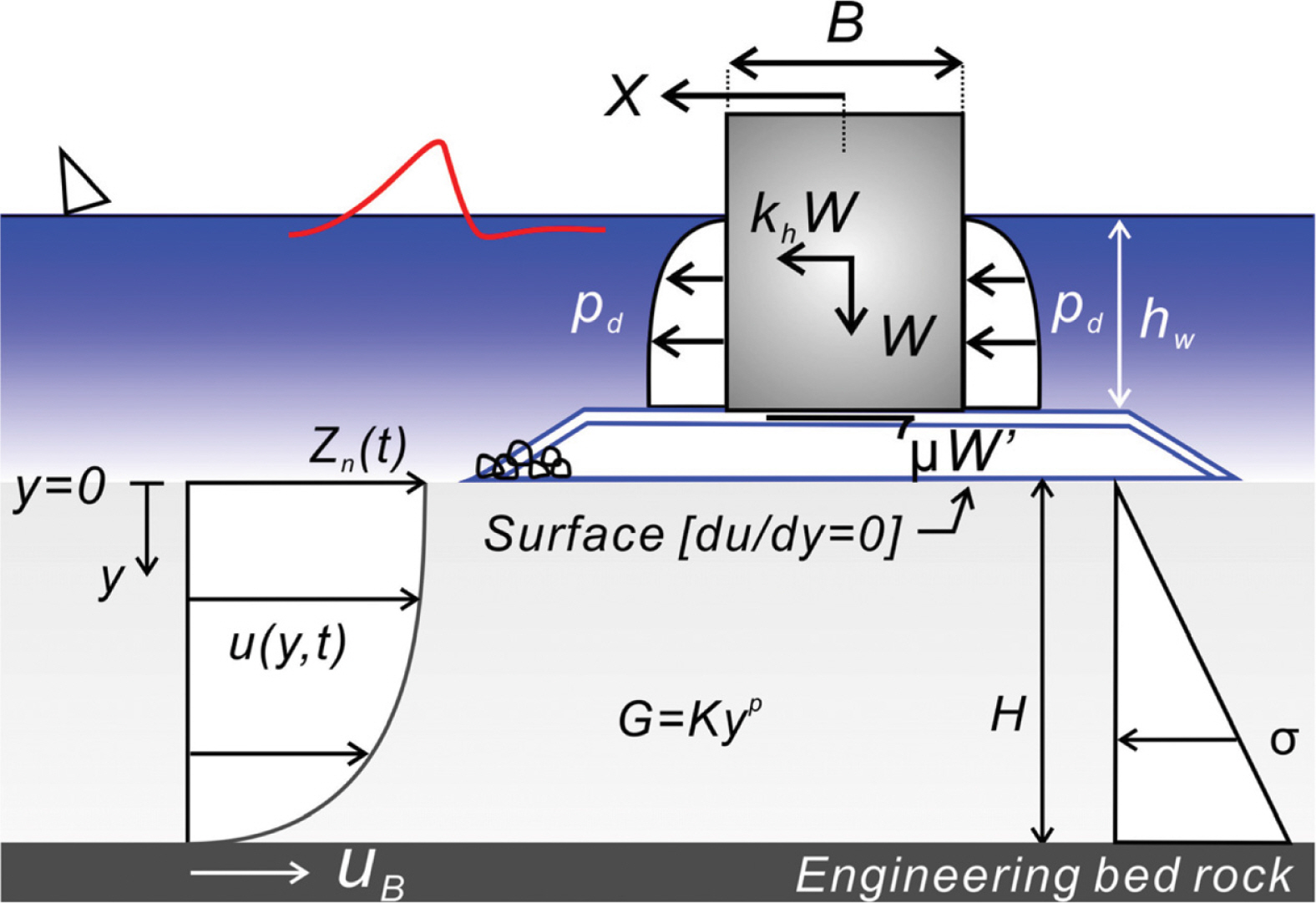
수치모의에 사용된 운동 방정식을 기술하면 다음과 같으며
여기서 W는 케이슨 자중, W'는 케이슨 수중 무게, g는 중력가속도, k h = u ¨ B / g
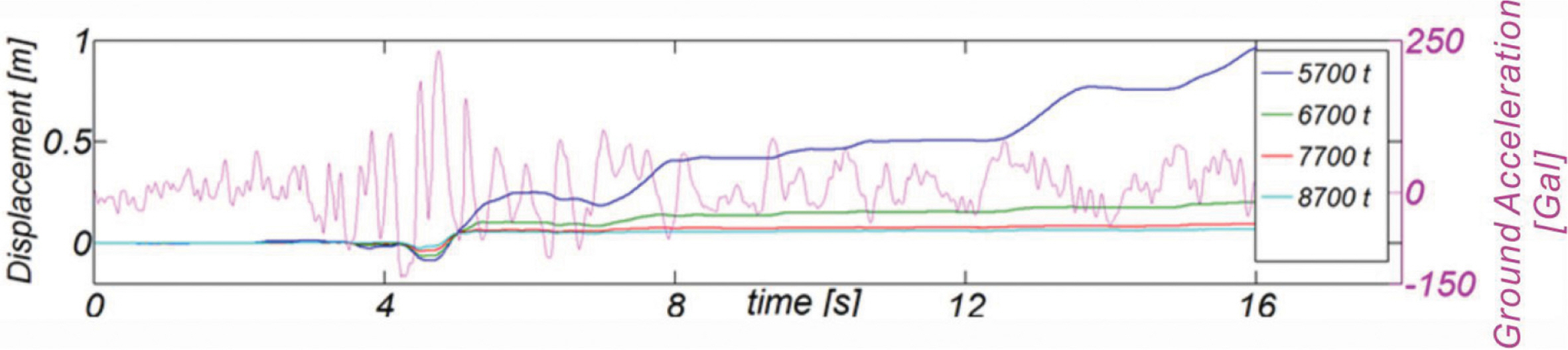
식(1)에 기술된 운동방정식은 Newmark-β 방법을 사용하여 수치해석 하였으며, 수치모의 과정에 우리나라에서 기 운영 중인 직립식 방파제의 해양환경을 고려하여 hw, Gmax는 각각 12 m, 200 Mpa로 취하였다. 모의된 수치결과는 Fig. 3에 도시하였으며, Hachinohe2와 경주를 제외하면 직립 방파제의 활동량은 0.02~0.04 m 정도로 미미하나 Hachinohe2의 경우 활동량은 최대 1.2 m까지 모의되어 지진으로 인한 전단파 특성이 지니는 영향이 상당함을 알 수 있다. 이러한 결과는 부산 신항 서방파제(Busan Port Construction Office, 2007)를 대상으로 Jeong et al.(2014) 등이 제시한 활동량 0.5 m를 상회하나 부산 신항 서방파제가 사석경사식이라는 사실을 고려하면 수용할 수 있는 범위로 판단된다. Fig. 4에는 방파제 활동량이 가장 크게 모의된 Hachinohe2를 대상으로 케이슨 자중이 미치는 영향을 파악하기 위해 케이슨 자중 5700 t, 6700 t, 7700 t, 8700 t에 대해 모의된 결과를 함께 도시하였으며, 케이슨 자중 증가 시 상당한 수평저항력으로 활동량이 급속하게 감소하는 것을 알 수 있다[Fig. 3(d), (e) 참조].
전단파 특성이 직립 방파제의 활동량에 미치는 영향을 보다 확연하게 드러내기 위해 FFT[Fast Fourier Transform] 기법에 준거하여 지진으로 인한 전단파 가속도 스펙트럼을 산출하였으며 그 결과는 Fig. 5에 도시하였다. Hachinohe 2의 경우 진앙 심도가 상대적으로 깊어 전이과정에서 단파 성분은 감쇠되어 장주기파가 우세하며, 이 경우 직립 방파제 변위량은 상대적으로 크게 나타나 지반 응답 스펙트럼의 주파수 대역폭은 직립 방파제 응답 특성에 상당한 영향을 미치는 것으로 나타났다.
3. 직립식 방파제 성능기반 내진 설계를 위한 제언
예비수치모의 결과 장주기 대역 전단파가 항 외곽시설 활동량에 미치는 영향은 작지 않다는 것을 확인할 수 있었다. 또한 기반암과 지표간의 이격거리가 상당한 항만시설의 특성상, 지진으로 인한 전단파는 전파과정에서 지표면 방향으로 증폭, 장주기 대역으로 이동된다. 따라서 항 외곽시설의 성능 기반 내진 설계가 구현되기 위해서는 국지적 지반특성이 반영된 전단파 누적 횟수에 따른 지반 강도 감소와 이로 인한 전단파 증폭 현상을 기술할 수 있는 항 외곽시설 시간이력 동적 해석이 필요해 보인다. 이와 더불어 내진 관측의 역사가 일천한 우리나라의 경우 항 외곽시설의 성능기반 내진설계는 전단파 파속이 400 m/s 이상인 기반암을 대상으로 정의된 설계 응답스펙트럼으로 진행되어야 할 것으로 판단된다(Otani et al., 2000).
전술한 검토결과에 기초하여 도출한 항 외곽시설의 성능 기반 내진설계 과정을 정리하면 다음과 같다.
4. 기반암을 대상으로 한 설계 가속도 응답스펙트럼
지진관측의 역사가 일천한 우리나라의 경우 항 외곽시설의 성능기반 내진설계는 전단파 파속이 400 m/s 이상인 기반암을 대상으로 정의된 설계 응답스펙트럼으로 진행되어야 할 것으로 판단되며(Otani et al., 2000), Fig. 6에는 이해를 돕기 위해 설계 응답스펙트럼을 도시하였다. 첫 번째, 두 번째 고유주기는 각각 다음과 같이 정의된다.
여기서 Ca와 CV는 기반암의 종류[강성암(SA), 일반암(SB), 연암(SC) 등]와 과거 지진활동 빈도에 따라 분류된 영역별 지진계수로 Table 1에 정리하여 수록하였다.
5. 기반암 설계 가속도 응답스펙트럼을 활용한 기반암 가속도 시계열자료의 Monte Carlo 시뮬레이션
5.1 감쇠율이 반영된 등가 PSD[Power Spectral Density Function]
항 외곽시설의 성능기반 내진설계가 기반암을 대상으로 정의된 설계 응답스펙트럼으로 진행되는 경우, 수치모형의 입력자료인 기반암 가속도 시계열 자료를 얻기 위해서는 먼저 선정된 기반암 설계응답스펙트럼 SA(ω, ζ)은 감쇠율 ζ이 반영된 등가 PSD pj [j = 1, 2, …, m]로 변환되어야 되며 그 변환과정을 정리하면 다음과 같다(Park, 1995).
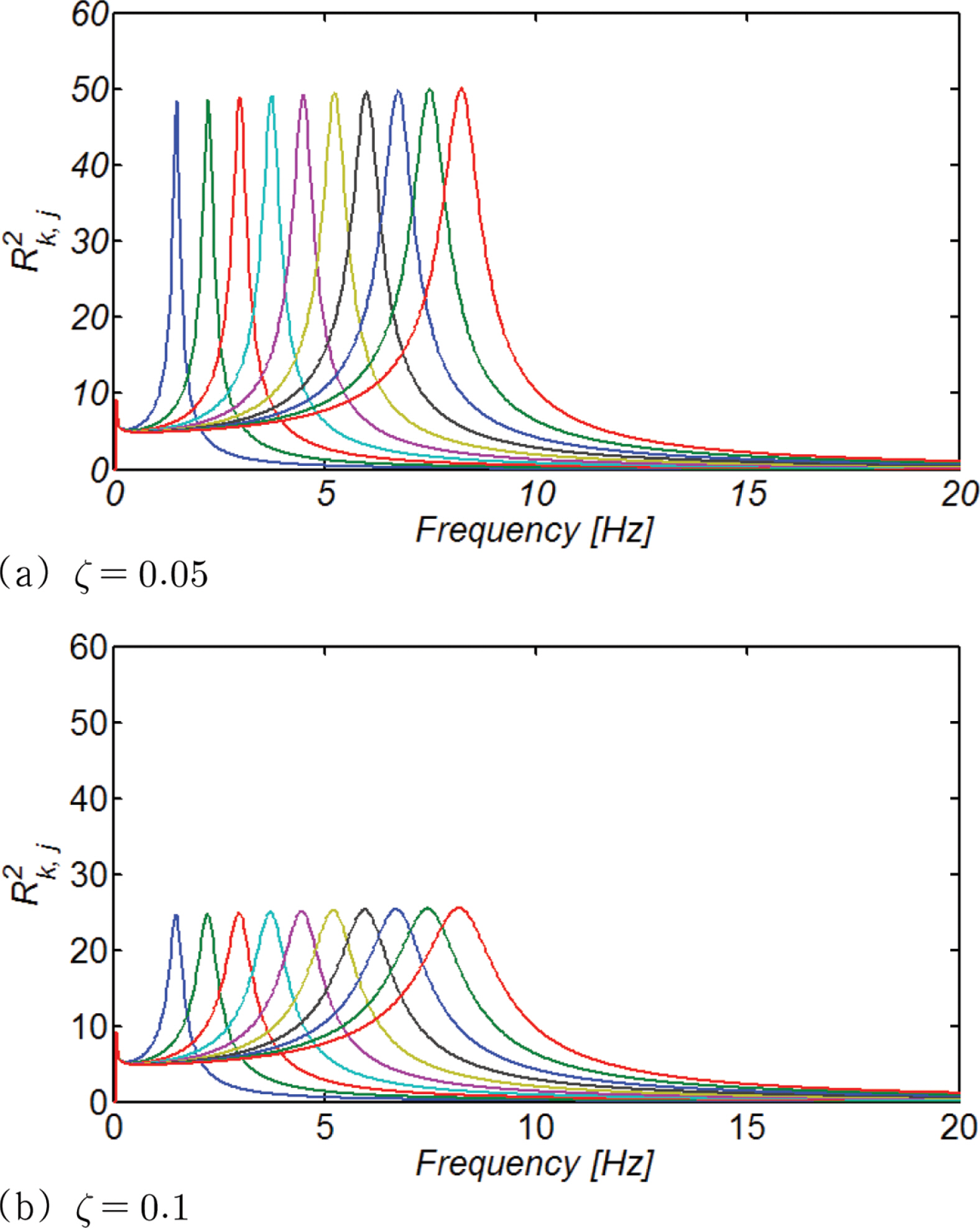
상기 식에서 pj, Rk, j, νj, χ는 각각 다음과 같이 정의되며
여기서 Rk, j는 고유주파수가 ωk, 감쇠율이 ζ이며 단일한 자유도를 지니는 구조계가 PSD가 δ(ωj)인 외력에 노출되는 경우 구조계의 첨두 가속도 응답, Δωj는 주파수 증분, G(ωj)는 PSD, ζ는 감쇠율, Te는 지진의 유효지속시간을 각각 나타낸다. 진폭 변조함수 I(t)가 주어진 경우 유효지속시간 Te는 다음과 같이 정의된다.
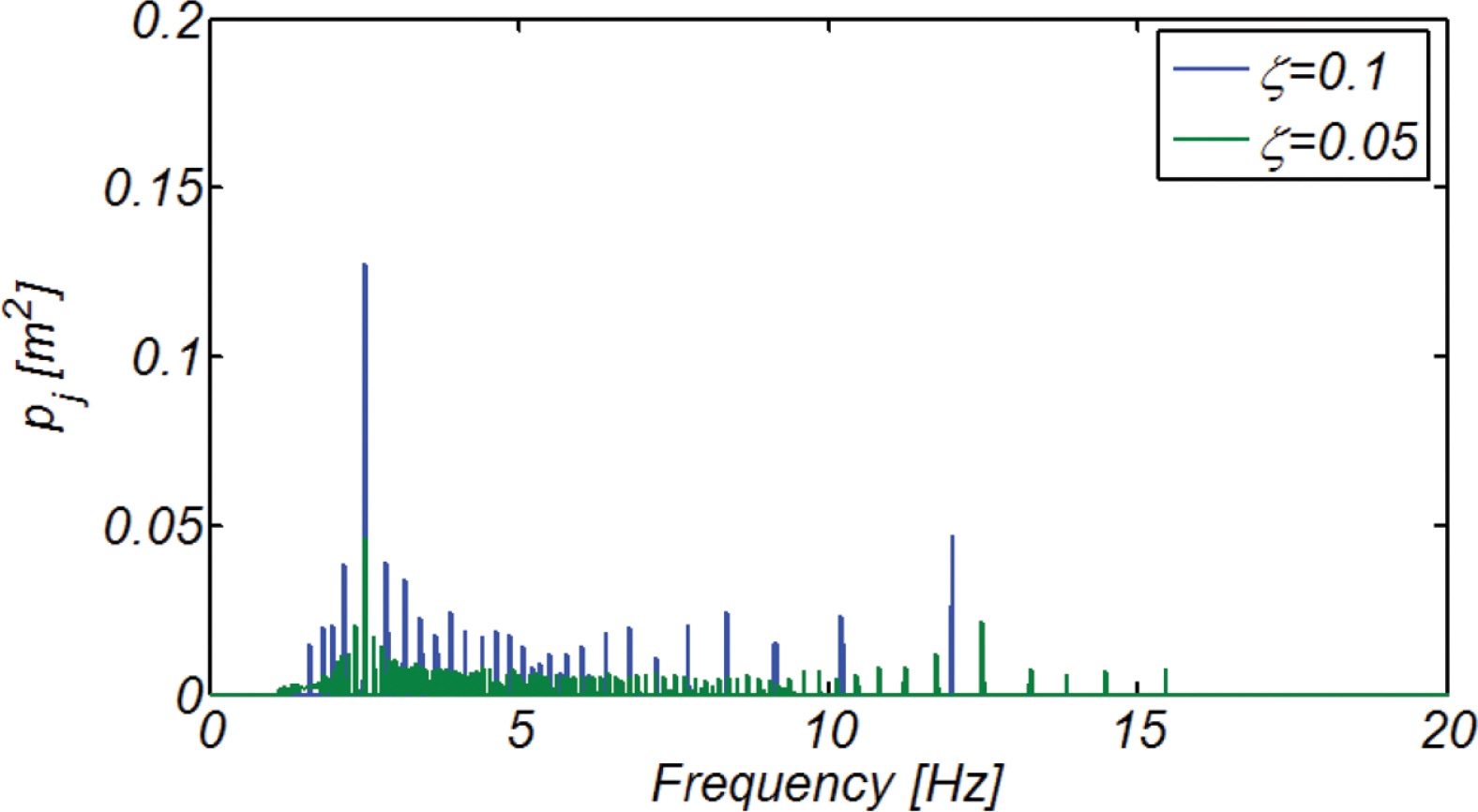
수치모형의 입력자료를 얻기 위한 기반암 가속도 시계열 자료모의 시 감쇠율을 ζ = 0.05로 취하며, 등가 PSD pj는 다음과 같이 정의되는 least squares problem으로 수치해석 될 수 있다.
5.2 진폭 변조함수
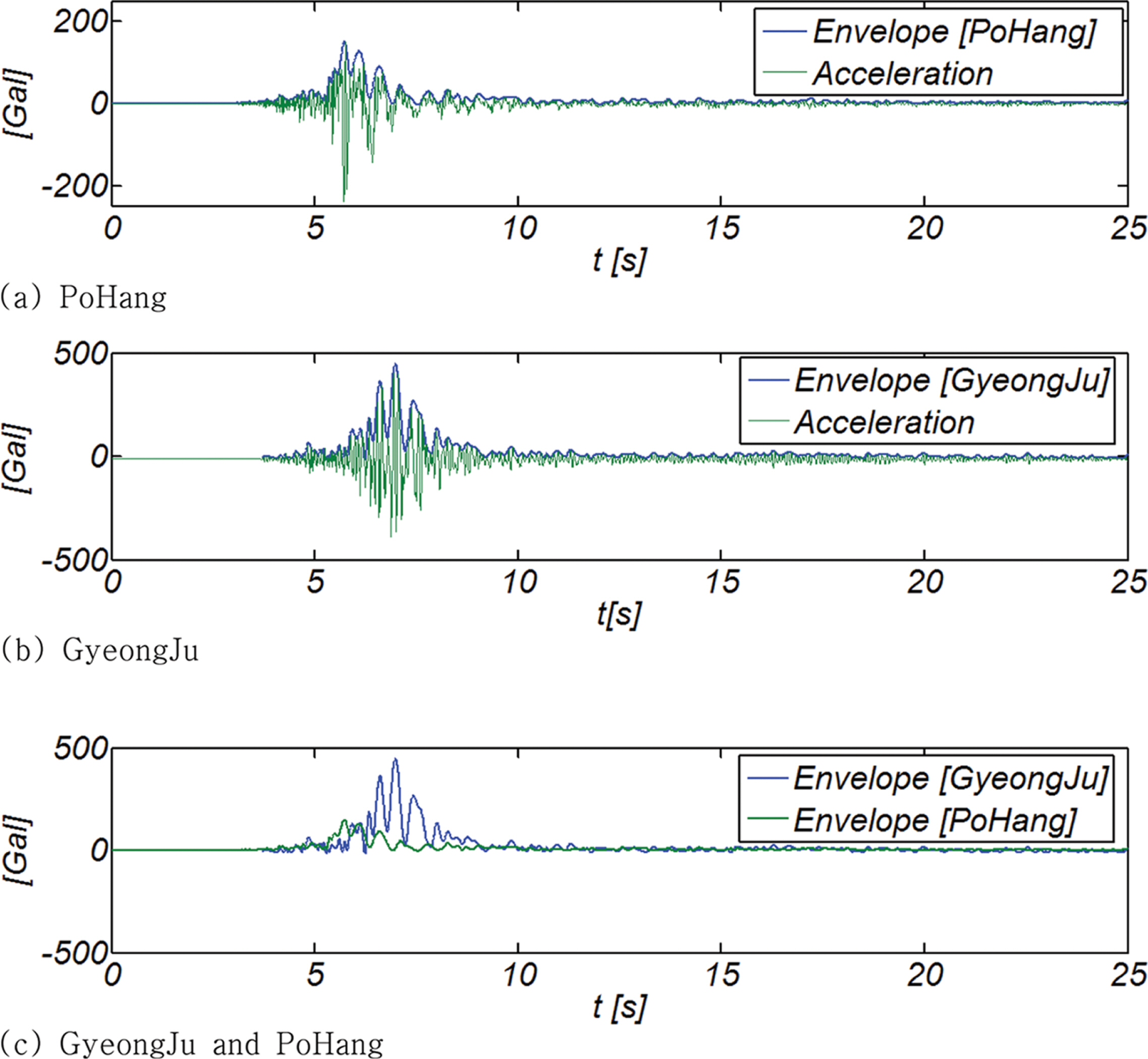
본고에서 사용될 가속도 진폭 변조함수 결정하기 위해 먼저 포항, 경주 가속도 관측 자료를 Wave by wave analysis를 통해 첨두 가속도 관측치를 분리하였으며, 그 결과는 Fig. 7에 도시하였다. 이어 이렇게 찾아낸 첨두 가속도 관측 값들을 Cubic spline 함수로 보간하여 가속도 진폭 포락함수를 산출하였으며 Fig. 8에는 최종 산출된 가속도 진폭 포락함수를 도시하였다. 이를 통해 가속도 진폭 포락함수 I(t)의 leading front는 이차함수 형태로 증가, 첨두부는 일정하게 유지, tail part는 지수함수의 형태로 감소하는 것으로 가정하였으며 이를 기술하면 다음과 같으며
이 경우 Te = 16.8s로 산출된다.
5.4 기반암 가속도 시계열자료의 Monte Carlo 시뮬레이션
Random phase method에 준거한 기반암 가속도 시계열자료의 Monte Carlo 시뮬레이션 과정을 정리하면 다음과 같다.
A Nyquist 주파수 fN보다 작은 주파수를 지니는 성분파에 대해 총 N개의 복소수 Fourier 계수 C(fi) = A(fi) + iB(fi)를 산출하며 이 때 A(fi)와 B(fi)는 각각 다음과 같이 정의된다.
여기서 ψ[fi]는 0과 2π 사이에 균일하게 분포하는 무작위 변량으로 i번째 성분파의 위상을 나타낸다.
B Nyquist 주파수 fN보다 우월한 주파수 성분파에 대해서는 전 단계에서 산출한 Fourier 계수의 mirror image를 투영한다.
여기서 윗첨자 *는 complex conjugate을 나타낸다.
C C(fi)에 대한 Inverse Fourier transform을 수행하는 경우 damping이 반영된 기반암 가속도 시계열자료 X(t)는 다음과 같이 산출될 수 있다.
6. 지반을 통한 전단파 전파과정 해석을 위한 전단파 파동 방정식
6.1 파동 방정식
전단파 파속 VS가 400 m/s 이상인 경우 기반암으로 정의되며(Otani et al., 2000), 현재 항 외곽시설은 연약지반에 거치되기 마련으로 액상화에 대비하기 위한 지반개량이 수행된 경우가 대부분이다. 이 경우 지반은 모래로 치환되며 이처럼 지반이 균질한 경우 지반을 통한 전단파의 전이과정은 파동방정식에 의해 기술될 수 있으며, 파동방정식의 유도과정을 정리하면 다음과 같다.
먼저 해석의 편의를 위해 단일 자유도 문제로 전환하기 위해 지반변위 u(y, t)를 변수분리법에 준거하여 다음과 같이 기술하면
여기서 ψn(y)는 형상함수, Zn(t)은 지표면에서의 수평변위를 각각 나타내며, Zn(t)은 다음과 같이 정의되는 운동방정식에 의해 기술될 수 있다.
여기서 Γ [ ]는 Gamma 함수, J−b( )는 b차 제 일종 Bessel 함수, βn은 J−0.4(βn) = 0의 해로 정의되며[β1 = 1.751, β2 = 4.8785, β3 = 8.0166, β4 = 11.157], H는 지반 심도, ωn는 고유주파수[radian/s], ζ는 감쇠율을 나타내며 각각 다음과 같이 정의된다.
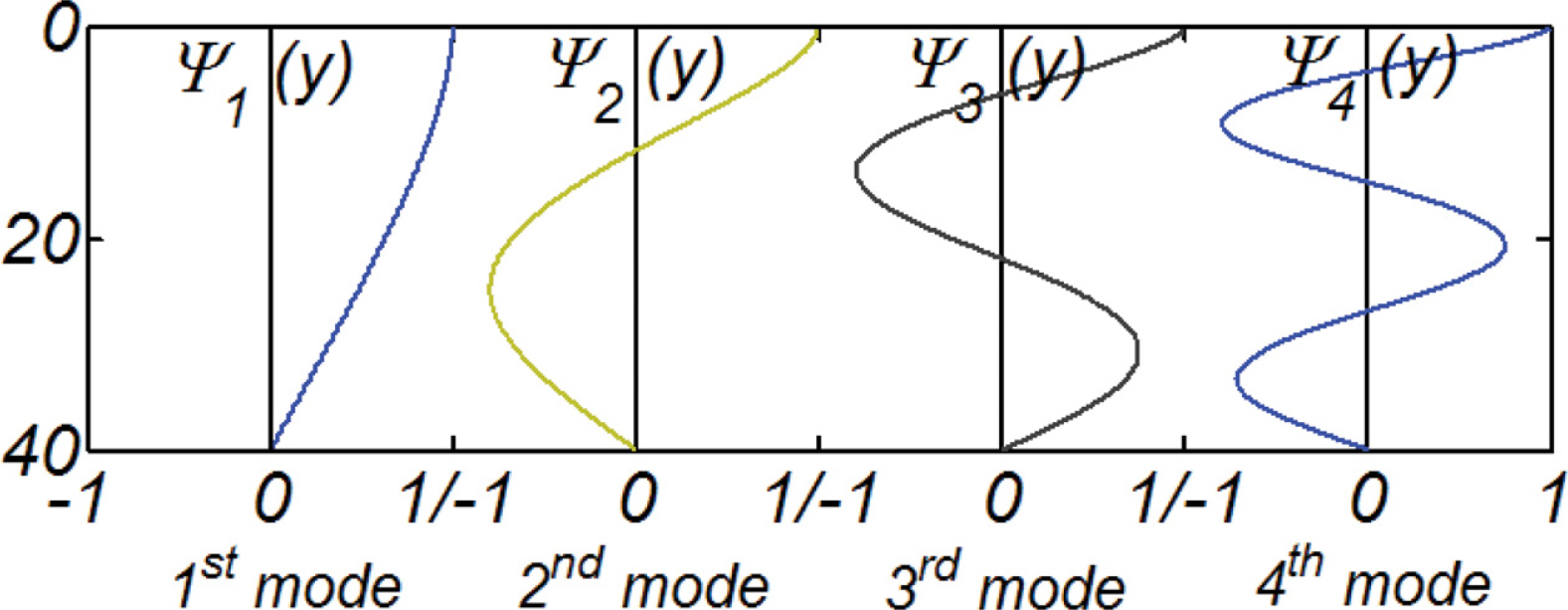
여기서 G는 shear modulus, Tn은 고유주기, y는 지표면으로부터의 이격거리를 각각 나타낸다[Fig. 3 참조].
Fig. 11에는 이해를 돕기 위해 본고에서 사용된 1st, 2nd, 3rd, 4th mode의 형상함수 ψn(y)를 도시하였다.
6.2 전단파 횟수 누적에 따른 지반 강도 감소
현재 지반 전단계수의 내습한 전단파 횟수 누적에 따른 지반 강도, 즉 전단계수의 감소를 기술할 수 있는 모형으로 가장 선호되는 것은 Hardin과 Drnevich(1972) 모형으로 보인다. Hardin과 Drnevich(1972)는 먼저 전단 변형률을 기준 전단변형률[Reference shear strain]로 정규화하고, 누적 횟수에 따른 전단계수의 감소는 정규화된 전단 변형률을 누적 횟수에 종속하는 계수를 포함한 쌍곡형 전단 변형률[Hyperbolic shear strain]로 변환하는 경우 전단계수 감소량과 쌍곡형 전단 변형률은 간단한 함수관계를 구성하다는 사실을 정교하게 구성된 실험을 통해 입증 하였으며, 이 후 Hardin과 Drnevich(1972) 모형은 지반을 통한 전단파 전파과정 해석에 큰 흐름을 구성한다. Hardin과 Drnevich(1972) 모형 유도과정을 정리하면 다음과 같다.
Hardin과 Drnevich(1972)는 범용 해석모형 구축하기 위해서는 정규화 과정이 필요하다는 것을 인식하고, 정규화를 위해 기준 변형률 γr을 도입하였으며 이를 기술하면 다음과 같다.
여기서
식(24)에서 e는 공극률, OCR은 과압밀비, σ o σ o
여기서 c ϕ σ y
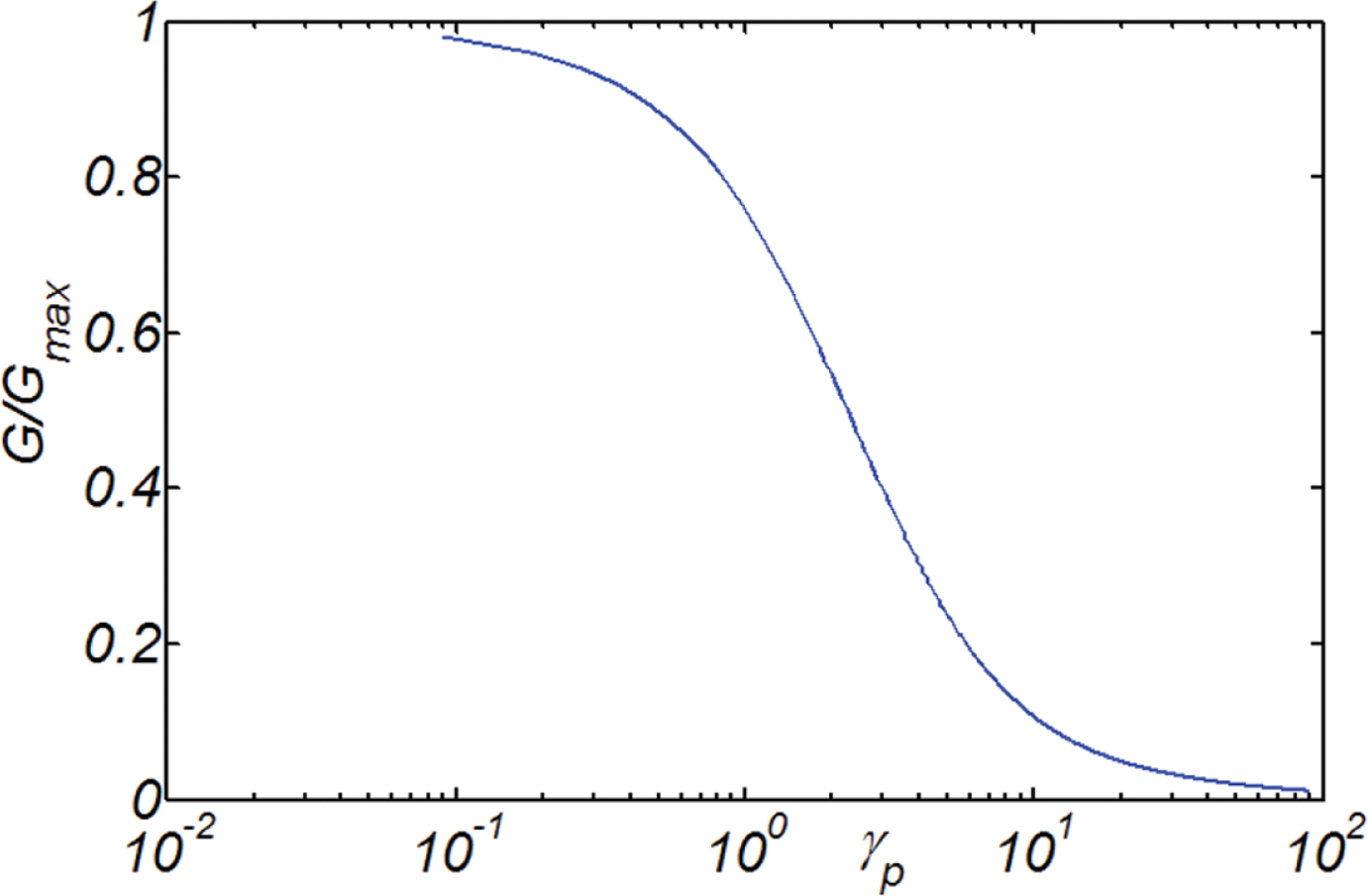
최종적으로 전단계수 G와 감쇠계수 ζ는 다음과 같이 기술될 수 있으며
여기서 γh는 내습한 전단파 횟수 누적에 따른 지반 강도, 즉 전단계수의 감소를 기술하기 위해 Hardin에 의해 도입된 쌍곡형 변형률로 다음과 같이 정의된다.
7. 수치해석 및 수치결과
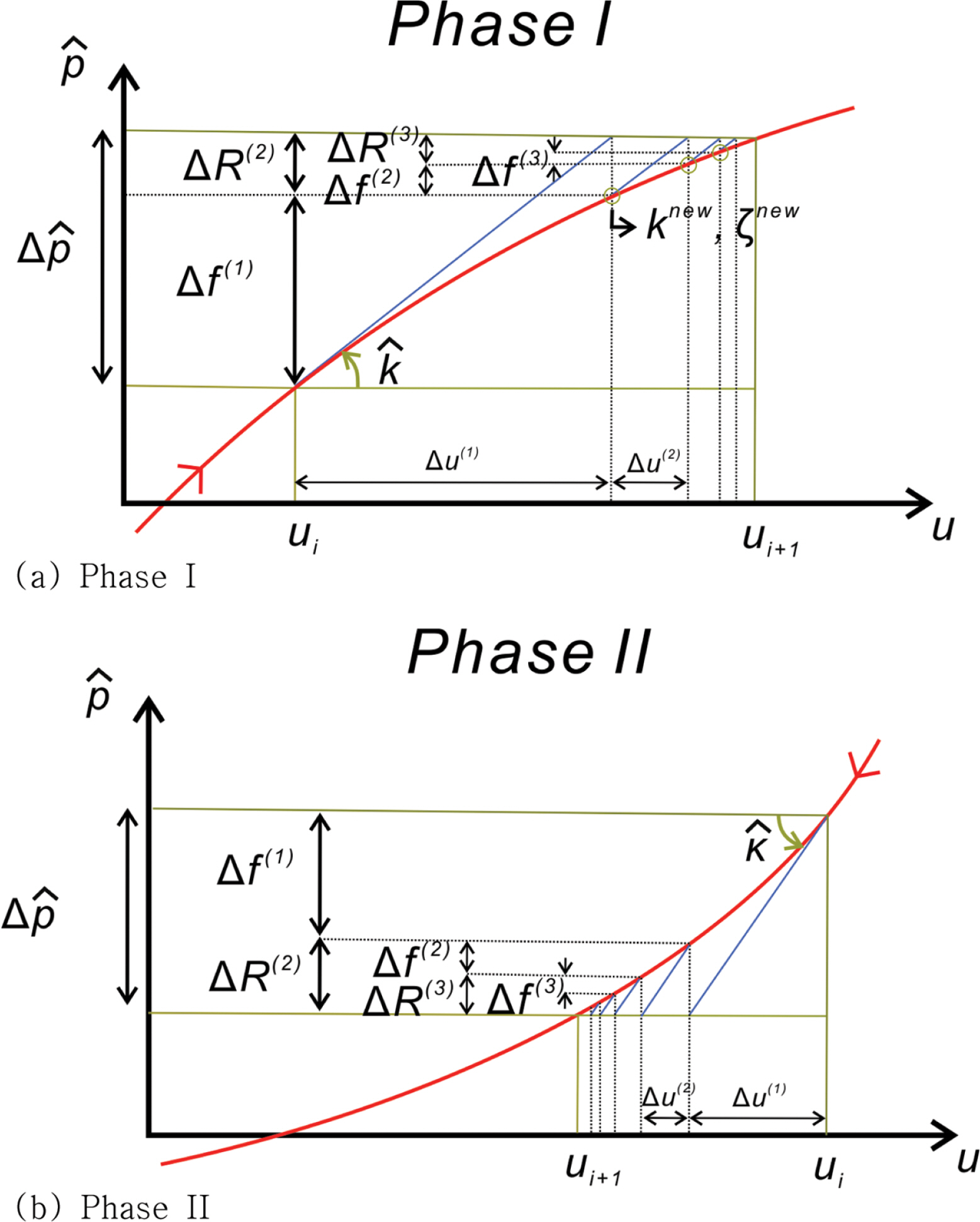
식(18)에 기술된 파동 방정식은 강 비선형 쌍곡형 형태로 초기 가정치를 토대로 해석이 시작되며, 반복 과정을 통해 남은 잔차력 ∆ R j + 1 = ∆ p ^ - ∆ f j
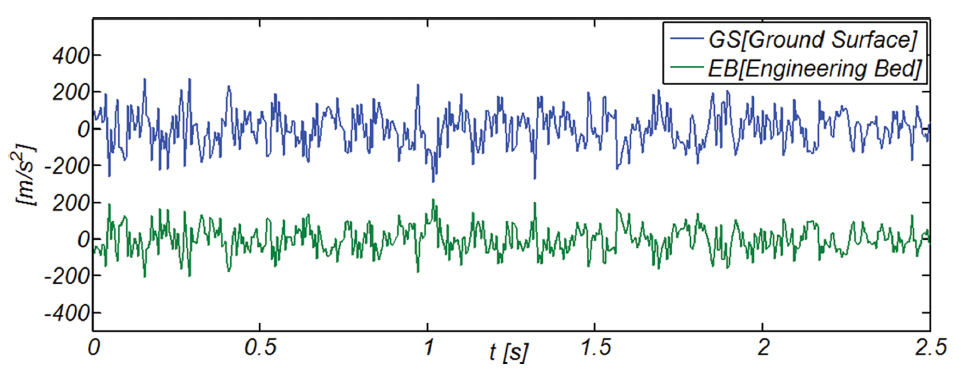
Fig. 14에는 비교를 위해 Monte Carlo 시뮬레이션 기법을 통래 모의된 기반암[ζ = 0.05]에서의 가속도 시계열 자료와 식(18)을 수치 적분하여 얻은 지표면에서의 가속도 시계열 자료를 함께 도시하였다. 육안으로는 우리가 예상 할 수 있는 전단파 증폭 현상은 미세하게 관측되나 지표면 방향으로 상당한 지진에너지가 장주기 영역으로 표류하는 현상은 확연하게 드러나지 않는다.
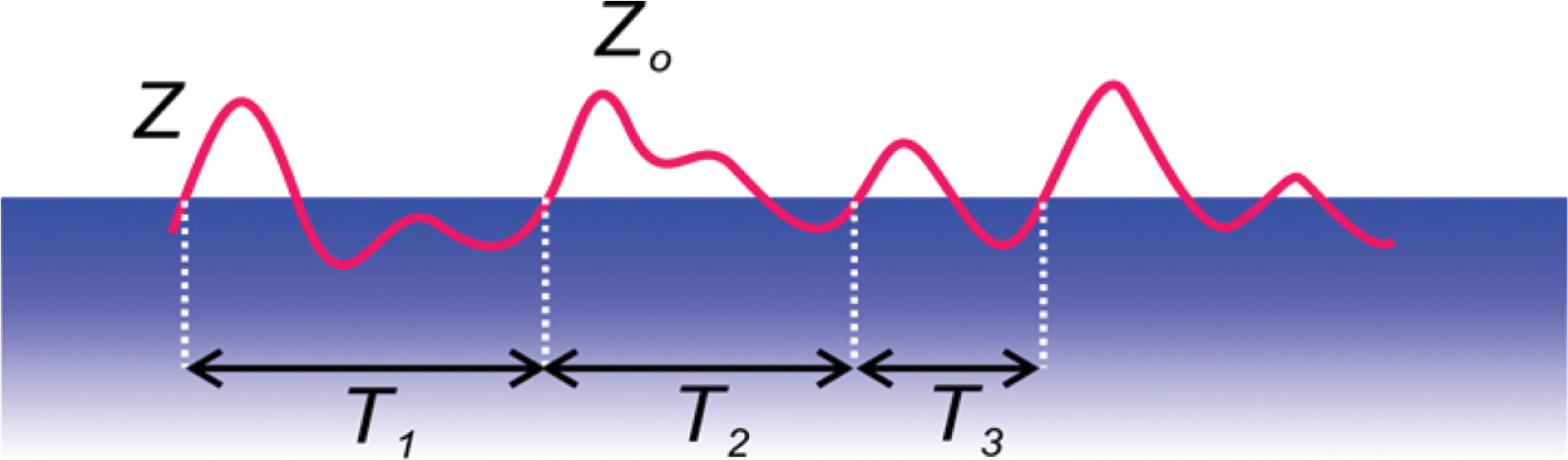
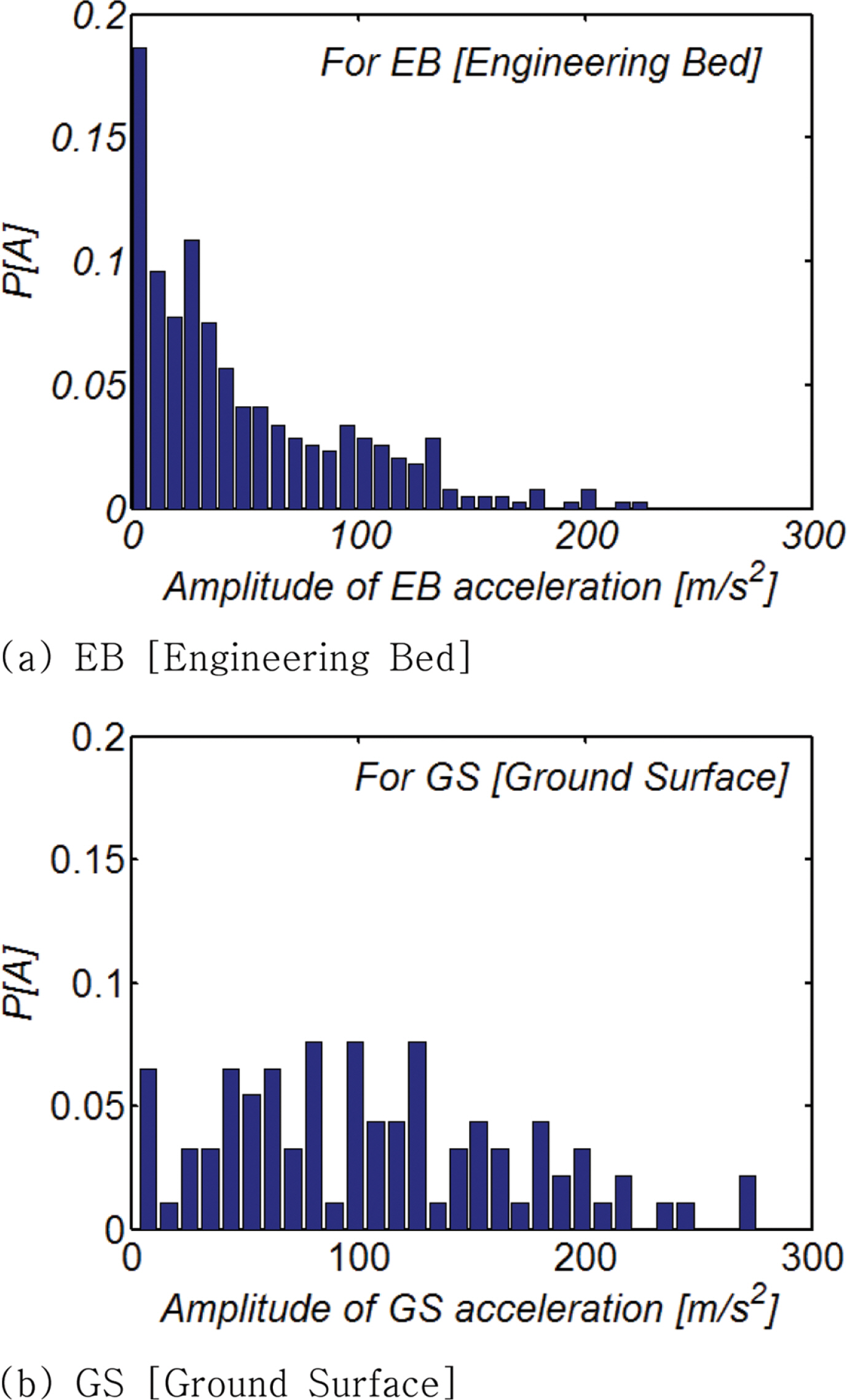
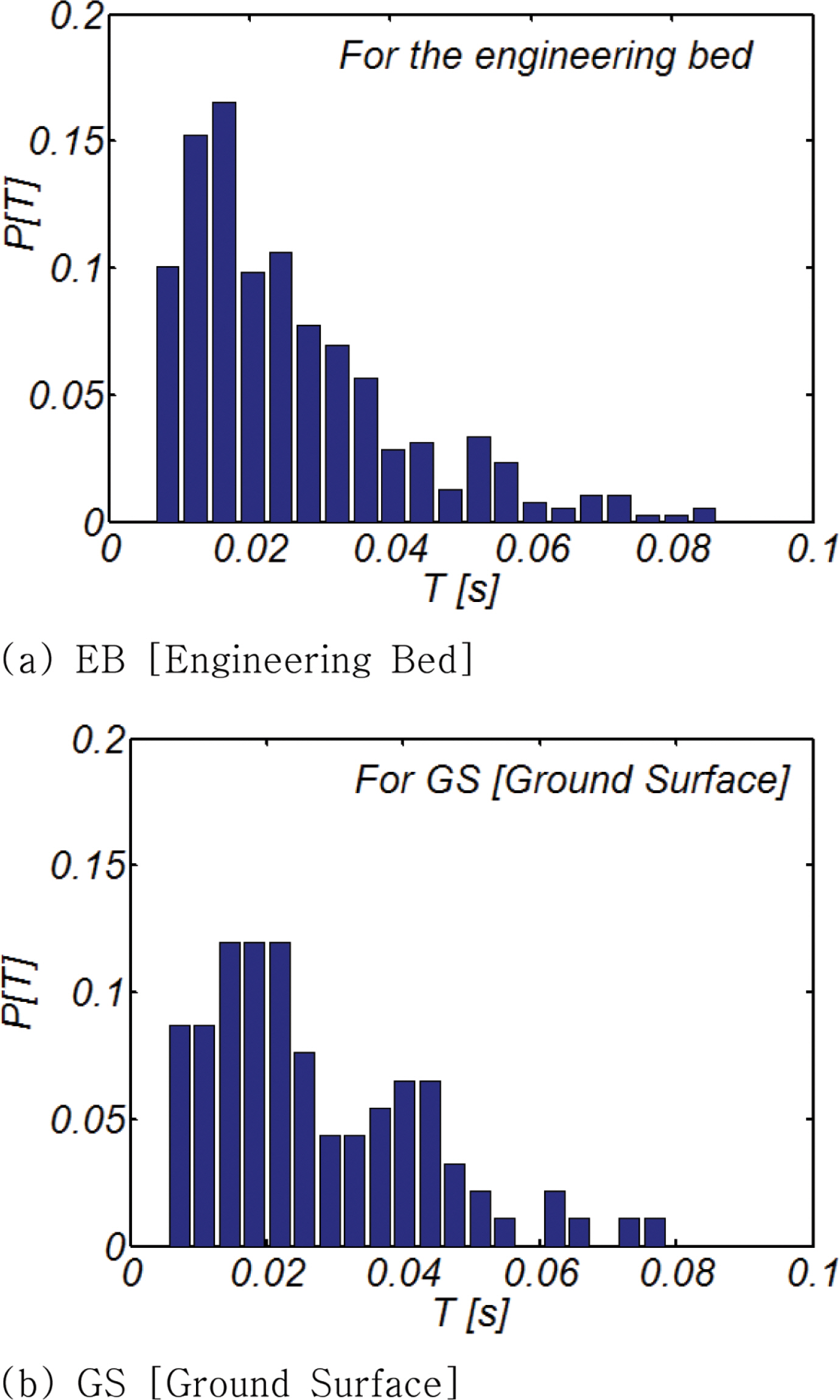
이러한 육안관측의 한계를 보완하기 위해 수치모의된 지표면에서의 가속도 시계열 자료를 대상으로 기준치 상향 통과법[zero-crossing method]에 기반한 파랑 전수해석[Wave by wave analysis]을 수행하였으며[Fig. 15 참조], 이렇게 찾아낸 가속도 첨두치와 첨두치 사이의 주기를 빈도 해석하고, 그 결과는 가속도 첨두치의 경우 Fig. 16에 가속도 첨두치 사이의 주기의 경우 Fig. 17에 각각 제시하였다. 전단파가 지표면으로 전파되는 과정에서 상당한 확률 질량이 상대적으로 큰 진폭과 장주기 쪽으로 이동하는 것을 보다 확연하게 확인할 수 있다.
Fig. 18에는 수치모의 과정에서 관측된 전단계수 G와 감쇠계수 ζ의 변화를 도시하였으며, 비교를 위해 누적 지표면 변위도 함께 도시하였다. 우리의 예상대로 전단계수 G는 급속히 감소하였으며, 이에 반해 감쇠계수 ζ는 급격하게 최대치 ζmax = 0.25로 수렴하는 것을 확인할 수 있다. 또한 지표면은 t < 2.0s에서는 탄성운동을 유지하나 이후 상당히 감소된 전단계수 G로 인해 지표면 변위가 누적되는 것을 알 수 있다.
8. 결 론
지난 이십여 년 간 우리나라 연안에 집중적으로 거치된 직립식 방파제의 내진 성능을 검토하기 위한 예비 수치모의를 포항, 경주, Hachinohe1, Hachinohe2, Ofunato, 인공지진파를 대상으로 수행하였다. 예비 수치모의 결과 지진으로 인한 전단파가 지반을 통해 전파되는 과정에서 지진에너지가 장주기 대역으로 이동한 Hachinohe2의 경우 항 외곽시설의 활동량이 상당하다는 것을 확인하였다. 지진으로 인한 전단파는 항만시설이 거치된 지표방향으로 증폭되며, 지진에너지의 상당부분은 장주기 대역으로 이동된다. 이 중 지진에너지의 일부분이 장주기 대역으로 이동되는 현상은 지반의 점성 혹은 내부 마찰에 기인하며, 전단파 증폭은 구속 응력의 감소로 인해 지표면 방향으로 감소하는 전단계수와 내습하는 전단파 횟수 누적에 따른 지반 강도 감소에 기인하는 것으로 여겨진다(Das, 1993).
현재 전단파 횟수 누적에 따른 지반 강도 감소는 지진과 지반 상호작용 해석 시 가장 선호되어온 “SHAKE”(Schnabel et al., 1972)에서 간과 되어 왔으나, 지반 강도 감소는 전단계수 축소, 감쇠율 증가를 야기할 수 있어 전술한 기작이 외곽시설 활동량에 미치는 영향에 대한 정량적 평가는 상당한 공학적 의미를 지닌다. 또한 지반 상호작용 해석의 다른 큰 흐름을 이루는 Miura 등(2001)의 응답스펙트럼 법, Xing 등(2012)의 수정 응답스펙트럼 법과 같은 주파수 영역 모형 같은 경우 전술한 전단파 횟수 누적에 따른 지반 강도 감소 같은 천이현상은 설명할 수 없다는 한계를 지닌다.
이러한 인식에서 본고에서는 먼저 전단파 횟수 누적에 따른 전단계수의 감소의 기술이 가능한 Hardin과 Drnevich(1972) 모형과 파동방정식에 기초하여 수치모형을 구성하고, 이어 전단파 횟수 누적에 따른 전단계수의 감소가 전단파 전파과정에 미치는 영향을 정량적으로 평가하기 위한 수치모의를 수행하였다. 이 과정에서 비선형 응력-변형률 관계를 설명하기 위해 Newmark-β 방법과 수정 Newton-Raphson 방법을 차용하였다(Chopra, 1995).
지진관측의 역사가 일천한 우리나라의 경우 항 외곽시설의 성능기반 내진설계는 전단파 파속이 400 m/s 이상인 기반암을 대상으로 정의된 설계 응답스펙트럼으로 진행되어야 할 것으로 판단된다(Otani et al., 2000). 또한 연약지반에 거치되어 기반암과 지표간의 이격거리가 상당한 항만시설의 특성상 국지적 지반특성이 지진 전단파 전파 과정에 미치는 영향을 기술할 수 있는 시간이력 해석이 필요해 보인다. 이 경우 수치해석에 필요한 지반 가속도 시계열 자료를 얻기 위해서는 감쇠율[ζ = 0.05]이 반영된 설계 응답스펙트럼에 해당되는 PSD[Power Spectral Density Function] 산출이 선행되어야 한다. 본고에서는 상당히 효율적인 것으로 알려진 Park(1995)의 전환법에 준거하여 등가 PSD를 산출하였다. 이 과정에서 등가 PSD 산출과정에 필요한 변조하는 가속도 진폭 포락함수는 포항, 경주 관측 자료를 토대로 leading front는 이차함수 형태로 증가, 첨두부는 일정하게 유지, tail part는 지수함수의 형태로 감소하는 것으로 가정하였다. 산출된 등가 PSD는 지표면 방향으로의 구속력 감소와 감쇠계수 증가에 따른 전단파 증폭과 지진에너지의 상당한 부분이 장주기 방향으로의 이동이 정확히 모의되는 것을 확인하였으며, 이어 이렇게 산출된 등가 PSD로부터 기반암 가속도 시계열 자료를 Random phase method를 활용하여 모의하였다.
이어 국지적 지반특성이 지진 전단파 전파 과정에 미치는 영향을 살펴보기 위해 비선형 쌍곡형 형태의 파동 방정식을 Newmark-β 방법과 수정 Newton-Raphson 방법으로 수치 적분하여 지표면 가속도 시계열자료를 모의하였다. 지표면 방향으로의 전단파 증폭과 지진에너지의 장주기로의 이동을 보다 확연히 드러나기 위해 최종 모의된 지표면 가속도 시계열자료를 대상으로 기준치 상향 통과법에 기반한 파랑별 해석을 적용하였다. 이렇게 찾아낸 가속도 첨두치와 첨두치 사이의 주기를 빈도 해석하였으며, 빈도 해석 결과 전단파가 지표면으로 전파되면서 상당한 확률 질량이 상대적으로 큰 진폭과 장주기 쪽으로 이동하는 것을 확연하게 확인할 수 있었다.
또한 수치모의 과정에서 관측된 전단계수 G와 감쇠계수 ζ는 우리의 예상대로 지진으로 인한 전단파에 대한 노출시간이 길어질수록 전단계수 G의 경우 급속히 감소하였으며, 이에 반해 감쇠계수 ζ는 급격하게 최대치 ζmax = 0.25로 수렴하는 것을 확인하였다. 또한 지표면은 t < 2.0s에서는 탄성운동을 유지하나 이후 상당히 감소된 전단계수 G로 인해 지표면 변위가 누적되는 것을 확인할 수 있었다.