1. 서 론
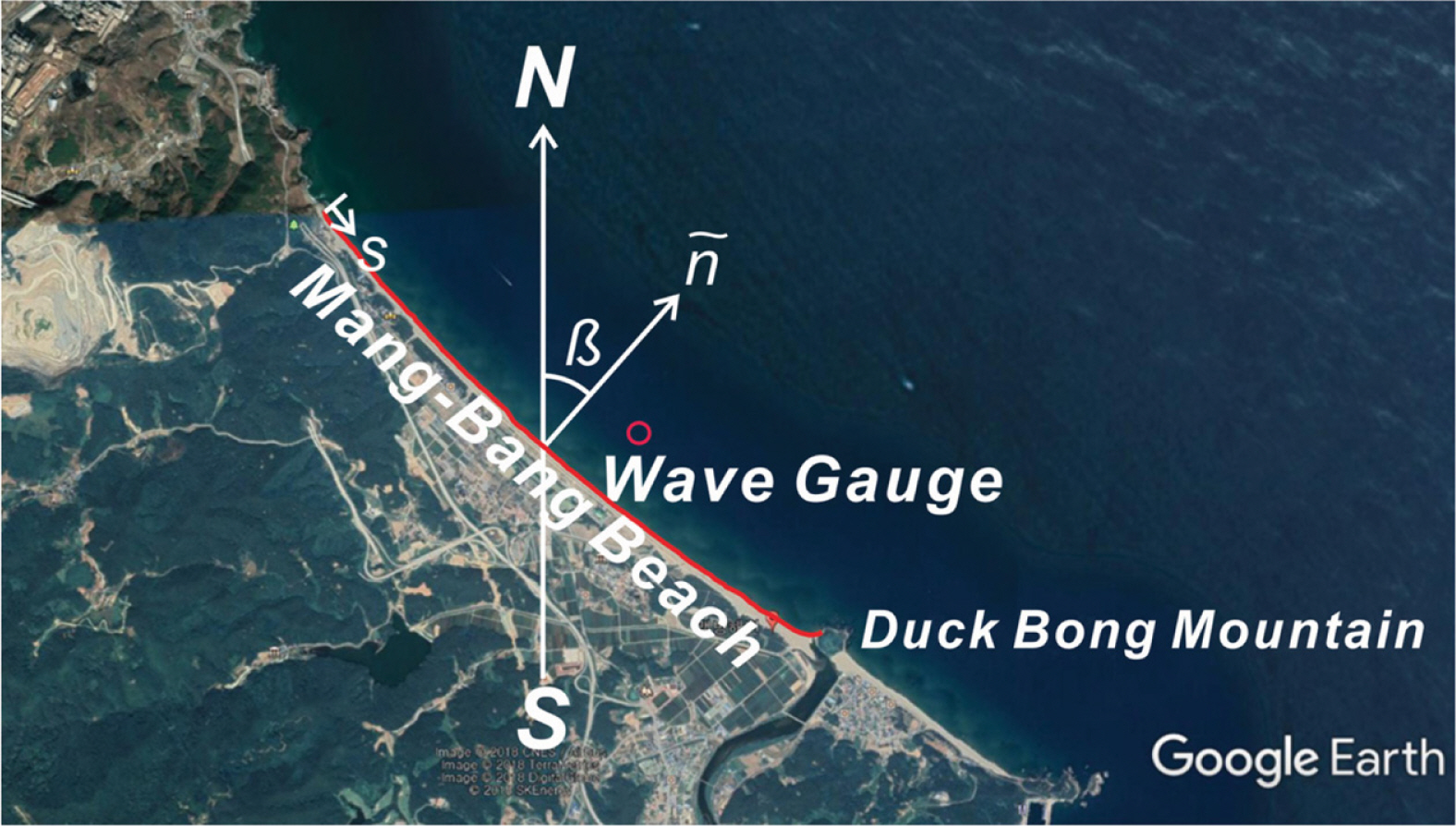
최근 해안 침식에 대응하기 위해 이안제, 돌제, 인공 곶(headland), 광폭잠제(artificial reef), 양빈(beach nourishment) 등이 거치 혹은 시행되고 있으나, 기대와는 달리 해빈 안정화 효과가 미미한 경우도 상당하다. 그러나 전술한 강성구조물의 해빈 안정화 효과가 보고된 경우도 작지 않아, 해안침식 대응방안은 해역별 파랑특성이 고려된 최적화 과정이 필요해 보인다.
해안침식 대응방안 최적화 과정에서 해역별 주 표사이송 모드와 모드별 년 표사 이송량에 관한 정보는 상당한 공학적 가치를 지니나, 현재 우리나라 각 해안의 주 표사이송 모드와 모드별 년 이송량을 정량적으로 평가하려는 노력은 부족해 보인다. 이러한 현상은 표사이송 문제에 내재한 난해함과 계측상의 어려움에 상당부분 기인하나 최근 3D 물리기반 지형모형(3D morphology model)이 개발되어 사주(sand bar)의 형성과정과 계절별 이행과정이 모의되는 등 상당한 성과가 이루어진 것으로 보인다(Jacobsen et al., 2012; Jacobsen et al., 2014). 그러나 전술한 3D 물리기반 지형모형을 우리나라 각 해안에 년 단위로 적용하는 것은 현재의 계산환경아래에서는 여전히 어려운 과제로 보인다. 따라서 3D 물리기반 지형모형에 비해 다소 거칠더라도 비교적 쉽게 각 해안의 주 표사이송 모드와 모드별 년 이송량에 대한 정보를 얻을 수 있는 platform 개발이 필요해 보인다.
이러한 시각과 결을 같이하는 연구로는 Walton and Dean(1973, 2010), Kim et al.(2001), Cho and Kim(2019) 등을 꼽아 볼 수 있다. Cho and Kim(2019)은 전술한 platform 구축을 위해 현재 침식이 진행되고 있는 맹방해빈을 대상으로 모드별 년 표사 이송량과 표사 장미도(littoral drift rose) 등을 제시한 바 있다. Cho and Kim(2019)은 연안 표사량의 경우 Energy flux 모형을, 횡단 표사량의 경우 Bagnold(1963)에 의해 초기 모형이 제시된 이래 Inman and Bagnold(1963)에 의해 개선되고 Bailard(1981)에 의해 완성된 Energy 모형을 차용하였다. 이 과정에서 Cho and Kim(2019)은 Bailard(1981)가 모형 검증과정에 활용한 미 California Torrey Pines 해빈 파랑자료와 우리나라 맹방 전면해역에서 관측되는 파랑자료 사이에 존재하는 구조적 상이성에 주목하고, Bailard(1981)가 간과한 주기가 반영된 수정모형을 비선형 Boussinesq Eq.(Frelich and Guza, 1984)에 기초하여 수치모의된 쇄파역 유속자료를 토대로 제시한 바 있다.
전술한 구조적 차이는 태평양에 직접적으로 노출되어있는 Torrey Pines 해빈의 경우 상당한 방위에서 파랑발달에 필요한 취송거리가 충분히 확보되나, 맹방해빈의 경우 반시계 방향으로 틀어진 형상의 동해에 노출되어있어 취송거리가 우월한 방위가 특정된다는 지형특성에 기인한다. 이 경우 상대적으로 긴 전파과정에서 단주기의 파랑은 느린 파속으로 파군으로부터 분리되어 후행하게 되어 Torrey Pines 해빈에서는 장주기의 너울이 우월하나, 맹방해빈에서는 다양한 주기의 너울이 관측된다. 이러한 차이로 인해 현재 Bailard(1981)의 횡단표사 모형에는 주기가 간과되어 있으나, 횡단표사의 이동방향을 가늠할 수 있는 Dean NO.에서 알 수 있듯 파랑 주기가 이안 표사에 미치는 영향은 결코 작지 않다. 따라서 Iribarren NO.를 차용하여 파랑 주기가 지니는 영향이 반영된 Cho and Kim(2019)의 연구는 다양한 주기의 너울이 관측되는 맹방해빈 표사이송 해석에 활용될 수 있을 것으로 기대되나 현재 계측상의 어려움으로 인해 검증과정이 결여되어 있어 향후 보다 많은 논의가 필요해 보인다.
전술한 연안 표사량에 대한 Energy flux 모형과 횡단 표사량에 대한 Bailard와 Inman(1981) 계열의 모형은 해안에서 쇄파역까지를 아우르는 전 수역에서의 표사이송을 다루며 검증에 필요한 자료를 얻기 위해서는 U.S. Army Corps of Engineers의 North Carolina Duck Project(Reniers et al., 2004)처럼 우리나라 각 해안에 집중관리수역을 설정하고 연속해서 관측할 필요가 있으나, 현재로서는 가용하지 않은 경우가 대부분이다. 그러나 해안선의 경우 지속적으로 monitoring한 자료가 상당량 축적되어 있어 모드별 년 표사 이송량에 대한 직접적인 검증은 어려우나 연안 표사에 횡단 표사가 더해져 진행되는 해안선 전진 혹은 퇴각되는 양의 계절적 변화를 통한 간접적인 검증은 가능해 보인다.
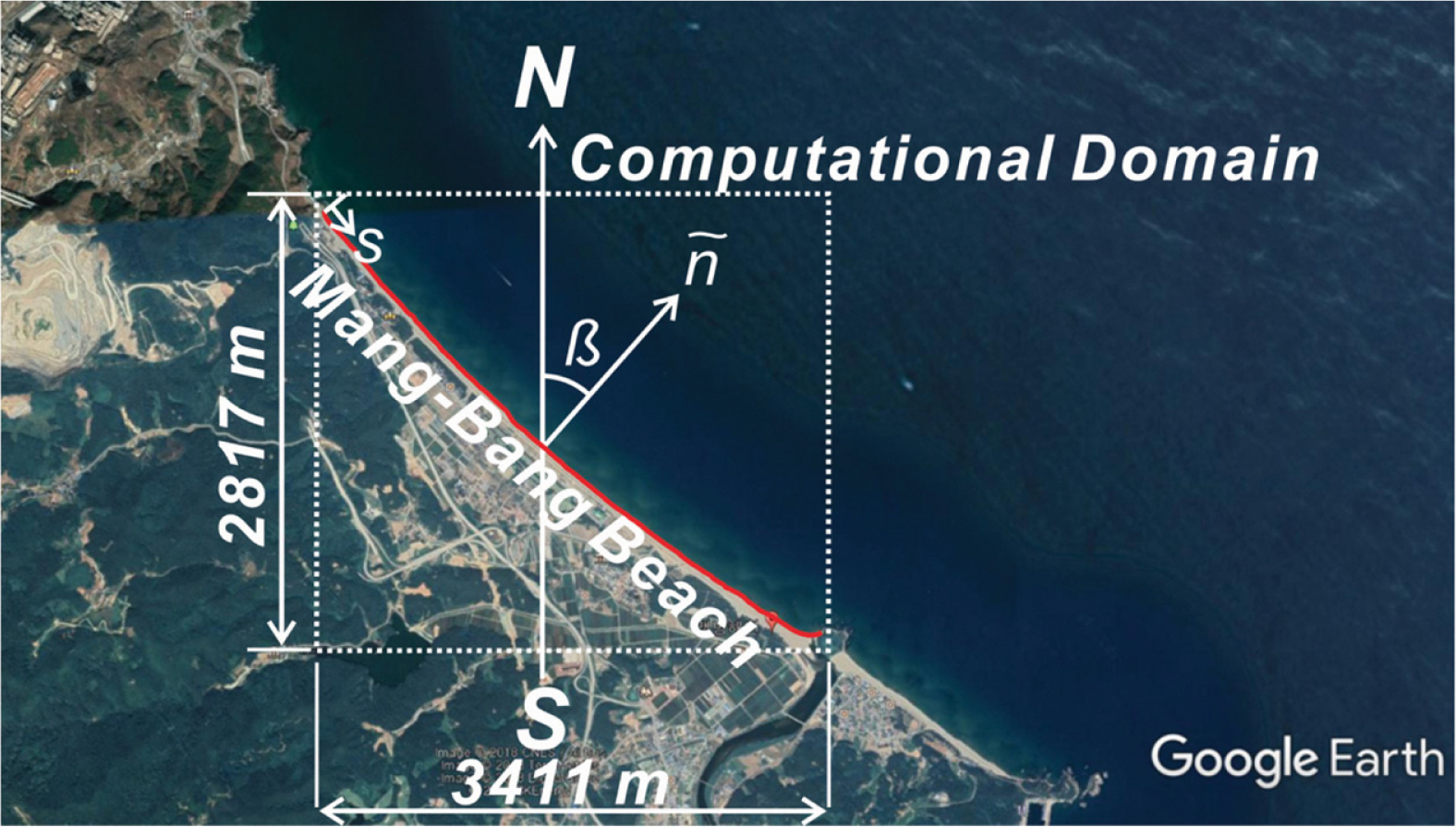
이상의 논의를 토대로 본고에서는 먼저 표사수지 개념으로부터 해안선 모형을 유도하고 이어 2017.4.26부터 2018.4.20까지 맹방해빈에서의 해안선 변화에 대한 수치모의가 수행된다. 이 과정에서 연안 표사량의 경우 Energy flux 모형, 횡단표사량의 경우 Bailard와 Inman(1981) 계열의 수정 모형(Cho and Kim, 2019)이 활용되며, 파랑자료는 맹방해빈 전면해역 수심이 26.5 m인 지점(Fig. 1 참조)에서 초음파식 파고계(Nortek)로 2017.4.26~2018.4.20 사이에 관측된 파랑 관측자료가 활용된다(129o13'34.56''E 37o24'11.22''N).
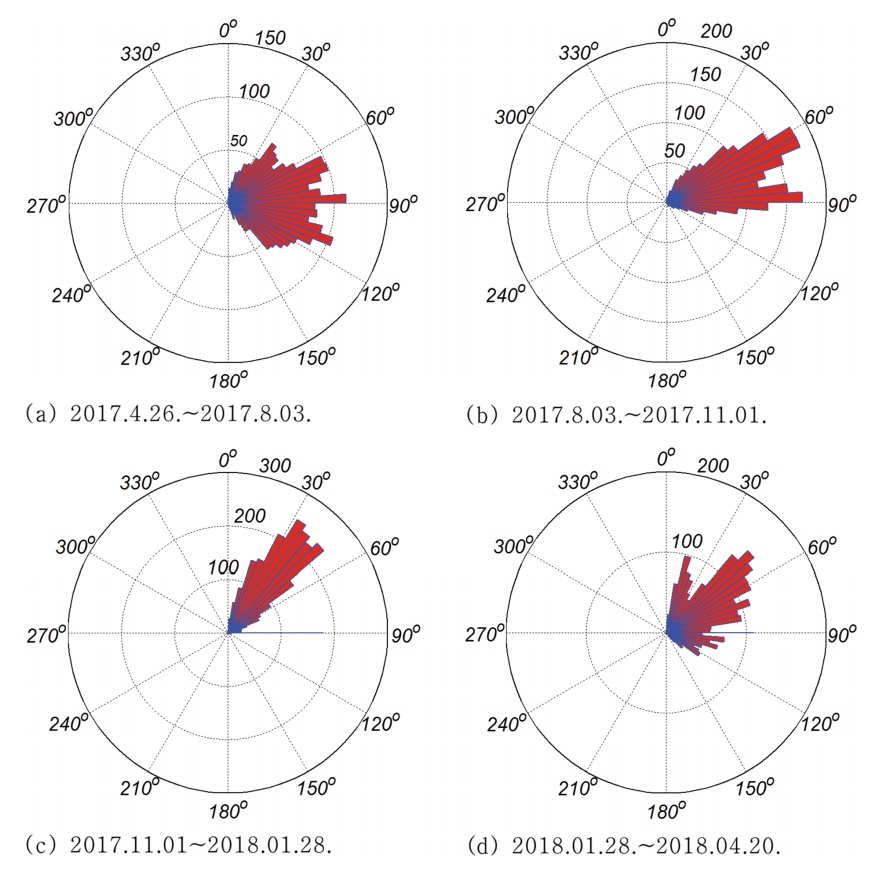
2장에서는 해안선 모형을 구성하는 중요 요소인 Energy flux 연안 표사량 모형, Bailard(1981) 계열의 수정 횡단 표사량 모형(Cho and Kim, 2019), 연안표사 장미도(littoral sediment drift rose)를 정리하였으며, 수치모의 결과는 3장에서 다루었다. 분기별 해안선 변화 추이를 이해하는 데 필요한 분기별 파랑 장미도, 입사각도별 파고 분포, 파향 벡터도는 Appendix에 정리하여 수록하였다.
2. 해안선 모형(One Line Model for shore line)
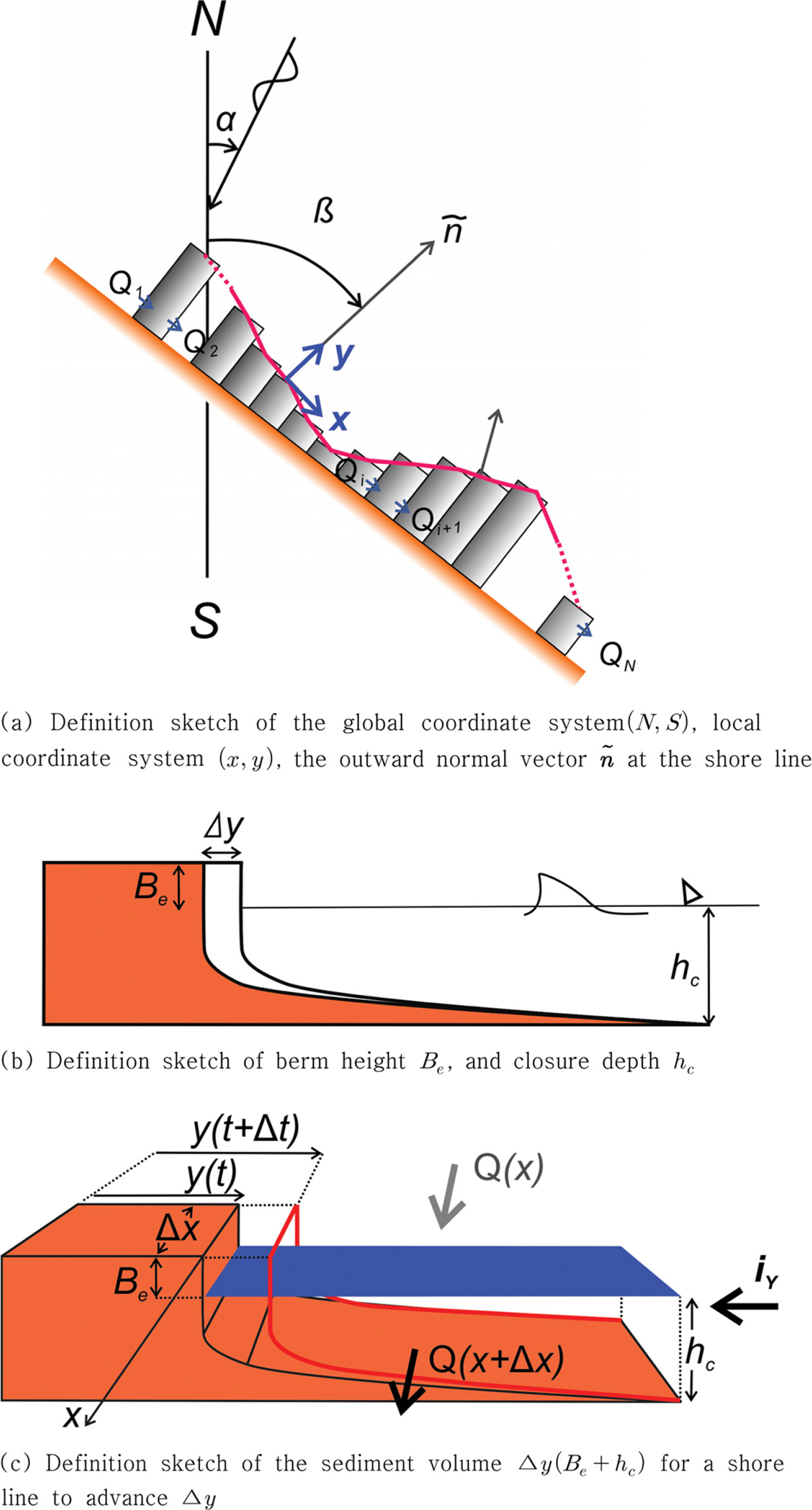
수치모의를 위해 이산화한 단위 격자에 표사수지와 해안선 전진 혹은 퇴각량 Δy는 서로 균형을 이룬다는 개념으로부터 해안선 모형(One Line Model for shore line)을 얻을 수 있으며 이를 기술하면 다음과 같다.
식(1)에서 y(t)는 해안선 위치, Be는 berm height, Q(x)는 연안 표사 이송률, iY는 횡단 표사 이송률, hc는 closure depth를 각각 나타낸다. Fig. 2에는 이해를 돕기 위해 수치모의에 사용된 전체 좌표계와 국지 좌표계, 해안선 외향법선 벡터 n ~
수치모의 결과를 해석하기 위해서는 수치모의에 사용된 연안 표사량 모형과 횡단표사량 모형, 연안표사 장미도(littoral sediment drift rose)를 이해할 필요가 있으며 이를 정리하면 다음과 같다.
2.1 연안 표사량
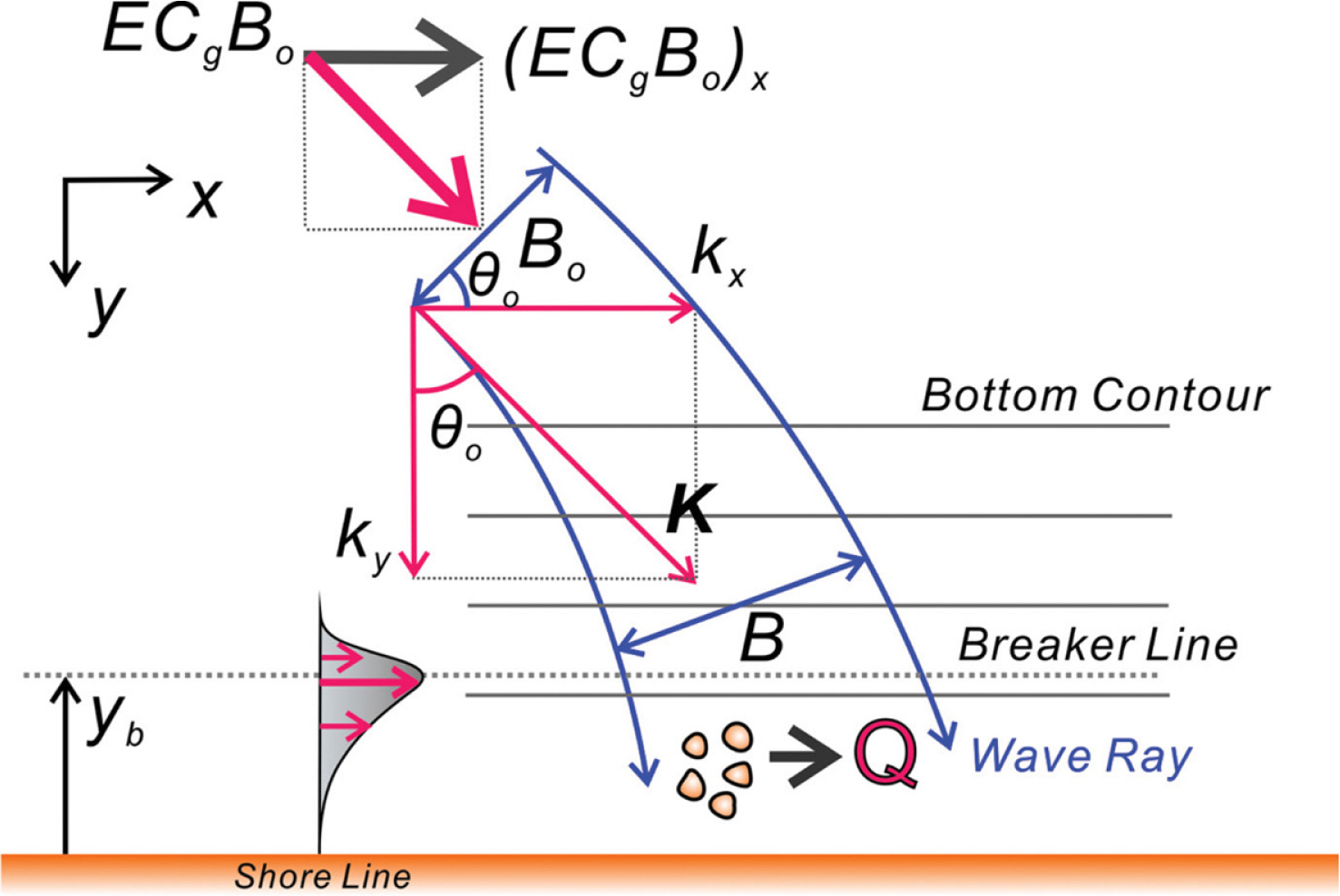
연안 표사량 Q는 가용한 파랑에너지 유입률 ECGB에 결과되는 것으로 해석하였으며, 사용된 Energy flux 모형을 기술하면 다음과 같다(Komar and Inman, 1970; Kraus et al., 1982; Dean et al., 1982; Dean and Dalrymple, 2002).
여기서, K는 계수, Ho는 심해 입사파고, g는 중력 가속도, T는 주기, θo는 심해 입사각도, S는 표사 비중, P는 공극율, κ = 0.79, θb는 쇄파역에서의 입사각도를 각각 나타내며(Fig. 3 참조), 식(2)의 유도과정에는 Snell’s Law가 활용되었다(Dean and Dalrymple, 2002).
2.2 횡단 표사량
횡단 표사량 iY는 현재 문헌에서 가장 빈번하게 언급되는 Bailard(1981)의 모형에 기초하여 산출하였다. Bagnold(1963)의 Energy 모형을 근간으로 표사를 부유사와 소류사로 분류하여 다룬 초기형태의 Bailard와 Inman(1981) 모형을 기술하면 다음과 같으며,
여기서, 〈 〉는 주기평균 연산자, Cf는 마찰계수, Φ는 마찰각도, β는 저면경사, εb와 εs는 각각 가용한 파랑에너지 중 소류사와 부유사 이송에 소요되는 비율, ρ는 밀도, u는 유속 벡터, i는 표사 이송량 벡터, w는 표사 침강속도, j는 해안방향을 가리키는 단위 벡터를 각각 나타낸다.
수치모의에는 유동계 u를 파동계 u ~ u ¯
여기서, δu, Ψ1, Ψ2, u3*, u5*는 각각 저류, 왜도, 정규화된 평균유속을 나타내며 다음과 같이 기술될 수 있다.
δu, Ψ1, Ψ2에 대한 해석해는 아직 가용하지 않으며, Bailard (1981)는 미 California Torrey Pines 해빈에서 관측된 자료로부터 전술한 적률에 대한 근사식을 제안한 바 있다. 최근 Cho and Kim(2019)은 Bailard와 Inman(1981) 이 모형의 검증과정에 활용한 미 California Torrey Pines 해빈 파랑자료와 우리나라 맹방 전면해역에서 관측되는 파랑자료 간에 존재하는 구조적 차이에 주목하고, Bailard와 Inman(1981) 이 간과한 주기가 반영된 수정모형을 비선형 Boussinesq Eq.(Frelich and Guza, 1984)에 기초하여 수치모의된 쇄파역 유속자료를 토대로 제시한 바 있다. Cho and Kim(2019)이 제시한 유동적률에 대한 근사식을 정리하면 다음과 같으며,
여기서 ξ는 Iribarren NO.를 나타내며 다음과 같이 기술될 수 있다.
3. 수치결과
3.1 표사수지
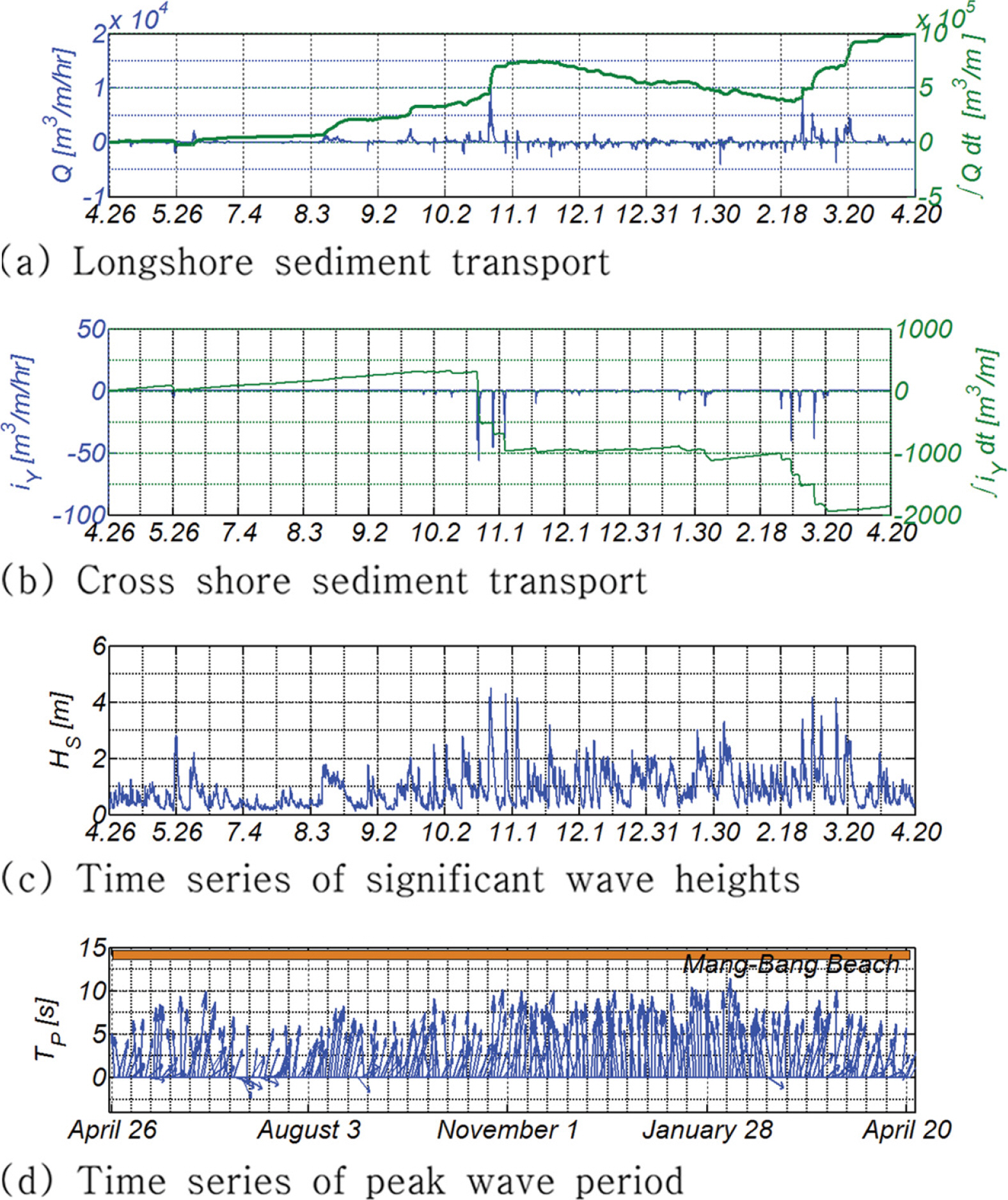
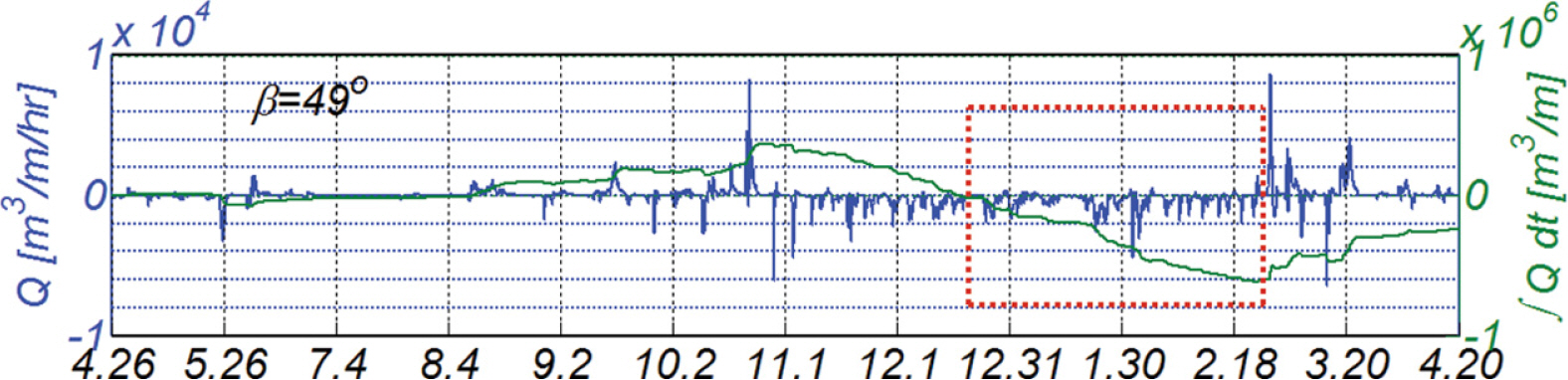
2장에서 다룬 Bailard(1981)의 수정 횡단표사모형, Energy flux 연안표사 모형에 준거하여 맹방해빈의 년 표사수지를 수치모의 하였으며 그 결과는 Fig. 4에 도시하였다(K = 0.2, P = 0.3, εs = 0.025, εb = 0.21, Cf = 0.005). Fig. 4(a), (b)에서 좌측은 instantaneous sediment transport rate을 나타내며 우측은 누적 sediment transport rate을 각각 나타낸다. Fig. 4에는 이해를 돕기 위해 유의파고 시계열자료와 파향 벡터도를 함께 수록하였으며, 파향 벡터도에서 크기는 주기를 나타내며 방향은 파향이 해안선 외향법선 벡터 n ~
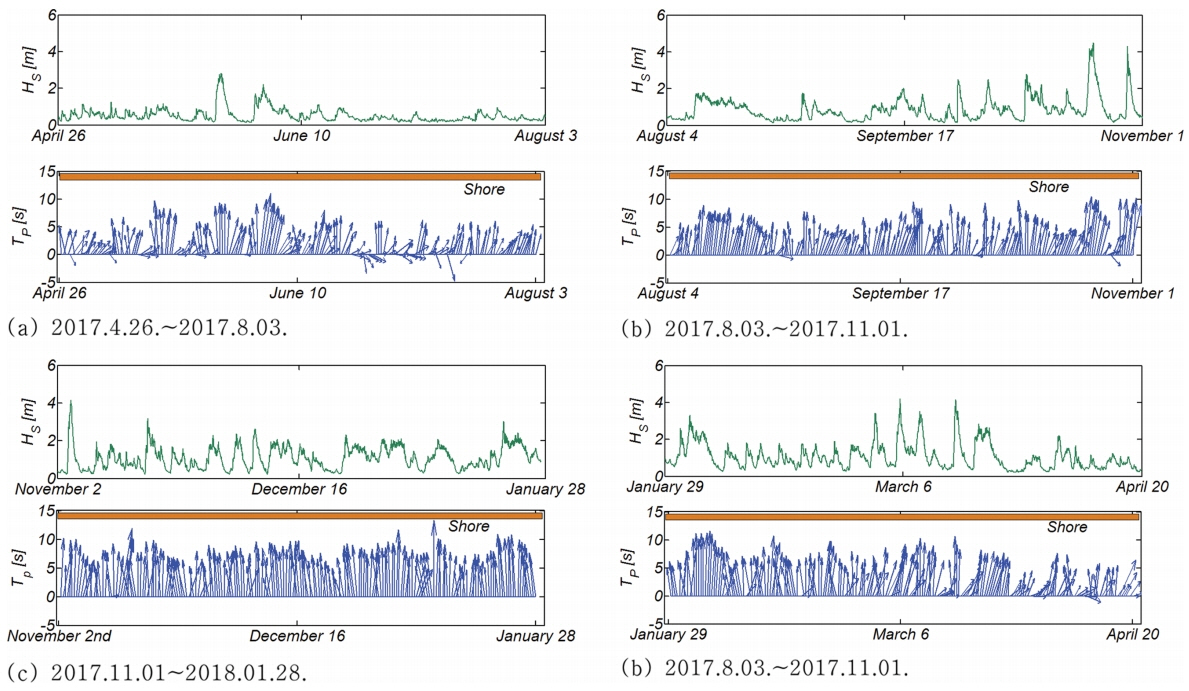
Fig. 4는 맹방해빈의 평균 방위 β = 41.6º을 대상으로 수행된 것으로 연안표사의 경우 북서진하는 연안표사가 우월하며 그 양은 년 100,000 m3/m에 달하는 것으로 모의 되었다. 횡단표사의 경우 4월부터 10월 중순까지는 연안방향으로의 퇴적이 점진적으로 진행되나, 10월말과 3월 중순에 단발적으로 발생한 고파랑에 의해 대규모의 침식이 진행된 것을 알 수 있다. 그러나 11월과 1월 30일 사이, 2월초에서 2월말 사이, 3월 20일 이후에는 연안방향으로의 표사 이송이 다시 복원되어 자연 해빈이 지니는 자기 복원능력을 부분적으로 확인할 수 있다.
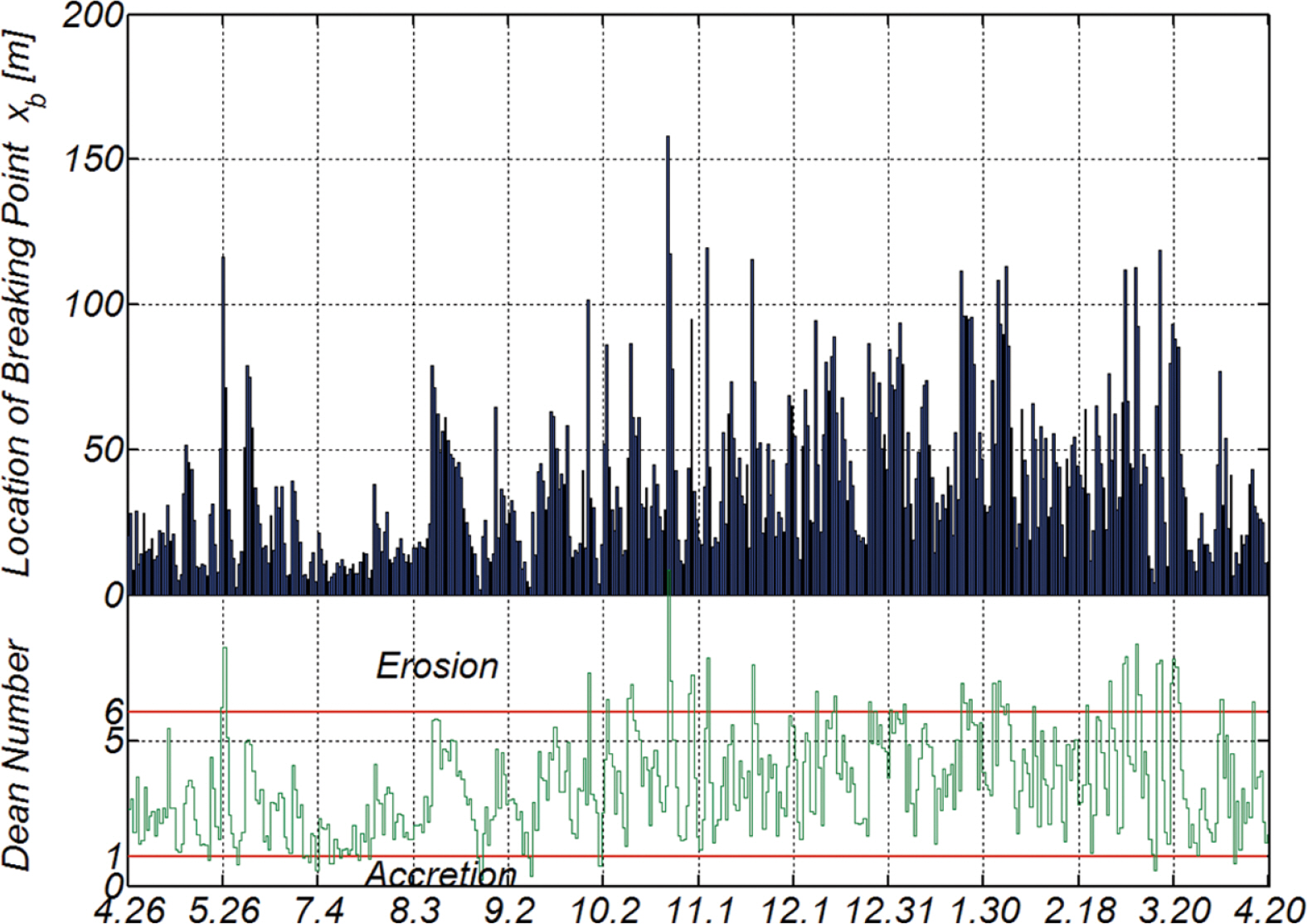
Fig. 5에는 비교를 위해 2017.4.26~2018.4.20 사이에 관측된 각 파랑에 해당되는 쇄파역의 해안으로부터의 이격거리 Xb와 횡단표사의 이동방향을 가늠할 수 있는 Dean NO. D를 도시하였다. Dean NO. D를 기술하면 다음과 같으며
여기서 Hb = κh는 쇄파역에서의 파고, h는 수심, w는 표사침강속도를 각각 나타내며 D > 6인 경우 침식이, D < 1인 경우 퇴적이 우세한 것으로 전해진다(Dean and Dalrymple, 2002).
전절에서 다룬 횡단표사에 의한 4월부터 10월 중순까지 진행되는 퇴적과 10월 말과 3월 중순에 단발적으로 발생하는 고파랑에 의해 대규모 침식이 Fig. 5에 제시된 Dean NO. D 시계열 자료에서도 상당히 근접하게 예측되는 것을 알 수 있다. 또한 쇄파가 시작되는 지점이 xb = 10 m에서 xb = 160m까지 상당히 넓게 포진하며, 이를 통해 해빈 표사가 발생하는 공간적 범위를 가늠해 볼 수 있다.
3.2 연안표사 장미도(littoral sediment drift rose)
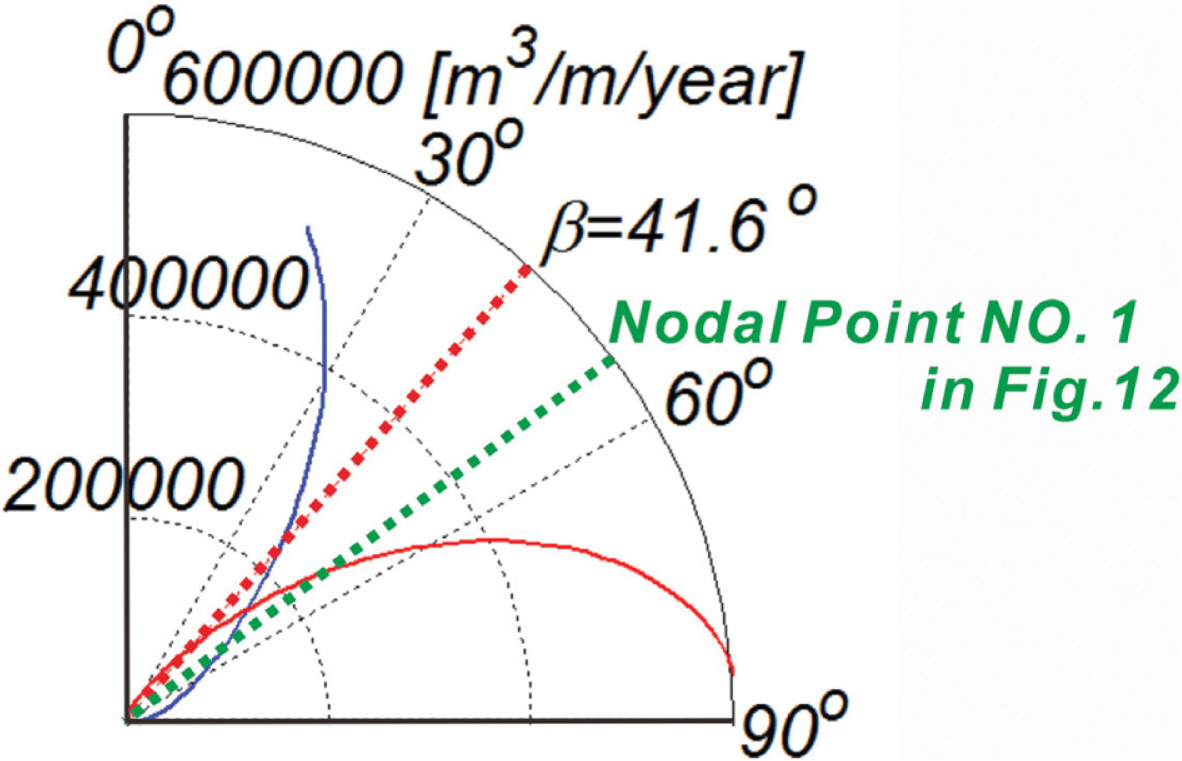
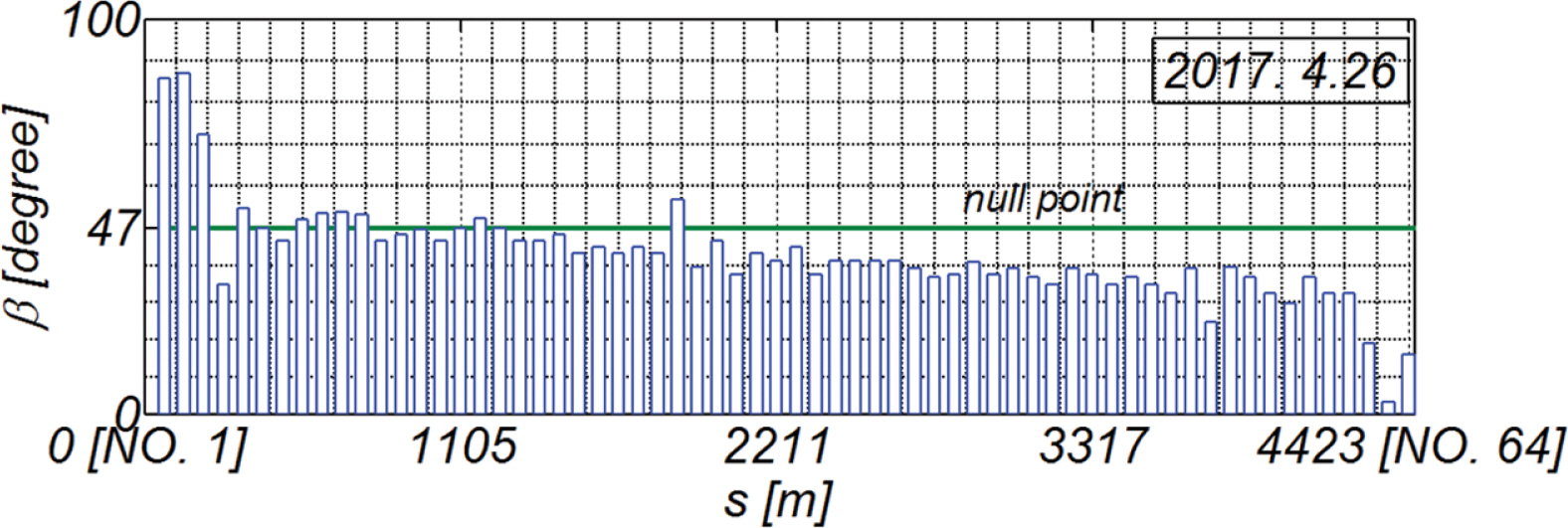
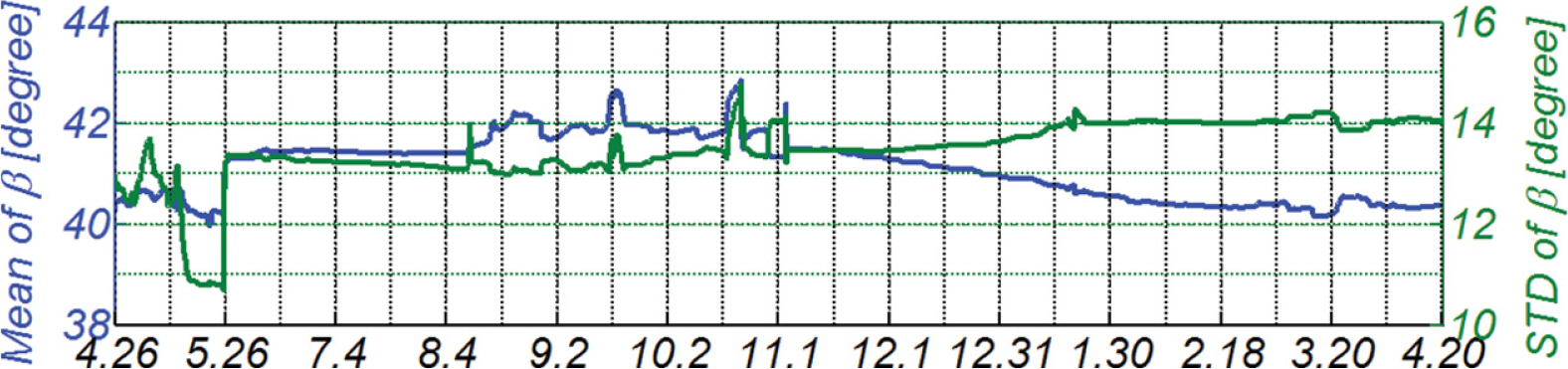
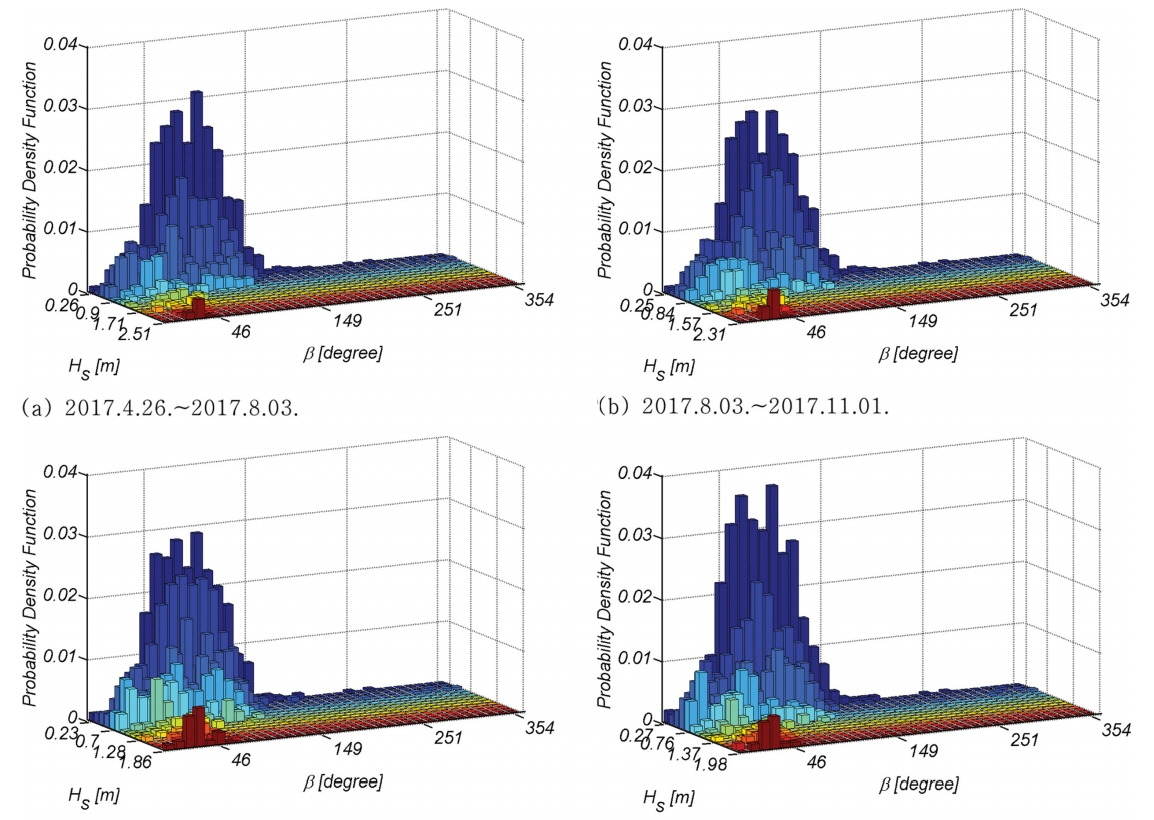
Fig. 6에는 2017.4.26~2018.4.20 사이에 관측된 파랑 관측자료를 대상으로 산출된 맹방 표사계의 연안표사 장미도를 도시하였다. 여기서 빨간 실선은 남동진하는 연안표사를 나타내며, 파란 실선은 북서진하는 연안표사를 나타낸다. 북서진하는 연안표사와 남동진하는 연안표사가 균형을 이루는 null point는 β = 47º에 위치하는 것을 알 수 있다. Fig. 7에는 수치모의가 시작되는 2017.4.26에서의 해안을 따라서 변하는 β를 도시하였으며, 대부분의 경우 null point β = 47º보다 작아 북서진하는 연안표사가 우월하다는 것을 알 수 있다(Fig. 6 참조).
3.3 Closure depth와 해안선
3.3.1 Closure depth
Fig. 5에서 확인하였듯이 표사이송이 진행되는 공간적 범위는 파랑에 따라 상이하며, 따라서 식(1)에 정의된 해안선 모형에서의 closure depth도 파랑에 종속하는 것으로 해석하는 것이 보다 큰 설득력을 지니나 현재 Genesis(Hanson and Kraus, 1989)로 대표되는 대부분의 지형모형에서는 이러한 파랑에 따른 closure depth의 변동성은 간과되어 있어 시정이 요구된다.
Hallermeier(1978)는 수조실험결과로부터 Shiled’s parameter ψ를 중심으로 closure depth hc를 다음과 같이 특정하고,
파랑에너지 보존식과 식(18)로부터 closure depth hc를 다음과 같이 심해 파랑조건으로 구성된 관계식의 해로 정의한 바 있다.
이 연구에서 Hallermeier(1978)는 상기한 관계식을 토대로 실해역의 경우 closure depth hc에 대한 근사식을 제안한 바 있으며 이를 기술하면 다음과 같다.
여기서 He는 년 중 초과기간이 12 hr인 유의파고로 정의되는 유효 파고(effective height)를 나타내며 다음과 같이 산출될 수 있다.
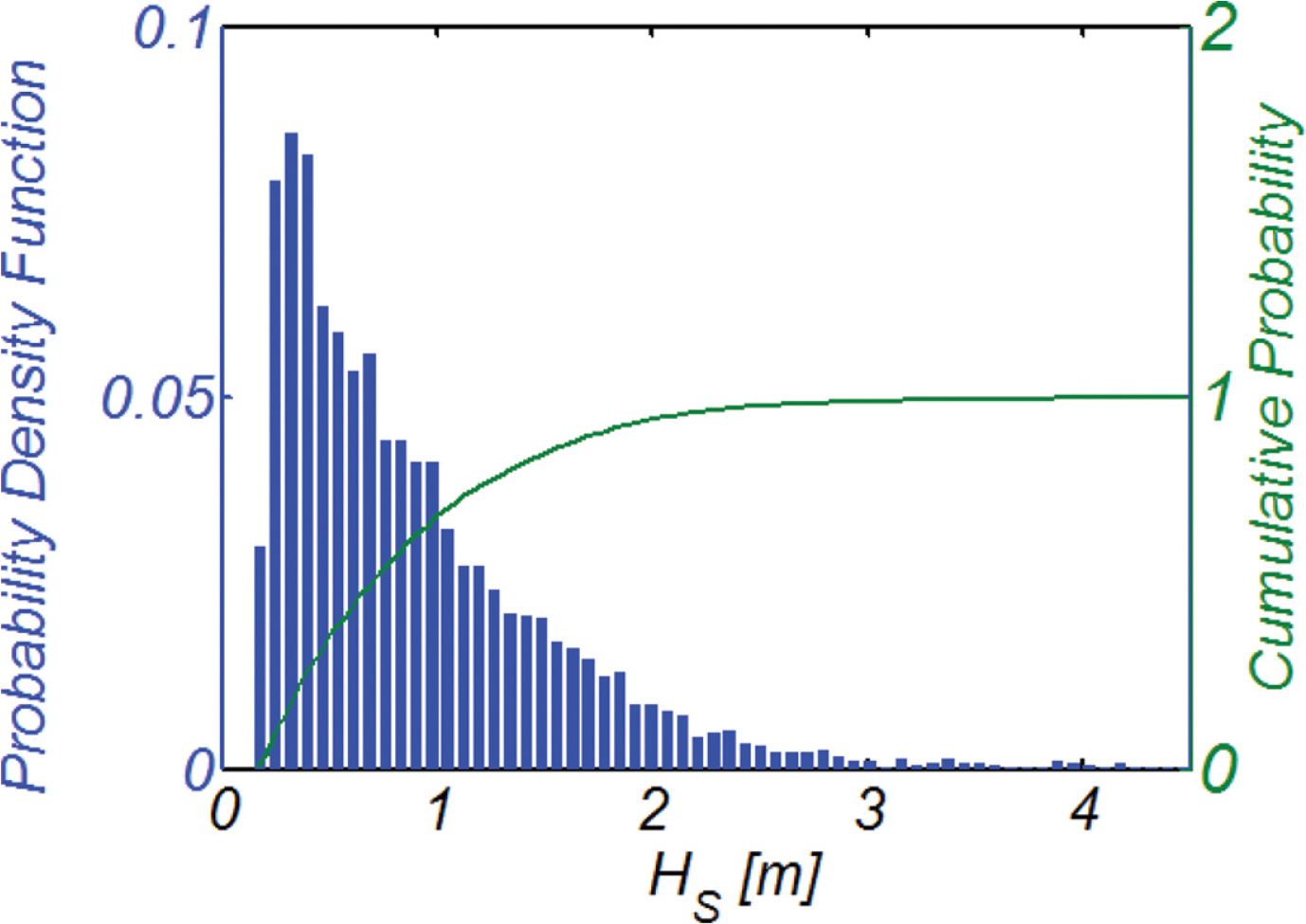
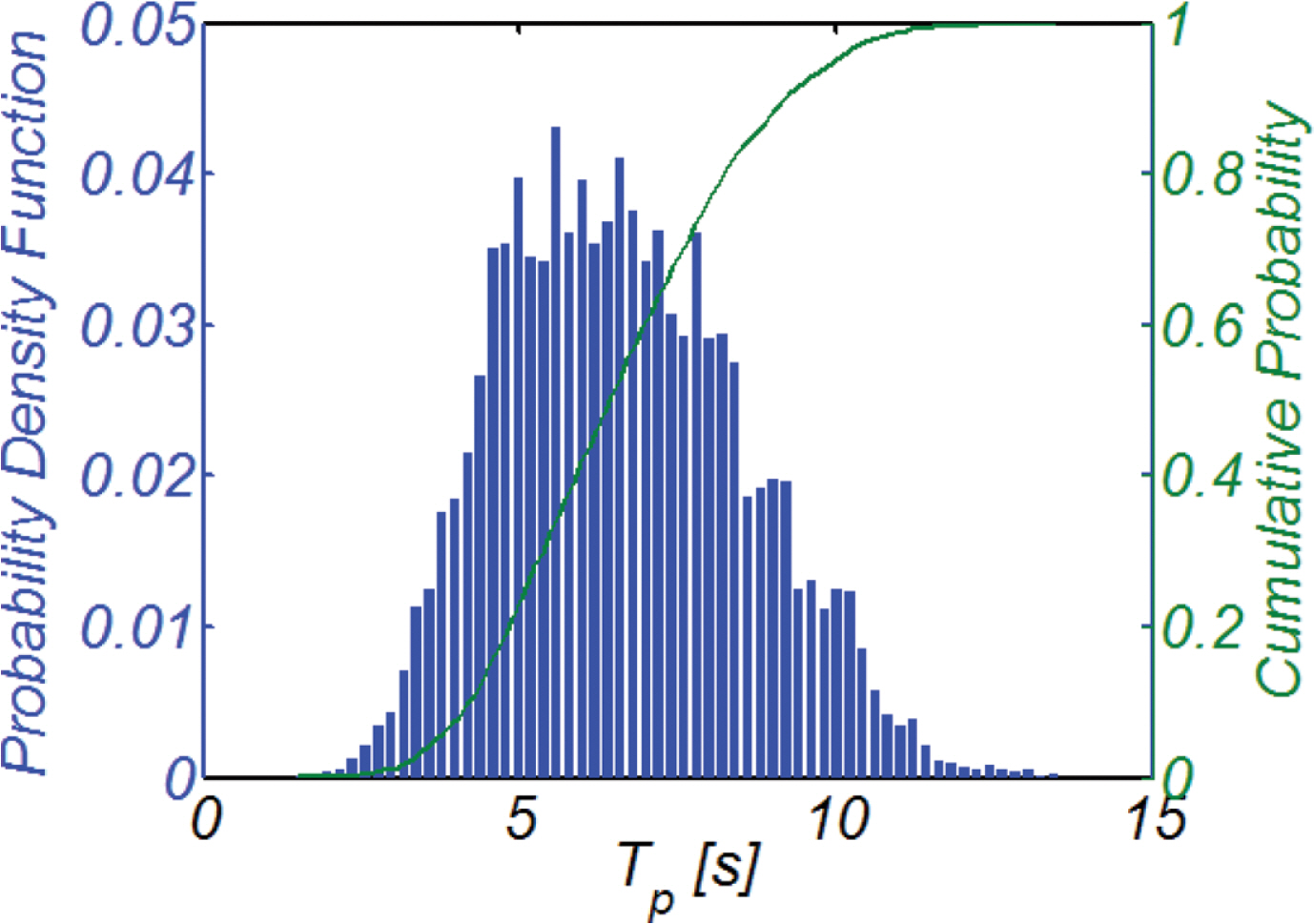
Table 1에는 식(20), (21)과 2017.4.26~2018.4.20 사이에 맹방해빈 전면해역에서 관측된 파고와 주기 관측치 빈도해석결과로부터 산출한 closure depth를 정리하였으며(Fig. 8, 9 참조), 방법론에 따라 편차가 상당하다는 것을 알 수 있다(Brutsch et al., 2016).
그러나 Hallermeier(1978)가 경험적 해석방법을 통해 제시한 식(20)에 맹방해빈에서의 파랑특성이 적절히 반영된 것으로 보기 어려워 관측치 빈도해석결과로부터 도출한 분포함수에 기초한 probabilistic method가 수월성을 지니고 있는 것으로 판단된다.
식(21)에서 확인할 수 있듯이 현재 대부분의 지형모형에서는 고파랑에 의한 표사이송이 가장 우월하다는 시각에서 closure depth가 결정되나, 이 경우 Fig. 4(b)에서 사월 말에서부터 시월 중순까지 관측되는 장기간에 걸쳐 너울에 의해 해안으로 회귀되는 표사로 인한 해안선 전진이 과소하게 평가될 수 있다(식(1), Fig. 4 참조).
식(19)에 기술된 Hallermeier(1978) 초기 모형은 그 유도과정에 단조해안이라는 가정이 수행되었으나, closure depth hc가 표사이송 여부를 가늠하는 데 예외 없이 활용되는 Shiled’s parameter에 근거한다는 점에서 상당히 강건한 물리적 기반을 지닌다. 또한 본고에서 다루는 우리나라 맹방해빈의 경우 상당한 부분의 파랑이 해안과 직각을 이루며 내습한다는 사실을 고려하는 경우 전술한 단조해안이라는 가정은 수용 가능해 보인다(Fig. 4(d) 참조).
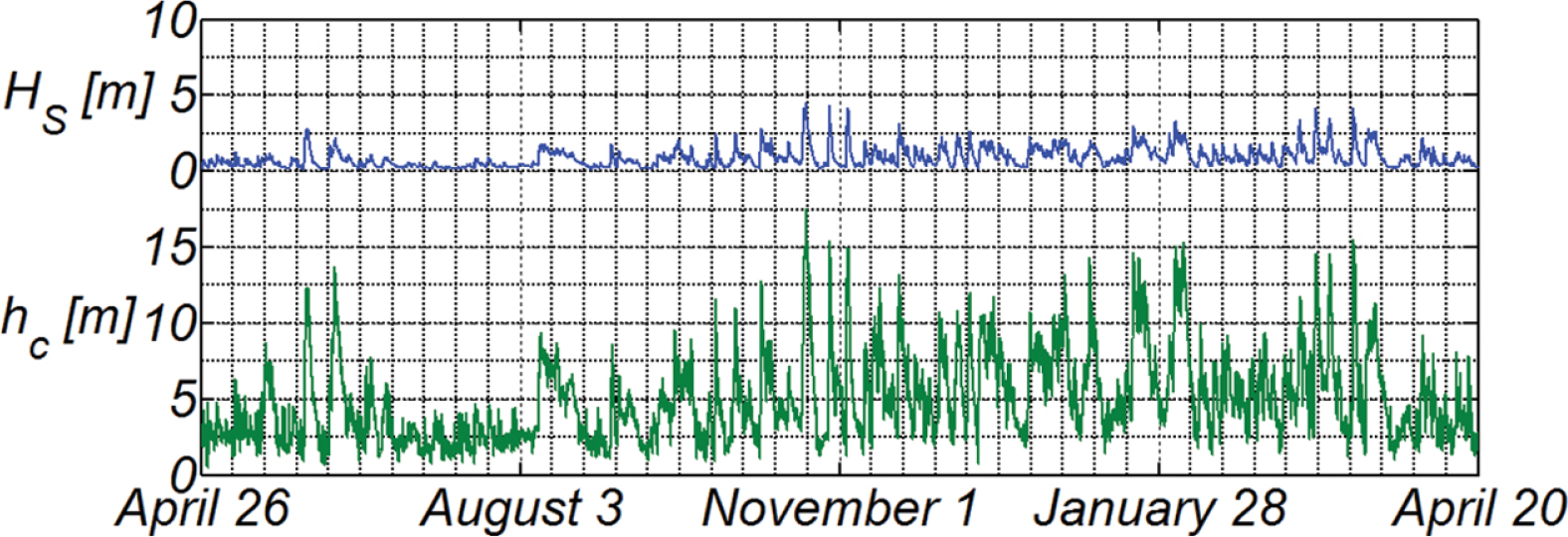
Fig. 8에는 식(19)에 준거하여 산출한 closure depth의 시계열 자료를 도시하였으며, 비교를 위해 파고 시계열자료도 함께 도시하였다. 예상대로 closure depth는 파고와 높은 상관성을 지니며 h c M I N h c M A X
3.3.2 해안선
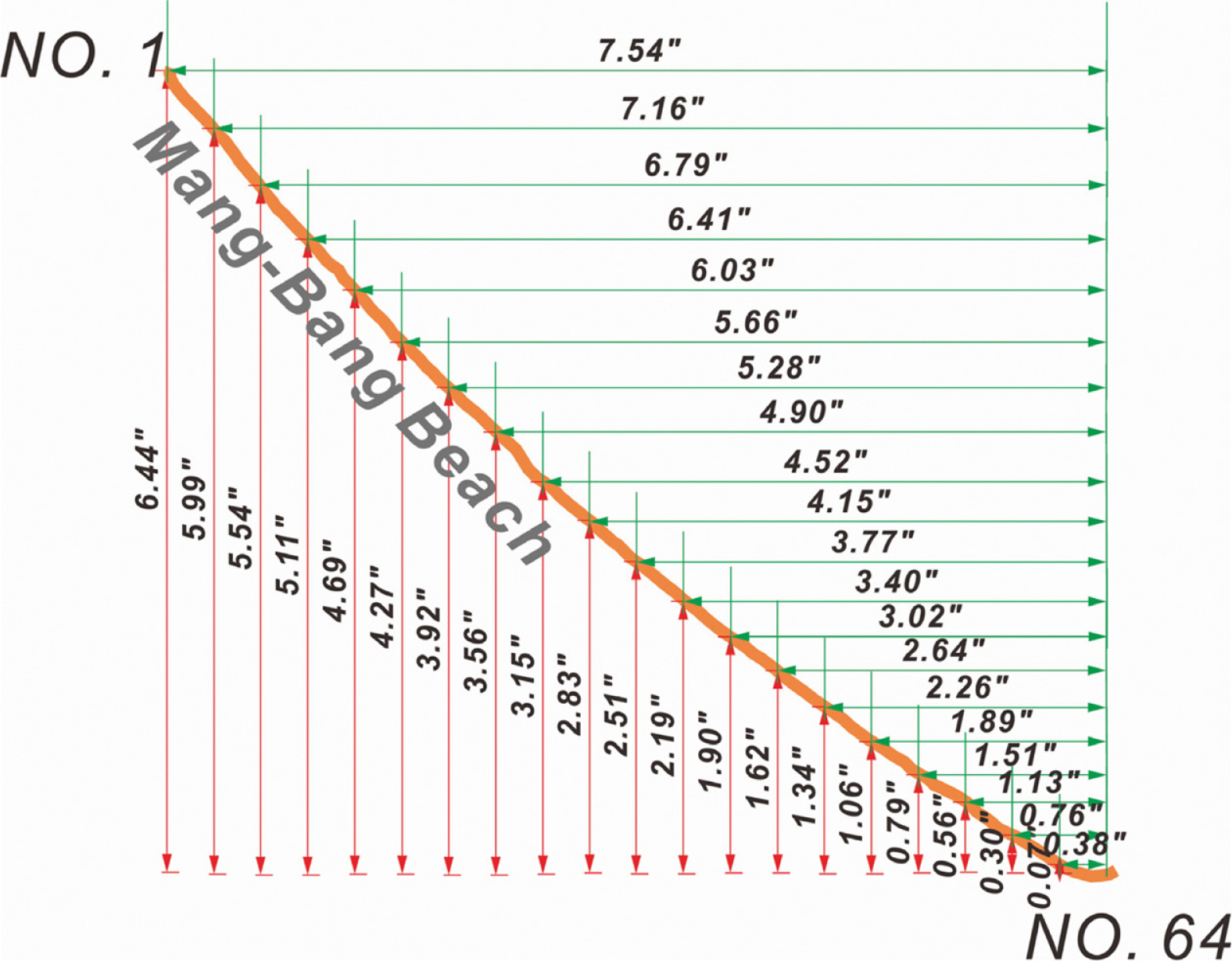
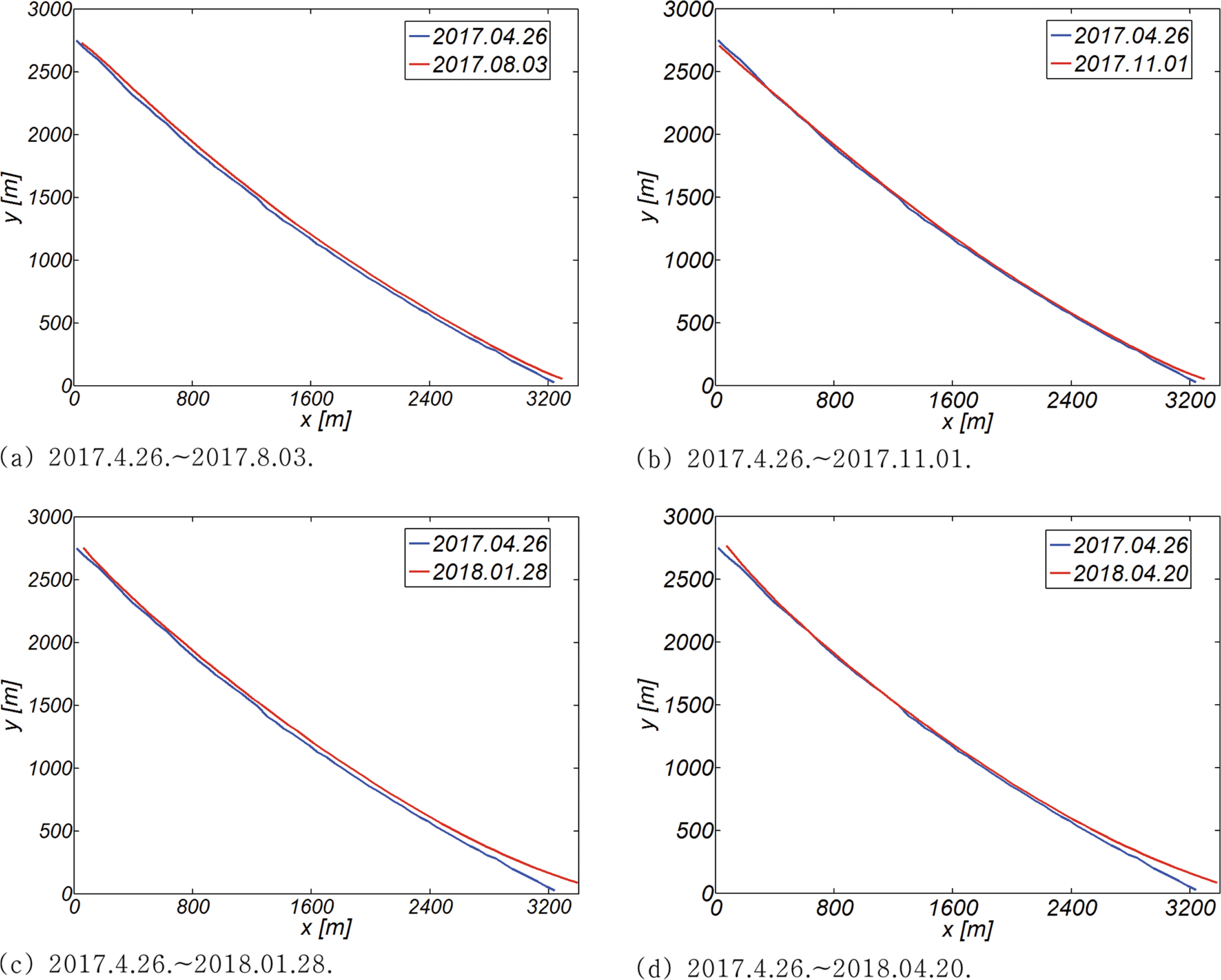
Fig. 11에 도시된 표사계의 총 4423 m에 이르는 해안선을 64개(Δx = 18.2~68.4 m)로 분할하여 2017.4.26부터 2018.4.20까지의 해안선 변화를 수치모의 하였다(Fig. 12 참조). 수치모의에는 closure depth가 파랑에 의해 결정되는 것으로 해석하였으며(RUN I), 비교를 위해 closure depth가 hc = 8.09m로 일정한 경우도 병행하여 수행하였다(RUN II).
Fig. 13에는 수치 모의된 해안선을 분기별로 도시하였으며 분기별로 해안선 변화추이를 정리하면 다음과 같다(RUN I).
A 2017.4.26.~2017.8.03.
B 2017.4.26.~2017.11.01.
하계 중순부터 추계 중순에 해당되는 이분기의 경우 해안선이 전체적으로 퇴각했으며 이는 시월 중순에 연이어 발생한 년 최대 고파랑에 의한 일시적 침식에 기인하는 것으로 보인다(Fig. 4, 5 참조).
C 2017.4.26.~2018.01.28.
추계 중순부터 동계 중순에 해당되는 삼분기의 경우 고파랑에 의해 일시적으로 침식되었던 해안선이 전체적으로 복원되었으며, 이러한 현상은 이 기간 동안 별다른 고파랑의 내습이 없었고 상대적으로 온화한 너울로 인해 횡단표사가 지속적으로 유입되어 발생한 것으로 보인다(Fig. 4, 5 참조).
D 2017.4.26.~2018.04.20.
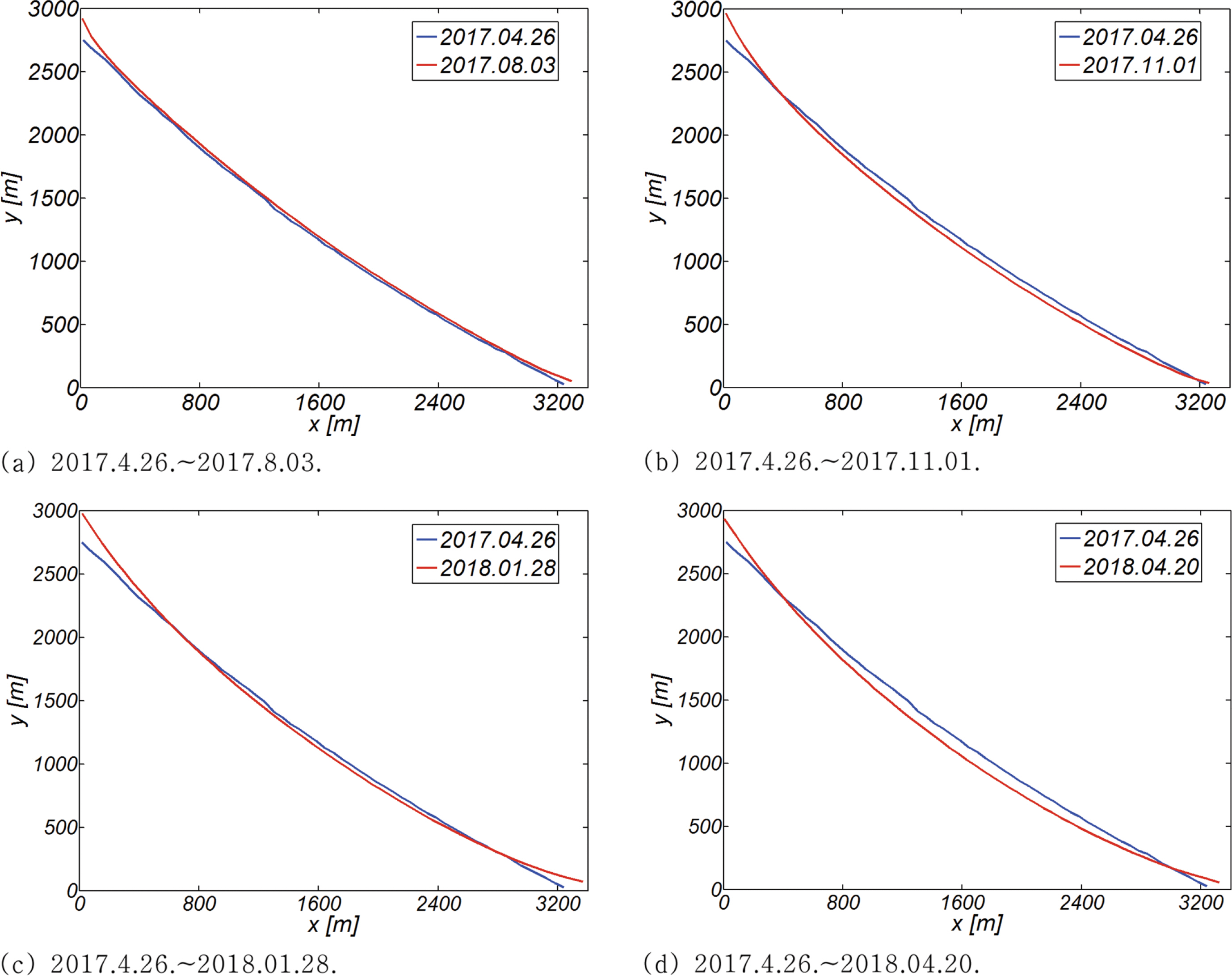
Fig. 14에는 RUN II에서 관측된 해안선을 분기별로 정리하였다. 계절별 해안선 변화 추이는 RUN I에서 관측된 경향: 춘계 말에서 추계 초입까지의 해안선 전진, 시월 중순에 연이어 발생한 년 최대 고파랑에 의한 해안선 퇴각, 추계 중순부터 동계 중순까지의 너울로 인한 횡단표사 유입과 이로 인한 해안선 복원, 삼월중순부터 삼월말까지 연이어 발생한 고파랑에 의한 해안선 퇴각 등이 유사하게 관측되나 해안선 전진 혹은 퇴각되는 양은 RUN I에 비해 상당히 증가되는 경향을 관측할 수 있다.
이러한 차이는 식(20), (21)에 기술된 Hallermeier(1978)의 경험식이 우리나라 맹방해빈의 파랑 특성을 반영하지 못해 발생한 것으로 보인다. 따라서 보다 강건한 물리적 기반을 지닌 Shiled’s parameter에 근거한 Hallermeier(1978, 1981) 해석모형을 토대로 파랑에 따라 closure depth를 수정(update)하는 과정이 필요해 보인다(Brutsch, 2016).
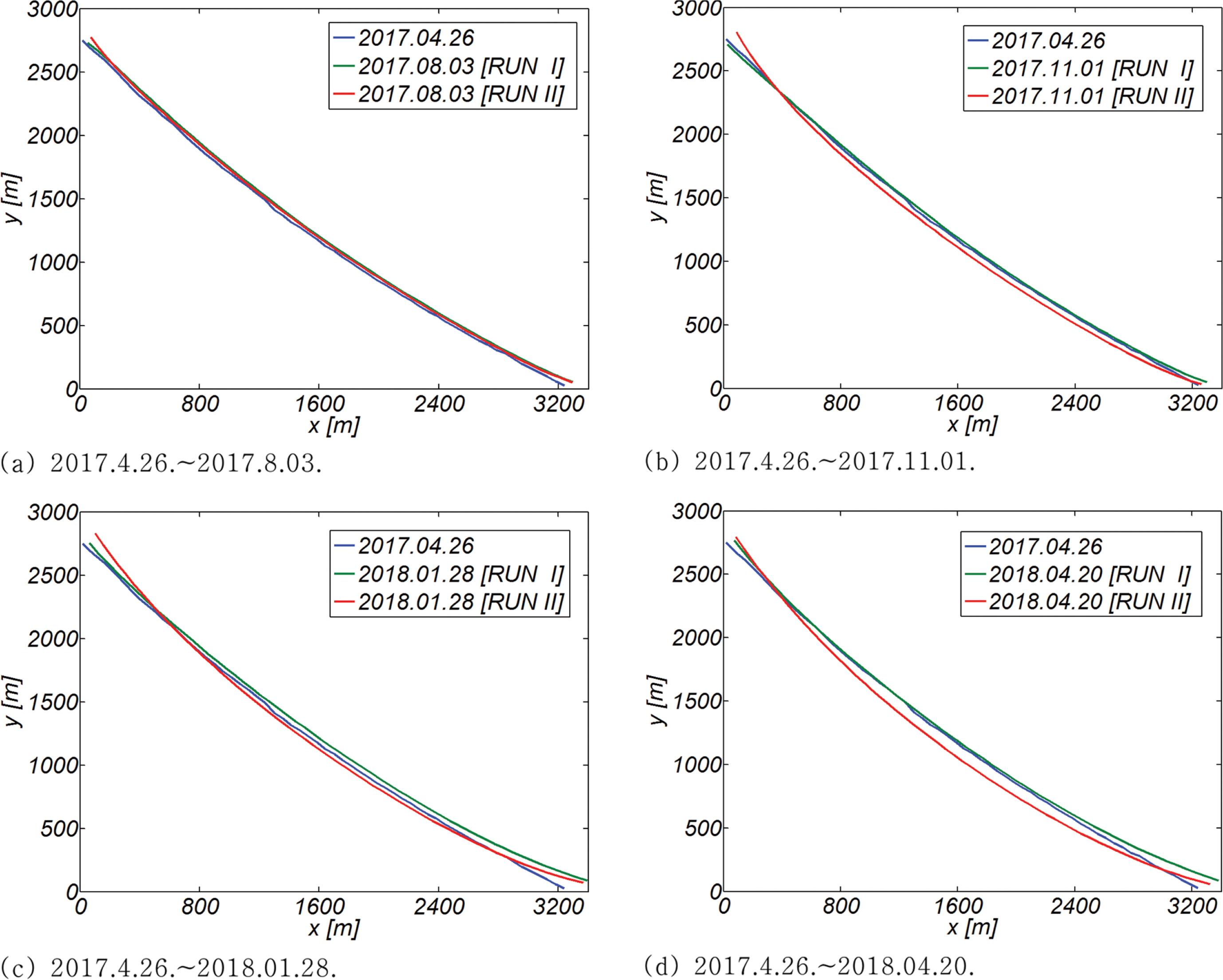
Fig. 15에는 파랑에 따른 closure depth의 변화가 해안선 거동에 미치는 영향을 보다 확연하게 드러내기 위해 RUN I, II에서 관측된 해안선을 분기별로 함께 도시하였다. 여기서 표사 장미도가 암시하듯 맹방 표사계가 안정적인 해빈이라면(Cho and Kim, 2019), 일 년여에 걸친 대순환 과정이 종료되는 시점에서 해안선은 원래의 위치로 회귀되어야 하며, 이러한 해안선 회귀는 RUN I에서 명징하게 관측되나 RUN II에서는 관측할 수 없었다(Fig. 15(d) 참조). 전술한 해안선 자기 회귀는 후술되는 해안선 측량 결과에서도 관측된다(Fig. 16(c) 참조).
이 밖에 수치모의된 해안선이 RUN I, II에서 절점 NO.1 인근에서 보이는 상이한 거동도 눈에 띈다. RUN II의 경우 2017년 11월 1일 해안선이 전진했으나, RUN I의 경우 해안선이 퇴각하였다(Fig. 15(b) 참조). 이러한 차이는 절점 NO.1 인근 해빈에서의 외향 법선 벡터 가 진북과 이루는 각도 β가 null point β = 47o보다 크며(Fig. 7 참조), 이 경우 남동진하는 연안표사가 우월하다는 사실(Fig. 6 참조)을 상기하면, RUN II에서의 해안선 전진은 지나치게 과다해 보이며, RUN I에서 관측되는 것처럼 해안선 후퇴가 보다 큰 설득력을 지닌 것으로 판단된다. 여기서 전술한 절점 NO.1 인근에서의 침식은 후술되는 해안선 측량 결과에서도 관측된다는 사실을 상기할 필요가 있어 보인다(Fig. 17(a), (b) 참조).
이와 더불어 RUN I에서 관측되는 절점 NO.64 인근에서의 해안선 전진(Fig. 15(d) 참조)은 맹방해빈 중앙부(점 NO.25~NO. 45)에서 2017년 12월 중순부터 2018년 2월 중순 사이에 발생하여 남동진하는 연안표사(Fig. 16 참조)가 돌출된 덕봉산(Fig. 1 참조)에 의해 차폐되고, 차폐된 표사가 누적되어 발생하는 것으로 보인다. 전술한 절점 NO.64 인근에서의 해안선 전진은 후술되는 해안선 측량 결과에서도 관측된다(Fig. 17(c) 참조).
Fig. 17에는 수치모형의 검증을 위해 2017년 4월5일, 9월 7일, 11월 7일, 2018년 3월 14일에 실측된 해안선 위치를 정리하였다. 수치모의에서 관측되는 춘계 말에서 추계 초입까지의 해안선 전진, 시월 중순의 해안선 퇴각, 동계 해안선 복원, 춘계 해안선 퇴각 등은 관측되나 그 양은 수치모의에 비해 현저하게 작아 보인다.
해안선 관측은 처오름(run-up)과 처내림(run-down)이 진행되는 swash-zone에서 진행되므로, 정확한 해안선 위치는 먼저 처오름 정점과 처내림 정점을 관측하고 그 중간 값으로 결정되어야 한다. 해안선 관측은 이처럼 꽤나 까다로운 과정을 거치며 처오름 정점과 처내림 정점이 제공되지 않는 한, 해안선 실측치에는 전술한 과정에서 수행된 여러 주관적 판단이 녹아있다고 보아야 한다.
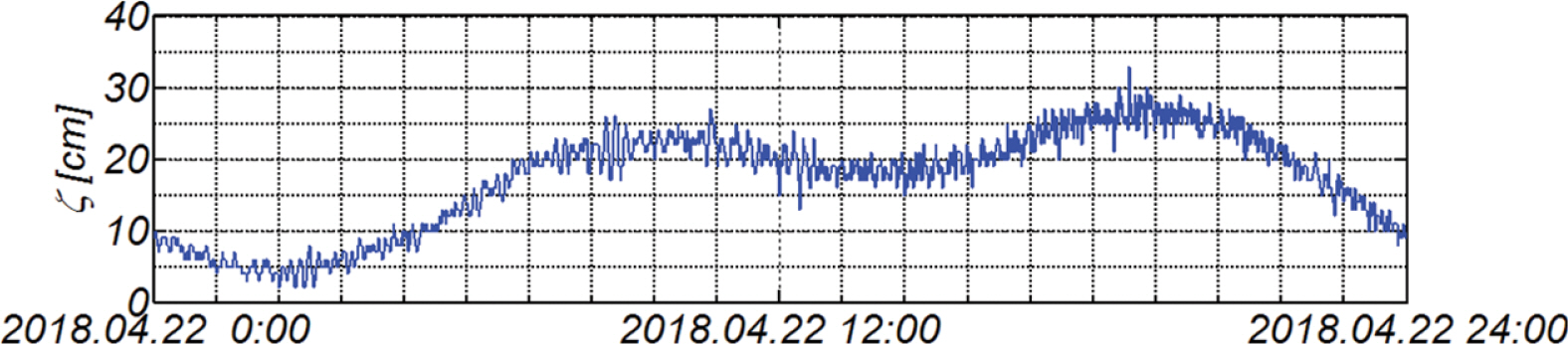
또한 0.3 m 내외인 맹방해빈에서의 조위차(Fig. 18 참조)를 고려하는 경우 해빈 경사를 맹방해빈 평균치인 1/30으로 취하면 참 해안선의 위치는 9 m 정도 보정되어야 하며, 고파랑 내습으로 상당한 침식이 진행된 경우 해빈 경사는 보다 완만해지며 이 경우 이격 양은 더욱 증가할 수 있다.
이와 더불어 맹방해빈의 경우 침식이 진행되고 있는 것으로 보고된 바 있으나 현재 측정된 해안선 위치는 년 중 변화가 지나치게 작으며, 특히 년 최대 고파랑 연이어 내습한 이후인 11월 7일에 측정된 해안선의 경우 퇴각량이 우리들의 인식과는 상당한 거리가 있다.
이상의 논의와 표사이송 문제에 내재한 난해함을 고려하는 경우 수치모의된 해안선 위치의 overshooting 문제는 수용 가능해 보이며, 본고에서는 실측된 해안선 위치는 정성적 변화에만 국한하여 수용하였다.
Fig. 19에는 이해를 돕기 위해 수치모의된 맹방해빈에서의 외향 법선 벡터 n ~
이상의 수치모의 결과 분석으로부터 얻은 결론을 정리하면 다음과 같다.
A. 자연 해빈이 지니는 자기 복원능력을 수치적으로 확인할 수 있다.
B. 수치모의에서 관측되는 일 년에 걸친 해안선 대순환과정이 자연계에서 실측된 해안선 위치에서도 유사하게 관측된다는 점에서 본고에서 제시한 진행된 해안선 모형은 부분적으로 검증된 것으로 판단된다.
C. Closure depth를 파랑에 의해 결정되는 것으로 해석하는 경우(RUN I), 자연계에서 실측된 해안선 위치에 보다 근접한 해안선 변화가 수치모의 될 수 있었다.
D. 따라서 본 고에서 제시한 해안선 모형은 해역별 최적 해빈 안정화 공법 선정 platform에 일정부분 기여할 수 있을 것으로 판단된다.
3.4 향후 연구과제
3.3.2절에서 다루었듯 본 논문에서 수치모의된 해안선 전진 혹은 퇴각양은 측정치를 overshooting하는 것으로 보인다. 이러한 편차는 연안표사량 모형에서 사용된 계수 K(식(2) 참조)와 Bailard(1981) 계열 수정 횡단표사모형 상의 εb, εs(식(3) 참조)를 맹방해빈의 표사 특성을 반영하여 최적화 하는 경우 일정 부분 조정이 가능한 것으로 보인다.
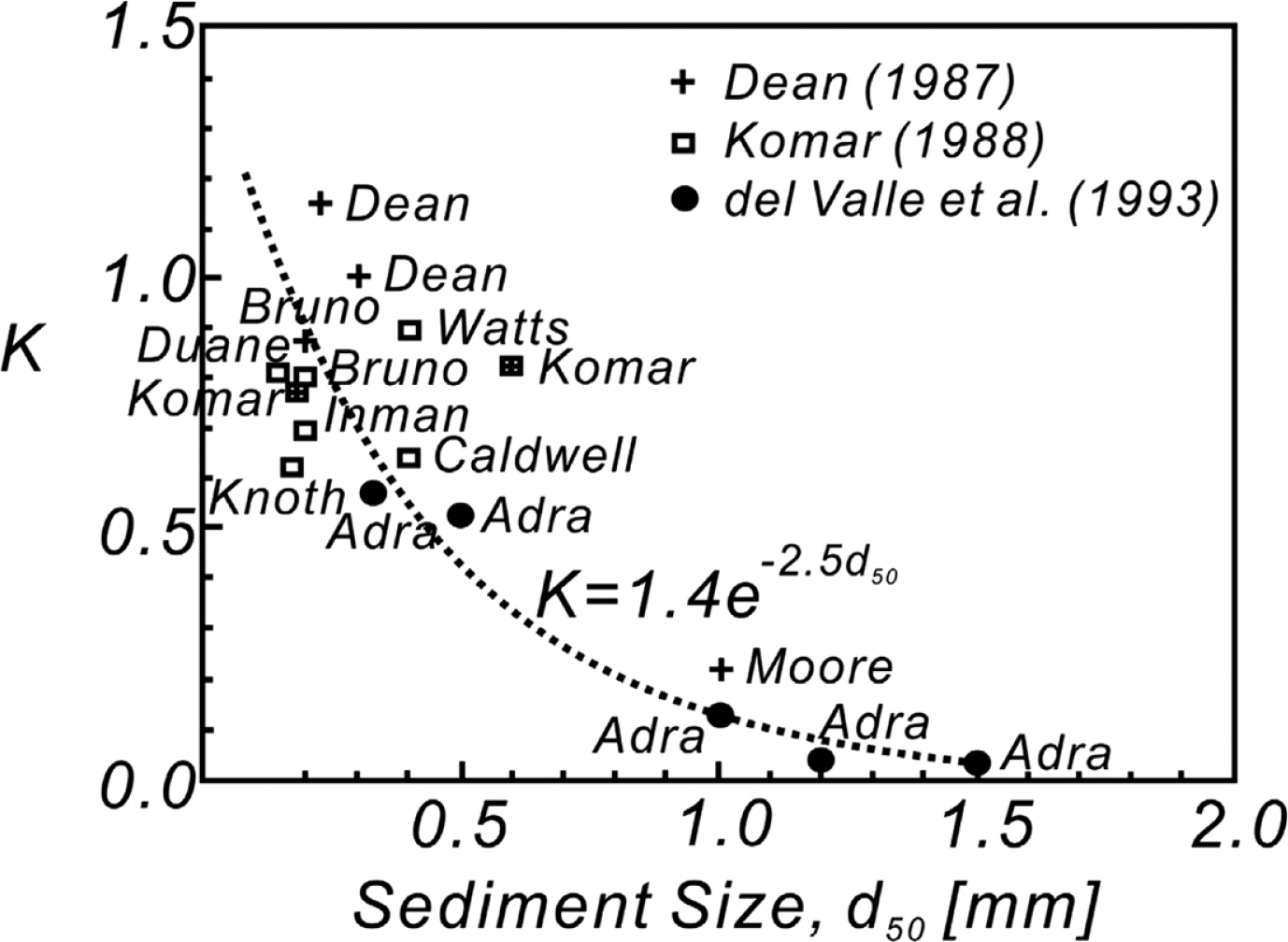
현재 해안 공학계에서는 전술한 K 값에 대한 여러 가지 이견이 상존하나, 가장 빈번하게 인용되는 수치는 K = 0.77로 보이며(Bodge and Kruss, 1991), 본 논문처럼 유의파고 HS를 중심으로 연안 표사량을 기술하는 경우 K 값은 전술한 수치의 35%(K = 0.26)를 취한다(Dean and Dalrymple, 2002).
그러나 Bailard(1984), Dean(1989), Kamphuis and Readshaw(1978) 등에 따르면 K는 상수라 볼 수 없으며, 표사 직경, 쇄파 형태를 결정하는 Iribarren NO. ξ(식(16) 참조)에 종속한다(Fig. 20 참조). 이러한 추정은 해빈표사 이송의 상당부분이 쇄파역 내에서 진행되며, 쇄파 형태는 Iribarren NO.에 의해 결정된다는 사실을 상기하면 상당히 강건한 물리적 기반을 지닌 것으로 보이며, 이 후 Bodge and Dean(1987)의 현장 관측 결과에서도 확인된 바 있다. 이 연구에서 K는 0.5 < K < 1.1 대역에서 Iribarren NO. ξ에 비례하여 증가하였다.
이상의 논의를 종합하면 제한된 기간(본 논문의 경우 2017.4.26~2018.4.20)에 한정해 K, εb, εs를 역추산하더라도 향후 예측 정확도가 담보된다고 볼 수 없으므로 보다 강건한 물리적 기반에 준거한 K와 Iribarren NO. ξ 사이의 인과관계를 규명하여 파고에 따른 K의 변동성을 반영하는 경우 상당한 정도의 해안선 변화 예측이 가능할 것으로 판단된다. 이와 더불어 가용한 파랑에너지 중 소류사와 부유사 이송에 소요되는 비율을 나타내는 εb와 εs에 대해서도 국내 표사 특성을 반영하려는 노력도 병행되어야 할 것으로 보인다.
4. 결 론
현재 상당한 침식이 진행되고 있는 맹방해빈을 대상으로 년간 해안선 변화량을 수치모의 하였다. 수치모의는 이산화된 해안선 단위 격자에 표사 순유입량과 해안선 전진 혹은 퇴각량은 서로 균형을 이룬다는 개념으로부터 유도한 해안선 모형(One Line Model for shore line)에 기초하여 수행하였다. 이 과정에서 연안 표사량의 경우 Energy flux 모형, 횡단 표사량의 경우 Bailard(1981) 계열의 수정 모형(Cho and Kim, 2019)이 활용되며, 파랑자료로는 맹방해빈 전면해역 수심이 26.5 m인 지점(Fig. 2 참조)에서 초음파식 파고계(Nortek)로 2017.4.26~2018.4.20 사이에 관측된 파랑 관측 자료가 활용되었다(129º13'34.56''E 37º24'11.22''N).
수치모의 과정에서 closure depth는 파랑에 종속하는 것으로 해석하였으며(RUN I), closure depth는 Shiled’s parameter에 기반 한 Hallermeier(1978)의 해석모형을 활용하여 산출하였다. 또한 비교를 위해 closure depth가 hc = 8.09m로 일정한 경우에 대한 수치모의도 병행하여 수행하였다(RUN II).
모의결과 너울이 우세한 2017.4.26부터 2017.10.15까지는 횡단 표사가 지속적으로 유입되어 해안선이 전진하는 것으로 모의되었다. 또한 10월 중순과 10월 말 사이에 연이어 발생한 년 최대 고파랑 내습에 따른 침식과 이로 인한 해안선의 일시적 퇴각, 이 후 파랑이 잦아들면서 다시 출현하는 너울에 의한 횡단표사 유입과 이로 인한 해안선 복원, 삼월중순부터 삼월말까지 연이어 발생한 고파랑에 의한 해안선 퇴각 등 일 년에 걸친 해안선 대순환과정이 상세하게 모의되었다.
전술한 해안선 대순환과정은 2017년 4월5일, 9월 7일, 11월 7일, 2018년 3월 14일에 측정된 해안선 위치에서도 유사하게 관측할 수 있다. 그러나 해안선이 전진 혹은 퇴각되는 양은 측정치에 비해 수치모의(RUN I, II)에서 크게 관측되며, 이러한 편차는 대부분의 지형모형(Genesis:Hanson and Kraus, 1989)처럼 closure depth를 hc = 8.09m로 일정하게 유지한 경우에 더욱 증가하여, 향후 해안선 모형(One Line Model) 운영 시 보다 강건한 물리적 기반을 지닌 Hallermeier(1978, 1981) 해석모형을 토대로 파랑에 따라 closure depth를 수정(update)하는 과정이 필요해 보인다(Brutsch, 2016).
해안선 관측은 처오름(run-up)과 처내림(run-down)이 진행되는 swash-zone에서 진행되므로, 정확한 해안선 위치는 먼저 처오름 정점과 처내림 정점을 관측하고 그 중간 값으로 결정되어야 한다. 해안선 관측은 이처럼 꽤나 까다로운 과정을 거치며 처오름 정점과 처내림 정점이 제공되지 않은 경우, 전술한 과정에서 수행된 여러 주관적 판단이 녹아있다고 보아야 할 것 같다. 또한 0.3 m 내외인 맹방해빈에서의 조위차(Fig. 18 참조)를 고려하는 경우 해빈 경사를 맹방해빈 평균치인 1/30으로 취하는 경우 참 해안선의 위치는 9 m 정도 보정되어야 하며, 고파랑 내습으로 상당한 침식이 진행된 경우 해빈 경사는 보다 완만해지며 이 경우 이격 양은 더욱 증가할 수 있다. 이와 더불어 맹방해빈의 경우 침식이 진행되고 있는 것으로 보고된 바 있으나 현재 측정된 해안선 위치는 년 중 변화가 지나치게 작으며, 특히 년 최대 고파랑 연이어 내습한 이후인 11월 7일에 측정된 해안선의 경우 퇴각량이 우리들의 인식과는 상당한 거리가 있다.
이상의 논의와 표사이송 문제에 내재한 난해함을 고려하여 측정된 해안선 위치는 정성적 변화에만 국한하여 수용하였다.
그러나 자연 해빈이 지니는 자기 복원능력이 수치적으로 확인되었다는 점과 closure depth를 파랑에 의해 결정되는 것으로 해석하는 경우(RUN I), 자연계에서 관측된 해안선 위치에 보다 근접하게 해안선 변화가 모의된다는 점, 수치 모의된 일 년에 걸친 해안선 대순환과정이 측정된 해안선 위치에서도 유사하게 관측된다는 점 등을 고려하는 경우, 본고에서 제시된 해안선 모형은 해역별 최적 해빈 안정화 공법 선정 platform에서 상당한 역할을 수행할 수 있을 것으로 기대된다.