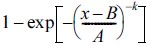Analysis of Confidence Interval of Design Wave Height Estimated Using a Finite Number of Data

Weon-Mu Jeong; Hong-Yeon Cho; Gunwoo Kim

doi:10.9765/KSCOE.2013.25.4.191

Abstract

It is estimated and analyzed that the design wave height and the confidence interval (hereafter CI) according to the return period using the fourteen-year wave data obtained at Pusan New Port. The functions used in the extreme value analysis are the Gumbel function, the Weibull function, and the Kernel function. The CI of the estimated wave heights was predicted using one of the Monte-Carlo simulation methods, the Bootstrap method. The analysis results of the estimated CI of the design wave height indicate that over 150 years of data is necessary in order to satisfy an approximately ±10% CI. Also, estimating the number of practically possible data to be around 25~50, the allowable error was found to be approximately ±16~22% for Type I PDF and ±18~24% for Type III PDF. Whereas, the Kernel distribution method, a typical non-parametric method, shows that the CI of the method is below 40% in comparison with the CI of the other methods and the estimated design wave height is 1.2~1.6 m lower than that of the other methods.

핵심용어: Design wave height, extreme value analysis, confidence interval, Bootstrap method, Kernel function, 설계파고, 극치해석, 신뢰구간, Bootstrap 방법, Kernel 함수

Abstract

부산항 신항에서 측정한 14년 동안의 파랑자료를 이용하여 재현기간에 따른 설계파고와 신뢰구간을 추정·분석하였다. 극치분석에 사용한 함수는 Gumbel 함수와 Weibull 함수, Kernel 함수이며, 각각의 방법으로 추정한 설계파고의 신뢰구간을 Monte-Carlo 모의기법 중의 하나인 Bootstrap 방법으로 추정하였다. 설계파고의 추정 신뢰구간을 분석한 결과, 약 ±10% 수준의 신뢰구간을 만족하기 위해서는 150년 이상의 자료가 필요한 것으로 파악되었다. 그리고 실질적으로 가능한 자료의 개수를 25~50개 정도(25~50년 동안의 추정자료)로 간주하는 경우, Type I 분포함수의 경우 허용오차가 ±16~22% 정도이며, Type III 분포함수의 경우, ±18~24% 정도로 파악되었다. 한편 비모수적 방법에 해당하는 Kernel 분포함수를 이용한 방법은 Type I과 III을 사용한 것에 비해 신뢰구간은 40% 이하 수준으로 우수한 결과를 보이는 반면, 설계파고는 1.2~1.6m 정도 낮게 추정하는 결과를 보여주고 있다.

핵심용어: Design wave height, extreme value analysis, confidence interval, Bootstrap method, Kernel function, 설계파고, 극치해석, 신뢰구간, Bootstrap 방법, Kernel 함수

1. 서론

해안·항만 구조물 설계에서 가장 중요한 인자 중의 하나는 설계파고이다. 항만 및 해안구조물 설계에 적용하는 기준파랑으로 항만설계의 경우 50년 재현빈도의 유의파고를 이용한다. 또한 다양한 해양시설 및 어항시설 설계에는 목적에 부합되는 여러 가지 재현빈도의 유의파고를 이용한다. 항만 및 어항 설계기준(Ministry of Oceans and Fisheries, 2005; 제2편 설계조건, 제4장 파랑)에서는 항만시설의 구조안정 검토에 사용되는 설계파고 산정기준으로 실측자료로서는 10년 이상의 자료가 바람직하나 실측 자료가 없는 경우에는 30년 이상의 기상자료를 이용하여 추산파고를 구하고, 이를 실측파고로 보정하여 사용하는 방법을 제시하고 있다. 한편 미국 공병단(USACE, 2002)에서는 20년(또는 20개) 이상의 실측자료 사용을 권장하고 있다. 또한 관측 자료가 제한된 경우에는 관측자료 기간의 2~3배 정도의 재현기간을 가지는 설계파고 추정이 바람직하다고 제시하고 있다.

제한된 기간일지라도 관측자료 또는 적절한 추산자료가 있다면 후보 극치분포 함수의 최적 매개변수를 추정하고 원하는 재현기간에 해당하는 설계파고를 추정할 수 있다. 그러나 한정된 자료를 사용하여 설계파고를 추정하는 경우에는 추정 결과의 신뢰구간이 사용 자료의 개수(또는 기간)의 영향을 크게 받기 때문에 어느 정도의 실질적인 허용 오차범위를 만족하지 못하는 추정 설계파고를 제시할 수 있다. 최적분포함수를 이용한 설계파고 추정연구는 활발하게 수행되고 있으나 추정 설계파고의 신뢰수준(불확실성) 분석에 관한 연구는 매우 미흡한 실정이다(Chae, 1980; Goda, 2000; Jeong et al., 2004; Lee and Jun, 2006; Suh et al., 2011; Jeong etal., 2012). 실질적으로 해안·항만구조물은 장기간의 극한 해양환경에서 안전이 확보되어야 하므로 신뢰할만한 설계파고 추정이 매우 중요하다.

따라서 본 연구에서는 한정된 자료를 이용하여 추정한 설계파고의 신뢰구간 분석을 통하여 설계파고 추정오차의 허용범위 만족을 위한 최소한의 “가용기간(분석에 사용되는 자료가 포함되는 기간[연 또는 자료의 개수])” 제시를 목적으로 수행되었으며, 신뢰구간 추정기법은 Monte-Carlo 모의(simulation)를 기반으로 하는 Bootstrap 기법(DiCiccio andEfron, 1996; Rubinstein and Kroese, 2008)을 사용하였다.

2. 장기파랑 관측 자료 및 설계파고 추정기법

2.1 설계파고 추정에 사용한 자료

본 연구에서 사용한 제한된 자료는 부산항 신항 동방파제전면(Fig. 1의 정점 W 참조)에서 측정된 파랑 자료이다. 정점 W의 위도는 35^o03'N, 경도는 128^o47'E였으며 설치수심은 M.S.L. 기준 약 15m였다. 여기서 1999년부터 2012년까지 14년 동안 30분 간격으로 관측된 파랑자료에서 연최대 유의파고 자료 14개(자료세트-I)와 연최대와 두 번째로 높은 유의파고 자료를 포함한 28개의 자료(자료세트-II)를 추출하였으며, 이들을 Table 1에 각각 정리하였다. 전통적인 POT 방법(Peak over Threshold; 어떤 기준 이상의 자료를 추출하는 방법)에 의하면 전체 자료에서 크기 순서대로 28개의 자료를 추출하여야 하나, 본 연구에서는 자료의 개수 증가에 의한 영향분석에 중점을 두어 간단하게 1년에 2개를 추출하는 방법(보다 일반적인 방법은 1년에 r개를 추출하는 방법; Soaresand Scotto, 2004)으로 자료개수를 2배로 증가시켜 자료세트-II를 구성하였다. Table 1에서 H_s는 유의파고(m), T_p는 첨두주기(sec.), T_z는 평균주기(sec.), 그리고 θ는 첨두주기에서의파향(^o)을 각각 나타낸다.

관측된 유의파고에는 동방파제로부터의 반사파가 일부 포함되어 있으므로 각각의 원시 자료(raw data)를 최대엔트로 피법(MEM)에 의하여 방향 스펙트럼을 분석하고 그 결과를 이용하여 입·반사파 분리를 실시하였다. 그 결과를 요약하면 관측된 입사파고에는 6~14%의 크기의 반사파고가 포함되어 있는 것으로 나타났으며 Table 1에 제시된 유의파고에는 분리된 입사파고를 제시하였다. 한편, Table 1에서 대표파향(θ)의 값이 없는 자료는 수압식 파고계로 관측된 자료이며 최대엔트로피법의 적용이 불가능하여 반사파고의 평균치를 관측된 값에서 빼고 입사파고로 표시하였다.

Fig. 1.

Location of the long-term wave monitoring station.

Table 1.

Wave data set for the estimation of the design wave height.

(a) Data set-I (annual maximum data)

Date		Characteristic wave parameters
Date		H_s	T_p	T_z	θ
1999	7/22 21H	2.03	9.12	5.71	S2.5^oW
2000	9/16 06H	4.28	14.07	8.14	S0.8^oW
2001	6/25 05H	1.71	7.75	6.21	S10.2^oE
2002	8/31 18H	5.34	12.73	9.10	S6.4^oE
2003	9/12 21H	7.42	16.56	11.06	S5^oE
2004	8/19 07H	5.06	13.66	10.33	S2.1^oW
2005	5/18 08H	2.38	8.53	6.93	-
2006	7/10 13H	5.28	12.71	9.51	S12.7^oE
2007	3/5 0H	2.31	8.68	6.70	S4.2^oE
2008	7/30 01H	2.03	13.84	12.28	S11.5^oW
2009	4/20 22H	2.73	10.28	7.59	S2.2^oW
2010	8/11 9H	3.65	12.71	7.81	S19.6^oW
2011	8/7 23H	3.81	8.89	7.59	S25^oW
2012	9/17 12H	6.30	12.80	8.32	-

(b) Data Set-II (annual maximum and second highest data)

Date		Characteristic wave parameters
Date		H_s	T_p	T_z	θ
1999	7/22 21H	2.03	9.12	5.71	S2.5^oW
1999	7/28 01H	1.76	8.15	5.48	S9.1^oE
2000	9/16 06H	4.28	14.07	8.14	S0.8^oW
2000	8/31 23H	2.34	11.90	7.19	S4.3^oE
2001	6/25 05H	1.71	7.75	6.21	S10.2^oE
2001	7/7 04H	1.20	12.76	10.38	S0.1^oW
2002	8/31 18H	5.34	12.73	9.10	S6.4^oE
2002	7/6 07H	2.85	10.36	6.62	S1.8^oE
2003	9/12 21H	7.42	16.56	11.06	S5^oE
2003	6/19 18H	3.64	15.03	10.50	S13.4^oE
2004	8/19 07H	5.06	13.66	10.33	S2.1^oW
2004	7/5 01H	2.33	11.64	7.35	-
2005	5/18 08H	2.38	8.53	6.93	-
2005	4/20 06H	2.36	8.53	7.57	-
2006	7/10 13H	5.28	12.71	9.51	S12.7^oE
2006	5/6 16H	2.26	7.53	6.71	-
2007	3/5 0H	2.31	8.68	6.70	S4.2^oE
2007	9/16 19H	2.19	12.80	10.82	-
2008	7/30 01H	2.03	13.84	12.28	S11.5^oW
2008	9/30 13H	1.40	11.93	11.31	S7.5^oW
2009	4/20 22H	2.73	10.28	7.59	S2.2^oW
2009	2/13 15H	2.42	8.23	7.08	S9.7^oE
2010	8/11 9H	3.65	12.71	7.81	S19.6^oW
2010	3/15 16H	2.35	9.61	7.81	S5.4^oE
2011	8/7 23H	3.81	8.89	7.59	S25^oW
2011	6/26 17H	2.77	11.92	9.25	S23.1^oW
2012	9/17 12H	6.30	12.80	8.32	-
2012	8/28 11H	4.36	14.22	7.96	-

2.2 설계파고 및 신뢰구간 추정 기법

설계파고 추정은 재현기간에 따른 설계파고를 추정한다는 의미이다. 재현기간은 어떤 특정파고를 상회하는 파랑이 나타나는 평균적인 연수로 확률적인 개념을 기초로 하고 있다. 확률파고를 추정하는 데는 연속적인 파랑관측 기록이 있으면 기준파고 등을 계산할 수 있으나, 일반적으로 장기간의 매년 최대파고를 극치통계자료로 이용하여 확률파고를 분석한다(Ministry of Oceans and Fisheries, 2005).

연 최대 파고 자료를 이용한 확률파고, 즉 재현기간에 따른 확률파고 추정은 극치해석 분야에서는 다음과 같은 정형화된 과정을 따른다.

- 제1 단계: 극치해석을 위한 자료(연 최대자료 또는 기준파고를 상회하는 자료 세트) 입력

- 제2 단계: 자료를 크기순으로 정렬하여 각각의 자료에 대한 초과(또는 비초과) 확률을 부여(확률 부여는 plotting position 공식을 활용)

- 제3 단계: 주어진 (확률, 파고) 세트 자료를 이용하여 후보 극치분포 함수에 대한 최적 매개변수 추정(최소자승법 등)

- 제4 단계: 극치 분포함수의 최적 추정된 매개변수를 이용하여 재현기간에 따른 초과확률과 확률파고(설계파고)를 계산

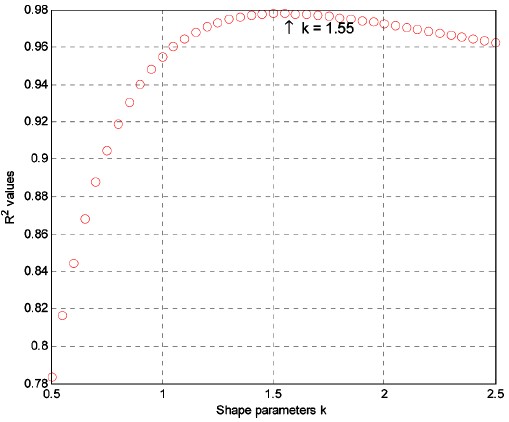
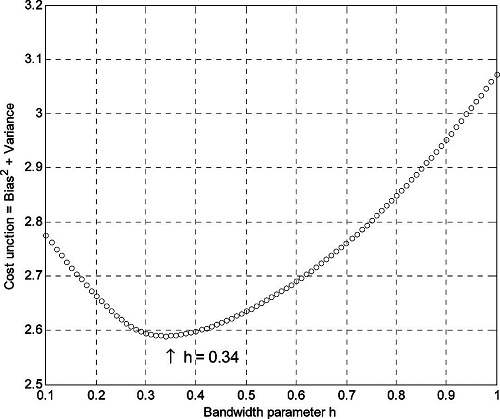
본 연구에서는 후보 극치분포함수로 연안 설계파고 추정에 널리 이용되는 Gumbel 분포함수와 Weibull 분포함수를 선정하였다. 또한 모수적 방법의 한계를 극복하기 위하여 제시되는 비모수적 방법을 적용하기 위하여 Kernel 분포함수도 선정하였다. 제3 단계의 최적 매개변수는 Gumbel 분포함수의 경우 간단한 변환과정을 통하여 최소자승법으로 추정하였으며, Weibull분포함수의 경우 형상 매개변수를 통상적인 0.5~2.0 범위에서 일정한 간격으로 변화시켜가며 최소자승법으로 추정된 다른 매개변수 조건에서 상관계수가 가장 크게 되는 형상매개변수와 그 조건에서의 다른 매개변수를 최적 추정하였다(Goda, 2000).Kernel 분포함수의 경우는 일반적으로 이용되는 (편의[bias])²+분산 수치를 최소(Wand and Jones, 1995)로 하는 매개변수를 선정하였다. Weibull 분포함수 및 Kernel 분포함수의 매개변수는 반복시행에 따른 최적 매개변수 추정과정이 필요하다.

추정 설계파고의 신뢰구간 추정은 제3 단계에서 결정된 극치 분포함수(모집단으로 가정)를 이용하여 가상의 파고를 발생(하나의 표본 집단으로 가정)시키고, 발생된 파고자료를 이용하여 각각의 재현기간에 따른 다수의 설계파고를 추정하는 과정이 추가된다. 여기서 추정된 다수의 재현기간에 따른 설계파고의 5~95% 영역이 ±5% 유의수준(significance level)에 대한 신뢰구간이 된다.

한편 추산자료(hind-casting data)를 이용하여 설계파고를 추정하는 방법도 가능하며, 일반적으로 파랑 관측기간보다 오랜 기간의 관측 자료가 있는 기상자료를 이용하여 장기간의 파랑자료를 추정하여 극치해석에 이용하는 방법이다. 극치해석 방법은 동일한 과정을 거치지만 극치해석에 이용되는 자료가 관측 자료보다 더 많기 때문에 신뢰구간이 감소하는 장점을 가지고 있으나, 극치해석에 이용되는 자료가 어느 정도(관측 자료의 관측 오차보다는 상당히 큰 정도)의 추정오차를 가지고 있는 단점이 있다. 따라서 관측 자료를 이용하는 설계파고 추정은 관측기간을 늘리는 것이 가장 중요하며, 추산자료를 이용하는 방법은 추산오차를 최소화하는 작업이 요구된다고 할 수 있다. 본 연구에서는 대표적인 설계파고 추정방법의 비교가 아니라 자료의 개수에 따른 설계파고 추정오차 변화 양상분석에 중점을 두고 있다.

2.3 이상 자료 검정(Outlier Test) 방법

한정된 파랑자료가 이상 자료(outliers)를 포함하는 경우에는 극치분포함수의 추정 매개변수가 이상 자료의 영향을 크게 받게 된다. 따라서 자료의 개수가 작은 경우에는 극치해석 이전에 자료에 이상 자료가 포함되어 있는 지를 검정할 필요가 있다. 이상 자료 검정방법은 대부분의 경우 정규분포를 가정하여 수행하고 있으나, 본 연구에서 사용하는 파고 자료의 경우 어떤 분포를 따르는지를 알 수 없기 때문에 분포 무관형 방법이 적합하다고 사료된다. 설계파랑 추정에 사용되는 자료의 개수는 보통의 경우 소 표본(small sample, 표본의 개수 25~30개 이하)에 해당되기 때문에 이상 자료의 영향이 매우 크게 나타날 수 있다. 특히 2003년 발생한 태풍 매미의 영향으로 발생한 남해 연안의 높은 파고는 이상 자료 여부에 대한 관심이 집중되는 자료이다. 본 연구에서 사용하는 부산항 신항 파랑자료도 태풍 매미의 영향을 받은 자료가 포함되어 있기 때문에 설계파랑 추정에 앞서 이상 자료에 대한 검정을 수행하였다. 이상 자료 검정은 다양한 방법이 제시되고 있으나 대부분의 경우 정규분포를 가정하고 있기 때문에 적용에 한계가 있다. 따라서 본 연구에서는 분포와는 무관한 Grubbs 검정(Grubbs,1969; Komsta, 2006)과 Fourth Spread 검정 기법(USACE,2008)을 이용하여 이상 자료 검정을 수행하였다. 이상 자료 검정은 주어진 자료에서 극값이 자료의 대표적인 위치에서 어느 한계 이상으로 떨어진 경우 이상 자료로 판단하는 개념에 근거하고 있다(USACE, 2008). 극치분석을 위한 파고자료에서 최대파고가 아래 조건에 해당하는 경우 이상 자료로 판단한다.

x₇₅+1.5(x₇₅−x₂₅)≤x₍₁₎ 조건을 만족하면 x₍₁₎=mild outlier

x₇₅+3.0(x₇₅−x₂₅)≤x₍₁₎ 조건을 만족하면 x₍₁₎=extreme outlier

여기서, x₍₁₎는 최대파고, x₂₅, x₇₅는 각각 25, 75 백분위수(percentile)로 사분위수(quartile)로는 제1, 제3 사분위수가 된다(제2 사분위수는 중간파고, median).

3. 연구 결과 및 토의

3.1 이상 자료 검정

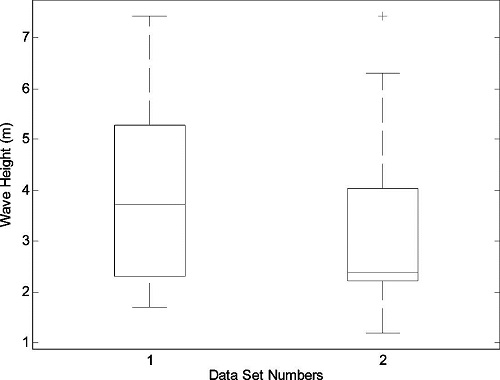
본 연구에서 사용한 자료를 이용하여 이상 자료를 검정한 결과, 5% 유의수준에서 자료세트-I에서는 2003년 매미에 의한 최대파고 자료가 이상 자료에 해당하지 않는 것으로 판단되었으나, 자료세트-II에서는 약한 이상 자료(mild outlier)로 판정되었다(Fig. 2 참조). USACE 방법이나, 자료의 정규분포 가정을 어느 정도 포함하고 있는 Grubbs 검정방법에서도 동일한 판정 결과가 제시되었다. 한편 범용적으로 이용되는 R 통계 프로그램의 ‘outliers’ PACKAGE(Komsta, 2006)를 이용하여 검정한 결과도 동일하였다. 이상 자료를 포함하는 경우, 이상 자료가 극치해석에 미치는 정량적인 영향은 이상 자료의 크기, 이상 자료를 포함한 자료의 개수 등에 따라 다를 수 있으며, 이상 자료가 극치해석 결과에 미치는 정량적인 영향분석이 필요한 분야로 판단된다. 이상 자료가 있는 경우에는 Robust 추정기법을 사용하거나 이상 자료를 제외하고 설계파고를 추정하는 방법이 필요하다(Rousseeuw and Leroy, 2003; Barnett and Lewis,1994). 본 연구에서는 이상 자료가 감지된 자료세트-II에서 이상 자료 개수가 전체 자료에서 차지하는 비중이 5% 이하로 작고, 잠재적 이상 자료(mild outlier)로 판단되어 이상 자료 제거 과정 없이 설계파고 추정을 수행하였다.

Fig. 2.

Outlier detection using the Fourth Spread Method (+ = mild outlier; Box-and-Whisker plot, max. Whisker length=1.5).

3.2 극치분포 함수의 적합도 검정 및 오차분석

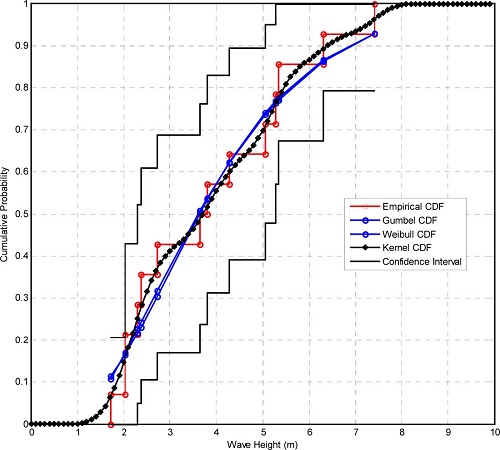
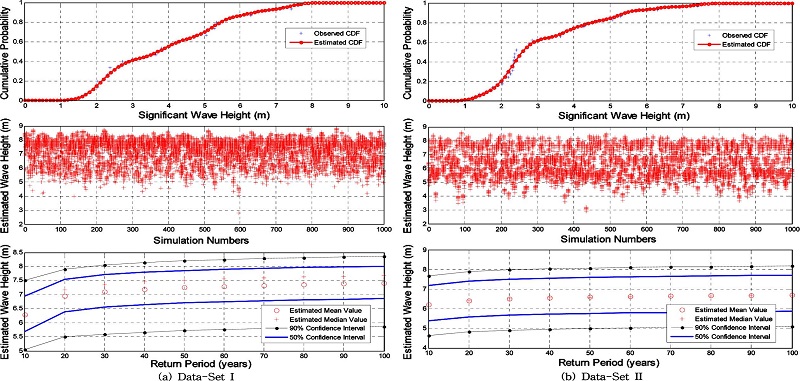
극치해석에 이용할 수 있는 분포함수는 매우 다양하다. 본 연구에서는 일반적으로 널리 이용되는 분포함수에 대하여 자료세트-I을 이용하여 매개변수를 추정하고 적합도 검정을 수행하였다. 적합도 검정에 사용된 극치분포함수는 Gumbel 함수(매개변수 2개) 및 Weibull 함수(매개변수 3개)이며, Kernel 분포함수(매개변수 1개)를 이용한 비모수적 분포함수도 이용하였다. 최적 매개변수는 극치분포 함수에 따라 다양한 확률 도시위치 공식이 제시되어 있으나, 본 연구에서는 Weibull 도시위치 공식(1−m/(n+1), m=파고의 순위[내림차순], n=자료의 개수)을 사용하여 추정하였다(Figs. 3~4 참조). 최적 추정된 매개변수 조건에서 관측 자료와 K-S 적합도 검정 및 Anderson-Darling 검정(Stephen, 1974; Stephen, 1986)을 수행한 결과 모든 극치분포함수가 적합한 것으로 파악되었으며, 관측 자료와 추정자료의 RMS 오차(Root mean-squared error)는 0.17~0.19 범위이다(Table 2. 참조). 관측 자료의 누적확률 도시는 경험누적함수(empirical CDF)를 이용하였으며, 본 연구에서 사용한 경험 누적함수와 추정 누적함수의 비교 및 90% 신뢰구간을 도시하였다(Fig. 5 참조). Type I, Type III 함수를 이용한 신뢰구간 추정 과정에서는 추정 결과의 편의(偏倚, bias)를 제거하기 위하여 제안된 도시위치 공식(Goda, 2000)을 이용하였다. Kernel 분포함수를 이용한 방법에서도 추정결과에서 0.4m 정도의 편의가 발생하고 있으나, 편의 저감(bias correction)에 이용되는 도시공식에 둔감하여 Weibull 도시위치 공식만을 사용하였다.

Fig. 3.

Optimal (Max R²) shape parameter (k=1.55) for the Weibull distribution.

Fig. 4.

Optimal bandwidth parameter (h=0.34) of the Kernel CDF.

Table 2.

Estimated parameters and RMS error of the goodness-of-fit test

Name of the function	Estimated parameters	RMS error (p-Value)
Gumbel pdf (Type I)	A=1.9428, B=3.3805	0.1886 (0.9971)
Weibull pdf (Type III)	A=3.4989 B=0.8472 k=1.55	0.1709 (0.9971)
Kernel pdf (Non-parametric)	h=0.3400	0.1766 (1.000)

Fig. 5.

Comparison of the observed and estimated CDFs.

3.3 재현기간에 따른 설계파고 추정

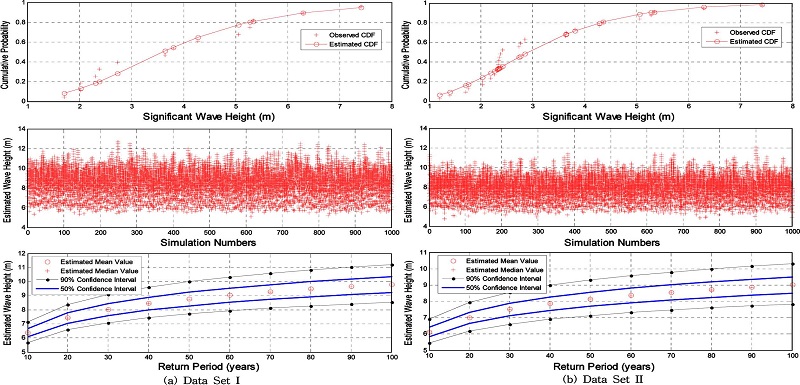
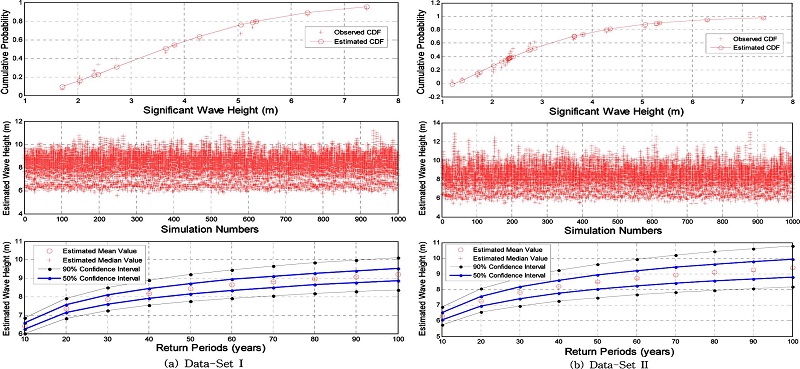
전 절에서 추정된 최적 매개변수를 포함하는 극치분포함수를 이용하여 재현기간에 따른 설계파고를 추정하였다. 설계파고를 추정한 재현기간은 10년부터 10년 간격으로 100년까지이며, 각각의 재현기간(T_R [년])에 대한 초과확률은 1−1/T_R이 된다. 사용한 극치분포 함수에 따른 재현기간과 설계파고는 Table 3에 제시되었다. 편의를 제거하는 도시공식을 이용한 경우, Type I 극치분포 함수의 경우 추정 설계파고는 전반적으로 감소하는 경향을 보인 반면, Type III 극치분포 함수의 경우에는 전반적으로 추정 설계파고가 증대되는 경향을 보이고 있는 것으로 파악되었으며, 설계파고 추정에 사용한 극치분포 함수에 의한 차이는 50년 빈도 설계파고(자료세트-I) 기준으로 1.66(=9.60−7.94)m에서 0.34m(8.78−8.44)로 크게 감소하였다. 한편, Monte Carlo 모의기법을 이용하여 추정한 50%, 90% 신뢰구간도 추정하여 제시하였다(Figs. 6-8 참조). 전체적으로 재현기간이 증가함에 따라 신뢰구간도 증가하고 있음을 알 수 있다. 자료세트-I을 이용하여 추정한 신뢰구간은 자료세트-II를 이용하여 추정한 신뢰구간보다 크게 나타나고 있으며, 이는 자료의 개수가 불확실성에 영향(자료의 개수가 적을수록 불확실성은 증가)을 미친 것으로 판단할 수 있다.

Table 3.

Estimated design wave heights (m) on the recurrence periods.

(a) Data Set I

Return Periods		10	20	30	40	50	60	70	80	90	100
Type I	BBC	6.81	8.03	8.73	9.22	9.60	9.91	10.17	10.40	10.60	10.78
Type I	ABC	6.36	7.42	8.02	8.45	8.78	9.05	9.27	9.47	9.64	9.80
Type III	BBC	6.08	6.93	7.39	7.70	7.94	8.12	8.28	8.41	8.53	8.63
Type III	ABC	6.43	7.35	7.85	8.19	8.44	8.64	8.81	8.96	9.08	9.19
Kernel		6.31	6.95	7.11	7.20	7.26	7.31	7.34	7.37	7.40	7.42

(b) Data Set II

Return Periods		10	20	30	40	50	60	70	80	90	100
Type I	BBC	6.44	7.39	7.94	8.33	8.63	8.88	9.09	9.27	9.43	9.57
Type I	ABC	6.13	7.00	7.50	7.86	8.14	8.36	8.55	8.72	8.86	8.99
Type III	BBC	6.03	6.93	7.45	7.80	8.08	8.30	8.49	8.65	8.79	8.92
Type III	ABC	6.31	7.27	7.82	8.20	8.49	8.73	8.93	9.10	9.25	9.39
Kernel		6.27	6.93	7.06	7.13	7.18	7.22	7.24	7.27	7.29	7.30

Ref. Type I, III = the Gumbel and Weibull distribution functions, respectively. Kernel = the kernel p.d.f.; BBC, ABC = before and after bias correction, respectively.

Fig. 6.

Estimated design wave height with the recurrence intervals (Gumbel distribution).

Fig. 7.

Estimated design wave height with the recurrence intervals (Weibull distribution).

Fig. 8.

Estimated design wave height with the recurrence intervals (Kernel distribution).

3.4 자료의 개수에 따른 신뢰구간 추정

추정 설계파고의 신뢰구간 추정은 설계파고 추정에 널리 이용되는 Type I, Type III 분포함수와 본 연구에서 도입한 비모수적 방법에 해당하는 Kernel 분포함수를 이용하여 신뢰구간을 추정하였다. 신뢰구간 추정은 연최대 파고 자료 조건을 가정하고, 25, 50, 75, 100개(년)의 조건에서 수행하였다. 연최대 파고자료는 부산항 신항 자료를 이용하여 최적 추정된 매개변수를 포함하는 극치분포 함수를 이용하여 가상의 표본 집단을 추출하는 Bootstrap 방법을 이용하였다. 신뢰구간은 재현기간에 따라 차이를 보이고 있으므로, 본 연구에서는 재현기간 50년에 대한 신뢰구간의 크기 변화를 중심으로 비교하였다(Table 4, Fig. 9 참조). 추정된 평균 설계파고는 Type I, Type III 함수를 이용한 경우 각각 8.78m, 8.44m로 자료의 개수에 무관하게 일정(Table 4 참조)하였다. 반면, Kernel 함수를 이용한 경우는 Type I, III 함수를 이용한 경우에 비하여 전반적으로 작은 추정 설계파고를 제시하였으며, 자료의 개수가 14개인 경우 7.26m에서 50개, 100개인 경우 각각 7.60m, 7.65m로 증가하는 경향을 보였다. 본 연구지역에서 도출된 결과를 다른 지역으로 확장하는 것은 한계가 있을 수도 있으나, 하나의 참고기준으로 활용하기 위하여 자료개수에 따른 신뢰구간의 크기를 추정 설계파고로 무차원화하여 제시하였다(Table 4. (c) 참조).

Table 4.

Confidence intervals of the 50-year design wave heights with the available wave data lengths.

(a) Upper and lower limits of the 90% confidence interval

No. of the data (years)	Type I (Gumbel pdf)			Type III (Weibull pdf)			Kernel pdf
No. of the data (years)	LL	Mean	UL	LL	Mean	UL	LL	Mean	UL
14	6.05	8.78	11.61	6.24	8.44	11.92	5.85	7.26	8.19
25	7.09	8.78	10.93	6.73	8.44	10.73	6.35	7.49	8.12
50	7.50	8.78	10.28	7.10	8.44	10.11	6.96	7.60	8.04
75	7.68	8.78	9.92	7.36	8.44	9.64	7.20	7.63	7.99
100	7.85	8.78	9.82	7.58	8.44	9.52	7.23	7.65	7.95
150	7.95	8.78	9.62	7.74	8.44	9.21	7.33	7.65	7.91
200	8.11	8.78	9.50	7.76	8.44	9.15	7.43	7.65	7.89

Ref. UL, LL are the upper and lower limits, respectively.

(b) Difference between (upper and lower) confidence limits

No. of the data (years)	90% Confidence interval			50% Confidence interval
No. of the data (years)	Type I	Type III	Kernel	Type I	Type III	Kernel
14	5.56	5.68	2.34	2.18	2.22	1.10
25	3.84	4.00	1.77	1.58	1.54	0.63
50	2.78	3.01	1.08	1.10	1.18	0.40
75	2.24	2.28	0.79	0.94	0.94	0.33
100	1.97	1.94	0.72	0.82	0.78	0.26
150	1.67	1.47	0.58	0.69	0.63	0.22
200	1.39	1.39	0.46	0.61	0.61	0.19

No. of the data (years)	90% Confidence interval			50% Confidence interval
No. of the data (years)	Type I	Type III	Kernel	Type I	Type III	Kernel
14	0.63	0.67	0.31	0.25	0.26	0.14
25	0.44	0.47	0.23	0.18	0.18	0.08
50	0.32	0.36	0.14	0.14	0.14	0.05
75	0.26	0.27	0.10	0.11	0.11	0.04
100	0.22	0.23	0.09	0.09	0.09	0.03
150	0.19	0.17	0.08	0.07	0.07	0.03
200	0.16	0.16	0.06	0.07	0.07	0.02

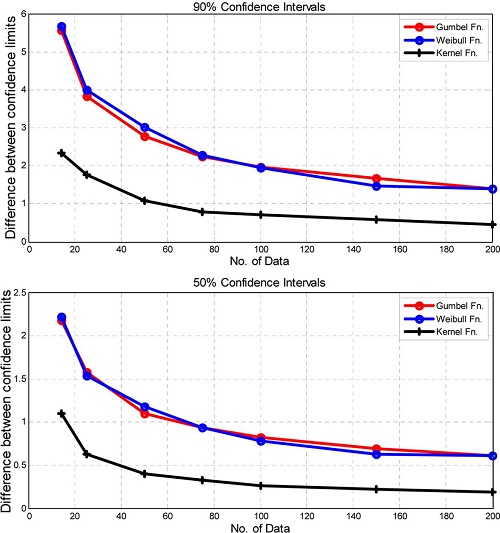
한편, 50년 재현기간에 대한 10% 유의수준에 대한 추정 설계파고 신뢰구간은 Table 4(a)에 보이는 바와 같이, Type I, Type III, Kernel 함수를 이용한 경우 각각 6.05~11.61m, 6.24~11.92m, 5.85~8.19m로 나타났다. 즉, Type I과 III 함수를 이용한 결과들은 서로 유사하였으나 비모수적 방법에 해당하는 Kernel 분포함수를 이용한 방법은 이들에 비해 40% 이하 수준으로 매우 작은 결과를 보여주고 있다. 그러나 신뢰구간이 작은 장점에도 불구하고 Kernel 함수를 이용하는 경우의 추정 설계파고는 Type I, III 함수를 이용한 경우보다 1.2~1.6m 정도 작은 값을 제시하고 있다.

자료의 개수 증가에 따른 50년 빈도 추정 설계파고의 신뢰구간은 하한은 증가하고 상한은 감소하여 신뢰구간의 크기(상한과 하한의 차이)는 모두 동등한 정도로 감소하는 경향을 보이고 있다. 따라서 목표 신뢰구간이 주어지는 경우, 그 조건을 만족하는 자료의 개수(기간) 추정이 가능하다.

우선 Type I(Gumbel 함수) 극치분포함수를 이용하는 경우, 추정 설계파고는 8.78m, 목표 신뢰구간을 추정 설계파고의 ±10% 조건을 적용하는 경우 약 ±0.88m(하한 7.90m, 상한 9.66m)가 된다. 이 조건을 만족하는 자료의 개수는 150개(150년 자료) 이상의 자료에서 만족하게 됨을 알 수 있다(Table 4(a) 참조). Type III(Weibull 함수) 분포함수를 이용하는 경우도 동일한 방법으로, 추정 설계파고 8.44m, ±10% 정도의 목표 신뢰구간을 적용하는 경우, 약 ±0.84m(하한 7.60m, 상한 9.28m)로 마찬가지로 대략 150개 정도의 자료가 필요하다.

반면, Kernel 분포함수를 이용하는 경우, 추정 설계파고 7.26m, 동일하게 ±10% 목표 신뢰구간을 적용하는 경우 ±0.73m(하한 6.53m, 상한 7.99m)로 25~50개 이상의 조건에서 허용오차를 만족하고 있음을 알 수 있다. 비모수적 방법에 해당하는 Kernel 분포함수는 가용한 자료에 최대한으로 접근시키는 방법이기 때문에 자료의 개수에 큰 영향을 받지 않는 방법이지만, 새로운 자료의 추가에 의한 영향이 크기 때문에 실질적인 문제 적용을 위해서는 보다 다양한 검토가 필요할 것으로 판단된다.

Fig. 9.

Confidence interval change plot with the no. of data.

한편, 실질적으로 설계파고 추정에 이용되는 자료의 개수를 25~50개 정도(25~50년 동안의 추정자료)로 간주하는 경우, Type I, III 분포함수의 경우 각각의 신뢰구간의 범위(Fig. 9 참조)는 3.84~2.78m, 4.00~3.01m이며, 50년 빈도 추정 설계파고를 기준으로 하는 비율로 환산하면 각각 32~44%, 36~47%가 된다. 상한과 하한신뢰구간의 크기를 대칭으로 가정하면 25~50개의 자료를 이용하여 50년 빈도 설계파고를 추정하는 경우 신뢰구간은 Type I, III 함수를 이용하는 경우 각각 ±16~22%, ±18~24% 수준이다.

4. 결론 및 제언

부산항 신항에서 14년 동안 관측한 파고자료를 이용하여 설계파고를 추정하고 신뢰구간을 분석하였으며 이상 자료 검정도 수행하였다. 태풍 매미에 의한 파고자료를 포함한 부산항 신항 파고자료는 연최대 유의파고 자료(자료세트-I)에서 이상 자료는 없는 것으로 파악되었으며, Type I, III 극치분포 함수를 이용하여 재현기간에 따른 설계파고를 추정한 결과, 50년 빈도 설계파고는 8.78m, 8.48m로 파악되었으며, Kernel 함수를 이용하는 방법은 신뢰구간은 가장 작은 반면 50년 빈도 설계파고로 7.26m가 추정되었다. Kernel 함수를 이용한 비모수적 방법은 그 활용빈도가 작기 때문에 최적 도시위치 및 신뢰구간 추정 기법 등에 대한 추가적인 연구가 필요할 것으로 판단된다.

또한 본 연구에서 사용한 14년 동안의 현장관측 자료를 이용하는 경우의 신뢰구간은 50년 빈도 추정 설계파고를 기준으로 ±30% 수준을 상회하는 것으로 파악되었으며, ±10% 수준의 목표 신뢰구간을 만족하기 위해서는 150년 이상의 자료가 필요한 것으로 파악되었다. 한편 실질적으로 가능한 25~50개(년) 정도의 자료를 이용하는 경우 Type I, Type III분포함수를 이용하는 경우 각각 ±16~22%, ±18~24% 정도의허용오차를 가지는 것으로 파악되었다. 그러나 비모수적 방법에 해당하는 Kernel 분포함수를 이용한 방법은 신뢰구간은 Type I과 III을 사용한 방법에 비해 40% 이하 수준으로 우수한 결과를 보이는 반면, 설계파고는 다른 방법에 비하여 1.2~1.6m 정도 낮게 추정하는 결과를 보여주고 있다.

현재 항만 및 어항 설계기준에 제시된 10년 이상의 관측자료를 이용하여 설계파고를 추정하는 경우, 관측오차는 무시할만한 수준일지라도 자료의 개수 제한으로 인한 허용오차는 매우 크기 때문에 50년 빈도 설계파고 추정을 위해서는 적어도 25개(년) 이상의 자료를 사용할 필요가 있으며, 이 경우의 허용오차는 ±22~24% 수준이 된다.