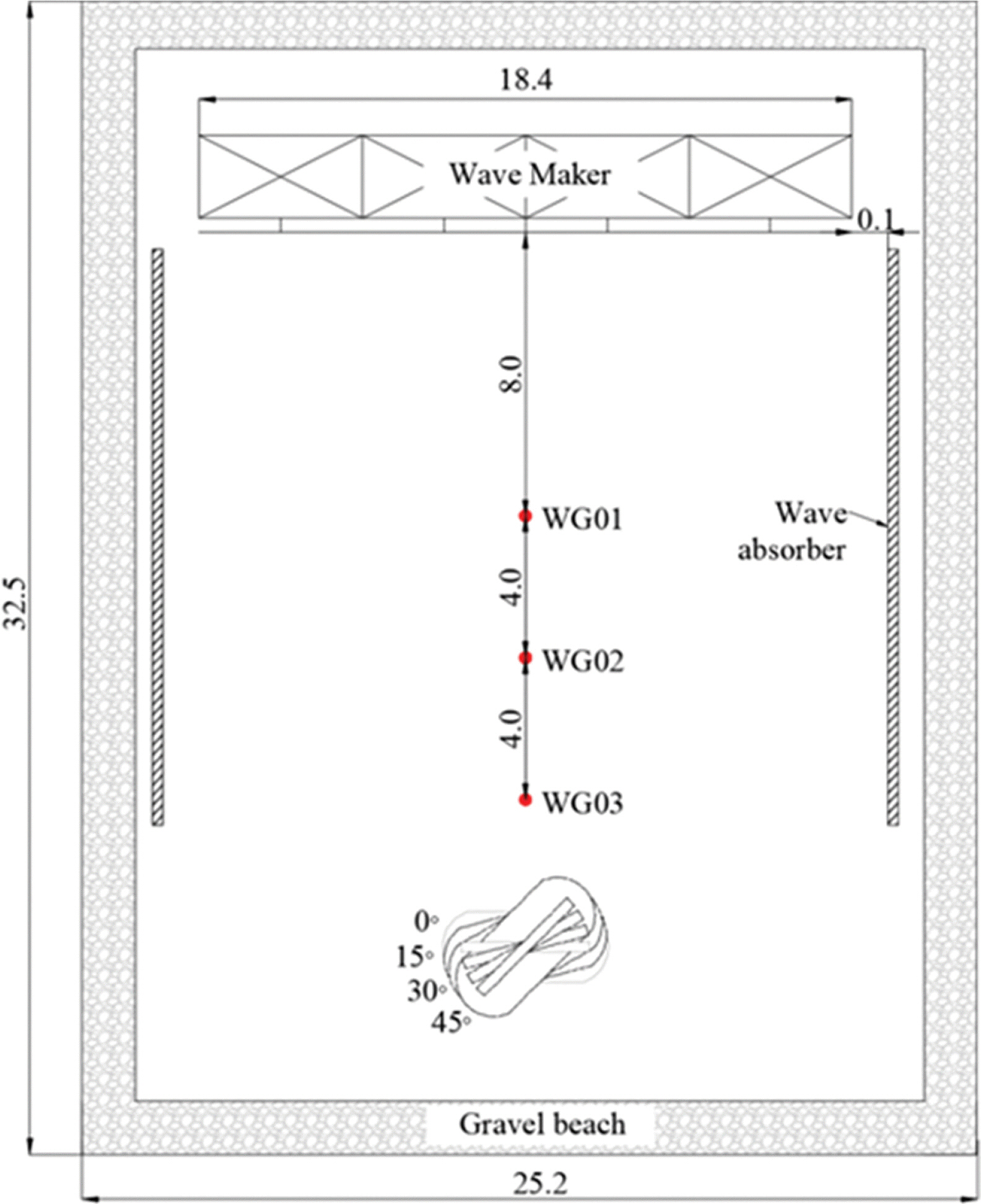
수리모형실험은 길이 33 m, 폭 30 m, 높이 1.2 m인 3차원 조파수조에서 수행되었으며, 본 연구에서는 실험 편의를 위해서 수조 길이 방향으로 32.5 m, 폭 방향으로 25 m 공간을 실험에 활용하였다. 파랑 생성을 위해 전기 서보 피스톤 방식으로 구동되는 일방향 조파기 4대를 사용하였으며 실험 영역을 둘러싼 모든 면에는 쇄석을 설치하여 반사파 발생을 억제하였다. 경사제 모형은 Fig. 1에 보인 것처럼 조파판으로부터 20 m 떨어진 지점에 설치하였고, 모형의 법선이 입사파향과 이루는 각도가 0°에서 45°까지 15° 간격으로 변화하도록 하였다. Fig. 2에는 서로 다른 입사파향별로 모형이 설치된 사진을 나타내었다.

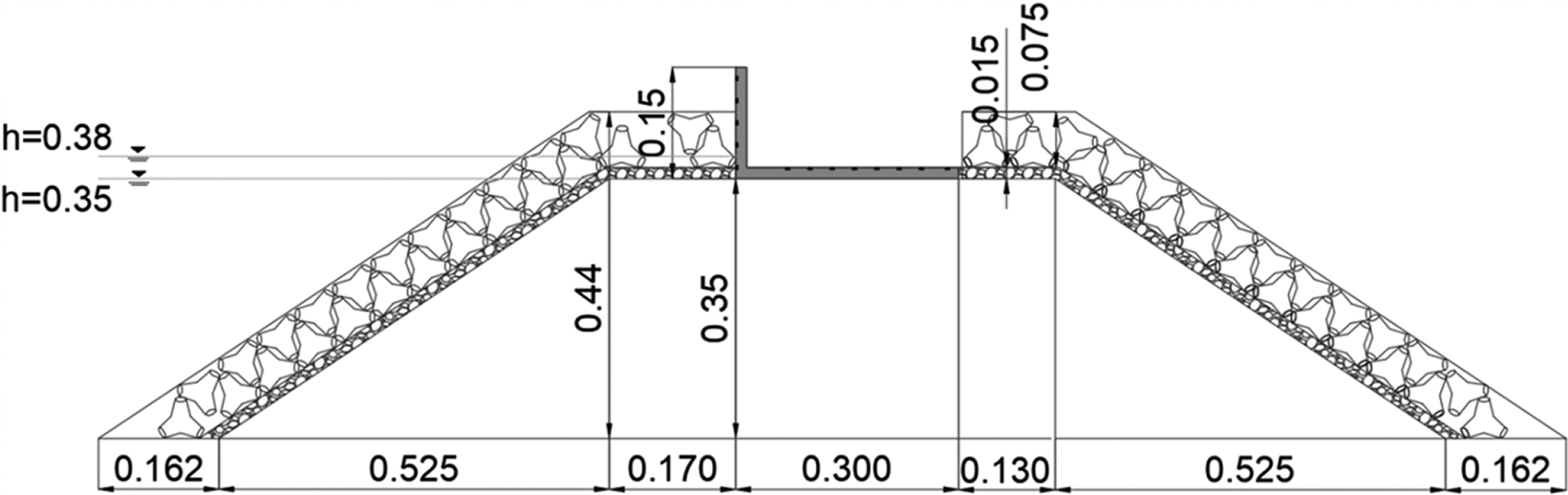
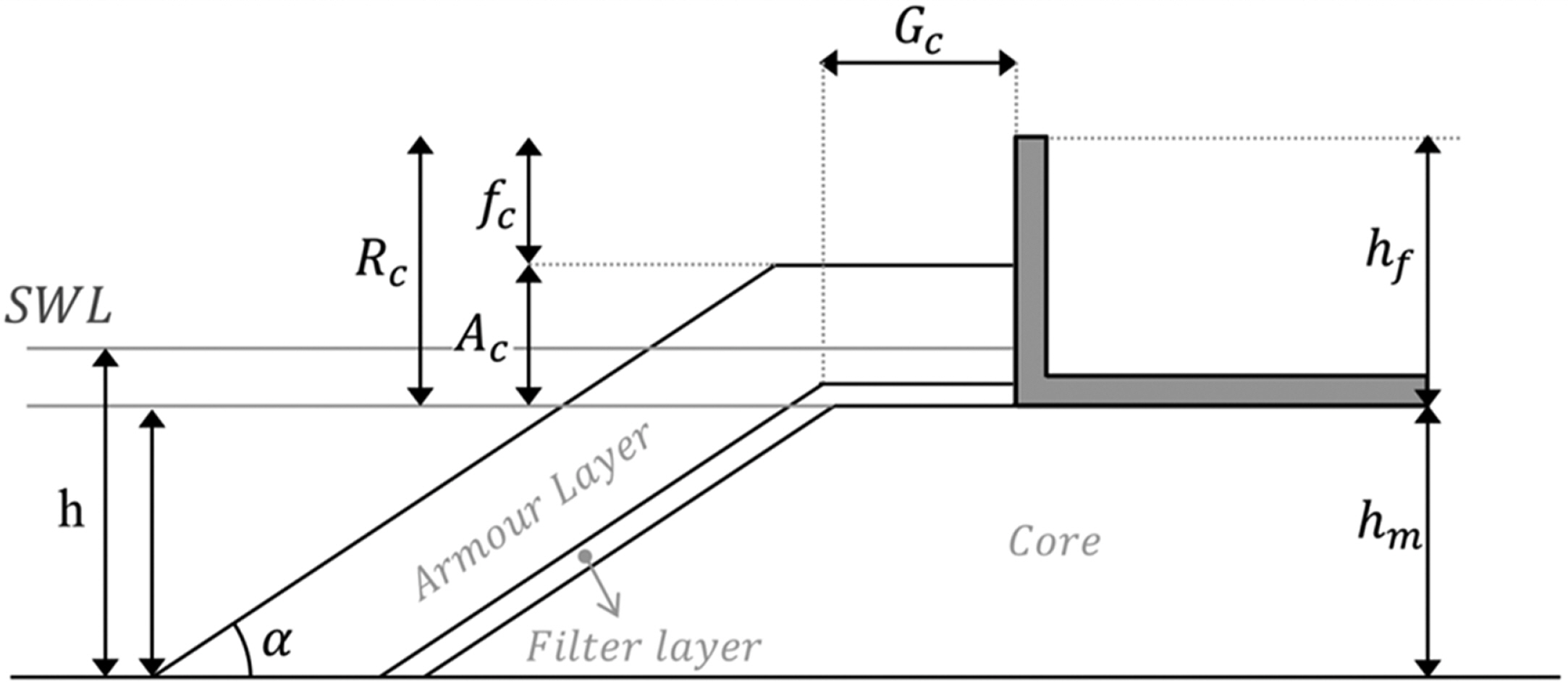
Fig. 3에는 실험 모형 단면도를 제시하였다. 사석마운드의 높이는 0.35 m이며 전면과 후면 경사는 모두 1:1.5로 평균 입경 1g의 기초 사석(Core) 위에 12 g의 중간 사석 피복층(Filter layer)을 쌓고 150 g 테트라포드 2열(Armour layer)로 피복하였다. ㄴ자 형태의 상부구조물은 높이 0.15 m, 폭 0.3 m이며 투명 아크릴로 제작하여 경사제 위에 설치한 후 움직이지 않도록 고정하였다. Fig. 4에는 Table 1에 보인 변수들에 대한 정의를 나타내었고, Table 1에는 이 변수들의 값을 제시하였다.

한편, 방파제 연장 방향으로의 아크릴 모형 길이는 0.6 m였으며, 아크릴 모형과 동일한 높이와 폭을 갖는 길이 0.3 m 콘크리트 블록을 모형 양측으로 각각 5개씩 일렬로 배치하여, 총 방파제의 연장 방향 길이가 3.6 m가 되도록 실험을 구성하였다.

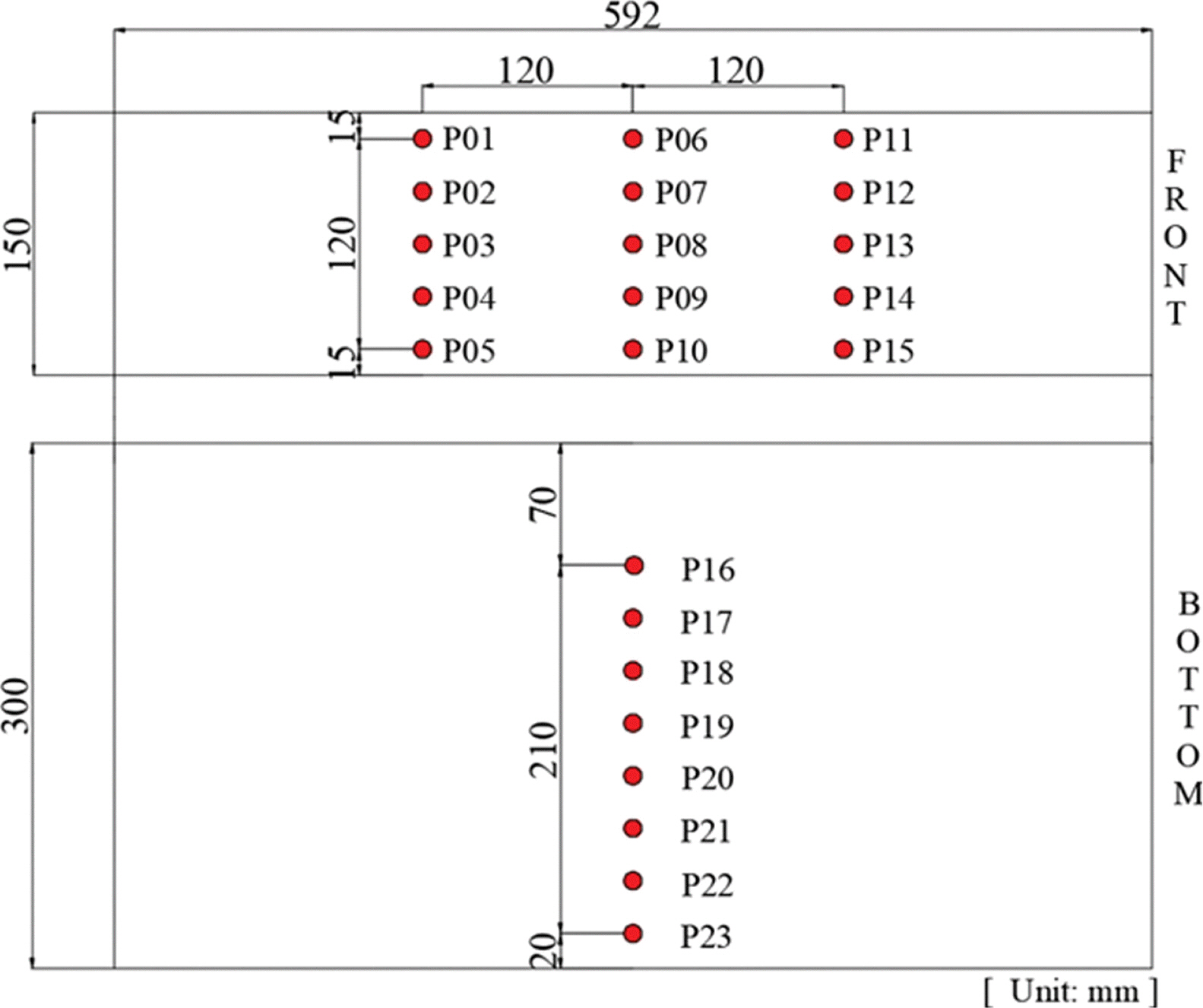
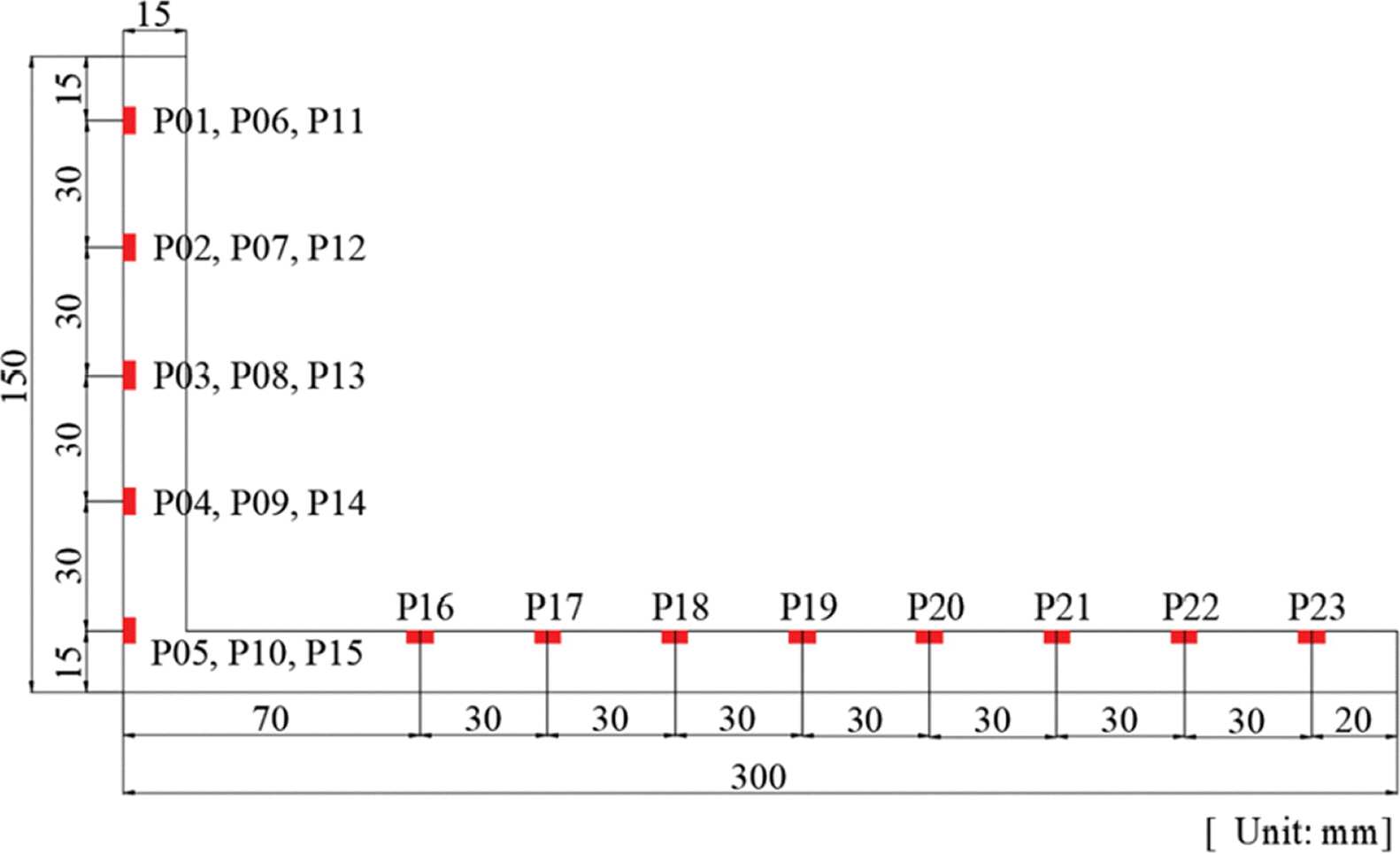
파고 계측은 Fig. 1에 나타낸 것처럼 평면수조 내 3곳에서 이루어졌으며, 이 중 방파제 모형에 가장 가까운 곳에 위치한 WG3에서 계측된 자료를 이용하여 유의파고(H_s) 및 유의 주기(T_s)를 평가하였다. 한편, 파압 계측은 Figs. 5와 6에 보인 것처럼 상부구조물 전면과 아랫면에 파압계를 부착하여 수행되었다. 파압계는 실험 모형에 매립하여 설치함으로써 파압계 표면이 모형 표면에서 돌출되지 않고 균일한 면을 이루도록 하였다. 테트라포드가 거치된 형태에 따라 상부구조물 전면 작용 파압이 달라질 수 있음을 고려하여 Fig. 5에 보인 것처럼 전면벽 파압 계측을 3개열에서 실시하고 각각의 높이 별로 3개열의 평균값을 계산하여 최종적인 전면 파압으로 평가하였다. 상부구조물 수평 및 연직 파압을 계측하기 위해 사용된 파압계의 개수는 23개였으며, 파압 및 파고 계측 자료는 800 Hz 간격으로 취득하였다.

Fig. 3에 보인 것처럼 수심(h)이 0.35 및 0.38 m인 두 가지 조건에서 계측이 이루어졌으며, 수심에 따라 Table 1에 보인 것처럼 R_c 및 A_c의 값은 달라지게 되었다.

실험은 스펙트럼 첨두증대계수 값이 γ = 2.0인 JONSWAP 스펙트럼을 따르는 불규칙파로 구성하였으며, 각 실험파별로 1,200파에 해당하는 시간 동안 조파하였다. 실험파는 수심 35 cm일 때에는 T_s = 1.0, 1.5, 2.0 s의 3 가지 조건에 대해서 H_s = 0.1 m였으며, 수심 38 cm일 때에는 위 3 가지 주기에 대해서 H_s = 0.08과 0.1 m의 두 가지 조건으로 변화시켰다. 따라서 총 실험파의 개수는 9개였다. 한편, 입사파향(θ)은 0°, 15°, 30°, 45°의 4가지 조건으로 변화시켰다. Table 2에는 실험파 조건 및 주요 무차원계수의 값 또는 범위를 정리하여 제시하였다.

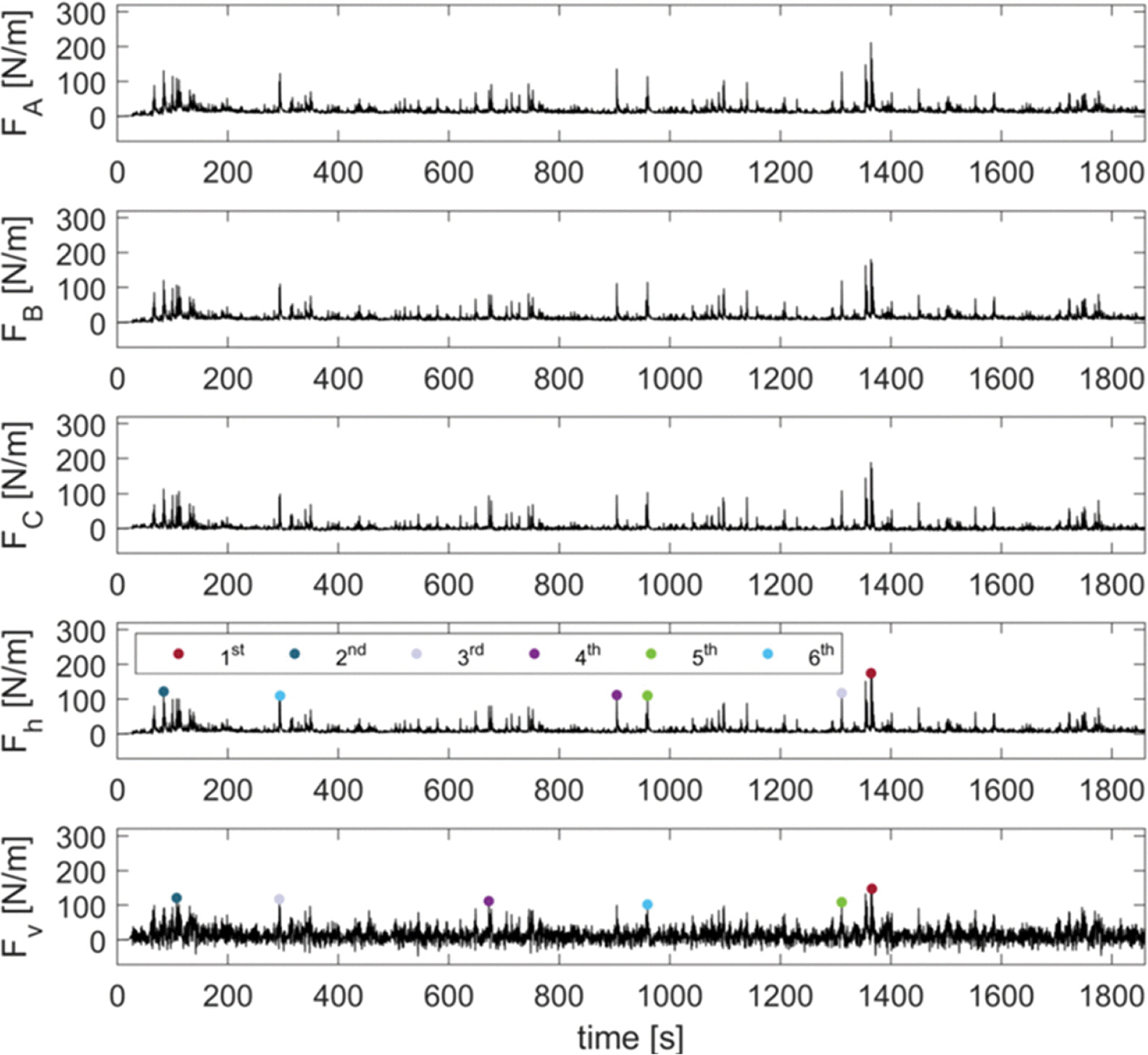
Fig. 7에는 T_s = 1.5 s, H_s = 10 cm인 파가 직각으로 입사했을 때 계측된 수평 및 연직 파력의 시계열을 제시하였다. 여기서 F_A는 전면벽의 좌측 열에 설치된 파압계 P01~P05, F_B는 가운데 열에 설치된 파압계 P06~P10, F_C는 우측 열에 설치된 파압계 P11~P15로부터 계측된 파압을 상부구조물 전체 높이에 대하여 적분하여 계산된 수평 파력을 나타낸다. F_A, F_B, F_C의 시계열을 보면 서로 매우 유사함을 알 수 있다. 그렇지만 위에서 언급된 것처럼 파압계 전면에 피복된 테트라포드의 형태에 따라 파압 계측값이 약간 차이가 있음을 확인할 수 있다. F_h는 F_A, F_B, F_C의 평균값으로서 본 연구에서는 이 값을 상부구조물 전면벽에 작용하는 수평 파력으로 평가하였다. 경사 입사 시에는 F_A, F_B, F_C에서 계측된 파력의 상대적 위상차가 발생할 수 있다. 그러나 좌측 열과 우측 열에 설치된 파압계의 거리가 입사파 파장에 비해 크지 않은 편이고, F_B를 기준으로 보면 평균값을 취하는 과정에서 위상차의 효과는 평활화된다고 볼 수 있다. 한편, F_v는 상부구조물 하부에 설치된 8개의 파압계(P16~P24)로부터 적분하여 계산된 연직 파력을 의미한다. F_h와 F_v의 시계열 그림에서 ○ 기호로 표시된 곳은 파력 계측값이 큰 순서로 상위 6개에 해당하는 값에 해당하며, 1,200파를 조파한 점을 고려하면 상위 0.5% 이내의 파력(F_0.5%)에 해당한다고 할 수 있다. F_h과 F_v의 상위 6개 파력이 발생한 시간은 일부는 일치하고, 나머지는 일치하지 않았다.

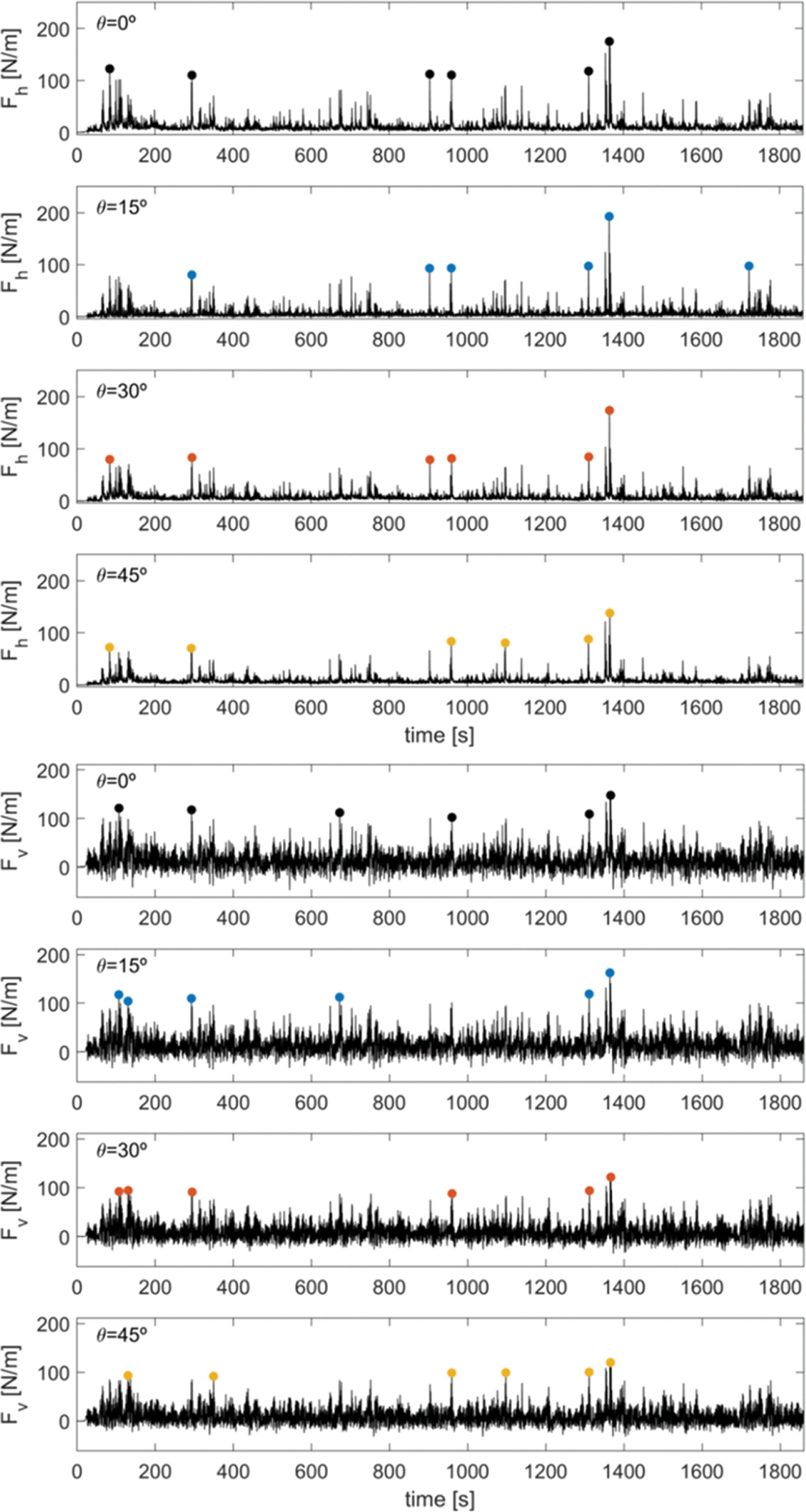
Fig. 8에는 Fig. 7에 보인 과정을 통해 계산된 수평 및 연직 파력을 서로 다른 입사파향에 대하여 비교하여 나타내었다. Fig. 8과 마찬가지로 파력이 큰 순서로 상위 6개에 해당하는 계측값(F_0.5%)을 ○ 기호로 표시하였다. 대체로 입사각이 증가함에 따라 구조물 전면 및 아랫면에 작용하는 파력이 감소하는 경향이 나타남을 직관적으로 확인할 수 있다.

한편, 본 연구와 같은 불규칙파 실험에서는 경사제 사면을 타고 처오름이 발생하는 과정에서의 쇄파 발생 여부 및 테트라포드 피복 상태가 파압 계측값에 큰 영향을 미치게 된다. 따라서 1,200파에 해당하는 전체 조파시간 동안의 수평 및 연직 파력 최대값을 기준으로 입사파향에 따른 파력 감소율을 평가할 경우 상당한 통계적 불확실성이 개입될 수 있다. 실제로 Fig. 7과 8에서도 개별 실험 조건에서의 상위 6개 파력값을 서로 비교해 보면 비슷한 경우도 있지만 때로는 제법 큰 차이를 보이기도 한다. 이러한 점을 고려하여 본 연구에서는 입사파향에 따른 수평 및 연직 파력 감소율을 평가할 때 초과확률 0.5%에 해당하는 상위 6개 파력값의 데이터를 이용하여 분석을 수행하였다.

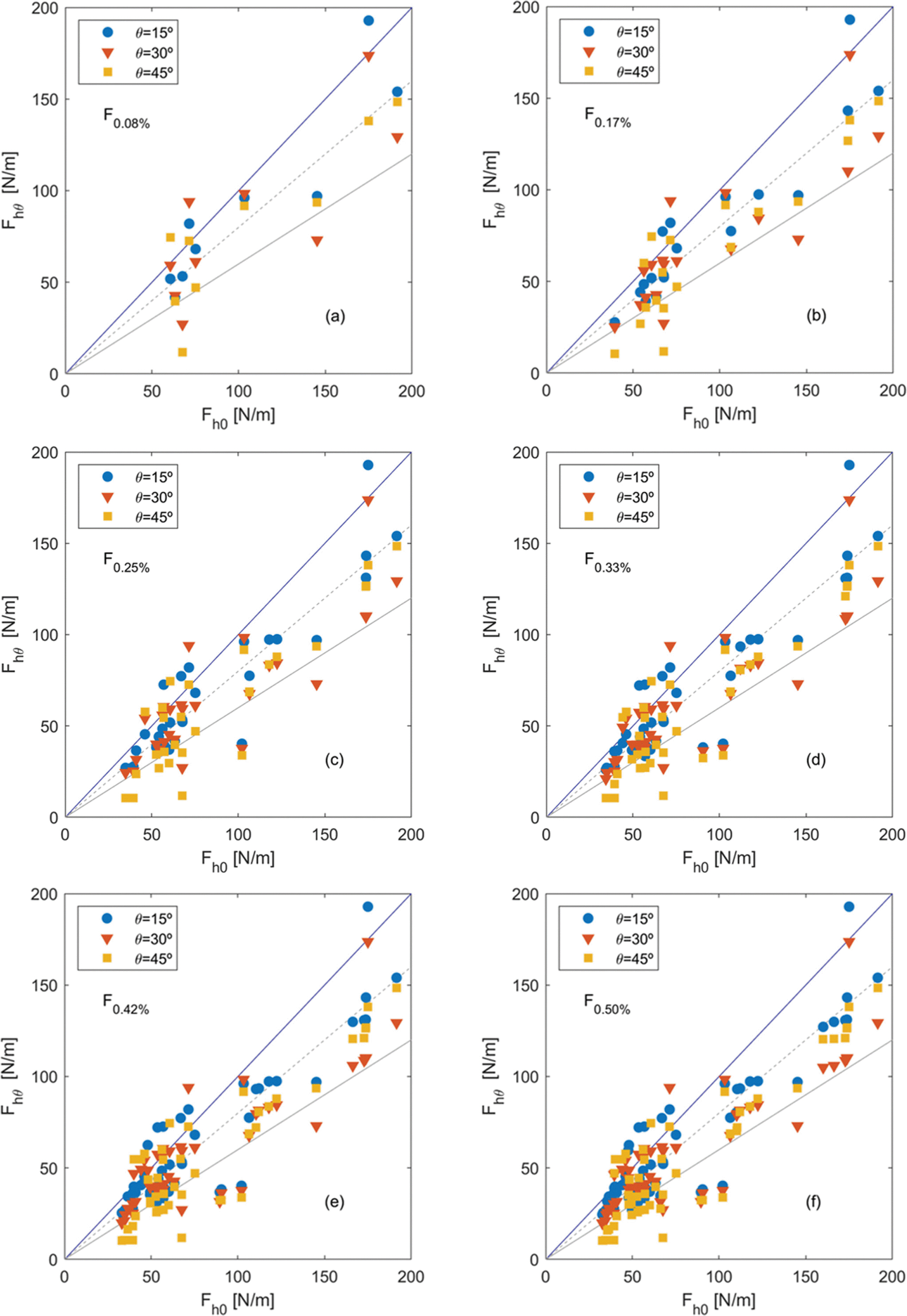
파력 감소율 산정에 앞서 상위 6개 계측 파력의 입사파향에 따른 변화 양상을 고찰하였다. Fig. 9에는 경사 입사 시(θ = 15, 30, 45°)와 직각 입사 시(θ = 0°)의 수평 파력을 비교한 그래프를 제시하였다. Fig. 9(a)는 각 실험조건 별 최대파력 값을 제시한 그림이며, Fig. 9(b)에서 9(f)는 순차적으로 상위 2개까지부터 6개까지의 파력값을 누적하여 각각 제시한 그림이다. 각각의 그림에서 가로축은 직각 입사 시 수평 파력(F_h0), 세로축은 경사 입사 시 수평 파력(F_hθ)을 나타낸다. 직각 입사 시 대비 경사 입사 시 파력의 크기를 쉽게 비교할 수 있도록 F_h0:F_hθ의 비율이 0.6, 0.8, 1.0을 나타내는 선을 각각 회색 실선, 회색 점선, 파란색 실선으로 도시하였다. Fig. 9로부터 전반적으로 파랑의 입사각이 증가함에 따라 상대적으로 파력이 감소하는 경향이 나타남을 확인할 수 있다. 최대파력 값만이 표시된 Fig. 9(a)에서도 이러한 경향을 알 수 있지만 Fig. 9(b)~9(f)에 걸쳐서 순차적으로 상위 2개까지부터 6개까지의 파력값들이 중첩되어 표시됨에 따라 더욱 선명한 경향성을 파악할 수 있다. 다만 일부 계측 자료에서는 경사 입사 시의 수평 파력이 직각 입사 시에 비해서 근소하게 큰 경우도 관찰되었다.

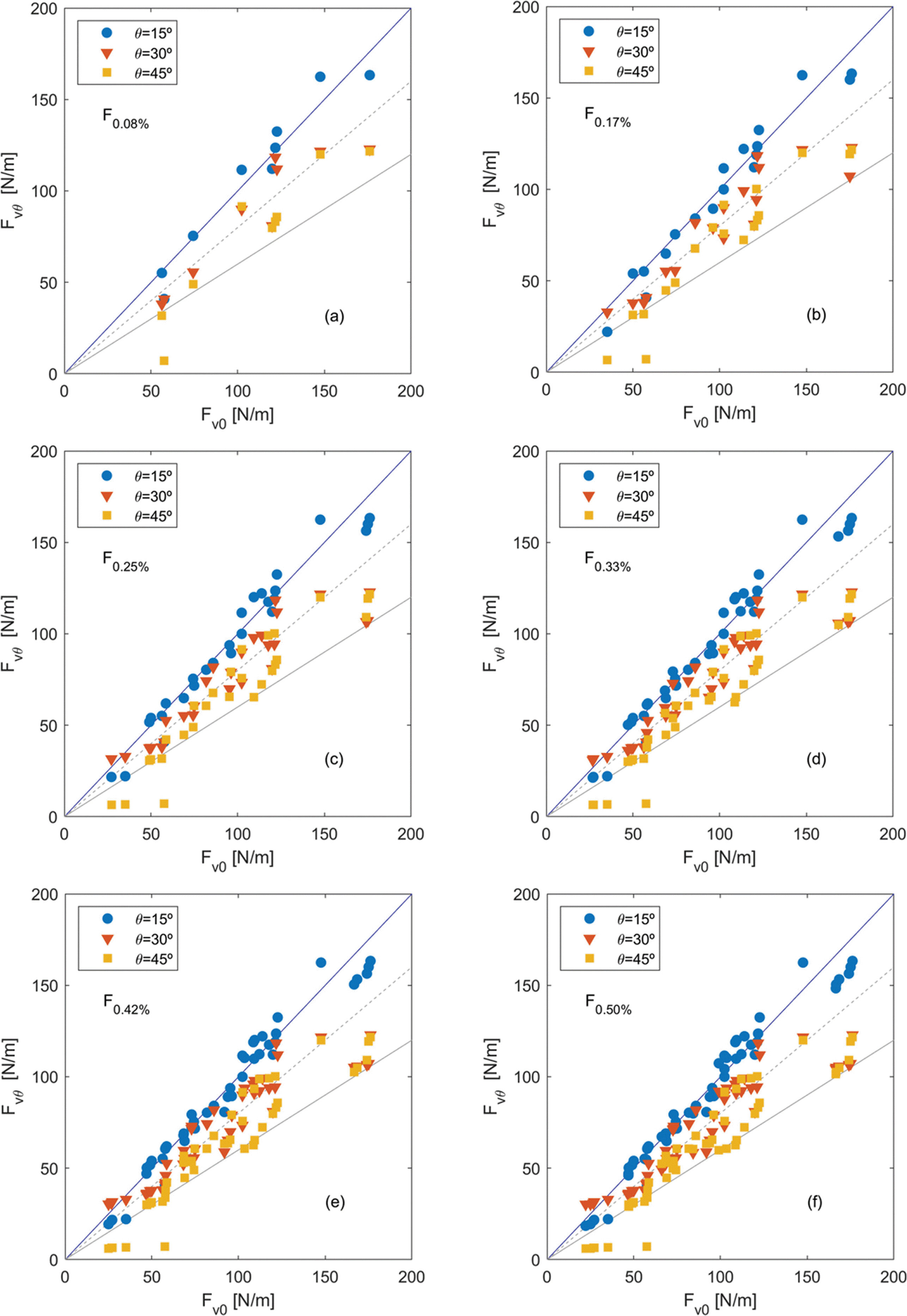
Fig. 10에는 상부구조물 아랫면에 작용하는 연직 파력에 대한 결과를 Fig. 9와 유사한 형태로 제시하였다. Fig. 10(a)부터 10(f)까지 각각의 그림에서 가로축은 직각 입사 시 연직 파력(F_v0), 세로축은 경사 입사 시 연직 파력(F_vθ)을 나타낸다. 연직 파력의 경우 입사각이 증가함에 따라 파력이 감소하는 경향이 수평파력에 비해 더욱 뚜렷하게 나타나며, 자료의 분산(scattering)도 훨씬 적음을 확인할 수 있다. 또한 입사각이 15°인 경우에는 직각 입사 시의 연직파력 값과 거의 차이가 없었다.

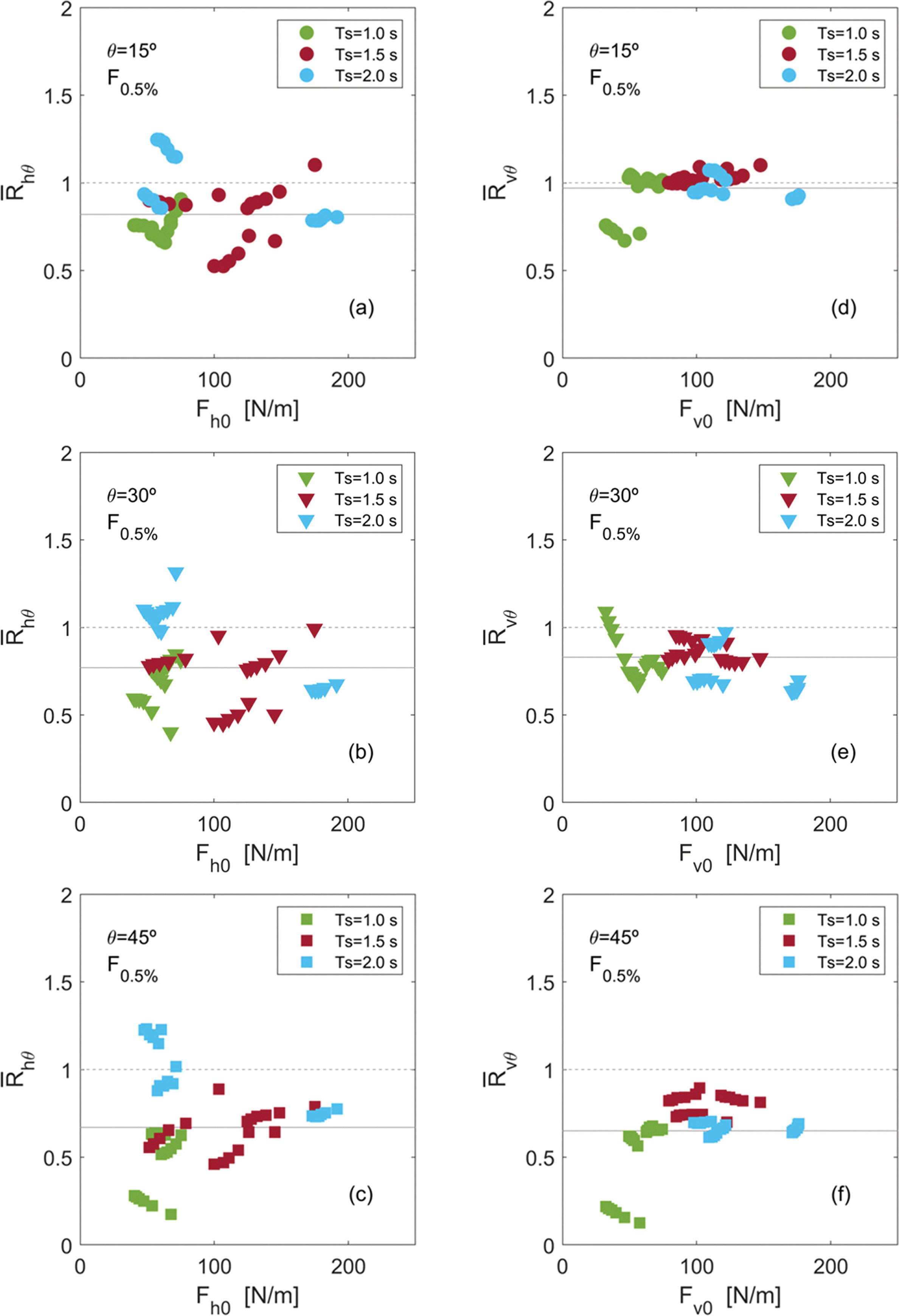
Fig. 11에는 초과확률 0.5%에 해당하는 상위 6개까지의 누적 파력값에 대하여 경사 입사 시 계측값을 직각 입사 시 계측값으로 나눈 비율에 대한 그래프를 제시하였다. 즉, Fig. 11은 Fig. 9(f)와 Fig. 10(f)의 데이터를 무차원화하여 입사각별로 도시한 것이다. 그림에서 R_vθ는 무차원 수평파력, R_vθ는 무차원 연직파력을 의미하며 회색으로 표시된 수평 실선은 그 평균값(R¯hθ, R¯vθ)을 나타낸다. 즉, R¯hθ 및 R¯vθ은 직각입사시 대비 경사입사 시의 수평 및 연직파력의 평균 감소율에 해당한다. Fig. 9와 10에서도 입사각이 증가함에 따라 수평 및 연직파력이 감소하는 경향을 알 수 있었지만 Fig. 11을 통해서 이러한 경향을 더욱 분명하게 파악할 수 있으며 R¯hθ 및 R¯vθ을 구하여 파력 감소율을 정량적으로 평가하는 것이 가능하다.

Fig. 11이 Fig. 9(f) 및 Fig. 10(f)와 대응되는 것처럼 Fig. 9(a)~(e) 및 Fig. 10(a)~(e)에 대응되는 무차원 수평파력(R_hθ)과 연직파력(R_vθ)을 유사하게 계산할 수 있으며, 각각의 경우에 대하여 그 평균값(R¯hθ 및 R¯vθ)을 계산함으로써 초과확률에 따른 파력 감소율을 개별적으로 산정하는 것이 가능하다.

Table 3과 4에는 이러한 계산을 통해서 구해진 수평 및 연직파력 감소율을 표로 정리하여 나타내었다. 평균값 계산에 사용된 데이터 수가 많아짐에 따라서, 즉 초과확률이 커짐에 따라서(F_0.08% → F_0.50%), R¯hθ 및 R¯vθ의 값이 일정하게 수렴해 감을 확인할 수 있다. 한편, 수평파력 감소율은 최대파력 값만을 사용하여 계산된 경우(F_0.08%)에 비해서 상위 6개까지의 파력값의 무차원 파력 비 평균을 사용한 경우(F_0.50%)에 더 커짐을 확인할 수 있다. 즉, F_0.08% 조건에서는 입사각이 15°일 때 13%, 30°일 때 19%, 45°일 때 25%의 감소율을 보이지만, 초과확률이 증가함에 따라 감소율이 커져서 F_0.50% 조건에서는 감소율이 18%, 23%, 33%로 수렴하였다. 반면에 연직파력 감소율은 F_0.08% 조건에서 입사각이 15°일 때 2%, 30°일 때 21%, 45°일 때 36%였고, F_0.50% 조건에서는 3%, 17%, 35%로 차이가 크지 않았다.

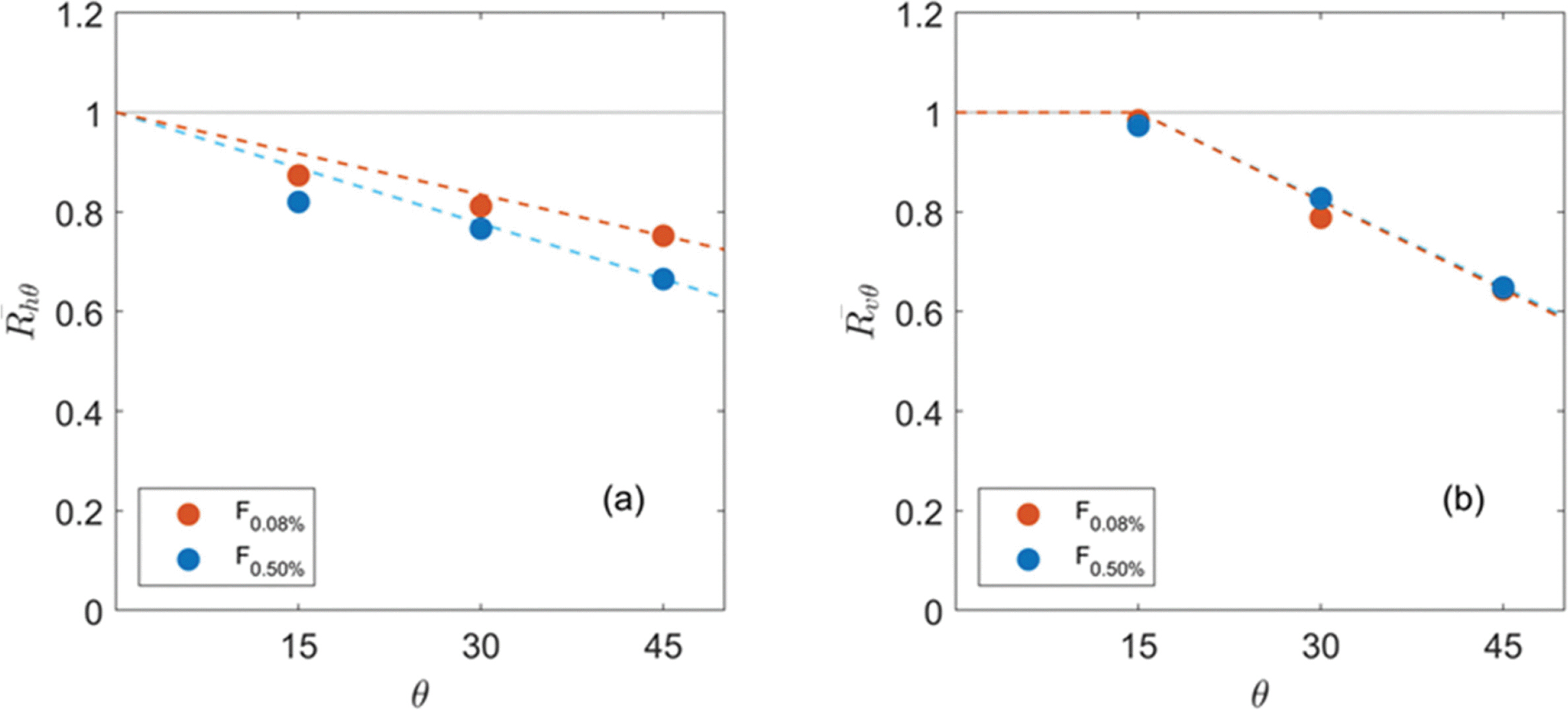
Fig. 12에는 F_0.08% 및 F_0.50% 조건에서의 R¯hθ와 R¯vθ값을 각각 그래프로 나타내었다. 위에서 언급한 것처럼 R¯hθ값은 두 조건에 따라 약간 차이가 있지만 R¯vθ값은 차이가 거의 없음을 뚜렷하게 확인할 수 있다. 또한 수평파력의 경우에는 입사각이 증가함에 따라 거의 선형적으로 비례하여 파력이 저감되는 반면, 연직파력의 경우에는 입사각이 15°일 때까지는 직각 입사 시와 큰 차이가 없다가 그 이후부터 파력이 급격하게 저감됨을 알 수 있다.

이러한 점을 고려하여 입사각에 따라 상부구조물에 작용하는 R¯hθ 및 R¯vθ의 회귀직선을 Fig. 12에 보인 것처럼 구할 수 있으며, 그 식을 식(1)~(3)에 나타내었다. 수평파력의 경우에는 F_0.08% 및 F_0.50% 조건에 따라 회귀곡선의 기울기, 즉 파력 저감율이 달라지게 되므로 식(1)과 (2)로 구분하여 제시하였다. 이처럼 초과확률에 따라 입사각에 따른 수평파력 저감율이 다르지만 설계 시에는 일반적으로 재현빈도가 극히 낮은 설계파 조건에 대하여 외력을 산정하게 되므로 식(1)을 사용하는 것이 바람직할 것이다. 수평파력 저감율 측면에서도 저감율의 기울기가 더 완만하기 때문에 파력을 더 보수적으로 산정하게 된다. 다만, 재현빈도가 통상적인 조건보다 상대적으로 높다면 Table 3 및 Fig. 12의 결과를 토대로 저감율을 식(1)보다 더 크게 평가하는 것도 가능할 것이다. 한편, 연직파력 저감율은 Table 4 및 Fig. 12에 보인 것처럼 초과확률에 따른 변화가 크지 않으므로 설계 시 식(3)을 보편적으로 적용해도 좋을 것이다.