요약해상에 설치된 관측타워에 미치는 환경 하중 변화에 따른 구조물의 동특성 파악은 구조물의 안전성 평가에 중요한 인자로 활용되고 있다. 이 연구에서는 새만금 방조제 인근에 위치한 만경해상관측타워(이하 만경타워) 구조물에 대한 현장계측실험을 통하여 동특성을 분석하고 수치해석모델을 구성하였다. 계측실험 결과, 조위가 하강할수록 고유주파수는 증가하는 추세를 보였다. 또한 동일한 모드가 2개의 주파수를 갖는 것을 확인하였으며, 이는 세굴에 의하여 파일과 지반이 접촉 시에 고유주파수가 일부 증가하는 현상으로 판단되었다. 수치해석을 위하여 구조물의 상부 질량, 가상고정점, 세굴 깊이 및 유체 영향을 고려한 부가 질량 등을 만경타워의 구조적 특성으로 반영하였으며, 추정된 고유주파수 및 패턴서치 알고리즘으로부터 수치해석모델에 대한 모델 개선 작업을 수행하였다. 개선된 해석모델로부터 추후 만경타워에 대한 안정성 검토 측면에서의 연구에 적용될 수 있을 것으로 기대된다.
AbstractIn the case of small observation towers located at sea, it is necessary to confirm the change in dynamic characteristics due to the influence of environmental loads. In this study, the dynamic characteristics were analyzed and the numerical analysis model was designed through field dynamic response measurement on the Mangyeong Offshore Observation Tower (Mangyeong Tower) located near the Saemangeum Embankment. As a result of the measurement, the natural frequency was found to increase slowly as the tide level is lowered. In addition, it was confirmed that the same mode has two frequencies, which was judged to be a phenomenon in which the natural frequency was partially increased when the pile and the ground contacted by scouring. For numerical analysis, the upper mass, artificial fixity point, scour depth and fluid influences are reflected in the structural characteristics of the Mangyeong Tower. In addition, the model updating from the estimated natural frequency and pattern search algorithm was performed. From the model updating, it is expected that it can be applied to future studies on stability of Mangyeong Tower.
1. 서 론기상 및 해양환경 변화 모니터링을 위한 해양관측시스템 구축이 활발히 이루어지고 있는 추세이다. 실시간 해양관측을 위한 시스템으로 해양관측부이, 해상관측타워 그리고 해양관측용 드론 등이 있고, 이를 토대로 연속적이고 장기적인 기상 및 해양환경 자료를 수집할 수 있다. 국내의 경우 이어도, 소청초 및 가거초 해양과학기지를 설치하여 운영하고 있으며, 이러한 대형시스템 외에도 여러 해역에서 중소형 관측시스템을 운영하고 있다. 새만금 방조제 외측 해역의 수질, 유속, 파랑, 파고뿐만 아니라 기상 특성에 대한 장기적인 관측을 위하여 가력해상관측타워와 소형 강관타워인 만경해상관측타워(이하 만경타워)를 설치하여 운영하고 있다.
전라북도 군산시 고군산군도 인근 해역에 위치해 있는 만경타워(Fig. 1 참조)는, 지난 2008년 새만금 해양환경보전대책을 위한 조사연구에서 해양환경(수질, 조류 등)과 해상기상 등을 상시 모니터링하기 위하여 설치한 소형 해상관측타워로서, Fig. 1(b)와 같이 단일 강관파일의 상부에 관측기기를 탑재하고 있다. 한편, 만경타워가 위치한 국내 서남해안의 경우 주로 점토지반 혹은 사질토지반이 넓게 분포하고 있고, 수심이 얕아 조류 및 파도에 의한 세굴 발생 가능성이 높으며, 만경타워 역시 기초 부근의 세굴이 발생하였을 가능성이 높다. 실제 만경타워 현장 사용자들에 따르면 파일의 진동이 갈수록 증가하고, 최근에는 높은 불안감을 제기해온 바가 있다. 만경타워의 운영기간이 10년 이상 경과함에 따라 강관파일이 상당히 노후화되어, 활용 측면에서의 사용성 검토뿐만 아니라 구조안전성 측면에서의 평가가 필요한 시점이다.
만경타워와 유사한 목적으로 설치되어 운영 중인 이어도, 소청초, 가거초 해양과학기지의 경우, 가거초 해양과학기지가 2011년 태풍 무이파에 의하여 심하게 손상된 이후, 이들 해양과학기지의 구조물 건전성 모니터링에 대한 중요성이 새롭게 인식되었다(Kim et al., 2017). 이후 이들 과학기지에 동적응답 계측시스템을 구축하였으며, 계측결과를 이용하여 환경조건에 따른 동특성 변화 및 구조해석모델 개선 등을 수행한 바 있다(Kim et al., 2018; Kim et al., 2019; Yi et al., 2020). 한편 세굴 깊이와 관련한 기존 연구로는 해상풍력터빈 기초부에 발생한 세굴을 고려하여 구조물의 고유주파수 변동을 분석한 연구(Yi et al., 2015, 2016)와 교각에 발생한 세굴의 깊이를 구조물의 고유주파수를 이용하여 분석하고자 한 사례가 있다(Park et al., 2005).
이 연구에서는 만경타워에 대한 구조 안전성 평가 측면에서 구조물에 대한 상시진동시험을 실시하여 가속도 응답을 계측하고, 계측자료에 대한 스펙트럼 밀도함수(power spectral density function, PSD)와 추계론적 부공간 규명법(stochastic subspace identification, SSI)을 이용하여 구조물의 동특성을 분석하였다. 그리고 세굴 깊이, 상부 질량 및 가상고정점(artificial fixity point) 깊이 등을 고려하여 해석모델을 구성한 후, 상시진동시험을 통하여 구한 만경타워의 계측 고유주파수와 패턴서치 방법(pattern search method)을 이용하여 수치해석모델을 개선하였다.
2. 이론적 배경2.1 스펙트럼밀도함수를 이용한 고유주파수 분석현장계측 시 신속한 모드해석을 위하여 스펙트럼밀도함수법을 이용하였다. 이는 구조물 응답 자료에 대한 PSD 함수 S(ω)의 정점(peak)에 해당하는 위치에서의 값을 비교함으로써 고유주파수와 모드형상을 구하는 방법이다. k번째 모드에 대한 계측자유도 a에서의 모드형상 값(
여기서 ωk는 k번째 모드의 고유주파수, Syayb는 기준이 되는 계측지점 b에서의 응답에 대한 계측지점 a에서의 응답 사이의 상호스펙트럼밀도함수(cross power spectral density function), Syayb는 기준이 되는 계측지점 b에서 계측된 자료의 자기스펙트럼밀도함수(auto power spectral density function), Nm은 계측된 자유도의 수이며 φ(k)는 k번째 모드의 모드형상 벡터이다.
2.2 추계론적 부공간 규명법을 이용한 동특성 추정하중에 대한 정보를 구하기 어려운 대형 토목구조물에서 주로 활용되는 기법인 추계론적 부공간 규명법(stochastic subspace identification, SSI)을 적용하여 보다 정밀한 모드분석을 수행할 수 있다. 이는 상시 진동실험을 통해 얻어진 응답을 이용하여 추계론적 상태-공간 모델의 변수를 추정하는 시간영역의 실험모드해석 방법이다. 식(2)와 같이 하중을 랜덤정규분포하중으로 고려했을 때의 추계론적 이산상태방정식으로부터, 식(3)과 같이 상호상관행렬(R(k))을 구하면, 상호상관행렬이 A, C, G와 같은 시스템행렬로 표현된다. 따라서 식(4)와 같은 블록행켈행렬을 구성하면 이는 식(4)의 마지막 항과 같이 가관측성행렬(observability matrix, On1)과 확장가제어성행렬(extended controllability matrix,
여기서, A, C는 시스템행렬(system matrix)이며, y는 계측벡터(observation vector), z는 상태벡터(state vector), w(k)와 v(k)는 서로 상관관계가 없는 랜덤 정규분포 하중벡터(load vector)와 관측변수에 대한 노이즈벡터(noise vector)이며 n1, n2는 모드추정에 사용된 R 행렬의 크기이다. 시스템행렬 A를 이용하여 구조물의 동특성을 아래와 같이 구할 수 있다(Jin, 2017; Yi et al., 2013; Yun et al., 2004).
여기서, λk, ωk, λk, φk는 각각 k번째 모드의 고유치, 고유주파수, 모드감쇠비 및 모드형상을 나타낸다.
2.3 모델개선(model updating)을 위한 패턴서치 방법(Pattern Search Method)의 도입도면이나 실측을 통하여 구축한 해석모델의 경우, 이 모델을 이용하여 계산한 고유주파수는 실제 계측에 의한 고유주파수와 일치하지 않는 경우가 많다. 이는 해석모델을 구축할 때 반영한 여러 물성치 및 치수 등이 실제와 다를 수 있고, 또한 비구조부재(non-structural member)의 경우 생략 또는 단순화하는 경우가 많기 때문이다. 따라서 해석모델로 구한 고유주파수가 실제 계측으로 구한 고유주파수에 가깝도록, 즉 실제 조건에 가까워지도록 모델을 개선하는 작업, 즉 모델개선(model updating)이 필요하다. 이러한 모델개선은 일종의 최적화 문제로 간주할 수 있으며, 이때 목적함수(objective function)는 계산된 고유주파수와 계측에 의한 고유주파수 사이의 차이 등을 이용하여 정의할 수 있다. 패턴서치 방법은 미분을 이용하는 기존의 최적화 방법과는 달리 목적함수 값 자체를 이용하는 직접탐색법(direct search method)의 일종으로, 최적해를 구하기 위하여 패턴을 반복하는 것이 효과적일 수 있다는 경험에 착안한 방법이다(Hooke and Jeeves, 1981). 패턴서치 방법은 다양한 최적화 문제에 적용하기가 용이하고, 실제 여러 분야에서 널리 이용되고 있다. 패턴서치 방법은 일반적인 방법에 비하여 탐색시간이 상대적으로 짧은 편에 속하며, 전역적 최적해를 찾을 가능성이 높은 방법이기도 하다. 기본적인 동작 순서로는 패턴의 생성, 격자 크기의 결정, 폴링(polling) 그리고 확장, 축소 등의 과정을 거치며, 패턴서치방법의 상세 이론은 기존 문헌 및 연구를 참고할 수 있다 (Hooke and Jeeves, 1961; Lewis et al., 2000; Manoharan and Shanmuganathan, 1999; Wetter and Wright, 2003; Zhao et al., 2006). 패턴은 임의의 집합에서 현재해보다 우수한 해를 찾기 위한 인접해를 결정하는 탐색 방향을 의미하며, 이러한 집합을 격자라 하고 그 격자 내부 인접해의 거리를 격자 크기라고 한다. 이 격자 크기는 다음 식(8)과 같이 결정된다.
여기서, ∆mk+1과 ∆mk는 각각 k + 1번째, k번째 탐색단계에서의 격자 크기이며, vk는 인접해와 현재해의 관계에 따라 격자 크기를 증가시키거나 줄여 주는 격자 크기 계수(mesh size factors)로서 0보다 큰 값이다. 폴링은 모든 인접해를 한번에 탐색한 뒤 가장 좋은 인접해를 다음 단계의 해로 선택하는 방법(complete poll)과 순차적인 탐색을 통하여 좋은 인접해가 나타나면 즉시 다음 단계의 해로 선택하는 방법(incomplete poll)이 있다. 폴링의 성공 또는 비성공 여부에 따라 각각 격자 크기가 증가 또는 감소한다.
3. 실험개요3.1 새만금 만경타워 개요만경타워는 새만금 방조제의 북서방향에 위치하고 있으며, 기본적인 해양환경 관측 및 사설항로표지 기능을 지니고 있다. 서론에서 소개한 바와 같이 만경타워는 단일 강관파일로 해상에 설치되어 있으며, 상부에 해양관측기기를 탑재하여 운영되고 있다.
강관파일의 규격은 Fig. 2와 같이 외경 1,016.0 mm, 두께는 17.5 mm이며, 파일의 총 길이는 43.0 m이다. 평균 해수면을 기준으로 해수면 상부 높이가 13.0 m이며, 평균해수면 아래 10 m 지점에 실트질의 해저지반이 놓여 있고, 충분한 구조적 안전성을 확보하기 위하여 파일을 기초지반 하부 20 m 지점까지 매입하여, 하단부가 암반층에 관입되도록 하였다.
3.2 현장계측 개요
Fig. 3과 같이 현장계측을 위해 기초로부터 최상부 높이의 위치에 대하여 중량의 비대칭성을 고려하여 배터리팩이 놓인 방향을 기준으로 X, Y 축을 설정하고 X 방향으로 2개, Y 방향으로 2개 등 총 4개의 1축 가속도계와 1개의 2축 경사계를 설치하였다. 또한 최상부로부터 약 4.8 m 하부에 X, Y 방향으로 각각 1개의 가속도계를 설치하였다(Fig. 3 참조). 계측에 사용된 센서는 MEMS형 가속도계 및 경사계로, 각각의 민감도는 2 V/g 및 60 mV/°이다. 계측주파수는 저차모드 고유주파수의 범위(수Hz)와 나이퀴스트 주파수(Nyquist frequency)를 고려하여 50 Hz로 설정하였다. 한 세트의 측정 시간은 신뢰성 있는 모드해석이 가능하도록 30분으로 고려하였고, 총 6회의 상시진동시험(ambient vibration tests)과 1회의 충격진동시험(impact vibration tests)을 수행하였다.
3.3 현장계측 자료 분석현장계측은 2019년 5월 30일 12시 40분부터 16시 10분까지 약 3시간 30분 동안 진행되었다. 국립해양조사원의 조석 예보에 따르면 계측 시작 시의 조위는 4.97 m이며, 종료 시의 조위는 약 3.12m로 조위가 낮아지는 낙조 상황이었으며, 측정된 상시진동 데이터를 30분 간격으로 분할하여 총 7회의 시계열 가속도 응답 세트를 얻었다. Fig. 4(a)와 4(b)는 첫 번째 세트와 마지막 세트에 대한 응답을 제시한 것으로, Fig. 4(b)의 충격진동시험은 현장 이동수단인 선박의 선미를 구조물에 충돌시켜 수행하였다.
Fig. 5는 획득한 시계열자료(time history data)로부터 주파수 영역에서의 응답을 분석하기 위하여 파워스펙트럼밀도(power spectral density)를 구한 것으로서, 정점(peak)을 읽어 각 모드의 고유주파수를 구할 수 있고, 대표적으로 타워 상부에서의 센서로부터 계측된 자료를 통해 고유주파수 계측값을 표시하였다. 조위가 4.97 m일 때 1차 고유주파수의 값은 0.8667 Hz, 조위가 3.52m일 때의 1차 고유주파수의 값은 0.9155 Hz로 고유주파수의 값은 조위가 감소함에 따라(부가질량의 효과가 감소함에 따라) 증가하는 것을 확인하였다.
3.4 추계론적 부공간 규명법에 의한 동특성 추정 및 분석보다 정밀한 동특성 추정을 위하여 시간영역 실험모드해석방법인 추계론적 부공간 규명법을 적용하였다. 4번째 계측자료 세트(14:10~14:40 30분 계측)에 대하여 추계론적 부공간 규명법을 적용하여 구한 안정화도(stabilization chart)를 Fig. 6에 제시하였으며, 이 안정화도로부터 보다 분명하게 모드를 추정할 수 있다. PSD의 경우, Fig. 5에서 제시한 바와 같이 0.9 Hz와 0.99 Hz에 각각 하나의 정점(peak)만 있는 것으로 확인되었으나, 실제 안정화도를 분석하면 이 주파수 대역에서 매우 근접한 두 개의 모드(close modes)를 찾을 수 있음을 알 수 있다. 이와 같이 매우 근접한 주파수 대역에서 발생하는 두 개의 모드는 강축과 약축 방향에 대한 두 개의 굽힘모드(bending mode)일 가능성이 높다. 실제 모드형상을 분석하면 Fig. 7에서와 같이 서로 직교하는 2개의 모드임을 알 수 있고, 이는 굽힘강성이 비슷한 두 축, 즉 강축과 약축에 대한 굽힘모드로 판단할 수 있다. Fig. 8에서 제시한 바와 같이 타워 상부에 위치한 중량인 배터리 팩의 위치가 중앙에 위치하지 않고 0.8 m 가량 한 방향으로 치우쳐져 약간의 비대칭성이 발생하여 근접한 두 개의 모드가 발생한다. 따라서 Fig. 6과 같이 0.9Hz의 고유주파수를 갖는 2개 모드와 0.99Hz를 갖는 2개 모드는 비대칭성에 의하여 발생한 것으로 분석할 수 있다.
한편, 1개의 굽힘모드가 0.9 Hz와 0.99 Hz 사이에서 각각 발생하는 원인은 세굴에 의한 것으로 판단된다. 즉, 강관파일이 세굴면에서 떨어진 경우(0.9 Hz)와 세굴면에 부착된 경우(0.99 Hz) 각각의 지반 강성 효과가 달리 작용하여 두 개의 굽힘모드로 분리된다(Fig. 9 참조). 따라서 Fig. 6의 0.9 Hz 부근의 두 개 모드는 각각 세굴면과 파일면이 분리되어 있을 때 약축, 강축 방향으로의 1차 굽힘모드이며, 0.99 Hz 부근의 두 개 모드는 각각 세굴면과 파일 면이 부착되어 있을 때 약축, 강축 방향으로의 1차 굽힘모드가 된다. Fig. 10(a)는 세굴면과 강관파일 접촉 조건을 단자유도 구조물로 간략화한 모식도를 나타낸다. k1과 k2는 각각 파일의 강성과 지반의 강성을 나타내는데, m의 질량을 가지는 파일이 지반과 접하지 않을 시, 즉 파일과 지반 사이의 거리인 xgap보다 실제 이동 거리 x가 작을 때 등가강성(k)은 k1임을 알 수 있다. 반면 파일이 지반과 접할 시 즉, x보다 xgap가 큰 경우, 등가강성(k)은 k1 + k2가 되어 고유주파수가 증가하게 된다. 이와 같은 비선형시스템의 경우 PSD는 Fig. 10(b)와 같이 두 개의 정점(peak)을 가지게 된다. Table 1은 SSI 법을 적용하여 도출된 각각의 모드 고유주파수를 제시하였으며, 전술한 1차 굽힘모드와 마찬가지로 고유주파수가 4.0 Hz와 4.3 Hz 사이 4개의 모드로 구성되는 2차 굽힘모드를 보여준다.
4. 해석모델 구성과 모델 개선4.1 해석모델 구성이 연구에서는 만경타워의 조위에 따른 주변 유체의 영향, 세굴깊이 등을 고려하여 구조물의 고유주파수를 해석할 수 있도록 수치해석모델을 구성하였다. 구조물의 고유주파수는 강성 및 질량의 함수로, 구조물의 자체 질량 및 주변 해수 등에 의한 부가질량 등을 정확하게 반영하는 것이 중요하다. 한편, 구조물 상부에 탑재된 태양광 패널, 리튬 전지 및 수납공간의 질량은 설치 도면이 부재하여 리튬 전지의 중량과 개수, 강재 함체의 사이즈 및 두께 등을 고려하여 상부 집중질량의 초기값을 600 kg으로 고려하였다. 또한 만경타워 강관 주변 조위에 따른 유체의 영향은 부가질량(added mass)으로 모델링하여 수치해석에 반영하였다. 이 연구에서는 일반적인 보요소에 부가질량 및 집중질량을 고려하여 모델링할 수 있도록 해석 프로그램을 작성하여 사용하였다.
한편, 지반-파일 상호작용(soil-pile interaction)을 고려하기 위하여 지반을 유한요소 등으로 모델링하거나 지반-파일 상호작용을 단순하게 가상고정점 모델을 이용하여 고려할 수 있는데, 이 연구에서는 해석의 편의성을 고려하여 파일에 수평하중(P)이 작용할 때의 가상고정점 모델을 적용하였다(Fig. 11 참조). 기초지반면으로부터 가상고정점까지의 깊이(ha)는 파일과 지반의 물성치를 이용하여 다음과 같이 구할 수 있다(Cho and Jeong, 2009; Jeong and Kim, 2013).
여기서, EI, D는 각각 파일의 휨강성 및 직경이며, kH는 횡방향 지반반력계수로 다음과 같이 구할 수 있다.
여기서, α, E0, BH는 각각 수평방향 지반반력계수 산정에 필요한 계수(평상 시 1, 지진 시 2), 표준관입시험의 N치를 통한 지반의 탄성계수, 하중작용방향에 직교하는 말뚝의 환산 재하폭을 나타낸다. 이 연구에서는 α 값으로 평상시의 값인 1을 적용하였고, BH는 만경타워 기초의 제원에 따라 0.469 m를 적용하였다. 한편 지반의 탄성계수는, 만경타워가 설치된 해역에 대한 지반조사 자료가 없기 때문에 서해안 점토지반에 대한 표준관입시험의 N 값의 범위를 고려하여 N을 10으로 가정하였으며, N 값으로부터 지반의 탄성계수는E0 = 28 N(tf/m2) 식을 이용하여 2.74 × 106 kN/m2으로 고려하였다(Chun et al., 2006; Kim et al., 2001). 수평방향 지반반력계수인 kH의 값은 1.188 × 105 kN/m3이고, 강관파일의 직경(D)과 휨강성(EI)(각각 1.016 m, 1.437 × 106 kN/m2)을 적용하여 구한 가상고정점의 깊이(ha)는 약 4.70 m이다.
4.2 해석모델 개선을 위한 목적함수구조물의 동특성을 이용한 수치해석모델 개선을 위하여, 구조물의 고유주파수와 패턴서치 방법을 이용하였다. 패턴서치방법을 이용하여 실제 구조물에 대한 모델개선을 수행하기 위해서는 추정하고자 하는 변수와 목적함수를 먼저 정의하여야 한다. 이 연구에서는 상부질량(mt), 세굴면에 닿았을 때의 가상고정점 깊이(ha1), 그리고 파일이 세굴면에 닿지 않았을 때의 세굴깊이와 가상고정점의 전체깊이(ha2)를 추정 변수로 고려하였으며, 이러한 변수를 추정하기 위하여 다음의 식(11)과 같은 목적함수를 고려하였다. 목적함수에 사용한 자료는 수심별, 세굴면과 파일 단면의 접촉, 비접촉 시 그리고 강축과 약축에 대한 1차, 2차 고유주파수이다.
(11)여기서,
4.3 수치시뮬레이션 결과를 이용한 모델 개선정확한 구조 제원을 알고 있는 경우에 대하여 수치시뮬레이션을 통하여 구한 고유주파수를 이용하여 부정확한 초기치를 반영한 모델을 개선함으로써 제안 방법의 적용성을 평가하고자 하였다. 다음 Table 2는 상부질량이 600 kg, 세굴면에 닿은 경우의 가상고정점 깊이(ha1) 5 m, 그리고 세굴면에 닿지 않은 경우의 가상고정점 깊이(ha2)를 6m로 고려하였을 때, 조위가 4.97 m, 4.82 m, 4.59 m, 4.28 m, 3.91 m, 3.52 m, 3.12 m인 경우에 따른 고유주파수의 값을 정리한 것이다. Table 2의 결과를 Table 1의 계측값과 비교하면, RMSE 값은 2.5827%에 이르는 것을 알 수 있다.
계측된 고유주파수를 사용하지 않고, 수치해석에 의한 고유주파수를 이용하여 사전에 참값으로 고려된 상부질량(mt), 가상고정점 깊이 1(ha1), 가상고정점 깊이 2(ha2)를 패턴서치 방법으로 정확하게 추정할 수 있는지 확인하였다. 상부질량은 500 kg, 가상고정점 깊이1은 4 m 가상고정점 깊이 2는 6 m를 참값으로 고려하였다. 초기값은 4.1절에서 설명한 바와 같이 상부질량 600 kg, 가상고정점 깊이 1, 2는 각각 5 m, 6 m로 고려하였으며, Table 3에 추정된 최종값(Final values)과 그에 따른 RMSE 값을 나타내었다. 패턴서치로 추정한 결과는 상부질량 500.2266 kg, 가상고정점 깊이는 세굴면에 닿은 경우와 떨어진 경우 각각 3.9987 m, 6.0000 m로 추정되어 추정오차가 0.0003% 미만이었으며, 이때의 고유주파수는 Table 3의 7번째 열과 같고, 이때 RMSE 값은 8번째 열에서와 같이 0.0741%로 목표 고유주파수와 매우 일치하는 결과를 얻을 수 있음을 확인하였다. Fig. 12는 패턴서치에 의하여 구한 RMSE 값의 수렴과정을 제시한 것으로 최적화에 의하여 RMSE 값이 감소하는 것을 알 수 있다. 한편, 최적화 과정에서 발생할 수 있는 유일해(unique solution)의 문제를 검토하기 위하여 Table 4와 같이 초기값을 4가지 경우로 고려하였을 때의 최종 결과를 비교하였다. 비교 결과 초기값을 다르게 고려하더라도 최종적으로 구한 값은 일치함을 알 수 있다.
4.4 계측결과를 이용한 패턴서치 방법의 적용4.3절에서는 수치시뮬레이션 결과를 이용하여 패턴서치의 적용성을 검증하였으며, 이 절에서는 계측결과를 이용하여 실제 만경타워에서의 상부질량과 가상고정점 깊이 1, 2를 추정한 내용을 정리하였다. Fig. 13(a)와 (b)는 조위가 3.12 m인 한가지 경우의 초기값에 의한 고유주파수(initial value)와 최종 추정된 값(final value)을 이용하여 계산한 고유주파수를 1, 2차 굽힘모드로 나누어 계측결과(measurement value)와 비교한 것으로 초기값을 이용한 경우에 비하여 최종 추정된 값을 적용하였을 때 고유주파수가 실제 계측결과에 더욱 근접함을 알 수 있다.
패턴서치에 의하여 구한 상부질량 454.2646 kg, 가상고정점 깊이는 세굴면에 닿은 경우와 떨어진 경우 각각 5.0000 m, 5.8679 m로 추정되었다. 세굴면에 닿았을 경우와 세굴면에 닿지 않았을 경우의 가상고정점 깊이를 이용하여 세굴깊이를 추정하면, 약 0.9 m 가량의 세굴이 발생하였을 것으로 유추할 수 있다. 그러나 이러한 세굴깊이는 세굴면에 닿았을 경우의 가상고정점 깊이와 세굴면에 닿지 않았을 때의 가상고정점의 깊이가 동일하다고 가정하였을 때의 결과이므로 정확한 세굴깊이는 실제 잠수부 등에 의한 측정이 필요할 것으로 사료된다. 그러나 실제 세굴깊이를 모르더라도 파랑하중에 의한 해석 또는 지진해석 등을 수행할 때 추정된 값을 이용하여 모델링함으로써 결과의 정확성을 높일 수 있을 것으로 사료되며, 향후 이 결과를 이용하여 만경타워의 구조적 안전성을 검토할 계획이다.
5. 결 론이 연구에서는 새만금 방조제 인근 만경타워 구조물에 대하여 현장계측을 통하여 동특성을 분석하였고, 계측 고유주파수와 패턴서치 방법을 이용하여 해석모델을 개선하였다. 주요 결론을 다음과 같이 정리하였다.
1) 타워 상부에 설치된 센서로부터 계측된 고유주파수의 값을 보았을 때, 조위가 하강할수록 1차 고유주파수의 값은 전체적으로 증가하였고, 이는 조위가 하강함에 따른 부가질량의 영향에 의한 것으로 확인되었다.
2) 추계론적 부공간 규명법 적용 결과, 동일한 주파수 대역에서 매우 근접한 두 개의 모드가 발생하였고, 이는 타워 상부 하중의 위치에 의하여 타워가 편심을 받아 강축과 약축이 발생하는 것임을 확인하였다. 또한 장기간 해·조류로 인한 세굴이 발생했다는 가정 하에 타워가 진동 중 세굴면에 부착된 경우와 떨어져 있는 경우가 각각 발생하여 1개의 굽힘모드에서 2가지 모드가 발생하는 것으로 판단하였고, 이를 해석모델 개선에 적용하였다.
3) 수치해석모델 개선을 위한 초기 단계로 계측값에 의한 고유주파수와 상부질량, 가상고정점 깊이 1 및 깊이 2를 가정한 경우의 수치해석에 의한 고유주파수를 비교한 결과, RMSE 값이 0.5068%에 이르는 것을 확인하였으며, 이에 수치해석에 의한 고유주파수와 패턴서치 방법을 이용하여 변수를 추정한 결과 반복횟수에 따른 RMSE 값은 0에 수렴하였고, 최종적으로 구한 변수는 실제 조건으로 고려한 값과 오차 수준 0.001% 이내의 해를 가지는 것으로 보아, 부정확한 초기치를 반영한 모델이 개선됨을 확인하였다.
4) 최적화 과정에서의 유일해 문제를 검토하기 위하여 초기값을 임의로 고려하여 추정한 결과, 초기값을 다르게 고려하더라도 최종적으로 구한 값은 일치하는 것을 확인하였다. 또한, 초기값에 의한 고유주파수와 최종 추정된 값을 이용하여 계산한 고유주파수를 현장계측된 고유주파수와 비교한 결과, 최종 추정된 값을 적용하였을 때 고유주파수가 현장계측된 고유주파수와 매우 근접해짐을 확인하였다.
추후 만경타워에 대한 세굴깊이를 실제 잠수부에 의하여 측정함으로써 본 연구에서 추정한 세굴깊이와 비교하는 것이 필요하며, 또한 모델 개선 결과에 대한 타당성을 모델 개선에서 사용한 자료 외의 다른 값을 이용하여 검증하는 것이 필요할 것으로 사료된다. 그러나 이 연구를 통하여 개선한 해석 모델은 파랑 및 바람에 의한 구조안전성 검토, 지진해석 등에 있어 기존의 도면을 바탕으로 작성한 해석 모델보다는 신뢰성이 높을 것으로 판단된다.
감사의 글이 논문은 2020년도 한국해양과학기술원의 지원을 받아 수행된 연구임(특정연구현장 설치 시설 운영(PO01386), 해양에너지 및 항만·해양구조물 실용화 기술개발(PE99831)).
Fig. 13.Comparison of measurement results of natural frequency (* D: detached condition, A: attached condition). 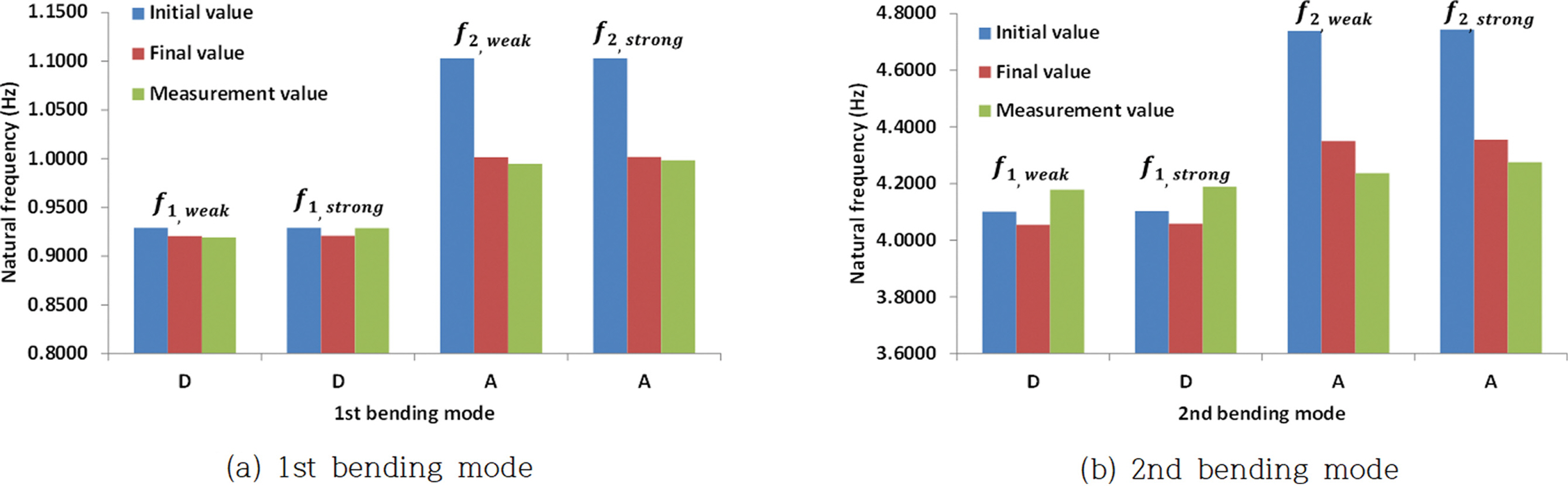
Table 1.Natural frequency derived by using SSI method Table 2.1st, 2nd natural frequency according to tide level Table 3.Convergence process and results estimated by pattern search Table 4.Comparing the results of the final estimate with different initial values ReferencesCho, J, Jeong, S (2009). Application of point of fixity and vertical spring for axial loaded piles, Proc. of KSCE 2009 Annual Convention, KSCE, 2833-2836 (in Korean).
Chun, B, Seo, D, Lee, Y (2006). A study on Prediction of the coefficient of horizontal subgrade reaction for pile using lateral pile loading test results, Journal of the Korean Geo-Environmental Society, 7, 15-24 (in Korean).
Hooke, R, Jeeves, TA (1961). “Direct Search” solution of numerical and statistical problems, Journal of the ACM (JACM), 8, 212-229.
Jeong, S, Kim, J (2013). Analysis of optimized column-pile length ratio for supplementing virtual fixed point design of bent pile structures, Journal of the Korean Society of Civil Engineers, 33, 1915-1933 (in Korean).
Jin, S (2017). Stochastic subspace identification: part 2. stochastic process and stochastic subspace identification, The Korean Society for Noise and Vibration Engineering, 27, 24-30 (in Korean).
Kim, B, Kim, C, Yi, J.-H (2019). Model updating for Gageocho Ocean Research Station structure using structural dynamic characteristics, Journal of Coastal Disaster Prevention, 6(3):103-110 (in Korean).
Kim, D, Lee, B, Kim, D, Yang, G (2001). Deformation characteristics of diaphragm wall induced by deep excavation(II) -numerical analysis-, Journal of the Korean Geotechnical society, 17, 107-115 (in Korean).
Kim, W, Yi, J.-H, Min, IK, Shim, J.-S (2017). Estimation of dynamic characteristics of Gageocho Ocean Research Station using long-term measurement data, Journal of Coastal Disaster Prevention, 4(SI):263-270 (in Korean).
Kim, W, Yi, J.-H, Min, IK, Shim, JS (2018). Monitoring of structural dynamic characteristics of Socheongcho Ocean Research Station, Journal of Coastal Research, SI, 85, 1191-1195.
Lewis, RM, Torczon, V, Trosset, MW (2000). Direct search methods: then and now, Journal of computational and Applied Mathematics, 124, 191-207.
Manoharan, S, Shanmuganathan, S (1999). A comparison of search mechanisms for structural optimization, Computers & Structures, 73, 363-372.
Park, B.-C, Oh, K.-H, Park, S.-B (2005). Integrity assessment of spread footing pier for scour using natural frequency, Journal of the Korean Society of Hazard Mitigation, 5(2):29-36 (in Korean).
Wetter, M, Wright, J (2003). Comparison of a generalized pattern search and a genetic algorithm optimization method, In Proc of the 8-th IBPSA Conference, 3, 1401-1408.
Yi, J.-H, Park, W.-S, Lee, S, Kim, J, Seo, C (2013). Evaluation of vibration characteristics of caisson-type breakwater using impact vibration tests and validation of numerical analysis model, Journal of Korean Society of Coastal and Ocean Engineers, 25, 1-10 (in Korean).
Yi, J.-H, Yun, C.-B (2003). A comparative study on modal parameter identification methods without input excitation information, Journal of the Korean Society of Civil Engineers, 23(2A):187-201 (in Korean).
Yi, J.-H, Kim, S.-B, Yoon, G.-L (2016). Reliability analysis of offshore wind turbines considering soil-pile interaction and scouring effect, Journal of Korean Society of Coastal and Ocean Engineers, 28(4):222-231 (in Korean).
Yi, J.-H, Kim, S.-B, Yoon, G.-L, Andersen, LV (2015). Natural frequency of bottom-fixed offshore wind turbines considering pile-soil-interaction with material uncertainties and scouring depth, Wind and Structures, 21(6):625-639.
Yi, J.-H, Min, I.-K, Shim, J.-S (2020). Analysis of structural dynamic characteristics of Ieodo Ocean Research Station using vibration measurement data, Journal of Coastal Disaster Prevention, 7(2):105-115 (in Korean).
Yun, C.-B, Yi, J.-H, Lee, J.-J, Lee, J.-S, Juhn, G.-H (2004). Modal based structural model modification using genetic algorithm, Computational Structural Engineering Institute of Korea, 17, 389-403 (in Korean).
|
|
|||||||||||||||||||||||||||||||||