요약우리나라 동해 남항진 해역에서 관측한 고파 파랑 스펙트럼 정보를 이용하여 수정 BM 스펙트럼과 JONSWAP 스펙트럼의 매개변수를 추정하였다. BM 스펙트럼의 매개변수 추정결과는 1.04, 0.27로 대푯값으로 제시된 1.098, 0.30과 유사하였으나 통계적으로는 유의미한 차이를 보였다. 한편 JONSWAP 스펙트럼의 경우에는 첨두증 대계수의 값이 통상적으로 적용되는 값인 3.3보다 매우 작은 1.4로 추정되었다. 두 스펙트럼의 적합 RMS 오차 차이는 0.2 정도로 미미한 수준이었으나, 두 스펙트럼 모두 첨두주파수보다 큰 주파수 영역에서의 에너지가 표준 스펙트럼 형태에 비해 상대적으로 완만하게 감소하는 양상을 보였다.
AbstractThe parameters of the modified BM and JONSWAP spectra are estimated using spectral data set off Namhangjin, located in the east coast of Korea, collected during high wave events. The parameters of the modified BM spectrum were estimated to be 1.04 and 0.27, which were similar to the conventional values of 1.098 and 0.30, but showed significant differences in statistical terms. On the other hand, the peak enhancement factor of JONSWAP spectrum was estimated to be 1.4, which was substantially small compared to the conventional value of 3.3. The RMSE differences from the fitted results of the two spectra were small, approximately 0.2. In the frequency range greater than the peak frequency, however, the spectral energy density showed relatively mild decrease with increase of the frequency, compared to the standard forms of the modified BM and JONSWAP spectra.
1. 서 론해상에서의 파랑은 시·공간적으로 불규칙하게 변하는 여러 성분파의 조합으로 이루어져 있으며, 이를 효과적으로 표현하는 통계적 방법이 파랑 스펙트럼이다. 파랑 스펙트럼을 통해 어떤 해역에 분포하는 각 성분파의 에너지량을 쉽게 파악할 수 있다. 지금까지 다양한 스펙트럼 형태가 제안되었으며, 그 중 PM 스펙트럼(Pierson and Moskowitz, 1964), BM 스펙트럼(Bretshneider, 1968; Mitsuyasu, 1970), JONSWAP 스펙트럼(Hasselmann et al., 1973), TMA 스펙트럼(Bouws et al., 1985)이 가장 대표적인 스펙트럼이다. 이 중 PM과 BM 스펙트럼은 충분히 발달한 파랑에 대한 스펙트럼이며, JONSWAP 스펙트럼은 취송거리(fetch)가 제한되어 충분히 발달하지 못한 파랑에 대한 스펙트럼이다. 한편, 수심 효과가 중요하게 다루어져야 하는 천해 지역에서는 유한 수심의 영향을 고려할 수 있는 TMA 스펙트럼의 사용이 권장되고 있다.
파랑이 완전히 성장하지 못한 경우 대부분의 에너지가 첨두주파수 근처에 몰려 있기 때문에 JONSWAP 스펙트럼은 PM 스펙트럼에 비해서 높은 첨두증대계수(γ) 값을 가지게 된다. JONSWAP 스펙트럼의 첨두증대계수의 표준값은 γ = 3.3 이며, PM 스펙트럼은 γ = 1에 해당한다. JONSWAP 스펙트럼이 북해 연안에서 관측된 파랑자료를 이용하여 제안되었기때문에 실제로 유럽 지역에서는 파랑이 완전히 성장한 경우가 아니라면 JONSWAP 스펙트럼에 γ = 3.3을 보편적으로 사용하고 있다. 그런데 우리나라에서는 JONSWAP 스펙트럼보다는 BM 스펙트럼을 사용하는 경우도 많다. 특히, 수리실험에서는 압도적으로 BM 스펙트럼을 사용한 경우가 많은데 (Jung and Yoon, 2019; Kim et al., 2019; Lee et al., 2016), 합리적인 근거가 있어서라기보다는 과거부터 관행적으로 적용해 왔던 방법이 그대로 이어져 온 것이라고 보여진다.
한편, 현장 관측자료 분석을 통해 첨두증대계수 값을 산정하기 위한 연구도 다양하게 이루어져 왔다. Ewans and Kibblewhite(1990)은 뉴질랜드 서해안에서의 파랑 관측자료를 분석하여 첨두증대계수의 평균값이 γ = 2.79라고 보고하였다. Lee et al.(1988)은 동해안의 후포 연안에서의 파랑자료를 분석하여 고파에 대하여 γ = 3.3 조건이 적절함을 제시하였다. 그리고 Suh et al.(2010)은 우리나라 주변 해역의 파랑 자료를 분석하여 γ = 2.14의 값을 얻었으며, 이 결과는 최근 국내에서 수행된 수리실험(Oh and Lee, 2010)에서 JONSWAP 스펙트럼에 γ = 2.0을 적용하는데 근거자료로 활용된 바 있다. Kang and Lee(2014)는 제주 북동부 연안에서 추계·동계에 관측된 파랑자료를 분석하여 JONSWAP 스펙트럼의 첨두증대계수의 평균값이 γ = 2.72임을 밝혔다. 이처럼 첨두증대계수의 값이 해역에 따라 조금씩 달라지게 되므로 우리나라 주변 해역에서의 첨두증대계수의 값을 보다 정확히 파악할 필요가 있다.
파랑 스펙트럼은 해역의 다양한 특성이 반영되어 발생하는 파랑으로 결정되는 정보이기 때문에 우리나라 해역의 스펙트럼 정보를 이용하여 기존에 사용되는 스펙트럼 형태 및 매개변수의 차이 등에 대한 검토가 필요하다. 일례로 Kweon et al.(2013)은 후포 연안의 파랑자료를 이용하여 스펙트럼 매개변수를 GEV 함수를 대상으로 추정, 제시한 바 있으며, Cho et al.(2015)은 마라도 파랑 자료를 이용하여 구간 파고에 대한 GEV 함수 형태의 스펙트럼에 대한 매개변수 변화 양상을 제시한 바 있다. 파랑 스펙트럼의 과거 매개변수 추정 연구는 스펙트럼 매개변수를 풍속, 취송시간 및 취송거리의 함수로 표현하는 방식으로 수행되어 왔으나, 최근에는 유의파고 및 첨두주기 정보를 포함하는 함수 형태에 대표 매개변수를 제시하는 유형이 일반적이다.
본 연구에서는 동해안의 남항진 해역(강원도 강릉시 강릉항에서 약 1.6 km 떨어진 해역, 수심 30.5 m)에서 초음파식 파고 파향계(AWAC: Acoustic Wave And Current meter)로 6년 동안 관측된 파랑 스펙트럼 정보를 이용하여 유럽과 일본에서 널리 사용되는 JONSWAP 스펙트럼 및 수정 BM 스펙트럼의 매개변수를 최적 추정하고 변동양상 및 차이를 분석하여 남항진 해역에 적합한 파랑 스펙트럼 매개변수 추정결과를 제시하였다.
2. 파랑자료 및 분석방법2.1 관측 파랑 스펙트럼본 논문에서 분석에 사용한 자료는 동해 남항진에서 관측된 파랑 스펙트럼이며, 파랑 관측은 초음파식 파고·파향계인 AWAC(Acoustic Wave And Current-meter, 600 kHz, Nortek, Norway) 장비를 사용하였으며, 설치 지점은 강원도 강릉시 남항진 해변에서 북동방향 약 1.6km 지점(37°46'33.5''N, 128°58'00.7''E)이며, 설치수심은 D.L. 기준 30.5 m 지점이다(Jeong et al., 2019). 본 연구에서는 2013년 1월부터 2018년 11월까지 약 6년 동안 관측된 파랑 자료 중에서 스펙트럼 추정값이 신뢰할만한 자료만을 선별하여 파고가 높은 순으로 상위 30개의 스펙트럼 자료를 분석에 이용하였다. 단, 선별된 자료의 관측 시각 사이는 최소한 하루 이상 서로 떨어져 있도록 하였다. Table 1에는 최종적으로 선별된 자료의 관측 시각 및 유의파고 값을 제시하였으며, 고파가 발생한 시기별 파고분포는 Fig. 1에 제시하였다.
남항진 파랑 스펙트럼 정보는 주파수에 따른 스펙트럼 수치로 구성되어 있으며, 주파수 범위는 0.02~0.99 Hz, 주파수 간격(df)은 0.01 Hz로 총 98개의 수치 자료이다. 파랑 자료를 이용한 스펙트럼 추정은 제작회사에서 제공하는 파랑분석 전용소프트웨어인 Storm64 프로그램을 이용하였으며, 스펙트럼 추정방법은 표준 FFT 분석기법(Window Span=64, default)에 기반을 두고 있다. 대표 파랑 매개변수에 해당하는 유의파고(Hm0)는 다음 식(1)을 이용하여 계산하고, 첨두주기(Tp= 1/fp)는 파랑 스펙트럼이 최대가 되는 주파수(fp)의 역수에 해당한다.
여기서, S(fk)는 파랑 스펙트럼이며, 하한절단주파수는 f1 = 0.02 Hz, 상한절단주파수 f98 = 0.99Hz이다.
고파로 선별된 30개 파고에 대한 파랑 스펙트럼을 모두 중첩하여 Fig. 2에 제시하였다. 그림에서 볼 수 있는 바와 같이 스펙트럼 형태는 첨두주기 영역의 위치에 따라 형태가 어느 정도 달라 보이지만, 전반적으로는 하나의 첨두를 가진 유사한 스펙트럼 형태를 보이고 있음을 알 수 있다.
2.2 스펙트럼 매개변수 추정방법매개변수 추정을 위한 대상 스펙트럼은 수정 BM 스펙트럼과 JONSWAP 스펙트럼이다. 매개변수 추정 관점에서는 두 스펙트럼 모두 함수 형태로 표현 가능하며, 식(2) 및 (3)에 각각의 식을 제시하였다. 스펙트럼 매개변수로 Hm0, Tp 대신 H1/3, T1/3를 사용하는 경우도 있는데, Hm0와 H1/3 및 Tp와 T1/3 간에 선형관계가 있으므로, 식(2)를 H1/3과 T1/3로 나타내더라도 스펙트럼의 계수는 달라지지만 함수 형태는 그대로 유지된다. 수정 BM 스펙트럼(식(2))에 비해서 JONSWAP 스펙트럼 모형(식(3))의 경우, 함수 형태 측면에서는 첨두 증대계수(γ, peak enhancement factor)를 도입하고 있는 점이 차이가 있다.
2.2.1 수정 BM 스펙트럼 매개변수 추정방법
Mitsuyasu(1970)에 의해 제안된 초기 BM 스펙트럼은 식(4)와 같으며, Tp≅1.05T1/3 조건을 적용하였다. 이 조건은 CERC(1984)에서 제안된 것이며 Ts = T1/3 = 0.95 Tp, 즉 Tp≅1.053T1/3 조건에 해당한다.
이후 Goda(1988)는 관측 자료를 이용한 추가분석을 통해 Tp≅1.1T1/3 조건을 적용하여 초기 BM 스펙트럼의 계수를 조정한 수정 BM 스펙트럼을 식(5)와 같이 제안하였다.
한편, 관측 스펙트럼 자료로부터의 매개변수 추정을 위해서는 H1/3 = Hs = Hm0 및 Tp= 1.1T1/3 조건을 적용하여 기존의 수정 BM 스펙트럼을 다음과 같이 식(6)으로 표현할 수 있다.
수정 BM 스펙트럼은 스펙트럼에서 추정되는 파고(Hm0)를 제외하는 경우, 식(2)에서 α, β, Tp가 추정 매개변수가 된다. 만일 첨두주기를 관측 스펙트럼에서 우선 추정하는 경우, 최적 추정 매개변수는 α, β의 2개로 한정된다. 첨두주기를 추정 매개변수로 포함하는 경우, 관측 스펙트럼으로부터 얻어진 첨두주기를 초기 추정값(initial guess)으로 가정하고, 상한 및 하한 주파수를 fp ± 0.1fp(fp= 1/Tp) 범위로 설정하여 3개의 매개변수를 최소자승법(least squares method)으로 추정하였다. 한편, 첨두주기를 추정 매개변수로 포함하지 않는 경우, 나머지 2개의 매개변수를 역시 최소자승법으로 추정하였다. 식(7)에는 최소자승법 추정을 위한 목적함수(L)을 나타내었다.
여기서, So(f)와 Se(f)는 각각 관측 스펙트럼과 추정 스펙트럼을 의미한다.
2.2.2 JONSWAP 스펙트럼 매개변수 추정방법JONSWAP 스펙트럼의 첨두증대계수(γ, peak enhancement factor)는 1.0~7.0 정도의 범위이나 평균 3.3의 값이 일반적으로 사용되고 있다. 수정 BM 스펙트럼 매개변수 추정에서 고려한 3개의 매개변수(α, β, Tp)에 γ, σa, σb까지 포함하면 추정 가능한 매개변수의 수는 총 6개가 된다. 그러나 본 연구에서는 첨두증대계수를 추정하는 것이 주된 관심사이므로 γ만을 추정 매개변수로 설정하여 분석을 진행하였다. 이 경우 추정 매개변수가 하나이기 때문에, 추정 매개변수의 값을 1.0에서 7.0 사이의 값에서 일정한 간격(0.01)으로 변화시키면서 RMS 오차를 계산하고, RMS 오차가 최소가 되는 조건에 해당하는 첨두증대계수 값을 구하였다.
3. 매개변수 추정 결과수정 BM 스펙트럼 및 JONSWAP 스펙트럼 매개변수 추정결과를 각각 구분하여 제시하였다. BM 스펙트럼의 경우 첨두주기를 매개변수에 포함한 경우와 포함하지 않은 경우의 추정 결과를 비교하여 제시하였다. 한편 JONSWAP 스펙트럼의 경우 평균 계수 3.3 조건과 본 연구에서 추정한 최적 매개변수와의 비교를 수행하였으며, RMS 오차도 비교·분석하였다.
3.1 수정 BM 스펙트럼 매개변수 추정 결과수정 BM 스펙트럼 형태의 함수에 대한 최적 매개변수 추정 결과는 Table 2에 제시하였다. Table 2에서 볼 수 있는 바와 같이, Tp를 각각의 관측자료에서 추정한 값으로 고정한 경우, α와 β의 추정값 평균은 각각 1.079, 0.284이며, 첨두주기는 평균 0.095이다. 한편, 3개의 매개변수를 추정한 경우, 첨두주기의 평균값은 0.096으로 2개의 변수만 추정한 경우와 큰 차이가 없으나 0.075~0.117 범위에서 다양한 값으로 추정되었다. 또한 α와 β의 평균은 각각 1.041, 0.273으로 추정되었다. 이 값은 식(5)에 제시된 표준형의 수정 BM 스펙트럼의 파라메터인 1.098, 0.300보다는 각각 5%, 9% 작은 값이다. 그러나 이 수치는 Table 1에 보인 것처럼 유의파고 3.6 m 이상의 고파만을 대상으로 얻은 결과이기 때문에 분석 대상 스펙트럼의 범위를 확장하여 유의파고가 더 낮은 파랑조건에서의 결과에 대해서는 추가적인 검토가 필요하다.
한편 추정 매개변수는 자료의 30개로 한정되어 있으나, Anderson-Darling 기법(R ‘nortest’package; Juergen and Uwe, 2015)을 이용하여 정규분포 검정을 수행한 결과, 첨두주기를 고정하고 2개의 매개변수만을 추정한 경우의 α 매개변수를 제외하고는 모두 “정규분포를 따른다”는 가설이 기각되었다. 전체적으로 추정 매개변수는 정규분포를 따르지 않는 것으로 판단된다. 한편 추정 매개변수의 Pearson 상관분석(Lee, 2019)을 수행한 결과, 매개변수 α, β 상관계수는 추정 매개변수와 2개인 경우, 3개인 경우 각각 0.898, 0.520 정도로 모두 상관이 있는 것으로 파악되었다. 추정 상관계수의 95% 신뢰구간은 각각 [0.96, 0.951], [0.197, 0.742]로 추정되었다. 추정 매개변수(α, β)와 첨두주기의 상관계수는 95% 신뢰수준에서 대략 0.3 이하로 매우 작은 것으로 파악되었다. 반면 추정 매개변수(α, β)와 파고의 상관관계는 추정 매개변수가 2개인 경우에는 거의 없는 것으로 파악되었으나, 첨두주기 변동 조건에서는 음(-)의 상관관계가 보이는 것으로 파악되었다. 이러한 상관관계 유무는 현재 제한된 자료 개수(= 30) 조건에서 수행하였기 때문에 다양한 조건에서 보다 많은 자료를 이용하여 심층 분석할 필요가 있을 것으로 판단된다.
한편, 수정 BM 스펙트럼에 대한 추정값의 평균제곱근오차(RMSE)를 다음 식(8)과 같이 계산하였다.
여기서,
그런데 일반적인 RMS 오차 계산은 모든 주파수 영역의 스펙트럼을 사용하기 때문에 작은 에너지 영역의 스펙트럼도 계산에 포함되기 때문에 RMS 오차를 저감하는 역할을 한다. 따라서 본 연구에서는 실질적으로 유의미한 수준의 에너지를 스펙트럼 첨두값의 1% 이상으로 가정하고, 이 범위 내의 스펙트럼 에너지만을 이용하여 아래 식(9)와 같이 수정 RMS 오차를 추가로 계산하였다.
여기서, k = k1, k2, …, km(≤ n)는 위에서 언급된 기준 S(f)≥max[S(fk)]/100을 만족하는 자료를 표시하는 인자이다. 수정 RMS 오차는 매개변수가 2개인 경우와 3개인 경우 모두 평균 1.73 m2/s, 최대 3.83 m2/s, 최소 0.69 m2/s 정도로 모든 주파수 영역의 스펙트럼 정보를 사용하는 경우에 대하여 계산된 RMS 오차에 비해서 대체로 2배 정도 크게 추정되었다. 이 경우에도 매개변수 개수가 2개인 경우와 3개인 경우의 조건에 따른 변화는 미미하였다.
Fig. 3은 수정 BM 스펙트럼을 이용하여 추정된 매개변수를 적용한 결과를 관측 스펙트럼과 비교한 결과이다. 전체 30개 자료 중에서 6개의 특성 자료(Target wave no. 1 =(Hm0)max case, 2 = βmin and fmin case, 4=fmax case, 12=αmin case, 29 = βmax case, 3 0= αmax and (Hm0)min case)에 대한 결과만을 나타내었다. 그림에서 볼 수 있듯이 첨두주파수 주변에서의 스펙트럼 에너지를 과소평가하는 경향이 나타나며 첨두에너지의 재현성이 미흡하였다. 또한, 관측 스펙트럼에서는 첨두주파수보다 고주파수 영역에서의 스펙트럼 에너지가 급격하게 감소하는데 수정 BM 스펙트럼은 이러한 경향을 반영하지 못하여 이 영역에서의 에너지를 관측 스펙트럼보다 과대평가하였다. 이처럼 첨두 주변에서의 에너지는 과소하게, 그보다 고주파수 영역에서의 에너지는 과대하게 평가하는 것은 수정 BM 스펙트럼의 한계인 것으로 판단된다.
3.2 JONSWAP 스펙트럼 매개변수 추정 결과JONSWAP 스펙트럼의 첨두증대계수에 대한 추정 결과 첨두증대계수의 평균은 일반적으로 제시되는 γ = 3.3에 비해서 크게 작은 평균 γ = 1.41로 계산되었으며, Fig. 4에 보인 것처럼 최소값 1.0에서 최대값 1.8 사이의 매우 좁은 범위에 분포하는 것으로 나타났다. 이처럼 첨두증대계수의 값이 JONSWAP 스펙트럼의 표준값인 γ = 3.3보다는 오히려 PM 스펙트럼에 해당하는 값인 γ = 1.0에 가깝게 제시되었다는 점은 동해안의 남항진에서 관측되는 파랑 스펙트럼이 비교적 잘 발달한 파랑의 성격을 가진다는 점을 시사한다.
Fig. 5는 JONSWAP 스펙트럼의 적합 결과를 대표적인 조건(Target wave no. 1 = (Hm0)max case, 26 = γmax(= 1.8) case, 7 = γmin(= 1.0) case, 10 = γmean(= 1.4) case)을 추출하여 제시한 그림이다. 모든 파고 스펙트럼에 대한 RMS 오차는 평균 0.94, 최대값 3.35, 최소값 0.42로 나타났다. 첨두 스펙트럼 에너지의 1% 이상의 에너지를 가지는 스펙트럼 영역의 자료만을 대상으로 계산할 경우의 수정 RMS 오차는 평균 1.93, 최대값 8.28, 최소값 0.81로 나타나서, 전체 스펙트럼을 사용하는 경우보다 대체로 2배 정도 크게 나타났다.
최적 추정된 JONSWAP 스펙트럼의 매개변수 조건에서는 첨두가 관측 자료에 적절하게 적합되어 있는 것으로 판단되지만, 고주파수 영역에서의 완만한 감소에 의한 차이가 뚜렷하다. 이는 BM 스펙트럼 적합 비교 그림에서도 명확하게 볼 수 있으며, 매개변수를 이용한 추정 스펙트럼의 첨두에너지 과소평가 및 첨두주파수를 벗어나는 영역, 특히 고주파수 영역(작은 주기 영역)에서의 완만한 감소에 대한 함수 형태의 수정·보완이 필요할 것으로 사료된다.
4. 결론 및 제언남항진에서 관측한 고파의 스펙트럼을 대상으로 수정 BM 스펙트럼과 JONSWAP 스펙트럼의 매개변수를 추정하고, 적합 수준을 평가하는 오차분석을 수행한 결과, 다음과 같은 결론을 도출하였다.
- 수정 BM 스펙트럼의 경우 매개변수 α, β는 표준값에 비해서 각각 5%와 9% 작게 추정되었다. 관측 스펙트럼과의 적합성(fitting)을 비교한 결과 첨두값은 과소추정하였고, 고주파수 영역에서는 관측 스펙트럼에 비해 에너지가 완만하게 감소하는 경향이 나타나 대체로 에너지를 과대추정하였다. 이러한 특성은 BM 스펙트럼이 가지는 한계인 것으로 판단된다.
- JONSWAP 스펙트럼의 첨두증대계수 추정결과, 표준값으로 제시되는 γ = 3.3에 비해 훨씬 작은 γ = 1.4로 나타났다. BM 스펙트럼에 비해 첨두에너지는 더 잘 부합되지만 고주파수 영역에서의 적합도는 여전히 차이를 보였으며, 이는 σa, b를 포함하는 매개변수 추정을 통해 개선이 가능할 것으로 판단된다.
- 본 연구와 선행연구들(Suh et al., 2010, Kang and Lee, 2014)의 결과를 종합해 보면 우리나라 해역에서 관측되는 파랑 스펙트럼은 BM 스펙트럼과 JONSWAP 스펙트럼의 중간 정도의 형태를 나타내는 것으로 보인다. 그러나 γ의 추정값에 상당한 편차가 존재하므로 향후 계절적 요소, 특히 태풍시와 비 태풍 시의 자료를 구분하지 않고 스펙트럼 파라미터를 추정하였는데 이를 구분하여 분석을 수행한다면 더욱 의미있는 결과를 얻을 수 있을 것으로 기대된다.
한편, 본 연구에서는 BM 스펙트럼과 JONSWAP 스펙트럼에 대해서만 분석을 수행하였는데 중간 수심역 또는 천해역에 대해서는 TMA 스펙트럼(Bouws et al., 1985)이 제안된 바 있으므로 우리나라 연안에서 관측된 파랑 자료에 대해서는 향후 TMA 스펙트럼을 이용한 매개변수 추정이 이루어질 필요가 있다. 또한, 남항진 해역 뿐 아니라 우리나라 여러 해역에서 다양한 파랑 스펙트럼 자료를 수집하여 지역별, 계절별 영향을 고려하여 최적 매개변수를 추정하는 연구가 지속적으로 수행될 필요가 있다.
Fig. 1.
Hm0 of the selected 30 wave spectra in terms of the observation time. The numbers indicate the ranking listed in Table 1. 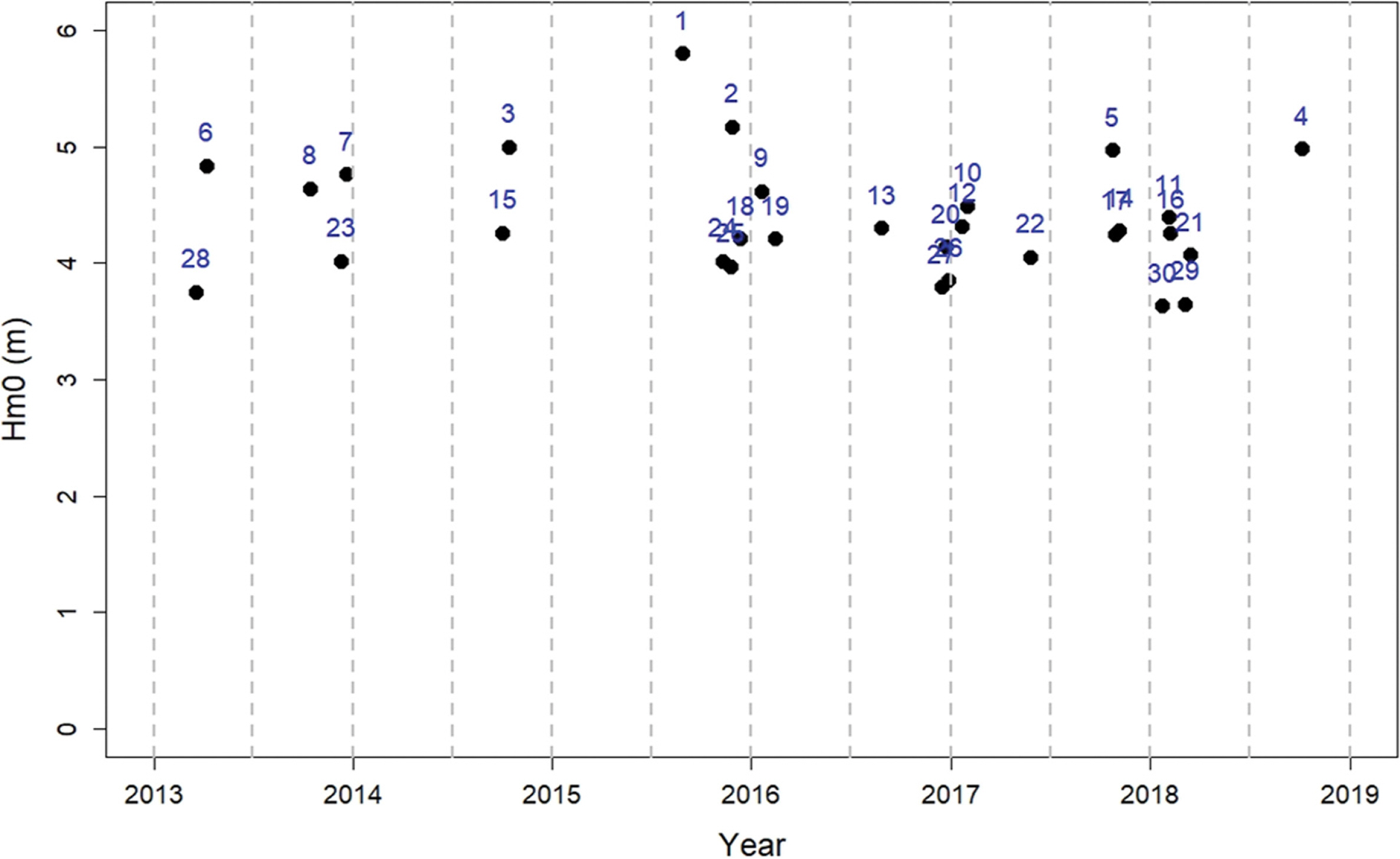
Fig. 5.Comparison of JONSWAP spectrum fitting between observed data, estimated spectra with optimized γ and estimated spectra with γ = 3.3. 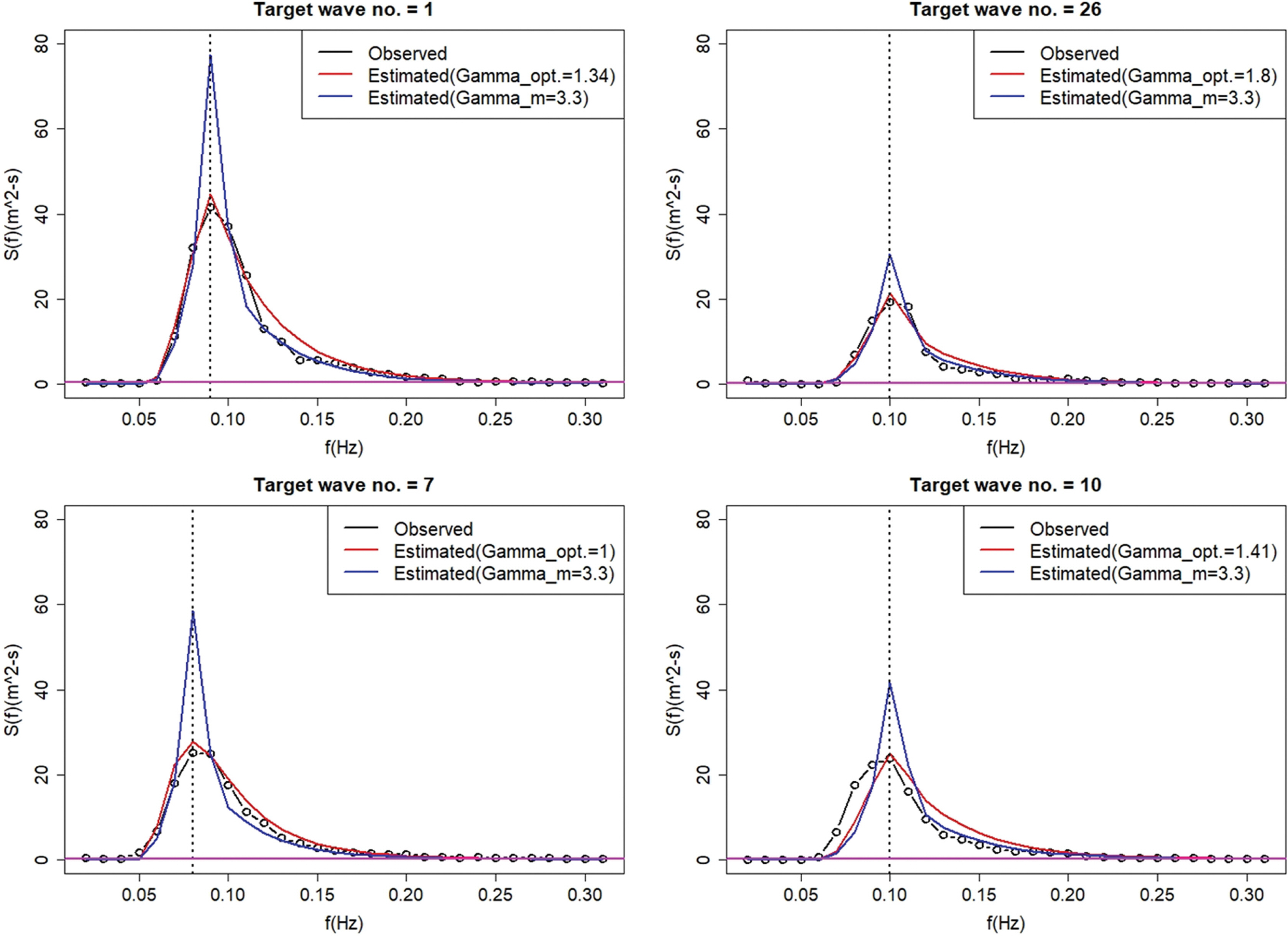
Table 1.List of top 30 wave heights (Hm0) with corresponding observation time of the spectra used in the analysis, which is ranked by Hm0
Table 2.Estimated optimal parameters of the modified BM spectrum type ReferencesBouws, E, Gunther, H, Rosenthal, W, Vincent, CL. (1985). Similarity of the wind wave spectrum in finite depth water, Journal of Geophysical Research, 90, 975-986.
Bretschneider, CL. (1968). Significant waves and wave spectrum, Ocean Industry, 40-46.
CERC. (1984). Shore Protection Manual. Coastal Engineering Research Center, US Army Corps of Engineers.
Cho, HY, Kwon, HM, Jeong, WM, Kim, SI. (2015). A study on the optimal equation of the continuous wave spectrum, Int J Nav Archit Ocean Eng, 7, 1,056-1,063 http://dx.doi.org/10.1515/ijnaoe-2015-0074.
Ewans, KC, Kibblewhite, AC. (1990). An examination of fetch-limited wave growth off the west coast of New Zealand by a comparison with the JONSWAP results, Journal of Physical Oceanography, 20(9):1,278-1,296.
Goda, Y. (1988). Statistical variability of sea state parameters as a function of wave spectrum, Coastal Engineering in Japan, 31(1):39-52.
Hasselmann, K, Barnett, TP, Bouws, E, Carlson, H, Carwright, DE, Enke, K, Ewing, JA, Gienapp, H, Hasselmann, DE, Kruseman, P, Meerburg, A, Muller, P, Olbers, DJ, Richter, K, Sell, W, Walden, H. (1973). Measurements of wind- wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP), Deutsches Hydrographisches Zeitschrift, 8(12):1-95.
Jeong, WM, Oh, SH, Cho, HY, Baek, WD. (2019). Characteristics of waves continuously observed over six years as offshore central east coast of Korea, J of KSCOE, 31(2):88-99 (in Korean).
Juergen, G, Uwe, L. (2015). nortest: Tests for Normality. R package version 1.0-4, https://CRAN.R-project.org/package=nortest.
Jung, JS, Yoon, JS. (2019). Experimental study for overtopping discharges of sea dike having Low Mound and High Wave Wall (LMHW), Journal of Korean Society of Coastal and Ocean Engineers, 31(6):335-343 (in Korean).
Kang, D.-H, Lee, B.-G. (2014). Evaluation of wave characteristics and JONSWAP spectrum model in the northeastern Jeju island on fall and winter, Journal of the Korean Society for Marine Environment and Energy, 17(2):63-69 (in Korean).
Kim, YT, Lee, JI. (2019). Hydraulic Experiments on Reflection Coefficients for Perforated Wall Caisson with Rock Fill, Journal of Korean Society of Coastal and Ocean Engineers, 31(6):403-408 (in Korean).
Kwon, HM, Cho, HY, Jeong, WM. (2013). Wave analysis and spectrum estimation for the optimal design of the wave energy converter in the Hupo coastal sea, J of KSCOE, 25(3):147-153 (in Korean).
Lee, DS, Ahn, HD, Chae, JW, Lee, KS. (1988). Characteristics of the wave energy distribution in Hupo coastal seas, Ocean Research, 10(2):43-49 (in Korean).
Lee, DS, Oh, S.-H, Cho, BS. (2016). Experimental investigation on the change of stability coefficient of Tetrapod according to difference in density, Journal of Korean Society of Coastal and Ocean Engineers, 28(3):124-131 (in Korean).
Lee, GS. (2019). Confidence interval estimation and significance test on correlation coefficient, KIDS Report, 1(2):5-10 (in Korean).
Mitsuyasu, H. (1970). On the growth of wind-generated waves (2) - spectral shape of wind waves at finite fetch, Proc. 17th Japanese Conf Coastal Eng, 1-7 (in Japanese).
Oh, SH, Lee, J. (2020). Experimental comparison of the wave force on crown wall of sloping breakwater armored with tetrapods under obliquely incident waves, Journal of Korean Society of Coastal and Ocean Engineers, 32(3):161-169 (in Korean).
|
|
||||||||||||||||||||||||||||||||||