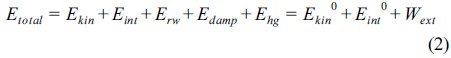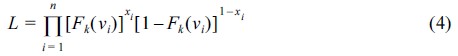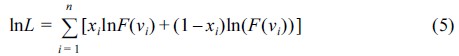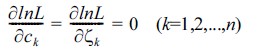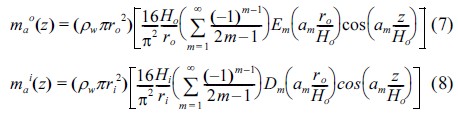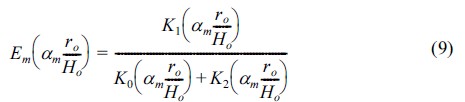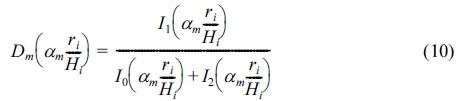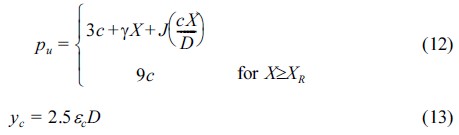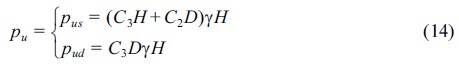1. 서론
해상풍력발전기는 구조물 자체가 매우 크고 해저지반에 설치되는 해상구조물로서 육상에 설치되는 풍력발전기의 외부하중과 함께 다양한 해양환경하중이 발생한다. 따라서 육상의 풍력발전기보다 상대적으로 설치 및 운영에 많은 비용이 소모되고 문제점이 발생한다. 또한 기술발전으로 해상풍력발전기의 발전용량이 증가하면서 전체 해상풍력발전기의 크기도 증가하고 있다. 해상풍력발전기의 안정성을 확보하기 위해 여러 가지 외부하중에 대한 평가방법을 설계기준으로 명시하여 해상풍력발전기의 설계에 반영하고 있지만 충돌하중에 대해서는 DNV-OS-J101, GL, IEC 61400-3과 같은 설계 기준에서 간략하게 언급되어 있다(Ren and Ou, 2009). 선박충돌은 매우 짧은 시간에 발생하는 사건으로 큰 질량을 가진 선박이 구조물과 직접적으로 부딪쳐 구조물에 하중으로 작용하기 때문에 충돌하중이 고려되지 않으면 선박충돌로 인한 해상풍력발전기의 기능적 손상 및 부분적 파손이 발생할 수 있다.
해상풍력발전기의 선박충돌에 대해 Florian(2005)는 3가지 형식의 지지구조물(모노파일형식, 트라이포드형식, 재킷형식)이 지지하는 해상풍력발전기에 탱크선과 컨테이너선, 화물선의 선박충돌해석을 수행하여 해상풍력발전기의 충돌거동을 확인하였고, Ren and Ou(2009)는 모노파일타입의 지지구조물을 갖는 해상풍력발전기에서 발생하는 충돌에너지를 최소화하기 위해 충돌방호공을 설치하여 충돌방호공의 설치 유무에 따른 충돌에너지를 비교하였다. Park et al.(2011)은 5MW급 해상풍력터빈을 나셀, 타워, 바닥판, 기초구조물로 나누어 모든 재료가 탄소성 거동을 보인다고 가정하여 충돌해석을 수행하였다. Dai et al.(2013)은 해상풍력발전기의 충돌위험과 충돌에 영향을 미치는 요인을 확인하여 선박충돌에 대한 위험도 평가방법을 제안하였다. 본 논문에서는 Ansys/Ls-dyna 구조해석 프로그램를 이용하여 충돌해석 시 API RP 2A(2000)에서 제시한 p-y곡선으로 해저지반의 비선형성을 고려하였고 충돌시 발생하는 충돌에너지를 확인하였다. 그리고 해상풍력발전기의 안정성을 평가하기 위해 선박과 해상풍력발전기가 충돌하는 위치의 응력을 확인하여 충돌속도에 대한 충돌취약도를 계산함으로서 해상풍력발전기 인근 해역을 통항하는 선박의 충돌속도를 제시하였다.
2. 연구 이론
2.1 해상풍력발전기-선박의 충돌해석
IEC 16400-3(2009)에서는 해상풍력발전기에 작용하는 충돌하중을 에너지 보존 법칙으로 계산하여 제시하였다. 선박에 의해 충돌하는 총 에너지는(E)는 식 (1)과 같다.
여기서, E는 총 에너지(J), a는 부가질량계수 (측면충돌에 대해서 1.4, 선수부 충돌에 대해서는 1.1로 가정), m은 선박의 질량(kg), vvessel는 선박의 충돌속도(m/s)이다. 하지만 본 연구에서는 Ansys/Ls-dyna 구조해석 프로그램을 사용하여 충돌선박을 모델링했기 때문에 해석 프로그램에서 계산하는 선박과 해상풍력발전기의 총 에너지는 식 (2)로 계산한다(LS-DYNA Support).
여기서, Etotal은 총 에너지, Ekin은 운동에너지, Eint은 내부에너지, Erw는 강체에 작용하는 에너지, Edamp는 감쇠에너지, Ehg는 격자의 변형에너지이다. 또한, Ekin0는 초기의 운동에너지, Eint0는 초기의 내부에너지, Wexternal은 외부에서 작용한 일이다.
2.2 충돌취약도
충돌취약도는 해상풍력발전기의 손상이 발생할 확률을 충돌속도로 나타낸 도표로서 선박충돌에 의한 해상풍력발전기의 손상수준을 의미하며 충돌취약도를 계산하기 위해 손상발생 유무를 통계자료나 구조해석을 통해 계산한다. Shinozuka et al.(2001)은 식 (3)과 같이 대수정규분포함수의 누적확률분포의 형태로 취약도 곡선을 표현하였다.
여기서, Φ(•)는 표준정규분포의 누적확률분포이며 v는 선박의 충돌속도, ck와 ζk는 각각 손상상태 k를 나타내는 충돌취약도(Fk)에 대한 누적확률분포의 중간값과 대수표준편차이다. ck와 ζk를 산정하기 위해 최우도 추정기법을 이용하였으며 식(4)와 같이 우도함수를 정의하여 i번째 자료에 대해 적용시킨다.
식(4)에서 xi는 타워 및 지지구조물의 재료인 강재의 항복응력을 기준으로 항복응력을 초과한 손상이 발생하면 1, 손상이 없으면 0을 입력하여 충돌해석단계에서 손상과 무손상의 확률을 누적시킨다. 우도함수인 식(4)를 대수함수로 표현한 최우도함수는 다음과 같이 식 (5)로 나타낸다.
식(3)의 중간값과 대수표준편차는 다음의 조건을 만족하는 최우도함수를 최대화하는 최적화 문제로 풀 수 있다.
3. 수치해석
3.1 해상풍력발전기
충돌과 같이 짧은 시간에 발생하는 문제를 해석하기 위해 본 논문에서는 explicit method를 사용하는 Ansys/Ls-dyna 구조해석 프로그램으로 충돌해석을 수행하였다. 블레이드, 로터 허브, 너셀, 타워, 모노파일 지지구조물은 163번 shell요소를 사용하여 모델링 했으며, 기초구조물 및 해저지반 스프링 모델은 161번 beam요소와 165번 link 요소를 사용하였다. 해상풍력발전기 모델은 2311개의 절점과 2496개의 요소로 모델링 되었다.
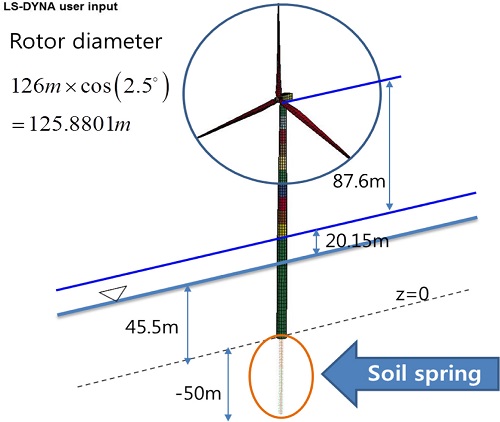
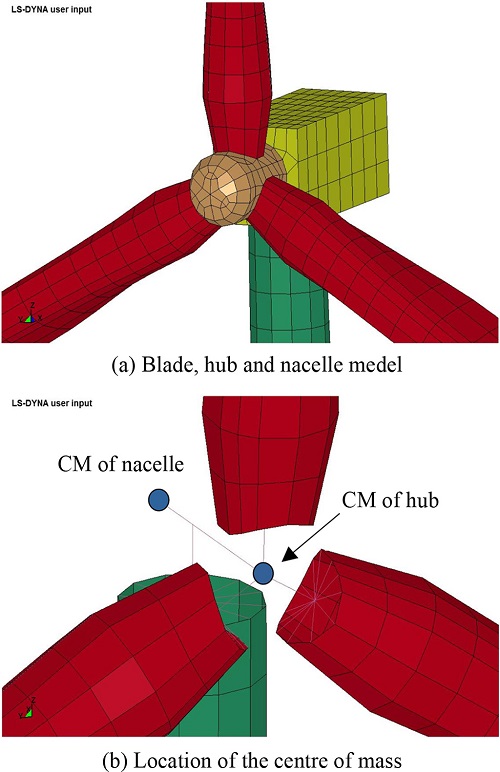
5MW 해상풍력발전기는 NREL(National Renewable Energy Laboratory)에서 제시한 참고용 모델로 수심이 45.5m이고 해저면에서 50m까지 관입된 모노파일 형식의 기초구조물에 지지되어 있다고 가정하였다. Fig. 1은 NREL 해상풍력발전기을 모델링한 그림으로 Fig. 2~3과 같이 3개의 블레이드와 허브, 너셀, 타워, 모노파일형식의 지지구조물로 구성되어 있다. 블레이드 1개의 길이는 63m이고 2.5o 기울어져 있다. 허브의 중심은 타워의 하단에서 90.0m 떨어진 최상부에 연결되어 있으며 너셀은 허브 중심에서 5m만큼 떨어진 위치에 각각 부가질량요소를 적용하여 모델링하였다. 허브와 너셀 및 블레이드는 선박충돌 발생 시, 타워의 거동에 의해 모사될 수 있도록 rigid 요소를 이용하여 연결시켰다. 해상풍력발전기의 너셀에 연결된 타워는 타워상부부터 지지구조물에 연결되는 타워하부까지 3.87m에서 6.0m의 직경으로 되어 있으며 10개 구간으로 나누어 각 구간별로 변단면을 고려해서 모델링하였다(Jonkman et al., 2009). 또한, 지지구조물은 6m의 직경을 갖는 모노파일형식으로 모델링하였다.
허브와 너셀의 질량은 부가질량요소로 표현하였으며 블레이드의 질량을 포함한 특성정보는 Table 1에 나타내었다.
타워를 지지해 주는 역할을 하는 지지구조물은 높이가 65.65 m, 외부 직경이 6 m, 두께가 0.0351 m인 원통형 실린더 타워이다. 본 연구에서 가정한 설계수심은 45.50m이고 평균해수면 위로 20.15 m인 위치에 TP(Transition piece)가 설치되어 있다고 가정하였다.
3.2 해수의 부가질량
해상풍력발전기는 해상에 설치되는 구조물로서 해수의 영향을 고려해야 한다. 본 연구에서는 간단하게 해상풍력발전기의 해수면 아래로 작용하는 수압을 등가의 부가질량으로 고려하는 부가질량법을 사용하였다. 부가질량법은 구조물이 강체이고 해수는 점성효과를 고려하지 않은 비압축성 유체라는 가정을 기초로 한다. Goyal and Chopra(1989)은 원통형 실린더 타워에 작용하는 해수의 부가질량을 식 (7), (8)로 표현하여 해수에 둘러싸인 타워에 작용하는 부가질량과 타워 내부에 작용하는 부가질량의 계산방법을 제안하였다.
여기서, mao와 mai는 지지구조물의 외부와 내부에 작용하는 해수의 부가질량이고 z는 해저면에서부터 평균해수면까지 지지구조물의 거리, ρw는 해수의 단위중량, ro와 ri는 지지구조물의 외부 및 내부직경, Ho와 Hi는 지지구조물의 외부 및 내부의 높이, am은 (2m−1)π/2이다. 또한, Em(amro/Ho)와 Dm(amri/Hi)는 식 (9)과 식 (10)을 이용하여 계산한다.
여기서, Kn는 계수가 n인 제2종의 수정된 베셀함수이고, In는 계수가 n인 제1종의 수정된 베셀함수이다.
식 (7)~(10)을 이용하여 계산한 모노파일형식의 지지구조물에 작용하는 해수의 부가질량은 Fig. 3에 나타내었다.
3.3 지반-기초구조물 모델
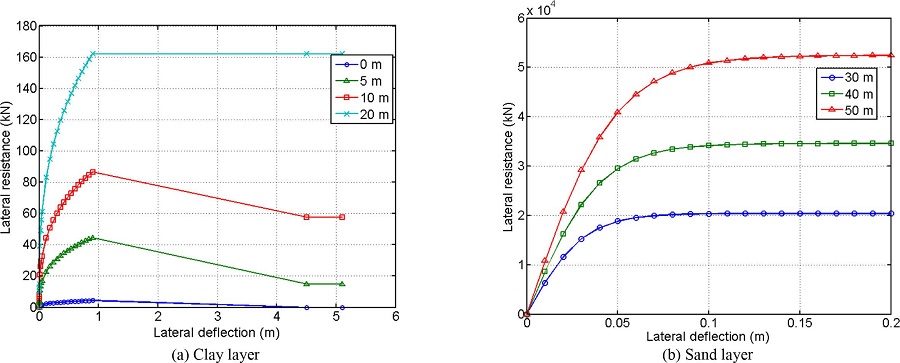
지반의 비선형 거동 특성을 고려하기 위해 API RP2A(2000)에서는 유효단위중량, 지반반력계수, 파일의 직경, 극한저항력 등을 이용하여 p−y곡선을 계산하도록 명시하였다. 이에 따라 제시된 점성토의 p−y곡선의 관계는 식 (11)과 같다.
여기서, p는 지반에 작용하는 하중, Pu는 극한지지력, y는 수평처짐, yc는 임계변위에 대한 매개변수이다. 식 (11)의 하중(p)를 구하기 위해 극한지지력(pu)과 임계변위에 대한 매개변수(yc)는 극한지지력(pu)과 임계변위에 대한 매개변수(yc)는 다음의 식 (12)와 식 (13)으로 계산한다.
여기서, X는 지표면에서의 깊이, c는 비배수 전단강도, D는 파일의 직경, γ는 유효단위중량, J는 경험상수, XR은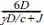 
로 계산되는 지표면 아래의 임계깊이, εc는 실험에 의해 결정되는 상수로 샘플의 비배수압축시험으로 구한 최대응력의 절반에서의 변형률을 의미한다.
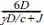로 계산되는 지표면 아래의 임계깊이, εc는 실험에 의해 결정되는 상수로 샘플의 비배수압축시험으로 구한 최대응력의 절반에서의 변형률을 의미한다.사질토에 대한 p−y곡선의 관계는 식 (14)와 같다.
여기서, A는 반복하중과 정적하중에 대한 계수, H는 말뚝의 관입깊이, k는 초기지반반력계수이다. 사질토에서 작용하는 극한지지력(pu)는 식 (14)로 계산할 수 있다.
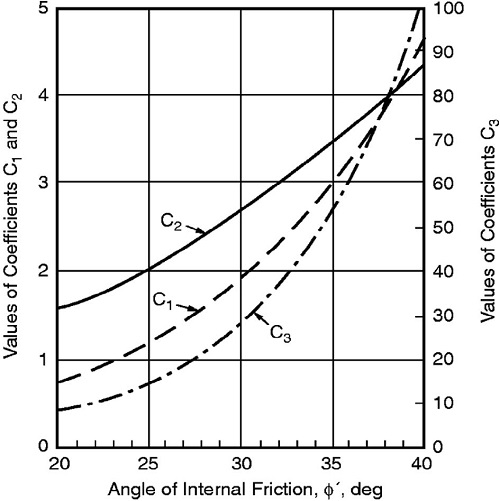
여기서, pus는 얕은 기초일 때의 극한지지력, pud는 깊은 기초일 때의 극한지지력이다. 내부마찰각의 함수로 표현된 계수인 C1, C2, C3는 Fig. 4로 추정할 수 있으며, 초기지반반력계수는 Fig. 5의 상대밀도에 따른 지반반력계수로 추정할 수 있다.
3.5 해석모델의 물성치
충돌해석에서 사용한 재료 물성치는 강재의 물성치 값인 탄성계수 2.1×1010Pa, 프와송 비는 0.3, 단위중량 8500 kg/m3을 사용하였다. 블레이드는 복합재료 물성치가 사용되어지지만 본 논문의 목적은 선박충돌에 의한 해상풍력발전기와 해저지반의 거동 특성을 확인하기 위한 것이므로 블레이드의 질량과 고유진동수를 유사하게 맞추어 해석에 적용하였다. 블레이드에 대한 질량과 고유진동수의 비교 자료로서는 Jonkman et al.(2009)의 NREL (National Renewable Energy Laboratory) 보고서에서 확인하였다. 그리고 Fig. 2의 허브와 너셀의 질량중심점(CM)에 대부분의 질량이 포함되어 있고 충돌거동 특성이 나타나도록 하였기 때문에 강재의 탄성계수와 프와송 비를 동일하게 사용하였다. 그리고 단위중량은 각각 1850 kg/m3, 8500 kg/m3을 사용하였다.
타워와 지지구조물, 기초구조물은 선박충돌시 해상풍력발전기의 전체 시스템에서 큰 영향을 미친다. 왜냐하면 지지구조물에서 직접적인 충돌하중이 전달되어 타워와 기초구조물에 작용하기 때문이다. 따라서 타워와 지지구조물, 기초구조물은 Cowper-Symonds 방정식을 이용한 strain rate dependent 비선형 물성치를 사용하였다. 탄성계수와 단위중량, 프와송 비는 강재의 물성치를 이용하였고 항복응력 345×106Pa, 접선계수 763×106Pa, 경화 매개변수 0.8, 변형 매개변수 C와 P는 Cowper-Symonds 변형률 매개변수로 각각 40.5와 5, 파괴변형값은 0.75를 사용하였다.
4. 해석결과
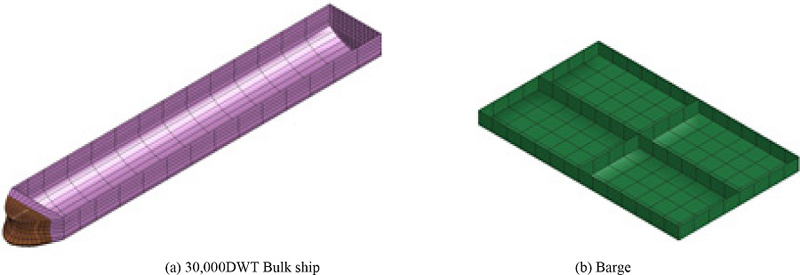
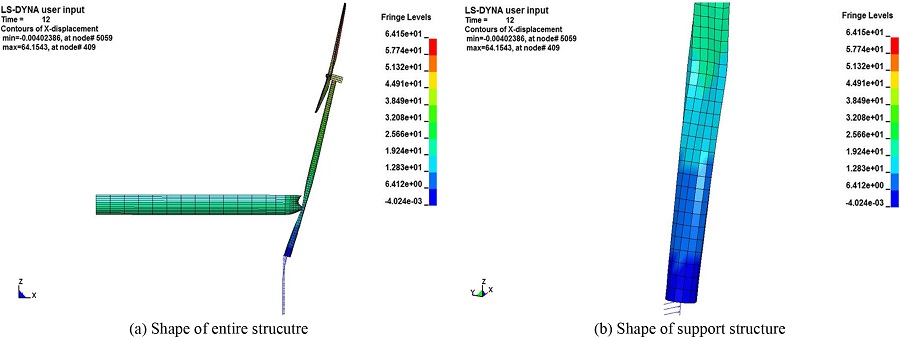
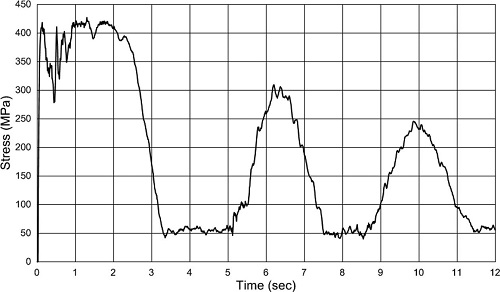
30,000DWT 충돌선박과 850ton barge선박을 이용하여 1~8 m/s의 충돌속도에서의 해상풍력발전기의 충돌해석을 수행하였다. Fig. 9와 Fig. 10은 5 m/s의 충돌속도에서 12초일 때 나타난 5MW 해상풍력발전기의 형상과 충돌이 발생한 위치에서의 응력에 대한 시간이력곡선으로 선박충돌에 의한 지지구조물의 국부적 변형이 발생하였다. 충돌속도가 각각 3 m/s와 5 m/s일 때, 1.9404 m, 3.9201 m의 최대변위가 해저면(z=0)인 위치에서 나타났으며 최대모멘트는 19 m 심도에서 각각 약 635.3 MN·m, 681 MN·m가 발생하였다.
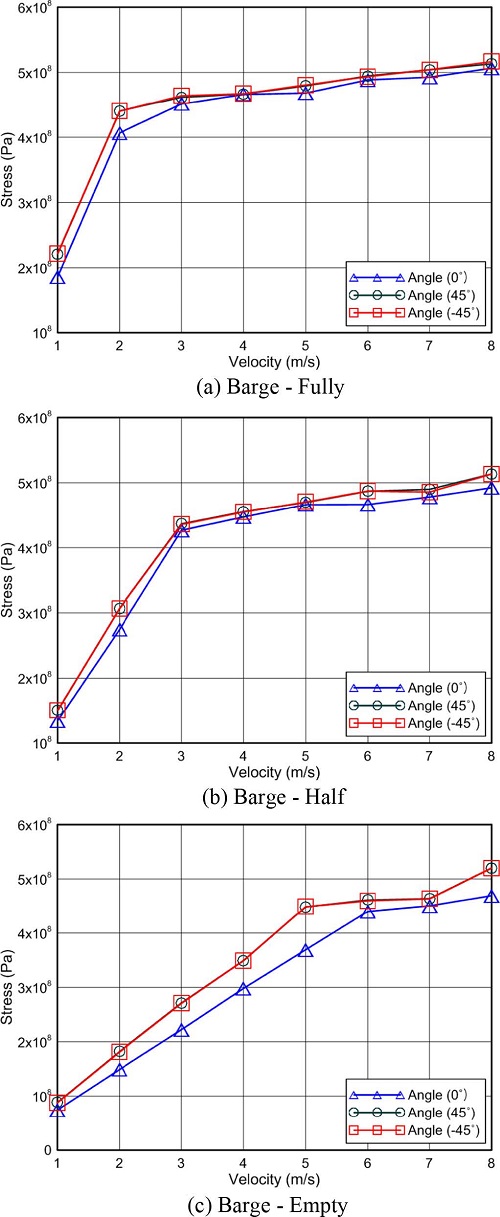
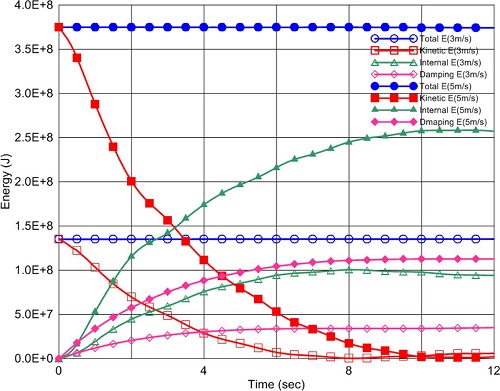
Fig. 11은 850ton barge 선박으로 충돌해석을 수행하여 충돌속도별 최대응력을 나타낸 그림이다. 지지구조물의 항복응력인 345 MPa을 초과하는 응력이 3 m/s이하의 속도에서 만선시, 상시, 공선시 모두 나타나는 것을 확인하였다. 또한 충돌각이 45o와 −45o일 때 충돌속도별 최대응력은 유사하게 발생하였다. Fig. 12는 30,000 DWT선박의 충돌과정에서 충돌속도가 각각 3 m/s, 5 m/s, 충돌각이 0o일 때 해상풍력발전기에 발생한 총 에너지와 운동에너지, 내부에너지, 감쇠에너지를 비교한 그림이다. 3 m/s일 때, 약 8초까지 선박충돌이 발생한 후 해상풍력발전기의 진동이 발생하는 것을 확인할 수 있으며 5 m/s일 때는 해석시간까지 계속 선박충돌이 발생하고 3 m/s에서의 내부에너지보다 큰 감쇠에너지가 발생한 것을 확인할 수 있다.
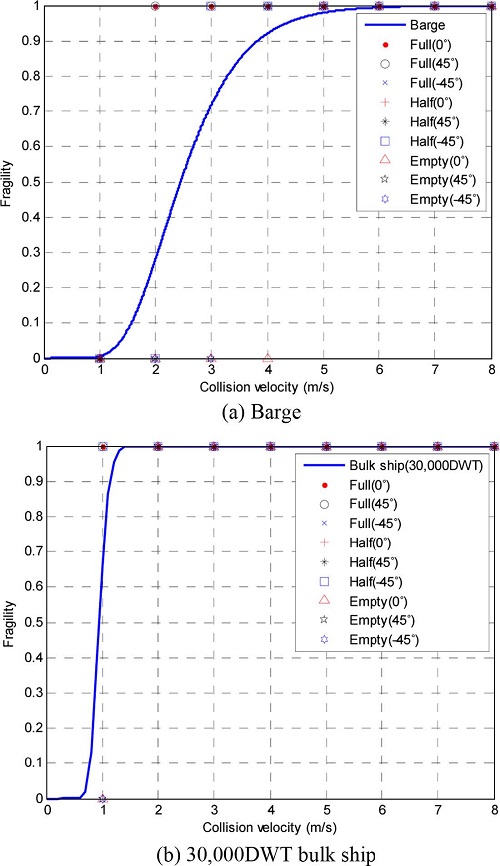
본 논문에서는 충돌취약도를 계산하기 위해 충돌 시 해상풍력발전기의 지지구조물에서 발생한 최대응력을 충돌취약도의 손상수준으로 설정하였다. 또한, 충돌취약도 곡선의 변동성을 고려하기 위해 충돌각과 선박의 질량을 만선시(full), 상시(half), 공선시(empty)로 구분하여 Table 4에 나타내었다. Fig. 13은 지지구조물의 항복응력을 손상기준으로 설정하여 구한 충돌취약도 곡선이다. Fig. 13(a)와 Fig. 13(b)의 충돌취약도 곡선을 비교하면 Fig. 13(b)의 곡선이 매우 급격하게 변화한 것을 확인할 수 있다. 이는 동일한 충돌속도일지라도 충돌하중이 클 경우 지지구조물에서 발생한 응력이 크게 나타남을 의미하며 Fig. 13(a)와 Fig. 13(b)의 누적확률분포 중간값인 0.5를 기준으로 확인했을 때 매우 큰 충돌속도의 차이를 확인할 수 있다. Table 5는 충돌취약도 곡선의 중앙값과 대수표준편차로 누적확률분포가 50%일 때 충돌속도를 나타낸다.
추정한 충돌취약도 곡선을 이용하면 해상풍력발전기 주변으로 통항하는 선박의 속도제어에 활용할 수 있다. 예를 들어, 통항하는 바지선에 의한 해상풍력발전기의 충돌파괴확률이 10%라고 가정했을 때 Fig. 13(a)와 같은 취약도 곡선을 참고하여 인근 해역을 통항하는 바지선의 속도를 파괴확률이 10% 이하가 되는 약 1.6 m/s이하의 통항속도로 제시하여 해상풍력발전기와 선박간의 충돌에 대비한 안전속도를 제시하는 것이다.
5. 결 론
본 연구에서는 1~8 m/s의 충돌속도에 대해서 충돌해석을 수행하여 해상풍력발전기의 충돌취약도를 계산하였다. 해상풍력발전기와 충돌하는 선박은 850 ton 바지선과 30,000 DWT 화물선으로 가정하였으며 충돌취약도의 손상유무는 충돌선박과 지지구조물의 충돌지점에서 발생한 응력이 항복응력을 초과하는지에 따라 결정하였다. 또한 충돌취약도 곡선의 변동성을 고려하기 위해 선박의 충돌각을 0o, −45o, 45o로 설정하고 선박의 중량을 만선시, 상시, 공선시로 구분하였다. 해상풍력발전기가 설치되는 해역의 지반조건은 API RP 2A(2000)에서 제시한 하중과 변위의 관계를 계산하여 이산화된 스프링으로 비선형성을 고려하였다. 바지선과 화물선에 대한 해상풍력발전기의 충돌취약도의 중앙값을 비교한 결과 바지선보다 화물선의 경우 약 0.93 m/s의 작은 값을 갖는다. 이는 화물선과의 충돌시 해상풍력발전기가 매우 취약함을 나타낸다. 또한 화물선보다 큰 중앙값을 갖는 바지선도 약 2.45 m/s에서 중앙값이 나타나므로 바지선과의 충돌에 대해 취약함을 확인하였다. 따라서 해상풍력발전기의 충돌에 대한 안정성을 높이기 위한 방안으로 수심이 깊은 곳에서도 사용이 가능한 충돌방지공을 개발할 필요가 있는 것으로 사료된다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation 
Print 
