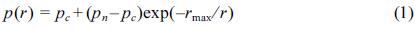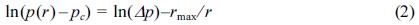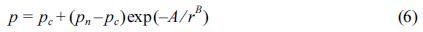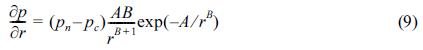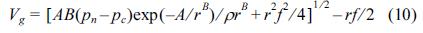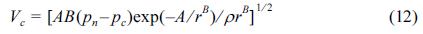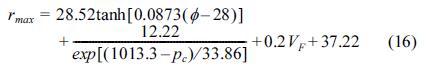1. 서 론
최근 활발한 연안 개발, 조류·파력 및 해상풍력 발전 등 다양한 해양에너지 개발에 따른 구조물 설치 등으로 해양 및 기상 설계 조건에 대한 관심이 높아지고 있다. 한반도는 북서 계절풍과 태평양 기단의 영향으로 매년 3~4개의 태풍이 빈번하게 출몰하며 해양 구조물에 미치는 영향도 상당하다. 이처럼 태풍은 극치 풍속을 결정하는 중요한 요소가 되어 극한 하중 형태로 작용하므로 설계 시 태풍의 영향을 신중하게 고려하여야한다. 한편, 극치 설계 풍속 산정을 위해서는 최소 30년 이상의 장기 풍속 자료가 필요하며 장기 바람 자료는 극치모델을 사용하여 50년 또는 100년 재현주기를 갖는 설계 풍속값을 예측하는데 사용할 수 있다. 그러나 육상과 달리 해상은 열악한 환경적 요인으로 인하여 장기 관측 자료의 확보가 어려워 태풍 모의기법(Kwon and Lee, 2008; Jung et al., 2012)을 이용하거나, 단기 관측(Kwon and Lee, 2009)을 통하여 대상 지점의 극치 풍속을 예측하고 있다.
태풍 모델 식들은 태풍을 모델링하는데 유용하지만 태풍에 대한 정보와 변수들간의 관계에 대해서는 잘 알려지지 않았으며 자료의 불확실성 등으로 인해 현실적으로 정확한 태풍을 모사하기란 거의 불가능하다. 그러나 태풍의 특성을 잘 반영한 태풍 모델은 어느 정도 현실성을 내포하고 있으며, 이러한 경우 태풍 모사를 위한 태풍 요소 정의가 매우 중요하다. 태풍 시 해상풍 모델의 입력자료로는 태풍 중심의 위치(매 3 내지 6 시간마다 태풍 중심 위치), 태풍 중심 기압, 태풍 외부의 기압, 최대풍속 반경, 태풍이 없을 경우 평균 바람장 등이 있다. 따라서 태풍에 의한 해상풍 추산을 위해서는 上記 파라미터들을 정확하게 추산하는 것이 가장 중요한 문제가 된다.
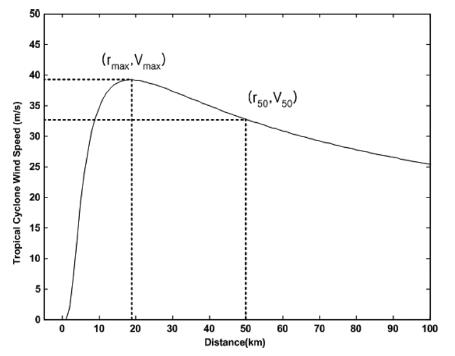
일반적으로 태풍은 기상학자들에 의하여 국가간 또는 세계적으로 예보되어 지며, 지역예보 센터는 세계기상기구(WMO, World Meteorological Organization)의 WWW(World Weather Watch) 프로그램에 의하여 설립되었다. 북태평양의 태풍 분석 및 예보는 JMA(2013)에 의해 운영되는 RSMC(Regional Specialized Meteorological Center) Tokyo-Typhoon Center가 수행하고 있으며 1951년 이후 태풍자료를 best tracks 형태로 제공하고 있다. 이 자료는 사전예보가 아닌 사후예보 자료로 모든 가용한 자료를 동원하여 예보하고 있으며, 1977년 이후에는 시각, 경도, 위도, 중심기압, 최대 풍속(kt), 최대풍속 50 kt(= 25 m/s)의 장반경 및 단반경, 최대풍속 30 kt(= 15 m/s)의 장반경 및 단반경 등의 자료를 제공하고 있다. 이 자료들은 태풍 모델의 입력 자료가 되어 태풍 모의에 활용되어진다. 한편, 태풍 모델의 주요 목적은 해상 구조물이 설치될 지점에서 발생하는 최대 풍속을 추정하는 것이기 때문에 태풍 정보를 이용하여 풍속 프로파일을 정확하게 정의할 필요가 있다. 태풍 시 풍속 프로파일과 최대풍속에 대한 정의는 Fig. 1에 나타내었다.
태풍 모델 식들은 태풍 파라미터의 함수로 정의되어지며 이중 최대풍속 반경(Radius of maximum winds, rmax)은 태풍 중심에서 최대 풍속이 발생하는 지점까지의 거리로서 태풍 산정에 있어서 매우 중요한 인자로서 작용하므로 합리적인 최대풍속반경 산출이 중요하다. 일반적으로 최대풍속반경을 결정하기 위한 방법으로는 항공기를 이용하여 직접 측정하는 방법과 위성자료를 이용하여 추정하는 방법, 그리고 경험 공식을 이용하여 산정하는 방법이 사용되고 있다(Anthes, 1982; Kieu, 2012). Hsu et al.(2000)는 태풍 눈 주변의 구름의 최저 온도에서 태풍 내의 최고온도까지의 거리로부터 최대풍속반경을 산정하였으며, Hsu and Babin(2005)는 위성 자료를 이용하여 2002년 멕시코만에 상륙한 허리케인 LILI의 최대풍속반경을 추정하였다. 그러나 이 방법은 태풍 눈이 구름으로 인해 식별이 곤란해지면 사용에 제약이 따른다. 또 다른 방법 중의 하나인 항공기를 이용한 직접 관측은 약 3 km 고도를 비행하는 항공기를 이용하여 태풍 특성을 관측한다. 그러나 이 방법 역시 고비용 및 위험성, 효율성 등의 문제가 발생하기 때문에 이용에 제약이 따른다.
국내의 경우, KORDI(2005)에서 최대풍속 태풍 반경을 산정한 바 있으며, 식 (1)과 같이 표현되는 Original Rankin vortex model(R. W. Schloemer model)의 해면기압 분포식을 이용하여 추정하였다.
여기서, p(r)은 태풍 중심으로부터 거리 r인 지점의 해면기압, pc는 중심기압, pn은 중립기압이며, rmax는 최대풍속반경이다.
식 (1)에서 pn - pc = ∆p라고 하고, 양변에 대수를 취하면 다음 식 (2)와 같이 정리할 수 있다.
식 (2)에서, ln(p(r) – pc)와 1 ⁄ r의 일차 관계식를 최소자승법으로 구하여 ln(p(r) - pc) 절편의 지수 값이 Δp, 기울기가 최대풍속 반경, rmax가 된다.
한편, 미국 해군에서 운영하는 하와이 소재 JTWC(2013)에서는 2001년부터 최대풍속 반경을 제공하지만 최대풍속반경 정보가 제외된 자료도 있으며, 2001년 이전의 태풍에 대해서는 결국 태풍 인자를 이용하여 최대풍속 반경을 산정하여야 한다.
본 연구에서는 Holland(1980) 모델의 파라미터 A, B와 rmax를 추정하기 위하여 일본 기상청의 RSMC 최적경로자료에서 제공하는 태풍 정보 중 국내 서남해안 지역에 영향을 미친 2010~2012년의 태풍 BOLAVEN(TY No. 1215), MEARI(TY No. 1105), KOMPASU(TY No. 1007) 정보를 이용하였으며 Holland 모델에 유한차분기법을 적용하여 최대풍속반경 매개변수인 A, B를 산정하였다. 또한 산정된 결과는 기타 최대풍속반경 산정 경험 공식들과 비교하였으며 각 방법들의 특성을 분석하였다.
2. 자료 및 방법
2.1 자료 특성
Table 1은 2001년 이후, 한반도에 영향을 미친 태풍과 출현 횟수를 정리하였다. 이는 한반도를 지나며 직접적으로 영향을 미친 태풍에 대한 정보이며, 이외에도 한반도를 관통하진 않았지만 인근 해상을 지나며 국내 해역에 영향을 미친 태풍의 수도 상당히 많다. 태풍의 영향 정도는 관심 대상 지점에 따라서 달라지며, 태풍 모의를 통해 대상 지점의 영향 정도를 파악할 수 있다.
Table 1.
Tropical cyclones that affect the Korean peninsula since 2001
태풍의 특성인자는 국내 기상청(KMA), 일본기상청(JMA) 그리고 미국합동태풍경보센터(JTWC) 자료를 활용할 수 있다. 국내 기상청의 자료는 다양한 태풍 특성을 제공하지 않고 있기 때문에 태풍 모의 목적용 자료로서는 부적합하다. 한편, JMA는 MTSAT 계열의 인공위성을 이용하여 태풍 정보를 수집하고 있으며 1951년부터 현재까지 북서태평양에서 중국해역까지(100oE and 180oE) 모든 태풍 정보를 3~6시간 간격의 RSMC 최적경로자료로 제공하고 있다. 한편, JTWC에서도 1945년부터 남반구, 북인도양, 북서 태평양 해역의 최적경로자료를 6시간 간격으로 제공하고 있다. RSMC 태풍경로 정보에는 최대풍속 반경을 제공하지 않고 있으며, JTWC에서는 2001년 기록부터 최대풍속반경을 제공하고 있다. 이 두 기관은 동일 태풍에 대해서 운영 목적, 해석 방법 등이 상이하여 서로 다른 특성 정보를 제공한다. JTWC의 경우, 1분 평균 풍속에서 최대지속풍속을 산출하는 반면, RSMC에서는 10분 평균 풍속을 사용하여 최대지속풍속을 산출한다. 또한 기상예측 수치모델로는 JTWC는 경압성(baroclinic model)과 순압성 역학 모델로 구성된 CONW라 불리는 수치 모델을 사용한다. 또한 경압성 모델로는 NOGAPS, GFDN, GFS, JGSM, UKMET, 그리고 ECMWF 모델을 사용하고 있으며 순압성 모델로는 the Weber Barotropic Model WBAR)을 사용하고 있다. 한편, JMA에서는 1959년 이래로 NWP(Numerical Weather Prediction) 모델을 사용하고 있으며 태풍 예측 모델로는 Typhoon Ensemble Model을 사용하고 있다. JMA의 태풍 모델은 태풍이 북서태평양에 진입하게 되면 하루에 4회, 즉 00, 06, 12 그리고 18시에 수행하게 된다.
JTWC는 WMO 태풍 프로그램에 의해 결정된 태풍이름과 번호를 사용하기 때문에 두 기관의 태풍번호는 동일태풍에 대해서 다른 태풍번호를 부여한다. 따라서 국내에서 이러한 태풍 인자를 사용하기위해서는 두 기관의 자료 특성을 파악하고 적합한 자료를 사용할 필요가 있다. Table 2에는 RSMC와 JTWC에서 제공하는 데이터를 정리하였다.
Table 2.
Contents of RSMC and JTWC best track data
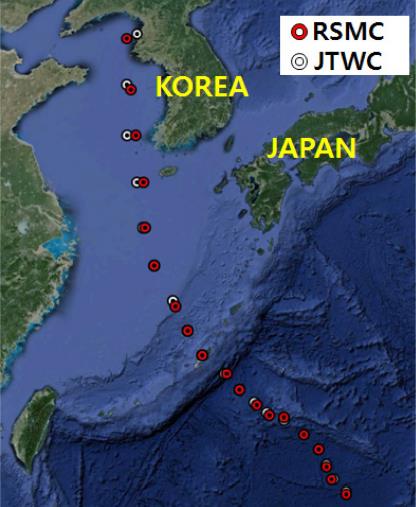
JTWC의 자료는 대부분 위성 사진을 Dvorak(1975) 방법에 의해 해석하여 사용하고 있으며, JMA 또한 위성 사진을 이용하고 있다. Fig. 2는 JMA에서 제공하는 태풍 BOLAVEN의 이동경로를 나타낸 것이며 태풍 중심 위치를 JTWC와 RSMC의 자료를 이용하여 비교하였으며 서로의 위치정보가 차이를 보이고 있다.
Table 3은 태풍 모의를 위해 필요한 최적경로자료의 내용을 BOLAVEN에 대해 발췌한 것으로 태풍은 시간과 공간에 따라 특성 인자들이 변화하고 있으며, 최대풍속 반경 산출시 이러한 시간과 공간에 따른 변화를 적절히 반영하여야 한다.
Table 3.
Tropical cyclone parameters of RSMC best track data(BOLAVEN)
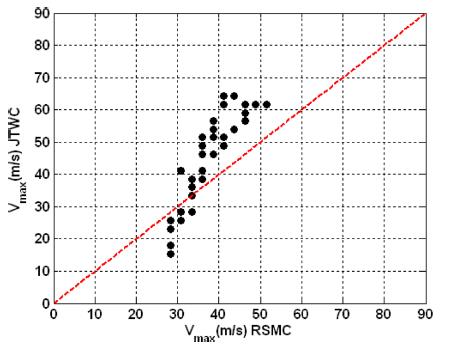
한편, 태풍 매개변수들 사이의 관계식을 수립하기 위해 지난 수십년간 많은 연구가 진행되었으며, 특히 풍속과 중심기압 사이의 경험적 관계식을 유도하고자 많은 연구결과가 발표되었다(Atkinson and Holliday, 1977; Dvorak, 1975; Thompson and Cardone, 1996; Kang et al., 2002). Ott(2006)는 2000-2003년 동안의 RSMC와 JTWC 최적경로자료를 비교하였다. JTWC의 경우, 1분 평균 풍속을 제공하는 반면 JMA에서는 10분 평균 풍속을 제공한다. 따라서 JTWC의 최대지속풍속은 JMA의 자료에 비해 약 14% 높게 추정되며, 중심기압의 경우 JTWC가 JMA에 비해 낮게 제시되고 있다. 이러한 차이는 다른 변수들의 산출에 더 큰 영향을 미칠 것으로 판단된다. 본 연구에서는 태풍 BOLAVEN, MEARI, KOMPASU의 RSMC와 JTWC 최적경로자료를 상호 비교해 보았으며 Fig. 3에 상기 3개 태풍의 최대풍속 비교 결과를 도시하였다. 그 결과 최대풍속의 경우, JTWC의 자료가 RSMC 자료에 비해 약 15.5 % 크게 산정되어 제시되고 있는 것으로 나타났으며 이러한 결과는 결국 식 (3)의 최대풍속과 중심기압과의 관계식으로부터 중심기압이 작게 산출되는 결과를 도출하게 된다.
여기서 Vmax는 최대풍속, pc는 태풍 중심기압, pn은 주변기압이며 a, b는 상수이다.
2.2 Holland model의 이론적 배경
태풍 매개변수를 이용하여 태풍을 모사할 수 있는 모델 중, Holland(1980) model은 관측 풍속장과 가장 유사한 값을 보여주고 있다(US Army Corps of Engineers, 2006). Schloemer(1954)는 중심기압과 주변기압의 차이로 인해 발생하는 변동성을 정규화 시키기 위해 다음과 같은 식 (4)를 제시하였다(US Army Corps of Engineers, 2006; Holland, 1980).
여기서 p는 임의 거리, r에서의 기압이다.
Holland(1980)는 위 식의 곡선이 직각 쌍곡선(rectangular hyperbolas)형태로 나타나는 것을 보이며 다음과 같은 식 (5)를 제시하였다.
여기서 A, B는 태풍 프로파일의 매개변수이다. 위 식을 p에 대하여 정리하면 식(6)과 같다.
한편, 경도풍, Vg에 대한 관계식(the gradient wind equations)을 태풍 중심에서 임의의 거리 r의 함수로 다음 식(7)과 같이 표시할 수 있다.
여기서 Vg는 거리 r에서의 경도풍이고, f는 코리올리 매개변수, ρ는 공기밀도이다.
식 (7)를 다시 경도풍에 대해 정리하면 다음 식 (8)과 같다.
한편, 식 (6)으로부터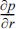 
를 구하면 식 (9)와 같다.
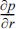를 구하면 식 (9)와 같다.
위 식 (9)를 식 (8)에 대입하면 다음 식 (10)과 같이 표현할 수 있다.
한편, 코리올리 힘은 식 (11)을 이용하여 계산하였다.
여기서, ϕ는 위도이며, ω는 지구자전 각속도로 7.2921159×10−5 rad/s이다.
원심력이 전향력에 비하여 큰 경우, 코리올리 힘은 무시할 수 있으며, 즉 선형풍(cyclostrophic wind)의 경우 풍속은 다음 식 (12)와 같이 표현할 수 있다.
dVc ⁄ dr = 0에 의해 rmax는 다음 식 (13)과 같이 표현된다.
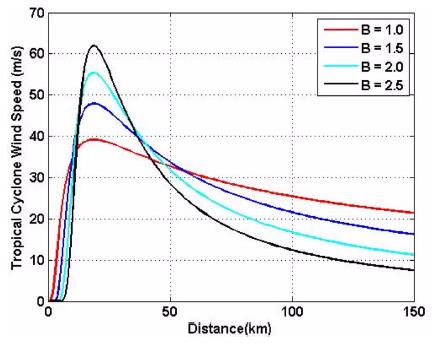
식 (10)에서 매개변수 B는 풍속의 첨두값을 제시하는 역할을 한다. Scholemer(1954)는 A = rmax, B = 1값을 사용하도록 제시하였지만 이는 실제값보다 낮게 추산되어 태풍 시 풍속의 저평가 원인이 된다. 따라서 Holland는 B의 값을 관측치로부터 회귀하여 값을 추정하도록 제안하였다(Holland, 1980). Fig. 4는 B값의 변화가 태풍의 최대풍속에 미치는 영향을 도시화 한 것이다. Fig. 4에서 보는 바와 같이 B = 1일 때, 풍속의 최대값이 가장 작게 산출되었으며, B의 값에 비례하여 최대치의 변화가 나타남을 알 수 있다. 이처럼 B의 선택이 태풍의 과대 또는 과소 평가의 중요한 역할을 하기 때문에 태풍의 특성을 고려하여 적합한 B의 값 산출이 필요하다. 본 연구에서는 RSMC 최적경로자료의 15 m/s와 25 m/s의 풍속과장반경 정보를 이용하여 A, B를 추정하였다. 두 값을 식 (10)에 대입하면 미지수, A, B에 대한 두 개의 비선형방정식이 나타난다. 이 비선형 방정식은 가장 널리 사용하는 수치해석법 중의 하나인 Newton-Raphson 법을 이용하여 근을 계산하였으며, 초기값을 가정(A = 150, B = 1)한 후, 반복계산을 수행하여 A, B를 산출하였다.
2.3 기타 경험공식
Anthes(1982)는 완전히 발달된 태풍에 대해서 거리 r에서의 풍속을 다음 경험식 (14)와 같이 제안하였다.
여기서, Vr은 거리 r 지점에서의 풍속 (m/s), Vmax는 최대풍속(m/s), rmax는 최대풍속반경(km), x는 풍속 산정을 위한 지수 값이다.
x의 값은 산정풍속의 위치가 해수면일 때는 0.5, 높은 고도일 경우에는 0.7의 값을 사용한다. 식 (14)를 최대풍속반경, 에 대해서 정리하면 식 (15)와 같다.
RSMC 최적경로자료 중 최대풍속과 25 m/s의 장반경을 이용하면 쉽게 최대풍속반경을 구할 수 있다. 그러나 위 식은 일반식으로서 지수 x의 값이 현장 상황을 얼마만큼 반영하는지에 대해서는 많은 불확실성이 내포되었을 것으로 판단된다.
한편, Graham and Nunn(1959)은 최대풍속반경 산정을 위해 다음 식 (16)과 같이 경험 공식을 제안하였다.
여기서, ϕ는 위도, VF는 태풍의 이동속도(m/s)이다.
3. 최대풍속반경, rmax 산정 결과
본 연구에서는 국내 서남해안 지역에 큰 영향을 미친 2010~2012년 태풍 BOLAVEN, MEARI, KOMPASU에 대하여 최대풍속반경을 산정하였다. 자료로는 A, B 추정이 가능한 비선형 방정식의 형태를 수립할 수 있는 정보(15 m/s와 25 m/s의 풍속과 장반경)를 제공하는 RSMC 데이터를 사용하였다. JTWC에서도 35, 50, 65, 100 kts(= 17.5, 25, 32.5, 50 m/s)의 풍속과 반경을 제공하지만, 본 연구에서 활용하기에는 부적합하다. Table 4는 본 연구에서 해석한 태풍과 기간 등을 요약하였으며, 결측기간 자료는 본 해석에서 제외하였다.
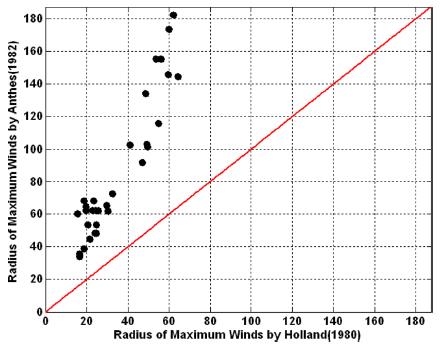
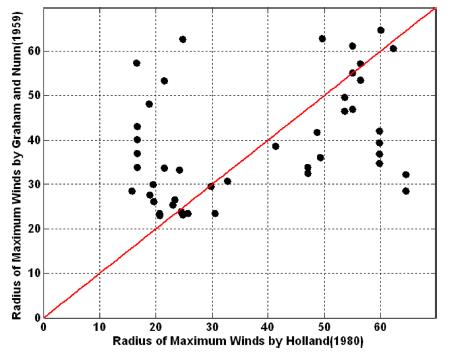
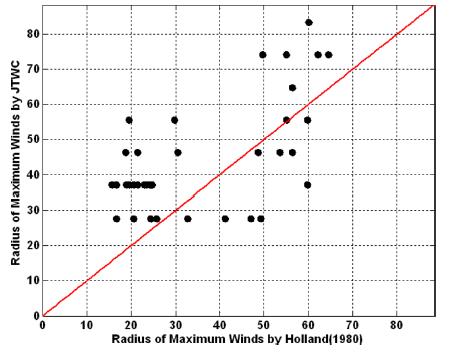
Fig. 5~7은 각 방법들에 의해 계산된 최대풍속 반경을 비교한 것이다. Anthes 식에 의해 계산 된 값은 Holland model에 의해 계산한 값보다 상대오차가 57.96 %로 상대적으로 큰 오차를 보이고 있었으며, Graham and Nunn과 Holland model에 의해 추산된 값들은 약 30.54%의 오차를 보였다. 또한 JTWC에서 제공하는 최대풍속반경과는 36.07%를 보였다. 이와 같이 최대풍속반경을 추산하는 식들 사이에도 많은 불확실성을 내포하고 있다.
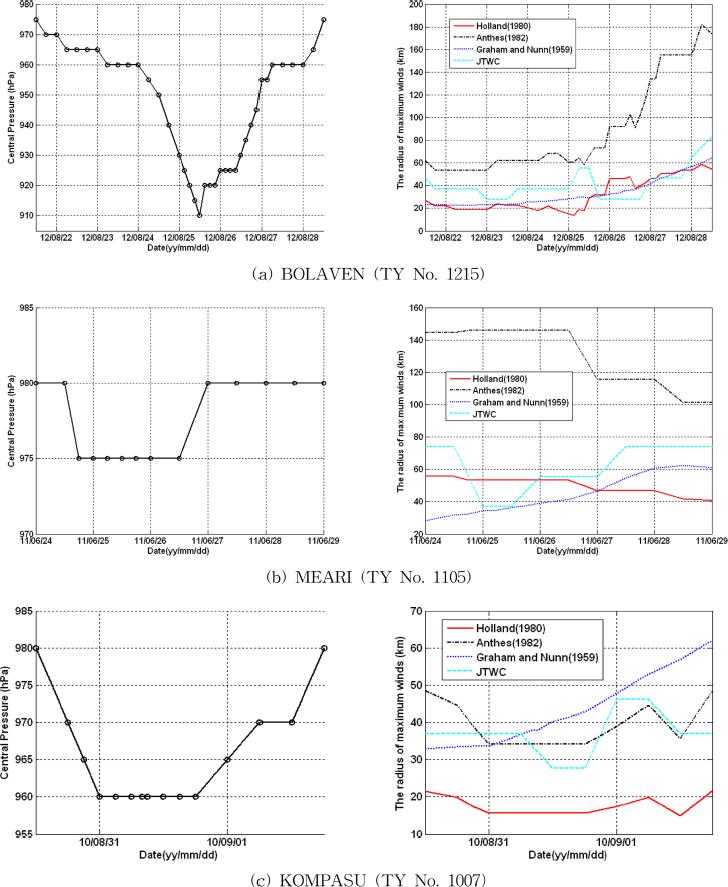
Fig. 8의 왼쪽 그림은 RSMC의 중심기압을, 오른쪽 그림은 4가지 방법에 따른 최대풍속반경을 시간별로 도시한 것이다. Fig. 8에 보이는 바와 같이 태풍의 이동 위치와 시간에 따라 태풍 특성이 변화하기 때문에 최대풍속반경도 달라지는 양상을 보인다. 2012년 태풍 BOLAVEN의 경우, Anthes의 식이 가장 큰 최대풍속반경을 산정하고 있으며, JTWC, Graham and Nunn 그리고 본 연구에서 제시한 Holland식이 비슷한 값을 보이고 있었다. 중심기압과의 관계에 따라, 중심기압이 상승하면 최대풍속 반경도 상승하는 태풍의 성향을 고려한다면, Holland와 Anthes의 식에 의해 추정된 값이 비슷한 경향을 보이며 중심기압에 대한 영향을 잘 표현하고 있는 것으로 나타났다. 2011년 태풍 MEARI의 경우, Holland 식을 이용한 방법과 Graham and Nunn, JTWC의 값이 Anthes의 식에 비해 작게 산정되었다. 그러나, Anthes와 본 연구에서 제시한 방법의 최대풍속반경은 큰 차이를 보이지만 경향은 비슷하게 나타났다. 2010년 태풍 KOMPASU의 경우, Anthes와 Graham and Nunn, JTWC의 값이 Holland 식에 의해 산정된 값에 비해 비교적 크게 산정되었으며, 이 경우 역시 Anthes와 Holland식에 의한 값이 비슷한 경향을 보이고 있었다. 전체적으로 Anthes와 Holland 식에 의한 값이 비슷한 경향을 보이며 중심기압의 영향을 잘 표현하고 있는 것으로 나타났으며, Anthes식의 경우 다른 방법에 비해 최대풍속반경의 값을 크게 산정하고 있다. 한편, Graham and Nunn 경험식에 의한 값은 중심기압의 변화와 상관없이 증가하는 성향을 보였으며, 태풍이 소멸 단계인 경우, 최대풍속 반경의 신뢰도가 저하되는 것으로 나타났다.
4. 결론 및 제언
태풍 모의는 설계 풍속 산정 등 장기간 태풍 자료가 요구될 때 수행하게 된다. 본 연구에서는 JTWC와 RSMC 최적 경로자료에 대하여 상호 비교 및 자료 특성을 파악하였으며, 최대풍속반경을 산정한 후, 기존 경험식들과 비교하였다. 이를 통하여 다음과 같은 결론을 도출하였다.
(1) 일본 기상청의 RSMC와 JTWC의 최적경로자료는 국내 태풍 모의 및 해일고 산정 등에 사용되어진다. 그러나 JTWC는 미국 정부의 필요 목적에 운영되어지고 있어 세계 기상 자료와는 상이한 정보를 제공한다. 최대풍속 산정의 경우, JTWC는 1분 평균 풍속을 제공하는 반면 JMA에서는 10분 평균 풍속을 제공하고 있어 JTWC의 최대지속풍속은 RSMC의 자료에 비해 약 15.5% 높게 추정되는 결과를 보였다. 이러한 차이는 다른 변수들의 산출에 더 큰 영향을 미칠 것으로 판단되며 태풍 모의시 이러한 특성을 적절히 반영할 필요가 있다.
(2) RSMC 최적경로자료는 25 m/s와 15 m/s의 풍속 및 장반경을 제공하고 있으며, 태풍 프로파일 모델인 Holland model에 적용하면 RSMC에서 정의한 태풍의 풍속 프로파일 작성이 가능하다. 따라서, RSMC 최적경로자료를 이용하여 태풍 모의를 수행할 경우, 태풍 모의 입력자료 특성의 일관성을 유지 할 수 있다.
(3) 최대풍속반경 산출 방법에는 항공기를 이용하여 직접 측정하는 방법과, 위성자료를 이용하여 추정하는 방법, 그리고 경험 공식을 이용하여 산정하는 방법(Anthes, 1982; Graham and Nunn, 1959)이 널리 사용되어진다. 한편, JTWC에서는 2001년 이후부터 최대풍속반경을 제공하고 있다. 본 연구에서는 태풍 BOLAVEN, MEARI, KOMPASU를 대상으로, 경험 공식과 JTWC의 최대풍속반경 정보 그리고 Holland model을 적용한 결과를 비교하였다. Holland model에 의해 산정된 값은 Anthes, Graham and Nunn, JTWC값과 각각 57.96%, 30.54%, 36.07%의 상대오차를 보이는 것으로 나타났다.
(4) 최대풍속반경의 시간적 변화양상을 살펴본 결과, Anthes식은 Holland model 값과 비슷한 경향을 보였으며, Anthes와 Holland model에 의한 추정값이 중심기압의 영향을 가장 잘 표현하고 있는 것으로 나타났다. 그러나 Graham and Nunn 식에 의해 추정된 값은 태풍의 변화를 무시한 채 계속 증가하는 형태를 보이고 중심기압의 변동영향이 크게 반영되지 않는 것으로 나타났다.
(5) 태풍의 대한 정확한 모의는 사실상 거의 불가능하다. 또한 자료의 명확한 해설과 관측값이 부족하기 때문에 각 결과치의 우수성을 논하기엔 무리가 있으며, 자료 특성을 파악하여 사용자가 목적에 따라 적절히 사용할 필요가 있을 것으로 판단된다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation 
Print 
