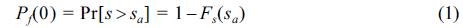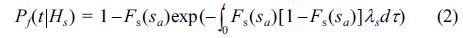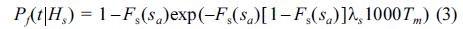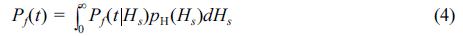1. 서 론
케이슨 활동 파괴는 직립방파제의 여러 가지 파괴모드 중에서 가장 지배적이기 때문에 이에 대한 많은 연구가 수행되었다. 일반적으로 케이슨 활동에 대한 설계법은 결정론적 설계법과 확률론적 설계법으로 나눠진다. 대표적인 설계법으로는 가장 전통적인 안전율 설계법(Goda 1974), 부분안전계수법을 포함한 신뢰성 설계법(Kim and Suh 2009a; Lee 2009; Lee et al. 2012), 그리고 성능설계법(Shimosako and Takahashi 2000; Takahashi et al. 2001; Kim et al. 2012a) 등이 있다. 앞에서 언급한 설계법 중에서 안전율 설계법을 제외하면 모두 확률론적 설계법이다. 이와 같은 다양한 확률론적 설계법의 출현 배경은 복잡하고 다양한 설계환경을 효과적으로 고려하지 못하는 전통적인 설계법의 한계 때문이다. 특히, 확률론적 설계법은 구조물의 설계뿐만 아니라 해석에서도 사용될 수 있다. 최근에는 신규 방파제의 설계보다 기존 방파제의 유지 및 관리에 대한 사회적 요구가 증가하고 있어 확률론적 설계법의 필요성이 더욱 높아지고 있다. 신뢰성 설계법과 성능설계법은 기초적인 유지·관리 기능을 가지고 있지만 다소 제한적이다. 이런 방법들은 설계수명 동안의 평균적인 파괴확률과 변위를 산정하지만 구조물의 생애기간 중간에 발생 가능한 피해를 예측할 수 없다. 이를 보완하기 위해서 최근 설계와 유지·관리 기능을 강화한 확률과정에 기반한 시간의존 성능설계법이 개발되었다(Suh et al. 2012; Kim et al. 2012b).
성능설계법에서는 방파제 수명 동안의 총 활동량의 기대값으로 계산되는 기대활동량(Takahashi et al. 2001), 총 활동량이 임의의 기준치를 초과할 확률(Shimosako and Tada 2003), 또는 설계폭풍 지속시간 동안의 기대활동량(Takahashi et al. 2001) 등을 계산하여 이들이 허용치를 초과하지 않도록 설계한다. 이 기준들은 모두 방파제의 수명 또는 설계폭풍 지속시간 동안의 누적활동량을 사용한다. 하지만 케이슨의 활동은 시간적으로나 그 크기에 있어서 매우 무작위하게 발생한다. 아주 큰 파들은 파의 주기보다 짧은 시간 동안에 케이슨의 활동을 발생시키며, 작은 파들에 의해서는 활동이 발생하지 않는다. 누적활동량에 대한 정보만으로는 몇 개의 파에 의해 활동이 발생하고 각 파에 의한 활동량이 얼마나 되는 지를 알 수 없다. 일반적으로 대부분의 파는 활동을 발생시키지 않으며, 소수의 큰 파에 의해 대부분의 활동이 발생한다. 개별 파에 의한 개별 활동량에 대한 정보를 알 수 있다면 매우 유용할 것이다. 월파에 대해서도 유사성을 찾을 수 있겠는데, 평균 월파량도 널리 사용되지만 개별 파에 의한 월파 부피 또한 중요한 변수이다. 본 연구에서 직립벽에 작용하는 파력은 개별파를 독립적으로 적용하여 산정하였다. 실제 파력은 개별파의 상호작용이 고려되나 본 모델은 이를 고려할 수 없는 한계가 있다.
최근 Kim et al.(2012b)은 설계폭풍 동안에 개별 활동량의 최초통과확률에 기초한 시간의존 성능설계법을 제안한 바 있다. 최초통과확률은 임의의 시간 동안에 개별 활동량이 허용활동량을 초과할 확률이다. 하지만 지금까지 개별 활동량의 허용치와 이에 대한 허용최초통과확률에 대한 기준이 제안된 바 없기 때문에 이 방법을 적용하기가 어렵다. 본 연구에서는 기존 설계법의 허용 기준을 검토하여 이에 상응하는 개별 허용활동량과 이에 대한 허용최초통과확률을 제시하고자 한다. 우선, 현행 설계법인 안전율 설계법과 세 가지 성능설계법(구조물의 수명 동안의 기대활동량 및 초과확률, 설계폭풍 동안의 기대활동량)을 사용하여 구조물을 설계하고 이 단면에 대해 개별 활동량의 최초통과확률을 산정 및 분석하여 개별 허용활동량과 허용최초통과확률에 대한 기준을 제안하고자 한다. 특히, 다양한 수심조건과 극치파고분포의 특성을 고려하여 일관성이 있는 허용최초통과확률을 개발하고자 한다.
2. 현행 설계법의 허용 기준
직립방파제의 설계는 케이슨 활동에 대한 안정성을 확보하는 것이 가장 중요하기 때문에 많은 연구자들이 활동에 대한 다양한 설계법과 허용기준을 제안하였다(Goda 1974; Shimosako and Takahashi 2000; Takahashi et al. 2001; Shimosako and Tada 2003). 현행 설계법은 안전율을 산정하는 결정론적 방법과 활동량과 확률을 계산하는 확률론적 방법으로 나뉜다. 안전율은 Goda(1974)에 의해 파압 산정 공식과 함께 제시된 것이며 허용기준으로 1.2를 사용한다. 이후 Goda 파압 산정 공식은 충격쇄파압을 고려하기 위해 Takahashi et al.(1994)에 의해 개선되었다. 안전율은 파압에 저항하는 구조물의 중량을 결정하는 것으로 계산 방법이 간단하여 지금까지 사용되고 있다(KPHA 2005). 한편, Shimosako and Takahashi(2000), Takahashi et al.(2001) 그리고 Shimosako and Tada(2003)는 안전과 파괴에 대한 이원론적 방법론을 넘어 구조물의 수명 동안에 발생하는 변위 또는 일정 변위의 초과확률을 어느 정도까지 허용할 것인가로 판단하는 성능설계법을 제안하였다.
성능설계법의 다양한 허용기준은 Tables 1부터 3에 제시되어 있다. Table 1은 구조물의 수명인 50년 동안의 기대활동량으로 구조물의 중요도에 따라 구분된다(Takahashi et al. 2001). Table 2는 구조물의 수명 동안에 평균적으로 한 번 발생하는 확률파와 구조물의 중요도에 따른 허용기준이다(Takahashi et al. 2001). Table 1의 기대활동량은 설계수명 동안에 발생하는 모든 폭풍파랑에 대한 누적활동량을 계산하지만 Table 2의 누적활동량은 설계기준에 해당하는 하나의 큰 확률파랑에 대한 활동량만 산정한다. 한편 Table 3은 구조물의 수명인 50년 동안에 Tables 1과 2에서 소개된 허용활동량을 초과하는 확률을 구조물의 중요도에 따라 제시하고 있다(Shimosako and Tada 2003). 특히, Table 3의 기준을 사용할 경우에는 세 가지 허용활동량을 초과하는 각각의 초과확률을 동시에 만족하도록 구조물을 설계해야 한다.
Table 2.
Allowable expected sliding distance of different storm events by Takahashi et al. (2001)
앞에서 케이슨 활동에 대한 서로 다른 4 가지 현행 허용기준을 살펴보았다. 본 연구에서는 구조물의 설계수명 50년과 재현기간 50년의 확률파랑, 그리고 보통의 중요도를 가지는 구조물에 대한 설계 기준을 사용한다. 다시 말하면, 현행 케이슨 활동의 허용기준으로 안전율 1.2, 구조물 수명 50년 동안의 기대활동량 0.3m, 50년 빈도파에 대한 폭풍 지속시간 동안의 기대활동량 0.1m, 그리고 50년 동안에 허용활동량 0.1, 0.3 및 1.0m를 각각 초과할 확률로 30%, 10%, 그리고 5%를 사용한다.
3. 허용개별활동량과 허용최초통과확률의 산정
허용개별활동량과 허용최초통과확률은 현행 설계기준을 만족하도록 설계한 전형적인 케이슨 단면에 대해 최초통과확률을 계산 및 분석하여 제안된다. 즉, 현행 설계기준에 상응하는 최초통과확률을 허용기준으로 결정하는 것이다. 다양한 수심조건과 파랑의 분포특성을 반영하기 위해 Shimosako and Tada (2003)를 참고하여 Table 4와 같이 파랑조건을 선택하였다. 50년 빈도 유의파고가 같은 조건에서 두 가지 확률분포함수와 γ50(= Hs50/Hs10)이 서로 다른 3가지 파랑분포를 사용하였다. 여기서 Hs10과 Hs50은 각각 10년과 50년 빈도의 유의파고이며 k, A, B, 그리고 λ는 형상, 척도, 위치 매개변수, 그리고 극치파고의 연간 발생율이다. 수심조건은 바닥경사 1:100에서 12 m에서 24 m까지 4 m 간격으로 4가지를 사용하였고 50년 빈도의 심해유의파고와 주기, 그리고 조위는 Kim et al.(2012a)의 값을 이용하였다.
3.1 현행 설계법에 따른 구조물 설계
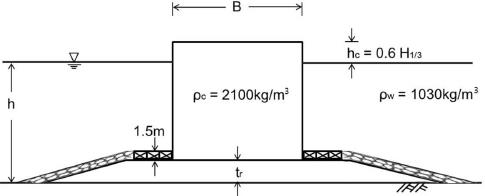
구조물의 단면 형상은 Fig. 1과 같이 전형적인 케이슨 단면이다. 수심은 Kim et al.(2012a)과 같이 수심 효과를 검토하기 위해 쇄파대(12m), 쇄파대 인근(16m), 그리고 비쇄파대(20m, 24m)로 나누었다. Table 5는 본 연구의 모든 설계법에서 공통적으로 사용되는 파랑, 수심, 그리고 기하학적 변수들이다. 기하학적 변수들은 Kim et al.(2012a)과 같이 천문조와 기상조를 고려하여 산정하였다. 여기서 hMSL는 평균해수면 기준으로 한 방파제 toe의 수심, H'0은 환산심해파고, Hmax는 최대파고(=H1/250), h(= hMSL+ tide)는 방파제 toe에서의 설계수심, h'{= h −max(0.2h, 3.0m)}는 마운드 위에서 수심, d(= h' − 1.5 m)는 근고공 위에서 수심, hc(= 0.6Hs)는 마루높이다.
Tables 6-8은 Table 4의 3 가지 경우에 대해서 Tables 1-3에서 정의한 안전율(S.F.), 한 확률 폭풍파 동안의 기대활동량(SES), 구조물 수명 동안의 기대활동량(SEL), 그리고 구조물 수명 동안의 허용활동량을 초과하는 확률(PE)을 사용하여 산정한 케이슨 단면 폭이다. 이 표에서 SL은 구조물 수명 동안의 누적활동량이다. 기본적으로 케이슨 단면은 연직 방향으로 동일한 기하학적 치수(Table 5)에서 케이슨 단면 폭만 여러 가지 설계법으로 결정하였다. 특히, 초과확률을 사용하는 경우의 단면 폭은 Table 3의 세 가지 조건을 동시에 만족하도록 결정하였다(Shimosako and Tada 2003). Tables 7, 8에서 안전율과 한 폭풍 동안의 기대활동량에 대한 단면 폭은 재현기간 50년의 확률파에 의해 결정되므로 Table 6과 동일한 값이 된다. 각 단면 결정시 허용기준의 오차범위는 안전율 ±0.001, 기대활동량 ±0.005 m, 그리고 초과확률 +0.005이다. 안전율을 제외한 나머지 세 가지 방법에서는 Shimosako and Takahashi(2000)의 모델에 기초하여 케이슨 활동량을 계산하였다. 본 연구에서 사용된 모델은 Shimosako and Takahashi(2000) 모델에 Kim and Takayama(2003)의 이중 절단 정규분포를 포함시키고 난수추출 방법을 개선한 것이다(Kim and Suh 2013; Kim and Suh 2009b). 또한 설계변수의 통계적 특성치는 Suh et al.(2012)의 값을 사용하였다.
Table 6.
Caisson widths designed by various methods for Case 1
Table 7.
Caisson widths designed by various methods for Case 2
Table 8.
Caisson widths designed by various methods for Case 3
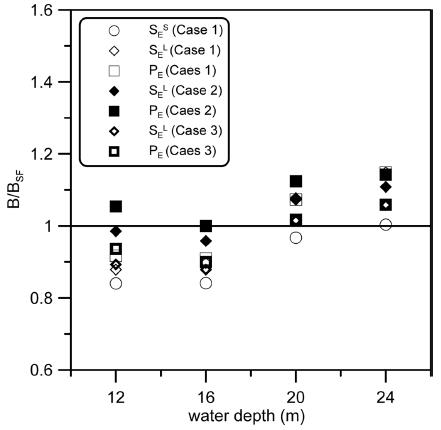
Fig. 2는 수심과 극치파고분포의 특성에 따라 다양한 방법으로 설계된 단면 폭을 안전율 1.2의 단면 폭으로 무차원화하여 비교한 것이다. 흥미로운 점은 수심과 극치파고분포의 특성, 그리고 설계 방법에 관계없이 설계된 단면 폭은 안전율 1.2의 단면 폭의 ±20%안에 분포하고 있다는 것이다. 즉, 지금까지 제안된 설계기준은 수심과 극치파고분포의 특성에 따라 단면 폭의 차이를 보이지만 일정한 범위 내에 존재하고 있다는 것이다. 상대적으로 수심이 얕은 쇄파대 인근(h = 16 m)과 쇄파대(h = 12 m)에서는 설계 방법과 극치파고 분포의 특성에 따라 단면 폭의 변동이 다소 크고 대부분의 경우 안전율 1.2의 단면 폭보다 작다. 반면 수심이 깊은 비쇄파(h = 20 m, 24 m)로 갈수록 단면 폭의 변동은 차츰 줄어들고 안전율 1.2의 단면보다 큰 단면이 산정되었다.
한편, γ50이 큰 Case 1의 한 폭풍파의 기대활동량(SES)으로 계산한 단면 폭이 하한 경계를 이루는 반면, γ50이 작은 Case 2의 초과확률(PE)에 의한 단면 폭은 상한 경계에 위치한다. 극치파고분포의 특성에서 보면 수심이 얕은 쇄대파 인근에서 γ50이 클수록 단면 폭이 작은 것을 확인할 수 있으며, 이는 심해에서 발생한 큰 파랑은 수심제한효과로 쇄파되지만 중간 크기의 파랑은 쇄파되지 않고 구조물 위치까지 전파되기 때문이다. 이와 같은 현상은 수심이 깊어질수록 점차 약해지는 것을 볼 수 있다.
3.2 최초통과확률의 산정
앞 절에서 다양한 설계법과 설계조건을 사용하여 케이슨 단면 폭을 산정하고 비교하였다. 이와 같이 설계된 케이슨 단면은 Kim et al.(2012b)이 제안한 확률과정에 기반한 시간의 존 신뢰성 설계법(혹은 최초통과확률법)으로 해석되며, 이 때 개별 허용활동량에 대한 최초통과확률이 산정된다. 최초통과 확률법은 하중의 발생과정과 피해과정을 정의하는 것이 중요하다. 본 연구에서 하중의 발생과정은 케이슨의 활동을 일으키는 큰 폭풍파의 발생으로 정의했으며, 폭풍파의 시간과 강도의 임의성에 근거하여 Poisson spike process로 정식화하였다. 동시에 피해과정은 개별파에 의한 활동량분포함수로 표현하였다. 여기서 활동량분포함수로 2모수 Weibull 분포함수를 사용했으며, 이는 형상 및 척도매개변수가 활동량분포함수를 잘 모사하기 때문이다. 사용된 2모수 Weibull 분포함수는 다양한 방법의 적합도 검증을 통해 개별활동량분포함수로서 적합함을 확인하였다.
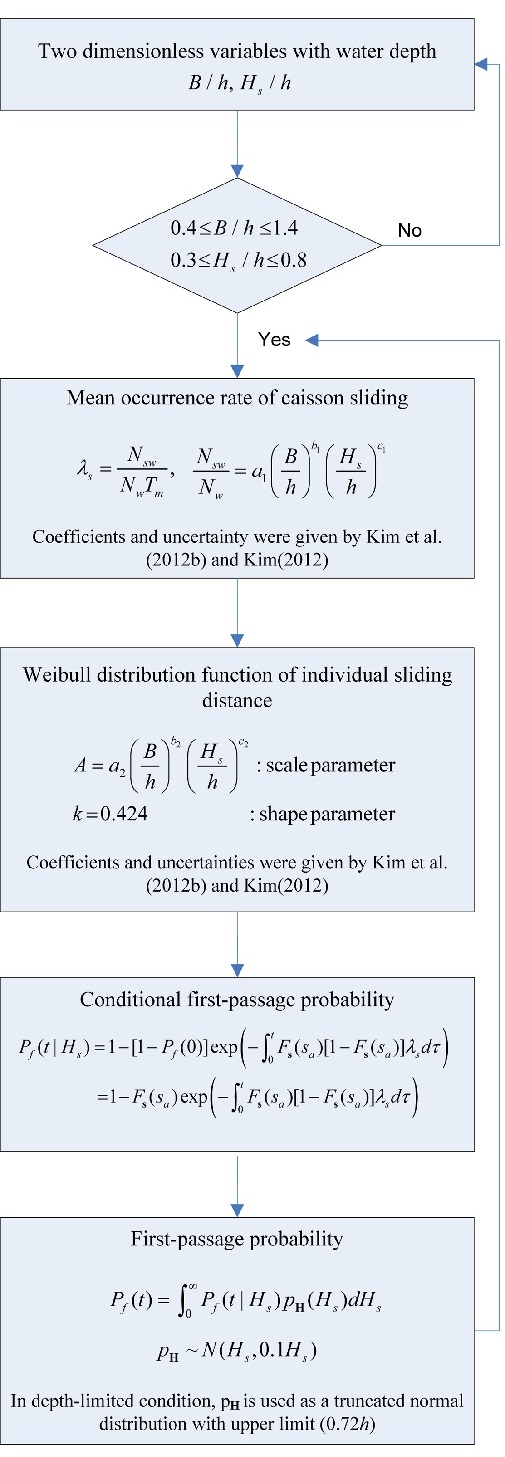
Fig. 3은 확률과정 신뢰성 설계법으로 최초통과확률을 산정하는 계산과정을 보여준다. 우선, 재현기간 50년 유의파고와 케이슨 단면 폭을 수심으로 무차원화하여 이 값들이 유의한 범위 내에 포함되는지 확인한다. 이 유의범위는 Kim et al.(2012b)의 연구에서 각종 매개변수들을 산정하는 데 사용되었던 자료의 범위를 나타낸다. 무차원화 한 두 변수가 유의범위 안에 포함되면 최초통과화률의 산정에서 가장 중요한 케이슨 활동의 평균발생률과 개별 활동량분포함수의 매개변수를 Kim et al.(2012b)에 주어진 계수를 사용하여 산정한다. 이 때 산정된 값은 평균값을 의미하며 이들의 불확실성에 대한 정보는 Kim et al.(2012b)에 자세히 제시되어 있다. 이와 같이 기초적인 정보를 산정하는 과정이 끝나면 최초통과확률을 계산하는 과정으로 넘어간다. 먼저, t = 0(혹은 시간 독립 조건)에서의 최초통과확률 Pf(0)은 하중으로 정의된 개별파의 활동량이 허용활동량을 초과하는 확률을 의미하며 다음과 같이 산정된다.
여기서 s와 sa는 각각 하중과 저항으로서 개별파에 의한 활동량과 허용활동량이며 Fs는 활동량의 누적분포함수이다. Kim et al.(2012b)은 FORM을 사용하여 구조물의 수명 동안에 파력(하중)이 구조물의 설계중량(저항)을 초과할 확률로서 Pf(0)를 계산하였다. 하지만 최초통과확률법의 설계개념은 개별파에 의한 활동량이 허용활동량을 최초로 초과하는 확률을 다루는 것이기 때문에 식 (1)을 사용하는 것이 보다 합리적이다. 위 식을 사용하여 주어진 유의파고 HS에 대한 조건부 최초통과확률은 다음과 같이 산정한다.
여기서 t는 폭풍지속시간으로 1000Tm을 사용하며 평균주기 Tm은 유의주기를 1.2로 나눈 값이다. 만약 폭풍지속시간 동안에 활동량분포함수 Fs와 평균발생율 λs가 변하지 않는다면 위 식은 다음과 같이 간단하게 된다.
본 연구에서는 주어진 유의파고 Hs에서 폭풍지속시간(1000Tm) 동안에 활동량분포함수와 평균발생율이 변하지 않는다는 조건으로 조건부 최초통과확률을 산정하였다. 최종적인 최초통과확률은 유의파고의 불확실성을 고려하여 다음과 같이 산정한다.
여기서 pH는 유의파고의 불확실성을 나타내는 확률밀도함수이다. 비록 제한적이지만 Kim et al.(2012a)와 Burcharth(1992)에 근거하여 이 변수의 분포를 정규분포로 가정하였고 평균은 주어진 유의파고이고 표준편차는 유의파고의 10%을 사용한다. 여기서 사용한 표준편차는 Burcharth(1992)가 제안한 하한 값에 해당한다. 표준편차에는 유의파고의 산정과정(심해파고, 파랑변형모형, 통계적 추산 등)에서 발생하는 다양한 불확실성이 포함되어 있다. 정밀한 관측장비를 사용하여 장기간 계측된 자료와 정확성이 높은 수치모형을 사용한다면 표준편차는 5% 이하로 줄어들 수 있을 것이다(Burcharth 1992; Kim et al. 2012a). 식 (4)에 의해 계산된 최초통과확률은 폭풍지속시간 t = 1000Tm 동안에 발생한 활동량 s가 허용활동량 sa를 최초로 초과할 확률이며 보다 상세한 계산과정은 Kim et al.(2012b)과 Kim(2012)에 소개되어 있다.
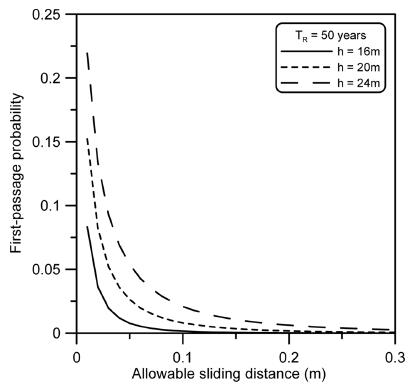
앞에서 언급했듯이 최초통과확률은 개별파에 의한 활동량이 허용활동량을 최초로 초과할 확률을 의미하기 때문에 최초통과확률을 산정하기 이전에 허용활동량의 크기를 정해야 한다. 여기서 허용활동량은 개별파에 의한 활동량을 의미한다. Kim et al.(2012b)이 허용활동량을 제안했지만 본 연구에서 식(1)을 사용하여 다시 검토하고자 한다. Fig. 4는 Kim et al.(2012b)과 동일하게 Table 6의 안전율 1.2로 설계한 단면에 대해서 산정한 최초통과확률이다. 비록 Kim et al.(2012b)은 허용활동량의 산정 시 FORM으로 계산한 Pf(0)을 사용하였지만 본 연구결과와 전반적인 경향성은 유사하게 관찰되었다. 왜냐하면 Pf(0)는 초기값을 결정하는 요소이기 때문에 허용활동량에 따른 최초통과확률의 변화에는 큰 영향을 주지 않는다. 따라서 허용활동량은 기존 연구와 동일하게 수리가능한계상태와 극한한계상태에서 각각 0.03 m와 0.1 m를 사용하였다.
Tables 9-11은 Table 1의 극치파고분포의 특성 조건과 다양한 수심에서 서로 다른 4 가지 설계법으로 산정된 케이슨 단면의 최초통과확률이다. Kim et al.(2012b)은 경험적인 방법으로 케이슨 활동의 평균발생율과 개별파에 의한 활동량분포함수를 제안했기 때문에 무차원화된 변수가 유효한 범위 안에 포함되어야 한다. 하지만 쇄파대 수심인 12 m에서 B/h가 상한값 1.4를 초과하는 경우가 발생하였다(Tables 9-11에서 기울임체로 표기함). 무차원 값 B/h가 상한값 1.4에서 멀어질수록 산정된 최초통과확률에 대하여 추가적인 검토 후에 신중하게 사용해야 할 것이다. 또한 유의파고의 불확실성의 분포함수로 정규분포를 가정했는데, 유의파고가 상한값 1.3Hs(= μHs + 3σHs )에 이르면 얕은 수심(h = 12 m)에서는 수심제한효과로 쇄파가 발생할 수 있다. 본 연구에서는 Burcharth and Sorensen(2005)이 제안한 Hs/h의 쇄파 상한값으로 0.72를 사용하였다. 이 값은 바닥경사가 가파를 경우에 적용되는 값으로 완만한 경사인 0.55보다 다소 크다. 한편, Smith et al.(1997)은 낙조류에서 불규칙파랑의 쇄파를 실험하여 쇄파한계파고(Hmomax = 0.1Ltanhkh)를 바닥경사와 관계없는 Miche(1951) 식의 형식으로 표현하였으며 이 값은 0.55와 0.72 사이에 존재한다. 따라서 본 연구에서는 바닥경사에 관계없이 일관성 있는 허용기준을 산정하기 위해 쇄파한계파고로 좀 더 보수적인 값을 채택하였다.
Table 9.
First-passage probability for different allowable sliding distances for Case 1
결과적으로 폭풍지속시간 1000Tm 동안에 허용활동량 0.03 m과 0.1 m를 최초로 초과하는 50년 빈도파 Hs의 최초통과확률을 각각 산정하였다. 이 때 개별파에 의한 허용활동량이 클수록 최초통과확률이 작아진다. 각 방법에서 산정된 값은 쇄파대(12 m, 16 m)와 비쇄파대(20 m, 24 m)의 구분 없이 상당히 일정한 범위 내에 분포하고 있다. 또한 허용활동량 0.03 m와 0.1 m를 각각 초과하는 확률은 대부분의 경우에 10%와 2%이 이내에 존재하는 것을 알 수 있다. 특히, 많은 경우에 허용활동량 0.1 m를 초과하는 경우는 거의 발생하지 않는다. 수심에 관계없이 가장 큰 최초통과확률은 γ50이 가장 큰 Case 1의 한 폭풍파의 기대활동량(SES)에서 관찰되었고 반대인 경우는 γ50이 가장 작은 Case 2의 초과확률(PE)에서 관찰되었다. 이는 Fig. 2에서 보인 바와 같이 전자의 단면이 가장 작았고 후자의 단면이 가장 컸기 때문이다.
3.3 허용최초통과확률의 결정
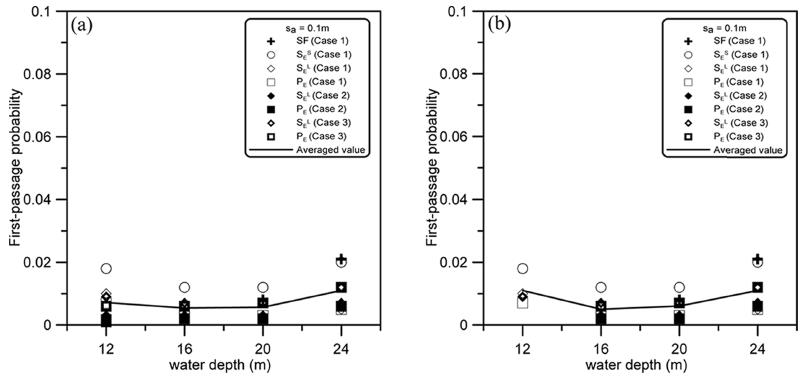
Figs. 5-6은 Tables 9-11을 수심에 따른 최초통과확률로 도식화한 것이다. 이들은 허용활동량 0.03 m와 0.1 m를 최초로 초과할 확률을 나타내고 있으며 확률값의 차이는 있지만 수심과 극치파고분포의 특성에 따른 경향은 유사하게 분석되었다. Figs. 5(a)와 6(a)는 B/h > 1.4인 경우를 포함한 경우이고 Figs. 5(b)와 6(b)는 유효한 범위 B/h > 1.4를 벗어나는 경우를 제외한 결과이다(B/h = 1.41의 경우는 포함시킴). 수심에 관계없이 두 경우 모두에서 최초통과확률은 일정한 범위 안에 분포하고 있다. 모든 수심에서 Case 1의 한 폭풍파의 기대활동량(SES) 조건으로 계산한 값이 가장 크고 Case 2의 초과확률(PE) 조건으로 계산한 값이 가장 작으며, 나머지 방법의 최초통과확률은 이 둘 사이에 존재하고 있다. 평균값과 가장 유사한 경우는 Case 3의 구조물 수명 동안의 기대활동량(SEL)과 초과확률(PE) 조건이다. 특히, 수심이 가장 얕은 12 m에서는 설계법에 따른 최초통과확률의 변동성이 가장 크게 나타났으며, 이는 쇄파효과와 B/h > 1.4인 경우를 포함하고 있기 때문이다. 그럼에도 불구하고 Figs. 5(a)와 6(a)에서 보듯이 유의범위를 벗어난 조건에서 산정된 최초통과확률도 전체적인 경향에서 크게 벗어나지 않아 허용최초통과확률의 산정 시 참고자료로 사용될 수 있다고 판단하였다.
Table 10.
First-passage probability for different allowable sliding distances for Case 2
Table 11.
First-passage probability for different allowable sliding distances for Case 3
본 연구에서는 여러 가지 설계법과 극치파고분포의 특성에 따라 산정된 최초통과확률을 평균하여 허용최초통과확률로 제안하였다. Table 12는 수심별로 평균한 최초통과확률과 수심에 관계없는 한계상태에 따라 제시한 허용최초통과확률이다. 결과적으로 수리가능한계상태 조건인 허용활동량 0.03 m와 극한한계상태 조건인 0.1 m를 최초로 초과하는 허용확률은 각각 5%와 1%로 제안한다. 구조물의 중요도에 따라 한계상태의 조건이 결정되며 이는 향후 연구에서 충분한 검토가 필요하다. 일반적으로 구조물의 변위를 많이 허용하지 않는 중요한 케이슨 방파제의 경우에는 수리가능한계상태를 사용할 수 있다.
Table 12.
Allowable first-passage probabilities in the present study
4. 구조물의 안정성 평가 사례
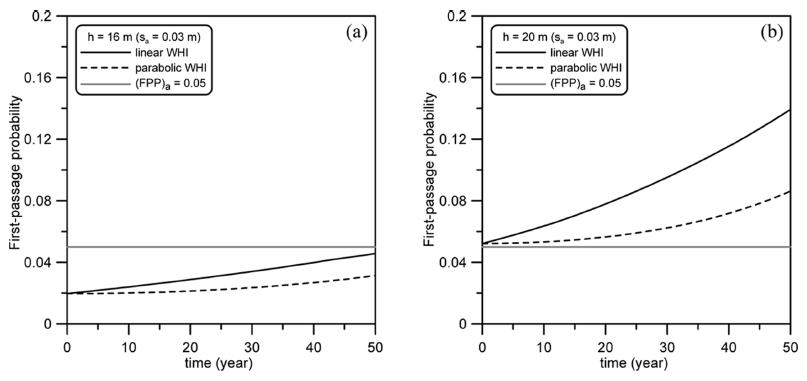
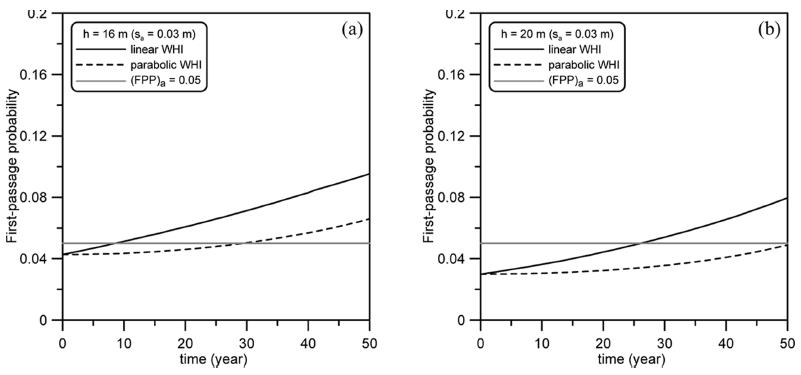
3절에서 각 한계상태에 따른 개별 허용활동량과 이에 대한 허용최초통과확률을 산정하였다. 본 장에서는 수리가능한계상태의 개별 허용활동량 0.03 m의 허용최초통과확률 5%를 사용하여 구조물의 안정성을 평가한다. 먼저, Table 6 (Case 1)의 안전율(S.F.)과 초과확률(PE)로 설계한 단면에 대해서 기후변화를 고려한 파랑 하중이 작용할 때의 최초통과확률을 산정하였다(Figs. 7, 8). 기후변화 효과는 Kim et al.(2012a)이 사용한 두 가지 심해파고 증가조건(포물선증가, 선형증가)을 사용하였다. 기후변화를 고려하면 심해파고와 그에 따른 주기와 폭풍지속시간이 변화하여 시간에 따라 최초통과확률이 변화한다. 전반적으로 기후변화로 인해 최초통과확률이 증가하며 특히 심해파고의 선형증가가 포물선 증가보다 큰 최초통과확률을 산정하다. Fig. 7은 수심 16 m와 20 m에서 안전율로 설계된 단면 조건에서 계산된 시간에 따른 최초통과확률이다. 수심 16 m에서는 기후변화를 고려하더라도 허용기준을 만족하지만 수심 20 m에서는 기후변화를 고려하지 않더라도 허용기준을 만족하지 못하고 있다. 이와 같은 현상은 안전율 설계법이 수심의 영향을 일관성 있게 고려하지 못하기 때문에 발생한다. 반면 성능설계법인 초과확률로 설계된 단면에서 계산된 최초통과확률은 수심의 영향을 상대적으로 덜 받는 것을 알 수 있다(Fig. 8). Fig. 8(a)에서는 기후변화를 고려하지 않을 경우에서는 허용기준을 만족하지만 기후변화로 인한 파고의 선형증가를 가정하면 10년 이후에 구조물은 불안정하게 된다. 같은 조건에서 파고의 포물선 증가를 가정하면 30년 이후에 구조물은 안정성을 잃게 된다. 한편, Fig. 8(b)인 좀 더 깊은 수심에서는 기후변화로 인한 파고의 선형 및 포물선 증가 시 각각 25년과 50년 이후에 구조물은 불안정하게 된다.
5. 결 론
본 연구에서는 직립방파제 케이슨의 개별 허용활동량과 이에 대한 허용최초통과확률의 기준을 수리가능한계상태와 극한한계상태에 대하여 제시하였다. 허용기준의 적용성을 높이기 위해 다양한 수심(쇄파대와 비쇄파대)과 극치파고분포의 특성을 반영하였다. 허용최초통과확률은 서로 다른 설계법으로 산정된 단면에 대해 최초통과확률을 산정하고 이를 평균하여 결정하였다. 여기서 수심에 관계없이 사용할 수 있는 허용기준을 제시하기 위해 약간 보수적으로 허용치를 선택하였다. 제안된 허용최초통과확률은 수리가능한계상태(개별허용활동량 0.03 m)와 극한한계상태(개별허용활동량 0.1 m)에서 각각 5%와 1%이다. 또한 결정론적 설계법과 성능설계법으로 설계된 단면에 대해서 허용최초통과확률을 적용하여 구조적 안정성을 평가하였다. 끝으로 보통의 중요도를 가지는 일반적인 직립방파제의 경우에서는 수리가능한계상태의 허용기준을 사용할 것을 권고한다. 본 허용기준으로 국내외에 시공된 방파제의 구조적 안정성을 평가하고 평가된 자료를 바탕으로 허용기준을 보완하고 개선해야 할 것이다. 이와 동시에 다양한 수리실험과 현장관측을 통해 허용기준을 평가하고 수정할 수 있을 것이다.