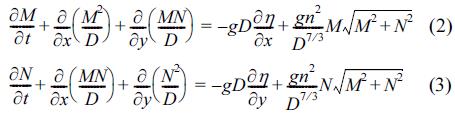1. Introduction
On 11th of March 2011, the Tohoku Earthquake with a magnitude of 9.0, which was the largest earthquake in the recorded history of Japan, occurred off the pacific coast of Japan. Tohoku region, which is located on the northern part of Honshu Island (the main island of Japan), has been devastated by some tsunamis in the past, such as the 1896 Meiji Sanriku Tsunami, the 1933 Showa Sanriku Tsunami, and the 1960 Chilean Tsunami. The countermeasures have been taken to prevent tsunami disaster. However, it was not sufficient against the tsunami generated by the Tohoku Earthquake. The tsunami caused catastrophic damages and a large loss of life. Sanriku coast, extending along the Pacific Ocean of Tohoku region, particularly suffered tsunami damages because of its indented coastline and the location close to the tsunami source. Mori et al. (2012) reported that the maximum inundation height exceeded 40 m in Miyako located along the Sanriku coast.
In western Japan, large earthquakes have occurred repeatedly along the Nankai Trough where the Philippine Sea Plate is subducting beneath the Eurasian Plate, as shown in Fig. 1. Five earthquakes occurred with a magnitude of 8 class in the last four centuries: the 1707 Hoei Earthquake, the 1854 Ansei Tokai Earthquake, the 1854 Ansei Nankai Earthquake, the 1944 Showa Tonankai Earthquake and the 1946 Showa Nankai Earthquake. Recently, there have been concerns about the occurrence of Tokai, Tonankai and Nankai earthquakes. Central Disaster Prevention Council (2003) estimated that the magnitude of these earthquakes would be at largest 8.7. However, it has been pointed out that the earthquakes with a magnitude of 9 class could strike in western Japan after the Tohoku Earthquake. Some studies have already investigated the tsunami characteristic of the earthquakes along the Nankai Trough (e.g., Imai et al., 2010; Furumura et al., 2011). However, there have been few studies about 9-magnitude earthquakes. The massive earthquakes could cause devastating tsunami damages in coastal areas where there have been no significant damages in the past, such as coastal land areas along three major bays of Tokyo Bay, Ise Bay and Osaka Bay.
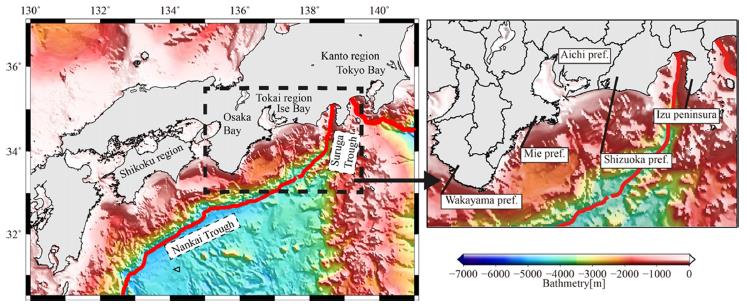
The purpose of this study is to investigate propagation characteristics of tsunamis generated by Tokai, Tonankai and Nankai massive earthquakes with magnitudes of 8.7 and 9.0 on the coasts of the three major bays and the Pacific coasts in western Japan, as shown in Fig. 2, by conducting numerical simulations using a depth-integrated two-dimensional numerical model.
2. Tsunami propagation simulation
2.1 Tsunami Propagation model
A depth-integrated two-dimensional numerical model based on nonlinear shallow water theory in Cartesian coordinate system was employed for numerical simulation of tsunami propagation due to Tokai, Tonankai and Nankai massive earthquakes. The numerical model adopted for simulating tsunami propagation in this study has been already validated through comparisons with the data collected during the tsunami events by 2011 East Japan Earthquake and 1983 central East Sea Earthquake (Lee et al., 2012). The governing equations consist of the continuity equation (Eq. 1) and the momentum equations (Eqs. 2 and 3) in the respective directions of x and y.
Continuity equation:
Momentum equation:
where η is the sea surface elevation, h is the still water depth, D=h+η is the total depth, and M and N are the horizontal components of the discharge flux. The discharge flux is a product of the total depth and depth-averaged velocity for each direction. g is the gravity acceleration, and n is Manning's roughness coefficient, which was assigned to the uniform value of 0.025 sm-1/3 in the sea area. The governing equations are solved by the staggered leap-frog method (Goto et al. 1997). The complete wave reflection condition was imposed as land boundary condition.
2.2 Tsunami Source
This study considers two different earthquake magnitudes, M8.7 and M9.0. The vertical sea bottom deformation data published by the Central Disaster Prevention Council (2003) was used as the tsunami source for M8.7. The tsunami source for M9.0 was estimated from that for M8.7 based on the Gutenberg-Richter relationship between seismic energy and magnitude (Eq. 4).
where E and M are seismic energy and earthquake magnitude.
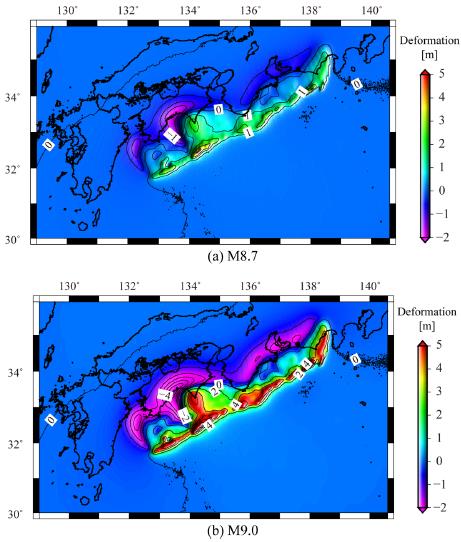
From Eq. 4, the seismic energy of M9.0 is 2.82 times as large as that of M8.7. Thus, the vertical sea bottom deformation in tsunami simulation for M9.0 was corrected by a factor of 2.82 under the assumption that the fault area of the Tokai, Tonankai and Nankai earthquakes, published by the Central Disaster Prevention Council (2003), does not change. Fig. 3 shows the spatial distributions of vertical sea bottom deformation due to the earthquakes, in which (a) and (b) denote M8.7 and M9.0. The uplifts of the bottom in M8.7 and M9.0 are 4.10 m and 11.56 m at largest, respectively. A significant uplift of more than 4 m is observed along the Nankai and Suruga Troughs in M9.0 showing in Fig. 3(b). For simplicity, the initial water level displacement is assumed to be equal to the vertical sea bottom deformation under the assumption that sea bottom instantly deforms after the initiation of the earthquakes.
2.3 Numerical condition
Tokai, Tonankai and Nankai massive earthquakes has large tsunami source area as indicated in Fig. 3, and the tsunami could propagate extensively. Numerical domain covers the Pacific coasts from Shikoku region to Kanto region and the coasts of the three major bays in this study, and was set up with consideration for computational load and the difference of high water level at each location. Four layers, namely Layers 1 (1350 m × 1350 m), Layer 2 (450m × 450m), Layer 3 (150m × 150m) and Layer 4 (50 m× 50m), were used in the numerical domain. Bathymetric of each resolution was provided by the Central Disaster Prevention Council, Japan. All the tide levels were assumed to be high water level. The numerical simulation was carried out for 360 min after the earthquake, and the computational time step was set to satisfy the CFL condition. Numerical conditions were summarized in Table 1.
3. Effect of earthquake magnitude on tsunami propagation characteristics
This chapter examines the effect of earthquake magnitude on tsunami propagation characteristics in the Pacific coasts and the three major bays by comparing the simulation results with two different magnitudes.
3.1 The Pacific coasts
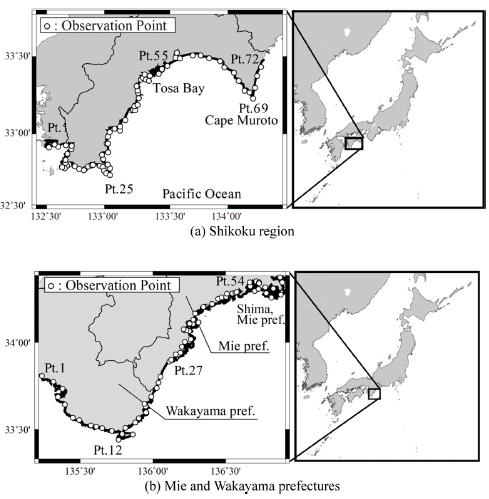
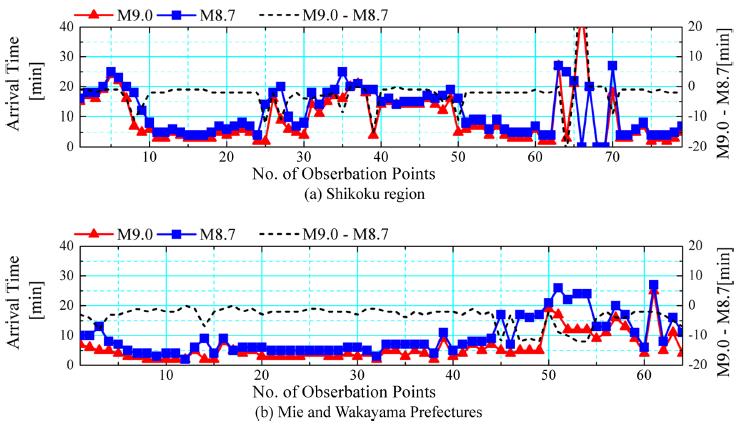
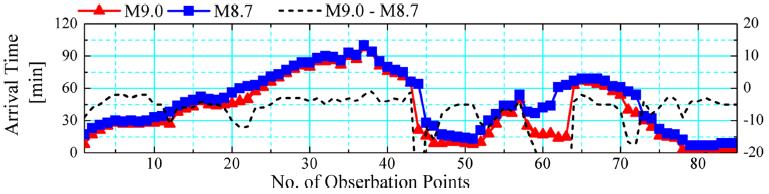
Observation points were set along the Pacific coast as shown in Fig. 4, and the tsunami height and the first tsunami arrival time were recorded at the observation points. The first tsunami arrival time was defined as the time when sea surface elevation was 20 cm higher than initial water level. The distributions of tsunami height and first tsunami arrival time on the Pacific coasts respectively are shown in Figs. 5 and 6, in which (a) and (b) indicate Shikoku region, and Mie and Wakayama prefectures. T.P. (Tokyo Peil) +0 m means the mean sea level in Tokyo Bay. Black dotted lines in Figs. 5 and 6 denote the ratio of the tsunami height for M9.0 to that for M8.7 and the difference in the first tsunami arrival time between M9.0 and M8.7.
It can be seen from Fig. 5, the tsunami height for M9.0 is found to be approximately twice as much as that for M8.7 on the Pacific coast. At the Cape Muroto, the tsunami height for M9.0 is more than three times, as shown in Fig. 5 (a). As indicated in Fig. 6, tsunami arrives within about 10 minutes after the earthquake at most of points in the case of M9.0 and M8.7, where there is little difference in terms of first tsunami arrival time between the two cases. Conversely, the first tsunami arrival time for M9.0 is slightly faster than that for M8.7 at the areas distant from the tsunami source, such as the coast of Shima, Mie prefecture. Although the relevant figures are not shown here, the first tsunami arrival time for M9.0 has been confirmed to be at most 20 minutes faster than that for M8.7 on the eastern coasts from the Izu peninsula. They are due to wave nonlinearity effect induced by the increase of tsunami height. Thus, the first tsunami arrival time is faster at some areas distant from the tsunami source. The tendencies of the first tsunami arrival time and the tsunami height presented herein are confirmed in other Pacific coasts in Japan.
3.2 The coast of three major bays
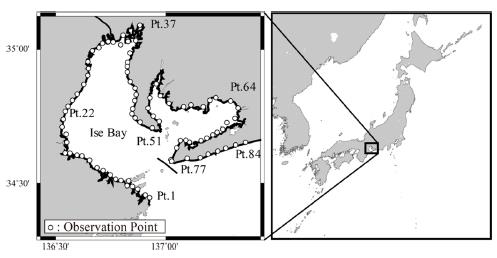
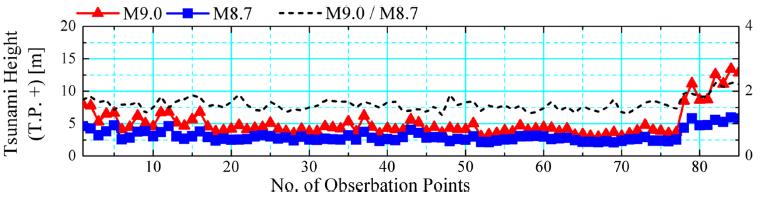
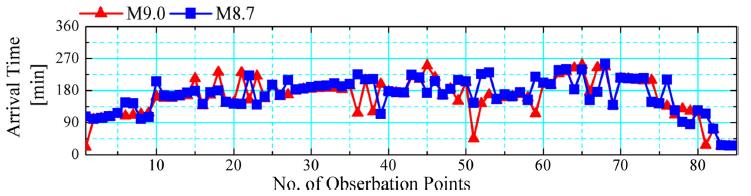
This section focuses on the coast of the Ise Bay as an example of the coast of the three major bays. The distributions of observation points, tsunami height, first tsunami arrival time and maximum tsunami arrival time on the coast of the Ise Bay are shown in Figs. 7~10, respectively.
It can be seen from Fig. 8 that the tsunami height for M9.0 is about one and a half times as compared to that for M8.7, and the ratio of the tsunami height for M9.0 to that for M8.7 decreases in comparison with the Pacific coasts. The tsunami height for M9.0 on the coast of Ise Bay (Pt. 1~77) is approximately T.P. +5 m, whereas it exceeds T.P. +10 m from the bay mouth to the Pacific coasts (Pt. 77~84). This is attributed to the narrow bay mouth, which prevent tsunami from propagating into the bay.
According to Fig. 9, the first tsunami arrival time for M9.0 is slightly faster than that for M8.7 at the bay head. As mentioned before, this is attributed to wave nonlinearity effect due to the increase of tsunami height. The effect becomes remarkable at the bay head because it is distant from the tsunami source, as shown in Fig. 3. The comparison between Figs. 9 and 10 shows that the maximum tsunami arrival time is much later than the first tsunami arrival time on the coast of the bay in the both cases of M9.0 and M8.7 while there is little difference on the Pacific coasts.
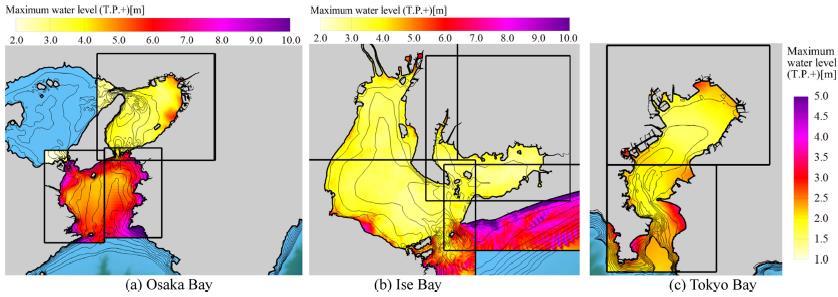
Results in the Osaka Bay and the Tokyo Bay, not shown here, are similar to those obtained in the Ise Bay. The tsunami height is approximately T.P. +5 m and T.P. +3 m on the coast of the Osaka Bay and the Tokyo Bay, respectively. The tsunami height of about T.P. +6 m at the head of the Ise Bay is the highest in the coasts of the three major bays.
4. Tsunami propagation characteristics of M9.0 Earthquake
4.1 The Pacific coasts
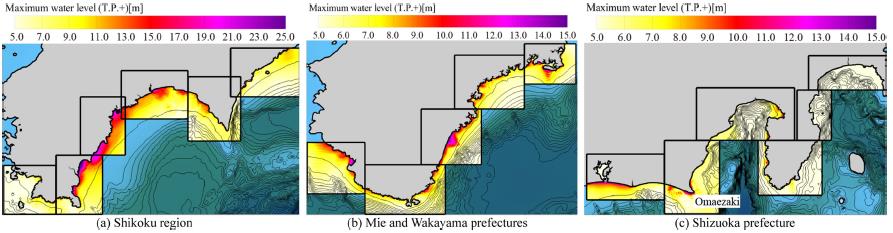
The spatial distributions of maximum water level in the case of M9.0 on the Pacific coasts are shown in Fig. 11, in which (a)~(c) denote the coast of Shikoku region, Mie and Wakayama prefectures, and Shizuoka prefecture. Maximum water level increases due to wave shoaling with decreasing water depth. The maximum water level in Shikoku region, which is close to the tsunami source, is found to be higher than compared to other Pacific coasts, and the maximum water level of more than T.P. +20 m is observed at the western coasts of Tosa Bay. In contrast, the maximum water level on eastern coasts from the Izu peninsula is much smaller than that on other Pacific coasts as shown in Fig. 11(c). The Izu peninsula acts as a natural breakwater, resulting in reducing tsunami height. Water level is found to be locally amplified on some coasts such as the coast of the Tosa Bay in Fig. 11(a), the coast of Mie Prefecture in Fig. 11(b) and the Omaezaki in Fig. 11(c). In Shima, Mie prefecture, the coast is a ria type one with indented coastline as well as the Sanriku coast of Tohoku region which was devastated by the 2011 Tohoku Earthquake tsunami. Around the Omaezaki, the shallow topography extends seaward in a tongue shape. The local geometry is assumed to lead to an amplification of water level. In the Tosa bay and the southern coast of Mie prefecture, it can be considered that the water levels are locally amplified because tsunamis are trapped and propagate along the coastline by forming edge wave.
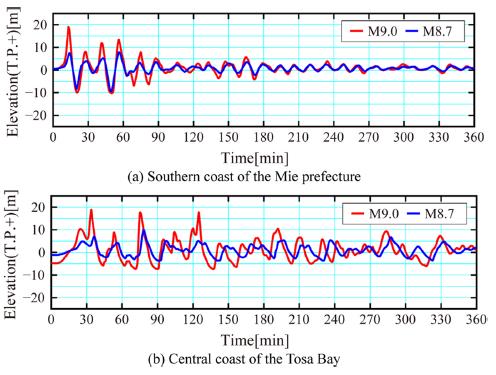
Fig. 12 shows the time series of water surface elevation on the Pacific coast, in which (a) and (b) denote the southern coast of Mie prefecture (Pt. 27 in Fig 4(b)) and the central coast of Tosa Bay (Pt. 55 in Fig 4(a)). As shown in Fig. 12 (a), the first tsunami wave is the largest at the southern coast of Mie prefecture. On the other hand, at the central coast of the Tosa Bay, the second wave arrives just after the first wave, which becomes the largest, as shown in Fig. 12(b). The period, when water level exceeds T.P. + 0 m in the first tsunami, reaches approximately 30 minutes at the central coast of Tosa Bay, which is long as compared to the southern coast of Mie prefecture. In addition, the water level exceeds T.P. + 5 m at approximately 5.5 hours after the earthquake at the central coast of the Tosa Bay, whereas sea surface elevation goes up and down at a short period at the southern coast of Mie prefecture. This result implies that it is important to consider not only maximum tsunami height but also tsunami duration in discussing tsunami hazard.
4.2 The coast of three major bays
Fig. 13 represents the spatial distributions of maximum water level in the three major bays in the case of M9.0, in which (a) ~ (c) denote the Osaka bay, the Ise Bay and the Tokyo Bay, respectively. The tsunami heights inside the bays are relatively small in comparison to the outside of the bays because the bays are enclosed by narrow bay mouths. However, the tsunami height locally increases at some area of the bay heads due to wave shoaling with local topography.
As an example of tsunami propagation in the bays, the time variation of tsunami propagation in Ise Bay is shown in Fig. 14. Tsunami arrives at the bay mouth at approximately 20 minutes after the earthquake and then propagates radially toward the bay head at 40 minutes after the earthquake. The tsunami propagation speed decreases inside the bay because of shallower water depth, and it takes more than an hour to arrive at the bay head from the bay mouth .The second tsunami approaches the bay mouth at 80 minutes after the earthquake. The second tsunami approaches from east and propagates along the Atsumi peninsula, whereas the first tsunami approaches the bay mouth from southeast. This is due to that the tsunami propagates in alongshore direction due to the bathymetry feature on the western coasts of Shizuoka prefecture. Furthermore, the tsunami repeatedly approaches the bay even after 120 minutes while the height of tsunami gradually decreases with time. Local amplification of tsunami is also found to be induced by wave reflection and refraction, and the sea level is recognized to stay high in the bay after 160 minutes.
Conclusions
In the present study, the numerical simulations of Tokai, Tonankai and Nankai massive earthquakes with two different magnitudes of earthquake of M8.7 and M9.0 are performed in order to investigate tsunami propagation characteristics on the Pacific coasts and three major bays of Tokyo Bay, Ise Bay and Osaka Bay using a depth-integrated two-dimensional numerical model. It was revealed from numerical results that tsunami heights for M9.0 were about twice as much as that for M8.7 on the Pacific coasts and the first tsunami arrival time for M9.0 is slightly faster in comparison with that for M8.7 at some areas distant from the tsunami source because of wave nonlinearity effect. In addition, high water level in the bays was also found to continue for a long time because of the enclosed bays.