1. 서 론
우리나라 남해안에서 관측되는 극치파랑(extreme wave)의 대부분은 태풍에 의해 생성되는 반면에 동해지역의 극치파랑은 폭풍에 의해 주로 발생되는 특성이 있다. 동해 폭풍은 계절풍 기후에 의하여 추계에서부터 이듬해 춘계 사이에 한반도에 영향을 미치며, 따라서 동해지역의 폭풍파랑 발생도 이 기간에 집중되는 특성이 있다. 특히 동해 폭풍파랑은 먼 바다에서 긴 취송거리를 통과하면서 너울성파랑의 형태로 전파하여 해안선의 현지 기상상태에 관계없이 내습하여 적지 않은 인명피해를 유발시키기도 한다(National Emergency Management Agency, 2013). 동해안에 내습하는 너울성파랑에 의한 피해를 줄이기 위해서는 이의 발생 가능성을 사전에 인지하고, 이를 바탕으로 위험 예상 지역 내에 있는 현지주민이나 관광객 들에게 경고를 하는 것이 필요하다. 이를 위해서는 실시간 파랑관측자료 또는 기상예보자료에 기반한 풍파 수치모의 실험 결과를 통해 너울성파랑의 원인이 되는 동해 심해역의 폭풍파랑을 예·경보할 필요가 있다. 그러나 국내의 경우, 동해 심해역에 대한 양질의 파랑관측자료가 거의 없는데다가 장기간의 동해 폭풍파랑 수치모의실험을 통한 수치모형을 검증한 사례가 많지 않아 이를 수행하기 힘든 실정이다.
특히 국내의 수치모의실험 연구사례를 보면, 3세대 풍파모형인 WAVEWATCH-III 및 SWAN에 기반한 동해 폭풍파랑 수치모의실험이 다수 진행되어 왔다(Kim et al., 2010; Lee et al., 2010; National Emergency Management Agency 2013). 이 중 Lee et al.(2010)은 심해역 파랑 수치모형인 WAVEWATCH-III를 이용해 2008년 2월에 발생한 동해 폭풍파랑을 계산하였는데, 너울성파랑에 의한 해난사고가 발생한 강릉항 및 일본 도야마만 지역에 대해서는 4단계 둥지형 격자(nested grid)를 도입하여 상세 파랑 계산을 수행하였다. 도야마만에 대한 Lee et al.(2010)의 계산결과는 관측결과와 잘 일치하고 있었지만, 강릉항에서의 계산 유의파고 및 유의파주기는 전반적으로 과소산정되고 있었다. 특히 유의파주기의 과소산정폭은 유의파고보다 큰것으로 나타났다. 한편 Kim et al.(2010)은 구조격자(structured grid) 및 비구조격자(unstructured grid) SWAN 모형을 이용해 Lee et al.(2010)과 동일한 기간에 대한 동해 폭풍파랑을 계산하였다. 이에 따르면, 격자 종류에 관계없이 최대 유의파고를 약간 과대산정하고 있었지만, 파주기는 반대로 과소산정하고 있었다. 특히 비구조격자를 사용하였을 경우에 대한 파주기의 과소산정 폭이 더욱 컸었는데, 이는 National Emergency Management Agency(2013)에서도 나타나고 있었다. National Emergency Management Agency(2013)은 2012년 12월에 대한 폭풍파랑을 계산하고, 후포지역에 대한 파랑계산결과를 관측결과와 함께 비교하였는데, 이에 따르면 유의파고의 RMSE는 0.45m에 지나지 않았지만, 첨두주기는 약 2.45 s 정도 과소산정하고 있었다. 이처럼 동해안 지역에 대한 폭풍파랑 수치모의실험 사례를 보면, 대체로 유의파고의 정확도는 어느 정도 만족할만한 수준이었지만, 파주기는 전반적으로 과소산정하고 있었다. 이와 같은 파주기의 과소산정 경향은 월파고의 과소산정으로 이어지기 때문에 동해안 지역에서의 너울성파랑에 위험정도를 실제보다 낮게 평가할 가능성이 높다.
이에 본 연구에서는 신속하고 정확한 너울성파랑을 예·경보하기 위한 기초 연구로 국립해양조사원의 KOGA-E01 파랑관측자료 분석을 통해 동해 심해역의 폭풍파랑 특성을 분석하였으며, 이에 대한 결과로 동해 심해역의 파랑특성 외에 파향에 따른 폭풍파랑의 유의파고 및 유의파주기 분포 특성 등을 제시하였다. 또한 효과적인 너울성파랑 예·경보를 위해 본 연구진이 개발한 심해부터 천해까지 적용 가능한 수정 WAM모형을 이용하여 동해 폭풍파랑 수치모의실험을 수행하였다. 본 연구에 사용된 Chun et al.(2006, 2007, 2008)의 수정 WAM모형은 유한차분법(finite difference method)에 기반하고 있기 때문에 천해지역에 대해 상세한 파랑계산을 얻기 위해서는 둥지형 격자가 추가적으로 필요하다. 그러나 둥지형 격자체계를 도입하게 되면, 계산속도가 현저하게 저하되는 측면이 있기 때문에, 본 연구에서는 5분 간격의 격자간격만을 사용하는 폭풍파랑 수치모의실험을 구축하였다. 이 때 구축한 수치모의실험으로 2013년에 발생한 주요 폭풍파랑들을 재현한 다음, 계산결과를 관측결과와 함께 비교하여 본 수치모의실험의 계산성능 및 정확도를 검증하였다. 수치모형의 검증은 심해역 뿐만 아니라 천해역에 대해서 수행함으로써 본 수치모형의 천해역 적용 정확성도 함께 검토하였다.
2. 동해 심해역 폭풍파랑 특성 분석
2.1 동해 심해역 파랑특성 분석
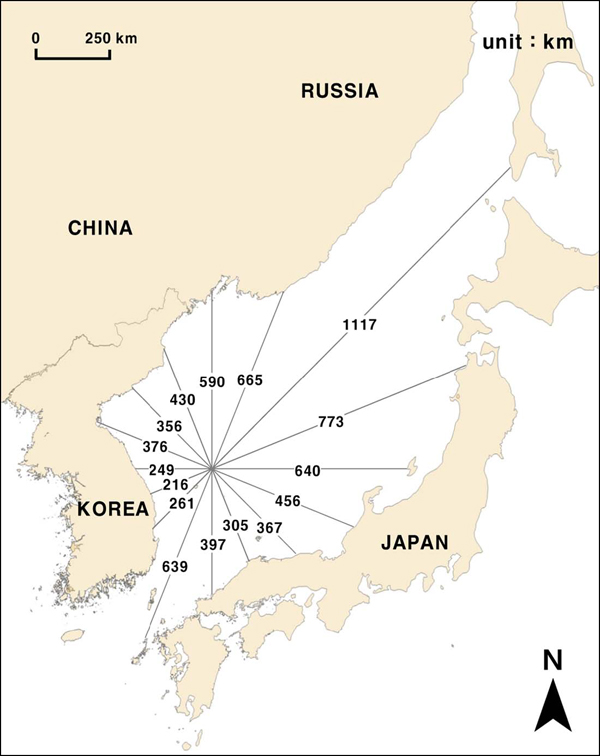
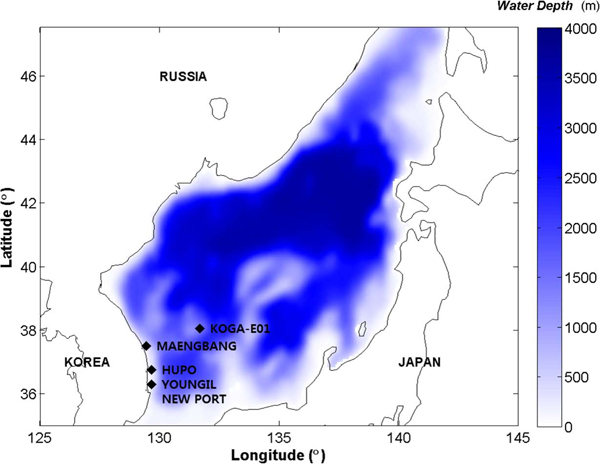
국립해양조사원의 KOGA-E01 파랑자료는 국립해양조사원이 2012년 11월 울릉도 북동쪽 해상에 설치한 부이형 파고계로 관측한 것으로, 이의 위치를 16방위에 대한 취송거리(wind fetch)와 함께 Fig. 1에 표시하였다. Fig. 1에서 볼 수 있듯이 파랑관측지점의 북쪽에서부터 동쪽 방향으로의 바람 취송거리가 길게 뻗어 있어, 본 파고계에서는 동계 계절풍에 의한 너울성 폭풍파랑을 관측하기에 적절하다. 이 외에 이 지점을 중심으로 남남서 방향에 대한 바람취송거리도 충분히 확보되어 있어 하계 계절풍에 의한 파랑현상도 관측하기에 적절해 본 파랑관측자료는 동해 전 해역의 파랑특성을 이해하기에 적절하다고 판단된다. 본 파랑관측자료는 2012년 12월 부터 자료가 공개되어 있어, 본 연구에서는 이 시점부터 2013년 12월까지 1년 정도의 자료를 입수하여 분석하였다.
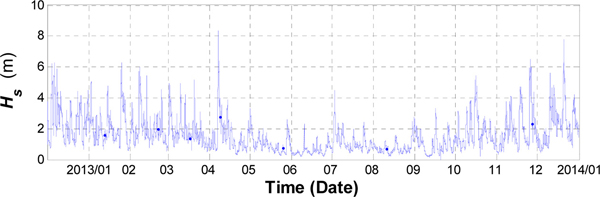
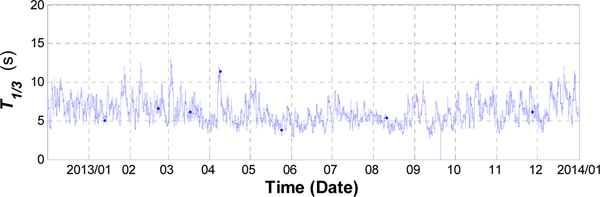
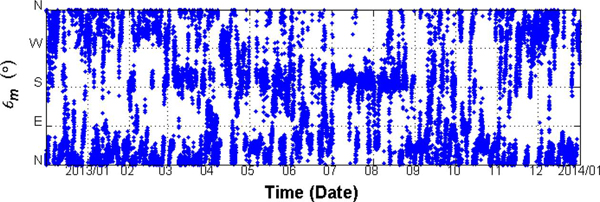
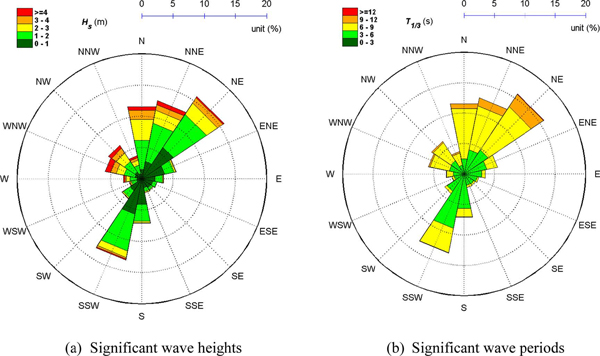
파랑관측자료 해석에 앞서 파랑관측자료 중 유의파고 Hs, 유의파주기 T1/3, 평균파향 θm 등의 시계열 자료를 Fig. 2~Fig. 4에 나타내었다. 이에 따르면 KOGA-E01 파랑관측자료에는 전형적인 계절별 특성이 반영되어 있는데, 5월~9월까지는 유의파고 및 유의파주기가 모두 낮게 나타나다가, 10월 부터 그 이듬해 4월까지 다시 증가하는 것을 볼 수 있다. 이러한 계절적 변화는 유의파고 및 유의파주기뿐만 아니라, 평균파향에서도 나타나고 있다. Fig. 4에서 볼 수 있듯이 NW~NE 계열의 파랑이 전반적으로 우세한 가운데, 하계시에 S 및 SSW 계열의 파랑의 출현율이 높게 나타나고 있다. 이러한 특성을 정리하여 Table 1에 나타내었다.
Table 1에서 보면, 계절에 따른 풍속 크기의 변화가 유의파고 및 유의파주기에 반영된 결과, 동계시에 비교적 큰 유의파고 및 유의파주기를 가진 파랑이 하계시에 다시 감소하는 특성을 보이고 있다. 그리고 평균파향의 평균값은 164.45o로 나타나고 있는데, 이는 N~E 계열의 파랑이 전반적으로 우세한 가운데, 하계시에 S계열 파랑 출현율이 높게 나타난 결과 때문이다.
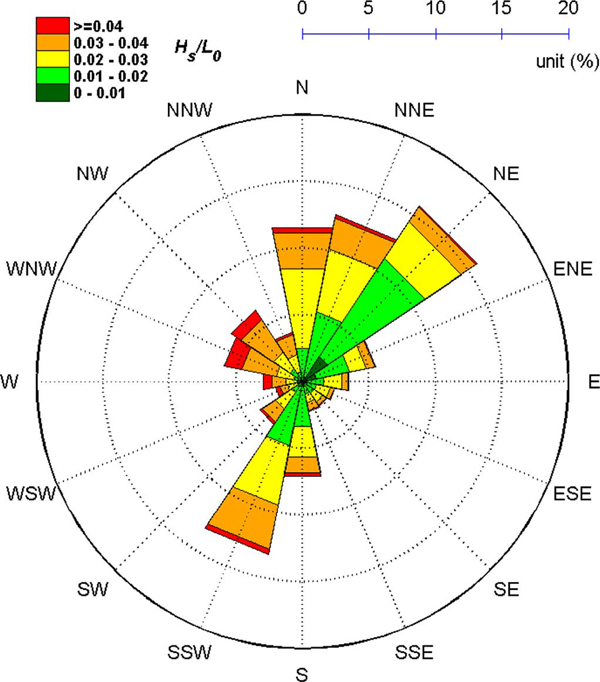
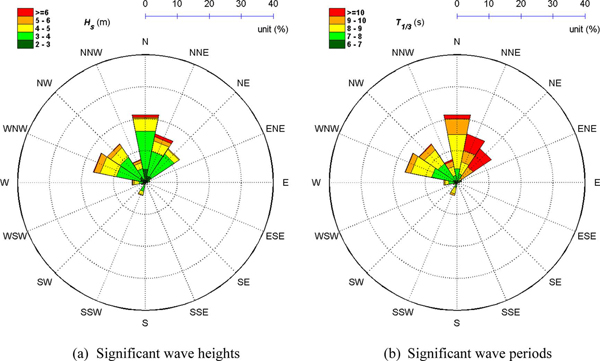
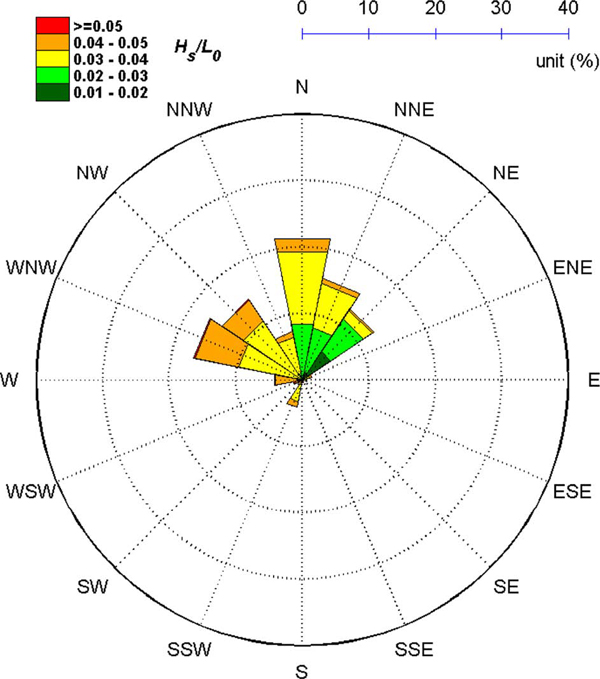
파랑에 대한 바람의 영향은 계절적 차이를 나타낼 뿐만 아니라, 파향에 따른 유의파고 및 유의파주기의 분포에도 영향을 미치는데, 이를 정리하여 Fig. 5에 나타내었다. 이에 따르면 동해 폭풍파랑의 주요 방향으로 알려져 있는 N~NE 계열의 파랑뿐만 아니라 SSW 계열 파랑의 출현율이 비교적 높은 것으로 나타나고 있다. 이 중 SSW 계열의 파랑은 파랑 출현율이 높은 데에 비해 고파랑 출현비율은 현저히 낮은 편이다. 이는 이들 파랑이 하계 계절풍의 작용에 의한 것으로, 하계시 남남서풍의 출현빈도가 높아 SSW계열의 파랑출현율이 높게 나타나지만, 하계시의 풍속은 크지 않아 유의파고는 낮은 것에서도 확인되는데, 6초 이하의 유의파주기의 비율이 다른 파향에 비해서 월등히 높아 전반적으로 유의파주기 또한 낮은 것으로 파악되고 있다. 한편 Fig. 5(a)의 유의파고 분포도를 보면, 4 m 이상의 유의파고는 WNW~NE계열의 파랑을 중심으로 높은 출현율을 보이고 있다. 이 중 WNW계열의 파랑에서 고파랑 출현율이 상대적으로 높게 나타나는 반면에, NE계열의 파랑에서는 고파랑 출현율이 비교적 낮게 나타나고 있다. 그러나 유의파주기의 분포는 이와 반대로, 9초 이상의 유의파주기는 NE 계열 파랑에서 가장 높은 출현율을 보이고 있다. 이러한 파랑 분포 특성은 파장 대비 파고의 비인 파형경사도에서도 확연하게 나타나는데, Fig. 6에서 보면, WNW, NW 계열의 파형경사도가 비교적 높은 반면에 NE 계열 파랑의 파형경사도가 상대적으로 낮게 나타나고 있다. 이는 북서방향의 짧은 취송거리를 따라 강한 북서풍이 작용한 결과로 인해 이들 방향에서는 풍파성향의 파랑이 발달한 반면에, NE계열의 파랑은 상대적으로 긴 취송거리로 인해 너울성파랑의 성향이 크게 나타난 결과로 파악된다.
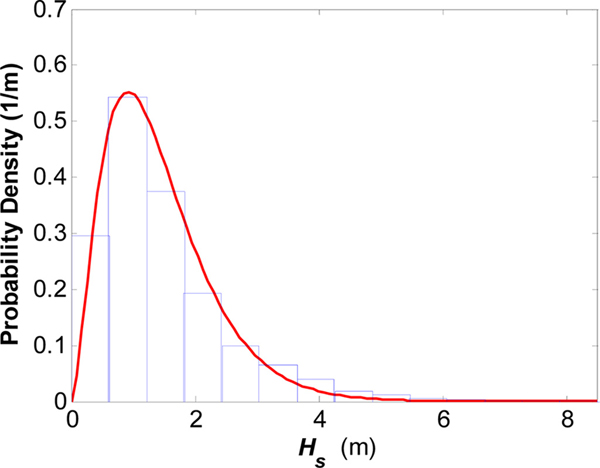
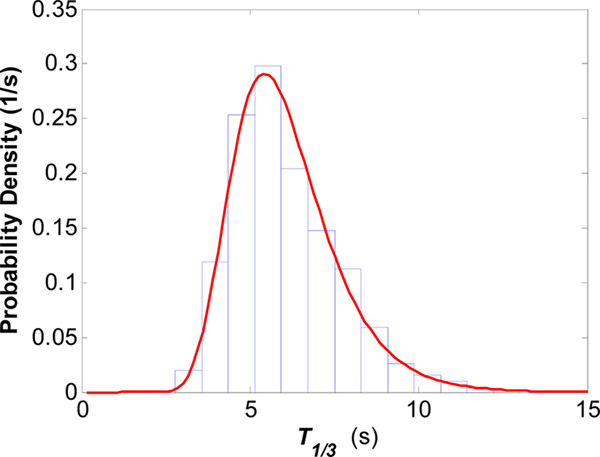
이 외에 본 연구에서는 KOGA-E01 파랑관측 결과 얻은 유의파고 및 유의파주기의 확률 분포 특성을 보기 위해 각각에 대한 확률밀도분포를 산정하고 그 결과를 Fig. 7과 Fig. 8에 각각 나타내었다. 이들에 나타나 있는 확률밀도분포함수는 각각 Generalized Gamma 분포 함수, Box-Cox 변환 함수로 이들 함수의 모수 산정 과정은 Ahn et al.(2013)에 소개되어 있어 본 논문에서 이에 대한 기술은 생략한다. Fig. 7과 Fig. 8에 있는 유의파고 및 유의파주기에 대한 확률밀도 분포함수식을 식 (1)과 식 (2)에 각각 나타내었다.
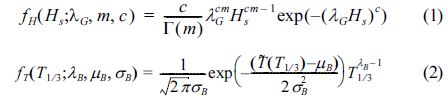
식 (1)에서 λG, m, c는 각각 Generalized Gamma 분포함수의 모수로 그 값은 각각 λG = 1.23, μB = 2.1 , σB = 1.12와 같다. 식 (2)에서 λB, μB, σB는 Box-Cox 변환함수의 모수로 그 값은 λG = -0.17, μB = 1.53 , σB = 0.18 과 같으며,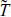 
는 Box-Cox 변환된 파주기를 나타내는데, 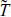= (TλB1/3 - 1) / λB와 같이 쓸 수 있다. 식 (1)과 식 (2)는 유의수준 0.05에서 K-S및 χ2-test 를 통과하였는데, 이로부터 특정 유의파고 또는 유의파주기의 확률을 구할 수 있을 뿐만 아니라, 각각에 대한 최빈도값(most probable value)도 구할 수 있다. 최빈도 유의파고 및 최빈도 유의파주기는 각각의 평균값과는 다른 것으로 통계적으로 출현빈도가 가장 높은 값을 나타내는데, 본 연구에서는 식 (1)과 식 (2)을 각각 미분한 ∂fH / ∂Hs = 0, ∂fT / ∂T1⁄3 = 0 을 만족하는 유의파고와 유의파주기를 각각에 대한 최빈도값으로 정의하였다. KOGA-E01 지점에서의 최빈도 유의파고 및 유의파주기는 식 (3)과 식 (4)와 같은 방법으로 산정하였다.
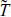는 Box-Cox 변환된 파주기를 나타내는데, 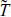= (TλB1/3 - 1) / λB와 같이 쓸 수 있다. 식 (1)과 식 (2)는 유의수준 0.05에서 K-S및 χ2-test 를 통과하였는데, 이로부터 특정 유의파고 또는 유의파주기의 확률을 구할 수 있을 뿐만 아니라, 각각에 대한 최빈도값(most probable value)도 구할 수 있다. 최빈도 유의파고 및 최빈도 유의파주기는 각각의 평균값과는 다른 것으로 통계적으로 출현빈도가 가장 높은 값을 나타내는데, 본 연구에서는 식 (1)과 식 (2)을 각각 미분한 ∂fH / ∂Hs = 0, ∂fT / ∂T1⁄3 = 0 을 만족하는 유의파고와 유의파주기를 각각에 대한 최빈도값으로 정의하였다. KOGA-E01 지점에서의 최빈도 유의파고 및 유의파주기는 식 (3)과 식 (4)와 같은 방법으로 산정하였다.
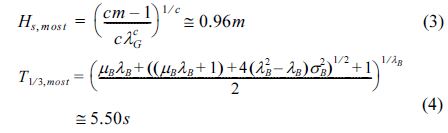
2.2 동해 심해역 폭풍파랑 특성 분석
동해안 폭풍파랑에 의한 너울성파랑을 예·경보하기 위해서는 먼저 폭풍파랑의 기준과 특성을 정량화할 필요가 있다. 폭풍파랑의 기준을 정량화하기 위해서는 장기간 측정된 파랑관측자료의 극치분석을 통해 정의하는 것이 타당하나, 현재 본 과업에서 확보하고 있는 파랑관측자료 길이가 길지 않아 차선책으로 식 (3)의 최빈도 유의파고보다 큰 유의파고를 가진 파랑자료의 시계열 자료를 분석하였다. 유의파고 시계열 자료는 30분 길이의 파랑자료의 유의파고로 이루어져 있다. 유의파고 시계열 자료 중에서 식 (3)의 최빈도 유의파고 보다 크며, 시계열에서 직전 및 직후의 유의파고 보다 큰 유의파고를 첨두 유의파고로 정의하였다. 본 논문에서는 폭풍파랑을 나타내는 기준 유의파고로 방금 전에 정의한 첨두 유의파고의 산술평균으로 정의하여 사용하였다. 이 때 추출된 표본의 폭풍파랑을 나타내는 기준 유의파고는 2.77 m 로, 본 연구에서는 기준 유의파고 보다 큰 파랑을 폭풍파랑으로 정의하였다. 이를 적용한 결과, 2012년 12월부터 2014년 1월까지의 13개월 동안 114건의 폭풍파랑이 KOGA-E01에서 관측된 것으로 집계되는데, 이는 연간 약 105개의 폭풍파랑이 발생한 것과 같다. 이 때의 폭풍파랑 발생빈도를 월별로 집계하여 Table 2에 나타내었으며, 이에 따르면 동계 계절풍이 한반도에 영향을 미치는 시기인 10월부터 이듬해 4월까지 폭풍파랑이 주로 발생하는 것으로 나타나고 있다. 그러나 하계인 7월에도 폭풍파랑이 일부 발생한 것으로 확인되는데, 이는 태풍의 소멸에 따른 저기압이 동해상에 진출한 결과이다. 이에 대한 예로 발생한 폭풍파랑으로 2012년의 경우 태풍 ‘카눈’의 소멸에 따른 저기압에 의해 동해 연안역에서 해난사고가 잇따라 발생한 경우를 들 수 있다.
폭풍파랑의 유의파고 및 유의파주기의 파향별 분포특성은 Fig. 9에 정리하여 나타내었다. 이에 따르면 폭풍파랑은 WNW~NE 방향에서 높은 출현율을 보이고 있으며, 이러한 경향은 Fig. 5에서 보여진 것과 대체로 일치하고 있다. 이는 각 파향별 폭풍파랑 출현율을 나타내는 Table 3에서도 확인된다. 전체 폭풍파랑의 86.9%이 WNW~NE방향에서 출현하고 있는데, 그 중에서도 N계열의 폭풍파랑 출현율이 가장 높은 것으로 파악되고 있다. 이는 너울성파랑의 근원이 되는 폭풍파랑이 NE파향과 같은 특정 방향에서만 발생한다는 일반적인 가정과 배치되는 것으로, 특정 파향을 가정해 너울성파랑을 예·경보하는 것은 보다 깊은 주의를 기울여야만 함을 시사한다. 한편 6 m 이상의 유의파고를 가진 폭풍파랑은 N, NNE계열을 따라 주로 출현하는 반면에, 너울성파랑의 주요 방향으로 알려져 있는 NE계열의 폭풍파랑에는 6 m 이상의 유의 파고가 나타나지 않는 것으로 파악되고 있다. 이러한 특성은 파향별 폭풍파랑의 평균값에도 반영되는데, NNW, N, NNE, NE 계열의 폭풍파랑 유의파고의 평균은 각각 4.6 m, 3.8 m, 3.6 m, 3.3 m 으로 NE 계열 폭풍파랑의 유의파고가 비교적 낮은 것으로 파악되고 있다. 이러한 유의파고의 특성은 동해기단계의 폭풍파랑이 NE계열에 대해서 출현하다가, 폭풍파랑이 완전히 발달했을 경우에 N 또는 NNE 등으로 파향이 바뀐다. 이로 인해 NE계열 폭풍파랑의 유의파고가 N계열 폭풍파랑의 유의파고보다 낮은 것으로 파악된다. 그러나 폭풍파랑의 유의파주기 분포 패턴은 이와 다른 분포 특성을 보이는데, NNW, N, NNE, NE 계열의 폭풍파랑의 유의파주기의 평균은 각각 8.7 s, 8.6 s, 8.7 s, 9.3 s 으로 오히려 NE계열의 폭풍파랑의 유의파주기가 가장 큰 것으로 나타나고 있다. 이는 북동방향의 긴 취송거리가 북동풍에 지속적으로 노출된 결과, NE계열 폭풍파랑의 유의파주기가 상대적으로 크게 발달하지만, N 또는 NNE 계열의 폭풍파랑은 강풍을 동반한 폭풍이 비교적 제한된 시간 내에 영향을 미쳐 유의파주기는 상대적으로 짧은 것으로 보여진다. 한편, 이와 같은 파향별 유의파고 및 유의파주기의 분포 특성으로 파향별로 서로 상이한 파향경사도 분포를 나타내며, Fig. 10에서 보면, NE 방향에 대한 폭풍파랑의 파형경사도는 비교적 낮아 너울성파랑 성향이 강한 반면에, 그 외 나머지 파향의 폭풍파랑은 풍파성향이 강한 것으로 파악되고 있다.
한편 본 연구에서는 폭풍파랑 유의파고의 유의성(significance)을 보기 위해 추출된 폭풍파랑 자료를 GPD (Generalized Pareto Distribution) 함수에 적용하여 각 폭풍파랑의 출현확률을 산정하였다. Chun et al.(2013)이 부산항에서의 극한파랑의 재현주기를 산정하기 위해 GPD함수를 도입한 바 있으며, 이의 확률밀도분포함수 및 누적확률분포함수를 식 (5)와 식 (6)에 각각 나타내었다.
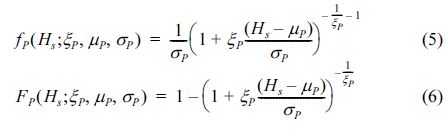
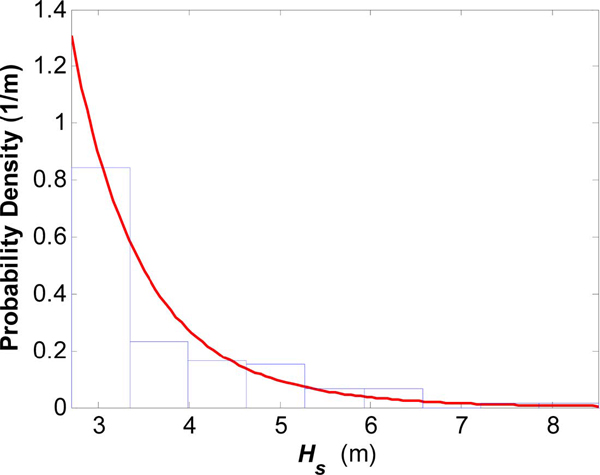
여기서 ξP, μP, σP Generalized Pareto 함수의 모수로 본 연구에서는 Singh and Guo(1995)의 최대엔트로피법(maximum entropy method)를 사용하여 이들을 산정하였다. 이 때 산정된 Generalized Pareto 함수의 모수는 ξP = 0.1, μP= 2.79, σP= 0.86 이며, 유의수준 0.05에서 K-S 및 χ2-test 를 통과하였다. 폭풍파랑 유의파고의 출현확률밀도를 식 (5)의 확률밀도분포함수와 함께 Fig. 11에 나타내었다.
연평균 폭풍파랑 발생 횟수가 산정되어 있기 때문에 식 (5)의 모수들을 식 (6)에 대입하여 각 유의파고에 대한 재현주기 산정이 가능하다. 그러나, 파랑관측자료의 길이가 길지 않기 때문에 이 때 산정된 재현주기의 신뢰도 또한 제한적이다. 예를 들면 2013년 4월 7일에 관측된 유의파고 크기는 8.34 m인데, 식 (6)에 의한 재현주기는 약 1.4년 정도 된다. 당시 기상현상이 이례적으로 극심하지 않아 이의 재현주기 또한 크지 않을 가능성이 높지만, 파랑관측자료의 길이가 비교적 짧아 재현주기가 낮게 산정되었을 가능성도 배제할 수 없다. 이에 본 연구에서는 식 (6)을 이용해 2013년에 발생한 주요 폭풍파랑의 출현확률만을 산정하여 관측된 폭풍파랑 유의파고의 유의성을 확인하였다. 2013년 4월 7일, 2013년 12월 20일에 KOGA-E01 에서는 8.34 m, 7.78 m 의 유의파고가 관측되었으며 이를 식 (6)에 적용한 결과, 각각에 대한 출현확율은 0.68%, 1.02%로 나타나고 있다. 그리고 동해 연안역에 큰 피해를 입힌 바 있는 2013년 10월 15일경의 폭풍파랑의 출현확율은 6.70 %로 나타나고 있다. 이에 본 연구에서는 이들 수치모의실험을 통해 이들 폭풍파랑을 재현하고자 한다.
3. 폭풍파랑 수치모의 실험
3.1 수정 WAM모형
본 연구의 수치모형인 수정 WAM모형은 Chun et al.(2006, 2007, 2008)이 기존 WAM 모형을 천해역에 적용할 수 있도록 확장한 것으로, 천해역의 파랑작용인 쇄파, 3파 상호 작용등이 포함되어 있을 뿐만 아니라, 음해법(implicit scheme)에 기반하여 효과적으로 파랑에너지의 전달을 계산할 수 있다. 이의 지배방정식은 SWAN또는 WAVEWATCH-III와 동일한데, 이를 식 (7)에 나타내었다.
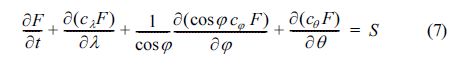
식 (7)에서 F는 파랑에너지 스펙트럼을 나타내며, 이 외에 λ, φ, θ는 각각 경도, 위도, 파향 등을 나타낸다. S는 파랑작용과정을 나타내는데, 바람에 의한 파랑에너지 생성 Sin, 쇄파에 의한 파랑에너지 감소 Sbr, 바닥 마찰에 의한 파랑에너지 감소 Sbf , 백파(white capping)에 의한 파랑에너지 감소 Sds, 4파 상호작용에 의한 파랑에너지 전달 Snl4, 3파 상호작용에 의한 파랑에너지 전달 Snl3등이 포함되어 있다. 수정 WAM모형의 파랑작용과정은 Chun et al.(2007, 2008)에 자세히 설명되어 본 논문에서 이에 대한 기술을 생략한다. 본 수치모형의 천해역 파랑계산 성능은 현장관측 및 수리모형실험과의 비교를 통해 이미 검증되었으며, 특히 Chun(2012)은 해빈류 계산을 위해 본 수치모형을 쇄파대에까지 성공적으로 적용한 바 있다. 그리고 식 (7)에서 cλ, cφ, cθ는 λ, φ, θ방향에 대한 파랑에너지의 전달속도를 나타내는 것으로 이에 대한 식을 식 (8)~식 (10)등에 나타내었다.
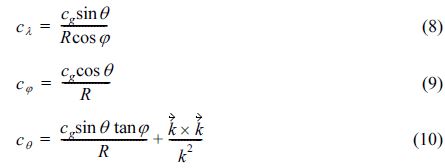
여기서, cg,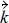 
, k는 각각 군속도, 파수벡터, 그리고 파수를 나타낸다. 그리고 R은 지구둘레를 나타내며 약 40,000 km 정도 된다. 한편, 식 (7)의 지배방정식 자체는 파랑작용 평형식(wave action balance equation)과 동일하나, 직각격자체계가 아닌 구면격자체계에 대한 것으로, 이 때문에 식 (7)의 cθ에는 파랑 굴절에 의한 파향변화 뿐만 아니라, 위도에 따른 파향 변화도 고려되어 있는데, 이는 식의 첫번째 항과 같다(Komen et al., 1994). 그런데, 식 (7)이 구면격자체계가 아닌 직각격가체계에 대해서 수치모의 실험을 실시할 경우, 식 (11)과 같은 과정을 통해, 이 항은 식 (7)의 세번째 항과 함께 소거되기 때문에 식 (7)이 구면격자체계에 대한 수치모형이지만, 직각격자체계에 대해서도 적용이 가능하다.
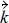, k는 각각 군속도, 파수벡터, 그리고 파수를 나타낸다. 그리고 R은 지구둘레를 나타내며 약 40,000 km 정도 된다. 한편, 식 (7)의 지배방정식 자체는 파랑작용 평형식(wave action balance equation)과 동일하나, 직각격자체계가 아닌 구면격자체계에 대한 것으로, 이 때문에 식 (7)의 cθ에는 파랑 굴절에 의한 파향변화 뿐만 아니라, 위도에 따른 파향 변화도 고려되어 있는데, 이는 식의 첫번째 항과 같다(Komen et al., 1994). 그런데, 식 (7)이 구면격자체계가 아닌 직각격가체계에 대해서 수치모의 실험을 실시할 경우, 식 (11)과 같은 과정을 통해, 이 항은 식 (7)의 세번째 항과 함께 소거되기 때문에 식 (7)이 구면격자체계에 대한 수치모형이지만, 직각격자체계에 대해서도 적용이 가능하다.
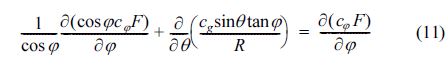
3.2 수치모의 실험 조건
본 연구에서는 효과적인 동해지역에서의 폭풍파랑 계산을 수행하기 위해, NOAA에서 제공하는 ETOPO5 수심자료를 이용하여 5분 간격의 수심도를 구성하였는데, 이를 Fig. 12에 나타내었다. 이의 계산영역은 경도 및 위도 방향으로 각각125oE ~ 145oE, 35oN~47.5oN 이며, 이에 대한 격자개수는 241×151이다.
파랑스펙트럼은 25개의 주파수와 48개의 파향 성분으로 나타내었다. 이는 Phadke et al.(2003)가 태풍파랑 계산을 위해 제안한 파랑스펙트럼의 성분개수와 동일하다. 본 연구의 수치모의 실험에서 사용한 파랑스펙트럼의 주파수를 식 (12)에 나타내었다.
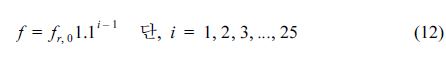
여기서 fr,0는 최소 주파수를 나타내며, 이 값은 0.04 Hz 와 같다. 이에 따라 본 연구의 수치모의실험은 2.5~25 s 사이의 주기에 대해 파랑계산이 가능하다. 한편 효과적인 파랑계산을 위해 본 연구의 수치모의 실험에서 시간격자간격으로 10분을 사용하였으며, 이에 따른 λ, φ, θ방향에 대한 최대 Courant number를 식 (13)에 나타내었다. 식 (13)에 따르면 θ방향으로의 Courant number가 10.4인데, 이는 공간 성분인 λ 및 φ에 비해서 확연히 높다. 이는 Fig. 12의 영역에 대한 파랑계산을 위해서는 군속도에 관계없이, cθ 때문에 시간격자간격을 1 분으로 해야만 함을 의미한다. 아니면 방향격자 개수를 줄여야만 하는데, 이 경우에는 불안정한 계산결과를 얻을 수도 있다(Phadke et al., 2003). 이는 기존 WAM모형의 계산시간의 약 10% 정도의 계산시간으로 본 연구의 수치모형이 구동됨을 의미한다.
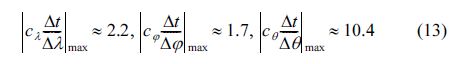
3.3 해상풍 자료
파랑은 바람에 의해 생성되기 때문에 정확한 파랑 후측모의를 수행하기 위해서는 정확한 바람장 정보가 먼저 제공되어야만 한다. 이에 본 연구에서는 일본 기상청의 바람 예보자료를 이용하여 파랑 계산을 수행하였으며, 일본 기상청의 바람장 정보는 중규모(Meso-Scale Model)의 수치모의 실험 결과로 제공되는 자료로 풍속 관측계(Wind profilers), 도플러레이다(Volume Vleocity Processing), ACARS(Aircraft Communications Addressing and Reporting System)등의 관측자료와 자료동화를 거쳐 비교적 높은 정확도를 확보하고 있다. 본 기상 자료는 경도 및 위도 방향으로는 3.75분, 3분 격자 간격으로 정의되어 있는 바람장이 1시간 간격으로 제공되고 있으며, 본 연구에서는 선형 내삽(linear interpolation)을 적용해 본 연구의 격자에 맞게 재구성하여 수치모의 실험을 실시하였다. 본 연구의 수치모의 실험 기간 중 주요 폭풍에 대한 바람장들을 Fig. 14, Fig. 16, 그리고 Fig. 18에 나타내었다.
3.4 2013년 3·4월 폭풍파랑 수치모의 실험
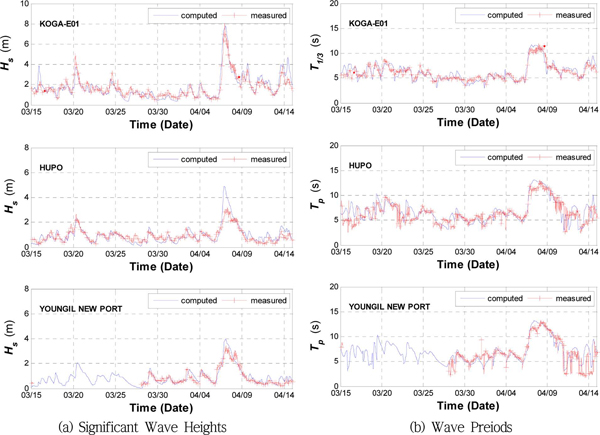
먼저 본 연구에서는 2013년 3월 15일부터 2013년 4월 15일 까지 파랑 수치모의실험을 실시하고, KOGA-E01, 후포항, 영일신항에 대한 유의파고 및 파랑주기 계산결과를 관측결과와 함께 Fig. 13에 나타내었다. 이 중 Fig. 13(a)는 유의파고에 대한 것으로, 2013년 4월 7일 07:30 시경에 KOGA-E01 에서 8.34 m 의 유의파고가 관측되었는데, 본 연구의 계산결과 얻은 유의파고 크기는 7.77 m 로 약 57 cm 정도 과소산정하였다. 하지만 동일한 시기에 대해 후포항 및 영일신항과 같은 천해역 지점의 유의파고 계산결과는 과대산정되고 있는데, 특히 후포항에서의 계산결과는 관측결과보다 1.83 m 더 큰 것으로 나타나고 있다. 이는 본 연구의 수치모의 실험에서 광역계산격자를 사용한 탓에 현지 수심 및 바람장을 고려하지 못하게 되었고, 이로 인해 바닥 마찰 및 백파(white-capping) 에 의한 파랑에너지 감소를 적절히 재현하지 못한 결과로 보여진다. 이 기간을 제외하고 본 연구의 수치모의 실험이 전반적으로 잘 일치하고 있으며, 이는 Table 4에서도 확인된다. Table 4는 파랑계산결과의 정확도를 bias, RMSE, SI, r등으로 정리하여 나타내었는데, 이는 Pilar et al.(2008), Rusu et al.(2008) 등이 수치모의실험의 정확도를 정량적으로 평가하기 위해 도입한 바 있다. 이들의 식을 식 (14)~식 (17)에 각각 나타내었다.
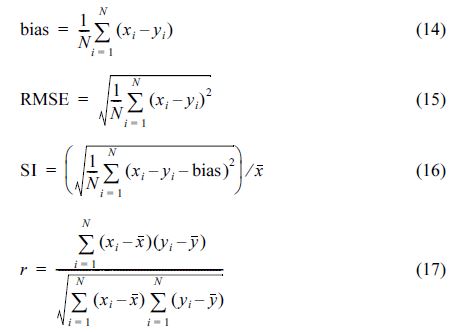
Table 4
Accuracy of the numerical simulation for March, 15, 2013 ~ April, 15, 2013
여기서 xi와 yi는 관측결과와 계산결과를 나타내며,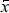 
와 
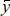는 각각의 평균값이다. Table 4 를 보면, 본 연구의 계산결과가 약 6~17 cm 정도 과소산정하고 있지만, Pearson 상관관계 계수 r은 0.85~0.92에 달하고 있어 본 연구의 계산결과의 정확도가 비교적 높은 것으로 파악되고 있다. 이를 보다 자세히 살펴보면 r은 천해역보다 심해역에서 더욱 높게 나타나고 있는데, 이는 본 연구의 수치모의 실험에서 사용한 계산 격자가 큰 탓에 천해역 파랑을 재현하는 데 한계가 있었기 때문이다. 그러나 평균제곱근오차 RMSE는 천해역보다 심해역에서 더욱 크게 나타나는데, 이는 KOGA-E01 지점에서의 유의파고 큰 탓에 오차 또한 크게 나타나는 결과로 파악된다. 실제로 KOGA-E01 에서의 SI는 0.29 정도 되는데, 그 크기는 영일신항 및 후포항의 58%~68%에 지나지 않는다.
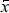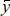와 는 각각의 평균값이다. Table 4 를 보면, 본 연구의 계산결과가 약 6~17 cm 정도 과소산정하고 있지만, Pearson 상관관계 계수 r은 0.85~0.92에 달하고 있어 본 연구의 계산결과의 정확도가 비교적 높은 것으로 파악되고 있다. 이를 보다 자세히 살펴보면 r은 천해역보다 심해역에서 더욱 높게 나타나고 있는데, 이는 본 연구의 수치모의 실험에서 사용한 계산 격자가 큰 탓에 천해역 파랑을 재현하는 데 한계가 있었기 때문이다. 그러나 평균제곱근오차 RMSE는 천해역보다 심해역에서 더욱 크게 나타나는데, 이는 KOGA-E01 지점에서의 유의파고 큰 탓에 오차 또한 크게 나타나는 결과로 파악된다. 실제로 KOGA-E01 에서의 SI는 0.29 정도 되는데, 그 크기는 영일신항 및 후포항의 58%~68%에 지나지 않는다.
Fig. 13(b)는 파랑계산결과 얻은 파주기를 관측결과와 함께 나타낸 것으로 KOGA-E01에서는 유의파주기에 대한 결과가 제시되어 있는 반면에, 후포항 및 영일신항에서는 첨두주기에 대한 결과가 제시되어 있다. 본 연구의 수치모형이 파랑스펙트럼 계산을 통해 파랑 에너지의 생성 및 전달을 예측하기 때문에 KOGA-E01 에서도 첨두주기를 비교해야만 한다. 그러나 KOGA-E01 에서는 파랑주기로 유의파주기만을 제공하기 때문에, 본 연구에서는 파랑계산결과 얻은 첨두주기를 유의파주기로 변환한 다음 이를 관측결과와 함께 비교하였다. Fig. 13(b)에 따르면 후포 및 영일신항의 경우, 일정 기간 동안 첨두주기가 4~8 초 사이에 불규칙한 패턴을 가지며 분포하는 것을 볼 수 있다. 이들 구간을 제외한 나머지 기간에 대한 계산결과는 관측결과와 잘 일치하고 있다. 실제로 Table 4 에서 보면, KOGA-E01 지점의 r은 0.90 정도 되며 천해역 지점인 후포항 및 영일신항 지역에서의 r은 0.79, 0.74 정도 되는 것으로 나타나고 있다. 천해역에서 낮은 상관관계 계수는 관측결과에 포함되어 있는 불규칙한 패턴의 첨두주기를 제대로 재현하지 못한 데에다가 연안역에서의 정확한 수심 및 바람장을 고려하지 못한 결과 상대적으로 정확도가 떨어진 것으로 파악된다. 그리고 유동장이 파주기에 영향을 미치는데, 본 연구의 수치모의 실험에서는 이를 고려하지 않아 파주기의 계산결과의 정확도가 낮은 것으로 보여진다. 이러한 경향은 본 연구의 계산결과뿐만 아니라, Pilar et al.(2008)에서도 확인되고 있다. Pilar et al.(2008)의 계산결과의 경우, 평균주기의 r이 0.70~0.78 사이에 분포하는 반면에 유의파고의 r은 0.81~0.93 사이에 분포하고 있는 것으로 파악되고 있다.
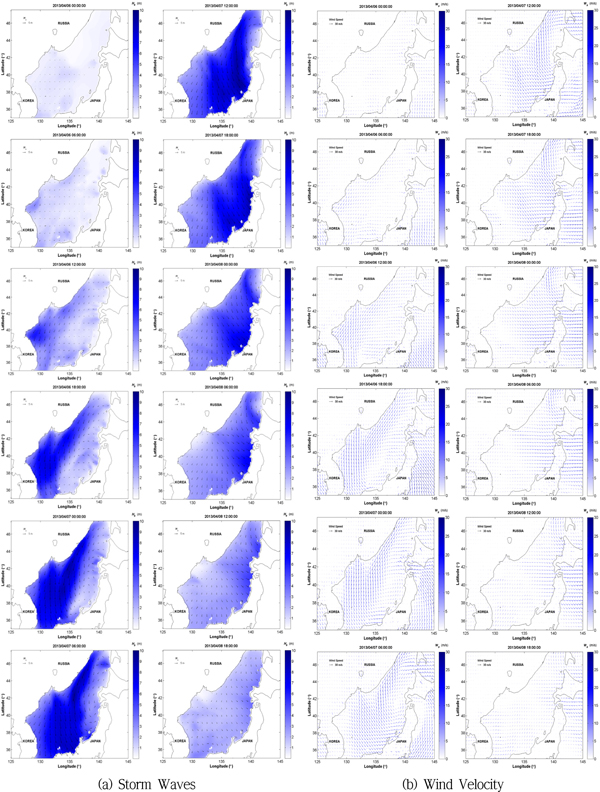
한편, 본 연구에서는 폭풍파랑 발달과정을 보기 위해 고파랑이 나타난 시점을 전후한 폭풍파랑 및 바람장의 분포를 Fig. 14에 나타내었다. 이에 따르면 2013년 4월 6일 06:00 시경에 러시아 연해주 연안을 따라 북동풍이 작용하고 있으며, 이로 인해 2013년 4월 6일 12:00 시에 강원도 지역을 중심으로 2~3 m 정도의 고파가 형성되어 있는 것을 볼 수 있다. 이 때 당시의 고파랑은 북동풍의 작용으로 더욱 크게 발달하는데, 2013년 4월 7일 00:00 시에는 일본 서해안을 제외한 동해 대부분의 지역에서 5~8 m 정도에 이르는 것을 볼 수 있다. 이 시점 이후 풍향이 북동풍에서 북서풍으로 서서히 바뀜에 따라, 파향도 NW계열의 파랑으로 전환되는데, 한반도 동해안에서의 유의파고 크기도 점차 줄어들어, 2013년 4월 8일 00:00시경에 동해 연안역의 유의파고 크기는 1~2 m정도 분포하고 있는 것으로 파악되고 있다. 그러나 일본 서해안은 북서풍의 직접적인 영향을 받아 당시 유의파고 크기가 5~6 m 정도 이르는 것으로 파악된다.
3.5 2013년 10월 폭풍파랑 수치모의 실험
2013년 10월 15일경에는 폭풍파랑의 작용으로 인해 우리나라 연안에서 해난사고가 다수 발생하였는데, 본 연구에서는 수치모의 실험을 통해 이를 재현하고, KOGA-E01, 맹방 해수욕장, 후포항에서 파랑 계산결과들을 관측결과와 함께 Fig. 15(a)를 보면, KOGA-E01에서의 유의파고는 5.42 m에 지나지 않았지만, 당시 맹방 해수욕장이나 후포항에서 각각 5.35 m, 4.19 m 의 유의파고가 관측되었다. 이처럼 당시 천해역 및 심해역에서의 유의파고는 거의 비슷한데, 이러한 특성은 Fig. 13의 경우와 확연히 다른 것으로, 이는 당시 러시아 연해주 일대에서 형성된 폭풍이 한반도 인근해역에 제한적인 영향을 준 결과로 보여진다. 당시의 폭풍파랑 및 바람장의 발달양상을 Fig. 16에서 나타내었으며, 이에 따르면 폭풍 바람장이 러시아 연해주 일대에서 형성되었다가 남하하면서 고파랑이 형성되는 것을 볼 수 있다.
Fig. 15(a)의 유의파고 계산결과를 보면, 본 연구의 계산결과가 관측결과와 전반적으로 잘 일치하고 있으나, 후포 및 맹방 해수욕장의 경우 고파랑이 나타난 2013년 10월 15일 당시의 본 연구 계산결과가 과대산정되고 있다. 고파랑 당시의 과대산정 경향은 3.4절에서 기술한 바와 같이 본 연구의 계산격자가 정밀하지 못한 결과로 보여지며, 본 수치모의실험의 정확도는 Table 5에서 확인되고 있다. 여기에 나타나 있는 본 수치모의실험의 정확도는 Table 4 의 것과 대체로 유사하며, 파주기의 계산결과의 정확도 또한 2013년 3~4월에 대한 계산결과 정확도와 유사한 것으로 파악되고 있다.
Table 5
Accuracy of the numerical simulation compared with wave measurements during October, 2013
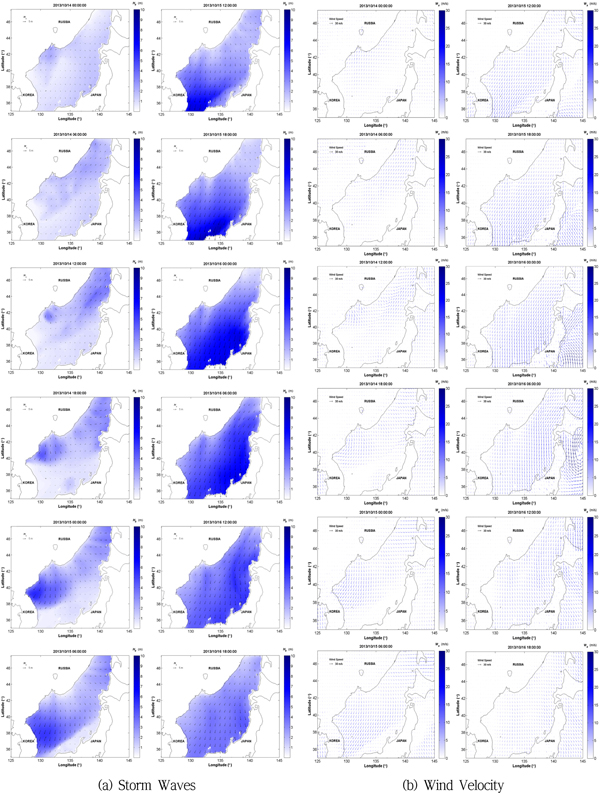
2013년 10월 15일 당시의 폭풍파랑 및 바람장의 발달양상을 Fig. 16에 나타내었다. 이에 따르면, 폭풍파랑이 발달하기 전인 2013년 10월 14일 12:00 시경에는 남서풍이 주도적이었는데, 이에 따라 당시 파랑 역시 SW계열의 파랑이 동해 전역에서 우세한 것으로 나타나고 있다. 이 후 러시아 연해주를 중심으로 북동 계절풍이 작용함에 따라 강원지역을 중심으로 고파랑이 발달해 있는 것을 볼 수 있는데, 북동풍 작용영역이 확대됨에 따라 한반도 동해안을 중심으로 고파랑이 발달하여 강원 지역의 경우 3~4 m 의 유의파고가 나타나고 있다. 그리고 동해 전역에서 북동계절풍이 나타나는 2013년 10월 15일 18:00 시경에는 울산 외해측에서 7~8 m 의 유의파고가 형성된 것을 볼 수 있다. 당시 울산지역에서는 고파랑에 의해 발생된 월파가 해안 저지대에서 침수를 야기한 바 있다. 이후 풍향이 북서풍으로 바뀜에 따라 유의파고도 낮아지면서 파향 또한 줄어드는 것으로 파악되고 있다.
3.6 2013년 12월 폭풍파랑 수치모의 실험
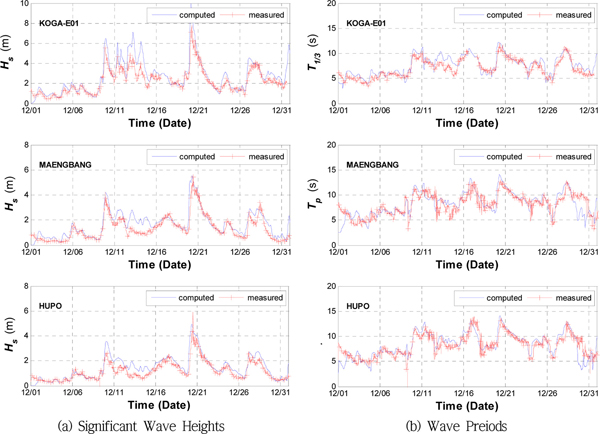
마지막으로 2013년 12월의 경우, 동해역에 진출한 온대성 저기압으로 인해 동해 전역에서 강풍을 동반한 고파랑이 발생하였는데, 본 연구에서는 이에 대한 계산결과를 관측결과와 함께 Fig. 17에 나타내었다. Fig. 17(a)의 유의파고 계산 결과를 보면, 고파랑이 나타난 2013년 12월 20일 경에 KOGA-E01 지점에서 본 연구의 파랑계산 결과가 약 2.22 m 정도 과대산정하고 있는 반면에, 맹방 해수욕장이나 후포항에서는 0.8 m 정도 과대산정하거나 1 m 정도 과소산정하고 있는 것으로 파악되고 있다. 이러한 계산결과 패턴은 이전 수치모의실험 결과들과 그 특성이 다른데, 이는 본 연구에서 사용한 바람장 분포에 의한 것으로 보여진다. Fig. 18(b)을 보면, 본 연구의 바람장 바람에너지가 KOGA-E01 지점을 중심으로 집중도가 높게 나타난 결과로 인해 연안역에서의 풍속은 비교적 낮고 심해역에서는 매우 높게 형성되어 있는 것을 볼 수 있는데, 이러한 바람장 분포 패턴이 KOGA-E01지점에 대한 파랑계산결과가 과대산정되고 있는 것으로 파악된다. Table 6에서 보면, 이 때 당시의 과대산정 결과로 KOGA-E01에 대한 평균 오차량 및 평균제곱근 오차 모두 크게 나타나고 있지만, 그 외 나머지 기간에 대한 계산결과가 관측결과와 잘 일치해 r은 0.94로 나타나고 있었다. 이는 KOGA-E01뿐만 아니라 후포항이나 맹방 해수욕장에서도 r이 0.90이상 나타나는 등, 2013년 12월에 대한 수치모의실험 결과가 다른 계산결과에 비해서 가장 정확한 것으로 파악되고 있다. 이 외에 Fig. 17(b)의 파주기 계산결과를 보면 전반적으로, 본 연구의 계산결과가 관측결과와 잘 일치하는 것으로 나타나고 있는데, Table 6에 따르면, 이의 정확도는 앞서의 계산결과들과 유사한 것으로 파악되고 있다.
Table 6
Accuracy of the numerical simulation compared with wave measurements for December, 2013
고파랑이 나타난 시점인 2013년 12월 20일을 전후한 파랑발달 양상을 당시의 바람장과 함께 Fig. 18에 나타내었다. Fig. 18(b)를 보면 태풍의 눈과 같은 온대성저기압의 중심점이 동해 중부역에서 지속적으로 남하하다가 2013년 12월 20일 18:00 시에 소멸한 것을 볼 수 있다. 이 때 당시의 폭풍파랑 패턴은 태풍파랑과 유사하나, 이와 달리 온대성 저기압 중심의 서쪽 영역을 따라 고파랑이 발달하는 것을 볼 수 있다. 이는 온대성 저기압이 남하함에 따라 온대성 저기압 중심점의 서쪽에 강풍이 형성된 결과로, 이들 지역에서 약 10 m정도되는 유의파고가 형성되어 있는 것을 볼 수 있다. 한편, 2013년 12월 20일 12:00 이후 온대성 저기압이 점차 소멸됨에 따라 동해역에서의 고파랑 또한 낮아지고 있지만, 온대성저기압에 뒤이어 작용한 북서계절풍이 동해역에 영향을 미쳐 한반도 동해안에는 약 2~3 m 의 유의파고가 형성되어 있는 것을 볼 수 있다.
4. 결 론
우리나라 동해안은 해마다 너울성파랑에 의한 피해가 발생하고 있는데, 이를 줄이기 위해서는 사전에 너울성파랑의 발생을 인지하고 예·경보하는 과정을 통해 너울성파랑에 의한 피해를 줄이는 것이 중요하다. 본 연구에서는 이를 위한 기초단계로 파랑관측자료를 바탕으로 너울성파랑의 원인이 되는 동해역의 폭풍파랑 특성을 분석하고, 수정 WAM수치모의 실험을 구축한 다음, 이를 이용하여 몇몇 폭풍파랑을 재현하여 파랑관측 자료와 비교하였다.
본 연구에서는 국립해양조사원의 KOGA-E01 파랑관측자료 분석 결과 얻은 최빈도 유의파고를 이용하여 폭풍파랑을 정의한 다음, 이를 바탕으로 동해 심해역의 폭풍파랑 특성을 규명하였다. 본 연구의 분석에 따르면 기존에 알려진 것과 달리 동해역의 폭풍파랑은 WNW~NE계열에서 주로 출현하며, 이 중에서도 N계열의 폭풍파랑 출현율이 가장 높은 것으로 분석되었다. 이는 파랑관측자료를 기반으로 너울성파랑을 예·경보할 때, 특정 방향을 가정하여 분석할 경우 세심한 주의가 필요함을 의미한다. 이 외에 폭풍파랑의 유의파고 및 유의파주기는 파향에 따라 서로 다른 분포 특성을 가지고 있었다. 예을 들면, KOGA-E01 지점에서 취송거리가 가장 긴 북동방향의 경우 6 m 이상의 유의파고를 가지는 폭풍파랑이 없었으나 유의파주기는 가장 큰 것으로 파악되고 있다. 이는 동해 폭풍파랑 발달 단계에 따라 나타나는 현상으로, 초기 단계에서는 북동풍의 지배를 받다가 폭풍파랑 발달단계가 진행됨에 따라 북풍 및 북북동풍의 영향을 받은 결과로 보인다. 이러한 파랑발달 과정은 본 연구의 수치모의실험에서 확인되었다. 한편 이처럼 서로 다른 파향별 유의파고 및 유의파주기의 분포특성 때문에 파향에 따라 폭풍파랑 성향도 다른 것으로 나타났는데, NE 계열의 폭풍파랑은 상대적으로 너울성 파랑의 성향이 강한 반면, 그 외 나머지 파랑은 풍파 성향이 강한 것으로 파악되고 있다.
이 외에 본 연구에서는5분 간격의 격자에 기반한 수치모의 실험을 구축하고, 이를 이용하여 2013년 3·4월, 2013년 10월, 2013년 12월에 대한 폭풍파랑 수치모의 실험을 실시한 다음, 천해역 및 심해역에서의 관측결과와의 비교를 통해 본 연구의 파랑계산 결과를 검증하였다. 본 연구의 계산결과에 따르면 유의파고의 평균제곱근 오차는 심해역보다 천해역에서 더욱 낮게 나타나고 있었지만, 상관관계 계수는 이와 반대로 천해역보다 심해역에서 더욱 높게 나타나는 특성이 있었다. 이는 심해역에서의 유의파고 크기가 천해역보다 큰 결과 오차가 더욱 크게 나타나는 결과로 SI값으로 확인된다. 한편 본 연구의 수치모의 실험을 통해 폭풍파랑의 발달 양상을 볼 수 있었는데, 본 연구의 계산결과에 의하면, 폭풍파랑이 발달할 시점에는 북동풍이 작용하다가, 이후 파랑발달과 함께 점차 풍향이 반시계 방향으로 바뀌면서 폭풍이 소멸될 무렵에는 북서풍이 지배적인 것으로 나타나고 있었다. 동해역의 폭풍파랑 역시 이러한 풍향 패턴에 연동하여 변화하는 것을 볼 수 있었다. 그리고 본 연구의 수치모의 실험에서 음해법을 차용한 결과 기존 WAM모형보다 시간적으로 10 배 정도 빨리 계산이 가능함을 확인하였다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation 
Print 
