1. 서 론
해양에서 관측되는 파랑 중 전형적인 해양파의 최대 파고의 범위를 초과하는 파랑에 대한 관심이 증가하고 있다. 이런 파랑을 freak waves (또는 rogue waves)라고 한다. 일반적으로 파고가 유의파고 보다 2배 이상 큰 단일파랑을 freak wave로 정의한다. Freak waves가 자연상태와 실험실에서도 존재한다는 증거가 꾸준히 제기되어 왔다 (Sand et al., 1989).
Rogue Waves 2008 Workshop (Olagnon and Prevosto, 2008)에서는 freak wave의 발생원인, 발생 메커니즘, 발생빈도 그리고 freak wave에 의한 해양구조물과 선박에 미치는 영향 등에 대한 다양한 논의가 있었다. Freak waves와 같은 극치파고와 관련된 위험요소는 선박 및 해양구조물 산업체의 주목을 끌었으며, 최근 Joint Industry Project CresT (Cooperative Research on Extreme Seas and their impact, http://www.marin.nl/web/JIPs-Networks/Public/CresT.htm)와 그 두번째 단계인 ShortCresT 그리고 EU project EXTREME SEAS (http://www.mai.ist.utl.pt/extremeseas/)와 같은 국제적인 연구 프로젝트가 수행되었다(Bitner-Gregersen and Toffoli, 2012).
최근 10여년 동안 이론적, 수치해석적, 실험적으로 freak waves의 발생원인과 메커니즘을 규명한 연구들이 발표되었다(Gramstad and Trulsen, 2007; Janssen, 2003; Kharif et al., 2009; Mori et al., 2011). Freak waves에 대한 연구는 결정론적인 방법과 추계학적인 방법의 2가지 접근방법으로 분류할 수 있다. 결정론적인 방법은 비선형 슈뢰딩거 파랑 방정식과 같은 비선형방정식을 통해 해석해와 비교함으로써 freak waves에 대한 발생 메커니즘을 이해하는 접근방법(Henderson et al., 1999)과 또는 강한 해류에 반사 또는 굴절되는 파랑의 집중과 같은 해석적이며 수치적인 접근방법(Kharif and Pelinovsky, 2003) 등이 이에 속한다. 한편 추계학적인 방법은 극치파고의 확률분포함수와 같은 확률분포함수를 통해 freak waves의 발생확률을 추정하는 통계적인 방법이다 (Mori and Janssen, 2006; Yasuda and Mori, 1997; Ahn et al., 2012; Stansell, 2005).
Freak waves에 대한 다양한 연구결과에도 불구하고 아직 freak waves의 발생 원인과 발생확률에 대한 명확한 합의된 이해가 이루어 지지 않고 있으며, 때로는 상충되는 연구결과도 존재한다. 예를 들면 파랑의 비선형성이 freak waves의 발생에 주요한 요인 인지에 대해서도 상충되는 측정자료의 분석이 제시되고 있다 (Ahn et al., 2012; Mori et al., 2011).
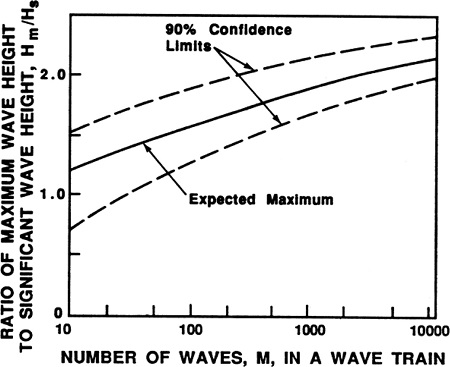
Dean (1990)은 freak waves의 존재여부는 파고의 확률분포함수인 Rayleigh의 극치파고분포의 초과확률(exceedance probability)에 근거하여 판단할 것을 제안하였다. Fig. 1은 파랑의 시계열 중 M개의 파고의 최대파고와 유의파고의 비율을 Rayleigh 분포함수에 따라 그린 것이다. 그림에 의하면 자연상태에서 파고의 분포가 Rayleigh 분포함수를 따른다고 가정하면, 파고의 개수가 약 2000개가 넘으면 최대파고(the most probable maximum wave height)가 유의파고의 2배 이상이 될 확률이 매우 높다는 것이다. 또한 최대파고와 유의파고의 비가 1.8보다 작거나 2.2를 넘을 가능성도 각각 5% 정도된다.
Fig. 1.
The most probable maximum wave height in a train of M waves expected to occur based on the Rayleigh distribution. (Dean, 1990).
Ahn (2012)은 ARSLOE(Atlantic Ocean Remote Sensing Land Ocean Experiment)에서 측정된 광범위한 파랑자료를 분석한 결과, 천해와 유한수심에서는 파고의 분포함수가 Rayleigh 분포함수에 잘 부합되지 않으며, 특히 최대파고는 Rayleigh 분포함수가 심각하게 과대평가한다는 것을 밝힌 바 있다. Ahn(2002)은 천해부터 심해까지 적용할 수 있는 파고의 분포함수를 새로이 제시하고, 이에 근거하여 최대파고(extreme wave height)의 분포함수를 아래와 같은 식으로 제시하였다.
여기서 A = exp(-λ0-λ12/4λ2)의 매개변수 λ0, λ1과 λ2는 파고의 1차와 2차 모멘트로부터 구할 수 있다. 만약 쇄파가 발생하는 해역일 경우에는 파고의 최대값이 쇄파고에 의해 제한되므로 아래의 3개의 방정식을 연립하여 매개변수를 구할 수 있다.
여기서 Hm=평균파고 Hrms=파고의 제곱평균제곱근 Hb=쇄파고; B(z)=φ(z)/Φ(z+
2 λ 2
Ahn et al. (2012)은 ARSLOE 프로젝트에서 측정된 파랑자료의 freak waves의 발생확률을 분석하였다. 해안선의 법선방향으로 25 m에서 12 km까지의 거리에 수심 1.4 m 부터 24.4 m 까지 설치된 8개의 파고계에서 측정된 파랑자료를 분석하였다. 1980년 10월 24일부터 26일까지 폭풍 시에 측정된 파랑자료를 분석하여 freak wave의 존재여부를 검토하였다. 약 900,000개의 파랑 중에 수심이 제일 깊은 24.4 m에서 2개의 freak waves가 발견되었다. 해안선으로 접근할수록 파랑의 비선형성이 증가하여 왜도와 첨도가 증가하지만 천해와 중간수심에서는 freak wave가 발생하지 않았다. 이는 파랑의 비선형성이 증가할수록 해수면의 첨도가 증가하고 또한 freak waves의 발생확률이 증가한다는 Mori et al. (2011)의 결과와 상충된다. ARSLOE 파랑분석 자료에 의하면 단순 계산으로 900,000개의 파고 중에 2개의 freak waves가 발생하였으므로 대략 O(10-5)의 발생확률이라고 하겠다.
2. 파랑자료의 분석
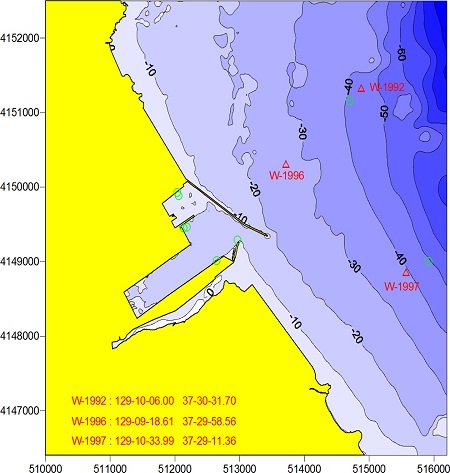
Freak waves의 출현확률분포 분석을 위해 본 연구에서는 동해항 전면 해역에서 1992년, 1996년 및 1997년에 측정된 파랑자료를 분석하였다. 네델란드 Datawell사의 부이식 파향파고계로부터 매 시간마다 0.78125초 간격으로 2,048개의 자료가 수집되었다. Fig. 2와 Table 1에 동해항 전면 해역의 파고계 설치 위치와 측정기간, 설치수심을 정리하였다.
Table 1.
Information of wave measurement stations
불규칙파의 분석 방법으로는 스펙트럼법 또는 파별분석법이 사용된다. 해수면 변위가 정규분포과정 (Gaussian random process)을 따르면 스펙트럼법에 의한 분석과 파별분석법에 의한 분석이 동일한 결과를 보여주지만, 해수면 변위가 비정규분포과정 (Non-Gaussian random process)인 경우에는 파별분석법에 의한 파랑분석이 Freak wave 분석에 더 적합하다. 본 연구에서는 파별분석법에 의한 영점상향교차법(zero up crossing method)를 사용하여 최대파고(Hm), 유의파고 (Hs), 유의파주기(Ts)을 구하여 Freak wave 분석에 사용하였다. 대표파향은 최우도법(Maximum likelihood method)에 의해 추정하였다. (Panicker and Borgman, 1974)
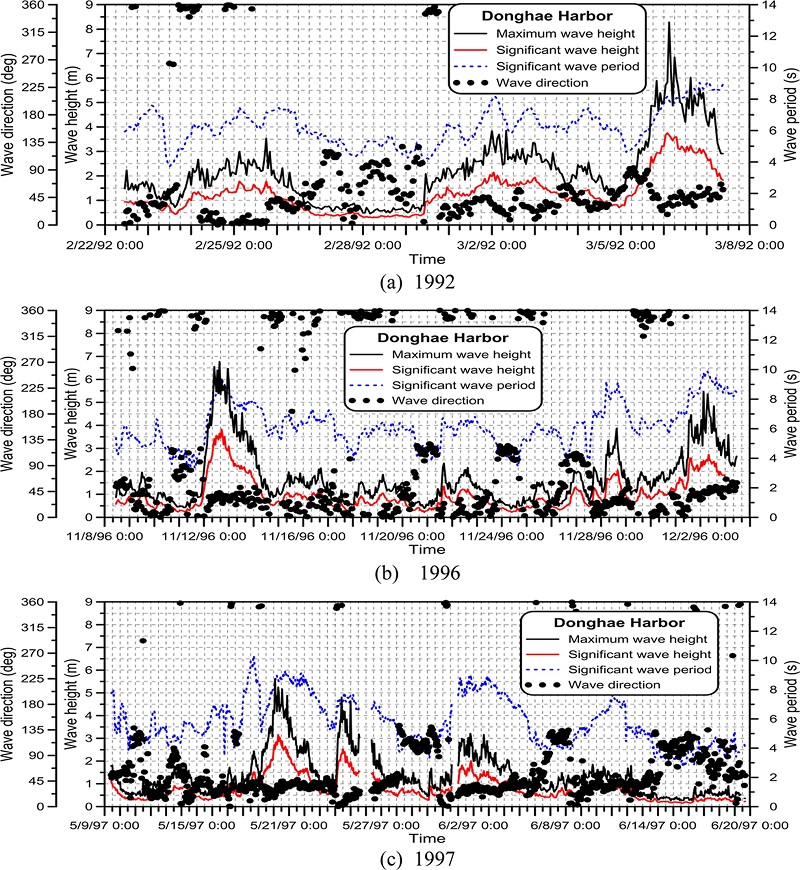
Fig. 3(a)~(c)에는 동해항 전면 해상에서 1992년 2~3월, 1996년 11~12월, 및 1997년 5~6월에 관측된 최대파고, 유의파고, 유의파주기 및 대표파향의 시간 경과에 따른 변화를 도시하였다. 관측된 최대 유의파고는 1996년 11월 12일 17시의 3.83 m (Hm= 6.01 m, Ts= 9.42초)로 기록되었다.
Fig. 3.
Time series of maximum wave height, significant wave height, significant wave period, and peak wave direction measured by directional waverider buoy near Donghae Harbor in 1992, 1996, and 1997.
동해항 전면 해상 수심 약 28 m~43 m 에서 매시간 1.28 Hz로 1600 sec 동안 측정된 파랑자료를 0.1 m 이하의 잡음을 제거하고 분석하였다. 자료의 샘플링 간격이 0.78125초이기 때문에 파고가 작고 평균주기가 5초 이하인 경우 파랑의 파봉과 파곡을 정확히 측정하지 못하기 때문에 최대파고와 유의파고의 정확도가 현저히 떨어진다. 이와 같은 경우에는 파랑자료의 부정확성 때문에 유의파고가 작은 경우에도 최대파고와 유의파고의 비율이 2.0이상인 경우가 많이 발생할 수 있다. 이런 이유로 본 논문에서는 유의파고가 2.5 m 이상인 파랑 중에서 최대파고와 유의파고의 비가 2.0 이상인 freak waves 만을 분석하였다. 3개의 freak waves가 발견되었으며, freak wave가 포함된 파랑의 시계열은 Fig. 4와 같다.
Fig. 4.
Time series of surface elevation including 3 freak waves with filtering threshold of 0.1 m measured at nearshore of Dongahe Harbor in the East Sea.
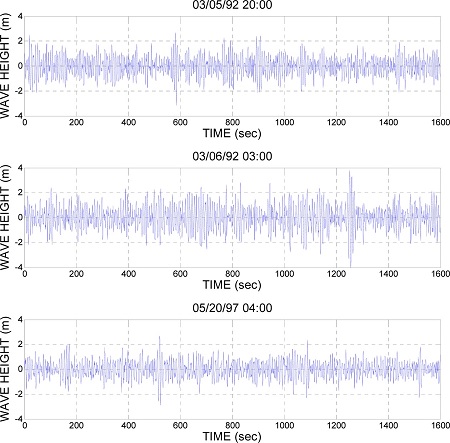
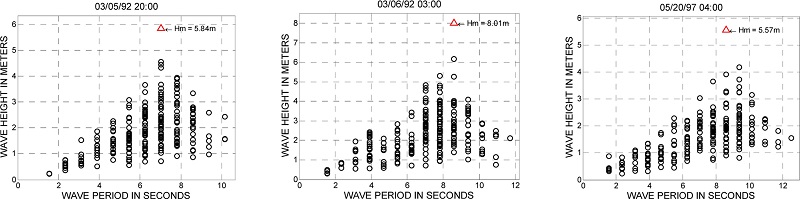
Freak waves가 포함된 시계열의 유의파고와 최대파고 그리고 왜도와 첨도 등의 각종 매개변수는 Table 2에 정리하였다. Fig. 5는 freak waves가 포함된 각 시계열의 파고와 그에 해당되는 주기를 도식한 것이다. Freak waves가 발생될 때의 주기는 최대 또는 최소 주기가 아니고 파고의 빈도가 가장 높을 때의 주기에 해당됨을 알 수 있다. 이러한 현상은 ARSLOE 프로젝트의 파랑자료에서도 동일하게 관찰되며(Ahn et al., 2012), 이에 대한 이유는 현재로서는 알 수 없으며, 향 후 연구의 대상이다.
Table 2.
Statistics of freak waves observed at nearshore of Donghae harbor in the East Sea.
3. Freak Waves의 발생확률
Freak waves의 통계적 분석을 위해 3개의 극치파고분포함수를 사용하여 비교하였다. 극치파고분포함수는 파고분포함수로부터 아래의 식을 이용하여 유도할 수 있다. (Ochi, 1998)
여기서 Hm은 n개의 파고 중 최대인 극치파고이며, f(H)와 F(H)는 각각 파고의 확률분포함수와 누적확률분포함수이다.
본 논문에서는 Rayleigh, Ahn, 그리고 Mori에 의해 제시된 극치파고분포함수를 비교 분석하였다. Rayleigh 극치파고 분포함수 g(Hm) 는 Rayleigh 확률분포함수 f(H) 와 식 (5)로부터 식 (7)과 같이 유도될 수 있다.
여기서 매개변수 R은 파고의 2차 모멘트이다.
여기서 m2 는 파고의 2차 모멘트이며 n 은 파고의 개수이다.
Mori (2004)는 단일파향의 비선형 불규칙 파랑에 대한 극치파고분포함수를 파고의 확률분포함수 f(H) 와 식(5)로부터 아래와 같이 유도하였다.
여기서 βi,j 는 매개변수로서 해수면 η(t) 의 왜도(skewness) μ3 와 첨도(kurtosis) μ4로 표시된다. 매개변수는 매우 긴 다항식으로 표기되며 Mori (2004) 논문을 참고하기 바란다.
여기서 A = exp(-λ0+λ12/4λ2) 이며 λ0, λ1 와 λ2 는 파고의 1차와 2차 모멘트로부터 구해진다.
Fig. 6에는 freak wave가 존재하는 시계열자료의 파고의 히스토그램과 Ahn, Rayleigh, 와 Mori의 파고분포함수와 극치파고분포함수를 도식하였다. Ahn, Rayleigh, 그리고 Mori의 파고분포함수는 큰 차이가 없는 것처럼 보이지만 극치파고분포함수는 서로 확연히 다름을 알 수 있다.
Fig. 6.
Comparison between histogram of wave height and the probability density functions of wave height by Rayleigh, Ahn, and Mori. The probability density functions of extreme eave height by Rayleigh, Ahn, and Mori are also shown in the figure.
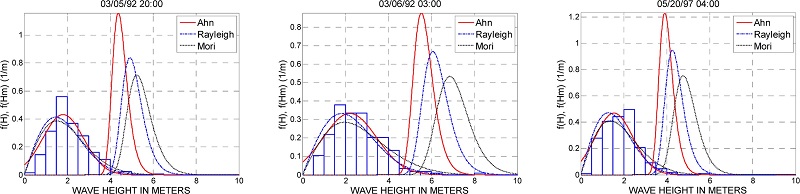
Fig. 7은 freak wave가 발생한 3개 시계열자료의 파고의 누적확률을 Ahn, Rayleigh, 그리고 Mori의 파고확률분포함수의 확률지에 나타낸 것이다. 각각의 확률지에 표시된 직선은 이론적인 누적확률을 나타낸다. 측정된 파고의 누적확률이 각각의 확률분포함수에 적합하면 직선 상에 표시되어야 한다. 그림에서 볼 수 있듯이 freak waves는 점선에서 매우 벗어난 지점에 나타난다. Freak waves를 제외한 나머지 파고자료들은 정도의 차이는 있지만 점선에 근접해서 나타나 는 것을 알 수 있다. 확률지 상에서 freak wave를 제외한 파고는 주어진 확률분포함수에 잘 부합한다.
Fig. 7.
Cumulative distributions of wave height by Rayleigh, Ahn, and Mori from left to right plotted on the probability paper, respectively, and compared with measured wave data including freak waves.
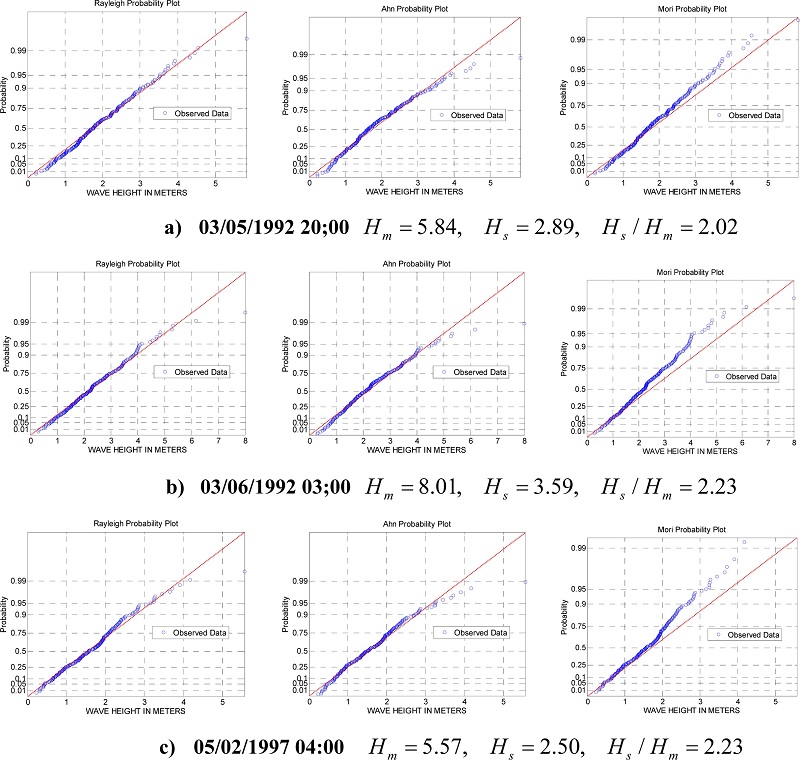
Table 3에서 볼 수 있듯이 freak waves가 포함된 파랑자료의 경우 3개의 경우를 제외하고 χ2 테스트를 통과하지 못했으나(표에서 회색으로 표시된 부분), freak wave를 제외하면 모든 경우 적합성 테스트(fitness test)를 통과했다. Table 4의 경우는 Mori의 Hm/Hs = 2.23인 경우(표에서 회색으로 표시된 부분)을 제외하고 나머지 경우는 K-S 테스트를 통과했다. Fig. 7과 Table 3, 4의 결과는 파고의 확률분포로부터는 freak wave의 발생확률을 예측하는 범위를 벗어난다는 의미이다. 즉 freak wave의 발생확률을 예측하기 위해서는 파고의 분포함수는 적합하지 않다는 의미이다.
Table 3.
χ2 test for the adequacy of probability distribution of wave height by Rayleigh, Ahn, and Mori with and without including freak waves (Shaded Box represents ‘ot accepted’by the test)
Table 4.
K-S test for the adequacy of probability distributions of wave height by Rayleigh, Ahn, and Mori with and without including waves. (Shaded Box represents ‘ot accepted’by the test)
Fig. 8은 Rayleigh, Ahn, 그리고 Mori의 파고 초과확률분포 (exceedance probability)를 freak wave를 포함한 파고측정자료와 함께 도식한 것이다. x축은 파고값을 유의파고로 나누어 무차원화했으며, y축은 파고의 초과확률을 Log 축척으로 표기한 것이다.
Fig. 8.
Exceedance probability of wave heights/significant wave height by Rayleigh, Ahn, and Mori plotted with observed wave height together with freak waves.
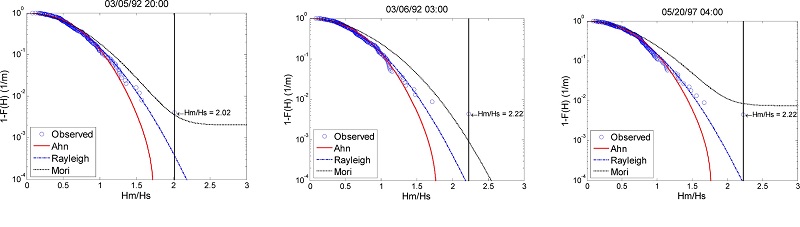
그림에서 볼 수 있듯이 freak wave (수직라인 상에 있는 O)는 측정된 파고의 범위를 벗어나 오른 쪽에 위치하고 있다. Freak wave가 Mori의 파고 초과분포 이론치에 가까이 있는 것은 Mori의 파고 분포함수가 극치값을 과대평가(극치값의 출현확률을 크게 평가)하기 때문이다.
Fig. 9는 극치파고분포함수의 초과확률 그래프이다. 측정된 파고의 초과확률 값과 같이 도식되어있다. 극치파고분포함수의 초과확률 그래프 상에서는 freak waves가 이론적인 그래프 값에 근접하여 위치하고 있음을 알 수 있다. Freak waves의 발생확률은 Mori식의 경우 파고의 시계열에서의 극치값이 freak wave가 되는 확률은 약 O(10-1)이며, Rayleigh 식의 경우 약 O(10-2), Ahn 식의 경우 약 O(10-3)임을 알 수 있다.
Fig. 9.
Exceedance probability of extreme wave heights/significant wave height by Rayleigh, Ahn, and Mori plotted with observed wave height with freak waves.
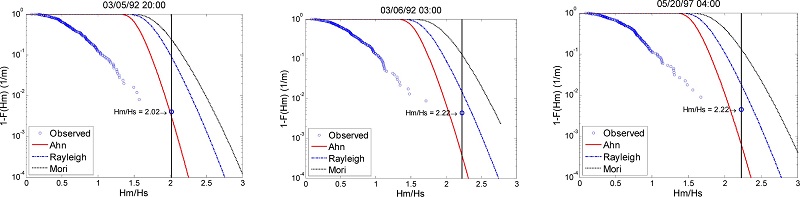
본 논문에서 동해항 인근 연안에서 측정된 파랑의 freak wave 발생확률의 분석결과는 Rayleigh, Ahn, 그리고 Mori에 의해 제안된 파고의 분포함수에 의해서는 발생확률을 예측할 수 없으나, 극치파고분포함수에 의해서는 발생확률을 예측할 수 있음을 제시하였다. Fig. 9에 의하면 동해항 전면해상에서 측정된 freak waves의 발생확률은 Rayleigh 극치파고분포의 O(10-2)와 Ahn 극치파고분포 O(10-3)의 사이에 분포함을 알 수 있다. 그러나 어떤 극치파고분포함수의 발생확률이 정확한지에 대해서는 더욱 많은 해역에서의 파랑자료의 분석이 필요하다.
4. 결 론
동해항 전면 수심 25 m, 40.5 m 그리고 43 m에서 측정된 파랑자료를 분석하여 freak waves에 대한 발생확률을 추정하였다. 유의파고 2.5 m 보다 크고 Hm⁄HS≥2인 freak waves 3개를 발견하였다. Freak waves의 발생확률을 추정하기 위해 Rayleigh, Ahn, 그리고 Mori의 파고 확률분포함수와 극치파고분포함수를 적용하여 비교하였다.
Rayleigh, Ahn,과 Mori의 파고 확률분포함수를 각각의 확률지에 도식한 후 freak wave가 포함된 파고 측정자료를 도식한 결과, 파고의 확률분포함수는 freak waves의 발생확률을 추정하기에는 적절하지 않음이 밝혀졌다. 반면에 극치파고분포함수는 freak wave의 발생확률을 추정할 때 사용하는 것이 적절하다고 판단된다.
Mori, Rayleigh, 그리고 Ahn의 극치파고분포함수에 의한 reak waves의 발생확률은 각각 약 O(10-1), O(10-2) 그리고 O(10-3) 정도이다. 본 논문에서 사용된 파랑자료의 freak waves의 발생확률은 O(10-2)와 O(10-3) 사이에 위치하였다. 그러나 Rayleigh와 Ahn의 극치파고분포함수 중에 어떤 분포함수가 정확한지에 대한 판단은 좀 더 다양한 해역에서의 freak waves에 대한 분석이 필요하다.