1. 서 론
연안으로 전파되는 외중력파(infra-gravity wave, IGW)는 항만에 계류되어 있는 선박의 거동 및 표사이동에 의한 연안지형변화에 직접적인 영향을 미치기 때문에 항만 및 연안관리에 매우 중요한 인자이다(Reniers et al., 2010; Thiebaut et al., 2013; Lopez and Iglesias, 2013). 그러나 약 3~25초 범위의 주기를 가지는 단주기파(short wave)에 관한 연구는 풍부한 반면, 외중력파에 대한 유의할만한 수준의 연구는 매우 미흡한 실정이다. 외중력파는 항만의 운영관리 측면에서 의 관점이나 전통적인 파랑 구분 기준에 의하면 지진해일이나 조석보다는 짧고 단주기파보다는 긴 주기를 가지는 파랑으로 구분되고 있다(Munk, 1950; Holthuijsen, 2007).
보통 풍파 범위를 벗어나는 파랑은 주기를 기준으로 3~25초 영역의 중력파(gravity wave, wind sea, swell), 25~300초 범위의 외중력파, 약 2~60분 정도의 주기를 가지는 FIG파(Far Infra-Gravity wave)로 구분되며(Thiebaut et al., 2013), 다수의 단주기파가 결합(grouping)되어 발생하기 때문에 단주기 파랑 정보와 높은 상관관계를 보이고 있다(Bowers, 1992). 따라서 대략 24~72시간 미리 발표되는 기상예보를 이용하면 파랑을 포함한 해황을 예측할 수 있으며, 이를 사용하여 단주기파로부터 유발되는 장주기파도 예측할 수 있다.
외중력파는 발생원인 및 전파 과정에 관한 이론적인 연구가 비교적 활발하게 수행되고 있다(Herbers et al., 1995). 반면 항만 내부의 외중력파 추정은 wind sea-swell 스펙트럼을 이용한 방법(Thiebaut et al., 2013), 수치모형을 이용한 방법(Reniers et al., 2010; Rijnsdorp, 2011), 통계기법에 해당하는 인공지능 방법(Lopez and Iglesias, 2013) 등이 있다. 또한 관측 자료의 분석과 그 자료를 이용한 기존 모형의 성능평가 연구도 수행되고 있으나(Okihiro and Guza, 1996; Bellotti and Franco, 2011), 장기 관측 자료를 이용한 통계 모형에 관한 연구는 가용한 자료의 제한으로 비교적 미흡한 실정이다.
본 연구에서는 항내로 침입하는 너울과 외중력파에 의하여 하역중단이 빈번하게 발생(포항지방해양항만청, 2010; 포항지방해양항만청, 2012)하는 포항신항의 항외 및 항내 지점에서 동시에 관측된 약 5년간의 외중력파 자료를 이용하여 통계적인 특성 및 전달함수를 이용한 전파 특성을 분석하여 항만의 외중력파 예측 모형의 성능평가를 수행하였다. 또한 외중력파 특성에 따라 변화를 보이는 전달함수의 매개변수와 외중력파의 파고, 주기, 파향 정보와의 관계도 분석하였다. 따라서 본 연구의 목적은 항외에서 예보된 파랑정보를 이용하여 항내의 외중력파 파랑정보를 추정하는 방법의 개발에 있다. 이 과정은 기상 및 파랑 예보치를 이용하여 항외 지점에서의 외중력파 정보를 추정하는 제1단계와 추정된 항외 외중력파 정보를 이용하여 항내 주요 지점의 외중력파 정보를 추정하는 제2단계로 구성된다. 본 연구는 항외 지점의 관측자료를 제1단계의 추정 외중력파 정보로 간주하는 경우 제2단계에 해당된다.
2. 관측자료 및 분석기법
2.1 관측자료 및 기본적인 통계정보
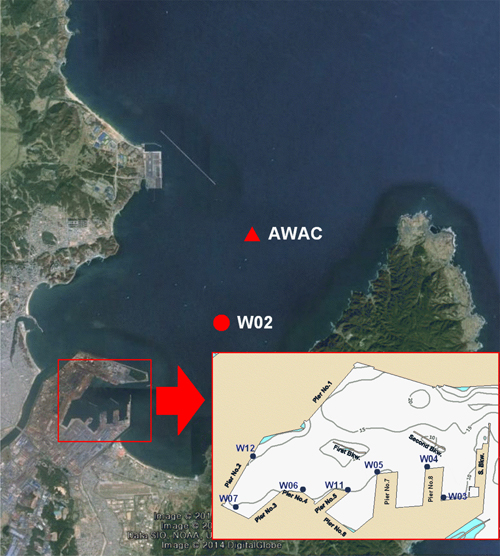
본 연구에서 사용한 포항신항에서의 파랑관측 자료는 한국해양과학기술원(KIOST)에서 2008년 9월 1일부터 2013년 8월 31일까지 5년 동안 수압식 파고계를 사용하여 0.5초 간격으로 연속적으로 측정한 자료이다(Table 1 및 Fig. 1 참조). 항만 내부로의 외중력파 전파 특성을 파악하기 위하여 항만 외부(정점 W02)와 내부(정점 W06) 지점의 자료를 선택하였다. 자료 결측은 항외 지점에서 2011년 4월 7일 18시 30분부터 6월 2일 15시 사이의 약 2개월 정도 발생하였다. 관측된 자료에서 주기가 30~300초 범위에 해당하는 자료만을 스펙트럼법(Cho et al., 2012)으로 추출하여 분석에 이용하였다. 한편 파향 정보는 영일만 입구(정점 AWAC)에서 초음파식 파향·파고계(AWAC, the Nortek)를 이용하여 관측한 정보를 이용하였다. AWAC로 취득된 파향 정보는 외중력파 분석에서 유의할만한 사상에 해당하는 시기의 값만 이용하였다.
Table 2에는 포항신항의 항외와 항내에서의 외중력파의 기본적인 통계 정보를 제시하였다. 기본 통계정보에서 알 수 있는 바와 같이 외중력파의 평균과 중간(median) 파고는 0.01~0.02 m 정도로 매우 미미한 수준이며, 주기는 60초 정도이다. 한편 파고의 변동계수는 항외, 항내 각각 1.09, 0.76정도이며, 주기의 변동계수는 각각 파고 변동계수의 22.9%, 27.6% 수준으로 매우 작게 나타나고 있다.
Table 2
Basic statistical information of the IGW wave monitoring data
2.2 전달함수 모형의 구성 및 매개변수 추정
항만 내외의 장주기파의 전파특성을 분석하기 위한 전달함수 모형은 항 외부의 파랑이 항 내부로 전파되고, 과거의 파랑이 현재에 영향을 미치기 때문에 다음과 같은 일반적인 차수를 가진 모형(Box et al., 2008)으로 구성하였다.
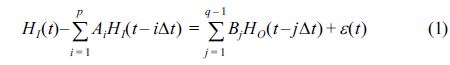
여기서, HI (t), HO(t)는 각각 항만 내부, 외부의 외중력파 파고(m)이며, A, B는 각각 자기상관(auto-regressive) 계수와 전달계수로 관측 자료를 이용하여 최적 추정되는 미지의 계수이며, ε(t)는 파고 추정 오차이다.
그러나 항만 내부의 외중력파 정보를 사전 추정된 항만 외부의 심해에서의 외중력파 정보만으로 추정한다는 제약조건이 있기 때문에 p = 0 조건이 부여된다. 따라서 본 연구에서 사용한 전달함수 모형은 다음과 같이 보다 간단한 형태로 구성된다.
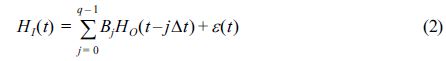
매개변수 Bj는 최소자승법을 이용하여 추정하였으며, 최적차수 q는 아래와 같이 계산되는 AIC(Akaike Information Criteria) 또는 BIC(Bayesian information criteria) 수치가 최소가 되는 차수로 결정하였다. 차수 변화에 따른 두 수치의 변화양상은 큰 차이가 없었으나, AIC 정보는 차수를 높이는 경향이 있고, BIC 수치는 낮추는 경향이 있기 때문에 간결한 모형 선택의 관점에서 추천되는 BIC 수치를 기준으로 모형의 최적 차수를 선택하였다(Storch and Zwiers, 1999).
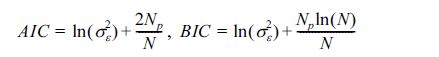
여기서, σ2ε는 표준 오차의 분산, Np는 추정 매개변수의 개수, N은 자료의 개수를 각각 나타낸다.
또한 모형의 매개변수는 유의미한 항내 외중력파 파고 0.1 m 이상에 해당하는 시점을 도출하고, 그 시점을 기준으로 전후 2일간의 자료를 하나의 사상으로 간주하여 각각의 사상에 대하여 추정하였다. Table 3에는 항내 외중력파 파고가 0.1 m보다 크게 나타난 경우의 시점과 그 시점에 해당하는 파고, 주기, 파향 등을 제시하였다. 단 여기서 파향은 영일만 입구 또는 포항신항 입구에서 AWAC 장비를 이용하여 관측된 단주기파의 파향 정보를 이용하였으며, 2009년 11월(사상 3, 4번)에는 AWAC 장비가 설치되지 않아서 가용한 파향 정보가 없다. 한편, 2011년 4월에 발생한 7번 사상은 항만 내부에서는 유의할만한 파고가 관측되었으나, 항만 외부 지점의 관측 자료가 없어 매개변수 추정에서 제외하였다.
Table 3
List of the significant IGW conditions (over 0.1 m)
2.3 매개변수와 파랑정보와의 관계
유의미한 파고를 중심으로 추출된 사상(Table 3) 자료를 이용하여 추정된 전달함수의 매개변수와 파랑정보와의 관계를 분석하였다. 파랑정보는 파고, 주기, 파향 정보만을 이용하였다. 상관관계분석은 다중 선형회귀분석 기법을 이용하였으며, 전달함수의 매개변수가 파랑정보의 선형조합으로 추정할 수 있다는 가정에서 다음과 같은 관계공식이 성립된다.

여기서, P = 매개변수 행렬(사상개수 ×매개변수개수), C = 미지의 계수 행렬(파랑정보개수 ×매개변수개수), W =파랑정보행렬(사상 개수 × [파랑정보개수 + 1(상수항)])이다. 미지의 계수행렬은 다음 식으로 최적 추정되며, 파랑정보행렬과 최적계수행렬  을 이용한 전달함수의 매개변수
을 이용한 전달함수의 매개변수 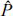 의 추정 결과는 다음과 같다.
의 추정 결과는 다음과 같다.
 을 이용한 전달함수의 매개변수
을 이용한 전달함수의 매개변수 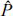 의 추정 결과는 다음과 같다.
의 추정 결과는 다음과 같다.

3. 분석결과 및 논의
3.1 항만 내외 파랑정보의 통계적인 특성
항만 내외의 파랑정보는 시계열 도시기법 및 Gaussian Kernel 함수를 이용하여 추정한 빈도분포의 형상을 이용하여 분석하였다(Figs. 2~3 참조). Kernel 함수를 이용한 빈도분포 추정은 추정결과가 연속적이고, 입력 매개변수가 단 1개(bandwidth parameter)이기 때문에 분포형태가 불연속적이고 입력 매개변수가 2개(starting point, bin numbers)인 막대그래프(histogram)보다 유리하다(Silverman, 1998). Kernel 함수의 최적 매개변수(h)는 Gauss 분포함수 조건에서 다음과 같이 자료의 표준편차와 개수의 함수로 계산된다(Silverman, 1998).

여기서  =Robust 추정 표준편차(=Median(|xi - Median(xi)|) /0.6745), Median(xi) =자료 xi의 중간값, n =자료의 개수이다.
=Robust 추정 표준편차(=Median(|xi - Median(xi)|) /0.6745), Median(xi) =자료 xi의 중간값, n =자료의 개수이다.
 =Robust 추정 표준편차(=Median(|xi - Median(xi)|) /0.6745), Median(xi) =자료 xi의 중간값, n =자료의 개수이다.
=Robust 추정 표준편차(=Median(|xi - Median(xi)|) /0.6745), Median(xi) =자료 xi의 중간값, n =자료의 개수이다.
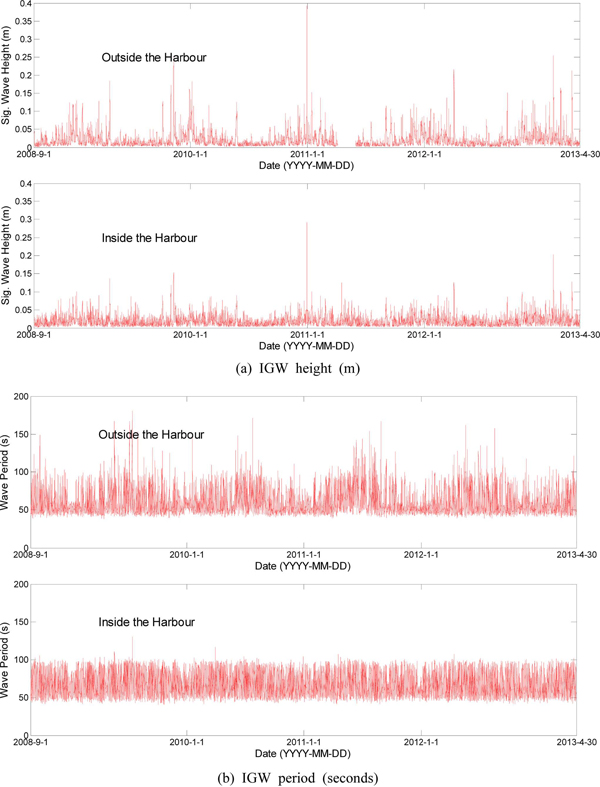
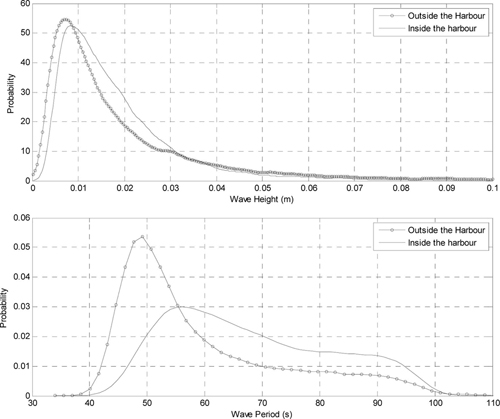
외중력파 자료는 항만 내외에서의 자료가 모두 가용한 시기에 해당하는 2008년 9월 1일부터 2013년 4월 30일까지의 기간에 대하여 도시하였다. Fig. 2(a)에서 볼 수 있는 바와 같이 항만 내부에서의 파고가 항만 외부에서의 파고보다 작게 나타나고 있다. 항외에서의 외중력파고의 최대치는 2011년 1월 1일의 0.39 m, 항내정점 W06에서의 최대치는 0.29 m로 제시되었다. 한편 Fig. 2(b)의 주기를 보면, 항만 외부는 50~170초의 넓은 범위에 걸쳐 분포하는 양상을 보이고 있으나, 항만 내부는 50~100초 사이의 범위로 주기 영역이 뚜렷하게 제한되고 있다. 한편 Kernel 함수를 이용한 빈도분포 함수(Fig. 3 참조)를 보면, 외중력파 파고의 경우 서로 유사한 형태를 보이고 있으나 파고 0.035 m를 기준으로 그 이하에서는 어느 정도 차이를 보이나 그 이상에서는 차이가 미미하다. 반면 주기분포는 항만 외부의 경우 50초 정도에 주기 발생빈도가 집중되어 있는 양상을 보이고 있으나, 항만 내부에서는 상대적으로 더 넓은 45~95초 영역에 분포하고 있다. 이처럼 항내에서의 주기가 항외에서보다 넓게 분포하는 원인은 구속파가 항입구를 통과하여 항내로 전파할 때 구속이 풀려 자유파로 전파됨으로써 보다 긴 주기의 파가 항내로 더 전파되었기 때문으로 사료되며 이에 관해서는 보다 심도있는 추가적인 연구가 요망된다.
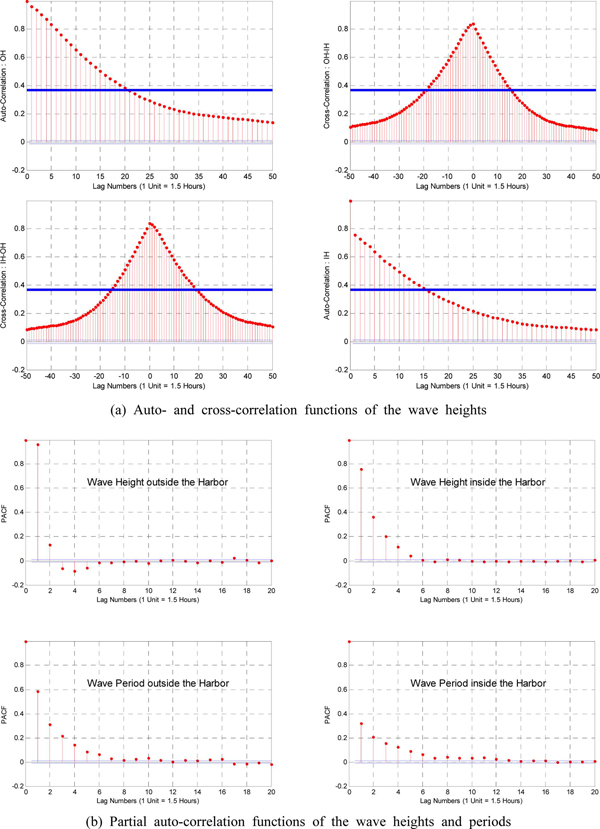
한편 외중력파 자료의 자기상관함수와 항만 내외의 교차상관함수를 계산하여 제시하였다(Fig. 4 참조). 항만 내외의 파고를 각각 IHH, OHH로 표현하는 경우, 자기상관함수(ACF)와 교차상관함수(XCF)는 다음과 같이 계산되며, 지체시간에 따른 상관계수로 표현된다.
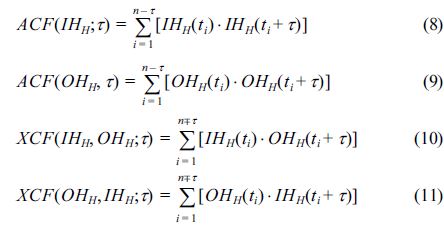
상관계수는 자료의 종속기간을 판단하는 지표로, 본 연구에서와 같이 어떤 사상이 발생한 시점(외중력파의 최대파고가 발생하는 시점)의 자료를 기준으로 이 자료에 영향을 미치거나 이 자료의 영향을 받았을 것으로 판단되는 기간을 대략적으로 결정하는데 이용할 수 있다. 외중력파 자료의 독립이 보장되는 기간은 이론적으로 95% 신뢰구간, 즉 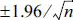 (n =자료의 개수) 범위에 포함되어야 하나, 본 연구에서는 실질적으로는 보다 완화된 e-Folding 조건에 해당하는 1 ⁄ e ≈ 0.37 조건을 이용하여 자료의 독립기간을 판단하였다. 그림에서 보이는 바와 같이 지체개수 16(시간으로 환산하는 경우 약 1일, 자료 관측간격 1.5시간 × 16 = 24시간) 이상 조건에서도 자기상관계수는 0.5 정도를 유지하고 있으며, 대략적으로 지체계수 20 정도(1~2일 사이)에서 e-Folding 조건을 만족하고 있는 것으로 판단된다. 반면 자기회귀모형(AR model) 계수 결정에 영향을 미치는 부분(또는 편, partial) 자기상관계수(Box et al., 2008)는 지체개수 5~6개 정도에서 95% 신뢰구간에 해당하는
(n =자료의 개수) 범위에 포함되어야 하나, 본 연구에서는 실질적으로는 보다 완화된 e-Folding 조건에 해당하는 1 ⁄ e ≈ 0.37 조건을 이용하여 자료의 독립기간을 판단하였다. 그림에서 보이는 바와 같이 지체개수 16(시간으로 환산하는 경우 약 1일, 자료 관측간격 1.5시간 × 16 = 24시간) 이상 조건에서도 자기상관계수는 0.5 정도를 유지하고 있으며, 대략적으로 지체계수 20 정도(1~2일 사이)에서 e-Folding 조건을 만족하고 있는 것으로 판단된다. 반면 자기회귀모형(AR model) 계수 결정에 영향을 미치는 부분(또는 편, partial) 자기상관계수(Box et al., 2008)는 지체개수 5~6개 정도에서 95% 신뢰구간에 해당하는 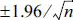 ≒ 0.01 정도로 근접하고 있다. 따라서 외중력파 자료의 AR 모형을 구성하는 경우, 대략적인 차수는 5~6 정도로 추정할 수 있다.
≒ 0.01 정도로 근접하고 있다. 따라서 외중력파 자료의 AR 모형을 구성하는 경우, 대략적인 차수는 5~6 정도로 추정할 수 있다.
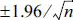 (n =자료의 개수) 범위에 포함되어야 하나, 본 연구에서는 실질적으로는 보다 완화된 e-Folding 조건에 해당하는 1 ⁄ e ≈ 0.37 조건을 이용하여 자료의 독립기간을 판단하였다. 그림에서 보이는 바와 같이 지체개수 16(시간으로 환산하는 경우 약 1일, 자료 관측간격 1.5시간 × 16 = 24시간) 이상 조건에서도 자기상관계수는 0.5 정도를 유지하고 있으며, 대략적으로 지체계수 20 정도(1~2일 사이)에서 e-Folding 조건을 만족하고 있는 것으로 판단된다. 반면 자기회귀모형(AR model) 계수 결정에 영향을 미치는 부분(또는 편, partial) 자기상관계수(Box et al., 2008)는 지체개수 5~6개 정도에서 95% 신뢰구간에 해당하는
(n =자료의 개수) 범위에 포함되어야 하나, 본 연구에서는 실질적으로는 보다 완화된 e-Folding 조건에 해당하는 1 ⁄ e ≈ 0.37 조건을 이용하여 자료의 독립기간을 판단하였다. 그림에서 보이는 바와 같이 지체개수 16(시간으로 환산하는 경우 약 1일, 자료 관측간격 1.5시간 × 16 = 24시간) 이상 조건에서도 자기상관계수는 0.5 정도를 유지하고 있으며, 대략적으로 지체계수 20 정도(1~2일 사이)에서 e-Folding 조건을 만족하고 있는 것으로 판단된다. 반면 자기회귀모형(AR model) 계수 결정에 영향을 미치는 부분(또는 편, partial) 자기상관계수(Box et al., 2008)는 지체개수 5~6개 정도에서 95% 신뢰구간에 해당하는 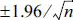 ≒ 0.01 정도로 근접하고 있다. 따라서 외중력파 자료의 AR 모형을 구성하는 경우, 대략적인 차수는 5~6 정도로 추정할 수 있다.
≒ 0.01 정도로 근접하고 있다. 따라서 외중력파 자료의 AR 모형을 구성하는 경우, 대략적인 차수는 5~6 정도로 추정할 수 있다.
3.2 전달함수를 이용한 항만 내부 파고 추정
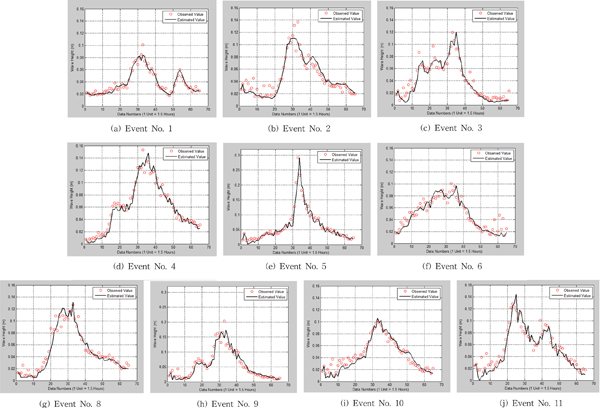
유의미한 파고를 대상으로 추출된 각각의 사상(Table 3)에서 대표적인 3개의 사상을 선택하여 모형 차수변화에 따른 BIC 수치변화를 파악하였다. 각각의 사상에 대한 BIC 수치는 관측 자료의 자기상관계수가 유의수준 이하로 감소하는 기간의 자료를 대부분 포함하기 위하여 최대 외중력파 파고 발생시점을 기준으로 ±2일, 파고기준 0.05 m 이상의 파고만을 이용하여 계산하였다(Table 4 참조). 모형의 차수 선택 기준이 되는 최소 BIC 수치(Storch and Zwiers, 1999; Box et al., 2008)는 사상 5, 11에서는 모형의 차수 2 조건에서 발생하고 있는 것으로 파악되었으며, 부분적으로 차수 1 조건이 최적으로 파악되는 경우도 있었다(사상 1번). 차수 1 조건이 선택되는 경우는 평균파고가 비교적 낮은 조건에 해당하기 때문에 본 연구에서는 차수 2 조건을 기준으로 하여 전달모형의 특성분석 연구를 수행하였다.
전달함수를 이용한 항만 내부의 파고추정은 전달함수에 포함되어 있는 계수의 최적 추정이 선행되어야 한다. BIC 값을 이용하여 선택된 최적 차수 2 조건에서 각각의 사상에 대한 최적 매개변수(B0, B1)를 추정하였다. 최적 추정을 위한 목적함수는 최소제곱오차이며, 일반적인 Gauss-Newton 반복기법을 이용하였다. 각각의 사상에 대한 최적추정 매개변수와 평균 RMS 오차 및 관측 최대파고와 추정 최대파고의 차이를 Table 5에 제시하였다. 유의할만한 외중력파 각각의 사상에 대한 최적 매개변수는 B0 계수가 B1 계수보다 크게 나타나는 경향을 보이고 있다. Table 5에서 볼 수 있는 바와 같이 최적 추정 매개변수는 사상에 따라 서로 다르기 때문에 추정 매개변수가 파랑의 영향을 받는다고 가정할 수 있으며, 다음 단계로 파랑정보와 전달함수 추정모형의 매개변수와의 관계분석을 수행하였다.
Table 5
Optimal parameters and RMS error of the transfer function model
한편 각각의 사상에 대한 관측파고와 추정파고를 비교하여 순서대로 제시하였다(Fig. 5 참조, 항외 관측 자료가 없는 사상 7 제외). 그림 및 표에서 볼 수 있는 바와 같이, RMS 오차는 0.007~0.024 m 범위로 나타나고 있으며, 평균 RMS 오차는 0.013 m이다. 최대파고의 추정 차이는 −0.016~0.031 m, 평균 차이는 0.006 m로 파악되었다. 이러한 오차 및 차이를 외중력파 사상 추출의 기준이 되는 0.1 m 수치에 대한 비율로 산정하면 평균 RMS 오차는 약 13% 정도(7~24%), 평균최대파고 추정 차이는 6%(−16~31%) 정도이다. 여기서 RMS오차는 각각의 사상기간 동안의 관측파고와 추정파고에 대한RMS (root-mean squared) 수치를 의미한다.
3.3 추정 매개변수와 파랑정보와의 관계분석
파랑정보와 매개변수의 상관관계 분석은 다중회귀분석법으로 수행하였다. 파랑정보는 파고, 주기, 파향으로, 파향 정보가 가용한 8개(사상 3, 4, 7 제외)의 사상에 대하여 수행하였다. 따라서 각각의 사상에 대한 전달함수의 매개변수 행렬 P(크기 = 사상개수 ×매개변수 개수 = 8 × 2), 회귀계수 행렬 C(파랑정보개수 ×매개변수개수 = 4 × 2), 파랑정보행렬 W(사상개수 ×파랑정보개수 = 8 × 4, 상수항 포함)를 각각 구성할 수 있다. 파랑정보에서 파향은 삼각함수로 변환(cosine 함수)하여 사용하였으며, 최종적으로 추정된 회귀계수 행렬은 다음과 같다.

따라서 전달함수 모형의 매개변수는 다음과 같은 파랑정보의 함수로 표현된다.
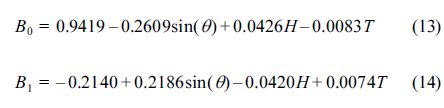
여기서, θ,H, T 변수는 각각 파향(radian), 파고(cm), 주기(초)이다.
각각의 사상에 대하여 추정된 최적 매개변수(P)와 파랑정보를 이용하여 추정한 매개변수(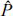 )의 상관계수(
)의 상관계수(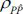 =
= 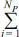 (Pi -
(Pi - 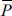 )(
)(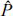 -
-  )/(
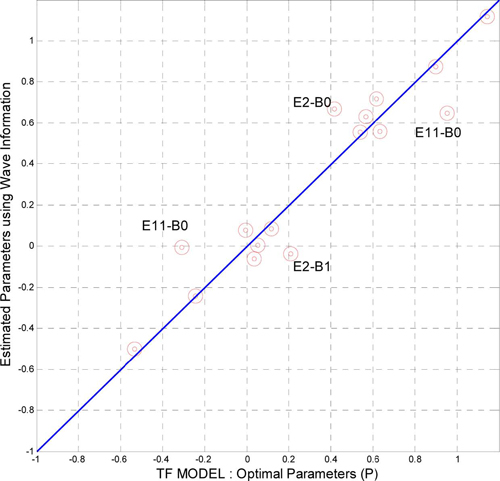
)/(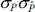 ), NP=추정 매개변수의 개수 = 8 × 2 = 16)는 0.95(Pearson coefficient)로 파악되었으며, RMS 오차는 0.15정도로 추정되었다(Fig. 6 참조). 사상 2, 11번(En, n =사상번호; Bm, m = 매개변수 번호)에서 매개변수 추정오차가 크게 발생하고 있으나, 전반적인 매개변수 추정수준은 양호한 것으로 파악되었다. 사상 2, 11번에서의 오차가 상대적으로 크게 발생한 원인을 분석하기 위하여 파랑정보와 비교·검토하였으나 뚜렷하게 원인으로 제시할만한 파랑 특성을 찾을 수 없었다. 추후 보다 다양하게 축적된 자료의 분석을 통하여 매개변수 추정오차의 원인을 자세하게 검토할 필요가 있을 것으로 사료된다.
), NP=추정 매개변수의 개수 = 8 × 2 = 16)는 0.95(Pearson coefficient)로 파악되었으며, RMS 오차는 0.15정도로 추정되었다(Fig. 6 참조). 사상 2, 11번(En, n =사상번호; Bm, m = 매개변수 번호)에서 매개변수 추정오차가 크게 발생하고 있으나, 전반적인 매개변수 추정수준은 양호한 것으로 파악되었다. 사상 2, 11번에서의 오차가 상대적으로 크게 발생한 원인을 분석하기 위하여 파랑정보와 비교·검토하였으나 뚜렷하게 원인으로 제시할만한 파랑 특성을 찾을 수 없었다. 추후 보다 다양하게 축적된 자료의 분석을 통하여 매개변수 추정오차의 원인을 자세하게 검토할 필요가 있을 것으로 사료된다.
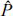 )의 상관계수(
)의 상관계수(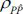 =
= 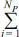 (Pi -
(Pi - 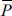 )(
)(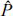 -
-  )/(
)/(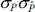 ), NP=추정 매개변수의 개수 = 8 × 2 = 16)는 0.95(Pearson coefficient)로 파악되었으며, RMS 오차는 0.15정도로 추정되었다(Fig. 6 참조). 사상 2, 11번(En, n =사상번호; Bm, m = 매개변수 번호)에서 매개변수 추정오차가 크게 발생하고 있으나, 전반적인 매개변수 추정수준은 양호한 것으로 파악되었다. 사상 2, 11번에서의 오차가 상대적으로 크게 발생한 원인을 분석하기 위하여 파랑정보와 비교·검토하였으나 뚜렷하게 원인으로 제시할만한 파랑 특성을 찾을 수 없었다. 추후 보다 다양하게 축적된 자료의 분석을 통하여 매개변수 추정오차의 원인을 자세하게 검토할 필요가 있을 것으로 사료된다.
), NP=추정 매개변수의 개수 = 8 × 2 = 16)는 0.95(Pearson coefficient)로 파악되었으며, RMS 오차는 0.15정도로 추정되었다(Fig. 6 참조). 사상 2, 11번(En, n =사상번호; Bm, m = 매개변수 번호)에서 매개변수 추정오차가 크게 발생하고 있으나, 전반적인 매개변수 추정수준은 양호한 것으로 파악되었다. 사상 2, 11번에서의 오차가 상대적으로 크게 발생한 원인을 분석하기 위하여 파랑정보와 비교·검토하였으나 뚜렷하게 원인으로 제시할만한 파랑 특성을 찾을 수 없었다. 추후 보다 다양하게 축적된 자료의 분석을 통하여 매개변수 추정오차의 원인을 자세하게 검토할 필요가 있을 것으로 사료된다.
Table 6
Parameter information of the transfer function model
3.4 전달함수 매개변수의 공간적인 분포
포항신항의 경우 ‘ ’ 형태의 접안부두(슬립, slip)가 다수 있으며(Fig. 1 참조) 이러한 수역에서는 외중력파의 주기가 수역의 고유진동주기와 유사하기 때문에 공진이 발생할 가능성이 크다. 따라서 접안선박의 하역중단에 따른 피해를 저감하기 위해서는 다중반사가 발생하는 슬립 내부에서의 파랑자료 분석도 필요한 것으로 판단된다. 본 연구에서는 항만의 슬립영역을 포함한 6개 지점(Fig. 1 참조)의 가용한 외중력파 자료를 이용하여 사상 5번(2011년 1월 1일을 중심으로 한 5일간)에 대하여 전달함수의 최적 매개변수를 각각 추정하였으며, 각각의 관측 자료는 시작시간을 동일한 시점으로 일치시켜 분석하였다. 추정된 매개변수 및 관측 지점의 최대파고 정보는 Table 6에 제시하였다. 표에서 볼 수 있는 바와 같이 정점에 따라 약간의 차이는 있으나 항외(외중력파고 = 0.39m)에서 항내로 전달된 외중력파 특성이 매개변수 및 최대파고에 따라 슬립 내부의 안벽에서는 증폭(W03, W07 지점)되고, 일자형 안벽에서는 감쇠(W04~W06, W11~W12)되는 두 가지 유형으로 분류되고 있음을 알 수 있다.
’ 형태의 접안부두(슬립, slip)가 다수 있으며(Fig. 1 참조) 이러한 수역에서는 외중력파의 주기가 수역의 고유진동주기와 유사하기 때문에 공진이 발생할 가능성이 크다. 따라서 접안선박의 하역중단에 따른 피해를 저감하기 위해서는 다중반사가 발생하는 슬립 내부에서의 파랑자료 분석도 필요한 것으로 판단된다. 본 연구에서는 항만의 슬립영역을 포함한 6개 지점(Fig. 1 참조)의 가용한 외중력파 자료를 이용하여 사상 5번(2011년 1월 1일을 중심으로 한 5일간)에 대하여 전달함수의 최적 매개변수를 각각 추정하였으며, 각각의 관측 자료는 시작시간을 동일한 시점으로 일치시켜 분석하였다. 추정된 매개변수 및 관측 지점의 최대파고 정보는 Table 6에 제시하였다. 표에서 볼 수 있는 바와 같이 정점에 따라 약간의 차이는 있으나 항외(외중력파고 = 0.39m)에서 항내로 전달된 외중력파 특성이 매개변수 및 최대파고에 따라 슬립 내부의 안벽에서는 증폭(W03, W07 지점)되고, 일자형 안벽에서는 감쇠(W04~W06, W11~W12)되는 두 가지 유형으로 분류되고 있음을 알 수 있다.
 ’ 형태의 접안부두(슬립, slip)가 다수 있으며(Fig. 1 참조) 이러한 수역에서는 외중력파의 주기가 수역의 고유진동주기와 유사하기 때문에 공진이 발생할 가능성이 크다. 따라서 접안선박의 하역중단에 따른 피해를 저감하기 위해서는 다중반사가 발생하는 슬립 내부에서의 파랑자료 분석도 필요한 것으로 판단된다. 본 연구에서는 항만의 슬립영역을 포함한 6개 지점(Fig. 1 참조)의 가용한 외중력파 자료를 이용하여 사상 5번(2011년 1월 1일을 중심으로 한 5일간)에 대하여 전달함수의 최적 매개변수를 각각 추정하였으며, 각각의 관측 자료는 시작시간을 동일한 시점으로 일치시켜 분석하였다. 추정된 매개변수 및 관측 지점의 최대파고 정보는 Table 6에 제시하였다. 표에서 볼 수 있는 바와 같이 정점에 따라 약간의 차이는 있으나 항외(외중력파고 = 0.39m)에서 항내로 전달된 외중력파 특성이 매개변수 및 최대파고에 따라 슬립 내부의 안벽에서는 증폭(W03, W07 지점)되고, 일자형 안벽에서는 감쇠(W04~W06, W11~W12)되는 두 가지 유형으로 분류되고 있음을 알 수 있다.
’ 형태의 접안부두(슬립, slip)가 다수 있으며(Fig. 1 참조) 이러한 수역에서는 외중력파의 주기가 수역의 고유진동주기와 유사하기 때문에 공진이 발생할 가능성이 크다. 따라서 접안선박의 하역중단에 따른 피해를 저감하기 위해서는 다중반사가 발생하는 슬립 내부에서의 파랑자료 분석도 필요한 것으로 판단된다. 본 연구에서는 항만의 슬립영역을 포함한 6개 지점(Fig. 1 참조)의 가용한 외중력파 자료를 이용하여 사상 5번(2011년 1월 1일을 중심으로 한 5일간)에 대하여 전달함수의 최적 매개변수를 각각 추정하였으며, 각각의 관측 자료는 시작시간을 동일한 시점으로 일치시켜 분석하였다. 추정된 매개변수 및 관측 지점의 최대파고 정보는 Table 6에 제시하였다. 표에서 볼 수 있는 바와 같이 정점에 따라 약간의 차이는 있으나 항외(외중력파고 = 0.39m)에서 항내로 전달된 외중력파 특성이 매개변수 및 최대파고에 따라 슬립 내부의 안벽에서는 증폭(W03, W07 지점)되고, 일자형 안벽에서는 감쇠(W04~W06, W11~W12)되는 두 가지 유형으로 분류되고 있음을 알 수 있다.
한편 W06 지점의 사상 5 조건에서의 매개변수와 RMS 오차가 다른 사상과 차이가 나는 이유는 자료추출간격의 차이에 의한 것이다. 다양한 사상에서 분석한 W06 지점의 매개변수는 30분 정도의 시차(항만 내·외 지점의 자료 추출시점의 차이)를 두고 있으나, 동일한 사상(사상 5) 조건의 다양한 지점에서의 비교는 시간차이가 없는 자료로 변환하여 비교하는 과정에서 발생하는 차이로, 추정 매개변수가 파랑전파시간의 영향이 크기 때문에 시차에 의한 영향이 반영되어 차이를 보이게 된다. 따라서 추정 전달함수는 추정 매개변수와 시차가 있을 경우 시차정보도 같이 제공하여야 한다. Table 5~6에 제시된 추정 매개변수는 각각 30분의 시차(항외 지점이 30분 이른 시간)와 무시차 조건에서의 값이다.
4. 결론 및 제언
동해안의 영일만 내부에 위치한 포항신항의 항외와 항내에서 장기간 관측한 외중력파 자료의 통계적인 특성을 분석하였으며, 항만 외부의 외중력파 정보를 이용하여 항만 내부의 외중력파고의 크기를 추정하는 전달함수 모형을 개발·적용하였다. 본 연구 수행을 통하여 얻어진 주요 결과는 다음과 같다.
(1) 외중력파의 주기분포는 항만 외부에 비하여 항만 내부에서 매우 크게 분산되는 양상을 보인다.
(2) 전달함수를 이용한 항만 내부의 외중력파 파고추정 모형은 차수 2 정도가 최적으로 파악되었으며, 차수 2 조건에서 최적 추정된 항만 내부파고의 평균 RMS 오차범위는 0.013 m이며, 최대 파고의 평균 추정 편차는 0.006 m이다.
(3) 전달함수 모형의 최적차수 2 조건에서 추정된 매개변수는 외중력파의 파랑정보와 강한 상관관계(상관계수 = 0.95)를 보이는 것으로 파악되었으며, 전달함수 매개변수(B0, B1) 추정 RMS 오차는 0.15 정도로 파악되었다.
(4) 항외에서 항내로 전달된 외중력파 특성이 매개변수 및 최대파고에 따라 slip 내부의 안벽에서는 증폭되고, 일자형 안벽에서는 감쇠되는 것으로 나타났다.
본 연구 성과는 항만 외부에서 사전 추정(예보)되는 단주기파 정보로부터 외중력파 정보를 추정하는 경우, 추정된 외중력파 정보를 이용하여 항만 내부의 외중력파 정보를 추정하는 도구로 사용할 수 있다. 그러나 어떤 특정한 사상에서는 매개변수 추정오차가 크게 발생할 수 있어 상당한 추정 편차가 예상되기 때문에 보다 다양한 사상에 대한 외중력파 파랑정보와 전달함수 매개변수의 관계분석 연구가 필요할 것으로 사료된다. 한편 실시간 정보를 이용하는 경우에는 항외 파랑이 항내로 전달되는 시간이 30분 이하로 짧기 때문에 실제적인 활용에는 제한이 있다. 그러나 동해 중부에 위치한 기상청의 해양기상부이 등에 의한 관측정보나 수치예보 결과를 활용하는 경우 본 모델의 활용성이 증대될 것으로 판단된다.