1. 서 론
최근 우리나라 주요 대형 항만에 건설되는 신규 방파제는 대체로 수심이 깊은 지역에 위치하고 있으며, 설계파고 및 주기도 커짐에 따라 매우 큰 파력이 방파제에 작용하게 된다. 이러한 설계조건으로 인해 해당 지역에는 종래에 많이 채택되었던 경사식 방파제보다는 케이슨 방파제가 압도적으로 많이 건설되고 있다. 그 중에서도 케이슨 내부에 유수실을 두고 케이슨 전면벽에는 긴 구멍(slit)을 내어 방파제에 부딪치는 파랑의 일부는 전면벽에서 반사되며, 나머지는 유수실 내부로 진입한 뒤 에너지 소산이 일어나게 함으로써 반사율 및 파력을 저감할 수 있는 유공 케이슨 방파제 형식이 대다수를 차지하고 있다. 특히, 설계시공 일괄입찰 방식 시행 이후 여러 회사에서 수리 성능 및 구조 안정성을 향상시키기 위한 목적으로 유공 케이슨의 형상 및 구조 형식을 변화시킨 다양한 방파제를 개발하고 있다.
이처럼 최근에 개발된 다양한 형상의 유공 케이슨 형식 중에서 일부는 케이슨 내부에 유수실이 두 개 있는 것들도 있다. 그런데, 유공 케이슨 설계 시 파력을 산정하는데 활용하는 Takahashi 파압 공식(Takahashi and Shimosako, 1994)은 유수실이 하나인 구조 형식을 대상으로 개발되었기 때문에 위와 같이 유수실 수가 한 개 이상인 경우에는 적용하는 것이 불가능하다. 현재로서는 유수실 수가 두 개인 이중유수실 케이슨 방파제의 파력을 산정하는 식은 개발되어 있지 않으며, 이로 인해 현재 설계 실무에서는 중간 유공벽에도 전면 유공벽에 작용하는 파력을 그대로 적용시키는 등 다소 임의적으로 설계가 이루어지고 있으며 일관된 기준이 확립되어 있지 않은 실정이다. 이러한 방법으로 설계가 이루어질 경우 케이슨 전체에 작용하는 수평파력이 무공케이슨에 작용하는 수평파력보다도 훨씬 크게 되어 유공케이슨 방파제의 도입 취지가 무색하게 된다.
이중유수실 케이슨 방파제의 파력을 산정하는 데 활용할 수 있는 공식은 아직까지 개발되어 있지 않지만, 이러한 형식의 방파제에 작용하는 파력에 관해서는 몇몇 연구자들의 연구 결과가 보고된 바 있다. Franco et al.(1998)는 이탈리아 Sardina지방의 Torres항에 건설된 다중 유수실 케이슨 방파제에 대한 약 3년 동안의 현장계측 결과를 토대로 Goda 파압식(Goda, 2010)에 대한 파력 저감계수 산정식을 제시하였다. 한편, Bergmann and Omeraci(2000)는 유수실의 개수가 1~3개로 서로 다른 방파제 실험모형에 작용하는 파력을 각각 계측하여 다중 유수실 방파제의 파력이 단일유수실 방파제 파력에 비해서 더 작다고 발표하였다. 또한, Chen et al. (2002)은 이중유수실 케이슨에 작용하는 최대 수평파력이 단일유수실 케이슨에 비해서 더 작으며, 따라서 중간벽이 파력을 저감시키는 효과가 있음을 보이는 수리실험 결과를 제시하였다.
이러한 선행 연구들은 공통적으로 유수실 수가 한 개보다 두 개 이상인 방파제 구조가 구조물에 작용하는 전체 파력을 저감시키는 효과가 있음을 보였다. 그러나 각 논문에 제시된 방파제의 형상이 서로 크게 다르며, 실험 또는 현장관측이 수행된 조건이 다양하지 못하기 때문에 어떠한 종합적인 결론이 도출되지는 못하였다. 특히, 위에서 언급한 것처럼 국내 실정 상 시급히 요청되고 있는 이중유수실 케이슨 방파제의 설계 시 활용할 수 있는 파압식이 개발되지는 못하였다. 이러한 점을 고려하여 본 연구에서는 이중유수실 케이슨 방파제에 작용하는 수평파력을 정밀하게 계측하는 수리실험을 수행하고 단일유수실 케이슨의 경우와 비교하여 파가 케이슨 방파제에 작용할 때의 위상에 따라서 각 벽체에 작용하는 파력의 저감 효과를 분석하였다. 본 논문에 제시된 결과는 향후 현업 실무에서 적용할 수 있는 이중유수실 파압 공식을 개발하는데 중요한 기본 자료로서 활용될 수 있을 것으로 기대된다.
2. 수리모형실험
2.1 실험시설 및 모형
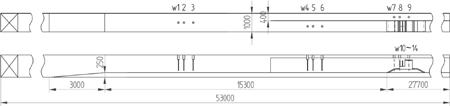
실험은 한국해양과학기술원(KIOST)에 있는 단면 조파수조(길이 53 m, 높이 1.25 m, 폭 1 m)에서 수행되었다. Fig. 1에 보인 것처럼 효율적인 실험을 위해서 수조의 종방향으로 연직 분할판을 설치하여 수조를 폭 0.6 m 의 광수로와 폭 0.4 m의 협수로로 분할하여 광수로에는 방파제 모형을 설치 하였고, 협수로에서는 통과 입사파를 계측하였다. 모형 방파제는 조파기로부터 25 m 떨어진 위치에 설치되었으며, 방파제 전면 바닥면은 평평하게 재현되었다.
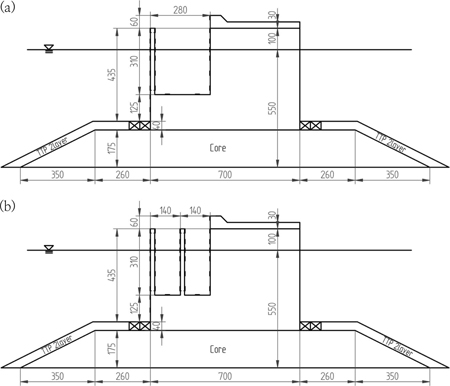
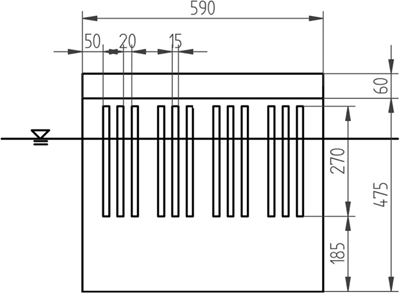
실험에 사용한 케이슨 방파제 모형은 전체 높이 53.5 cm, 폭 59 cm, 길이 70 cm이며, 투명 아크릴로 제작되어 사석 마운드 위에 설치되었다. Fig. 2에 보인 것처럼 유수실 수를 1개 또는 2개로 변화시킬 수 있도록 방파제 모형을 제작하였다. Fig. 2(a)에 보인 단일유수실 케이슨 모형은 Takahashi and Shimosako(1994)의 실험 모형과 매우 비슷한 형태이며, Fig. 2(b)의 모형은 단일유수실 케이슨의 유수실을 이등분하여 이중유수실 구조로 만든 형태이다. 즉, 이중유수실 케이슨의 유수실 2개를 더한 전체 폭은 단일유수실 케이슨 유수실의 폭과 같다. 한편, 사석 마운드의 높이(hM)는 17.5 cm였으며, 케이슨 전·후면벽으로부터의 사석 마운드 길이(BM)는 26 cm였다. 또한, 유수실 뒤쪽에는 마루높이 6 cm인 상치 구조물이 위치하였다. 한편 케이슨 전면벽 유공부의 유공률(ε)은 30%였으며, 이중유수실 케이슨의 경우 중간벽의 유공률 또한 30%로 동일하였다. Takahashi(2002)는 ε의 값이 통상적으로 15~30% 범위로 설계된다고 하였으며, 실제로 최근 국내에 건설된 유공 케이슨 방파제를 조사해 본 결과 대부분 ε = 20~30% 범위에 분포하였다. Fig. 3에 보인 것처럼 케이슨 전면벽의 유공부 위치는 케이슨 바닥으로부터 18.5 cm 높이로부터 케이슨 상단 아래 2 cm까지의 27 cm구간이며, 이는 케이슨 전면벽 높이 47.5 cm의 약 57%에 해당한다. 본 실험 모형의 제원을 최근 우리나라 대형 항만에 설치되는 실제 케이슨 방파제 구조물과 비교해보면 대략 1/40 정도의 크기에 해당한다.
2.2 계측기기의 배치 및 실험 방법
본 실험에서는 총 14개의 파고계를 사용하였으며 Fig. 1에 보인 것처럼 수조 내에 배치하였다. 한편, 파 작용 시 케이슨 벽에 작용하는 힘을 직접 계측하기 위해서 1축 하중계 (load cell)를 이용한 파력 계측 시스템을 구성하여 전면벽의 무공부 및 유공부, 중간벽(이중유수실의 경우)과 후면벽, 그리고 상치구조물에 작용하는 파력을 독립적으로 각각 측정하였다. 실험 수심(d)은 모형 설치 위치에서 55 cm였으며 주기(T)는 0.77~2.70 s, 파고(H)는 2.8~24.8 cm 범위에서 서로 다른 총 37개의 규칙파를 60초 동안 조파하였다. 모든 계측 자료를 PC의 저장장치에 기록한 시간 간격(sampling rate)은 800 Hz였다. 또한, 실험이 진행되는 동안 비디오 촬영을 함께 진행하여 자료 분석 시 활용하였다.
3. 파 작용 위상에 따른 최대 수평파력
유공케이슨 방파제의 경우 전면벽 및 후면벽에 각각 작용하는 수평파력의 첨두값이 동시에 발생하는 것이 아니라 시간 차를 두고 나타나게 된다. 이러한 점을 고려하여 Takahashi파압 공식(Takahashi and Shimosako, 1994)에서는 파가 단일유수실 유공케이슨에 작용하는 상황을 여섯 가지 서로 다른 위상에 따라 구분하였으며, 수평파력이 양의 값을 가지게 되는 경우에 대해서는 Fig. 4에 보인 것처럼 세 가지 파의 위상을 고려하였다. 여기에서 crest I은 유공케이슨 전면벽 유공부의 파력이 최대가 되는 위상, crest IIa는 유수실 후면벽에 충격적인 파력의 첨두값이 나타나는 위상, crest IIb는 유수실 후면벽에 비교적 완만하게 변화하는 파력의 첨두값이 나타나는 위상을 각각 나타낸다. Takahashi and Shimosako(1994)는 이 각각의 위상에 대해서 단일유수실 케이슨의 전면벽 유공부 및 무공부, 그리고 후면벽에 작용하는 파력의 크기를 무공 케이슨에 대해서 제안된 Goda의 파압공식과 비교한 바 있다.
Fig. 4.
Three differernt phases during the wave action on the perforated caisson defined by Takahashi and Shimosako(1994).
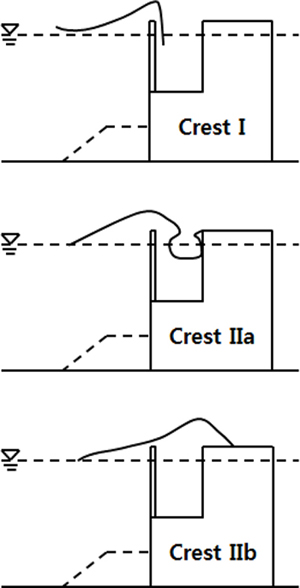
본 연구에서도 Takahashi and Shimosako(1994)와 유사한 방법으로 케이슨 각 부재에 작용하는 수평파력을 개별적으로 측정할 수 있는 계측시스템을 구성하였기 때문에 단일유수실 케이슨 전면벽의 유공부 및 무공부, 그리고 후면벽에 작용하는 수평파력을 파의 위상에 따라서 Goda의 파압공식과 비교하는 것이 가능하였다. 이에 더하여 이중유수실 케이슨의 경우에는 전면벽과 후면벽 사이에 위치한 중간벽에 작용하는 파력에 대해서도 동일한 분석을 수행하는 것이 가능하였다.
Fig. 5.
Typical time variation of the wave force for the single chamber caisson when T = 1.70 s, H = 16.5 cm.
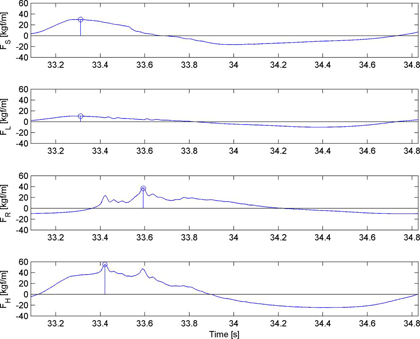
Fig. 5에는 Fig. 2(a)에 보인 단일유수실 케이슨에 T = 1.70 s, H = 16.5 cm인 파가 작용했을 때의 파력 시계열 예를 제시하였다. 여기서 FS와 FL은 케이슨 전면벽 상부 유공부 및 하부 무공부에 작용하는 파력을, FR은 케이슨 후면벽에 작용하는 파력을 각각 의미하며, FH는 케이슨에 작용하는 총파력을 의미한다. Fig. 5로부터 전면벽 상부 유공부와 하부 무공부에 작용하는 수평파력의 첨두값(그림에서 원으로 표시된 지점)이 거의 동시에 발생함을 알 수 있으며, 이는 Takahashi and Shimosako(1994)에서 crest I으로 정의한 위상에 해당한다. 한편, 후면벽 작용 파력의 경우 전면벽 첨두값이 발생한 시간보다 지체되어 첫 번째 첨두값이 나타나며(crest IIa), 이보다 더 늦게 파력의 최대값(그림에서 원으로 표시된 지점)이 발생하였다(crest IIb). Fig. 5에 보인 예에서는 crest IIa에서의 후면벽 첨두가 잘 나타났지만 주기가 길고 파고가 비교적 작은 파가 작용하는 경우에는 crest IIa에서의 첨두가 뚜렷하게 나타나지 않는 경우도 있다. Fig. 5로부터 이 실험파의 경우에는 Crest IIa 위상에서 총파력 값이 최대가 되었음을 알 수 있다.
Fig. 6.
Typical time variation of the wave force for the double chamber caisson when T = 1.70 s, H = 16.5 cm.
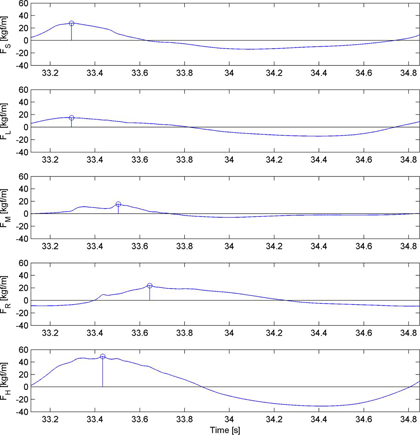
Fig. 6에는 동일한 파가 작용했을 때 이중유수실 케이슨에서 관측된 파력 시계열 예를 제시하였다. 이 경우에는 첫 번째와 두 번째 유수실 사이에 위치한 중간벽에 작용하는 수평파력에 대해서도 계측이 이루어졌으며, FM으로 표시되었다. Fig. 6에서 전면벽 상부 유공부 및 무공부에 작용하는 파력(FS 와 FL) 시계열의 모습은 대체로 Fig. 5에 보인 단일유수실 케이슨의 경우와 매우 비슷하였으나, 후면벽 작용 파력(FR)의 경우에는 상당한 차이를 보였다. 무엇보다 유수실 내에 침투한 파가 후면벽에 부딪칠 때 나타나게 되는 crest IIa에 해당하는 첨두가 뚜렷하게 관찰되지 않았으며, 첨두값의 크기도 단일유수실 케이슨의 경우에 비해서 작은 편이었다. 한편, 후면벽에서의 수위가 최대가 될 때에 대응되는 Crest IIb의 위상에서도 첨두값의 크기가 단일유수실 케이슨의 경우에 비해서 다소 감소하였으며, Crest I부터 Crest IIb까지의 시간 동안 파력이 완만하게 상승하는 경향을 보였다. 또한, 전면벽 첨두가 나타난 Crest I으로부터 Crest IIb까지의 시차가 단일유수실 케이슨의 경우에 비해서 증가한 것을 확인할 수 있다. 이처럼 이중유수실 케이슨의 경우 단일유수실 케이슨에 비해서 후면벽 작용 파력이 감소하며, 첨두값에 이르기까지의 시간이 지체되는 현상은 유수실 내부에 침투한 파의 에너지 일부가 중간벽에서 소산되기 때문일 것으로 추정할 수 있다. Fig. 6에 보인 중간벽 파력 계측 시계열에서도 후면벽에서의 Crest IIa 및 IIb와 유사하게 2번의 첨두가 나타남을 볼 수 있으며, 이는 각각 중간벽에 파가 부딪칠 때와 수위가 가장 높아질 때에 대응되는 시점이라고 해석할 수 있다. Fig. 6에서 중간벽의 파력 첨두값은 전면벽 유공부 및 후면벽에서의 첨두값에 비해서는 작음을 확인할 수 있으며 이에 관해서는 다음 장에서 보다 자세히 설명하였다. 한편, Fig. 6에 제시된 총파력 시계열을 Fig. 5와 비교해 보면 전체적으로 총파력이 매우 완만하게 상승하였다가 감소하는 경향이 나타나며, Crest IIa 및 Crest IIb 위상에서의 첨두값이 매우 미약하게 나타남을 확인할 수 있다. 이 경우에도 총 파력의 첨두값은 후면벽에서의 Crest IIa 위상에서 나타나는 것으로 보이지만, Fig. 5에 보인 단일유수실 케이슨의 경우에 비해서 그 크기는 더 작았다.
4. 케이슨 각 벽체에 작용하는 최대 수평파력
4.1 전면벽 작용 최대 수평파력
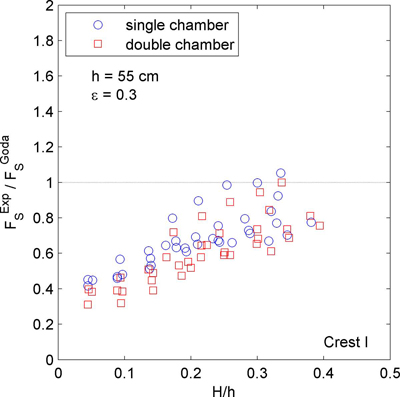
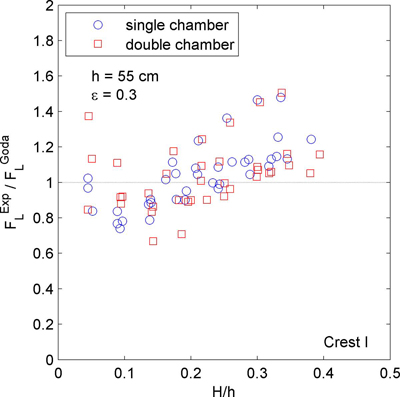
Fig. 7은 전면벽 유공부에 작용하는 수평파력이 최대가 되는 Crest I 위상에서 단일 및 이중유수실 케이슨 방파제의 전면벽 유공부 파력 계측값(FSEXP)을 Goda 파압식에 의해 계산된 파력(FSGoda)으로 나누어 무차원화한 결과를 비교하여 나타낸 것이다. 여기서 FSGoda는 전면벽 유공부의 단면을 무공벽으로 가정하여 Goda 파압식으로 계산한 결과에 해당하며, Takahashi and Shimosako(1994)에 제시된 방법과 동일하게 α2= 0으로 설정하여 계산을 수행하였다. 따라서, 무차원 파력(FSEXP/FSGoda)은 Goda 파압식에 의해 계산되는 무공벽 파력에 대한 유공벽 작용 파력의 비율을 나타낸다. 즉, Fig. 7에서 이 값은 단일 및 이중유수실 케이슨의 경우 모두 대체로 1보다 작은데, 이는 Crest I 위상에서 전면벽 유공부에 작용하는 파력이 무공 직립벽 파력 산정을 위해 제안된 Goda파압식에 의한 산정값에 비해서 더 작음을 의미한다. 한편, 이 그림으로부터 단일유수실 케이슨에 비해서 이중유수실 케이슨의 경우가 상대적으로 전면벽 유공부에 작용하는 파력이 더 작음을 알 수 있다. 평균적으로는 이중유수실 케이슨에 대한FSEXP/FSGoda의 값이 단일유수실 케이슨에 비해서 10.9% 작게 나타났다. 또한 H/h의 값이 증가함에 따라서 단일 및 이중유수실 케이슨의 무차원파력이 대체로 증가하는 경향을 나타내었다.
파의 위상이 동일한 Crest I에서 전면벽 무공부에 작용하는 수평파력(FLEXP) 계측 결과를 Fig. 8에 제시하였다. Fig. 5에서 설명한 것처럼 전면벽 무공부 파력도 Crest I 위상에서 최대값을 가지게 된다. Fig. 8로부터 FLEXP/FLGoda의 값은 평균적으로 1근처에서 형성됨을 확인할 수 있으며, 이는 실험에서 계측된 파력이 Goda의 파압 공식 계산 결과와 대체로 일치함을 의미하는 것이다. 또한, 이 경우에는 Fig. 7에 보인 전면벽 유공부의 결과와는 달리 단일 및 이중유수실 케이슨에 따른 파력의 차이가 뚜렷하게 나타나지 않았다. Table 1에는 전면벽 유공부와 무공부를 비롯하여 후면벽 및 중간벽(이중유수실 케이슨의 경우)에 작용하는 무차원 파력의 평균 및 표준편차 계산 결과를 제시하였다.
4.2 후면벽 작용 최대 수평파력
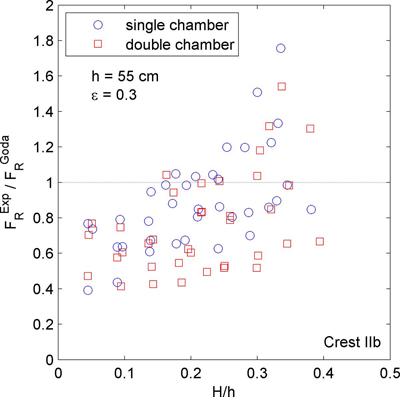
유수실 안쪽 후면벽에 작용하는 파력은 먼저 유수실 내 수위가 저하되는 상태에서 전면벽 슬릿을 통과한 파에 의해 다소 충격적 파력의 첨두가 발생한 후(Crest IIa), 유수실 후면벽을 월파하는 파에 의해서 비교적 완만하게 변화하는 파력 첨두값(Crest IIb)이 2차로 나타나게 된다(Takahashi and Shimosako, 1994). 그러나 파고가 작거나 주기가 긴 경우에는 충격적 파력이 잘 발생하지 않기 때문에 Crest IIa의 위상은 모든 파랑 조건에서 항상 나타나는 것은 아니다. Fig. 9에는 Crest IIb 위상에서 유수실 후면벽에 작용하는 파력 계측값(FREXP)을 Goda 파압식에 의해 계산된 파력(FRGoda)으로 나누어 무차원화한 결과를 제시하였다. Fig. 9로부터 FREXP/FRGoda의 값은 평균적으로 1보다 다소 작으며, 대체로 H/h의 값이 증가함에 따라서 그 크기가 근소하게 증가함을 확인할 수 있다. Takahashi and Shimosako(1994)에서는 파고가 커짐에 따라서 후면벽에 작용하는 무차원파력 값이 작아지는 경향을 보였으며, 이는 본 실험과 상반된 결과로서 향후 이와 관련해서는 추가적으로 면밀한 고찰이 필요하다. 한편, Fig. 9에서 일부 실험파를 제외하면 단일유수실에 비해서 이중유수실 케이슨의 경우가 파력 계측값이 더 작음을 확인 할 수 있으며, 이는 Fig. 7에 제시된 전면벽 유공부 작용 파력 계측 결과에 상응하는 것이다. 평균적으로는 이중유수실 케이슨에 대한 FREXP/FRGoda의 값이 단일유수실 케이슨에 비해서 14.6% 작게 나타났다.
4.3 중간벽 작용 최대 수평파력
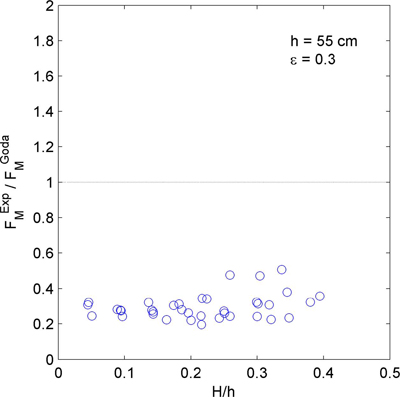
전면벽 작용 파력에 대한 분석 방법과 동일하게 이중유수실 케이슨의 중간벽에 작용하는 최대 수평파력에 대해서도 중간벽에서의 파력 계측값(FMEXP)을 Goda 파입식에 의한 계산값(FMGoda)로 나누어 무차원화한 결과를 Fig. 10에 제시하였다. 즉, FREXP/FRGoda는 중간벽 유공부의 단면을 무공벽으로 가정하여 Goda 파압식으로 계산한 결과에 해당한다. 이 결과는 중간벽에 작용하는 파력이 최대가 되는 파 위상, 곧 Fig. 6에서 FM이 최대가 되는 시점에 해당하는 결과이며, 단일유수실 케이슨의 경우에는 중간벽이 없기 때문에 오직 이중유수실 케이슨에 대해서만 계산 결과를 제시하였다. Figs. 7~9에 보인 전면벽 및 후면벽 작용 파력의 경우와는 달리 중간벽에 작용하는 최대 수평파력은 대체로 Goda 파압식에 의한 파력 산정값의 20~40%에 분포하여 상대적으로 매우 작았다. 이처럼 중간벽에 작용하는 최대 수평파력이 현저하게 작은 이유는 중간벽은 전면벽처럼 파가 처음으로 부딪치면서 큰 에너지를 전달하는 구조물이 아니면서, 동시에 유공 형식이기 때문에 후면벽처럼 유수실 내로 침투한 파에 의한 파력에 최종적으로 저항하는 구조물도 아니기 때문이다. 즉, 중간벽은 유수실 내로 침투한 파의 에너지를 부분적으로 소산시키면서 후면벽에 작용하는 파력을 일부 저감시키는 역할을 담당한다고 볼 수 있다. 따라서, 중간벽은 전면벽과 유사한 유공 구조물 형식이지만 전면벽에 비해서는 구조적으로 요구되는 강성이 훨씬 작을 수 있으며, 설계 시 이러한 점을 고려할 필요가 있다.
5. 토의 및 결론
5.1 단일 및 이중유수실 케이슨에 작용하는 최대 수평파력 비교
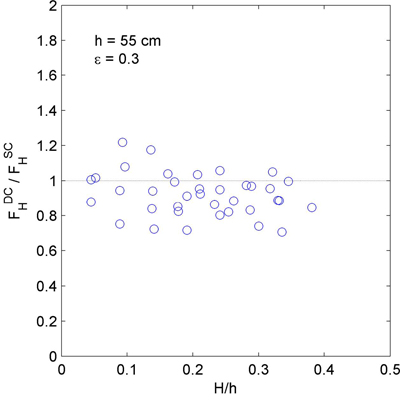
3장과 4장에서는 파의 위상에 따라서 유공 케이슨 각 벽체에 작용하는 최대 수평파력을 개별적으로 고찰하여 보았으며, 이는 부재 설계 및 케이슨 자체의 안정성 평가에 매우 중요한 정보를 제공한다. 그런데, 현업 설계에서는 이에 더하여 단일 및 이중유수실 케이슨에 작용하는 전체 파력의 크기에도 관심을 두게 된다. Fig. 11에는 단일 및 이중유수실 케이슨에 작용하는 전체 수평파력이 최대가 되는 순간의 계측값을 상대 비교한 결과를 나타내었다. 이 그림에서 FHDC는와 FHSC는 각각 이중 및 단일유수실 케이슨에 수평 방향으로 작용하는 최대 전파력을 의미한다. Fig. 11로부터 상당수의 실험파 조건에서 FHDC/FHSC의 값이 1보다 작음을 확인할 수 있으며, 이는 이중유수실 케이슨에 작용하는 파력이 단일유수실 케이슨에 비해서 더 작음을 의미한다. 평균적으로는 FHDC의 값이 FHSC에 비해서 8.2%가 더 작았다.
한편 Table 1에는 단일 및 이중유수실 케이슨에 작용하는 최대 수평파력 계측값을 Goda 파압공식으로 무차원화한 결과(FHEXP/FHGoda)를 추가로 제시하였다. 여기서 최대 수평파력이 작용하는 파의 위상은 Fig. 5 및 Fig. 6에서 FH가 최대가 되는 시점에 해당한다. Table 1으로부터 본 실험에서는 단일 유수실 케이슨 작용 파력이 Goda 파압공식에 의한 산정 결과의 93.4%에 해당함을 알 수 있으며, 이는 무공케이슨에 비해서 6.6% 파력이 저감되는 효과가 있음을 나타낸다. 이중유수실 케이슨의 경우 최대 수평파력 계측값이 Goda 파압공식에 의한 수평파력 대비 84.4%였으며, 단일 유수실보다 더 큰 15.6%의 파력감소 효과를 나타내었다. 한편, 이 두 값을 비교하면 이중유수실 케이슨의 무차원 수평파력이 단일유수실에 비해서 9.6% 작았다. 이 값이 바로 위에서 살펴본 결과(평균적으로 FHDC의 값이 FHSC에 비해서 8.2% 작음)와 차이가 나는 이유는 단일 및 이중 유수실 케이슨에 대한 실험에서 동일한 실험파를 조파하더라도 계측된 입사파가 미세하게 다르기 때문에 그에 따라서 FHGoda의 값이 서로 약간씩 다르게 계산되기 때문이다. 이러한 점을 고려할 때 단일 및 이중 유수실 케이슨 수평파력의 상대비교는 후자(무차원 수평파력 FHEXP/FHGoda의 비교)에 근거한 결과를 참고하는 것이 엄밀한 의미에서 더 타당하다고 할 수 있다.
지금까지 위에서 고찰한 것처럼 이중유수실 케이슨의 경우 중간벽이 존재하여 파 에너지를 소산시키는 기능이 있기 때문에 유수실 전체 폭이 동일한 단일유수실 케이슨에 비해서 최대 수평파력이 작아지게 된다는 점을 주지할 필요가 있다. 간혹, 현업 설계에서 이중유수실 케이슨 설계 시 중간벽 작용 파압 분포를 전면벽 파압 분포와 유사하게 적용한 후 파의 위상에 대한 고려 없이 단순하게 합침으로써 단일유수실 케이슨의 경우에 비해서 훨씬 큰 파력을 산정하는 경우가 있는데, 이러한 설계법은 근본적인 오류를 내포하고 있기 때문에 설계 시 피해야 할 것이다.
5.2 결론
본 연구에서는 단면 수리모형실험을 수행하여 단일 및 이중유수실 케이슨 방파제에 작용하는 수평파력을 로드셀을 이용하여 계측하고, Takahashi and Shimosako(1994)의 방법을 준용하여 파의 위상별로 케이슨 전면벽, 후면벽 및 중간벽(이중유수실의 경우)에 작용하는 최대 수평파력을 분석 및 비교하였다. 본 연구를 통해서 이중유수실 케이슨의 2개 유수실 전체 폭이 단일유수실의 폭과 동일한 경우 이중유수실 케이슨에 작용하는 총파력이 더 작음을 확인할 수 있었다. 이러한 파력 저감 효과는 이중유수실 케이슨의 경우 전면벽 유공부를 통과하여 유수실 내로 침투한 파 에너지가 중간벽에서 추가적으로 소산되면서 후면벽에 부딪치기까지의 시간이 더욱 지연되어 전면벽 및 후면벽에서 수평파력이 최대가 되는 위상 사이의 시간 차가 더 크게 되기 때문에 발생하는 것이다. 향후 마운드의 높이, 방파제 전면 수심, 케이슨 전면벽 유공률 등이 본 수리실험 조건과 다른 추가 실험을 수행하여 본 연구에서 얻어진 결과를 검증할 필요가 있으며, 이를 바탕으로 설계 현업에서 활용할 수 있는 이중유수실 파압 공식을 개발할 필요가 있다.