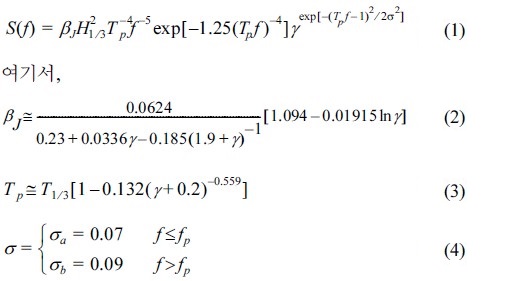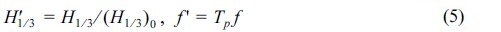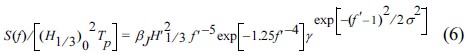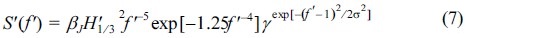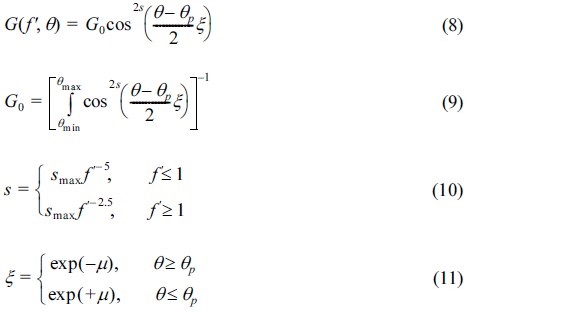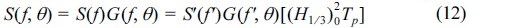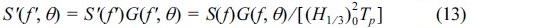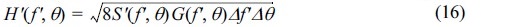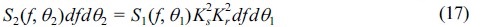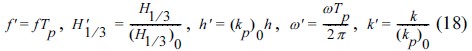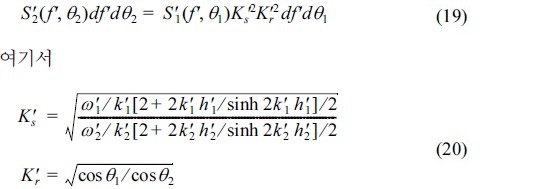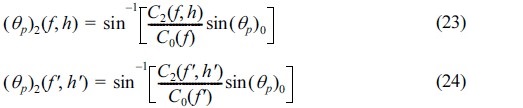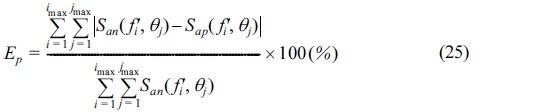Article information

Abstract

Trans Abstract

1. 서 론

심해에서 바람에 의해 생성된 파랑은 다양한 주기와 방향성이 존재한다. 심해에서 생성된 다방향 불규칙파랑은 천해로 전파해 오면서 해저 지형의 변화에 따른 굴절, 섬이나 해양 구조물에 의한 회절, 수심 감소에 따른 천수 등의 다양한 과정을 겪으면서 주기와 방향에 대한 에너지 분포, 즉 스펙트럼이 변화한다.

심해에서의 다방향 불규칙파랑은 주기 스펙트럼으로 Pierson-Moskowitz 스펙트럼(Pierson and Moskowitz, 1964), Bretschneider-Mitsuyasu 스펙트럼(Bretshneider, 1968; Mitsuyasu, 1970), JONSWAP 스펙트럼(Hasselmann et al., 1973) 등이 있으며, TMA(Bouws et al., 1985) 스펙트럼은 천해역의 천수 효과가 고려된 것이다. 방향 분포함수로는 cos²(θ − θ_p)형(Pierson et al., 1952), cos^2s[(θ − θ_p)/2]형(Longuet-Higgins et al., 1961), cos^2sθ − θ_p)형(Borgman, 1969) 등이 있으며, Mitsuyasu et al.(1975)은 첨두주파수(peak frequency)에서의 방향분포함수의 폭이 다른 주파수에서의 것보다 좁은 형태를 제안하였다. 앞에서 θ는 파랑의 입사각을 뜻하며, θ_p는 첨두주파수에서의 주입사각, s는 방향분포 매개변수를 뜻한다. Hwang et al.(2000)은 스펙트럼 밀도의 첨두값이 2개의 주파수에 존재하는 쌍봉(bimodal)형 방향 스펙트럼을 제안하였고, Lee et al.(2010)은 굴절에 의한 방향의 좌우 비대칭성을 고려한 방향스펙트럼을 제안하였으며, 관측 결과를 토대로 천해에서 방향의 비대칭성이 발생함을 확인하였다.

이처럼 최근 다양한 형태의 방향 스펙트럼이 제안되었는데, 이는 불규칙파랑의 대표값(예를 들어, 유의파고, 유의파주기, 첨두주기 등)은 같을지라도 해안선이나 해안지역에 건설된 구조물의 영향을 받아 그 형태가 상당한 차이가 나기 때문이다. 특히, 불규칙파랑의 방향 비대칭성의 경우 주파향을 기준으로 에너지 분포가 넓은 방향으로 구조물에 부딪치는 경우 또는 그 방향으로 항 내로 파랑이 전파하는 경우 구조물에 미치는 파력 또는 항내정온도가 방향의 비대칭성을 무시한 경우에 비하여 크게 발생할 것이다. 이를 무시한 경우 과소평가로 인하여 안전성에 문제가 발생할 수도 있다. 또한 해안선 근처에서 방향의 비대칭성이 이안류 및 연안류의 형성에도 영향을 미치게 될 것이다. 입사파랑의 방향 비대칭성이 구조물에 미치는 영향에 대해서는 이 등(2009) 및 Jung et al.(2011)에 의해 상세히 연구된 바 있다. 따라서, 수심 조건에 따른 스펙트럼의 형태를 나타내는 다양한 계수들을 미리 계산하여 이를 이용한다면 천해에서의 스펙트럼의 형상을 간과함으로써 발생하는 문제들을 사전에 방지할 수 있을 것이다. Lee et al.(2010)은 등수심선이 나란한 경우 천해에서 굴절이 발생하면서 다방향 불규칙파의 방향 비대칭 매개변수(μ) 및 최대 방향분포 매개변수(s_max)가 변하는 값을 제시하였다. 그런데, 그들의 결과는 유의파고가 5.0 m, 유의파주기가 10초, 첨두신장인자(peak enhancement factor)가 γ = 3.3인 경우에 대해서 제시하였다.

본 연구에서 Lee et al.의 연구를 확장하여 해안선이 나란한 경우 굴절이 발생하면서 다방향 불규칙파의 방향비대칭 매개변수 및 최대 방향분포 매개변수의 일반화된 값을 제시하여 해안공학 실무자와 연구자들이 활용할 수 있게 하였다. 일반화를 위해 계산과정과 결과들을 심해에서의 유의파고, 첨두주기, 극대주기에 대응되는 파장 등으로 무차원화 하였다. 파랑의 굴절은 에너지 스펙트럼 성분을 8,145개 규칙파 성분(45개 주기 성분 × 181개 방향 성분)으로 분해하였으머, Snell의 법칙을 따르는 해석해를 적용하여 계산하였다. 그리고, Lee et al.(2010)이 제안한 스펙트럼의 근사화를 통해 상대수심에 따른 비대칭 매개변수와 최대 방향분포 매개변수를 계산하였다. 무차원화된 불규칙 파랑의 굴절은 제2장에서, 상대 수심에 따른 비대칭 매개변수 및 최대 방향분포 매개변수의 근사화는 제3장에서 상세히 소개하였다. 제4장에서는 심해에서 다양한 입사각과 최대 방향분포 매개변수, 첨두 신장인자에 따른 천해에서의 최대 방향분포 매개변수와 비대칭 매개변수의 변화된 값을 실무자들이 적용할 수 있게 그림으로 제안하였으며, 이에 대한 설명을 추가하였다. 마지막으로 제5장에서는 결론 및 향후 추가 연구사항 등에 대해 언급하였다.

2. 불규칙파 스펙트럼의 무차원화

본 연구에서는 심해에서 다방향 불규칙파랑의 주파수스펙트럼으로 JONSWAP 스펙트럼을 채택하였다. JONSWAP 스펙트럼 식은 아래와 같다.

위 식에서 H_1/3은 유의파고, T_p는 첨두주기, f 는 주파수, f_p는 첨두주파수를 의미한다. 그리고, γ 는 첨두신장인자로 주파수 스펙트럼의 폭을 결정한다. γ 가 클수록 에너지 밀도의 첨두값이 커지고 밀도폭이 좁아진다. 위의 스펙트럼식을 일반화하기 위해 다음과 같은 무차원 변수를 정의한다.

여기서, (H_1/3)0은 심해에서의 유의파고를 의미한다. 식 (5)의 무차원변수를 식 (1)에 대입하면 식 (6)과 같다.

여기서, 무차원 주파수 스펙트럼을 S'(f') = S(f)/((H_1/3)₀²T_p)로 정의하면 식 (6)은 다음과 같다.

통상적으로 방향분포함수는 차원이 없기 때문에 무차원화가 필요치 않다. 하지만, Mitsuyasu et al.(1975)에 의해 제안된 방향분포함수와 비대칭효과를 고려한 Lee et al.(2010)의 식은 주기 성분에 따라 분포형태가 달라지기 때문에 주기에 대해서 무차원화가 필요하다. 식 (5)의 무차원 변수를 사용하면 Lee et al.의 방향분포함수는 다음과 같다.

여기서, s는 방향분포 매개변수, s_max는 최대 방향분포 매개변수, μ는 비대칭 매개변수이다. 비대칭 매개변수가 양수이면 방향 스펙트럼 형상은 주파향보다 각도가 큰 방향(즉, 왼쪽 방향)의 분포함수값이 주 파향보다 각도가 작은 방향에 비해 더 크다. 즉, 비대칭 매개변수를 이용하여 방향에 대해 비대칭 형상인 에너지 분포를 나타낼 수 있다. 비대칭 매개변수와 방향스펙트럼의 왜도(skewness)에 대한 상관관계는 Lee et al.(2010)의 결과를 참고할 수 있다.

다방향 불규칙파랑의 에너지 분포를 나타내는 스펙트럼은 주파수 스펙트럼과 방향 스펙트럼의 곱으로 표현되며 다음과 같다.

따라서, 다방향 불규칙파랑의 무차원 스펙트럼식은 다음과 같다.

여기서, S'(f')는 식 (7)과 같으며, 식 (4)는 다음과 같이 고쳐 쓸 수 있다.

다방향 불규칙파랑의 스펙트럼에서 각 주파수 및 방향 성분에 대한 파고 성분은 다음과 같은 식을 만족한다.

여기서, Δf 및 Δθ 는 주파수 및 방향에 따른 계산간격을 뜻한다. 식 (5)를 이용하여 식 (15)을 무차원화 하면 다음과 같다.

3. 최대 방향분포 매개변수 및 비대칭 매개변수의 근사화

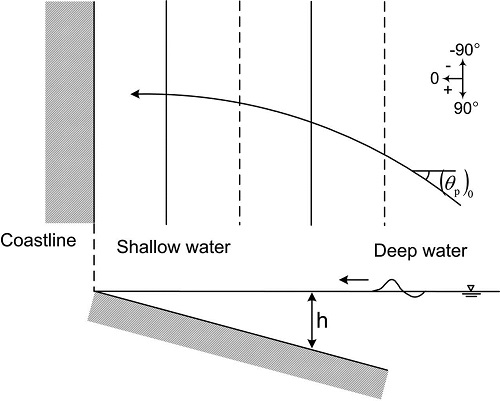
심해에서 방향 대칭인 불규칙파랑이 등 수심선에 비스듬히 입사할 경우 수심변화에 따라 굴절이 발생하게 된다. 이와 같은 불규칙파랑이 천해로 전파해 옴에 따라 주파향각을 중심으로 양쪽의 굴절 정도가 달라져서 방향 비대칭이 발생하게 된다. 심해에서 천해역으로 전파해 오는 다방향 불규칙파랑 스펙트럼은 다음과 같은 식을 통해 해석적으로 계산할 수 있으며, 이는 Fig. 1을 참고할 수 있다.

Fig. 1.

Definition sketch of refraction of random waves.

여기서, K_s (= 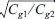)는 천수계수이고, K_r ( = 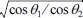)은 굴절계수이다. 그리고, C_g( = C[1 + 2kh/sinh2kh]/2)는 파의 군속도, C( = ω/k) 파의 위상속도 이다. 식 (17)을 이용해서 심해에서부터 천해로 단계적으로 스펙트럼을 계산할 수 있는데, 아래첨자 1은 심해 쪽에 위치한 변수를 의미하고, 아래첨자 2는 천해 쪽에 위치한 변수를 의미한다.

굴절에 따른 스펙트럼의 변화를 나타내는 식 (17)을 무차원화 하기 위한 무차원 변수는 다음과 같다.

여기서, (k_p)₀는 심해에서 첨두 주파수에 해당하는 파수를 뜻한다. 식 (18)을 이용하여 식 (17)을 무차원화 하면 최종적으로 다음과 같은 식이 성립한다.

식 (19)를 풀기 위해서는 k'와 ω'를 구하여야 하고, 그 전에 분산관계식을 풀어야 한다. 무차원화 된 분산관계식은 다음과 같다.

그리고 심해에서의 분산관계식과 식 (21)을 이용하여 정리하면, 식 (22)와 같은 무차원 분산관계식을 구할 수 있다.

여기서, h'₀는 다방향 불규칙 파랑이 출발하는 심해 수심 이며, h'₀ = (k_p)₀h₀이 성립한다.

그리고, Lee et al.(2010)에 의해 제시된 것처럼 각 주기별로 굴절의 정도가 달라지기 때문에 에너지가 가장 큰 주 파향각 θ_p가 주기 및 수심에 따라 상이한 값을 갖게 된다. 따라서, 이를 고려하여야 하는데 이는 식 (23)과 같으며, 이를 무차원화 한 식은 식 (24)와 같다.

식 (19), (22), (24)을 적용하여 다방향 불규칙파랑의 굴절에 대한 해석해를 계산할 수 있다. 해석적으로 계산된 다방향 불규칙파랑 스펙트럼이 어떠한 비대칭 매개변수 값과 최대 방향분포 매개변수를 갖는지를 알기 위해 정형화된 스펙트럼 식을 근사화 하는 과정이 필요하다. 이는 다음과 같은 식으로 제안된 퍼센트 오차가 최소가 되도록 하는 비대칭 매개변수와 방향분포 매개계수를 시행착오법을 통하여 계산하였다.

여기서, E_p는 퍼센트 오차를 뜻하며, S_an(f_i^', θ_j)는 i번째 주파수 및 j번째 파향각에 해당하는 해석해에 의한 스펙트럼을 뜻한다. 그리고, S_ap(f_i^', θ_j)는 i번째 주파수 및 j번째 파향각에 해당하는 근사화된 스펙트럼을 나타낸다. 본 연구에서 i_max는 f ' = 0.2에서 2.4까지 45를 적용하여 Δf ' = 0.05이며, j_max는 θ = −π/2에서 π/2까지 181을 적용, Δθ = π/180이다.

4. 천해역에서 최대 방향분포 매개변수 및 비대칭 매개변수

본 연구에서는 심해에서 출발한 방향 대칭인 다방향 불규칙파랑이 천해역으로 전파해 오면서 상대수심에 따른 최대 방향분포 매개변수와 비대칭 매개변수를 계산한다. 과거 Goda and Suzuki(1975)는 방향 비대칭을 무시하고 상대 수심에 따른 최대 방향분포 매개변수를 제안하였다. Lee et al.(2010) 은 이후 굴절에 의한 비대칭까지 고려한 결과를 제시하였으나, 특정한 몇몇 경우에 대해서만 결과를 제시하였다. 따라서, 본 연구에서는 실무에 보다 편리하게 적용할 수 있게 무차원화를 통해 계산과정을 일반화하였으며, 또한 심해에서의 보다 다양한 불규칙파랑에 대해 천해에서의 결과를 제시한다.

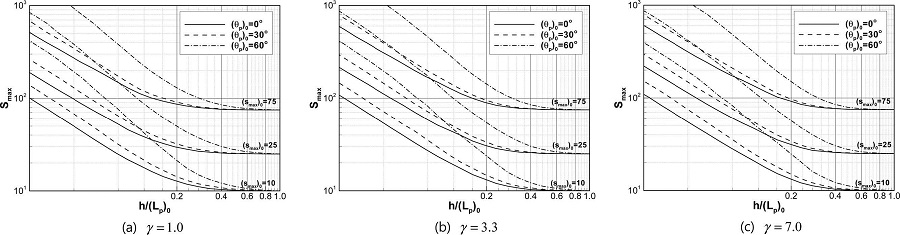
Fig. 2는 각각 γ = 1.0, 3.3, 7.0 인 경우에 대한 계산 결과이다. 그리고, 각각의 그림은 심해에서의 최대 방향분포 매개변수, (s_max)₀=10, 25, 75 및 심해에서의 주파향 각 (θ_p)₀ = 0^o, 30^o, 60^o인 경우에 대해 상대수심에 따른 최대 방향분포 매개변수를 나타낸다. Fig. 2를 통해 상대수심이 감소할수록 최대 방향분포 매개변수는 급격히 증가하며, 심해에서의 주파향각이 클수록 증가율이 더욱 커지는 것을 알 수 있다. 이는 주파향각이 클수록 해저지형에 의한 굴절이 더욱 크게 발생하여 방향스펙트럼의 폭이 더욱 좁아지기 때문이다.

Fig. 2.

Variation of maximum spreading parameter with relative water depth.

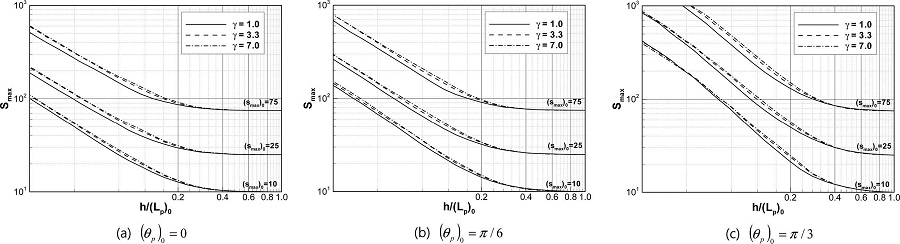
Fig. 3 역시 상대수심 변화에 따른 최대 방향분포 매개변수를 나타낸 그림으로, 첨두신장인자의 변화에 따른 최대 방향분포 매개변수의 변화를 보다 보기 쉽게 나타낸 그림이다. Fig. 2와는 달리 첨두신장인자에 대해서는 상대수심에 따른 최대 방향분포 매개변수의 변화가 크게 발생하지는 않았다. 즉 주파수 스펙트럼의 형상은 최대 방향분포 매개변수의 변화에 큰 영향을 주지는 않는 것으로 나타났다. 하지만 전반적인 경향은 첨두신장인자가 클수록 최대 방향분포 매개변수 역시 적은 값이지만 크게 계산된다. 이는 첨두신장인자가 증가할수록 첨두 주파수로 에너지가 집중되어 비교적 규칙파에 가까워지기 때문이다.

Fig. 3.

Variation of maximum spreading parameter with relative water depth.

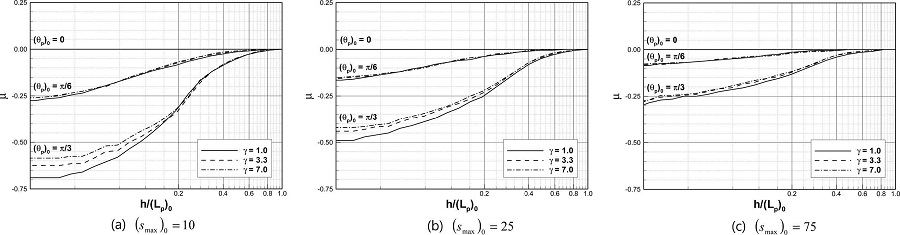
Fig. 4는 상대수심 변화에 따른 비대칭 매개변수의 변화를 나타낸 그림이다. 그림을 통해 심해에서의 주 파향각이 크고, 첨두신장인자(γ)가 작을수록 그리고, 상대수심이 감소할수록 비대칭 매개변수의 절대값은 증가하는 것을 볼 수 있으며, 첨두신장인자보다는 심해에서 주 파향각의 크기가 비대칭 매개변수에 더욱 큰 영향을 주는 것을 알 수 있다. 그리고, Fig. 4(a), (b), (c)는 각각 심해에서의 최대 방향분포 매개변수가 다른데, 최대 방향분포 매개변수가 작을수록 천해역에서 비대칭 매개변수의 절대값은 더욱 커짐을 알 수 있다. 최대 방향분포 매개변수가 작으면 주파향각을 중심으로 넓게 분포하는 형태가 되는데, 굴절의 영향을 크게 받는 성분, 즉 등수심선에 수직인 방향과 각도의 차이가 큰 성분이 많기 때문에 최대 방향분포 매개변수가 작을수록 비대칭성이 강해지는 현상이 발생하게 된다.

Fig. 4.

Variation of asymmetry parameter with relative water depth.

5. 결 론

본 연구에서는 천해역에서 다방향 불규칙파랑의 굴절에 의해 발생하는 비대칭성 매개변수와 최대방향분포 매개변수의 변화에 대해 연구하였다. 굴절의 해석해는 무차원화를 통해 더욱 일반화된 식을 사용하였으며, 파랑의 방향 비대칭성을 추가로 고려한 Lee et al.(2010)이 제안한 방향 스펙트럼을 이용하여 근사화하였다. 근사화를 위한 수치해석 결과 상대수심이 작아질수록 최대 방향분포 매개변수와 비대칭 매개변수의 절대값은 증가하였다. 특히, 첨두신장인자가 증가할수록 천해에서의 최대 방향분포 매개변수는 증가하였다. 반면 심해에서의 입사각이 클수록, 그리고, 첨두신장인자가 작을수록 천해에서 비대칭 매개변수의 절대값은 증가하였다. 첨두신장 인자가 커지면 첨두 주파수로 파랑 에너지가 집중되어 보다 규칙파에 근접해진다. 따라서 천해에서의 최대 방향분포 매개변수는 보다 크게 계산되며, 반면 비대칭 매개변수는 작게 나타난다. 입사각이 큰 경우에는 천해로 접근해 오면서 굴절에 의한 파랑 변형이 크게 발생하므로 비대칭 매개변수 역시 크게 계산된다.

본 연구를 통해 제시된 그림에서는 Goda and Suzuki (1975)의 연구에 파랑의 비대칭성과 첨두신장인자의 변화를 추가로 고려하였으며, Lee et al.(2010)의 연구를 더욱 일반화 하였기 때문에 실무자들이나 연구자들이 보다 쉽게 활용할 수 있을 것이다. 또한, 이를 통해 해안 구조물의 설계나 해안환경의 변화에 있어서 그 동안 간과되어 왔던 파랑의 방향 비대칭성이 추가로 고려될 수 있을 것이다. 그리고 향후에는 항내 정온도나 해안 구조물에 작용하는 파력 등에 있어서의 방향 비대칭 효과에 대해 추가 연구가 필요할 것으로 사 료된다.

Article information Continued