Article information

Abstract

Trans Abstract

1. 서 론

해안의 퇴적물 이동은 입사파의 쇄파와 쇄파대에서 발생하는 해빈류(wave-induced currents)의 영향을 크게 받는다. 해빈류는 해안선과 나란한 방향의 연안류(longshore currents)와 해안선과 직각방향으로 외해쪽으로 향하는 이안류(rip currents) 성분으로 나눌 수 있다. 쇄파로 인한 강한 난류에 의하여 발생한 부유사(suspended load)는 이러한 해빈류에 의하여 수송된다. 한편 쇄파대내 파의 소상영역(swash zone)과 쇄파대 밖에서는 파동에 의한 유체운동에 의하여 소류사(bed load) 형태로 퇴적물이 수송된다. 이러한 물리적인 과정에 의하여 퇴적물이 수송되고 해안의 침식과 퇴적이 발생하게 되는데 이를 연안과정(coastal processes)이라고 한다. 연안과정에서 퇴적물 수송에 영향을 미치는 흐름은 파랑에 의한 해빈류 이외에도 조석에 의한 흐름(조류) 및 하천유출수 등이 있다. 본 연구대상인 해운대 해수욕장은 해안부근에서 비교적 조류가 약하고 하천유출수의 영향을 받지 않는 해안으로서 연안과정에서 해빈류가 지배적인 역할을 한다. 해빈류의 수치 모의 방법은 크게 두 가지로 나눌 수 있는데 일반적으로 파랑에 의한 radiation stress를 구하여 천수방정식의 외력항으로 평가하여 수치모의하는 방법이 널리 사용되고 있다(Lee et al., 2005). 최근에는 직접 파랑변형을 수치계산하여 시간적분을 통하여 해빈류를 수치모의하는 방법이 많이 사용되고 있다. Choi et al.(2011)과 Choi(2015)는 Boussinesq-type 방정식에 의한 FUNWAVE(Fully Nonlinear Boussinesq Wave Model) 모형을 이용하여 다방향 불규칙파 조건에서 해운대 해수욕장의 이안류를 예측하였다. Boussinesq-type모형은 천해역의 천수변형, 굴절, 회절, 반사, 쇄파, 파-흐름 상호작용과 비선형효과 등의 고려가 가능하며 다른 후처리 과정 없이 일정시간동안 평균된 유속을 구하여 해빈류를 계산할 수 있다는 장점을 가지고 있다. 그러나 전통적인 수심적분 Boussinesq-type 모형은 심해영역에서 주파수 분산의 정확도가 저하된다는 문제점을 가지고 있으며, 수심평균된 2차원 흐름의 결과만을 얻을 수 있다. 해운대해수욕장에서 해빈류에 대한 연구는 해안표사이동의 원동력으로서의 해빈류에 관한 연구(Lee et al., 2007a; Lee et al., 2007b; Lim et al., 2014)와 최근에는 이안류발생기구등 연안방재와 관련된 연구가 활발하게 진행되고 있다(Kim et al., 2010; Ha et al., 2014; Shin et al., 2014). 한편, 본 연구에서 사용하는 SWASH(Surface WAves till SHore) 모형(The SWASH team, 2010)은 연직방향으로 층을 나누어 준3차원적인 결과를 얻을 수도 있으며, 층을 증가시켜 심해영역까지 분산효과의 정확성을 증대시킬 수 있다. SWASH 모형에 의한 해빈류에 관한 해외연구는 Vilani et al.(2012) 의 연구사례가 있으며, 국내에서는 진하해수욕장의 해빈류에 대한 Jang et al.(2014)의 연구와 해운대해수욕장의 이안류에 대한 Yoon(2014)에 의한 연구가 있다. 해운대해수욕장의 해빈류에 관한 기존 연구결과를 보면 연안 침식·퇴적과정(beach processes) 해석을 위한 연구와 해수욕장의 안전과 관련한 이안류발생기구 및 예측에 관한 연구로 대별할 수 있다. 이안류에 관한 연구에서 Kim et al.(2010)은 실시간 파랑관측자료를 이용하였으며, Yoon(2014)는 다양한 수심과 파랑조건 하에서 이안류 발생여부를 검토하였다. 한편, beach processes와 관련한 연구에서는 장기간에 걸친 해안선변화예측 또는 폭풍으로 인한 단기간의 해빈변형예측 등과 같은 연구목적에 따라서 사용하는 대표파의 제원이 달라진다. 따라서 기존의 해운대해수욕장의 해빈류수치시뮬레이션에 적용한 입사파랑조건이나 수심보정 등이 각각 다르다. 본 연구에서는 해운대해수욕장의 계절적인 해빈류특성을 파악하기 위하여 해운대해수욕장에서 1차 양빈이 끝난 2014년 5월 측량한 수심자료를 사용하여 2014년 1년간에 걸친 파랑관측 자료로부터 구한 계절별 유의파의 최대값에 해당하는 대표파를 평균해수면 조건에서 수치시뮬레이션하였으며 사계절 결과중에서 입사파향이 서로 다른 하계와 동계의 해빈류패턴을 비교하였다. 한편, 입사파랑조건은 규칙파와 불규칙파를 대상으로 시뮬레이션을 행하여 양자를 비교한 결과 불규칙파의 시뮬레이션결과가 보다 타당성이 있는 결과로 판단되어 Choi(2015)와 같이 불규칙파랑에 대한 해빈류의 시뮬레이션결과를 제시하였다.

2. 대상지역의 특성

2.1 대상지역의 위치

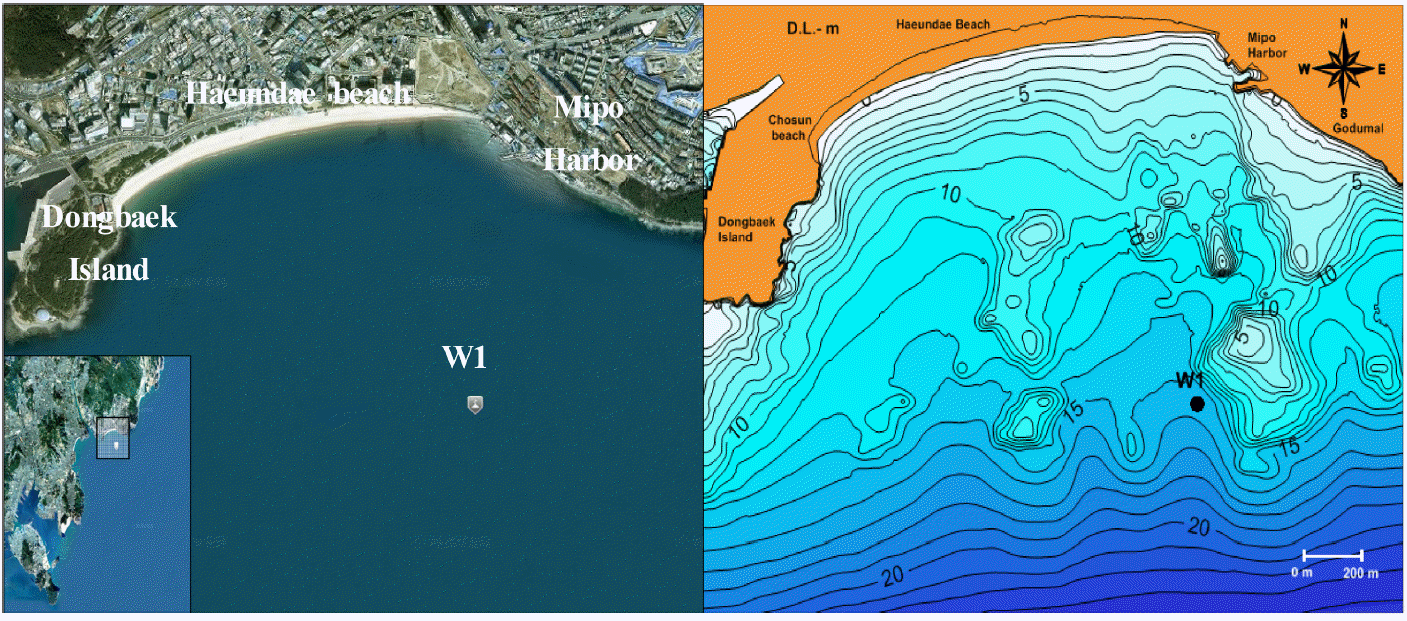
해운대 해수욕장은 부산광역시 해운대구에 위치하고 있으며 연안정비사업으로 인해 양빈사업이 지속적으로 시행되어 2014년 11월에는 평균 해빈폭이 80 m까지 증가하였다. 해운대 해수욕장의 동측에는 미포항, 서측에는 동백섬이 위치하고 있으며 해운대 해수욕장의 침식과 미포항의 매몰문제가 문제시 되고 있는 상황이다. 해운대 해수욕장의 중앙부근과 미포측의 전면은 암반과 천퇴로 인한 복잡한 해저지형을 나타낸다. 본 연구에 적용한 해운대해수욕장의 수심자료는 1차 양빈 후에 측량한 2014년 5월에 관측된 수심관측 자료를 적용하였다(Fig. 1).

Fig. 1.

Topography (left) and bottom bathymetry of May, 2014(right) in Haeundae Beach (KHOA).

2.2 계절별 대표파랑 선정

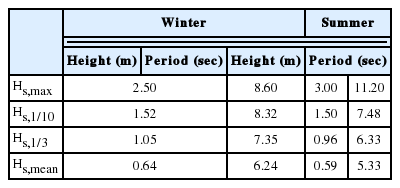
해운대 해수욕장의 계절별 대표파랑을 선정하기 위해 2014년 1년간 국립해양조사원의 파랑관측자료를 사용하였으며 그 위치는 W1과 같다(Fig. 1). 관측부이가 위치한 수심은 15.6 m 이며, 1시간단위의 파랑관측자료를 이용하여 대표파랑을 선정하였다. 파랑관측자료를 분석한 결과, 동계(12월 ~ 2월) ESE 계열과 하계(6월 ~ 8월) S 계열의 파랑이 지배적으로 나타났다(Fig. 2). 동계와 하계의 1시간단위 파랑관측자료를 이용하여 유의파의 최대치 H_s,max, 1/10 최대파 H_s, _1⁄10, 1/3 최대파 H_s, _1⁄3, 평균파 H_s,mean 및 그에 상응하는 주기를 나타내었으며 대표파랑은 유의파의 최대값으로 선정하였다(Table 1).

Fig. 2.

Wave rose diagrams in Haeundae Beach, 2014 (winter and summer).

Table 1.

Characteristics of seasonal wave in Haeundae Beach (Winter, Summer)

2.3 계절별 흐름 및 표사이동 특성

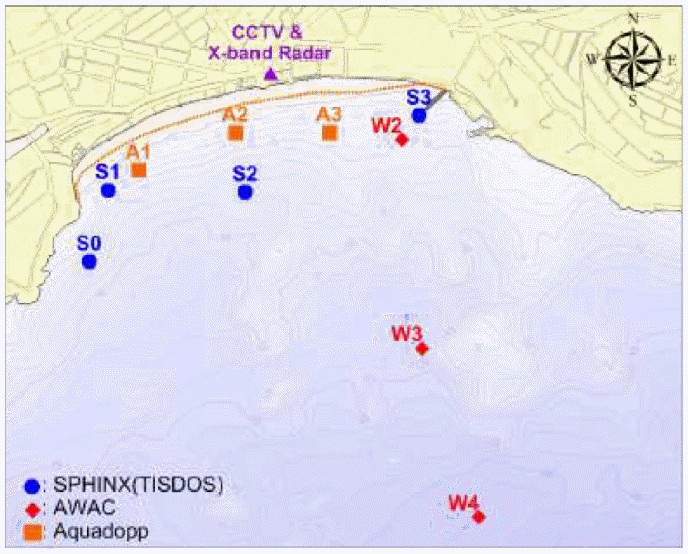
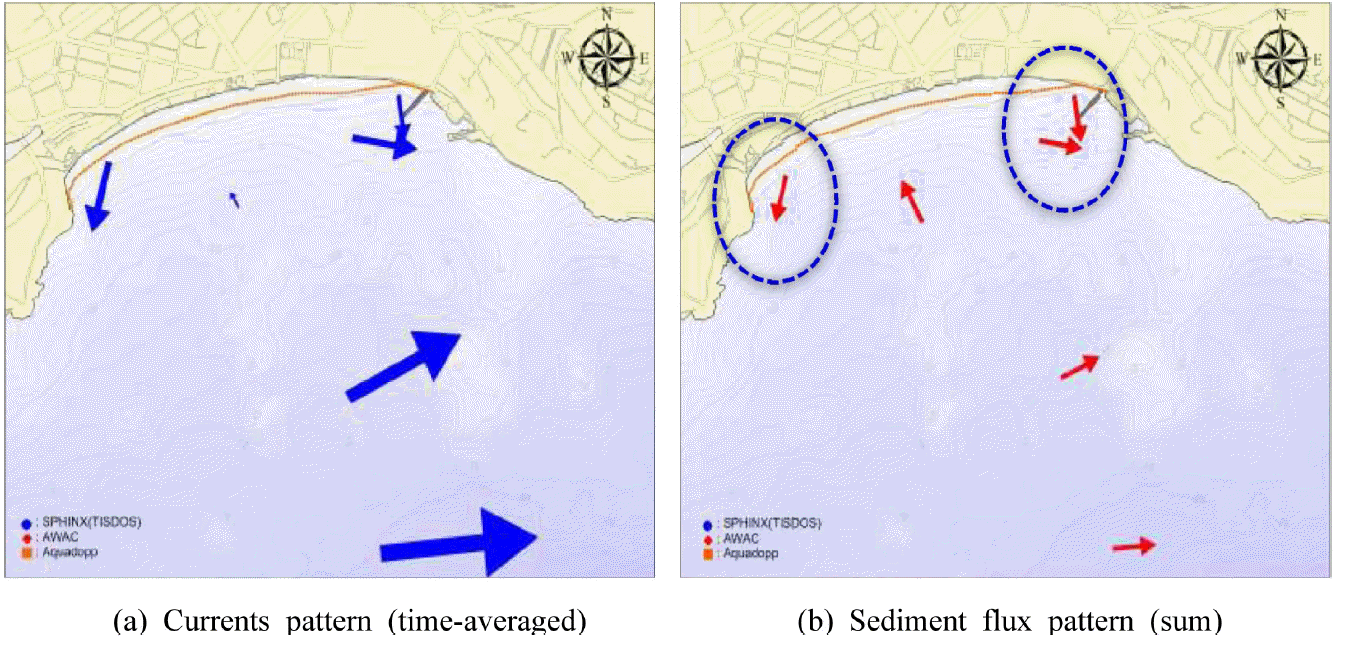
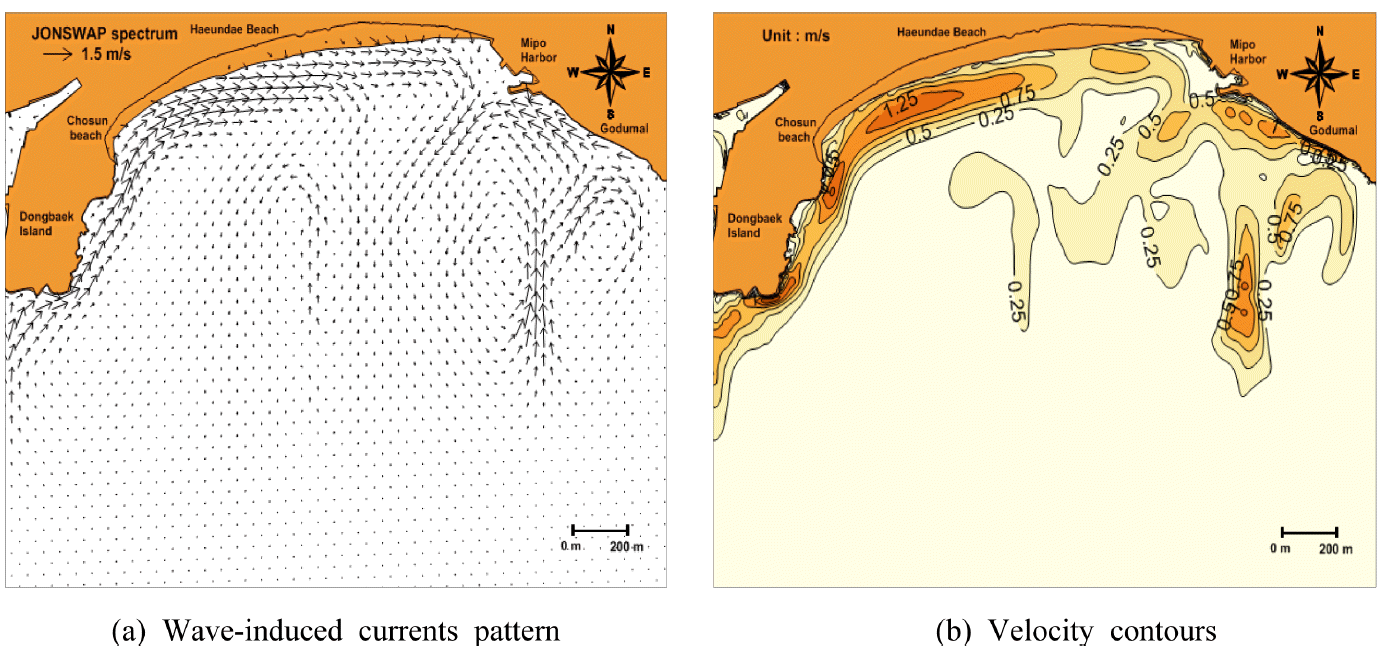
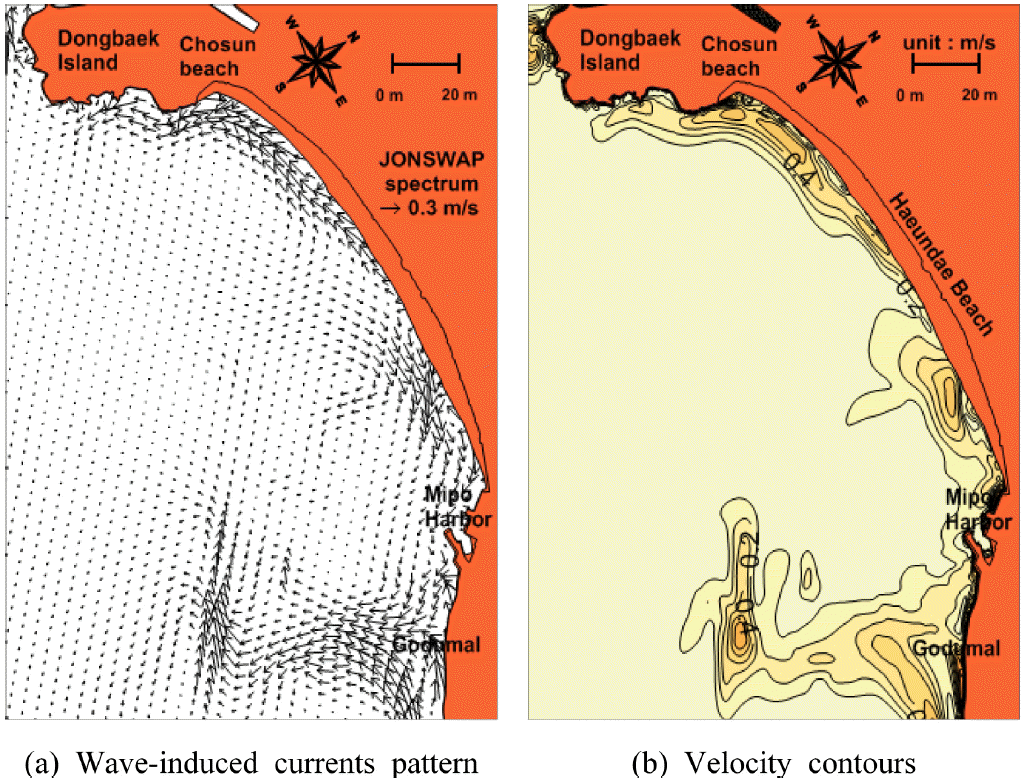
해양수산부 연안침식 대응기술개발 연구단은 동계(2014년 2월 12일 ~ 2014년 4월 10일)와 하계(2014년 8월 22일 ~ 2014년 9월 11일)에 AWAC, SPHINX, TISDOS 등의 장비를 이용하여 흐름패턴 및 표사이동 flux를 관측하였으며 관측위치는 Fig. 3과 같다(Do et al., 2015). 동계와 하계의 흐름패턴과 표사이동 flux의 관측결과는 Fig. 4와 Fig. 5와 같다. 흐름패턴은 시간평균된 결과를 나타내며 표사이동 flux는 누적된 합을 나타낸다. 표사이동 flux는 동계와 하계 모두 흐름패턴과 유사하게 나타났으며 흐름이 퇴적물 이동에 큰 영향을 미친다는 것을 알 수 있다.

Fig. 3.

Observation points for currents and sediment fluxes.

Fig. 4.

Observed currents (left) and sediment flux (right) patterns from SPHINX, AWAC and TISDOS during the winter season in Heaundae Beach(MOF, 2015).

Fig. 5.

Observed currents (left) and sediment flux (right) patterns from SPHINX, AWAC and TISDOS during the summer season in Heaundae Beach (MOF, 2015).

동계(Fig. 4)의 흐름패턴 및 표사이동 flux의 관측결과 동백섬측과 미포측에서 외해방향으로 이동되는 것으로 나타났으며 해운대 해수욕장 중앙부근 전면에서 유입되는 패턴이 나타났다. 또한, 외해방향에서 관측된 결과는 조류의 방향과 유사하게 나타났다. 이 시기에는 미포측의 돌제가 건설되기 전이기 때문에 미포측에서 돌제를 가로질러서 외해방향으로 이동되는 패턴이 관측된 것으로 사료된다. Do et al.(2015)의 관측결과 최대유속의 크기는 S2지점에서 관측기간 중 최대 유의파고는 1.2 m 정도이었으며 유속은 ± 20 cm/s 이내로 관측되었다.

하계(Fig. 5)의 흐름패턴 및 표사이동 flux의 관측지점이 동계와 다소 차이가 있는 것은 이 시기에 미포측의 돌제가 완공되어 동일한 위치에서 관측이 불가능하여 변경된 것으로 판단된다. 하계의 관측결과, 동백섬측과 미포측에서 외해방향으로 이동되는 것으로 나타났으며 해운대 해수욕장 중앙부근에서 외해로 이동되는 것으로 나타났다. Do et al.(2015)의 관측결과 최대유속의 크기는 S2지점에서 관측기간 중 최대유의파고는 1.1 m 정도이었으며 유속은 ±20 cm/s 이내로 관측되었다. 그리고 해운대 해수욕장 중앙부근의 이동패턴은 이안류에 의한 영향으로 사료된다.

그러나 현지 해빈류는 불규칙 입사파랑 조건과 해저 수심 분포에 따라서 많은 영향을 받기 때문에 시·공간적으로 변동이 매우 커다란 불규칙한 변동특성을 나타낸다. 따라서 장기간의 정밀한 현지관측으로도 어떤 일정한 패턴을 찾아내기가 매우 어렵다는 것은 Do et al.(2015)의 연구에서도 확인할 수 있다.

3. SWASH 모형의 소개

SWASH 모형은 Stelling and Zijlema(2003), Stelling and Duinmeijer(2003), Zijlema and Stelling(2005, 2008), Smit et al.(2013)의 연구를 기초로 개발되었다. 2차원의 해석방법은 수심평균, 비정수압, 자유수면 흐름을 Navier-Stokes 방정식의 질량·운동량보존조건으로 유도된 다음과 같은 비선형 천수방정식을 적용한다.

여기서, x와 y는 정수면에 위치하고 있으며 t는 시간, ζ(x,y,t)는 정수면을 기준으로 자유수면까지의 높이, d(x, y)는 정수면하 수심, h = ζ + d는 총 수심, q(x, y, z, t)는 비정수압 압력성분, u(x, y, t) v(x, y, t)는 x, y 방향에 대한 수심평균유속, g는 중력가속도, c_f는 저면마찰계수로서 Manning의 조도계수를 사용하여 평가하였다. τxx τxy τyx τyy는 수평난류응력, ν_t (x, y, t)는 쇄파와 난류성분에 의한 수평와점성계수, l_m는 혼합거리이다.

SWASH 모형의 지배방정식에서 운동량방정식의 비정수압항의 처리는 다음과 같다.

여기서 q_b는 저면의 비정수압을 나타내는 항이다.

4. SWASH 모형을 이용한 수치모형실험 결과

4.1 입력자료

SWASH 모형을 이용하여 해운대 해수욕장의 계절별 이상 파랑에 의한 파랑변형 및 해빈류 특성을 파악하기 위하여 적용된 조건은 Table 2와 같다. 입사파랑조건은 1시간단위 파랑관측자료의 유의파의 최대값과 그에 상응하는 주기를 사용하였으며 주 파향은 하계의 경우 S 계열, 동계의 경우 ESE 계열을 적용하였다. 조위는 국립해양조사원에서 제공하는 기본수준점 성과표를 참고하여 2013년 6월 21일부터 7월 21일까지 관측된 해운대의 조위를 사용하였다. 계산격자의 선정은 전파방향의 격자의 경우는 관심영역의 최대수심의 파장을 고려하여 파고를 고려하여 결정한다. 일반적으로 1/50에 상응하는 크기의 격자간격으로 충분하다. 그러나 파고가 큰 경우에는 1/100 정도의 격자간격도 권장하고 있다(The SWASH team, 2010). SWASH 모형은 경계에서 직각으로 입사파랑이 전파되는 것을 권장하기 때문에 계산영역은 입사파랑이 입사경계에서 직각으로 전파되도록 설정하였다. 하계(S 계열)의 경우 계산영역의 방향 변화가 없지만 동계(ESE 계열)의 경우는 계산영역을 회전시켜 적용시켰다. 따라서 Table 2와 같이 하계와 동계의 계산영역의 크기가 다르다. 하계의 경우는 전파방향의 격자의 크기가 CFL조건을 만족시키도록 선정하였다. 동계의 경우는 하계보다 파고가 작아 최대수심에 대한 파장의 1/50에 해당되는 정격자로 선정하여 모의하였다. 시간 격자는 CFL 조건을 만족하는 범위에서 결정하였으며 SWASH 모형에서는 안정조건을 만족시키도록 자체적으로 시간격자를 결정하게 된다. 불규칙파 입사파랑은 SWASH 사용자 매뉴얼에서 선택 가능한 스펙트럼중에서 JONSWAP spectrum을 적용하여 모의하였다. 그 이유는 입사파의 경계 지점의 최대수심이 약 30 m 정도로서 주기 8.6초에 대한 상대수심이 0.28 로서 심해와 천해의 중간수심역에 해당하고 시뮬레이션 대상파랑이 외해쪽으로 열린 해역에서 태풍이나 폭풍에 의한 파랑인 점을 감안하고, 해운대연안정비사업 모니터링용역의 선행연구(MOF, 2015)에서도 JONSWAP spectrum을 적용하였기 때문에 비교를 위하여 동일한 스펙트럼을 적용하였다. 입사경계를 제외한 투과성 경계에서는 반사를 최소화하기 위하여 파장의 3~5배에 상응하는 길이의 sponge 층을 설정하여 반사를 최소화하였다. 계산시간은 입사파의 군속도가 해안에 내습하여 반사파가 입사경계에 되돌아오는데 걸리는 시간보다 충분히 길게 잡았으며 해빈류가 안정상태에 달하는데 걸리는 시간을 체크한 결과 30분 정도면 충분하다는 결과를 얻었다. 따라서 불규칙파의 경우 스펙트럼 한 주기에 해당하는 시간 약15분을 추가로 계산하여 이에 대한 시간평균값을 최종결과로 산출하였다. 따라서 전체 시뮬레이션 시간은 45분이 된다.한편, SWASH 모형은 연직방향으로 다층 모델이 가능하지만(Zijlema et al., 2011) 다층모델링을 하면 그만큼 계산시간이 많이 소요된다. 본 연구에서는 입사파의 주기가 길어 쇄파대 부근이 천해영역에 해당하므로 단층모델을 적용해도 무방한 관계로 단층모델을 적용하였다. 약간의 조위차가 해빈류에 미치는 영향이 미미할 것으로 판단되며 동일한 수심조건에서 하계와 동계의 해빈류 변화를 파악하기 위해 조위조건은 하계와 동계에 동일한 평균해면을 사용하였다.

Table 2.

Numerical simulation conditions

4.2 하계의 이상파랑에 의한 해빈류 특성

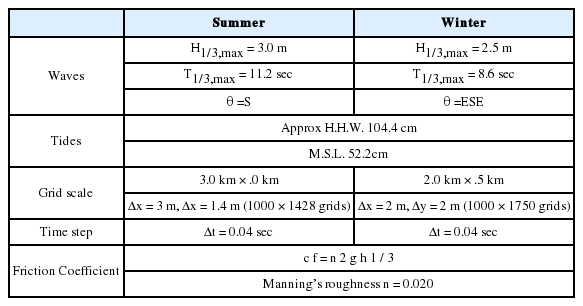
4.2.1 파봉선 및 파고분포

JONSWAP spectrum을 적용한 파봉선 및 파고분포는 Fig. 6과 같다. 계산된 파봉선을 보면 파랑이 내습되면서 육지에 의한 약반사 및 천퇴영역에 의한 파의 산란 등 파랑변형의 형태가 잘 묘사되고 있는 것을 볼 수 있으며 투과성 개경계의 sponge 층의 효과로 경계에서의 반사와 같은 불필요한 파랑변형이 나타나지 않음을 알 수 있다. 파고분포를 보면 Fig. 1의 등심선과 유사하게 분포하는 것을 볼 수 있다. 하계의 경우 S계열의 커다란 파고와 주기를 갖는 파랑이 해안에 직접적으로 내습하게 되어 해운대 해수욕장의 연안과정에 큰 영향을 미치게 될 것으로 사료된다.

Fig. 6.

Calculated wave crest lines and wave height distribution during the summer season.

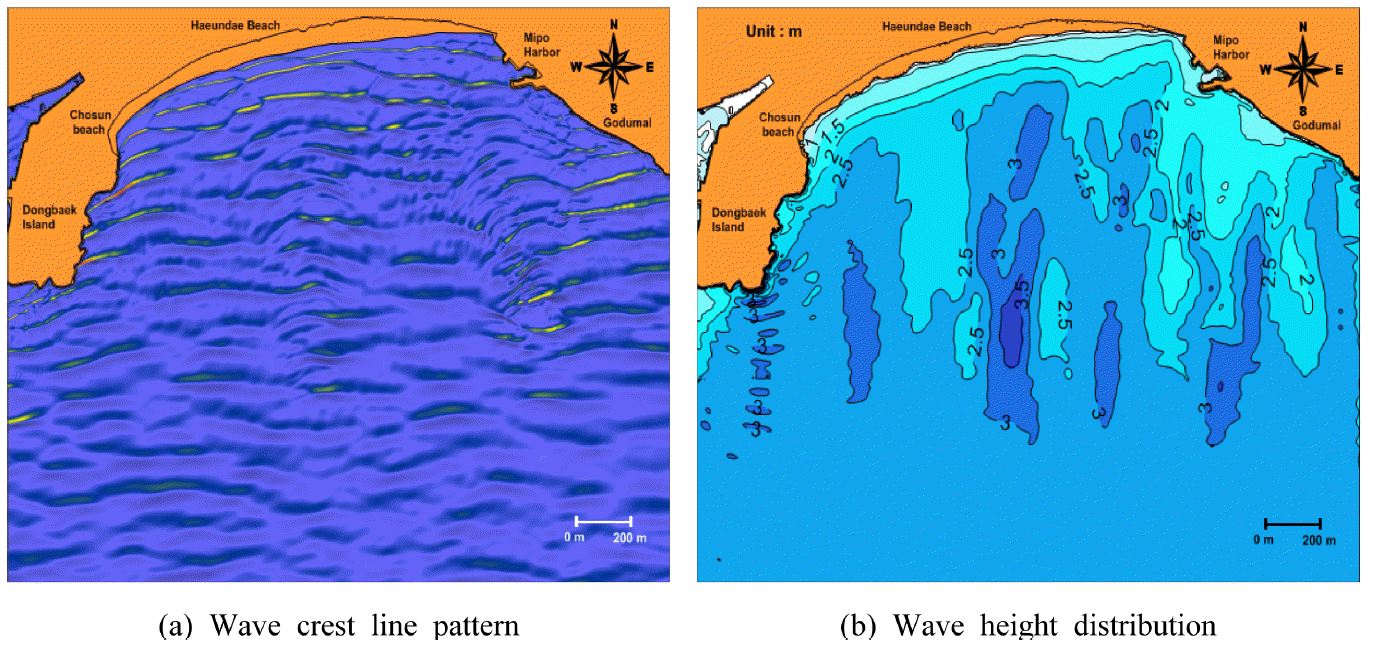
4.2.2 해빈류 패턴 및 유속분포

JONSWAP spectrum을 적용한 해빈류 패턴 및 유속분포는 Fig. 7과 같다. 해빈류는 최종적으로 안정상태에 도달하였을 때의 결과를 얻을 수 있도록 spectrum에 의한 계산시간의 마지막 한 주기의 계산 결과를 평균하여 나타내었다. 계산된 해빈류 패턴을 보면 동백섬측에서 미포측으로 향하는 연안류가 지배적으로 나타나고 있으며 해운대 해수욕장 중앙부근에서 이안류가 나타났다. 또한 미포항 동쪽 고두말에서 발생된 흐름은 미포부근에서 해수욕장까지 도달하지 못하고 외해로 빠져나가는 패턴이 나타났다. SWASH 모형을 이용하여 산정된 해빈류 패턴과 Fig. 5의 관측결과를 비교해 보았을 때 미포측의 흐름패턴 및 이안류의 발생위치는 잘 묘사하였지만 동백섬측은 차이가 나타났는데 Fig. 5의 하계 관측시는 입사파랑이 H_s < 0.6 정도로 본 계산조건과 달리 비교적 작았기 때문인 것으로 사료된다. 유속분포를 보면 동백섬측에서 최대 약 1.5 m/s까지 가장 빠르게 나타났고 미포측까지 0.5~1.0 m/s의 범위의 유속이 나타났으며 미포측에서는 0.1 m/s 이하까지 낮게 나타났다. 그러나 하계 이상파랑과 같은 고파랑 조건하에서 현지 해빈류의 관측결과가 전혀 없는 관계로 시뮬레이션 결과의 검증은 할 수 없었지만 Fig. 6의 파봉선분포와 파고분포로부터 Fig. 7과 같은 해빈류 패턴이 예상된다. 이러한 해빈류 패턴과 유속분포를 통하여 동백섬측에서 미포측까지 연안류에 의해 퇴적물이 이동하여 미포측에서 유속이 감소함에 따라 퇴적물이 미포측에 퇴적될 것으로 예상된다. 또한, 동백섬측과 해운대 해수욕장 중앙부분은 전반적으로 강한 연안류와 이안류에 의하여 침식이 발생될 것으로 예상된다.

Fig. 7.

Calculated wave-induced currents and velocity contours during the summer season.

4.3 동계의 이상파랑에 의한 해빈류 특성

4.3.1 파봉선 및 파고분포

JONSWAP spectrum을 적용한 파봉선 및 파고분포는 Fig. 8과 같다. 계산된 파봉선을 보면 파랑이 직접적으로 연안에 내습하는 것이 아닌 육지와 천퇴영역에 의해 반사 및 산란된 파랑변형을 통하여 간접적으로 연안에 내습되는 것을 볼 수 있다. 파고분포의 형상도 경계와 직각의 분포를 나타내다가 미포측의 천퇴영역에서 굴절과 산란에 의한 파랑변형을 통해 연안으로 내습되는 것을 볼 수 있다.

Fig. 8.

Calculated wave crest lines and wave height distribution during the winter season.

4.3.2 해빈류 패턴 및 유속분포

JONSWAP spectrum을 적용한 해빈류 패턴 및 유속분포는 Fig. 9와 같다. 동계 이상파랑조건에서 관측한 해빈류 조사자료가 없는 관계로 계산결과의 검증은 할 수 없지만 Fig. 8 과 같은 파봉선과 파고분포로부터 개략적인 해빈류패턴을 예상할 수 있다. 계산된 해빈류 패턴을 보면 해운대 해수욕장 중앙부근에서 동백섬측으로 발생 되는 연안류와 미포측으로 발생되는 연안류가 나타났다. 미포항 동쪽 고두말에서 발생된 흐름은 미포측까지 도달하지 못하고 외해로 빠져나가는 패턴을 보였다. SWASH 모형을 이용하여 산정된 해빈류 패턴과 Fig. 4의 관측결과를 비교해 보았을 때 동백섬 측과 미포측에서 외해로 이동하는 패턴을 잘 묘사한 것으로 나타났다. 유속분포를 보면 고두말에서 최대 약 1.5 m/s까지 가장 빠르게 나타났으며 동백섬측과 미포측에 약 0.3 ~ 0.5 m/s의 범위로 유속이 나타났다. 해빈류 패턴과 유속분포를 통하여 해운대 해수욕장 중앙부근에서 발생되는 연안류로 인하여 동백섬측과 미포측으로 퇴적물이 이동하여 지형적인 영향 및 유속저감의 영향으로 동백섬측과 미포측에 퇴적될 것으로 예상된다. 또한 해운대 해수욕장 중앙부근은 동백섬측과 미포측으로 발생되는 연안류로 인하여 침식이 발생될 것으로 사료된다.

Fig. 9.

Calculated wave-induced currents (left) and velocity contours (right) during the winter season.

5. 결론 및 요약

본 연구의 주목적은 비정수압 SWASH 모형을 이용하여 불규칙파에 의한 해운대 해수욕장의 해빈류를 수치모의하고 그 적용성을 검토하는 것이다. 연구대상지역인 해운대 해수욕장의 외력조건 및 지형특성을 분석하여 가장 큰 영향을 미칠 것으로 예상되는 동계 ESE 계열, 하계 S 계열의 이상파랑을 대상으로 수치모의를 실시하였다.

하계 이상파랑의 경우, S 계열의 파랑이 태풍에 의하여 비교적 커다란 파고와 주기로 직접적으로 내습하는 것으로 나타났다. SWASH 모형을 이용하여 산정한 해빈류 패턴은 동백섬측에서 미포측까지 연안류가 발생하여 미포측에서 외해로 빠져나가는 패턴이 나타났으며 중앙부근에서 외해로 빠져나가는 이안류가 나타났다. 해운대해수욕장의 동쪽 고두말에서 발생된 흐름은 해운대 해수욕장까지 도달하지 못하고 외해로 빠져나가는 패턴을 보였으며 유속은 동백섬측에서 약 1.5 m/s까지 가장 크게 나타났으며 미포측에서 약 0.1 m/s 이하로 낮게 나타났다. 해빈류 패턴과 유속을 통하여 동백섬측과 해운대 해수욕장 중앙부근에서 침식과 미포측의 퇴적이 발생될 것으로 사료된다.

동계 이상파랑의 경우, ESE 계열의 파랑이 파랑변형을 통해 내습하는 경향이 나타난다. SWASH 모형을 이용하여 산정한 해빈류 패턴은 해운대 해수욕장 중앙부근 서측에서는 동백섬으로 연안류가 발생하고 해운대해수욕장의 동쪽에서는 미포측으로 연안류가 발생하였다. 고두말에서 발생된 흐름은 해운대 해수욕장까지 도달하지 못하고 외해로 빠져나가는 패턴을 보였다. 유속분포는 고두말에서 최대 약 1.5 m/s까지 나타났으며 해운대 해수욕장에서는 전체적으로 약 0.3 ~ 0.5 m/s의 범위로 나타났다. 해빈류 패턴과 유속을 통하여 동백섬측과 미포측이 퇴적과 해운대 해수욕장 중앙부근의 침식이 발생될 것으로 사료된다.

본 연구에서 적용한 이상파랑 조건하에서 현지 해빈류의 관측결과가 없는 관계로 수치모의 결과의 검증은 이루어지지 않았지만 파봉선과 파고의 공간적인 분포로부터 어느 정도 해빈류의 패턴은 예측할 수 있을 것으로 사료되며 향후 해운대 해수욕장 연안정비사업이 완료되어 돌제나 잠제등의 구조물이 설치된 후 해빈류 패턴이 양빈전과 비교하여 어떻게 변할 것인가를 파악하기 위한 사전 연구로 가치가 있을 것으로 사료된다. 아울러 앞으로 beach processes의 연구를 위하여 이상파랑 조건하에서의 현지 해빈류 관측이 반드시 필요할 것으로 본다.

Article information Continued