유한 단층 모델 및 순환 경계조건을 이용한 전지구 지진해일 예측 시스템 개발
Development of the Global Tsunami Prediction System using the Finite Fault Model and the Cyclic Boundary Condition
Article information
Abstract
본 연구에서는 원거리 지진해일에 대응하기 위한 기초 연구로써 유한 단층 모델과 순환 경계조건을 이용한 전지구 지진해일 예측 시스템을 제안하였다. 제안한 전지구 지진해일 예측 시스템을 2014년 칠레 지진해일에 적용하여 원거리 지진해일에 대한 대응 시스템으로써의 가능성을 검토하였다. 전지구 지진해일 예측 시스템의 경계조건, 지배방정식, 격자 크기, 단층 모델에 따른 지진해일 파고와 도달시각을 DART 부이, 조위관측소 관측 자료와 비교함으로써 유한 단층 모델과 순환 경계조건의 중요성을 확인하였다.
Trans Abstract
A global tsunami prediction system was suggested for a distant tsunami using a finite fault model and a cyclic boundary condition. The possibility of the suggested system as a distant tsunami response system was checked by applying it into the case of 2014 Chile tsunami. A comparison between the numerical results(tsunami height and arrival time) with different conditions (boundary condition, governing equation, grid size and fault model) and measured data (DART buoy, tide station) showed the importance of the finite fault model and the cyclic boundary condition.
1. 서 론
지진해일은 주로 해저지진에 의해 유발되는 장주기의 파이다. 지진해일이 상대적으로 수심이 얕은 해안으로 접근하면 천수효과에 의해 처오름이 발생하여 엄청난 인명과 경제적 피해를 발생시킬 수 있다(Cho and Suh, 2001). 우리나라에서도 일본 서쪽 근해에서 발생한 1983년 동해 중부 지진과 1993년 북해도 남서외해 지진에 의한 지진해일로 인해 인적·물적 피해를 입은 바 있다(Kim et al., 2007a). 기상청은 이에 대비하기 위하여 한반도 주변해역 시나리오 지진해일 DB(Database)를 활용한 지진해일 통보시스템을 운영하고 있다(Park and Lee, 2014). 지진해일 통보시스템을 이용하여 2005년 3월 20일 일본 후쿠오카 해역 지진(규모 7.0) 발생 당시 우리나라에 해수면으로부터 0.5 m의 파고로 예상되는 지진해일 주의보를 발령할 수 있었다(Park and Cho, 2012).
2004년 인도네시아 수마트라 지진(규모 9.2), 2010년 칠레 지진(규모 8.8)과 같은 대규모 지진에 의해 유발된 지진해일은 태평양을 횡단하여 전지구적인 피해를 초래하였다(Fritz et al., 2011; Ha et al., 2007). 이와 같은 대규모 지진에 의한 지진해일에 신속히 대응하기 위하여 태평양 지진해일 경보센터(PTWC, Pacific Tsunami Warning Center), 해양대기국 지진해일 연구센터(NCTR, NOAA Center for Tsunami Research) 등은 원거리 지진해일 예·경보 체계를 구축하여 운영 중이다. 그러나 우리나라의 경우 한반도 주변해역 시나리오 지진해일 DB에 포함되지 않은 지진해일에 대하여 외국 기관의 통보문에 의존하여 대응하고 있다. 2011년 동일본 대지진(규모 9.0)의 경우 일본 동쪽 해역에서 발생하여 제주도와 남해안에 최대 0.3 m의 작은 지진해일이 관측되었으며, 지진해일에 의한 피해는 없었으나 외국 기관의 통보문에 우리나라에 대한 지진해일 정보가 포함되어 있지 않아 정량적인 예보가 이루어지지 못하였다(Bae et al., 2012; Yoon et al., 2012). 따라서 태평양에서 발생하는 대규모 지진해일에 의한 한반도의 지진해일 피해를 정량적으로 분석하여 한반도에 지진해일이 도달하기 전에 정보를 제공하는 시스템(이하 지진해일 예측 시스템)이 요구된다.
지진 발생 직후 지진해일 정보를 가장 신속하게 제공할 수 있는 방법은 전지구 영역에 대하여 시나리오 지진해일 DB를 구축하는 것이다. 그러나 지진해일을 발생시킬 수 있는 지진대와 지진규모를 모두 고려하려면 시나리오 지진해일에 대한 경우의 수가 매우 방대해진다. 또한 같은 지진대, 같은 규모의 지진이라도 지진 매개변수에 따라 지진해일 초기 해수면 변위의 형상이 달라져 해안가에서의 지진해일 파고는 달라질 수 있다(Sim et al., 2009). 예를 들어 같은 규모의 지진이라도 주향의 변화에 따라 해안가에서의 지진해일 파고는 7배 이상 차이날 수 있다(Lee et al., 2005). 따라서 전지구 영역에 대하여 모든 지진대, 지진규모, 지진 매개변수를 고려한 시나리오 지진해일 DB를 구축하는 것은 수치모의 작업량과 DB 저장 공간 등의 문제로 현실적이지 못하다. 따라서 범람역 산정과 같은 상세한 계산이 불가하여 상대적으로 정확도가 낮지만 신속한 결과를 줄 수 있는 큰 격자의 광역 선형 수치 모형을 이용하여 지진 발생 즉시 수치모의를 수행하는 방식으로 전지구 지진해일 예측 시스템을 구축하는 것이 적절하다(Bae and Yoon, 2010; Ha and Cho, 2015).
국내에서 진행된 대부분의 지진해일 수치모의 관련 연구는 한반도에 피해를 줄 가능성이 높은 지진공백역에 대하여 균일한 변위량을 갖는 1~2개의 단층면을 가정하여 초기 파형을 계산하거나, 지진을 분석하여 발표한 논문의 지진 매개변수와 경험식에 의한 균일한 단층 변위량으로 구한 초기 파형을 이용하였다(Bae et al., 2012; Kim et al., 2007a; Kim et al., 2007b; Kim et al., 2008; Lee et al., 2012; Park and Cho, 2012). 그러나 단층의 크기가 수백km인 대규모 지진의 경우 1개의 단층면으로 지진해일 초기 파형을 설명할 수 없는 경우도 있으며, 단층면상의 위치에 따라 변위가 크게 달라 균일한 단층 변위량을 가정했을 때와 초기 파형이 크게 달라질 수 있다. 미국지질조사소(USGS, United States Geological Survey), 일본 나고야 대학 지진화산연구센터, 논문 등에서 지진 분석을 통한 단층 변위량(slip distribution)이 발표되나, 지진 발생 후 상당한 시간이 지난 이후 발표되어 지진해일 예·경보에 사용하기 어렵다. 조위관측소 관측 자료를 이용하여 지진해일 초기 파형을 추정하는 방법도 있으나, 지진해일이 관측되기 위해서는 이미 상당한 시간이 경과한 후여서 지진해일 예·경보에는 적합하지 않다(Gusman et al., 2015; Tsushima et al., 2012). 지진파는 지진해일보다 상당히 빠른 시간 안에 먼 거리를 전파하므로 지진파 분석을 통하여 지진해일 초기 파형을 추정하는 것이 보다 효과적이다.
대부분의 지진해일 수치모의 관련 연구는 일부 지역에 한정하며 영역 경계조건으로 지진해일이 영역 밖으로 빠져나가는 방사 경계조건(radiation boundary condition)을 사용한다. 그러나 전지구 지진해일 예측 시스템의 경도 방향 경계조건으로는 한 쪽 경계를 통과한 지진해일이 반대편 경계로 입사하는 순환 경계조건(cyclic boundary condition)이 필요하다(Kowalik et al., 2005; Kowalik et al., 2007).
본 연구에서는 원거리 지진해일에 대응하기 위하여 단층에서의 변위량 정보를 제공하는 유한 단층 모델과 전지구 지진해일 수치모의 수행 조건인 순환 경계조건을 고려한 전지구 지진해일 예측 시스템을 제안하고자 한다. 이를 위해 2014년 칠레 지진(규모 8.2)을 대상으로 경계조건, 지배방정식, 격자크기, 단층 모델의 영향력을 분석하고 실시간 지진해일 예·경보에 적합한 입력변수 조건을 평가하고자 한다.
2. 전지구 지진해일 예측 시스템
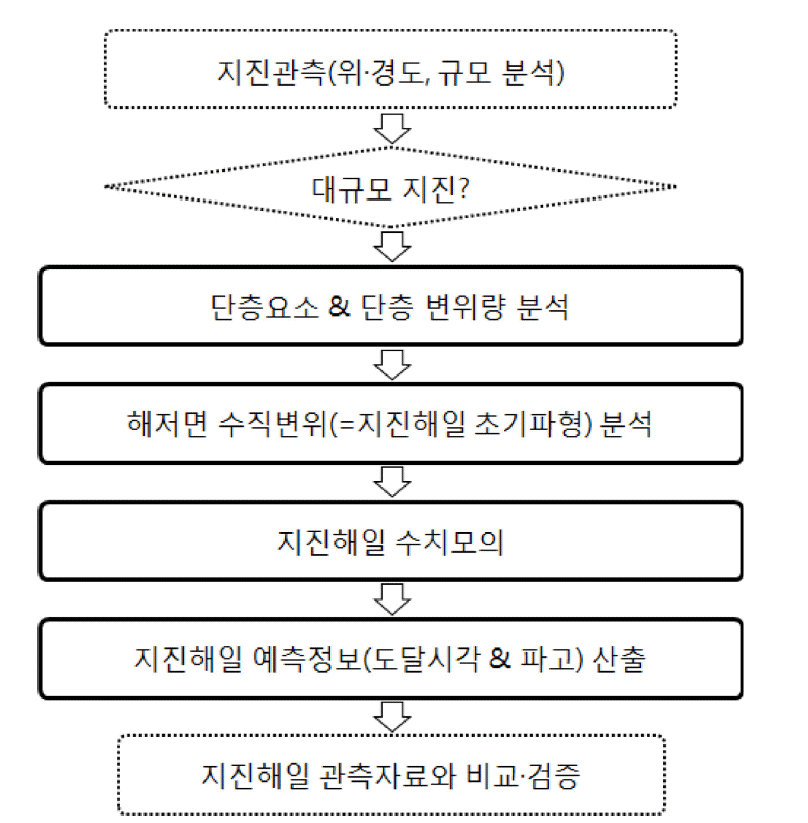
본 연구에서 제안하는 전지구 지진해일 예측 시스템의 자료 처리 및 분석 흐름도는 Fig. 1과 같다. Fig. 1에서 실선으로 표시된 부분이 전지구 지진해일 예측 시스템의 분석 체계를 나타내며, 점선 부분은 전지구 지진해일 예측 시스템과 연동되는 작업을 나타낸다. 지진파 분석을 통해 지진발생 위치(위·경도, 깊이)와 지진의 규모가 분석된 후 해역에서 발생한 대규모 지진으로 판단되면 지진해일 예측 시스템이 가동되도록 한다. 이 때 대규모 지진에 대한 기준이 필요한데, 일반적으로 지진의 규모가 7 이상일 경우 지진해일이 발생하기 때문에 분석된 지진규모가 7 이상일 경우 대규모 지진으로 판단하도록 설정할 수 있다. 필요에 따라서는 그보다 작은 규모로 설정할 수 있으며, 기술적으로는 지진파의 다양한 위상을 이용하여 얻어지는 여러 가지 지진규모 중에 어떤 값을 기준으로 할 것인지에 대한 판단도 필요하다. 이에 대해서는 시스템 운용 시 고려할 필요가 있으며, 이 논문에서는 그에 대한 논의를 생략하고자 한다.
대규모 지진이 발생한 것으로 판단되면 지진파형 분석을 통해 해당 지진을 일으킨 단층의 기하학적 요소(주향, 경사, 단층 길이와 폭 등의 매개변수; 이하 단층요소)와 단층면상의 위치에 따른 변위량을 분석한다. 이 과정에 사용되는 지진파나 분석기법에 따라 단층요소와 단층 변위량의 분석 결과를 얻기까지 상당한 시간이 필요한 경우도 있으며, 신속한 지진해일 정보 제공을 위해서는 지진분석 시간을 최소한으로 단축시킬 필요가 있다. 지진파 분석을 통해 단층요소와 변위량 분석 결과를 얻으면 단층에서의 변위량을 이용하여 해저면에서의 수직 변위를 계산할 수 있으며, 해저면에서의 수직 변위가 지진해일의 초기파형과 같다는 가정 하에 지진해일 수치모의를 수행한다. 이 때 지진해일 예·경보를 위해서 필요한 지점에 대한 지진해일 도달시각과 파고를 모의한다. 지진해일 수치모의 결과는 관측자료와 비교하여 검증을 수행한 후 필요한 경우 지진해일 정보를 갱신하는 체계로 전지구 지진해일 예측 시스템을 구성하고자 한다.
2.1 유한 단층 모델
지진 발생 후에 가장 먼저 관심을 갖게 되는 것은 언제(진원시), 어디서(진원), 얼마나 큰(규모) 지진이 발생했는가 하는 것이며, 관측되는 지진파형의 분석을 통해 이에 대한 정보가 제공된다. 지진의 규모가 작은 경우는 그 지진을 발생시키는 단층의 크기도 작아서 하나의 점으로‘어디서’를 표현해도 무방하다. 그러나 지진의 규모가 큰 경우 그 단층의 크기가 커서 하나의 점으로 지진발생 위치를 나타낼 수 없게 된다. 예를 들어 2011년 동일본 대지진은 규모 9.0으로 단층의 길이가 400~500 km인 것으로 분석되었는데(e.g. Koketsu et al., 2011, Mori et al., 2011, Yokota et al., 2011), 동일본 대지진과 같이 단층의 크기가 큰 경우 진원(진앙 및 깊이)은 지진이 시작된 지점을 나타내고 진원으로부터 파괴가 진행되어 최종적으로 전체 단층이 움직이게 되는 것이다. 단층의 파괴가 이루어지는 과정에서 수백km나 되는 단층면상의 모든 곳에서 동일한 단층운동을 한다는 것은 비현실적이며, 단층면상의 응력 수준이나 유체의 유무 등 조건에 따라 단층운동이 일어나기 쉬운 곳에서는 변위량이 크게 나타나고 단층운동이 일어나기 어려운 곳에서는 변위량이 작아지며 결과적으로 더 이상 변위를 일으키지 못하게 되면 지진이 멈추게 된다. 이러한 단층면상에서의 불균일한 단층운동을 표현하기 위하여 단층을 여러 개의 작은 소단층으로 나누고 각 소단층에서의 변위량과 방향, 변위가 일어나는 시간(진원시간함수) 등을 추정하는 방법이 사용되고 있는데, 이러한 단층 모델을 유한 단층 모델이라 한다.
유한 단층 모델을 이용한 단층 변위량 분석에는 지진파 중 P파나 S파, 표면파를 이용하거나 GPS에 관측된 지표변위 등 지진파 이외의 자료를 이용하기도 한다. 본 연구에서는 전지구 지진해일 예측 시스템 개발을 위하여 전세계에 널리 분포되어 전세계 어디에서 지진이 발생하더라도 비교적 균일한 분포의 관측자료를 획득할 수 있는 지진파형을 이용하고자 한다. 지진파형을 이용한 분석방법 중 원거리 실체파(P, S파) 역산방법(Kikuchi and Kanamori, 1982; Kikuchi and Kanamori, 1986; Kikuchi and Kanamori, 1991)이 널리 사용되고 있어 본 연구에서는 이를 이용하여 전지구 지진해일 예측 시스템 개발에 필요한 최적의 입력변수 조건을 평가하였다. 여기서, 원거리 실체파는 진원으로부터 지구중심각 약 30o ~90o 떨어진 곳에 위치한 지진관측소에서 관측된 P파 또는 S파를 의미하는데, 지구중심각 30o 보다 가까운 곳에서는 지구내부의 저속도층 등 복잡한 내부구조에 의한 파형을 재현하는데 어려움이 있으며, 90o 이상의 거리에서는 지구내부를 전파하던 P파가 맨틀-외핵 경계면에서 회절되거나 S파가 외핵을 통과하여 전파되지 못 하는 등 이론파형 계산이 어려워지기 때문에 30o ~90o 사이의 지진파를 주로 사용한다. Kikuchi and Kanamori(1982, 1986, 1991)의 원거리 실체파 역산에서는 단층을 여러 개의 소단층으로 나누고 각 소단층에서 지진관측소까지 전파하는 지진파형을 이론적으로 계산한 다음 각 소단층에서의 지진모멘트를 곱하여 전체 소단층에 대해 합산하는 형태로 이론합성파형을 계산한다. 각 관측소의 이론합성파형과 관측파형의 차가 최소가 되도록 역산을 수행하며 결과적으로 각 소단층에서의 지진모멘트를 포함한 단층요소를 결정한다. 최종적으로 구해진 각 소단층에서의 지진모멘트와 단층요소를 통해 변위량 및 방향을 얻을 수 있다.
2.2 지진해일 전파 모델
지진해일은 수심에 비해 파장이 매우 길어 천해파(장파)로 간주되며, 대부분의 해역에서 수심에 비해 수면변위가 매우 작아 비선형성을 무시할 수 있다(Cho and Ha, 2010). 이러한 이유로 대부분의 지진해일 수치모의에는 천해 가정으로부터 연속방정식과 Navier-Stokes 방정식을 연직방향으로 적분한 선형 천수방정식(linear shallow-water equations)을 지배방정식으로 사용한다. 수심에 비해 지진해일의 진폭이 큰 경우 비선형성이 증대하여 해안과 같이 수심이 얕은 영역에서의 지진해일 수치모의에는 비선형 천수방정식(nonlinear shallow-water equations)을 지배방정식으로 사용하기도 한다(Cho, 1995).
지진해일의 장주기 성분이 단주기 성분보다 전파 속도가 빨라 발생하는 분산 효과(dispersion effect)와 지구의 곡률 효과, 그리고 자전에 의한 전향력 효과(Coriolis effect)는 먼 거리를 전파하는 대규모 지진해일의 파두(wave front)와 방향에 많은 영향을 준다(Dao and Tkalich, 2007; Glimsdal et al., 2013; Kirby et al., 2013). 천수방정식은 유도 과정에서 분산항이 생략되나 Boussinesq 방정식은 분산항을 포함하고 있어 분산 효과를 고려할 수 있다. 2013년 산타크루즈 지진(규모 8.0)에 대하여 Boussinesq 방정식을 지배방정식으로 하여 지진해일을 수치모의 한 경우 분산을 고려하지 않은 경우 보다 최대파고가 0.4 m 이상인 영역이 약 34% 감소하는 차이가 발생하였다(Miyoshi et al., 2015). 그러나 Boussinesq 방정식은 긴 연산 시간을 요구하는 음해법(implicit method)을 이용해야 한다는 수치기법의 한계가 존재하여 전지구 지진해일 예측 시스템에 적합하지 않다(Yoon, 2002). Imamura et al. (1988)과 Cho (1995)는 천수방정식을 차분하는 과정에서 발생하는 수치분산 오차를 이용하여 물리적 분산 효과를 얻는 방법을 개발하였다. Cho et al. (2007)와 Yoon et al. (2007)은 각각 실용적인 분산보정기법과 2차원 선형 Boussinesq형 파동방정식을 개발하여 수심이 변하는 지형에서도 분산 효과가 고려되도록 개선하였다.
지구 곡률 효과는 보통 1000 km 이내의 영역에서 무시될 수 있으나, 더 넓은 영역에서는 지진해일 수치모의에 영향을 준다(Cushman-Roisin and Beckers, 2011). 2004년 수마트라 지진해일 수치모의에서는 지구 곡률에 의하여 최대 30%의 최대파고 차이를 보였으며, 특히 고위도 또는 진원으로부터 먼 거리로 갈수록 지구 곡률에 의한 차이가 증가하였다(Dao and Tkalich, 2007). 전향력은 지진해일이 대양을 횡단하는 방향에 영향을 주어 2011년 동일본 지진해일 수치모의에서 최대 5%의 최대파고 차이를 보였으며 해령에 지진해일의 에너지가 집중 되는 현상(energy trapping)에 영향력을 미쳤다(Dao and Tkalich, 2007; Kirby et al., 2013; Kowalik et al., 2005; Løvholt et al., 2008). 그러므로 전지구 지진해일 예측 시스템은 분산, 지구 곡률 그리고 전향력을 고려한 수치모델을 사용하여야 한다.
COMCOT(COrnell Multi-grid COupled Tsunami Model)은 천수방정식을 지배방정식으로 사용하고 유한차분법을 이용한 수치모델로 많은 지진해일 연구에 사용되고 있다(Lima et al., 2010; Megawati et al., 2009; Wang and Liu 2006; Wijetunge, 2012; Wijetunge et al., 2008). COMCOT은 Yoon (2002)의 방법을 개선하여 분산 효과를 고려하며, 전향력을 고려한 지배방정식과 지구 곡률을 고려한 구면 좌표계를 지원한다(Wang, 2008). 그리고 유한 단층 모델로 구한 지진해일 초기 파형 자료를 사용할 수 있어 전지구 지진해일 예측 시스템에 적합하다. 본 연구에서는 순환 경계조건을 적용하기 위하여 경도 방향 경계 격자의 수면 변위와 체적 유량(volume flux) 정보가 반대쪽 경도 방향 경계 격자로 전달되도록 수정한 COMCOT을 사용하였다. 지진해일 전파 모델에 대한 보다 자세한 설명은 Liu et al. (1998)을 참조할 수 있다.
3. 2014년 칠레 지진해일
2014년 4월 1일 23시 46분(UTC) 칠레 북부에 위치한 항구도시 이키케(Iquique) 북서쪽 해역에서 발생한 규모 8.2의 지진은 2014년 미국지질조사소에서 발표한 지진 중 가장 큰 규모의 지진으로 나스카 판이 남아메리카 판으로 섭입되는 판 경계부에서 발생하였다. 지진과 지진해일에 의해 최소 7명이 사망하고 200여 명의 부상자가 발생하였으며 가옥 13,000여 채가 파손되는 등 막대한 피해가 발생하였다. 지진해일은 칠레에서 약 4.25 m, 하와이에서 약 1.13 m, 일본에서 약 0.34 m의 파고를 보이는 등 태평양을 횡단하여 전지구적으로 영향을 미쳤다(Hayes et al., 2014; Heidarzadeh et al., 2014). 본 연구에서는 전지구 지진해일 예측 시스템을 이용하여 지진 분석 및 지진해일 수치모의를 수행하였다.
3.1 지진 분석
유한 단층 모델 방법을 이용한 2014년 칠레 지진의 단층변위량 분석을 위하여 지구중심각 30o ~90o 범위에 위치한 16 개소의 지진관측소를 선정하여 지진학연구연합체(IRIS, Incorporated Research Institutions for Seismology)로부터 관측자료를 수집하였다. 단층운동에 의해 사방으로 방사되는 지진파는 같은 위치에서 발생하더라도 단층의 기하학적 형태(예: 주향, 경사)와 단층운동 형태(예: 역단층, 주향이동단층)에 따라 관측되는 방향마다 다른 모양으로 나타난다. 본 연구에서는 진앙을 중심으로 360o 방향으로 관측소를 골고루 분포시켜 방향에 따른 지진파형의 서로 다른 특성을 반영함으로써 역산 결과의 신뢰도를 높였다(Fig. 2, Table 1). 분석에 사용된 진앙은 지진학연구연합체에서 발표한 19.64o W, 70.82o S를 사용하였고, 수집된 지진파형 중 지진에너지가 충분히 포함되도록 150초의 P파 자료를 이용하였다. 그리고 전 지구 지진을 대상으로 높은 정확도를 가지고 지표의 모든 지 점에 도달하는 P파 시각을 예측한 Jeffreys-Bullen 속도구조 모델(Jeffreys and Bullen, 1958)을 적용하여 단층에서 관측소까지 전파하는 이론 지진파형을 계산하였다. 역산을 위해 15 km × 20 km 크기의 50개 소단층으로 구성되는 단층면을 가정하였다. Fig. 3는 역산 결과를 나타내는데, 여기서 M0는 단층운동으로 방출된 총 에너지인 지진모멘트이며 구해진 지진모멘트와 규모와의 관계식을 통해 모멘트규모(Mw)가 8.0으로 분석되었다. H는 진원깊이, var.(variance)는 관측파형과 이론합성파형 간의 오차를 의미하는 값이다. 진원깊이는 지진학연구연합체에서 발표한 20 km를 초기값으로 역산을 수행한 다음, 결정된 단층면해를 이용하여 15 km에서 25 km 사이에서 이론파형과 관측파형의 오차가 최소가 되는 진원깊이를 찾았으며, 진원깊이 19 km일 때 최소오차를 나타내었다. Source time function은 진원시간함수(초)로, 단층운동에 의해 지진에너지가 방출된 총 시간 뿐 아니라 시간에 따른 에너지 방출 양상도 파악할 수 있다. 2014년 칠레지진의 진원시간함수는 약 100초이며, 지진발생 직후 많은 에너지가 방출된 것을 알 수 있다. Focal mechanism(단층면해)은 단층의 기하학적 형상과 운동방향을 하나의 원에 나타내는 것이며, 원 안의 점들은 분석에 사용된 관측점의 진원으로부터의 방위각과 거리에 따른 위치를 표시한다. 또한 Strike는 주향, Dip은 경사, Rake는 면선각으로 단층의 기하학적 형상(단위: o)을 표현한다. 지진파형 역산을 통해 결정된 최적의 단층면 해는 주향 340o와 경사 37o이며 횡압력에 의해 발생하는 역단층으로 나타났다. 분석된 단층변위량 분포(Slip distribution)는 진원(별표)에서 다소 떨어진 영역에서 최대 변위량을 보였으며, 최대 변위량은 5.4 m로 역산되었다. 그림에서 등치선은 최대변위량을 기준으로 5등분한 변위량을 나타낸다. 가로축은 주향 방향, 세로축은 경사방향이며, 각 소단층의 중심을 점으로 표현한다. 점에 이어지는 화살표는 각 소단층의 운동방향과 변위량을 나타낸다. 화살표 방향은 대부분 주향에 대해 수직방향으로 나타나며 이는 역단층 운동을 보이는 단층면해를 통해서도 알 수 있다. 지진은 진원에서 시작하여 사방으로 전파되었으며 10~30 km 떨어진 곳에서 가장 큰 변위량을 나타내다가 차츰 줄어들어 진원에서 약 100 km 거리에서 단층운동이 멈춘 것으로 해석된다. Fig. 3의 오른쪽에는 분석에 사용된 각 관측점에서의 관측파형(굵은 실선)과 계산된 합성파형(가는 실선)이 표출되어 있으며, 위쪽에 파형의 길이와 표출되는 변수에 대한 예시가 같이 나타나있다. 여기서 P는 각 관측소의 수직성분 관측자료 중 P파가 분석에 이용된 것을 나타낸다. 지진파형은 모두 P파의 초동이 10초 시점에 오도록 배열되어 있는데, 약 50초 부근에서 진폭이 큰 것을 알 수 있다. 이렇게 진폭이 큰 것은 단층변위가 큰 영역에서 방출되는 에너지가 관측소에 전해진 것으로, 진원에서 다소 떨어진 곳에서 변위가 크게 나타났기 때문에 P파의 초동에서 바로 진폭이 커지지 않고 어느 정도 시간이 지난 후에 진폭이 커진 것이다. 이와 같은 방법으로 구한 단층변위 분포를 이용하여 주변 지각의 운동량을 계산하기 위해서는 Okada(1985)가 널리 사용되는데, 지진해일 수치모의를 위해 지진분석 결과와 Okada 모델을 이용하여 단층운동에 따른 해저면에서의 수직변위를 구하였다. 지진은 지진해일에 비해 순식간에 발생하여 해저면에서의 수직 변위가 해수면 변위와 동일하다고 가정할 수 있으며, 이를 지진해일 초기 해수면 변위로 간주하였다. Fig. 4a와 Fig. 4b는 각각 10분 간격의 수심 격자와 4분 간격의 수심 격자를 사용했을 때의 지진해일 초기파형으로 최대파고가 각각 1.728 m, 2.146 m이다.

Slip distribution and waveform fit of the 2014 Chile earthquake. The contour lines and arrows present slip distribution and slip vector.
유한 단층 모델을 이용한 지진해일 수치모의 결과와의 비교를 위하여 COMCOT에서 제공하는 단층 모델(이하 COMCOT 단층 모델)을 사용하였다. 이 모델로는 진원, 지진 규모, 단층의 주향과 경사, 단층의 크기와 변위량 등의 지진 매개변수를 입력하면 그 변위량을 단층면에 대해 균일하게 적용하여 해저면 변위를 계산하며, 이를 지진해일 초기 해수면 변위로 가정하여 지진해일 수치모의를 수행할 수 있다. Table 2에 COMCOT 단층 모델을 사용하기 위한 지진매개변수를 정리하였다. 유한 단층 모델과 동일한 지진학연구연합체의 진앙(Epicenter)을 이용하고, 이 밖에 깊이(Focal depth), 주향, 경사, 면선각, 규모는 미국지질조사소 자료를 이용하였다. 지진 분석을 통하여 구한 단층의 크기와 변위 정보 또한 미국 지질조사소에서 얻을 수 있으나 지진 발생 후 상당한 시간이 지난 후에 정보를 검색할 수 있다. 따라서 지진 발생 즉시 수치모의를 수행해야하는 전지구 지진해일 예측 시스템에 적용할 수 있도록 지진규모를 이용하여 단층의 크기와 변위량을 계산할 수 있는 경험식을 도입하였다. Tatehata(1998)가 제안하고 기상청의 한반도 주변해역 시나리오 지진해일 DB 구성에도 사용된 식 (1)~(3)을 이용하였다. 이 식은 일정한 강성률과 응력강하 가정 하에 유도된 식으로 지진규모로부터 단층의 크기와 변위를 구할 수 있다.
여기서, M은 지진규모, L은 단층의 길이(km), W는 폭(km), 그리고 D는 단층의 변위(cm)를 나타낸다. Fig. 4c는 COMCOT 단층 모델로 구한 지진해일 초기파형으로 최대파고는 1.804 m로 유한 단층 모델과 유사하나 높은 파고가 더 넓은 범위에 분포하고 있으며 서쪽 방향으로 완만한 경사를 보인다.
3.2 지진해일 수치모의 조건
수치모의 격자수가 증가함에 따라 수치모의에 소요되는 연산 시간이 증가하므로 목적에 따라 적절한 수심격자를 구성하는 것이 중요하다. COMCOT은 서로 다른 간격의 격자를 이용하는 중첩 격자(Nested grid) 기능을 제공한다. COMCOT과 같이 편미분 방정식을 유한차분법으로 풀어 해가 수렴하기 위해서는 공간격자 간격과 시간 간격의 관계식인 CFL 조건(Courant-Friedrichs-Lewy condition)을 만족해야 하며 작은 공간격자 간격일수록 작은 시간 간격을 요구하며, 이는 수치모의 연산 시간을 증가시킨다. 따라서 상대적으로 긴 연산 시간이 필요한 중첩 격자 기능은 전지구 지진해일 예측 시스템에 적합하지 않다. 본 연구에서는 NOAA의 지구물리 자료센터(NGDC, National Geophysical Data Center)에서 제공하는 2가지 간격(4분, 10분)의 전지구 수심 자료를 이용한 동일한 간격의 격자망을 사용하였다.
Table 3는 격자 간격, 경계 조건, 지배방정식, 단층 모델에 따른 차이를 비교하기 위하여 수행한 5가지 경우의 지진해일 수치모의 조건이다. 여기서 Cyclic은 순환 경계조건, Radiation은 방사 경계조건, Linear는 선형 천수방정식, Nonlinear는 비선형 천수방정식, Finite는 유한 단층 모델, COMCOT은 COMCOT 단층 모델을 나타낸다. 이 밖에 수치모의에 공통적으로 사용한 조건은 Table 4와 같다. 지진해일이 충분히 전파되어 전지구 영역에 도달할 수 있도록 40 시간을 모의했으며, 수치모의 결과를 저장하는 빈도와 가짓수도 연산 속도에 영향을 주므로 동일하게 설정하였다. 또한 지구 곡률 효과를 고려한 구면좌표계를 사용했으며 CFL 조건을 만족하는 시간 간격으로 1초를 사용하였다.
3.3 지진해일 관측 자료
지진해일 수치모의 결과를 관측값과 비교하기 위하여 NOAA의 지구물리 자료센터에서 제공하는 조위관측소 101개소에서의 지진해일 도달시각 정보와 NOAA데이터부이센터(NDBC, National Data Buoy Center)의 DART(Deep-ocean Assessment and Reporting of Tsunamis) 부이 시계열 자료를 수집하였다(National Oceanic and Atmospheric Administration, 2005). 수치모의에 사용하는 격자망이 매우 조밀하지 않으면 관측 지점과 격자점이 일치하지 않을 수 있다. COMCOT은 관측 지점 주변 4개의 격자점 시계열을 선형보간하는 방법으로 관측 지점과 동일한 지점에서의 시계열을 출력한다. 이 방법은 격자점 이외 지점의 시계열을 출력할 수 있다는 장점이 있으나, 선형보간하는 주변 4개의 격자점 중 1개라도 육지인 경우 지진해일 파고를 과소평가한다. 또한 복잡한 해안가를 표현하지 못하는 큰 간격의 격자를 사용하면 해상도 문제로 인하여 지진해일 관측 지점이 수치모의 격자망에서 육지로 가정되는 경우도 있다. 따라서 본 연구에서는 조위관측소 101개소 중 수치모의를 통해 도달시각을 산출할 수 있는 75개소를 선별하였다(Fig. 5a의 노란색 원).
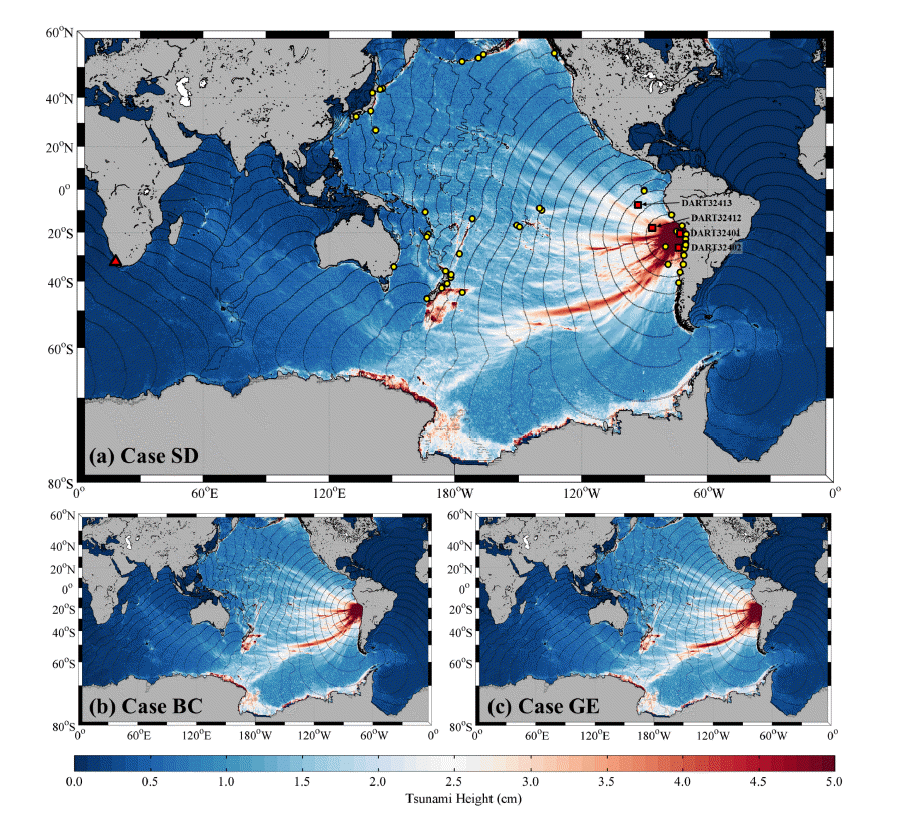
Maximum tsunami height with tsunami travel map for (a) Case SD, (b) Case BC, and (c) Case GE. Red squares, yellow circles and red triangle indicate locations of DART buoys, tide stations and Cape Town, Republic of South Africa, respectively.
DART 부이는 수심이 깊은 외해에 설치되어 평소에는 15분 간격의 자료를 전송하며, 지진해일 감지 시 15초 간격의 자료를 전송한다(Meinig et al., 2005). 이러한 자료 특성 때문에 진원으로부터 멀리 떨어져 지진해일을 감지하지 못한 DART 부이는 수치모의 결과와 비교하기에 적합하지 않다. 따라서 본 연구에서는 지진해일이 감지된 4개의 DART 부이를 선별하였다(Fig. 5a의 빨간색 사각형). DART 부이 시계열에는 지진해일뿐만 아니라 조석과 같은 다른 요인에 의한 파고 변화도 포함되어 있으나 수치모의 결과에는 오직 지진해일에 의한 파고 변화만 존재한다. 따라서 지진해일 수치모의 결과를 지진해일 관측값과 비교하기 위해서는 DART 부이 시계열 자료에 포함된 조석성분을 제거할 필요가 있다. 지진해일에 비해 상대적으로 장주기인 조석 성분을 제거하기 위해 기존 연구에서는 고역 필터(High-pass filtering) 또는 다항식 접합(Polynomial fitting)과 같은 수학적 방법을 이용하였다(An et al., 2014; Bae et al., 2012; Heidarzadeh et al., 2014). 반면 본 연구에서는 긴 시간의 시계열 자료가 필요하지만 조수의 본질적인 특성을 이용한 조화 분석(Harmonic analysis) 프로그램인 T_TIDE를 이용하여 DART 부이 시계열로부터 조석 성분을 제거하였다(Pawlowicz et al., 2002).
3.4 지진해일 수치모의 결과
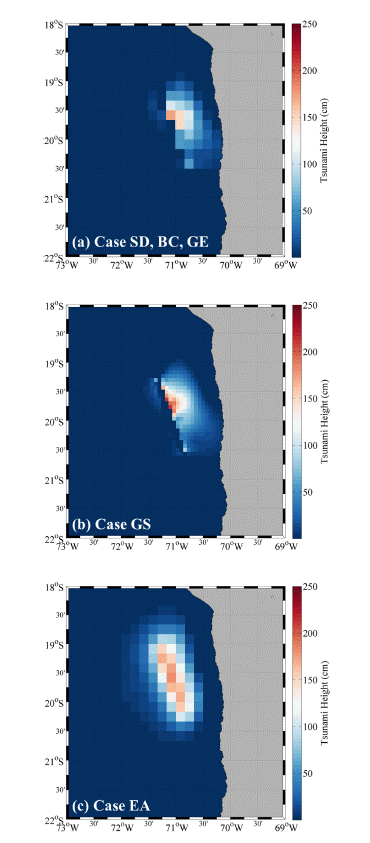
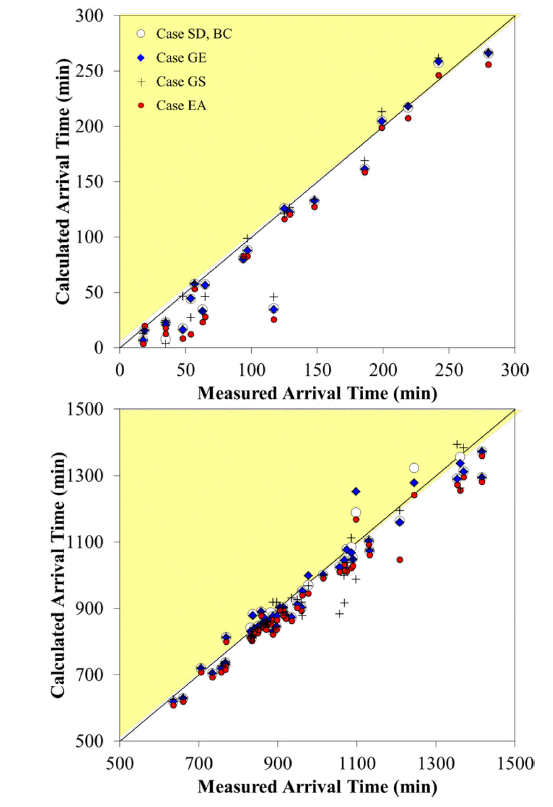
3.2절에서 설명한 5가지 조건에 대하여 전지구 지진해일 예측 시스템의 경계 조건, 지배방정식, 격자 간격, 단층 모델에 따른 차이를 비교하였다. Fig. 5는 지진해일 최대파고분포도와 1시간 간격의 전파도이다. 여기서 최대파고분포도는 지진해일이 40시간 전파하는 동안 각 격자점에서 보인 최대 파고를 나타낸 것이며, 전파도는 매시간 파고 자료에서 파고가 0 cm를 초과하는 지점을 연결한 선이다. Fig. 6는 지진 발생 전후 약 1개월(2014년 3월 17일 ~ 2014년 4월 15일)의 DART 부이 시계열을 이용하여 조석 성분을 제거한 시계열과 수치모의로 얻은 시계열을 비교한 것이다. Fig. 7은 75개소 조위관측소의 도달시각과 수치모의로 예측한 도달시각을 비교한 것이며 오차와 상관도를 Table 5에 정리하였다. 여기서 RMSE는 평균 제곱근 오차(Root Mean Square Error), MAE는 평균 절대 오차(Mean Absolute Error), r은 상관계수(Correlation coefficient)를 나타내며 식 (4)~(6)으로 계산된다.
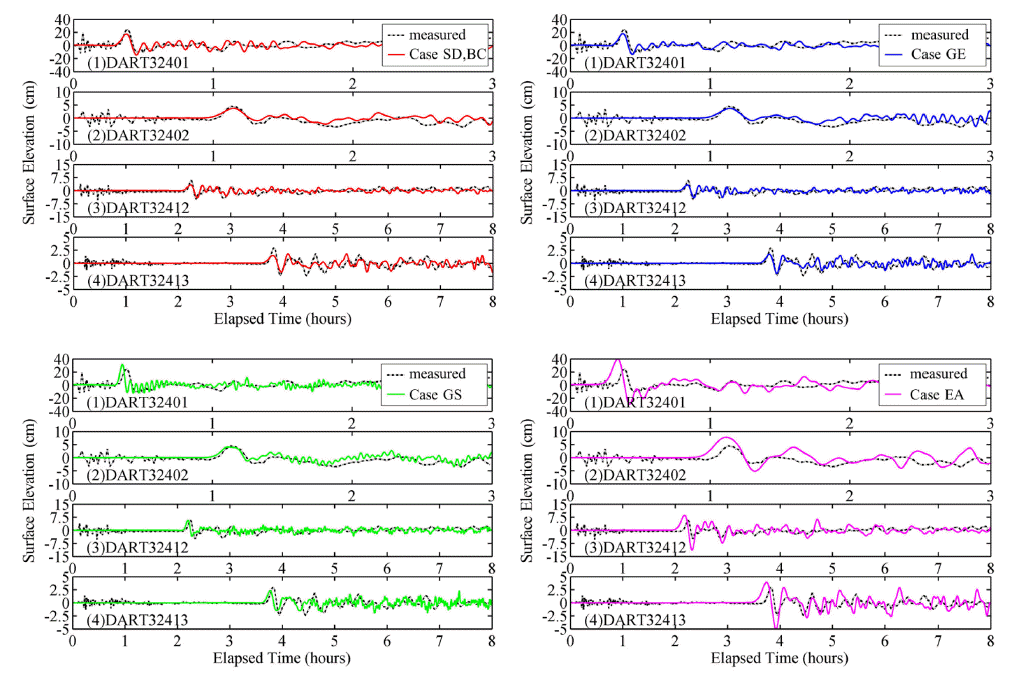
Comparisons between measured (black dash lines) and calculated (colored lines) water elevation at four DART buoys.
여기서 yi는 예측 도달시각, xi는 관측 도달시각,
Case BC는 지진해일 수치모의에 있어 순환 경계조건의 영향력을 알아보기 위하여 방사 경계조건을 적용한 경우로써 Case SD에 비해 지진해일 전파를 1시간 모의하는데 약 1분 씩 짧게 소요되었다. 최대파고분포도를 보면 Case SD의 경우 순환 경계조건에 의해 남아메리카와 남극 사이를 통과한 지진해일과 태평양을 횡단한 지진해일이 지진 발생 약 20시간 후 경도 70oE 부근에서 만난다(Fig. 5a). 그러나 Case BC는 순환 경계조건을 적용하지 않아 남아메리카와 남극 사이를 통과하여 우측 경계에 도달한 지진해일이 좌측 경계로 전달되지 못하고 그대로 영역 밖으로 빠져나간다(Fig. 5b). 그로 인하여 남아프리카공화국 케이프타운(Fig. 5a의 빨간색 삼각형)의 지진해일 도달시각이 Case SD는 지진 발생 약 16시간 후인 반면 Case BC는 지진 발생 약 28시간 후로 12시간이라는 큰 차이가 발생한다. 비교에 사용된 모든 DART 부이와 조위관측소가 태평양에 위치하기 때문에 경계조건에 따른 DART 부이 시계열과 조위관측소의 도달시각은 차이가 없다(Fig. 6, Fig. 7). 모든 DART 부이에서 수치모의된 지진해일 첫 파의 파고가 관측 파고보다 작으며, 대부분의 조위관측소에 지진해일이 관측된 도달시각보다 빠르게 도달하였다.
Case GE는 지진해일 수치모의에 있어 비선형성의 영향력을 알아보기 위하여 비선형 천수방정식을 지배방정식으로 사용한 경우로써 Case SD에 비해 지진해일 전파를 1시간 모의하는데 약 15분이 추가로 소요되었다. 지진해일 최대파고분포(Fig. 5c)를 살펴보면 칠레 부근에서 지진해일이 넓게 전파하는 양상을 보인다. DART 부이 시계열의 경우(Fig. 6) 시간이 경과할수록 Case SD와 차이가 발생하나 지진해일의 에너지 중 대부분을 차지하는 첫 파는 거의 동일하다. 조위관측소 도달시각의 경우 지진해일이 도달하는데 300분 이하 소요되는 가까운 지점은 Case SD보다 미소한 차이로 잘 예측하였으나 500분 초과의 먼 지점은 Case SD보다 오차가 커, 전체적으로 오히려 Case SD보다 정확도가 낮다(Fig. 7, Table 5).
Case GS는 지진해일 수치모의에 있어 수심 격자 크기의 영향력을 알아보기 위하여 4분 간격 격자를 사용한 경우로써 Case SD에 비해 지진해일 전파를 1시간 모의하는데 약 50분이 추가로 소요되었다. Case GS의 경우 32401을 제외한 세 DART 부이에서 첫 파의 파고를 Case SD보다 잘 예측하였다(Fig. 6). 그러나 모든 DART 부이에서 지진해일이 더 빨리 도달하고 단주기 성분이 증가하여 전체적인 오차가 Case SD보다 크다. 유한 단층 모델을 이용한 지진분석 결과, COMCOT 단층 모델에 비해 경사각이 23o 크게 분석되었으며 전체 단층 중 진원 부근에만 변위가 크게 나타났다. 이로 인해 COMCOT 단층 모델을 이용한 경우에 비해 좁은 범위에서 초기 해수면 변화가 발생한 것으로 분석되며(Fig. 4), 4분 수심격자를 사용한 경우 10분 격자에 비해 초기 해수면 변화가 민감하게 반영되어 지진해일의 단주기 성분이 증가하는 것으로 보인다. 조위관측소 도달시각의 경우 지진해일 도달시각 300분 이하의 가까운 지점은 Case SD보다 미소한 차이로 잘 예측하였으나 500분 초과의 먼 지점은 Case SD보다 오차가 커, 전체적인 정확도가 Case SD보다 낮다(Fig. 7, Table 5).
Case EA는 지진해일 수치모의에 있어 지진 분석의 영향력을 알아보기 위하여 COMCOT 단층 모델을 사용한 경우이다. DART 부이 시계열의 경우 Case SD보다 첫 파의 도달 시각을 짧게 예측하고 파고를 과대하게 예측하였다(Fig. 6). 조위관측소 도달시각의 경우 전체적으로 Case SD보다 약 10분의 큰 오차를 보인다(Fig. 7, Table 5).
4. 토 의
4.1 격자망 및 경계조건
수심이 급격히 변하거나 지형이 복잡한 해안가에서는 차분 과정에서 발생하는 수치 오류에 의하여 해가 발산할 수 있다. 구면좌표계의 천수방정식을 수치해석 기법으로 해석하는 과정에서 발생하는 극점의 특이점(Singularity) 문제도 전지구 격자망 구성을 어렵게 한다(Purser, 1988). 본 연구에서는 발산과 특이점이 지진해일 전파에 영향을 주지 않는 위도를 시행 착오 방법으로 제한하여 사용하였다. 그러나 위도를 제한한 격자망으로는 고위도 지역에서 발생한 지진해일이 알류샨 열도 및 북극에서 반사되어 지진해일 전파에 영향을 줄 수 있으므로 향후 고위도까지 고려한 전지구 격자망을 이용할 수 있는 수치모델에 대한 연구가 필요하다. 그리고 천수방정식을 차분하는 과정에서 발생하는 수치분산 오차를 이용하여 물리적 분산 효과를 얻기 위해서는 정사각형 격자가 되어야 하나 본 연구에서는 동일 간격의 위경도 격자망을 사용하였다. 향후 Bae et al. (2012)에서 사용한 위도 보정 방법 등과 같은 고위도 지역까지 분산 효과가 적절히 고려되는 방법에 대한 연구가 필요하다.
2014년 칠레 지진해일의 경우 태평양을 전파하며 대부분의 에너지가 소산되어 순환 경계조건 적용 여부에 따른 지진해일의 차이는 거의 없었다. 대부분의 대규모 지진해일은 2014년 칠레 지진해일과 같이 태평양을 중심으로 발생하고 우리나라에 영향을 줄 수 있는 지진해일이 태평양 지진해일임을 감안할 때, 대서양을 잘라 펼친 격자망을 이용한다면 순환 경계조건이 큰 역할을 하지 못할 것이다. 그러나 순환 경계조건을 적용하면 남아프리카공화국 등의 경계 주변 지역에서 격자망 경계를 통과한 지진해일을 고려할 수 있어 인근 지역에 거주 또는 여행하는 재외국민의 피해를 막을 수 있다. 또한 순환 경계조건은 일부 대서양 주변에서 발생한 지진해일 또는 규모 9.0 이상의 대규모 지진에 의한 지진해일 발생 시 전지구 영역에 대하여 매번 새로운 격자망을 구성할 필요 없이 기존의 발산과 특이점 문제를 고려한 격자망을 사용할 수 있게 한다.
4.2 격자 간격
지진해일 파형을 충분히 모사하기 위해서는 지진해일 파장에 대해 최소 20개의 격자가 필요하다(Shuto et al., 1986). 수심이 얕은 해안선 근처에 도달한 지진해일은 에너지 보존 법칙에 따른 천수효과에 의해 파장이 감소하여 더욱 조밀한 격자가 요구된다. 그러나 본 연구에서는 4분 간격 격자망을 사용한 Case GS에서 DART 부이 시계열과 조위관측소 도달 시각의 정확도가 진원에 가까운 일부 지점을 제외하고는 Case SD의 정확도보다 오히려 낮다. 이는 상대적으로 조밀한 4분 간격 격자망 또한 연안의 지진해일 도달시각 예측에는 충분하지 않으며, 지진 분석에 의한 오차, 수치모델에 의한 오차 등 다양한 원인의 오차들과의 상호작용에 의한 것으로 판단된다. 우리나라에 가까운 곳에서 발생한 지진해일 예측에는 상세한 격자망이 필요할 것이나 본 연구와 같은 전지구 지진 해일 예측에는 10분 간격 격자망이 4분 간격 격자망보다 합리적이다. 그러나 10분 간격 격자망을 이용하여 수심이 얕은 해안에서의 파고를 수학적으로는 계산할 수 있으나 물리적으로 타당하지 않으므로 충분한 검토가 필요하다. 일본 기상청(JMA, Japan Meteorological Agency)은 일반적으로 천수 가정이 성립하는 수심 50 m 지점의 파고를 천수방정식으로 구한 후, Green’s Law를 적용하여 연안의 지진해일 파고를 예측한다. Green’s Law는 에너지 보존 법칙에 따른 수심과 파고의 관계식으로, 다방향 반사파가 중첩되는 복잡한 해안가에서는 지진해일 파고를 과대평가할 수 있으나 신속히 연안의 파고를 예측할 수 있어 일본 지진해일 예·경보 시스템을 위해 사용되었다(Kamigaichi, 2009). 향후 Green’s Law와 같이 격자 간격에 의한 오차를 개선할 수 있는 방법에 대한 연구가 필요할 것이다. 또한 본 연구에서는 동일한 간격의 격자망을 이용하였으나 태평양에서 발생한 대규모 지진해일에 의한 한반도의 지진해일 피해를 정확히 예측하기 위하여 가변 격자를 이용한 한반도 주변 해역의 상세 수심을 적용하는 연구가 필요할 것이다.
4.3 단층 모델
유한 단층 모델로 분석한 2014년 칠레 지진 변위 분포에서 상대적으로 큰 변위를 보인 것은 진원을 포함한 하나의 영역으로 표현할 수 있다(Fig. 3). 또한 유한 단층 모델에서 얻어진 단층의 주향과 COMCOT 단층 모델을 위해 가정한 주향이 동일하다. 그로 인해 1개의 단층면에 균일한 변위량을 가정하는 COMCOT 단층 모델로 구한 지진해일 초기 파형이 유한단층 모델에 의한 초기 파형과 유사한 경향을 보인다(Fig. 4). 만약 1개의 단층면으로 설명할 수 없을 정도로 복잡한 대규모 지진이라면 유한 단층 모델을 이용한 지진 분석이 지진해일 예측에 큰 영향을 미칠 것이다. Wang and Liu(2006)는 2004년 수마트라 지진해일에 대하여 COMCOT 단층 모델과 유한 단층 모델로 구한 지진해일 초기파형을 이용한 수치모의 결과 비교를 통해 대규모 지진에 있어 유한 단층 모델의 중요성을 보였다.
본 연구에서 단층모델을 구하기 위해 사용한 원거리 실체파 역산방법(2.1절)은 단층의 기하학적 형상과 단층면에서의 변위 분포를 구하기 위한 단계적인 분석을 수행하도록 구성되어 있다. 또한 분석대상 지진의 특성에 따라 초기 입력변수를 변화시키거나 시행착오 방법으로 분석결과의 오차를 줄여나갈 필요도 있기 때문에, 분석자의 숙련 정도에 따라 분석결과를 얻는데 수십 분에서 수 시간이 소요될 수 있다. 따라서 실시간으로 운용되어 지진과 지진해일 분석결과를 신속하게 생산해야 하는 전지구 지진해일 예측 시스템을 위해서는 이러한 일련의 과정을 단순화하거나 자동화시킬 필요가 있다. 이를 위해 미리 계산된 이론파형을 이용하여 지진파 역산을 수행하는 방법을 검토 중에 있으며, 이 방법이 적용될 경우 수 분 이내에 단층변위량 분석이 가능할 것으로 생각된다.
지금까지 일반적으로 사용된 지진해일 수치모의는 지진해일의 초기파형이 지진에 의한 해저면 변위와 동일하며 전체 단층에서의 변위가 일순간에 발생한다고 가정한다. 그러나 이 가정은 지진해일의 파장에 비해 수심이 충분히 얕은 경우에만 성립하며 가파른 경사(steep dip)로 인해 지진해일의 파장이 짧거나 쓰나미 지진(tsunami earthquake)과 같이 지속시간이 긴 경우 적용할 수 없다(Saito and Furumura, 2009). 또한 수심이 지진해일의 파장에 비해 충분히 얕은 경우라 하더라도 시간 이력을 무시한 단층운동모델은 지진해일 초기 파형의 최대파고와 단주기 성분을 과대 산정할 수 있다. 지진이 시작된 진원에서 멀어질수록 단층운동이 일어나는데 시간이 필요하며 특히 단층의 길이가 긴 경우 시간 경과에 따라 변위가 일어나는 지역이 뚜렷하게 달라진다. Dutykh and Dias (2009)는 2차원 평면에서 시간이력을 고려한 경우와 고려하지 않은 경우에 대한 지진해일의 차이를 보였다. Suppasri et al.(2010)과 Ohmachi et al.(2001)은 파열 속도(rupture velocity)가 느리고 단층에 가까운 지역일수록 시간이력을 고려함에 따른 지진해일의 차이가 증가함을 확인하였다. 또한 수분의 시간차를 두고 발생하는 대규모 지진의 경우 단층운동의 시간이력에 따라 지진해일이 해안에서 증폭될 수 있다(Imai et al., 2010). 그러나 단층파괴에 대한 시간이력을 고려할 경우 연산 시간이 길어 일부 연구에서는 초기파형을 필터링하는 필터 모델을 개발하여 이 문제를 보완하기도 한다(Glimsdal et al., 2013; Saito and Furumura, 2009). 대규모 지진해일 대응을 위한 전지구 지진해일 예측 시스템의 정확도 향상을 위해서는 단층운동에 대한 시간이력을 고려한 지진해일 수치모의에 대한 연구와 그 결과의 반영이 필요할 것으로 보인다.
4.4 지진해일 파고 및 도달시각
Fig. 6를 보면 2010년 칠레 지진해일, 2011년 동일본 지진해일과 마찬가지로 지진해일 첫 파에서 최대파고가 나타났다(Shevchenko et al., 2014; Yamazaki and Cheung, 2011). 그리고 지진해일 예상 도달시각 이전에 파고 변화가 생기는 지진해일 전조파(tsunami forerunner)가 관측 시계열에 나타났다. 지진해일 전조파 현상은 수치모의 결과에는 모사되지 않았는데, 단층의 수평변위, 해저면 경사 그리고 지진 지반 운동 등에 의해 전조파 현상이 나타나는 것으로 판단되며(Murotani et al., 2014) 지진해일 수치모의에는 이것이 충분히 반영되지 않는 것으로 생각된다.
지진해일이 실제로 도달하는 시각보다 늦게 도달할 것으로 통보하면 예상하지 못한 시각에 지진해일이 내습하여 큰 피해가 발생할 수 있다. 반면 지진해일이 실제로 도달하는 시각보다 빨리 도달할 것으로 통보하면 필요 이상으로 대응할 수 있으나, 미리 대비할 수 있는 시간을 더 많이 확보할 수 있어 경보 차원에서는 의미가 있다고 하겠다. 본 연구에서는 평균적으로 85%의 지점에서 예측한 시각보다 늦게 지진해일이 도달하였다(Fig. 7). 이는 물의 압축과 팽창 그리고 지진해일의 탄성 하중에 의한 시간 지연 현상 등에 의해 예측시각보다 늦게 도달하는 것으로 판단된다(Watada et al., 2014).
4.5 연산 속도
국립기상과학원 서버(CPU: E5-2697(2.8 GHz), RAM: 128 GB)에서 Case SD를 모의하는데 약 4시간 30분이 소요되었다. 지진 분석에서 결과 표출까지 고려한다면 대규모 지진 발생 후 약 5시간이 경과해야 지진해일 예측 정보를 생산할 수 있다. 2014년 칠레 지진해일의 경우 지진 발생 약 25시간 후 한반도에 도달하므로 현재의 연산 속도로도 충분히 대비할 시간이 있다. 그러나 현재의 연산 속도라면 남아메리카 대륙에는 이미 지진해일이 도달하여 인근 지역에 거주 또는 여행하는 재외국민에게 지진해일 정보를 제공하기에는 느리며, 2011년 동일본 대지진과 같이 한반도 주변에서 발생한 지진해일에는 대응할 수 없다.
병렬화란 순차적으로 진행되는 계산을 여러 프로세서에서 동시에 수행되도록 하는 것으로 수치모의 정확도는 유지하며 연산 속도를 획기적으로 늘릴 수 있는 방법이다. FVCOM(Finite-Volume primitive equation Community Ocean Model)과 GeoClaw(Geophsical Conservation laws)는 각각 MPI(Message Passing Interface)와 OpenMP(Open Multi-Processing) 방법으로 병렬화되어 천수방정식을 유한체적법으로 해석하는 수치모델로 지진해일의 분산성이 상대적으로 중요하지 않은 연안에서의 지진해일 모의에 사용되었다(Chen et al., 2014; Melgar and Bock, 2015). 최근 Lin et al. (2015)은 COMCOT 코드의 최적화 및 병렬화를 수행하여 기존보다 최소 10배 빠른 iCOMCOT을 개발하였다. 향후 원거리 지진해일에 대한 신속한 대응을 위하여 병렬 프로그래밍을 통해 지진해일 수치모의 연산속도를 증대시키고 유한 단층 모델에 의한 지진분석과 그 결과의 지진해일 수치모의에 반영하는 과정 등을 신속하게 연동시킬 수 있는 방안을 개발하는 것이 추가로 요구된다.
5. 결 론
지진해일은 인명과 재산에 직접적인 영향을 주는 자연재해로 잘못된 정보는 큰 혼란을 일으킬 수 있다. 따라서 지진해일 예측 및 통보에는 신속성과 정확성이 동시에 요구되어 지진해일 통보시스템 구축이 쉽지 않다(Titov et al., 2005). 본 연구에서는 원거리 지진해일에 대응하기 위한 기초 연구로써 유한 단층 모델과 순환 경계조건을 이용한 전지구 지진해일 예측 시스템을 제안하였다. 또한 2014년 칠레 지진해일에 적용하여 원거리 지진해일에 대한 대응 시스템으로의 가능성을 검토하였다. 전지구 지진해일 예측 시스템의 경계조건, 지배방정식, 격자 크기, 단층 모델에 따른 결과를 DART 부이, 조위관측소 관측 자료와 비교하였다. 그 결과 지진해일 정확도와 연산 속도를 고려할 때 10분 간격 격자에 선형 천수방정식을 지배방정식으로 사용하는 것이 합리적이며, 유한 단층 모델과 순환 경계조건이 중요함을 확인하였다. 향후 고위도를 고려한 격자망, 격자 간격에 의한 지진해일 오차, 단층운동시간을 고려한 단층 모델, 지진해일 전조파 및 시간 지연 현상, 병렬 프로그래밍 등에 관한 추가 연구를 통해 정확성과 신속성이 확보된 전지구 지진해일 예측 시스템의 구축이 가능할 것으로 기대된다.
Acknowledgements
이 연구는 국립기상과학원 ‘관측·지진기술 지원 및 활용 연구’의 지원에 의해 수행되었습니다. 본 논문을 심사하고 유익한 조언을 해 주신 익명의 세 심사위원과 편집위원께 감사 드립니다.