역기압 효과를 반영한 동해 연안 수위 변동 수치 재현
Numerical Simulation of Water Level Change at the Coastal Area in the East Sea with the Inverted Barometer Effect
Article information
Abstract
일반적으로 해수위 변동은 조석, 기상, 수온, 염분, 파랑, 지형 등 다양한 요인에 의해 영향을 받는다. 비조석 외력 조건 중 대기압 변화는 수위 변화를 유발하는 큰 요인 중 하나이다. 수위 변동을 예측함에 있어 서해와 달리 조차가 작은 동해 연안은 조석 성분만을 외력 조건으로 고려하여 관측 수위를 재현하기는 현실적으로 어렵다. 본 연구에서는 동해 연안의 수위 예측 및 재현 시 대기압의 시간적 변화가 수위의 변화에 미치는 영향을 검토하고자 Telemac-2D 모형에 역기압 효과(IBE, Inverted Barometer Effect)를 반영하여 수치 모의를 실시하고 그 결과를 검토하였다. 역기압 효과와 조석을 동시에 반영한 예측 결과는 조석만을 반영한 예측결과보다 관측 자료와의 상관도가 크게 증가함으로 동해 연안 관측 수위의 수치 재현에 역기압 효과가 반드시 반영되어야함을 확인하였다.
Trans Abstract
Sea water level variations are generally influenced by a variety of factors such as tides, meteorological forces, water temperature, salinity, wave, and topography, etc. Among non-tidal conditions, atmospheric pressure is one of the major factors causing water level changes. In the East Sea, due to small tidal range which is opposite to large tidal range of the Yellow Sea, it is difficult to predict water level changes using a numerical model, which consider tidal forcing only. This study focuses on the effects of atmospheric pressure variations on sea level predictions along the eastern coast of Korea. Telemac-2D model is simulated with the Inverted Barometer Effect(IBE), and then its results are analyzed. In comparison between observed data and predictions, the correlation of prediction with IBE and tide is better than that of tide-only case. Therefore, IBE is strongly suggested to be considered for the numerical simulations of sea level changes in the East Sea.
1. 서 론
해양에서 레저, 관광, 연안 및 항만 개발 등 다양한 인간 활동이 증가함에 따라 보다 안전한 활동을 보장할 수 있는 해황 예측·재현 기술의 개발이 매우 중요해 지고 있다. 서해 및 남해안에 비해 조석이 작은 동해 연안의 경우도 개발이 활발해 짐에 따라 보다 정확한 해황 예측이 요구된다. 특히, 수치모형을 이용한 수위 예측 연구에서는 조석 성분뿐만 아니라 비조석 성분도 고려하여 관측 수위를 재현하는 수요가 증가하는 추세이다.
일반적으로 해양에서 해수위의 변동은 조석, 기상(바람, 기압 등), 밀도(수온, 염분), 파랑, 지형, 지각변동 등 다양한 요인에 영향을 받아 발생한다. 특히 조석의 크기가 작은 동해 연안의 경우는 조석 이외의 해수면 변동에 영향을 주는 성분을 파악·반영하여 수치모의 함으로써 관측수위를 보다 정확하게 재현하는 방법을 고려할 필요가 있다.
Kim and Kim(2013)은 2003~2009년의 우리나라 연안 해수면자료로 조위편차를 산출하고 해면기압과 바람이 조위편차 변동에 미치는 영향을 분석하였다. 그 결과, 해역별로 조위편차에 영향을 주는 주요 요인이 서해안에서는 남-북 방향의 바람성분이고 남해안에서 동해안으로 갈수록 해면기압이 바람보다 밀접하게 영향을 주고 있음을 보고하였다. 또한 Han et al.(2013)은 동남극 테라노바 만의 조위모델 정밀도 평가 연구를 통해 대기압과 평균대기압의 차이로부터 산출한 역기압 효과 보정을 실시한 결과 실측 조위와 모델 계산 조위간의 평균제곱근오차(RMSE, root mean square error)가 감소함을 보고한 바 있다. 아울러, Jung et al.(2008)은 1999~2005년까지 7년간의 해수면과 대기압 자료 분석을 통해 동해 연안의 종관주기 해수면 변동 특성을 분석하였으며 해수면과 대기압 간 교차 스펙트럼 분석을 통해 종관주기 해수면 변동의 생성에 있어 역기압 효과(IBE, inverted barometer effect)가 중요한 요인임을 밝힌 바 있다.
항만 개발, 설계, 환경영향 평가 등 공학적인 목적으로 수치모델을 이용하여 동해 연안을 모의하는 경우, 수위 예측은 1개월 또는 그 이내의 기간을 예측하는 경우가 대부분이다. Jung et al.(2008)이 동해에서 3-20일 정도 주기의 종관주기 해수면 변동성이 대기압과 연관이 큼을 보고한 바, 수치모델을 이용하여 1개월 이내의 단기 관측 수위를 예측·재현할 때 대기압에 의한 역기압 효과를 반영하는 것이 실측 수위에 더 가까운 계산 결과를 도출할 수 있을 것이라 판단된다. 따라서 본 연구에서는 국립해양조사원의 동해 연안 4개소(후포, 묵호, 동해항, 속초)의 2014년 11월에서 2015년 10월까지 365일간의 1시간 관측 수위자료 및 대기압 자료를 수집·분석하고, Telemac-2D 모형을 이용하여 동계(2015년 2월)와 하계(2015년 7월)에 대한 수치모의를 실시하여 동·하계의 대기압 변화에 의한 역기압 효과가 동해 연안 수위의 변동에 미치는 영향을 분석·검토하였다.
2. 관측 자료 및 분석
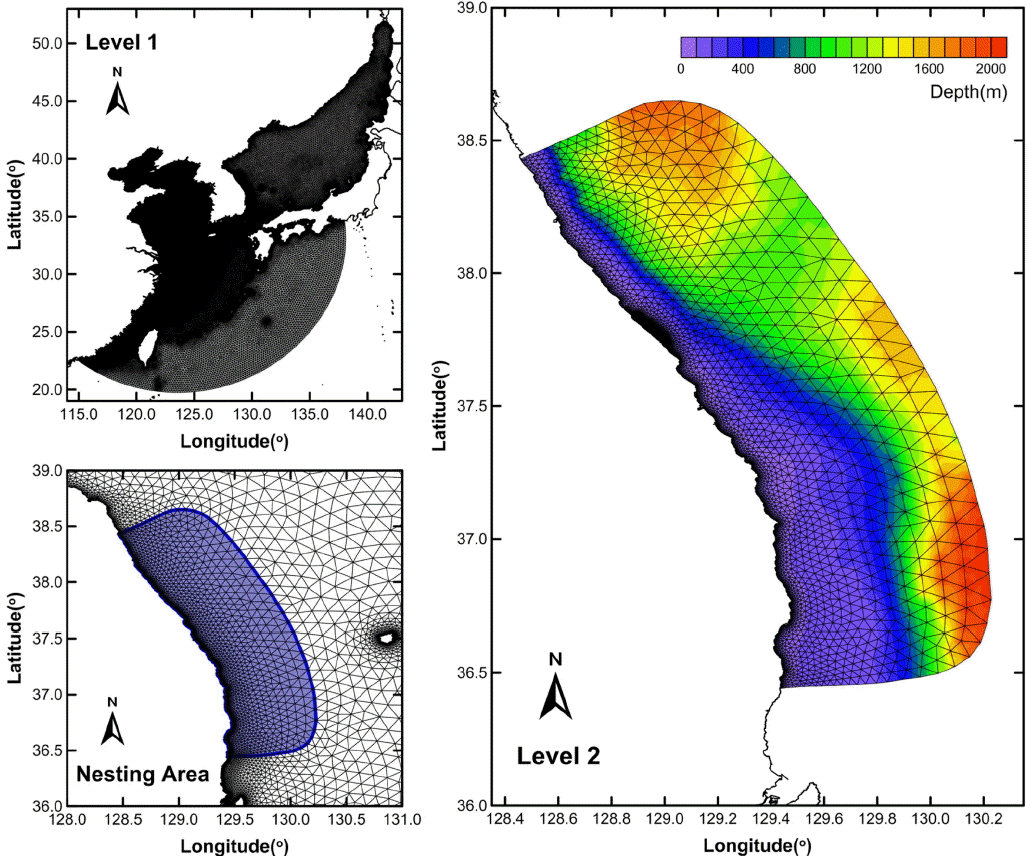
동해 연안에서 수위 변동에 영향을 미치는 조석 및 비조석 성분 분석 및 수치 모형의 계산 결과 검토를 위해 국립해양조사원(Korea Hydrographic and Oceanographic Administration)의 동해 연안 기준검조소 4개소(후포, 묵호, 동해항, 속초)에서 관측한 자료를 수집하였다(Fig. 1). 관측자료 중 수위 자료는 2014년 11월 1일부터 2015년 10월 31일(GMT 기준)까지 365일간의 1시간 간격의 자료를 수집하였고, 대기압 자료는 동기간의 검조소 관측 1분 자료를 수집한 후 이를 1시간 간격으로 추출하였다.
일반적으로 해양의 해수면 변동은 다음과 같이 평균해면, 주기적이고 예측 가능한 조석과 불규칙적으로 변동하는 비조석 성분인 조위편차(잔차)의 합으로 구성된다(Kim and Kim, 2013).
여기서, ζ(t), MSL, T(t), R(t)는 각각 해수면, 평균해면, 조위, 조위편차이다. f(t)는 달의 공전주기인 18.61년 동안 달의 적위에 따라 변화하는 노달 팩터(nodal factor), 아래첨자 i는 i번째 분조, n은 분조의 개수, ω는 각속도, t는 시간, φ는 위상이다.
관측 자료로부터 비조석성분인 조위편차에 미치는 대기압의 영향을 검토하고자 TASK-2000(Tidal Analysis Software Kit-2000; Bell et al., 1999) 패키지를 이용하여 수집된 1년 간의 수위 관측 자료의 조석조화분해를 실시하였다. 분석된 조석조화상수 중 수치모델의 외력조건에 해당하는 주요 8개 분조의 분석결과는 Table 1에 제시된 바와 같다. 분석된 조화상수를 바탕으로 추후 논할 수치모델의 예측 기간인 동계(2015년 2월 1일 ~ 3월 2일) 및 하계(2015년 7월 1일 ~ 30일)의 기간에 대해 각 기준검조소별 산술평균해면(A0)을 계산한 후 평균해면상의 관측수위, 대기압, 조위 및 조위편차를 분석하고 시계열로 제시하였다(Fig. 2, Fig. 3).

Calculated major tidal harmonic constituents at four tidal stations from Nov. 1st. 2014 to Oct. 30th, 2015: A (amplitude, cm), P (phase, °, GMT).
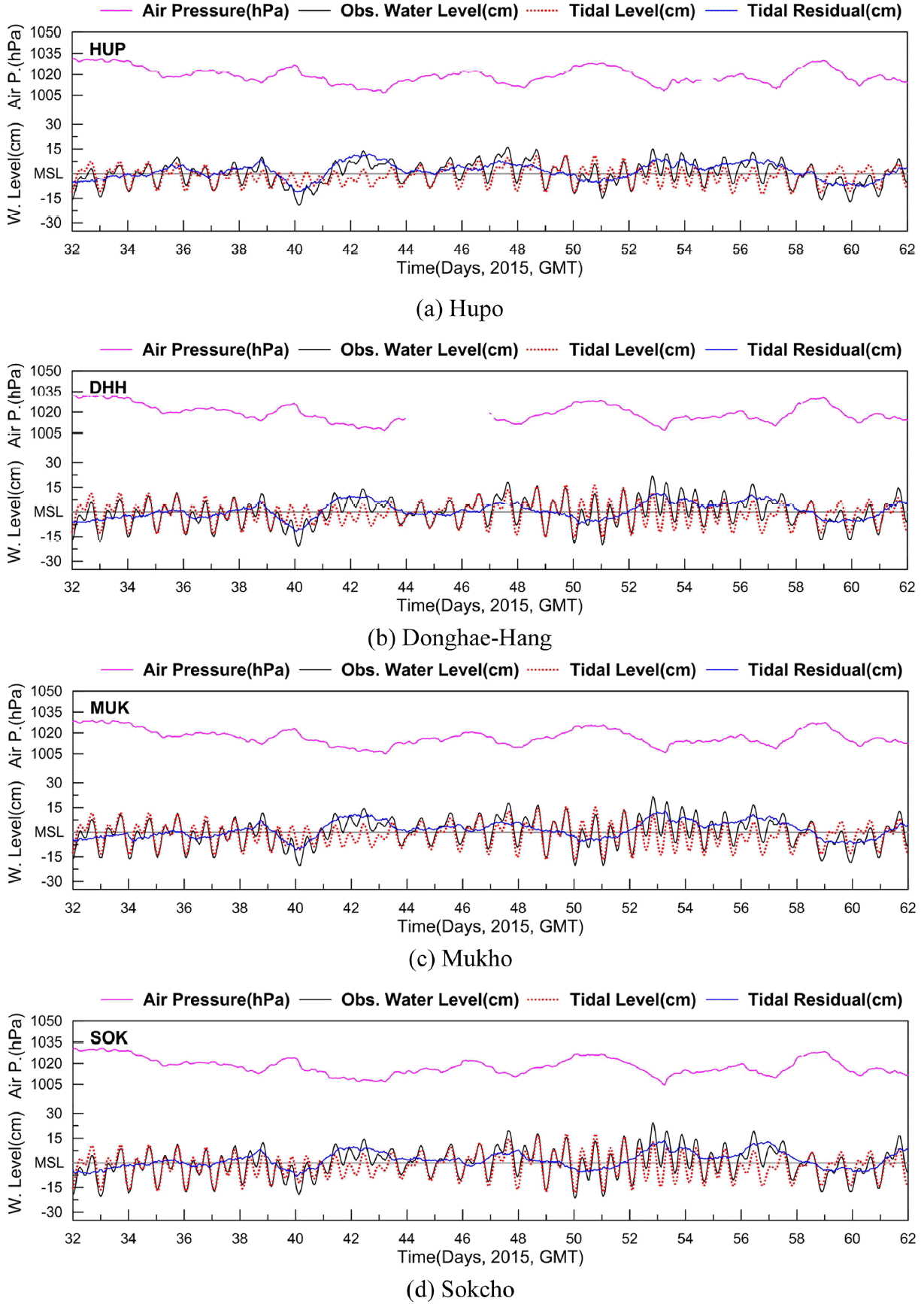
Time series of observed water level (black line), tidal level (red dot), tidal residuals (blue line), and air pressure (purple line) at four tidal stations from Feb. 1st to Mar. 2nd 2015.
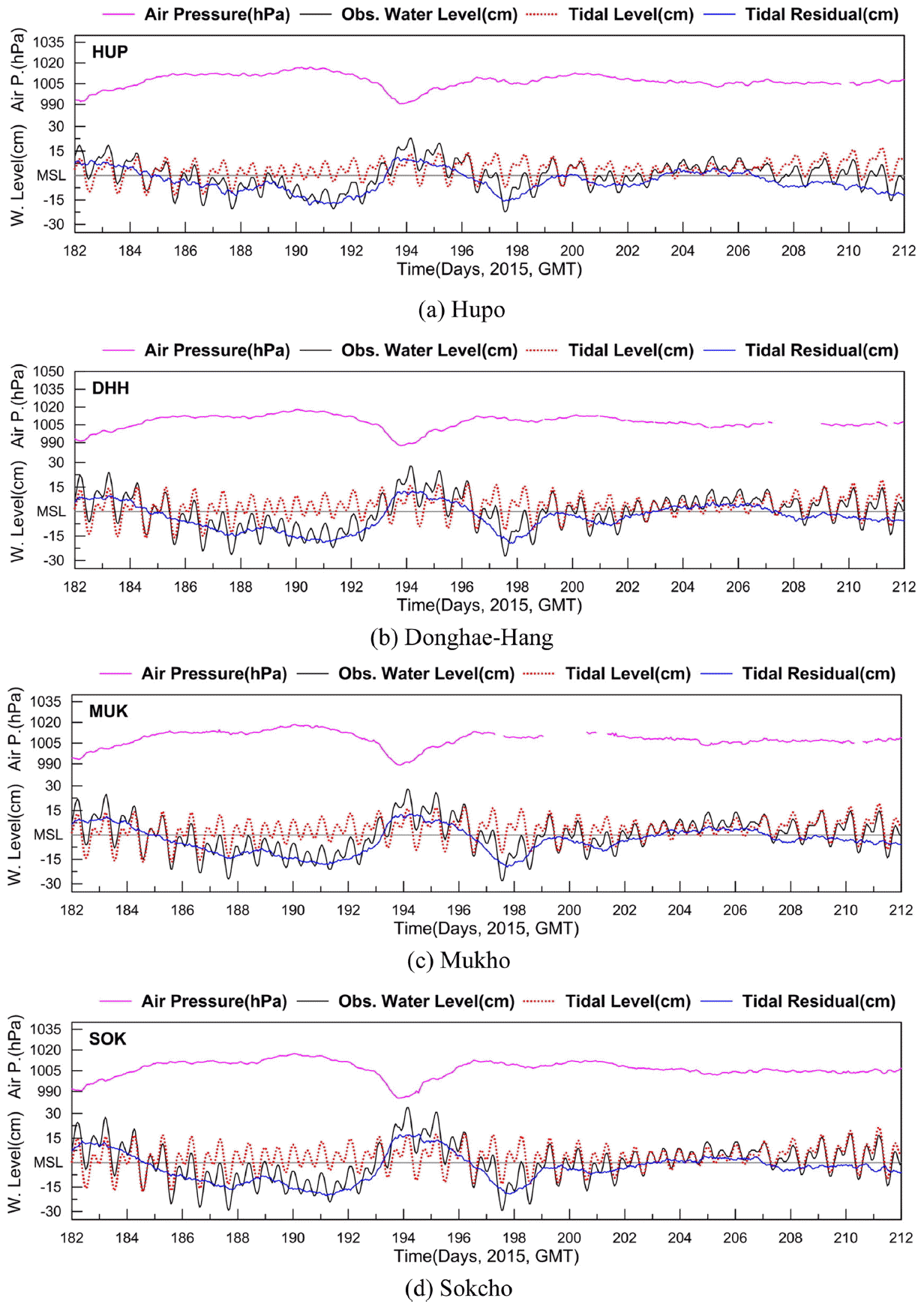
Time series of observed water level (black line), tidal level (red dot), tidal residuals (blue line), and air pressure (purple line) at four tidal stations from Jul. 1st to Jul. 30th 2015.
대기압에 따른 해수면의 반응은 대기압이 증가(감소)하면 해수면은 하강(상승)하는 역관계를 가지며 이러한 현상은 “역기압 효과(inverted barometer effect)” 라고 알려져 있다. 역기압 효과에 의한 해수면 변화(∆η)는 해수밀도에 영향을 받으며 다음과 같이 계산할 수 있다(Bowden, 1983; Pugh, 1987; Dorandeu and Le Traon, 1999).
여기서, ρ는 해수밀도, g는 중력가속도, Pa는 대기압이다. Pref는 기준 대기압으로 평균기압 또는 1013.0 등의 상수를 적용한다. 해수밀도 자료가 존재하지 않을 경우 경험적인 방법으로 대기압 변화에 따른 해수면 변화를 계산할 수 있다. 대기압이 1 변화할 때 해수면은 1.01 cm 변화함을 가정할 때 역기압 효과에 의한 해수면 변화는 다음과 같이 계산할 수 있다(Kantha et al., 1994).
후포, 동해항, 묵호, 속초의 4개 기준검조소에서 관측된 수위 자료 중 조석성분이 제거된 조위편차 내 역기압 효과의 영향을 검토하고자 관측된 1시간 간격의 대기압 자료에 식(4)를 적용하여 수위 변화를 계산하였다. 수위 변화 계산 시 기준 대기압(Pref)은 동·하계 수치모델의 예측 기간 평균치를 계산하여 후포, 동해항, 묵호, 속초에서 각각 동계에 1019.2, 1019.2, 1017.0, 1017.9 을 적용하였고 하계는 1007.0, 1007.2, 1007.9, 1006.4 으로 적용하였다. 분석된 조위편차와 역기압 효과에 의한 수위 변화의 정량적 분석은 다음과 같이 평균제곱근오차(RMSE)를 계산하여 검토하였으며 분석 시 대기압 자료의 결측 구간은 계산에서 제외하였다.
여기서, Xo는 관측 값이고 Xp는 식(4)를 이용한 계산 결과값이다.
Fig. 4와 5는 계산된 역기압 효과에 의한 수위 변화와 조위편차를 시계열로 비교한 것이다. 제시된 그림에서 4개 관측점 모두 동·하계 대기압에 의한 수위변화는 조위편차의 크기 및 경향성과 밀접한 관계가 있음을 보여준다. 동계의 경우 역기압 효과에 의한 수위 변화와 조위편차간의 평균제곱근오차는 후포 4.6 cm, 동해항, 묵호, 속초에서 4.3 cm로 계산되었고 하계의 경우 평균제곱근오차는 후포 5.9 cm, 동해항 5.8 cm, 묵호 5.6 cm, 속초에서 5.9 cm로 계산되었다. 이는 분석 기간 내 조위편차의 최대 변화폭이 4개 관측점 평균 동계 22.9 cm, 하계 33.0 cm 임을 고려할 때 역기압 효과에 의한 수위 변화와 조위편차간의 오차는 크지 않다고 판단되며, 추세선의 변화를 함께 고려할 때 대기압의 변화가 동해 연안 조위편차에 상당한 영향을 주고 있음을 가늠케 한다.
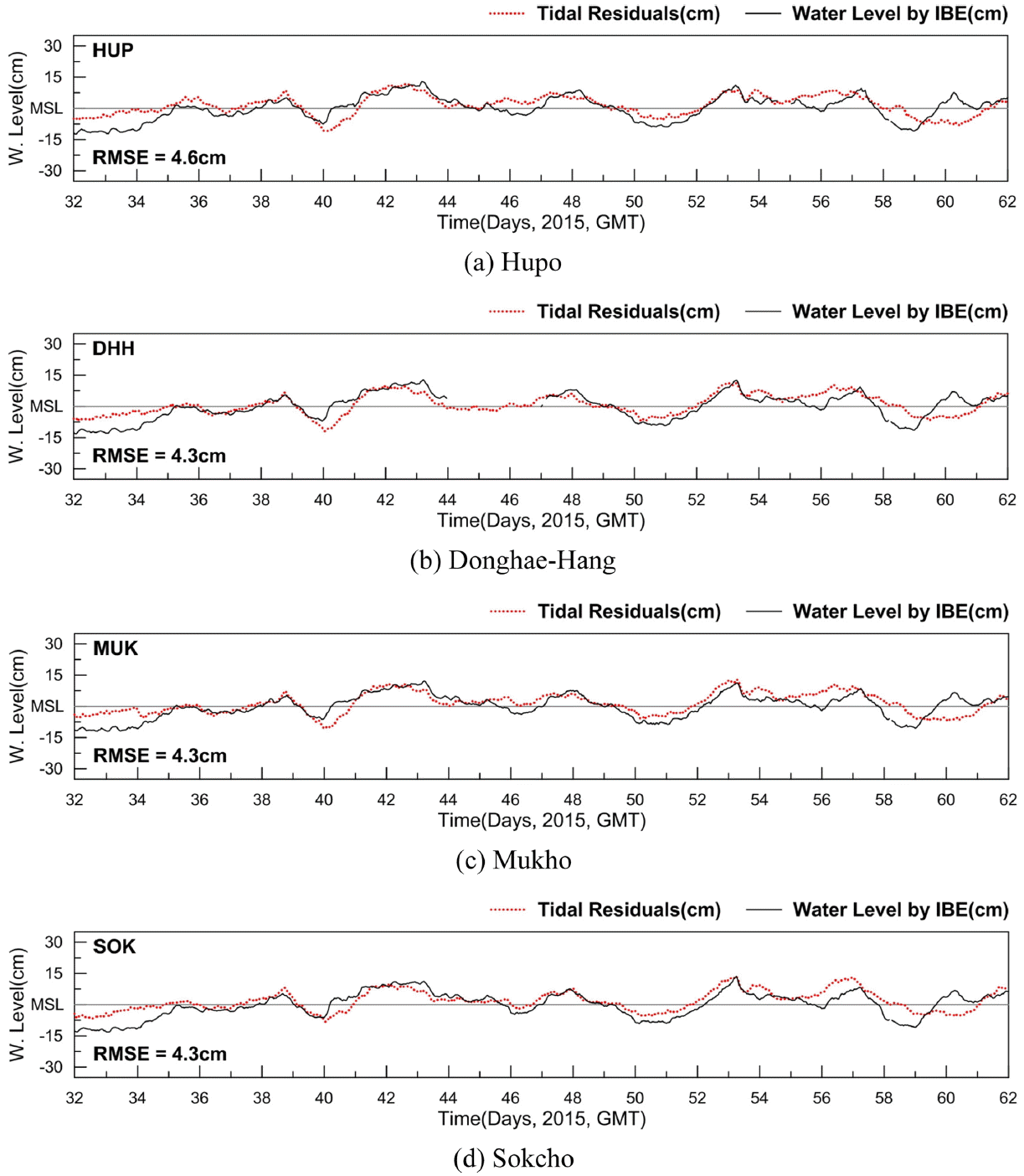
Time series comparison of observed tidal residuals (red dot) and water level (black line) calculated by the inverted barometer effect (IBE) method from Feb. 1st to Mar. 2nd 2015.

Time series comparison of observed tidal residuals (red dot) and water level (black line) calculated by the inverted barometer effect (IBE) method from Jul. 1st to Jul. 30th 2015.
이상의 결과로부터 동해 연안에서 기압 시계열 변화를 수치 모델에 고려하는 것이 조석만을 외력조건으로 고려하는 경우보다 수치 모델의 수위 변동 재현 정밀도가 향상될 수 있음을 예상할 수 있다.
3. 수치 실험
3.1 사용 모델
대기압 변화가 동해 연안 수위 변화에 미치는 영향의 검토를 위한 예측실험은 공개 모델인 Telemac-2D 모델을 이용하여 실시하였다. TELEMAC 모델은 1990년대 후반 프랑스의 EFD-R&D(Research and Development Directorate of the French Electricity Board)의 LNHE(Laboratoire National d'Hydraulique et Environnement) 연구소에서 개발되어진 후 현재는 유럽 컨소시엄에 의해 개발·검증되고 있는 모형으로 2010년 오픈소스 버전으로 공개된 공개 모델이다. 공개된 TELEMAC-MASCARET 시스템은 2·3차원 유동 및 침·퇴적, 파랑 및 반사파를 고려한 항내파랑, Delft3D 모델의 수질 모듈(DELWAQ)과 연계한 수질 예측 등 다양한 현상에 적용이 가능한 모듈들을 보유하고 있다.
본 실험의 유동해석에 적용된 Telemac-2D 모델은 수심적분 자유표면 방정식을 계산하는 2차원 모형으로 해양과 하천 수리 분야에 다양하게 적용되었으며(Asaro and Paris, 2000; Hervouet, 2000), 비선형효과를 포함한 장파의 전파, 저면 마찰, 지구 자전, 기압과 바람 등 기상 효과, 난류, 밀도, 홍수, 조간대 효과, 입자 추적과, 라그란지안 부표 추적, 지진 해일, 유류 확산, 연안류 계산 등 다양한 현상을 고려할 수 있는 모델이다(Hervouert, 2007). Telemac-2D 모델에서 연속 방정식, 방향의 운동방정식은 각각 다음과 같다.
여기서, h는 수심(m), u, v는 각각 x, y 성분의 속도(m/s), 는 중력가속도(m/s2), νt는 운동량 확산계수(m2/s), Z는 자유 표면 고도(m), t는 시간(s), Sh, Sx, Sy는 유체 및 운동량의 생성·소멸항이다. 본 연구에 적용된 Telemac-2D 모델에 대한 자세한 사항은 EDF-R&D(2014)에 기술되어 있다.
3.2 모델 구축
동해 연안 수위 재현을 위한 모델은 연안역에 대한 해상도 향상과 효과적인 역기압 효과 반영을 위해 다중격자시스템인 2단계의 네스팅(nesting) 기법을 도입하여 모델을 수립하였다. 모델 구축 시 광역의 1단계(Level 1) 모델은 우리나라 동·남·서해 및 일본, 중국, 대만 등을 포함하는 영역에 대하여 비구조격자 모델을 구축하였고 이를 일방향 네스팅(one-way nesting) 방법으로 2단계(Level 2) 모델에 연계하였다. 동해 연안의 2단계 모델은 국립해양조사원의 동해 연안 4개 기준검조소를 포함하는 영역에 대하여 상세 비구조격자 모델을 구축하였다. 수치 모델 모의 시 적용된 수심 및 해안선은 국립해양조사원 간행 수치해도 자료를 기본적으로 사용한 후 Seo(2008) 및 영국 해양자료 센터(BODC, British Oceanographic Data Centre)의 GEBCO 30(General Bathymetric Chart of the Oceans 30 arc-second global grid of elevations) 수심 자료를 사용하여 보완하였다(Fig. 6).
광역의 1 단계 모형의 개방경계에서 외력 조건으로 고려된 조석은 1/12도 격자의 NAO.99jb(Matsumoto et al., 2000) 결과로부터 추출·보완된 M2, S2, K1, O1, N2, K2, P1, Q1의 8개 분조를 외력 조건으로 사용하였으며, 상세역의 2단계 모형은 광역의 1단계 모형에서 계산된 조위 및 유속 결과를 입력조건으로 사용하였다. 실험 시 모델의 초기조건으로 해수면과 각 격자에서의 유속은 0(cold start)으로 설정하였고, 폐경계 조건으로 육지경계면을 가로지르는 유속은 없음을 가정하였다.
수위 예측 실험은 상세역인 2단계 모형을 이용하여 실시하였으며, 역기압 효과에 의한 수위변화 양상 검토를 위해 실험은 외력으로 조석만을 반영한 경우와 조석과 역기압 효과를 동시에 반영한 경우로 구분하여 실시하였다. 수치모형 실험은 동계 및 하계로 구분하여 실험을 실시하였으며 수치 모델의 결과 및 관측 자료와의 비교·분석은 모델의 안정화 기간을 고려하여 7일간의 안정화 기간을 모의한 후 도출되는 30일간(동계 : 2015년 2월 1일 ~ 3월 2일, 하계 : 2015년 7월 1일 ~ 30일)의 결과를 사용하여 실시하였다.
역기압 효과 반영 실험 시 기압 관측 자료는 대기압의 공간 변화를 무시하고 묵호 기준검조소의 1시간 간격의 기압 자료를 공간적으로 균일하게 적용하였으며 기압 자료의 결측 구간은 인근역의 동해항 기준검조소의 기압 자료를 사용하여 보완 및 내삽하여 적용하였다. 역기압 효과에 의한 수위 변화는 식(4)를 Telemac-2D 모델 내에 반영하여 계산하였으며 계산 시 기압 변동의 기준이 되는 기준기압(Pref)은 묵호 기준검조소의 기압 자료 중 분석 기간 30일간의 평균값인 동계 1017.0 hPa, 하계 1007.9 hPa로 적용하였다.
3.3 결과 분석
수치 모델에 의한 조석 예측 결과의 적절성을 검토하고자 조석 조건만을 외력조건으로 고려한 실험의 예측 결과를 다음과 같이 비교·검토하였다. 동계 및 하계의 예측 결과와 관측 자료의 조석조화분해로 계산된 조화상수 중 모델 계산 시의 외력조건에 해당하는 8개 분조 조화 상수(Table 1)를 TASK-2000 팩키지를 이용하여 분석 기간과 동일하게 합성한 후 이를 비교·검토하였다(이후 동계 비교시를 Case W1, 하계 비교시를 Case S1로 칭함). 이러한 비교 방법은 공학적인 목적으로 동해 연안의 조위를 재현하는 경우에 적용하는 일반적인 비교 방법이다. Fig. 7과 Fig. 8은 동·하계의 예측 조위와 관측 조석조화상수의 합성 조위간의 시계열 비교 및 상관관계 검토 결과를 제시한 것으로 4개 관측점에 대한 예측 결과는 관측 자료의 경향성을 잘 재현하고 있음을 알 수 있다. 평균제곱근오차(RMSE) 및 상관계수(R-Squared) 분석에 있어서도 동계 및 하계의 평균제곱근오차는 각각 0.9~1.0 cm, 0.9~1.1 cm로 오차가 작았으며 상관계수는 동계 0.9541~0.9826, 하계 0.9593~0.9839로 높게 분석되어 모델의 예측 결과가 8개 조석조화분조에 의한 관측 조위를 잘 재현하고 있음을 알 수 있다.

Comparison of tidal level time series between regenerated by observed 8 tidal harmonic constituents (red dot) and calculated (black line) data from Feb. 1st to Mar. 2nd 2015(Case W1).
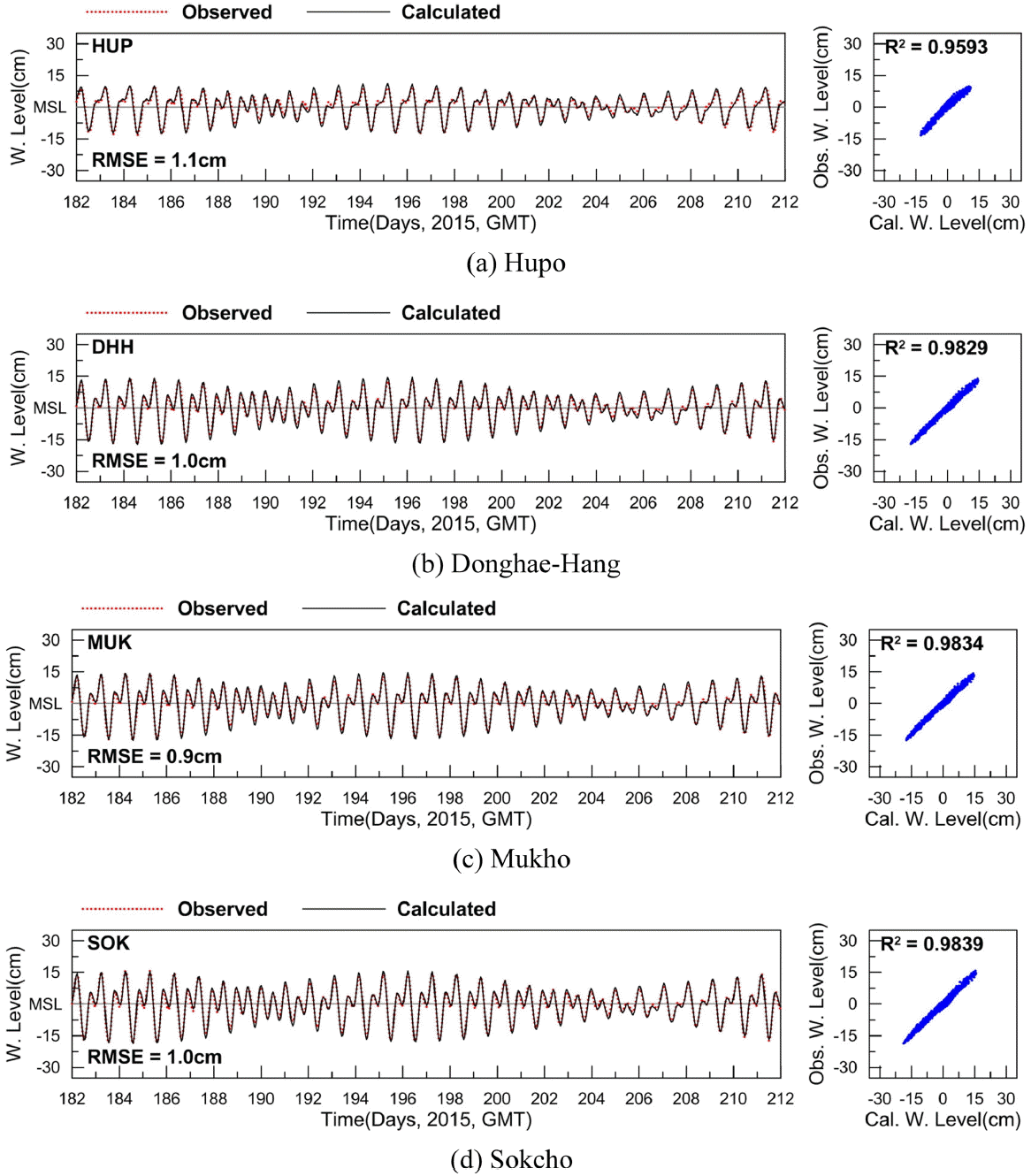
Comparison of tidal level time series between regenerated by observed 8 tidal harmonic constituents (red dot) and calculated (black line) data from Jul. 1st to Jul. 30th 2015(Case S1).
비록 조석에 의한 예측 결과가 관측 자료를 바탕으로 하는 8개 조석조화상수의 합성 조위를 잘 재현하였지만 이러한 결과가 합성 조위가 아닌 실제 관측된 수위의 시간변화 역시 잘 재현할 것인지에 대한 검토가 필요할 것이다. 이의 검토를 위해 조석 조건 하에서 예측된 동·하계의 예측 조위와 관측 수위를 평균해면상에서 비교·분석하였다(이후 동계 비교시를 Case W2, 하계 비교시를 Case S2로 칭함). Fig. 9와 Fig. 10은 동·하계의 예측 조위와 관측 수위를 시계열로 비교하여 제시한 것이다. 동계의 경우 4개 관측점에서 예측 조위와 관측 수위간의 상관계수는 0.4973~0.6705, 평균제곱근 오차는 4.8~5.0 cm로 계산되어 Case W1의 결과 보다 오차가 크게 증가하였다. 하계의 경우도 4개 관측점에서 상관계수는 0.3484~0.3840, 평균제곱근오차는 7.0~9.2 cm로 분석되어 Case S1의 결과와 비교 시 동계보다 큰 폭의 오차가 증가함을 알 수 있다. 특히 하계의 오차 증가는 시간에 따른 비조석 성분의 변화폭이 동계보다 하계에 크기 때문에 발생하고 있으며 이러한 분석 결과로부터 상대적으로 조석의 크기가 작은 동해 연안에서 비조석 성분에 의한 영향이 수위 변동에 상당한 영향을 주고 있음을 알 수 있다.

Comparison of water level time series between observed (red dot) and calculated (black line) data from Feb. 1st to Mar. 2nd 2015(Case W2).
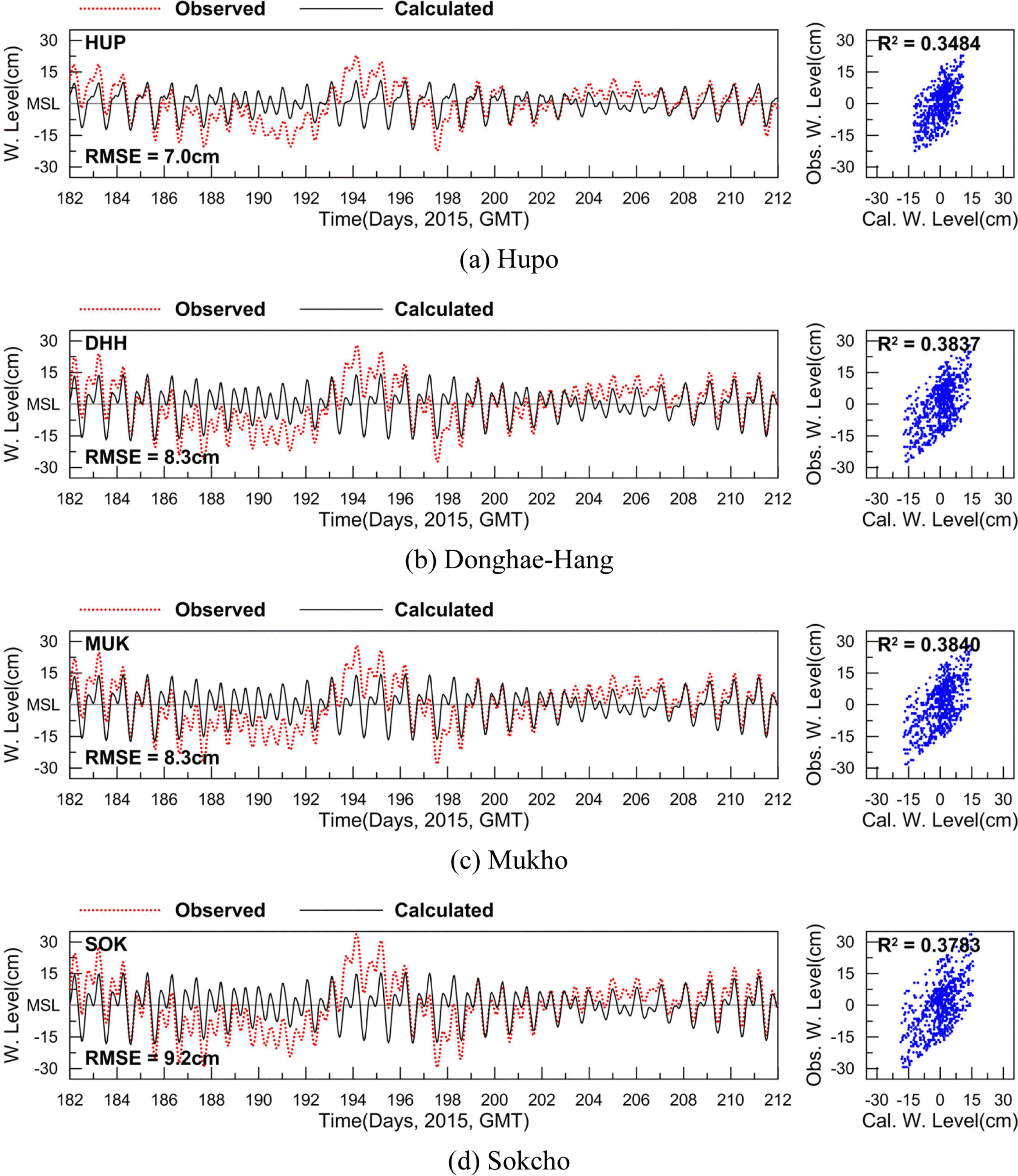
Comparison of water level time series between observed (red dot) and calculated (black line) data from Jul. 1st to Jul. 30th 2015(Case S2).
앞서 언급된 바와 같이, 해수위의 변동에 영향을 미치는 비조석 성분은 바람과 기압 같은 기상 조건과 수온 및 염분의 변화, 파랑, 지형, 지각 변동 등 다양한 요인의 영향에 의해 발생한다. 이러한 요인 중 대기압 변화가 동해 연안의 수위 변동에 미치는 영향을 검토하고자 수치모형의 외력조건으로 8개 분조의 조석 조건에 역기압 효과를 반영한 예측 실험을 동계 및 하계에 실시하고 앞선 비교 시와 마찬가지로 예측 결과를 평균해면상에서 관측 수위와 비교하여 기압이 수위 변화에 주는 영향을 검토하였다(이후 동계 비교시를 Case W3, 하계 비교시를 Case S3으로 칭함). Fig. 11과 Fig. 12는 역기압 효과가 반영된 예측 결과를 동계 및 하계에 대해 관측 수위와 시계열로 비교하여 제시한 것이다. 그림에서 보여지듯 역기압 효과 반영 시 수위 변화의 시계열은 동·하계 모두에서 Case W2와 Case S2의 경우보다 추세선의 변화 양상에 관측 수의의 시간 변화 경향성이 반영되고 있음을 알 수 있다. 예측 수위와 관측 수위간의 상관도 분석에서도 상관계수는 동계의 경우 후포 0.5761, 동해항 0.7398, 묵호 0.7321, 속초 0.7968로 4개 관측점 평균 0.7112로 계산되어 Case W2의 평균값인 0.6144보다 약 0.10 증가하였으며, 하계의 경우는 후포 0.7709, 동해항 0.7916, 묵호 0.7919, 속초 0.8007로 4개 관측점 평균 0.7888로 계산되어 Case S2의 평균값인 0.3736보다 약 0.42 증가하여 기압 효과 미반영시 보다 큰 폭으로 상관도가 증가하였다. 예측 수위와 관측 수위 간의 평균제곱근오차 분석에서 평균제곱근오차는 동계의 경우 후포에서 5.0 cm로 분석되어 Case W2 분석 시 보다 0.1 cm 증가하였으나, 동해항, 묵호, 속초의 경우는 각각 4.4 cm, 4.6 cm, 4.1 cm로 분석되어 Case W2 분석 시 보다 0.2~0.9 cm 감소하였으며 4개 관측점의 평균값은 약 0.35 cm 감소하였다. 하계의 경우 평균제곱근오차는 후포 4.1 cm, 동해항 4.8 cm, 묵호 4.8 cm, 속초 5.3 cm로 분석되어 Case S2 분석 시보다 2.9~3.9 cm 감소하였으며 4개 관측점의 평균값은 약 3.45 cm 감소하여 오차가 크게 감소함을 보였다.
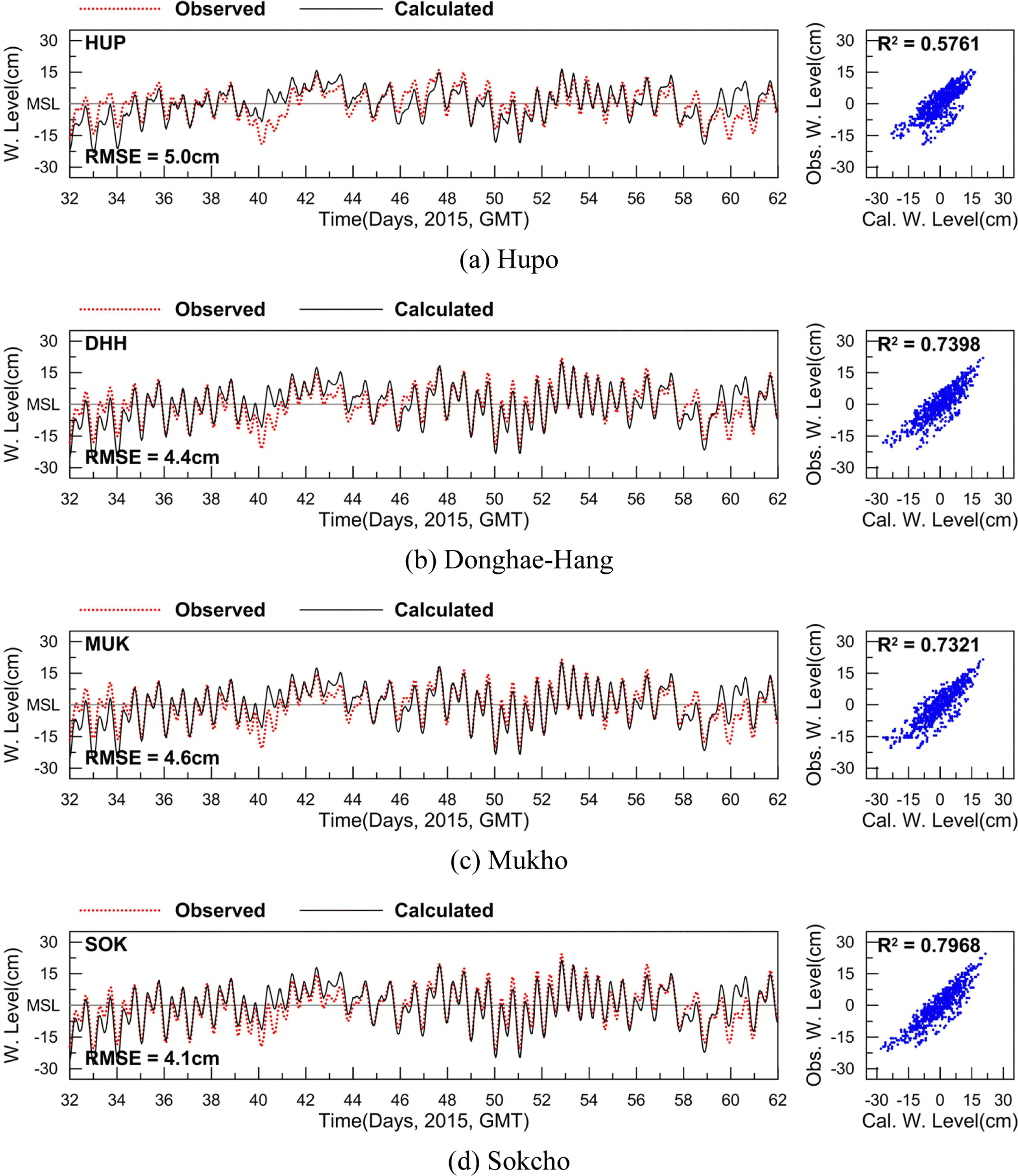
Comparison of water level time series between observed (red dot) and calculated (black line) data from Feb. 1st to Mar. 2nd 2015(Case W3).
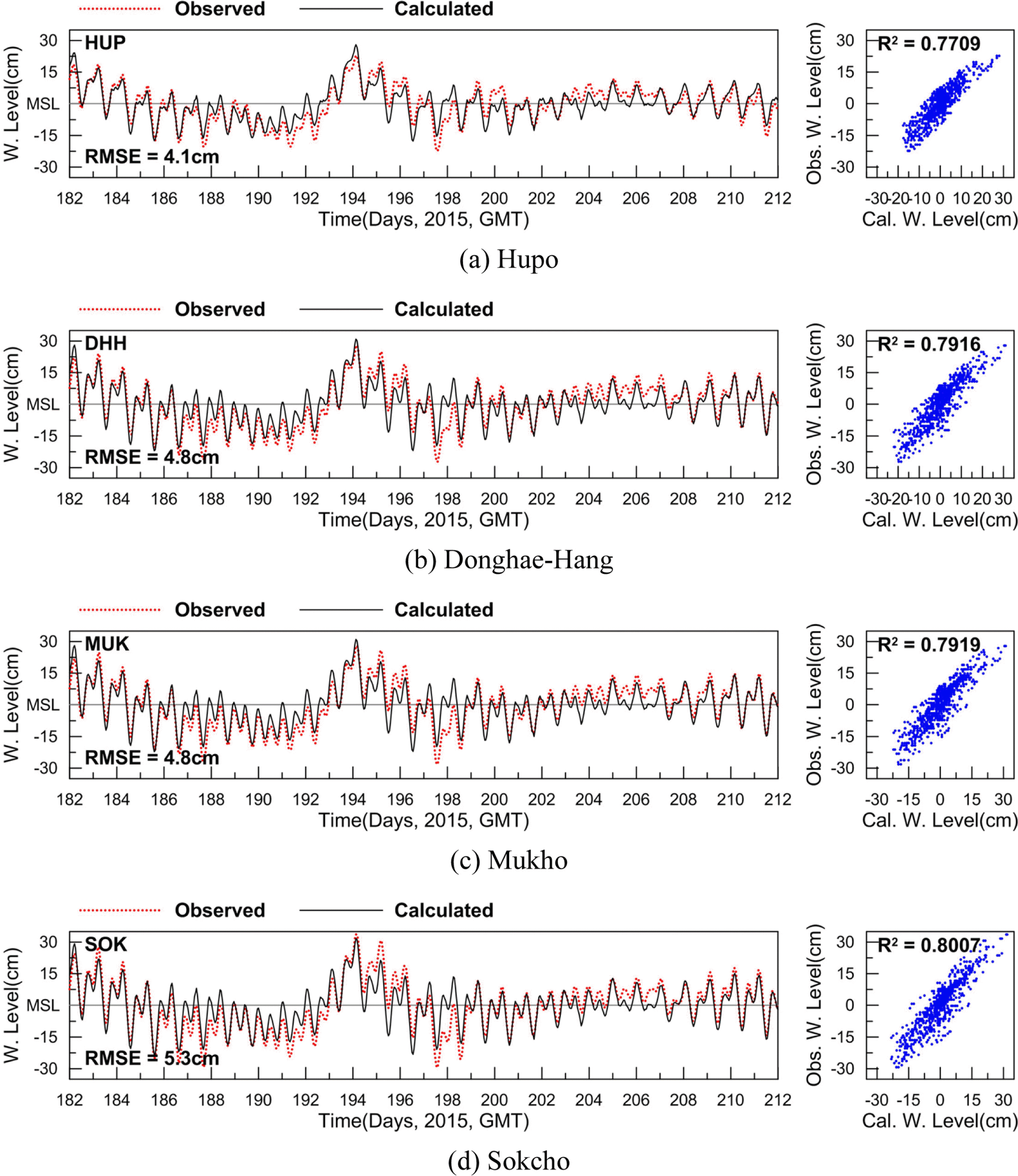
Comparison of water level time series between observed (red dot) and calculated (black line) data from Jul. 1st to Jul. 30th 2015(Case S3).
역기압 효과를 반영한 실험에서 동계 후포의 예측 결과는 관측 수위간의 상관도가 다른 3개 관측점 예측 결과보다 낮게 분석되고 있으며 특히 동계의 경우가 하계의 경우보다 상관계수가 더 낮게 분석되었다. 이러한 원인은 본 연구에서 고려된 대기압 자료가 묵호 기준검조소에서 관측된 기압 자료를 공간적으로 균일하게 적용함에 따라 입력된 기압 자료가 후포 인근 역의 기압 변화에 따른 수위 변화 양상을 잘 반영치 못함이 하나의 원인으로 판단되며, 특히 2월 초와 말의 수위 변동치의 오차 증가가 미미하지만 평균제곱근오차의 증가를 유발한 것으로 판단된다. 그렇지만 후포의 경우에서도 역기압 효과를 반영한 Case W3의 분석 결과는 기압을 미반영한 Case W2의 분석 결과보다 경향성의 재현도 및 상관도의 증가를 나타내므로 역기압 효과의 반영이 수위 변화 예측 시 필요함을 확인할 수 있다.
이상의 결과로부터 수치 모델을 이용한 동해 연안의 관측 수위 예측에 있어 조석이외의 성분 즉, 비조석 성분에 의한 수위 변화 양상을 반영하는 것이 상당히 중요함을 알 수 있으며 특히 대기압 효과에 의한 수위 변화 양상을 반영하여 수치 모델을 실시함으로써 관측 수위 변화 대비 예측 결과의 정확도가 향상됨을 확인하였다.
4. 결론 및 토의
해수면의 변동은 일반적으로 평균해면, 조석, 불규칙적으로 변동하는 비조석 성분인 조위편차(잔차)의 합으로 표현할 수 있다. 서해안과 같이 조차가 큰 해역에서는 비조석 성분을 고려하지 않고 조석만을 고려하는 방법으로도 수위 변화량의 대부분을 설명할 수 있을 것이다. 그렇지만, 서해안에 비해 조석의 효과가 미미한 동해안의 경우 수위의 변동에 비조석 성분인 조위편차가 미치는 영향은 상당히 크며 조석만을 입력 조건으로 적용하는 수치 모델을 이용한 수위 예측 방법으로 는 관측 자료의 경향성을 재현하는데 한계가 존재한다.
일반적으로 공학적인 목적으로 수치 모델을 이용하여 동해 연안을 모의하는 경우 수위의 예측은 1개월 또는 그 이내의 기간을 예측하는 경우가 대부분이다. 따라서 본 연구에서는 수치모델을 이용하여 1개월 이하의 단기 관측 수위를 예측·재현함에 있어 조석 외력 조건이외의 비조석 성분 중 하나인 대기압에 의한 역기압 효과를 반영함으로써 수치 모델의 예측 결과의 정확도가 상당부분 향상될 수 있음을 보였다.
현실적으로 실제 해수면 변동의 수치 모델에 의한 재현은 해수 범람, 월파 등 연안 방재 활동에 있어 매우 중요한 예측 수단이 될 수 있을 것이다. 한반도 전체 또는 본 연구에서와 같이 동해 연안 전체를 수치 모의하는 경우 보다 정밀한 예측 결과의 획득을 위해서는 연안의 정밀 지형 및 정확한 평균해면을 반영하고 이를 기본으로 조석 및 비조석 성분 등의 외력 조건을 반영함이 수치모델을 이용한 해수면 변화 예측에 필요할 것이다. 본 연구의 경우 대기압의 공간 변화를 반영하지 않고 공간적으로 균일한 대기압 관측 자료를 반영하여 역기압 효과를 고려함으로써 후포 관측점의 경우는 동해항, 묵호, 속초 관측점보다 예측 정확도가 다소 낮게 예측되는 결과가 산출되었다. 특히 태풍 시와 같이 대기압이 공간적으로 급격하게 변화하는 경우는 폭풍해일 계산을 포함하여 광역 모형으로부터 계산된 예측 결과의 연결과 공간적으로 변화하는 대기압을 반영하는 예측이 필요할 것이다. 그렇지만, 본 연구에서 적용된 네스팅 기법을 적용하여 후포항, 동해항, 묵호항, 속초항 등과 같이 공간적인 대기압의 변화를 무시할 만하고 대표적인 평균해면을 적용할 수 있는 협소 해역을 모의하는 경우 본 연구에서 적용한 바와 같이 대표적인 대기압 자료를 반영하여 계산한 역기압 효과를 수치 모델에 포함하여 해수위 변화의 예측 정확성을 상당 부분 향상시킬 수 있으리라 예상된다.
앞서 언급된 바와 같이 해수면 변화에 영향을 주는 요소는 매우 다양하므로 앞서 고려한 조석과 대기압 두 요소가 해수면 변동 재현을 100% 반영하기는 어렵다. 그렇지만, 본 연구로부터 대기압에 의한 역기압 효과 고려가 동해 연안 수위 변동 예측에 있어 재현 결과의 정확성을 상당부분 향상시킴을 확인하였으므로 추후 바람(wind set-up), 파랑(wave set-up), 수온 및 염분 등의 비조석 성분과 동해 연안에서 상당히 크게 영향을 주는 장주기 조석 성분인 Sa, Ssa, Msf, Mm 분조 등의 추가적인 조석 외력조건을 고려하는 수치 예측 연구를 수행함으로써 동해 연안 해수면 변동 예측의 정확도 향상을 도모할 수 있을 것이다.
Acknowledgements
본 연구는 해양수산부의 재원으로 한국해양과학기술진흥원의 지원을 받아 수행된 연구입니다(연안침식 대응기술 개발-2013023).