2.1 실험적 진동특성 분석 방법

가속도 등의 구조물 응답자료만을 이용한 동특성 추정 방법에는 여러 방법이 있으며, 지난 2000년 연구에서는 주파수영역 분해법을 적용한 바 있다(Brinker et al., 2000; 한국해양연구원, 2001). 이번 연구에서는 좀 더 정밀한 분석을 위하여 시간영역 실험적 모드해석 방법 가운데 응답자료의 상관행렬을 요소로 가지는 블록 행켈 행렬을 이용하여 모드계수를 추정하는 추계론적 부공간 규명법을 적용하고자 하였으며(Peeters and de Roeck 1999), 이 방법은 아래의 식 (1)과같은 추계론적 이산상태방정식으로 식 (2)의 상호상관행렬(R(k))을 구하는 것으로 시작된다.

여기서, z(k)와 y(k)는 각각 상태변수(state variable)와 관측 변수(observed variable)이며, w(k)와 v(k)서로 상관관계가 없는 랜덤 정규분포를 갖는 하중 벡터와 관측 변수에 대한 노이즈벡터이다. 한편A, B, C는 시스템 행렬이며, G = E[z(m + 1)y(m)^T] 는 상태변수와 관측 변수 사이의 상관행렬이다. 식 (2)와 같은 상호상관행렬을 요소로 갖는 블록 행켈 행렬을 식(3)과 같이 구성하면, 이는 마지막 등호관계와 같이 가관측 성행렬(observability matrix)(_n1)과 확장 가제어 성 행렬(extended controllability matrix)(_n2)로 분해할 수 있음을 알 수 있고, 이는 행켈 행렬을 Q-R분해함으로써 실현(realization)할 수 있다.

여기서, 가관측성 행렬을 구하기 위하여 행켈 행렬을 특이치 분해하면 아래와 같이 구할 수 있고, 식 (4a)의 마지막 관계로부터 가관측성 행렬 _n1를 식 (4b)에서와 같이 구할 수 있다.

최종적으로, 가관측성행렬의 상부 첫 번째와 두 번째 블록으로부터 시스템 행렬 A와 C를 구할 수 있고(식 (3) 참조), 이로부터 이산상태방정식에 대한 고유주파수, 모드감쇠비, 모드형상 등의 모드계수는 다음과 같이 구할 수 있다.

최종적으로 우리가 구하고자 하는 연속상태방정식의 고유치(λ_k), 고유진동수(ω_k)와 모드감쇠비(ζ_k) 및 계측 자유도에서의 실제 모드벡터(φ_k)는 아래와 같이 구할 수 있다.

2.2 수치해석적 진동특성 분석 방법

케이슨 방파제 구조물의 진동특성을 분석하기 위하여 다음Fig. 1과 같은 유체-구조물-지반 상호작용을 고려한 동적해석을 수행하였다. 구조물과 근역지반의 경우 유한요소를, 원역지반의 경우 동적 무한요소를 적용하였다. 한편 유체의 경우, 전단강성이 없는 비점성 비압축성 유체요소와 유체 원역 경계에서의 점성 감쇠 등을 고려하여 모형화 하였다.

Fig. 1

Modeling of fluid-structure-soil interaction system.

우선 구조물과 근역지반의 동적강성행렬(S^SN(ω))은 2차원 평면변형 유한요소의 강성행렬(K^FE)과 질량행렬(M ^FE)을 이용 하여 다음과 같이 구할 수 있다.

여기서, i = 이고, h는 이력감쇠비이며, ω는 원주파수이다. 유한요소를 이용하여 구조물과 근역지반을 모형화 하는 과정은 통상적인 유한요소해석과 동일하며, 다만 지반이 포화된 경우 포아송비가 0.5에 가까워 수치적 불안정성이 커질 수 있는데, 이를 해결하기 위하여 선택적 감차적분, B-bar 방법 또는 혼합정식화를 이용한 유한요소를 사용할 수있으며, 이 연구에서는 체적 변형에 대한 잠김 현상(locking phenomenon)을 피하기 위하여 선택적 감차적분 방법을 사용하였고, 포화지반의 거동을 잘 모사할 수 있도록 하였다. 한편 원역지반의 동적강성행렬((^F(ω)))은 다음과 같이 동적무한요소의 강성행렬(^IE(ω))과 질량행렬(^IE(ω))을 이용하여 구성할 수 있다(양, 1992; 김, 1995; 김, 1999; 서, 2007).

여기서 동적무한요소의 강성행렬과 질량행렬은 다음과 같이 구할 수 있다(윤 등, 1997).

여기서, ω와 D는 각각 변형도-절점 변위 관계 행렬과 응력-변형도 관계 행렬로 유한요소법에서와 정의가 동일하고, ρ 는 밀도이며, ω은 무한요소의 형상함수 행렬로서 복소 파동함수를 포함하고 있다. 원역 공간의 수평층상지반과 저면의 반무한지반에 대하여 각각 수평무한요소(HIE, Horizontal Infinite Element)와 수직무한요소(VIE, Vertical Infinite Element)를 적용하여 모형화 하였고, 모서리측 지반의 경우는 모서리 무한요소(CIE, Corner Infinite Element)를 적용하여 모형화 하였다. 한편, 전단강성이 없는 비점성인 압축성 유체의 동적평형방정식은 다음과 같다(Kim and Yun, 1997).

여기서 u_f는 유체의 변위벡터이고, P_f는 유체의 질량밀도이며, K_f 는 유체의 체적계수를 나타낸다. 식 (11)을 경계조건 등을 적용하여 약형(weak form)으로 나타내면 다음과 같다.

여기서, w는 가중함수, 는 경계 상(_p)에서의 압력, n은 각각의 경계 상에서의 수직방향벡터이고, n_g는 중력방향을 나타내는 벡터이며, g는 중력가속도 값이다. 식 (12)에 유한요소법을 적용하여 행렬식으로 표현하면 다음과 같다.

이 때, M, K, S는 각각 유체의 질량행렬, 체적변형과 관련된 강성행렬, 슬로싱(sloshing)과 관계된 강성행렬이며, f 는 하중벡터이다. 유체를 사변형 4절점 변위형 유체요소로 고려하는 경우, 질량행렬과 강성행렬을 각각의 요소에서 평면변형 모드와 휨 모드의 중첩으로 아래와 같이 나타낼 수 있다.

이 때, 휨 모드는 체적변형에 관계되는 유체요소의 정확성을 감소시키므로, 강성행렬 구성 시 (1 × 1) 감차적분을 적용하고, 질량행렬 구성 시 질량투영법(mass projection)을 사용하여 이러한 문제를 해결하고, 회전변위에 관련된 영 에너지 모드는 비회전 운동조건을 벌칙 기법(penalty method)을 강제 적용하여 해결하였다. 결과적으로 사변형 4절점 변위형-유체요소의 강성행렬과 질량행렬은 다음과 같이 구한다.

위에서와 같이 구한 강성행렬 및 질량행렬 등을 이용하여 유체-구조물-지반 상호작용계의 충격하중에 의한 운동방정식은 다음과 같이 나타낼 수 있다.

여기서 아래첨자 f 는 유체영역, n은 유체와 구조물의 경계면, s는 경계면을 제외한 구조물과 근역지반, i는 근역지반-원역지반(또는 유한요소-무한요소) 경계면, e는 원역지반 만의 자유도를 나타내며, S(ω)와 (ω)는 각각 유한요소와 무한요소에 의한 동적강성행렬을 나타낸다. 그리고 f_n(ω)는 구조물에 가해지는 하중벡터이다. 아울러 지반 외에 유체영역 역시 상류방향으로 에너지의 적절한 방사가 이루어져야 하는데, 이를 위하여 본 연구에서는 원역의 유체영역 경계에 점성감쇠기(viscous damper)를 적용하였다. 이때 점성감쇠장치의 감쇠계수 C_p값은 p-파의 전파속도(V_p), 질량밀도( ρ), 경과통계면의 면적(A)을 고려하여 다음과 같이 계산할 수 있다(Lysmer and Kuhlemeyer, 1969).

3.1 적용 대상 구조물 재원 및 실험 개요

지난 2000년 오륙도 방파제 케이슨에 대한 정밀안전진단의 일환으로 진동기반의 구조물 건전성 평가를 실시한 바 있고(한국해양연구원, 2001), 당시 실험에서는 파도에 의한 응답을 이용하는 상시진동시험과 함께 예인선에 의한 충격진동 시험을 동시에 수행하였다. 또한 방파제를 구성하는 총 46기의 케이슨에 대하여 연속한 3기의 케이슨을 하나의 그룹으로 묶고, 3개 케이슨 중 가운데 케이슨에 200톤급 예인선을 이용하여 충격을 가하여, 이로부터 3기 케이슨에 대한 진동을 계측하고, 그 특성을 평가하였다. 케이슨의 번호 및 세트별 해당 케이슨은 Fig.2 및 Table 1과 같고, 케이슨 상부에 설치된 가속도계의 위치 및 계측 방향 등은 다음의 Fig.3(a)와 같다. 한편 오륙도 방파제는 지난 2005년 천단고를 4 m 높였으며 이와 같이 구조가 변경된 상태에서의 진동특성을 분석하기 위하여 지난 2011년 18번 케이슨에 대하여 소형 선박을 이용한 충격진동시험을 추가적으로 수행하였으며, 이때의 가속도계 배치는 다음 Fig.3(b)과 같다

Fig. 2

Location of target breakwater and impact vibration tests.

Table 1

Test cases and Caisson IDs

Fig. 3

Experimental setups.

3.2 천단고 변경 이전 케이슨에 대한 진동실험 결과 분석

2011년 실험에서의 대상 케이슨(18번 케이슨)과 가장 인접한 Case 3과 Case 4에 대하여 충격진동시험에 의한 가속도 응답을 다음의 Fig. 4와 같이 정리하였다. Fig. 4(d)는 추계론적 부공간 규명법에 의한 실험모드해석 과정에서 고유주파수와 모드감쇠비를 구할 때 사용한 안정화도(stabilization chart)를 보여준 것이다. Fig. 4(d)에서 볼 수 있듯이 오륙도 방파제 케이슨의 고유주파수는 1.5 Hz와 2.7 Hz 부근에서 찾을 수 있으며, 이번 연구 결과를 2001년 보고서에서 제시된 값과 함께 Table 2에서 제시하였다. 한편, 괄호 안의 값은 모드감쇠비를 나타낸다.

Fig. 4

Measured impact responses and stabilization chart.

Table 2

Identified and calculated natural frequencies for vibration tests in 2000 (Hz)

한편 동일한 크기의 케이슨 구조물인 Case 2-Case 13의 경우 Fig. 5에서와 같이 뒤채움(Fig. 9(b)의 Sand Fill 참조) 깊이가 깊을수록 고유주파수가 작게 나타나는 것을 알 수 있다. 이는 곧 뒤채움 깊이가 깊을수록 시스템 전체가 유연해 지는 것을 의미하며, 이는 뒤채움 지반의 강성이 기반암의 강성보다 작고 따라서 이러한 뒤채움 지반이 깊을수록 전체 시스템이 유연해 지기 때문이다. 한편 Fig. 6은 실험 케이스에 따른 모드감쇠비를 정리한 것으로 모드감쇠비의 경우 케이스에 따라 차이는 있지만 어떠한 경향성을 찾기는 어려운 것으로 판단된다. 다만 일부 케이스를 제외하면 2차 모드의 감쇠비가 1차 모드의 감쇠비보다 큰 것을 알 수 있다. 그리고 일반적인 구조물의 모드감쇠비인 3-5%보다 큰 4-15%의 감쇠비를 가지고 있는 것을 알 수 있는데, 이는 지반이 일반적인 콘크리트나 강재보다는 감쇠비가 크기 때문이며, 또한 케이슨 주변에 존재하는 유체가 가지고 있는 동수역학적 감쇠가 포함되었기 때문인 것으로 판단된다.

Fig. 5

Identified natural frequencies and depth of sand fill (○: FDD, ●: SSI).

Fig. 9

Section of breakwater and numerical modeling of breakwater after installation of parapet.

Fig. 6

Identified modal damping ratios and depth of sand fill (○:1st mode, ●: 2nd mode).

3.3 천단고 변경 이후 구조물에 대한 동특성 분석

한편 아래의 Fig. 7과 Fig. 8은 2011년 실시한 18번 케이슨에 대한 진동실험 결과이다. 이 실험에서는 유선 계측 시스템 대신 최근 상용화가 이루어지고 있는 무선 계측 시스템을 사용하였고, 총 7개의 가속도계를 이용하였다. 한편 사용된 가속도계의 계측범위 및 민감도는 각각 ±0.5g, 10 V/g이며, 샘플링은 100 Hz으로 설정하였다. 그 외의 모든 조건은 2000년도에 실시한 실험과 동일하며, 상시진동을 추가적으로 3분 동안 계측하였다. 상시진동 및 충격진동시험으로부터 구한 구조물의 고유주파수 및 모드감쇠비는 Table 3과 같다.

Fig. 7

Measured responses and stabilization chart for ambient vibration tests.

Fig. 8

Measured responses and stabilization chart for impact vibration tests.

Table 3

Identified natural frequencies after installation of parapet

고유주파수의 경우 상시진동시험 결과를 이용하였을 때, 1.471 Hz, 2.753 Hz로 고유주파수를 구할 수 있었고, 충격진동시험 결과를 이용하였을 때는 1.430 Hz, 2.695 Hz로 구할 수 있어, 충격시험의 경우 1차와 2차 모드의 고유주파수가 각각 2.8%와 2.1% 작게 평가되는 것을 알 수 있다. 이는 상시진동의 경우 매우 작은 외력이 작용하고, 응답 역시 매우 미소한 수준으로 발생하여 하중-변위 관계에서 상대적으로 좀더 큰 기울기를 갖는 초기 강성효과가 포함된 것이라 판단된다. 이와 유사한 연구결과는 Boroschek 등(2011)의 연구에서도 찾아 볼 수 있는데, 이들의 연구에서 강제진동시험으로 실시한 긴장 후 완화시험(pull-back test)의 결과가 1.63 Hz, 2.74 Hz로, 상시진동시험 결과인 1.68 Hz, 2.82 Hz에 비하여 각각 2.9%, 2.8% 작게 분석된 바 있다. 따라서 이와 같은 기존 연구사례와 함께 이 연구의 결과를 통하여 강제진동계측에 의한 고유주파수의 경향을 살펴보면 응답 수준이 매우 작은 상시진동시험에 비해서 2-3% 정도 작은 결과를 구할 수 있다는 것을 알 수 있다. 실제 태풍 등의 설계 외력이 작용하는 경우 상시진동시험보다는 강제진동시험에 가까운 하중 상태에 놓이게 되므로 상시진동시험 결과를 이용하여 구조물의 상태를 평가하는 것은 역으로 어느 정도의 과대평가 가능성이 있음을 의미하며, 가능하다면 강제진동시험을 수행하는것이 바람직할 것으로 판단된다.

한편, 이 결과를 2000년도 결과와 비교하면 다음과 같다(Table 4 참조). 우선 18번 케이슨에 대한 1차 모드와 2차 모드의 고유주파수는 2000년도 실험에서는 1.494 Hz와 2.743 Hz이었으며, 2011년도 진동시험에서는 1.430 Hz와 2.695 Hz로 분석되었다. 따라서 천단고 증고에 따른 구조 변화는 고유주파수에 대하여 1.7-4.3% 감소시키는 결과를 가져왔으며, 이는 천단고를 높이기 위하여 추가 설치한 시설물의 질량 효과가 반영된 결과라 할 수 있다.

Table 4

Change of identified natural frequency after installation of parapet

4.1 수치해석 개요

다음 Fig. 9(a)는 천단고를 높인 오륙도 방파제의 단면도이며, Fig. 9(b)는 이를 바탕으로 천단고 변경 후 구조물을 대상으로 한 수치해석 모델이다. 이 모델은 2000년도에 수행한 연구에서 사용된 기존 2차원 수치해석 모델에 외항 측의 추가적인 시설물에 대하여 4절점 평면변형 요소를 적용하여 추가한 것이다. 대상 케이슨인 18번 케이슨의 경우, 뒤채움 깊이가 14.5 m이며, 구조물과 뒤채움 등의 근역지반은 2차원 평면변형 유한요소로 모델링하고, 유체영역은 의사 영 에너지모드(pseudo zero energy mode)들이 제거된 사변형 4절점변위형-유체요소를 사용하여 모델링 하였다. 그리고 평행층상반무한 원역지반은 2차원 동탄성 무한요소를 이용하여 모델링 하였고, 유체영역에서 상류방향으로의 에너지 방사를 위하여 상류방향의 유체영역 경계에 점성 감쇠를 설치하여 유체거동을 모사하였다.

수치해석 모델에 사용된 물성치들은 Table 5에서 정리한 바와 같이, 상치 콘크리트, 케이슨, 콘크리트 블록 및 해수의 물성치는 일반적으로 적용되는 콘크리트 및 해수의 물성치를 사용하였고, 사석과 뒤채움, 반무한 지반의 물성치들은 2000년도에 실시한 강제진동시험 결과를 이용하여 추정한 물성치를 사용하였다. 이 물성치들은 2000년도에 실시한 수치해석 모델에 적용된 것과 동일한 값이다.

Table 5

Material properties of caisson and soil for numerical analysis

4.2 해석 결과

이 연구에서는 2차원 유체-구조물-지반 상호작용을 고려한 2차원 구조물에 대한 강제진동해석을 위해 원자력 발전소 격납구조물, 교량 구조물 등 다양한 구조물에 대하여 성능이 검증된 바 있는 KIESSI(A computer program for soil-structure interaction analysis using finite and infinite element techniques) 프로그램을 이용하였다(양 등, 1994; 김, 1999; 윤 등, 2000; 김 등, 2000; 서 등, 2008). 이 프로그램은 2차원, 축대칭 및 3차원 좌표계에서의 유체, 구조물, 지반, 설비 등의 상호작용을 고려한 해석 프로그램으로, 무한영역에 대해서 파동이론을 접목한 동탄성 무한요소가 장착되었고, 시간 및 주파수영역 해석이 가능하다. 이 프로그램을 이용하여 천단고를 높힌 방파제에 대한 강제진동해석을 수행하고, 이를 변경 전 구조물에 대한 해석결과와 비교하였으며, 아울러 충돌시험에 의 한 진동 특성 분석결과와도 비교하였다.

강제진동해석에서 입력하중은 전 주파수영역에 동일한 단위 하중(1(ω))을 갖는 이상적인 충격하중을 사용하였고, 이를 다음의 식 (18)과 같이 정적 응답(U(0))에 대한 동적 응답(U(ω))의 비를 나타낸 복소 주파수응답함수(Frequency Response Function: H(ω))를 구하였다.

그리고 수평방향 강제진동의 위치는 내항 쪽 상치콘크리트 상단(Fig. 9(b)의 A 지점)이며, 응답을 산정하는 관심지점은 외항 쪽 상치콘크리트의 상단(Fig. 9(b)의 B 지점)이다. 이 때 계산한 수직과 수평 방향의 주파수응답함수 및 가속도, 속도, 변위 응답을 아래 식으로 산정하였다.

Fig. 10과 Fig. 11은 각각 수치해석에 의한 외항 쪽 상치콘크리트 상단의 수직 가속도 성분의 응답신호와 이의 주파수응답함수를 제시한 그림이다. 천단고를 높이기 전의 1차와 2차 공진 대역은 각각 1.514 Hz와 2.441 Hz이었으며, 천단고를 높인 후의 공진대역은 각각 1.416 Hz와 2.344 Hz로 분석 되었다. 이들 값을 진동시험에 의하여 추정한 고유주파수와 비교하면 다음의 Table 6과 같다. 수치해석 결과와 진동시험결과를 비교하면 1차 모드의 경우 차이가 1% 내외로 매우 정확한 반면 2차 모드의 경우 10% 내외의 차이를 보이고 있어 향후 추가적인 모델 개선이 가능함을 알 수 있었다. 한편 천단고 변경 전후의 변화율을 살펴보면 진동시험의 경우 1.7-4.3% 감소하는 것으로 분석된데 비하여 수치해석에서는 4.0-6.5% 감소하는 것으로 분석되었다. 향후 이와 같은 차이에 대한 추가적인 분석이 필요하리라 사료된다.

Fig. 10

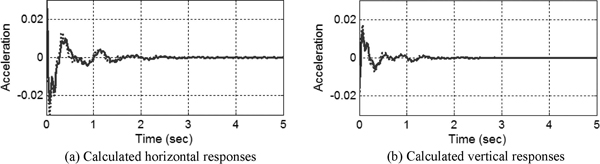
Impact responses at top of caisson by FSSI analysis (dotted line: before installation, solid line: after installation).

Fig. 11

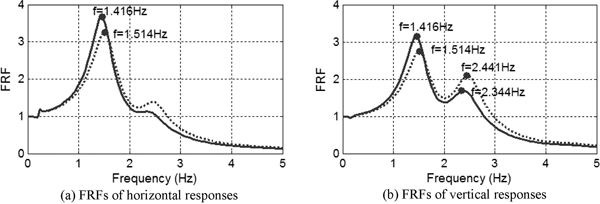
FRFs of responses at top of caisson by FSSI analysis (dotted line: before installation, solid line: after installation).

Table 6

Calculated and identified natural frequencies after installation of parapet