비중 차이에 따른 테트라포드 안정계수 변화에 관한 실험적 연구
Experimental Investigation on the Change of Stability Coefficient of Tetrapod According to Difference in Density
Article information
Abstract
이 연구에서는 수리실험을 통해 비중이 서로 다른 테트라포드의 Hudson식에 의한 안정계수(KD) 변화 특성을 고찰하였다. 수리실험은 사면 경사 1:1.5인 경사식 방파제에 대하여 반복실험 없이 1회 수행되었으며, 본 실험 조건에서는 고비중 테트라포드의 안정계수가 더 크게 나타났다. 이는 테트라포드 안정계수가 비중에 따라서 달라지게 됨을 보여주는 결과이다. 향후 보다 많은 실험을 통해서 테트라포드의 비중이 안정계수에 미치는 영향을 자세히 고찰할 필요가 있다.
Trans Abstract
In this study, a physical experiment was performed to investigate the change in the stability coefficient, defined by Hudson equation, for the tetrapod of different specific densities. The experiment was carried out once (with no repetition) for a rubble mound breakwater with 1:1.5 slope. In this experiment, the stability coefficient for the high-density tetrapod was greater than that for the normal-density tetrapod. This indicates variability of the stability coefficient according to change in the density of tetrapod. Further experiments and detailed analysis are required to investigate the effect of the density on the stability coefficient of tetrapod.
1. 서 론
제철 공정에서 발생하는 부산물인 슬래그(slag)는 철광석에서 철 성분을 분리해 내고 남는 맥석 성분을 주성분으로 하는 고로슬래그와 선철 중의 규소 등을 분리해낼 때 발생하는 제강슬래그로 구분된다 (Yang et al., 2004). 최근 철강 제품의 다품종화 및 조업 과정의 다변화에 따라 제철 공정에서 발생하는 부산물에 대한 처리 공정도 합리적으로 변화하고 있다 (Cho and Lee, 2013). 한편, 시멘트 콘크리트 제조 산업은 그 특성상 고온의 소성 과정이 필요하며 이로 인해 전세계 CO2 배출량의 약 8%를 차지하고 있기 때문에 이러한 환경 부하를 저감시키기 위해서 슬래그 등 산업 부산물의 활용성을 높이면 상대적으로 시멘트 사용량을 줄일 수 있어 CO2 발생 저감 효과를 얻을 수 있다. 이러한 이유로 일부 국가에서는 콘크리트 구조물에서 슬래그 콘크리트 사용량이 일반 포틀랜드 시멘트 콘크리트 사용량에 거의 육박하고 있으며, 국가적 차원에서도 관련 설계기준을 정비하여 슬래그 콘크리트 사용을 권장하고 있는 추세이다 (Jeon and Yoon, 2013).
건설 산업과 관련해서 고로슬래그는 시멘트 원료로서의 사용 비중이 크고, 제강 슬래그는 도로용 골재 및 토목용 골재로 주로 활용되고 있다. 그 중에서도 해양 토목 분야의 적용 사례로서 가장 대표적인 것은 제강슬래그를 이용하여 어초용 블록 또는 소파블록을 제작하는 것이며, 이러한 블록들은 일반 콘크리트 블록에 비해 해조류들이 잘 부착하여 성장하는 특성으로 인해 해중림 조성을 위한 구조물로서 활용 가치가 높다고 알려져 있다 (Yang et al., 2004). 슬래그를 이용하여 해양 구조물을 제작할 경우의 또 다른 이점으로는 장기 내구성을 향상시킬 수 있다는 점이다. 최근 연구에 의하면 콘크리트 배합 설계 시 슬래그 함유율을 70~80%까지 높일 경우 해양 콘크리트의 장기 내구성이 증대되는 효과가 극대화되며, 그 이유는 슬래그 함유율이 높은 콘크리트는 보통 포틀랜드 시멘트 콘크리트에 비해 동결융해 및 염화물 이온 침투 저항성능이 향상되기 때문이다 (Kim et al., 2014).
슬래그 사용 콘크리트의 또 다른 특징으로는 슬래그 자체의 비중이 크기 때문에 보통 포틀랜드 시멘트 콘크리트에 비해서 고비중 콘크리트를 제조할 수 있다는 점이다. 이러한 특징을 활용하여 최근 항만 시설의 방파 구조물에 주로 쓰이는 소파블록에 슬래그를 혼합한 고비중 콘크리트를 적용하는 사례가 증가하고 있다. 특히 기후변화 등 해양환경 변화로 인해 설계파가 증대되고, 항만 시설이 점차 수심이 깊은 곳에 설치되는 사례가 증가하면서 고중량 소파블록의 사용 필요성 또한 높아지는데, 고비중 콘크리트 소파블록을 사용할 경우 블록의 규모를 유지하면서 고중량 블록을 제조할 수 있기 때문에 최근 그 활용 범위가 점차 증가하고 있다. 포르투갈 Sines항 서방파제 제두부에는 단위중량 3.1 tf/m3인 90톤급 Antifer Cube가 사용되었으며, 일본에서는 1990년대부터 다수의 항만 건설공사에 다양한 범위의 고비중 소파블록(단위중량 2.45~3.0 tf/m3)이 활용된 바 있다 (Aqua Product Co., 2016). 국내의 경우 2009년부터 울산북방파제 축조공사, 여수 소두라항 및 남해군 장포항 방파제 보강공사 등에 고비중 소파블록이 적용되었는데, 이 때 사용된 블록의 단위중량은 모두 2.8 tf/m3에 해당하였다 (Mecca Ocean Research & Institute Co., 2016).
이처럼 최근 고비중 소파블록의 적용 사례가 증가하고 있지만 고비중 소파블록으로 피복된 방파제의 사면안정성에 관해서는 선행 연구가 많지 않은 편이다. Helgason and Burcharth (2005)는 단위중량이 2.65 - 3.30 tf/m3인 사석을 이용하여 1:1.5 및 1:2 사면 경사에 대한 수리실험을 수행한 바 있다. 이 결과에 따르면 1:2 사면에서는 소파블록의 공칭직경과 파고 비의 세제곱이 수중에서의 블록 상대 밀도의 세제곱의 역수에 비례하여
그런데 우리나라 방파제 건설공사에서 가장 많이 사용되는 테트라포드에 대해서는 고비중화에 따른 안정계수 변화 특성에 관한 연구가 이루어진 바가 없는 것으로 파악된다. 이러한 점을 고려하여 본 연구에서는 수리실험 자료를 분석하여 일반비중 및 고비중 테트라포드의 안정계수를 비교, 평가하는 연구를 수행하였다.
2. 사면 안정성에 영향을 미치는 요소들
소파블록으로 피복된 사면에 작용하는 여러 외력 성분은 Fig. 1과 같이 나타낼 수 있으며, 여기에서 FL은 양력, FD는 항력, FI는 관성력, FG는 중력을 각각 나타낸다. 이 중 앞의 세 힘은 블록의 움직임을 유발하는 힘이며, 중력에 의한 블록의 자중 및 블록 간의 마찰력과 맞물림(interlocking)은 블록 안정화에 기여하는 힘이다. 이 힘들은 모두 근본적으로 사면 경사의 함수이며, 블록 안정화에 기여하는 힘의 경우 사면 경사가 급해짐에 따라서 자중의 영향은 상대적으로 감소하고 마찰력과 맞물림이 더 중요한 요소가 된다 (Burcharth, 1993). 따라서 각 성분의 기여도는 정확하게 정의되지는 않지만, Fig. 2에 제시된 Price (1979)의 연구 결과를 통해서 어떠한 사면경사에서의 자중과 나머지 힘(마찰력과 맞물림)의 상대적인 크기를 대략 파악할 수 있다.
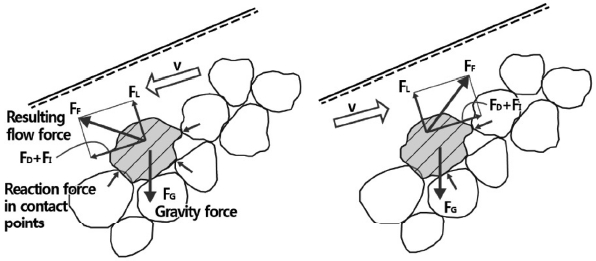
Schematization of forces on armour units under wave attack (after Burcharth 1993).
Influence of slope angle on the stabilizing effects of gravitational force, interlocking and surface friction (after Price 1979).
Fig. 2로부터 맞물림이 좋은 피복재의 경우 사면경사가 대략 55º정도까지는 경사가 급해질수록 맞물림과 표면 마찰력이 빠르게 증가하므로 사면 안정성이 좋아짐을 알 수 있다. 반면에 맞물림이 거의 없는 피복재는 경사가 대략 30º를 넘기 시작하면 사면 안정성은 오히려 감소한다. 이러한 이유로 사석 또는 이와 유사한 형태의 피복재는 일반적으로 1:2(26.6º) 경사로 설치되며, 맞물림이 강화된 인공블록은 이보다 더 경사가 급한 1:1.5 (33.7º) 또는 1:1.33 (36.9º) 경사로 설치되고 있다 (Burcharth, 1993). 즉, 블록의 종류(형상) 및 경사각에 따라서 사면 안정성이 달라질 수 있다.
한편, 주어진 파고에 대하여 사면에서 안정한 피복재의 중량을 예측하기 위해서는 일반적으로 식(1)의 형태로 표현되는 Hudson식을 사용한다.
위 식에서 W는 피복재의 소요 중량, V는 피복재의 부피, γr은 피복재의 단위 중량, Sr은 피복재의 해수에 대한 비중, H는 설계파고, KD는 피복재의 안정계수, α는 사면이 수평면과 이루는 각도를 각각 나타낸다. 식(1)에서 피복재의 비중에 관련된 항은 (Sr – 1)로 나타난다. 안정계수(KD)란 주어진 파고에서 피복층의 피해가 발생하기 시작하는 피복재의 최소 중량에 상응하는 Hudson식의 계수를 의미하며, 피복재의 안정계수 값이 클수록 주어진 파에 대하여 피복재의 소요 중량은 작게 된다.
Fig. 1에 보인 여러 외력 성분들 중에서 항력, 양력, 중력은 Hudson식에서 고려되었다. 반면에 유체의 관성력, 블록 간의 마찰력 및 맞물림은 고려되지 않았지만 이 요소들도 블록의 사면 안정성에 영향을 미치게 된다. 만일 피복재의 비중이 변화하면 피복재의 상대비중(Sr – 1) 및 그에 따른 영향을 받게 되는 블록 간 마찰력과 맞물림의 사면 안정성에의 기여도가 달라지게 된다. 그런데 Hudson식에서는 마찰력 및 맞물림에 대한 효과를 수식으로서 포함시키지 않았기 때문에 비중 변화의 영향은 결국 KD값의 변화로 나타나게 된다.
3. 수리모형실험
3.1 실험시설 및 모형
수리모형실험은 길이 53 m, 폭 1 m인 2차원 조파수조에서 수행되었다. 수조 종방향으로 연직 분할판을 설치하여 수조를 폭 0.6 m의 광수로와 폭 0.4 m의 협수로로 분할하여 광수로에는 방파제 모형을 설치하였고, 협수로에서는 통과 입사파를 계측하였다. 실험 여건을 종합적으로 고려하여 현장에 설치되는 일반 테트라포드 (단위중량 2.3 tf/m3 기준)의 규모를 공칭중량 5톤급 (실중량 4.6톤)으로 선정하였고, 모형은 원형의 길이를 1/40로 축소 제작하였다. 한편, 고비중 테트라포드는 단위중량 2.8 tf/m3을 가정하여 제작하였으며, 모형의 부피는 동일하므로 일반 테트라포드의 단위중량이 2.3 tf/m3임을 고려할 때 현장에 설치되는 중량 규모는 실중량 5.6톤에 상응하는 것이다. 본 수리모형실험에서는 중력과 관성력이 가장 지배적인 힘으로 작용하게 되므로 모형 축척에서의 물리량 크기는 Froude 상사법칙을 이용하여 변환되었다.
일반 및 고비중 테트라포드의 비중은 수리실험이 담수(fresh water)로 수행되는 점을 고려하여 현장에 설치될 경우의 비중인 2.3 및 2.8에 비해서 약 3% 정도 작게 제작함으로써, 실험 환경에서의 안정성이 현장에서도 재현되도록 하였다. 일반 및 고비중 테트라포드 모형의 수중포화 상태에서의 중량 평균값은 각각 69.7 g과 84.9 g이었으며, 이에 따른 모형의 비중은 각각 2.22 및 2.70에 해당한다. 본 실험에서는 고비중 및 일반비중 모형 단면의 크기 및 부피를 동일하게 하였는데, 이는 블록에 작용하는 유체력(항력, 양력 및 관성력)을 변화시키지 않도록 함으로써 오직 비중 변화에 따른 블록의 거동 변화를 평가하기 위해서였다.
3.2 모형 설치
실험 수조 내에 설치된 콘크리트 불투과면 위에 기초사석과 중간피복석을 쌓고 모형 테트라포드를 거치하여 방파제 형상을 재현하였다. 방파제의 마루높이는 실험파 작용시 월파가 발생하지 않는 조건으로 설정하였으며, 제체의 폭이 넓어서 투과성이 작기 때문에 제체 후면으로의 전달파고가 매우 작았으므로 본 실험 조건은 방파제는 물론 호안의 경우에도 상응하는 조건이라고 볼 수 있다. 방파제 전사면 경사는 수평1.5, 연직1의 비율인 1:1.5로 설정하였다. 기초사석은 현장 규모로 0.015~0.03 m3/EA 크기의 사석을 선택하였으며, 중간 피복석은 현장 규모로 0.2 m3/EA 크기의 사석을 사용하여 기초사석 위에 2층으로 피복하였다. 테트라포드는 2층으로 피복하였으며, 한 열에 하층 14개, 상층 13개를 설치하였다. 한편, 테트라포드 하층 제1열의 미끌림을 방지하기 위한 구조로 제체를 축조하였다.
3.3 실험 방법
3.3.1 비쇄파 조건 실험
비쇄파 조건이란 파가 피복재로 피복된 사면에 도달하기 전에는 수심 제한으로 인해 쇄파되지 않는 조건이다 (U.S. Army Corps of Engineers, 2011). Fig. 3에는 비쇄파 조건에 대하여 일반 테트라포드를 사용하여 축조된 방파제 전경을 제시하였으며, 이 경우 모형 앞쪽 바닥면의 경사는 1/34.3이었다.
A photograph of the breakwater model for non-breaking wave condition.
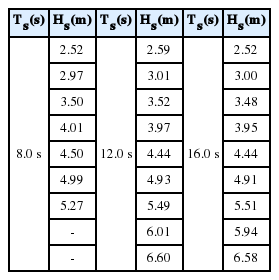
실험파는 수심이 깊은 구간에서 Bretschneider-Mitsuyasu 스펙트럼을 따르는 불규칙파를 사용하여 조파하였으며, 모형 설치 위치 협수로에 설치한 파고계 3개를 이용하여 입사파를 평가하였다. 실험 수심은 방파제 전면에서 42.5 cm로 하였으며, 본 실험의 축척을 1/40로 하였으므로 현장에서의 수심은 17 m에 해당된다. 실험파의 유의주기(Ts)는 우리나라 해역에서 재현빈도 50년 빈도의 설계파 주기가 대부분 8~16 s 범위인 점을 고려하여 현장 조건으로 8, 12, 16 s의 3 가지로 변화시켰다. 유의파고(Hs)는 약 2.5 m로부터 설정된 수심에서 재현이 가능한 최대파고까지 약 0.5 m 간격으로 변화하도록 하였다. 위 조건들로부터 상대파고 (relative wave height: Hs ⁄ d) 및 상대수심 (relative water depth: d ⁄ L)의 값을 계산하면 0.15<Hs ⁄ d<0.39 및 0.09<d ⁄ L<0.20의 범위에 해당하며, 육안으로 관측하였을 때 실험파가 방파제 전사면의 끝(toe)에 도달할 때까지 거의 쇄파가 발생하지 않았다. 한편, 실험파의 조파 시간은 29분 30초였으며, 이를 현장 크기로 환산하면 항만 및 어항 설계기준 (2005)에서 태풍 시 항만구조물의 피복재 피해량 추정 기간으로 언급된 3시간에 상응한다. Table 1에는 현장 규모로 환산한 실험파 조건을 제시하였다.
Test waves for non-breaking condition.
3.3.2 쇄파 조건 실험
쇄파 조건이란 수심의 제한으로 인해 파가 피복재로 피복된 사면에 도달하기 전에 부서지는 조건으로 (U.S. Army Corps of Engineers, 2011), 이 경우 사면에 쇄파압이 크게 작용하게 된다. 쇄파 실험을 수행하기 위해서는 어떠한 수심 및 파고, 주기 조건에 대해 경사제 사면에 가장 격렬한 쇄파가 발생하는 상태에서 소파블록의 안정성을 평가하는 방법이 이상적이다 (Carver and Davidson, 1982). 그러나 이러한 실험을 수행하기 위해서는 파고 및 주기를 미세 조정하면서 많은 반복실험을 거쳐야 하므로 실험에 매우 많은 시간이 소요된다. 본 연구에서는 이러한 어려움을 감소시키기 위하여 파고가 작은 파의 경우에는 쇄파가 발생하지 않지만 어느 정도 파고가 커짐에 따라서 쇄파가 발생하는 수심을 찾은 후 실험을 수행하였다. 쇄파 조건 실험의 경우에도 방파제 제체 폭은 정수면 높이에서 비쇄파 조건 실험과 거의 동일하게 하였다. Fig. 4에는 일반 테트라포드를 사용하여 축조된 방파제 전경을 제시하였다. 이 경우에는 모형 앞쪽 해저면 경사는 비쇄파 조건보다 급한 1/26.2로 설정하였다.
A photograph of the breakwater model for breaking wave condition.
실험파는 현장 조건을 기준으로 유의파주기(Ts)는 12, 16 s의 두 가지로 변화시켰으며, 파고는 약 2.5 m부터 조파가 가능한 최대파고까지 약 0.5 m 간격으로 변화하도록 결정하였으나 비쇄파 조건 실험에 비해서 파고 간격을 균일하게 설정하는 것이 훨씬 어려웠다. 또한 이 경우에는 쇄파가 발생하기 때문에 모형 설치 위치에서의 파랑은 Bretschneider-Mitsuyasu 스펙트럼 형상을 따르지 않는다. 한편, 위 조건들로부터 상대파고 (relative wave height: Hs ⁄ d) 및 상대수심(relative water depth: d ⁄ L)의 값을 계산하면 0.39<Hs ⁄ d<0.65 및 0.05<d ⁄ L<0.08의 범위이며, 육안으로 관찰하였을 때 대부분의 실험파가 방파제 전사면의 끝(toe) 근처에서 부서지는 현상이 발생하였다.
쇄파 실험에서의 실험 수심은 일반 테트라포드로 피복된 사면에 대해서는 17.5 cm, 고비중 테트라포드로 피복된 경우에는 22.5 cm로 하였으며, 본 실험의 축척이 1/40인 점을 고려하면 현장의 수심은 각각 7 m와 9 m에 해당된다. 이 경우 일반비중 및 고비중 테트라포드 실험에서의 주기 및 파고 조건은 비슷하더라도 수심이 다르기 때문에 파장도 다르므로 파형경사(H⁄ L)의 차이가 발생할 수 있다. 그러나 고비중 테트라포드 실험에서는 더 큰 파고 조건까지 실험이 이루어졌기 때문에 실험파의 파형경사 범위는 일반 테트라포드의 경우 0.023~0.046, 고비중 테트라포드의 경우 0.024~0.054로 큰 차이가 없었다. 따라서 고비중과 일반 비중 실험 시의 파형 경사 차이가 실험 결과에 미치는 영향은 거의 없을 것으로 판단된다. Table 2에는 일반 테트라포드 및 고비중 테트라포드에 대하여 각각의 실험 수심에서의 실험파 조건을 현장 규모로 제시하였다. Table 2에서 *를 붙인 것은 쇄파가 발생하지 않는 비쇄파 조건에서 실험이 수행된 것을 나타낸다. 실험파 작용 시간은 비쇄파 조건 실험과 동일하게 29분 30초로 하였다.
Test waves for breaking condition.
4. 사면 안정성 평가 방법
4.1 피해 모드
실해역에서 경사식 방파제 피복재의 최종 피해는 일반적으로 피복재가 제자리를 이탈하거나 파괴되는 현상으로 나타나지만 축소 수리모형실험에서는 피복재가 파괴되지는 않으므로 사면의 안정성을 검토할 때에 일반적으로 피복재 자체의 파괴는 고려하지 않고 단지 피복재가 제자리에서 이탈한 양으로 피해량을 평가한다. 따라서 실험실에서 경사식 방파제 사면의 피해라고 하면 제체의 사면에 설치된 피복재가 파력을 받아 최종적으로 제자리를 이탈하는 정도만을 의미하는 것으로 이해하기가 쉽다. 그러나 현장에서는 사면에 설치된 피복재가 제자리를 이탈하지 않더라도 제자리에서 움직임(Rocking)이 심한 경우 피복재가 부러지는 등 피해가 발생하므로 실험에서도 Rocking이 심하게 발생하는 경우에는 피복재의 파괴로 간주하여 피해량에 포함시키는 것이 바람직하다.
본 수리실험과 같이 단면 형상이 구체적으로 결정되지 않은 상태에서 피복층의 피해량을 평가하거나 피복재의 안정계수를 추정하는 데에는 매우 오랜 시간과 많은 실험이 소요되며 범용적으로 사용할 수 있는 결과를 얻는 데 어려움이 따른다. 본 연구에서는 Ministry of Maritime Affairs and Fisheries (2001)에 제시된 안정성 평가 항목에 근거하여 일반 및 고비중 테트라포드로 축조된 방파제의 사면 안정성을 검토하였다. Ministry of Maritime Affairs and Fisheries (2001)에서는 피복재의 피해 모드를 다음 세 가지로 제시하고 있다. 첫 번째는 개별 피복재가 과도한 제자리 움직임(Rocking)을 하는 경우이다. 두 번째 피해 모드는 피복재가 제자리에서 이탈된 후에 다시 복원되는 경우로서, 큰 파가 사면에 내습하게 될 경우 피복재가 위로 솟구친 후 다시 제자리로 떨어지거나 또는 일단 자리를 이탈해서 사면 위에 머물다가 다음에 내습하는 큰 파에 의해 원래의 자리로 되돌아가는 현상이 발생하기도 한다. 세 번째 피해 모드는 피복재가 제자리에서 최종적으로 이탈되는 것이다. 일반적으로 피복재가 원래의 위치에서 피복재의 특성길이(characteristic length)의 1/2배 이상 이동한 경우 이탈로 간주한다. 통상적으로 소파블록의 특성길이는 공칭직경(nominal diameter)과 같은 의미를 가지며, 중량을 단위중량으로 나눈 값의 세제곱근으로 계산된다. 본 수리실험에서는 이 세 가지 피해모드에 의한 피해를 모두 고려하여 사면안정성을 평가하였다.
4.2 안정계수 평가 방법
사석방파제 및 호안의 사면에 피복된 테트라포드의 안정계수를 평가하기 위하여 실험파를 파고가 작은 파로부터 파고가 큰 파의 순서로 제체에 작용시켰다. 사면에서 테트라포드의 이탈 피해가 발생하기 시작하면 그 때의 실험파의 파고보다 파고가 더 큰 실험파 2~3개를 더 작용시킨 후 실험을 종료하였다. 피복재의 제자리 회전 및 움직임(Rocking) 현상에 따른 피해를 평가하는 데 일반적으로 통용되는 정량적인 기준이 없기 때문에, 본 수리실험에서는 테트라포드가 제자리에서 순간적으로 180 o이상 회전하는 현상이 반복적으로 발생하는 경우에는 파괴로 인한 피해로 간주하였다.
피해가 발생하기 시작한 실험파보다 파고가 한 단계 더 큰 실험파를 작용하였을 때 누적 피해량이 크게 증가하는 경우에는 실제로 피해가 발생하기 시작하는 파고는 실험에서 피해가 최초로 관측된 실험파보다 낮을 수 있다. 이러한 점을 고려하여 이러한 경우에는 안정계수 산정을 위한 피해 시작파고는 피해가 발생하기 시작한 실험파와 그보다 파고가 한 단계 작은 실험파의 파고의 중간값으로 추정하였다. 반면에, 피해가 발생하기 시작한 실험파보다 파고가 한 단계 더 큰 실험파를 작용하여도 피해량이 크게 증가하지 않은 경우에는 최초에 피해가 발생한 실험파부터 실제로 피해가 발생한다고 판단하였다. 만약 준비된 실험파를 순차적으로 모두 작용하여도 피해가 발생하지 않는 경우에는 피해 시작파고 및 안정계수를 판정할 수 없었다.
5. 안정계수 평가
5.1 비쇄파 조건
Table 3~5에는 Ts= 8.0 s, 12.0 s 및 16.0 s의 실험파를 작용하였을 경우에 일반 및 고비중 테트라포드의 파고별 누적 피해량 및 피해 시작파고 판정결과를 각각 제시하였다. 4.2절에서 언급한 것처럼 테트라포드의 피해가 최초 발생하기 시작하는 파고를 포함하여 그 보다 높은 파고 조건 2개 이상에서의 피해 발생 결과를 종합적으로 고려하여 피해 시작파고를 판정하였다. 예를 들어 Table 5의 경우 파고 5.51 m와 5.94 m에서의 테트라포드 피해 수량은 각각 5개 및 6개인데, 파고 5.51 m에서의 피해 수량은 다른 실험에 비하여 상대적으로 많은 편이지만 한 단계 높은 파고(5.94 m)에서의 피해 수량이 급격히 증가하지 않았다. 또한 이 2개 파 조건에서 피해량으로 판정된 블록 중에는 상대적으로 경미한 흔들림을 보인 것이 3~4개 포함되어 있다. 이러한 점들을 고려하여 Ts= 16.0 s에서의 피해 시작파고를 5.51 m 로 평가하였다.
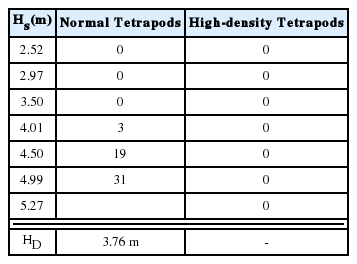
Cumulative number of damaged blocks and decision of design wave height under non-breaking wave condition (Ts = 8.0 s)
Cumulative number of damaged blocks and decision of design wave height under non-breaking wave condition (Ts = 12.0 s)
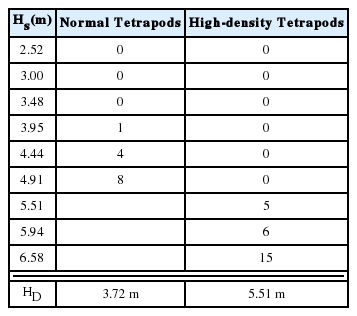
Cumulative number of damaged blocks and decision of design wave height under non-breaking wave condition (Ts = 16.0 s)
한편, Table 3~5에 보인 것처럼 피해 시작파고는 주기별로 다소 차이를 나타낼 수 있으므로 그 중에서 최소값을 선정하여 최종적인 피해 시작파고로 평가하였다. 따라서 피해 시작파고는 비중 2.3인 일반 테트라포드의 경우 3.72 m (실험실 조건에서 9.30 cm), 비중 2.8인 고비중 테트라포드의 경우 5.49 m (실험실 조건에서 13.73 cm)로 평가되었다. 일반 및 고비중 테트라포드에 대하여 안정계수를 계산하면 각각 KD= 9.4 및 KD= 11.2의 결과가 얻어진다. 이 결과로부터 비쇄파 조건에서 비중 2.8의 고비중 테트라포드는 비중 2.3의 일반 테트라포드에 비하여 안정계수가 약 19% 증가되는 것으로 나타났다.
5.2 쇄파 조건
Table 6~7에는 Ts= 12.0 s 및 16.0 s의 실험파를 작용하였을 경우에 일반 및 고비중 테트라포드의 파고별 누적 피해량 및 피해 시작파고 판정결과를 제시하였다. Table 6~7에 보인 것처럼 피해 시작파고는 주기별로 다소 차이를 나타낼 수 있으므로 최소값을 선정하여 최종적인 피해 시작파고로 평가하였다. 피해 시작파고는 일반 테트라포드의 경우 3.46 m (실험실 조건에서 8.65 cm), 고비중 테트라포드의 경우 5.12 m (실험실 조건에서 12.80 cm)로 산정되었다. 이 결과값들을 Hudson식에 대입하면 일반 테트라포드는 KD= 7.6, 고비중 테트라포드는 KD= 9.0의 결과가 얻어진다. 즉 쇄파 실험 조건에서는 고비중 테트라포드의 KD값이 일반 테트라포드에 비하여 약 18% 크게 나타났으며, 이는 비쇄파 조건에서의 결과(KD값 19% 증가)와 유사한 결과이다.
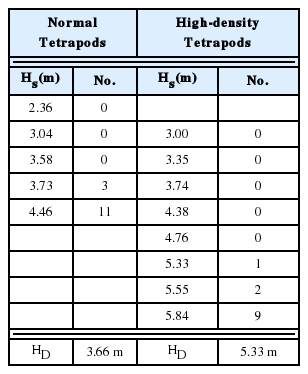
Cumulative number of damaged blocks and decision of design wave height under breaking wave condition (Ts =12.0s).
Cumulative number of damaged blocks and decision of design wave height under breaking wave condition (Ts = 16.0 s).
5.3 토의
본 연구의 수리실험에서 사면경사 1:1.5인 경우 비쇄파 조건에서의 안정계수 값은 일반 테트라포드에 대하여 KD= 9.4, 고비중 테트라포드에 대하여 KD= 11.2로 평가되었으며, 쇄파조건에서의 안정계수 값은 일반 테트라포드에 대하여 KD = 7.6, 고비중 테트라포드에 대하여 KD= 9.0으로 평가되었다. 즉, 비쇄파 조건과 쇄파 조건에서 모두 비중 2.8인 고비중 테트라포드가 비중 2.3인 일반 테트라포드에 비하여 비중이 약 22% 증가됨에 따라 안정계수 값은 약 18~19% 증가되는 것으로 나타났다. 그러나, 안정계수 산정값은 파형경사, 상대수심, Reynolds수, 항력계수 등(Hudson, 1959) 이외에도 해저면 경사, 중간 피복재의 특성, 파랑 스펙트럼의 형태, 파고 간격, 파고 판정의 정밀도, 파의 지속시간, 블록과 필터층의 쌓기 방법에도 영향을 받는다. 특히 피해율을 어떻게 정의하느냐에 따라서도 큰 편차를 보일 수 있다 (van der Meer, 1988).
Table 5에 보인 것처럼 Ts= 16 s인 경우 고비중 테트라포드의 실험에서 피해가 최초로 관측된 파고와 이보다 한 단계 낮은 파고간의 간격은 0.64 m로 다른 경우들에 비해서 컸다. 그런데 만약 이 구간에서 파고 간격이 더 작았다면 피해 시작파고가 현재보다 더 작게 나타났을 가능성이 있다. 그 경우 값 계산에 사용된 피해 시작파고는 Table 4에 제시된 5.49 m보다 작은 파고로 결정되어 고비중 테트라포드의 KD값이 11.2보다 작게 평가되었을 가능성이 있다. 즉, 고비중 테트라포드의 경우 일반 테트라포드에 비해서 피해 시작파고가 더 크기 때문에 파고의 세제곱에 비례하는 Hudson 공식의 특성상 파고 간격이 KD값 산정에 미치는 영향도 더 커지게 된다. 따라서 보다 엄밀하게 KD값을 평가하기 위해서는 파고 간격을 더 세밀하게 선정한 실험을 수행해야 할 필요가 있다. 그러므로 블록의 비중 증가가 KD값에 미치는 영향을 정밀하게 고찰하기 위해서는 가능한 파고 간격을 좁게 설정하여 실험을 수행하는 것이 바람직하다. 또한 축척이 다른 모형을 각각 제작하여 블록의 중량(크기) 및 파랑 조건이 다른 조건에서 실험을 반복 수행할 필요가 있다.
한편, 비중 2.3인 일반 테트라포드의 안정계수 값으로 우리나라 항만 및 어항 설계기준해설 (Ministry of Oceans and Fisheries, 2014)에는 비쇄파 조건에서는 KD= 8.0, 쇄파 조건에서는 KD= 7.0이 제시되어 있는데, 미국 설계기준 (U.S. Army Corps of Engineers, 2002)에는 비쇄파 조건에서 KD= 8.3, 쇄파 조건에서는 KD= 7.2로 제시되어 있다. 한편, 한국항만협회에서 발행한 책자인 “Tetrapod 설계·시공”에는 일본 테트라포드 주식회사의 실험 결과가 수록되어 있는데, 사면경사 1:1.33의 비쇄파 조건에서는 KD= 10.2, 쇄파 조건에서는 KD= 8.3으로 제시되었다. 이처럼 문헌에 따라서도 안정계수의 값이 다르게 제시되어 있는데, 이는 실험단면의 사면경사, 실험파의 종류(규칙파 또는 불규칙파) 및 모형의 거치방법 등에 따라서 실험결과가 영향을 받을 수 있기 때문이다. 또한 안정계수 값은 방파제의 사면안정성과 직결되는 중요한 파라메터이므로 다소 보수적으로 평가하는 경향이 있기 때문에 본 연구에서의 실험을 통해 비중 2.3인 일반 테트라포드에 대하여 산정된 값이 항만 및 어항 설계기준·해설(Ministry of Oceans and Fisheries, 2014)에 제시된 값보다 다소 큰 것은 납득할 수 있는 결과라고 사료된다.
위에서 언급한 여러 측면의 내용을 고려할 때 본 연구에서 산정된 안정계수 값들은 그 절대적인 값 자체보다는 일반비중 및 고비중 테트라포드의 안정계수 값이 다르게 나타날 수 있으며, 특정 사면경사(본 연구에서는 1:1.5)에서는 고비중 테트라포드의 안정계수가 더 크게 나타날 수 있다는 점에 의미를 부여하는 것이 바람직하다. 따라서 제한적인 조건에서 반복 실험 없이 수행된 본 연구 결과를 근거로 실무에서 고비중 테트라포드의 안정계수를 바로 설계에 적용하는 것은 현재로서는 바람직하지 않으며, 향후 이와 관련된 충분한 후속 연구를 통해 비중이 테트라포드의 안정계수에 미치는 영향을 다각도로 검토 및 확인한 후에 적용 방향을 검토해야 할 것 이다.
6. 결 론
사면경사 1:1.5인 단면에서 테트라포드의 비중 차이에 따른 사면안정성의 차이를 검토할 목적으로 비중 2.3인 일반 테트라포드 및 비중 2.8인 고비중 테트라포드에 대하여 각각 비쇄파 및 쇄파 시의 단면 수리실험을 수행하고 Hudson식에 의한 안정계수를 평가하였다. 그 결과 비쇄파 및 쇄파 조건에서 모두 비중 2.8인 고비중 테트라포드가 비중 2.3인 일반 테트라포드에 비해 안정계수 값이 크게 나타나는 경향을 발견하였다. 본 실험에서는 약 18~19% 증가되는 것으로 평가됨으로써 안정계수 증가율이 비중의 증가율과 유사하게 나타났지만, 소파블록의 안정계수 평가값은 실험 여건에 따라 편차가 발생할 수 있기 때문에 향후 보다 다양한 실험조건에서 여러 차례 반복 실험을 통해 본 연구에서 제시된 결과를 검증할 필요가 있다. 특히, 보다 엄밀한 안정계수 값 산정을 위해서는 파고 간격을 좁게 설정하여 실험을 수행하는 것이 바람직하다. 또한, 본 실험은 사면 경사 1:1.5인 사석 방파제에 대하여 수행되었으므로 사면 경사가 이와 다른 경사 조건에서의 고비중 테트라포드 안정계수는 해당 경사에서의 추가적인 실험을 통해서 산정해야 할 것이다.
Acknowledgements
본 연구의 수리실험은 POSCO (재)포항산업과학연구원의 연구비 지원을 받아 2009년에 수행되었으며, 추가 분석 및 논문 작성에 한국해양과학기술원 주요사업(PE99424)의 지원을 받았습니다. 특별히 본 논문 내용을 자세히 읽고 여러 귀중한 조언을 해주신 3분의 심사위원께 깊이 감사드립니다.