우리나라 연안의 기온과 수온 분포함수 추정 및 비교평가

Estimation and Comparative Analysis on the Distribution Functions of Air and Water Temperatures in Korean Coastal Seas

Article information

J Korean Soc Coast Ocean Eng. 2016;28(3):171-176

Publication date (electronic) : 2016 June 30

doi : https://doi.org/10.9765/KSCOE.2016.28.3.171

조홍연^*, 정신택^,^**

^*Department of the Coastal Engineering, Korean Institute of Ocean Science and Technology

^**Department of the Civil and Environmental Engineering, Wonkwang University, Iksandae-ro 460, Iksan, Jeonbuk, 54538, Korea

Corresponding author: Shin-Taek Jeong, Department of the Civil and Environmental Engineering, Wonkwang University, Iksandae-ro 460, Iksan, Jeonbuk, 54538, Korea, Tel:+82-63-850-6714, Fax:+82-63-857-7204, stjeong@wku.ac.kr

Received 2016 June 2; Accepted 2016 June 27.

Abstract

기온과 수온의 분포형태는 발생빈도의 양상을 결정하는 기본적이고 필수적인 정보이다. 또한 기후변화에 의한 기온과 수온의 장기변화 양상 파악에 유용하다. 기온과 수온의 전형적인 분포형태는 다수의 첨두(mode)를 가지는 형태로 일반적으로 널리 사용되는 정규분포로 표현하기에는 한계가 있다. 본 연구에서는 Gaussian 혼합함수와 Kernel 분포함수를 보다 기온과 수온의 보다 적합한 분포함수 형태로 제안한다. 제안된 분포함수를 우리나라 연안 기온과 수온자료를 이용하여 추정-평가한 결과, 관측 자료의 분포는 꼬리 영역에서 크게 차이를 보이고 있는 것으로 파악 되었다. 높은 수온영역과 낮은 기온 영역에서 꼬리 영역이 길게 나타나고 있다. 또한 본 연구에서 제안한 분포함수 추정 및 비교는 기온과 수온의 상호 변동관계 및 장기적인 변동양상을 파악할 수 있다. 그러나 평균 기온 및 수온 그리고 정규분포 함수 형태로는 이러한 변화 양상의 파악은 크게 제한되고 있다.

Trans Abstract

The distribution shapes of air and water temperatures are basic and essential information, which determine the frequency patterns of their occurrence. It is also very useful to understand the changes in long-term air and water temperatures with respect to climate change. The typical distribution shapes of air and water temperatures cannot be well fitted using widely used/accepted normal distributions because their shapes show multimodal distributions. In this study, Gaussian mixture distributions and kernel distributions are suggested as the more suitable models to fit their distribution shapes. Based on the results, the tail shape exhibits different patterns. The tail is long in higher temperature regions of water temperature distribution and in lower temperature regions of air temperature distribution. These types of shape comparisons can be useful to identify the patterns of long-term air and water temperature changes and the relationship between air and water temperatures. It is nearly impossible to identify change patterns using only mean-temperatures and normal distributions.

Keywords: 분포 형태; 기온과 수온; 다중첨두 분포; Kernel 분포; Gaussian 혼합분포

Keywords: distribution shapes; air and water temperatures; multimodal distribution; kernel distribution; Gaussian mixture distributions

1. Introduction

Water temperature is regarded as the most important environmental and ecological (E&E) factor in coastal seas. This factor is highly expected to change in the long term owing to climate change. In-depth analysis of water temperature change patterns is essential to understand E&E change patterns. However, such analysis usually depends on air temperature change patterns because air temperature data are more abundant than water temperature data.

Although air and water temperatures are of relatively high importance compared to other E&E parameters, the distribution shape and change patterns show considerable differences owing to the typical hysteresis and density difference (Cho & Lee, 2012). In this study, it is suggested that E&E change estimation based only on air temperatures has basic limitations by making a comparison and analysis of the change pattern and distribution shape between air and water temperatures. In general, the overall occurrence distribution shape of air and water temperatures does not show a normal distribution but rather a multimodal or skewed distribution (Toth and Szentimery, 1990; Grace and Curran, 1993; Harmel et al., 2002; Jeong et al., 2013; Jeong et al., 2014). This is why the distribution shape and change pattern analysis is somewhat limited in the case of meanonly estimation. The distribution shape can be used as a reference to understand the changes of the shift-pattern, the modal locations, and the tail shapes in the probability density distribution of the air and water temperatures. Donat and Alexander(2012) examined the shifting probability distributions of global temperatures.

2. Air and water temperature data

The current level of monitoring of air and water temperature data is sufficient, but the simultaneously measured data sets are slightly limited. In this study, four representative data sets collected in 2009 supported by the KHOA (Korea Hydrographic and Oceanographic Administration) are selected to consider the diverse coastal characteristics at the sites Incheon (strong-tide, N 37-27, E 126-35), Mokpo (N 34-46, E 126-22, Gadeokdo (N 35-01, E 128-48), and Mukho (weak-tide, N 37-33, E 129-07) shown in Fig. 1. The data are taken at 1-min intervals. To reduce the data size and utilize the reference data, the raw data are transformed to hourly data through a 1-hour median filter. This data transformation does not change the overall distribution shapes even though the wiggles (small fluctuating patterns) disappear. Outliers are removed by using the efficient outlier detection method by Cho et al. (2014). The basic statistical information is arranged in Table 1. As shown in Table 1, the mean air and water temperatures are highly dependent on the latitude of the stations. Moreover, the dispersion indicators, such as standard deviation, are closely related to the tidal conditions. As the tide strength decreases in a particular order-namely, Incheon, Mokpo, Gadeokdo, and Mukho stations, the dispersion indicators decrease significantly.

Fig. 1.

Map of air and water temperature monitoring stations.

Table 1.

Basic statistics of air and water temperature data

3. Results and discussion

3.1. Relationship between air and water temperatures

Fig. 2 shows the time series plots and scatterplots of the air-water temperature data. The upper panels show the time series plots of the data. The fluctuations of air temperature are stronger than those of water temperature, as expected. The mild increase and steep decrease patterns also represent clear typical temporal changes. In the scatterplots in the lower panels, the water temperature barriers (WTB) are shown in the lower and higher regions, which are defined as nearly constant water temperature periods. In this region, the water temperature does not increase any further, even though the air temperature increases. Based on the rough graphical estimation, the lower WTBs in Incheon, Mokpo, Gadeokdo, and Mukho, are approximately 2, 4, 8, and 8℃, respectively. The WTBs in the western coast are much lower than those in the eastern coast because of the physical environment of the seas. In addition, the Incheon WTB is much lower than the Mokpo WTB because Incheon is located at higher latitude than Mokpo. The WTB differences are attributed to the flow and location characteristics. The WTB can be used as a key indicator of the water temperatures for long-term climate change even though in-depth analysis is needed using more temperature data sets in many locations.

Fig. 2.

Time series plots and scatterplots of air-water temperature data set (Upper panel : Blue solid line = water temperatures, Red symbols = air temperature).

3.2 Comparison of the distribution shapes between air and water temperatures

Estimation methods for the distribution function can be classified as parametric and nonparametric methods. Jeong et al. (2013, 2014) suggested that the Gaussian mixture model (order = 2) is more suitable than the normal distribution to fit the air and water temperature data distribution. The model parameters are estimated using the least-square methods in Jeong's study. Another typical parameter estimation method is an EM (expectation-maximization) algorithm (Bishop, 2006), which is available using R-packages (“mixtools”, “mclust”), Matlab function “gmdistribution.fit,” and others. This is the typical parametric method. In this study, the kernel distribution functions are compared with the Gaussian mixture models whose parameters are estimated by a typical EM algorithm. However, the Gaussian model shows relatively poor fitting results in the tail areas and multi-peaks. In order to reduce these limitations, the nonparametric method using kernel functions is used in this study. This method is regarded as a very powerful and flexible method (Silverman, 1998). The bandwidth parameter of the kernel function can be estimated using the following formula, as shown in Eq. (1):

(1) hopt=1.06σ^n−1/5

in which h_opt = optimal bandwidth parameter, σ^ = standard deviation, and n=number of data.

Another typical nonparametric method is the histogram. This has been a widely used method even though it shows a discontinuous distribution shape and is sensitive to the bin width (i.e., bin numbers) and data starting point. Moreover, the kernel distribution is continuous and has only one parameter. The histogram method is not used in this study because of these drawbacks.

Fig. 3 shows the comparison plot of the probability distribution function between air and water temperatures. As shown in Fig. 3, all distribution shapes exhibit obvious double peaks. The longer-tailed shapes and asymmetric patterns are shown in each air temperature distribution. With regard to the air temperature distribution shape, the peak probability of the lower temperature is smaller than that of the higher temperature, whereas the peak probability of the higher water temperature becomes smaller than that of the lower water temperature. The probability change pattern between peaks is also different between the air and water temperatures. Even though the distribution shapes using Gaussian mixture model exhibit double peaks and roughly similar shapes suggested by Jeong et al. (2014), the location and probability of the peaks and the gradient of tail regions show considerable differences.

Fig. 3.

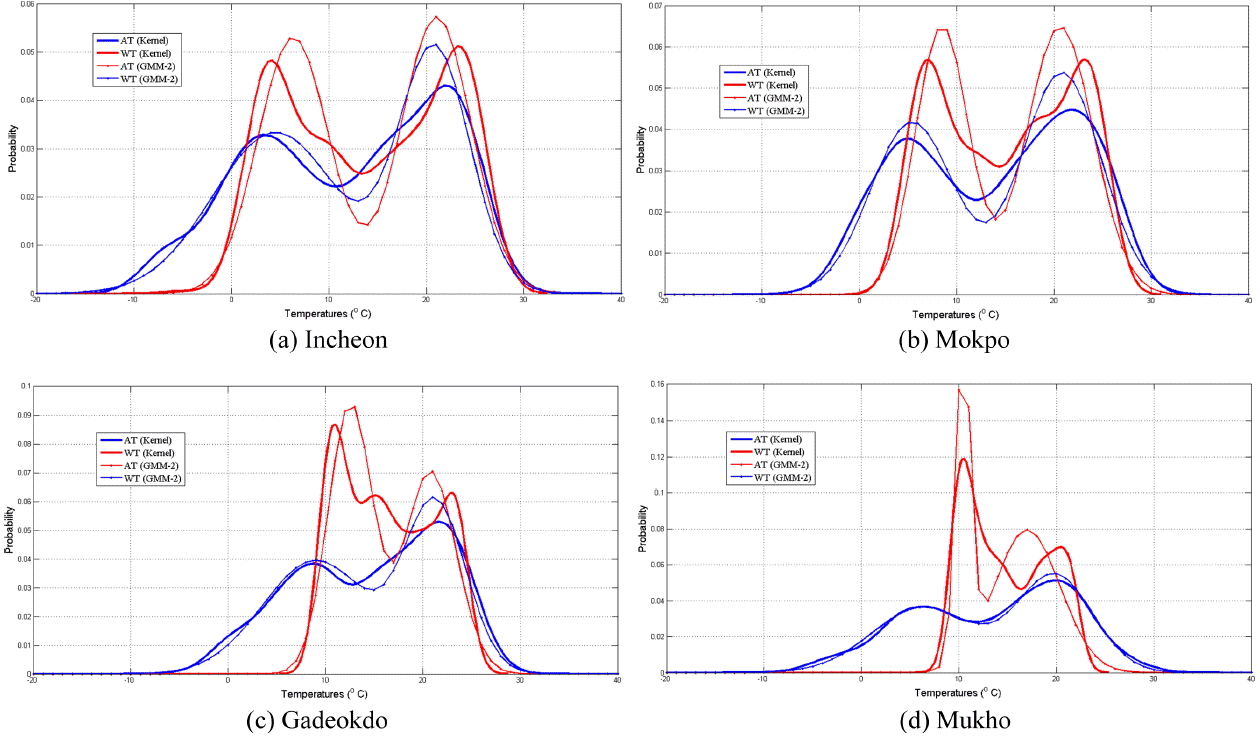
Kernel and Gaussian mixture density distribution plots of the air and water temperatures (AT = air temperature, WT = water temperature, GMM-2 = Gaussian mixture model of order 2).

Fig. 4 shows the comparison plot of the cumulative distribution between air and water temperatures. In this figure, the difference in the lower temperature region can be detected with ease. This means that the dominant temperature difference derived in the lower temperature regions because the water temperature scarcely decreases as the air temperature decreases. The water temperature maintains nearly constant values as already shown in the scatterplot (Fig. 2), corresponding to the newly suggested temperature barrier in this study. This value can be regarded as the characteristic value in the coastal zone, which is dependent on the coastal environmental conditions, such as the latitude, tidal strength, water depth (and/or mixing layer thickness), and other seawater properties.

Fig. 4.

Time-series and scatter plots of the air-water temperatures data set.

4. Conclusions and recommendations

The information from the probability distribution function (or occurrence frequency) is useful to quantify the contribution of the air and water temperature changes from climate change. All air and water temperature data show similar change patterns because of the dominant annual components. However, there is a large difference between the local change pattern and occurrence distribution because of the difference in the air and water temperature change drivers. Therefore, rough E&E parameter estimation based only on air temperature might be reasonable. Conversely, estimation based on long-term small changes, such as water temperature change due to climate change, could lead to the erroneous conclusions. Thus, it is unreasonable to estimate the water temperature and E&E parameters using air temperature change patterns due to climate change. The E&E parameters in the coastal zone should be estimated using water temperature change patterns.

Acknowledgements

This research was funded by the KIOST Basic Research Project (PE-99424).

References

Bishop CM. 2006. Pattern Recognition and Machine Learning, Chap. 9, Springer Science+Business Media, LLC.

Cho HY, Lee KH. 2012;Development of an air-water temperature relationship model to predict climate-induced future water temperatures in estuaries. Journal of Environmental Engineerng 138(5):570–577.

Cho HY, Jeong ST, Ko DH, Son KP. 2014;Efficient outlier detection of the water temperature monitoring data. Journal of of Korean Society of Coastal and Ocean Engineers 26(5):285–291. (in Korean with English abstracts).

Donat MG, Alexander LV. 2012. The shifting probability dsitribution of global daytime and night-time temperatures. Geophysical Research Letters 39L14707.

Grace W, Curran E. 1993;A bimodal model of frequency distributions of daily maximum temperaturem. Australian Meteorological Magazine 42(4):151–161.

Harmel RD, Richardson CW, Hanson CL, Johnson GL. 2002;Evaluating the adequacy of simulating maximum and minimum daily air temperature woth normal distributions. Journal of Applied Meteorology 41:744–753.

Jeong ST, Cho HY, Ko DH, Oh NS, Son KP. 2013;Estimation of probability distribution functions for water temperature data in Korean coasts. Journal of Korean Society of Coastal and Ocean Engineers 25(1):11–19. (in Korean with English abstracts).

Jeong ST, Cho HY, Ko DH, Hwang JD. 2014;Estimation on the distribution function for coastal air temperature data in Korean coasts. Journal of Korean Society of Coastal and ocean Engineers 26(5):278–284. (in Korean with English abstracts).

Silverman BW. 1998. Density Estimation for Statistics and Data Analysis Chapman & Hall/CRC. London, UK:

Toth Z, Szentimrey T. 1990;The binormal distribution: A distribution for presenting asymmetrical but normal-like weather elements. Journal of Climate 3:128–136.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.