2.1 실험장비

동적원심모형실험은 대전 K-water연구원에 설치되어 있는 대형 빔형 원심모형실험장비(유효반경 8 m, 용량 800 G-ton)에 탑재된 진동대를 활용하였다. 지반재료의 경우, 일반축소모형실험을 수행하게 되면, 토립자의 자중에 의한 응력(body force) 효과가 제대로 재현되지 않기 때문에, 흙의 거동이 제대로 재현되기 어려운 점이 있다. 이는 흙의 역학적거동이 응력수준(Stress level)의 지배를 받기 때문으로, 이를 극복하기 위하여 원심모형실험이 개발되어 사용되어왔다(Schofield, 1980). 원심모형실험은 1/N으로 제작된 축소지반구조물모형을 중력가속도의 N배의 원심력장을 부여하여 지반모형체 내부의 응력수준을 실규모지반구조물과 유사하게 만드는 실험이다. 또한, 본 연구에서 사용하는 동적원심모형실험은 원심력을 만들어내는 원심모형실험기에 진동대가 탑재되어, 지반구조물 모형체를 수평방향으로 흔들어 지진하중을 모사할 수 있는 실험이다. 지진모사장치는 세계 최대규모 원심모형시험용 지진모사시스템으로서, 최대 진동가속도는 적재하중이 없을 경우 60 g, 최대적재하중 1,800 kg에 대해서는 22 g가 재현가능하다. 국내 내진설계기준 설계지반가속도 이상의 지진파를 모사할 수 있으며, 원형스케일(Prototype)에서 최대가속도 0.55 g의 기반암 지진동을 재현할 수 있다. 원심모형실험장비와 진동대의 자세한 사항은 Kim et al.(2014b)과 Segismundo et al.(2014)을 참조한다. 원심모형실험에서 사용되는 상사비는 Table 1과 같다.

Table 1.

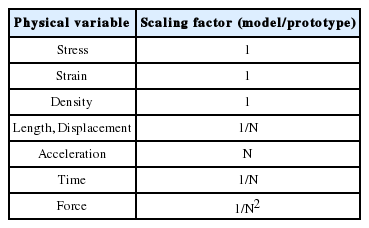
Scaling factors for centrifuge modeling (Schofield, 1980; Taylor, 1995).

원심모형시험에서 모사되는 모형지반은 유한한 크기의 토조안에 조성되기 때문에, 유한한 경계조건을 가질 수밖에 없고, 무한경계에 가까운 현실조건과는 차이를 가진다. 이러한 이유로 지진하중을 모사하는 원심모형실험에서는 Laminar박스 또는 ESB(Equivalent Shear Beam)박스를 사용하여 경계면효과를 고려하고 있고, 본 연구에서는 ESB박스를 사용하였다. ESB박스의 기본개념을 Zeng and Schofield(1996)가 처음 제안하였으며, 본 연구에서 사용한 ESB박스의 내측 크기는 1,440 mm (L) × 440 mm (W) × 631 mm (H)이다. ESB박스는 10개의 알루미늄 프레임으로 구성되며, 각 프레임은 볼베어링과 고무로 연결되어있다. 지진하중 작용시 모형지반을 담고 있는 ESB 벽체가 변형이 가능하여 모형지반과 유사하게 변형되고, 따라서, 지진파가 전달되는 무한경계 지반의 변형을 유사하게 재현한다. 본 연구에서 사용된 ESB박스는 프랑스 Actidyn사에서 제작되었고, 동일 모델이 Lee et al.(2013)에 의해 검증된 바 있다.

2.2 실험모형

석션기초의 스커트(skirt)길이 영향을 비교하기 위하여, Fig. 1과 Table 2에 나타낸 바와 같이 스커트의 길이(L)와 직경(D)의 비를 0.5:1, 0.75:1, 1:1의 비율을 가지는 세 개의 구조물(Model-1~Model-3)에 대하여 동적원심모형실험을 수행하였다. 사용된 석션기초 모형은 스커트의 길이를 제외하고 모두 동일한 제원을 가진다. 모형석션기초의 형상 및 제원은 해상풍력지지구조물로 개발되는 콘크리트석션기초를 차용하였다. 직경 17 m, 스커트 근입깊이 13 m의 석션기초로 자세한 제원은 Choo et al.(2014)을 참조한다. 대상구조물은 ESB박스의 크기 제약으로 1/240크기로 축소제작되었다. 반면, 원심모형실험기에 장착되는 진동대의 제약으로 60G에서 실험이 수행되었다. 결과적으로 대상구조물의 1/4크기의 석션기초에 대해서 실험이 수행된 것과 같다(Table 2).

Fig. 1.

Suction foundation models: (a) Model-1 (L/D) = 0.5, (b) Model-2 (L/D) = 0.75, (c) Model-3 (L/D) = 1.

Table 2.

Dimensions of suction foundation models used in dynamic centrifuge model tests.

상부구조물은 타워와 터빈 등으로 구성되고, 이에 대한 주요 제원은 Upwind Design Basis(Fischer et al., 2010)을 참조하였다. 상부구조물은 타워와 터빈을 대신하여 상부구조물의 공진주파수를 재현하는 단순한 단자유도 구조물로 모사하였다. 상부구조물 모형은 상단에 질량체를 달고 있는 금속봉으로 제작된 단자유도 구조물이다. 자세한 모델링과정은 Olalo et al.(2015)을 참조한다.

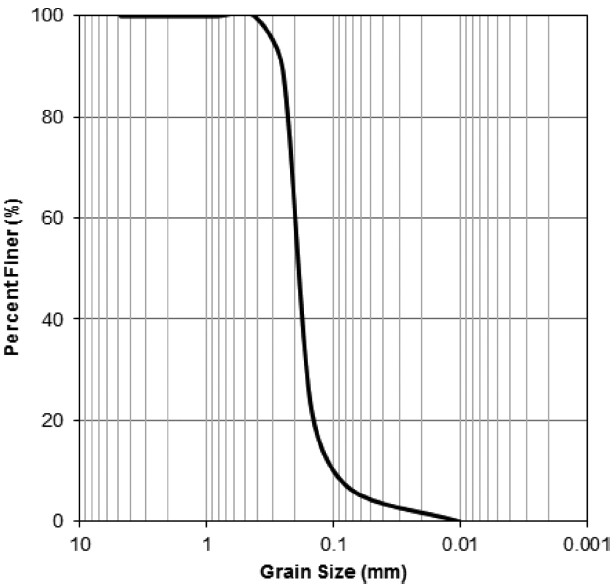
모형지반을 조성하기 위하여 사용된 흙재료는 통일분류법으로 SP로 분류되는 깨끗한 모래를 사용하였다. 모래시료의 입도분포곡선은 Fig. 2와 같다. 최대입경 0.4, 평균입도(D₅₀)은 0.19, 균등계수(c_u)는 2.27, 곡률계수(C_c)는 1.38의 시료이다. 모형지반은 낙사법(Air-pluviation method)을 이용하여 조성되었다. 낙사법은 균질한 모래 지반의 조성이 가능하고, 낙사 높이 및 모래입자의 낙하속도를 조절하여 모형지반의 밀도를 조절할 수 있는 모래 조성방법이다.

Fig. 2.

Particle size distribution of sand used in the experiment.

모형지반은 건조밀도 1.55 t/m³의 매우 조밀한 조건으로 전체 높이는 600 mm로 ESB박스안에 조성되었다. 모래지반의 조성이 완료되면, 모형지반이 담겨있는 ESB박스는 원심모형실험장비의 진동대 위에 탑재되고, 구조물을 설치한 후, 원심가속하여 입력지진파를 가진하였다. 모형지반은 건조상태에서 동적원심모형실험이 수행되었다. 수중모래지반의 경우 지진동으로 인한 과잉간극수압이 발생하여 지반-유체 상호작용의 영향이 있기때문에, 본 연구에서는 이를 배제하기 위하여, 완전배수조건을 목표로 건조상태에서 실험이 수행되었다.

2.3 실험절차

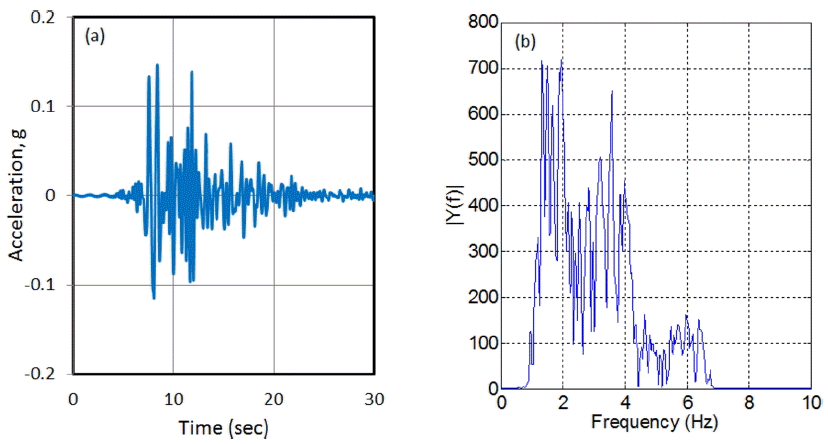
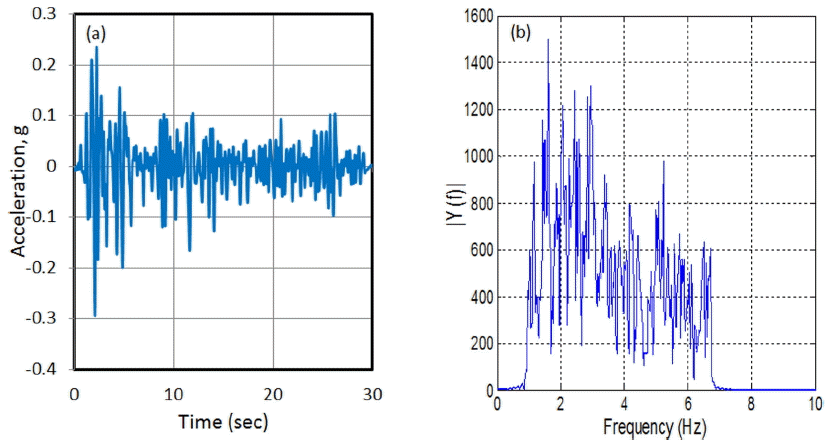
본 연구에서 사용된 입력지진파는 Kobe지진 (Fig. 3)와 El Centro지진 (Fig. 4)이다. Kobe지진은 1995년에 KJMA Station 090에 계측된 지진기록이고, El Centro지진은 Chopra(2000)에 제공되는 지진기록을 사용하였다. 장주기가 지배적인 Kobe지진과 전체 주기특성이 고르게 분포하는 El Centro지진을 선정하였다.

Fig. 3.

(a) Time history and (b) frequency contents of Kobe earthquake (prototype scale).

Fig. 4.

(a) Time history and (b) frequency contents of El Centro earthquake (prototype scale).

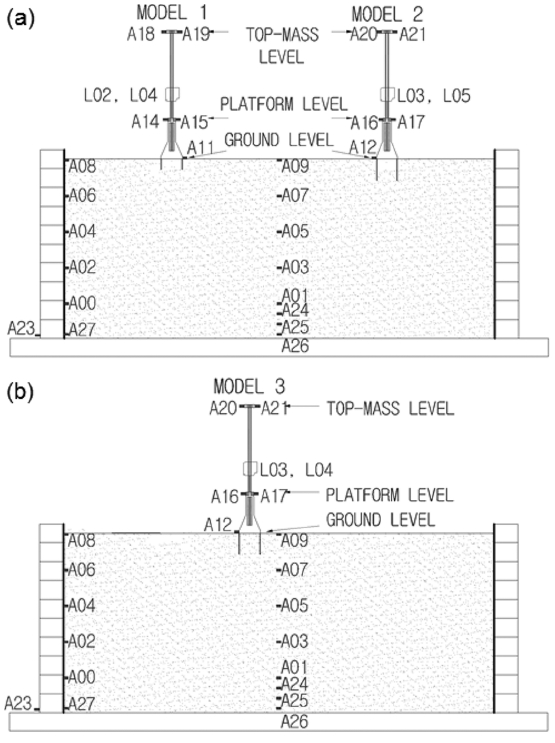
동일한 모형지반조건에서 두 번의 지진실험이 수행되었다. 1차실험에서는 스커트길이/석션기초직경(L/D)비가 0.5인 버켓 기초(Model-1)와 스커트길이/석션기초직경(L/D) = 0.75인 석션기초(Model-2)가 함께 설치되어 실험되었다(Fig. 5a). 2차 실험은 Fig. 5b와 같고, 스커트길이가 가장 긴 케이스로 스커트길이/석션기초직경(L/D)가 1인 석션기초(Model-3)가 실험되었다.

Fig. 5.

Model setup with instrumentation: cross-sections of (a) Model-1 and Model-2; and (b) of Model-3.

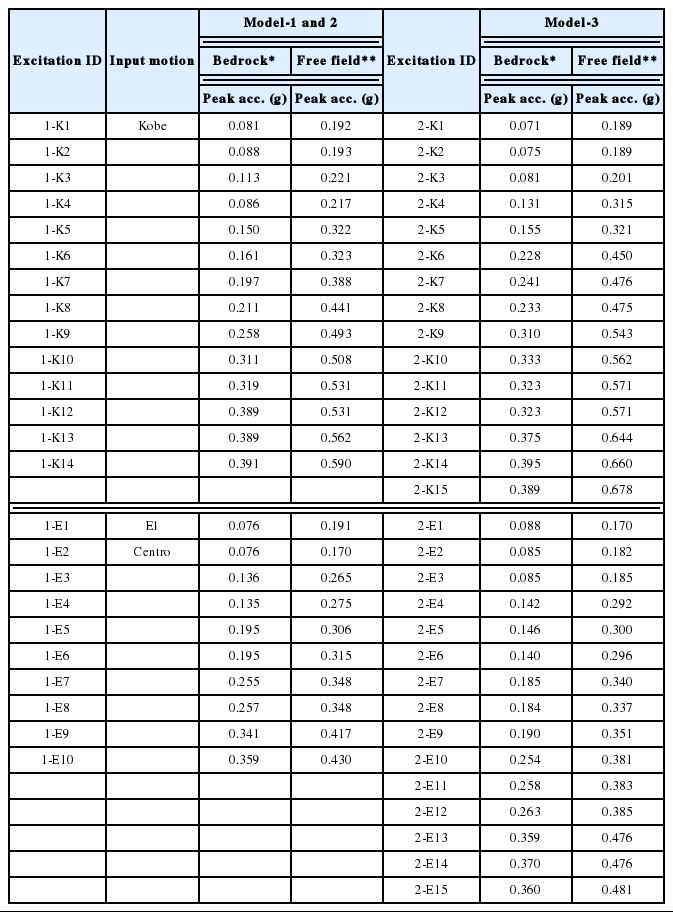
기준이 되는 지진파의 최대가속도(peak acceleration)를 목표한 최대가속도 수준으로 비례적으로 스케일하여 생성한 지진파를 모형지반에 가진하였다. 입력지진파는 ESB박스의 바닥판에 입력되었고, 즉, 바닥판이 제어점(control point)이면서 기반암(bedrock)으로 가정된다. 각 실험에서 Kobe지진과 El Centro지진이 최대가속도를 원형스케일에서 0.071 g에서 0.30 g로 스케일한 지진파을 순차적으로 제어점에 입력하여 지진모사실험이 수행되었다. 최종적으로 지반증폭으로 인하여 지표면최대가속도(Free field PGA)는 0.17 g에서 최대 0.5 g까지의 지진이 모사되었다. Table 3은 1차실험인 Model-1과 Model-2의 가진순서와 2차실험인 Model-3의 가진순서를 나타낸다. 각 지진파는 가장 작은 최대가속도로 스케일된 지진파를 최초로 모형지반에 가하고, 이후, 최대가속도가 크게 스케일된 입력지진파를 동일한 모형지반에 차례로 가진하였다. Model-1과 Model-2에 대하여, 1-K1~1-K14 까지의 지진이 가진되었고, 이후, 1-E1~1-E10의 지진이 가진되었다. Model-3의 경우, 2-K1~2-K15를 가진하고나서 2-E1~2-E10을 가진하였다.

Table 3.

Excitation records (prototype scale).

실험에서 사용된 센서들의 배치는 Fig. 5와 같다. 지진하중이 작용시 모형지반의 거동을 파악하기 위하여, 모형지반의 중앙에 깊이방향으로 지표면으로부터 여러 개의 가속도계를 매설하였다. 이중 A09는 지표면에 위치하여 지표면가속도(자유장가속도)를 측정한다. 또한, 모형지반의 기반암에 해당하는 ESB박스의 바닥판 외측에 가속도계가 부착되어, 기반암 가속도를 측정하였다(Fig. 5의 A21).

모형구조물의 동적거동을 파악하기 위하여, 총 3개의 위치에 가속도계를 설치하였고, 기초의 동적거동을 측정하기 위하여 기초-지반접속부 부분(Fig. 5의 PA1으로 표시; A11과 A12), 지지구조물와 타워의 접속부(Fig. 5의 PA2으로 표시; A14와 15; A16과 A17), 상부질량체(Fig. 5의 PA3으로 표시; A18과 A 19; A20과 A21)에 설치하였고, 가속도계의 질량이 상대적으로 무거워 모형구조물의 거동에 영향을 줄 가능성이 있어 동일한 종류의 가속도계를 대칭이 되는 위치에 쌍이 되도록 부착하였다.

레이저변위센서를 사용하여 지지구조물의 수직변위를 측정하였다(Fig. 5의 L02, L03, L04, L05). 지진하중의 직교방향 중앙선을 따라 구조물의 양옆에 설치되었고, 지지구조물 모형의 지표면부분에 타겟을 옆으로 튀어나도록 설치하여, 구조물의 수직변위량을 측정하였다.

3.1 최대가속도 증폭특성

본 연구에서 지지구조물의 3가지 높이 PA1, PA2, PA3에서 최대가속도가 비교되었다. Fig. 6과 7은 구조물 Model-1, Model-2, Model-3의 3측점 PA1, PA2, PA3에서 측정된 최대가속도를 지표면에서 측정된 자유장최대가속도에 대한 그래프를 나타낸다. Fig. 6은 Kobe지진의 결과이고, Fig. 7은 El Centro지진의 결과이다. 모든 구조물에서의 최대가속도가 자유장최대가속도와 거의 선형적인 관계를 보인다.

Fig. 6.

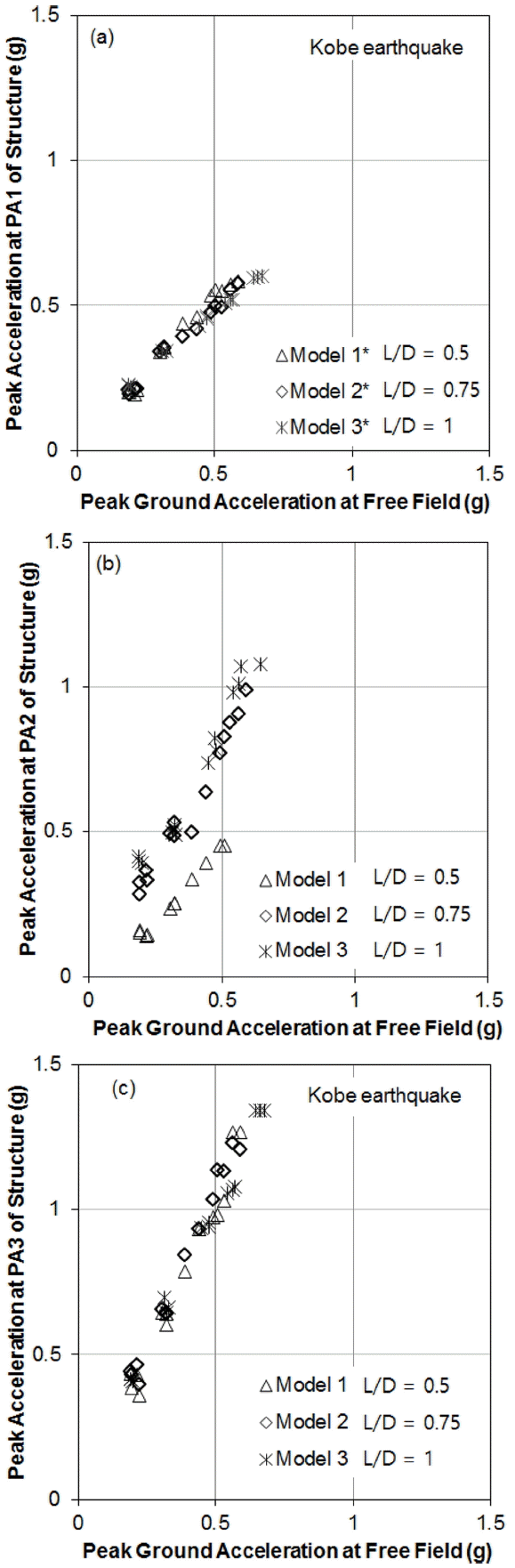
Peak accelerations measured at (a) PA1, (b) PA2, (c) PA3 versus free field PGA subjected to Kobe earthquake.

Fig. 7.

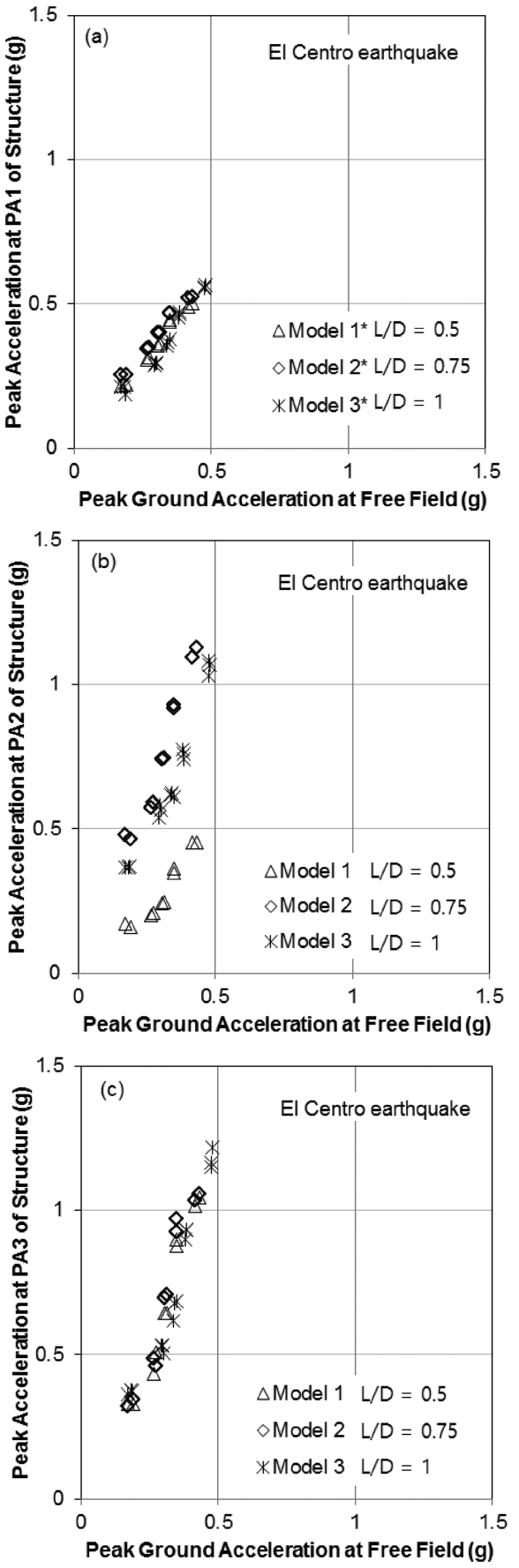
Peak accelerations measured at (a) PA1, (b) PA2, (c) PA3 versus free field PGA subjected to El Centro earthquake.

두 지진 모두, Model-1, Model-2, Model-3의 스커트길이 차이에도 PA1과 PA3은 거의 차이가 나타나지 않았다. PA1은 석션기초 구조물의 지표면위치에서의 가속도로, 지중에 정착되어 있는 스커트로 인해서 가속도증폭이 거의 발생하지 않고 지표면가속도와 유사하게 나타났다. PA3은 타워의 상대적으로 큰 연성이 지배적으로 나타나서, 타워 상단 질량체(터빈부에 해당하는 질량체)에서의 가속도가 석션기초의 스커트길이와 관계없이 유사해지는 것으로 판단된다.

반면, 지지구조물의 플랫폼 레벨인 PA2에서는 구조물에 따라 뚜렷한 차이를 보이고 있다. Kobe지진과 El Centro지진 모두에서, 스커트가 가장 얕은 Model-1의 가속도증폭이 작게 나타났고, 스커트가 깊어지는 Model-2와 Model-3는 증폭은 커지나, 유사한 값을 보였다. 스커트의 근입깊이가 얕은 Model-1의 경향은 스커트의 근입깊이 부족으로 인하여 rocking모드의 영향이 커짐에 따라 발생하는 것으로 판단된다.

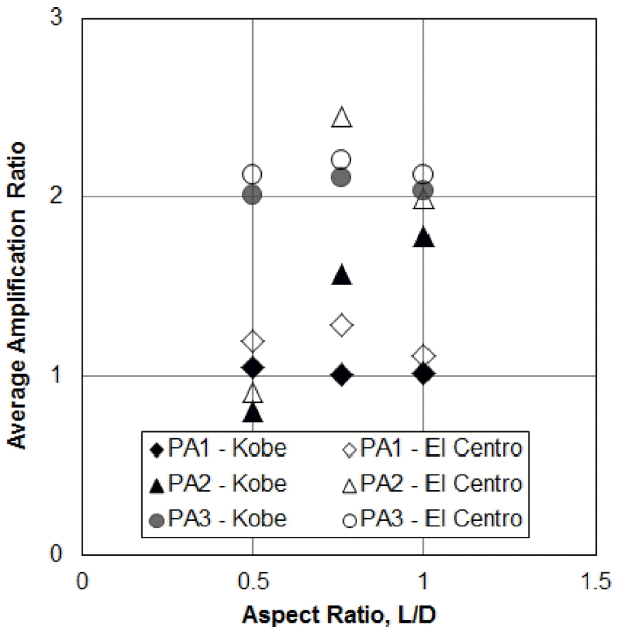
최대가속도증폭특성을 분석하기 위하여, 각 측점 PA1, PA2, PA3에서의 계측된 최대가속도를 자유장최대가속도로 나눈 증폭비를 Fig. 8에 나타내었다. 구조물에서의 최대가속도가 자유장최대가속도에 선형적인 관계를 보였기 때문에, 증폭비는 대체로 일정한 값을 보였다. 따라서, PA1, PA2, PA3에서의 증폭비 평균값을 구하여 스커트길이/석션기초직경비(L/D)에 따라 Fig. 9에 나타내었다. 앞서 확인한 바와 같이, PA1과 PA3은 스커트길이에 관계없이 거의 유사한 값을 보였다. 반면, PA2는 스커트길이가 가장 짧은 Model-1(L/D = 0.5)에서 가장 증폭비가 작고, Model-2와 Model-3에서 커지는 것을 확인하였다. PA2에서의 증폭비가 스커트길이가 길어짐에 따라서 수렴할 것으로 예상되나, 이를 확인하기 위해서는 추가 연구가 필요하고 판단된다. El Centro지진파가 Kobe지진보다 모든 측점에서 증폭비가 다소 큰 것을 확인되어, 석션기초의 증폭은 지진파의 영향을 받았다.

Fig. 8.

Amplification ratio of Kobe earthquake: (a) PA1, (b) PA2, and (c) PA3.

Fig. 9.

Average amplification ratio vs aspect ratio of suction foundation.

3.2 잔류수직변위

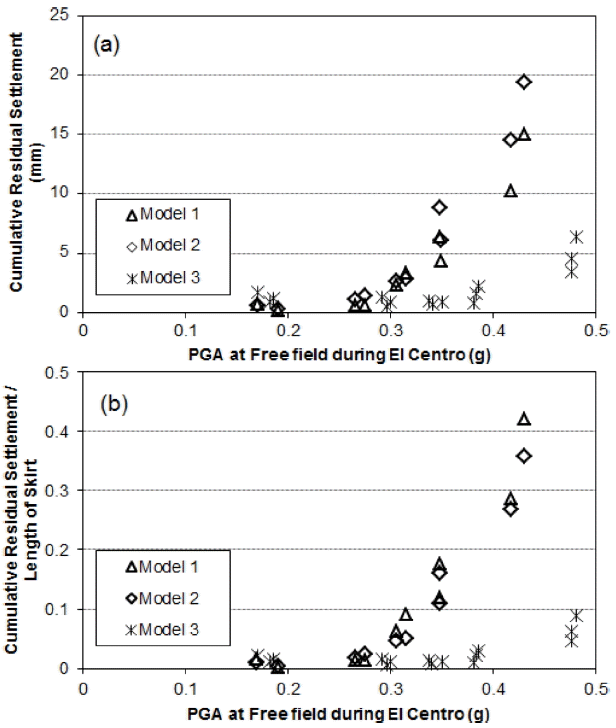
Fig. 10은 El Centro지진파의 순차적인 가진에 따른 기초의 누적잔류수직변위량의 변화추이를 나타낸다. Table 3의 1-E1~1-E10의 가진과 Table 3의 2-E1~2-E15의 가진에 따라 발생하는 누적잔류침하량을 도시하였다. 잔류침하량은 각 지진하중이 지나간 후에 잔류되는 침하량을 나타낸다. Kobe지진 가진중에는 계측기의 문제로 측정이 제대로 이루어지지 않았다. Fig. 10에 표시된 값의 (+)는 인발을, (-)는 관입을 나타낸다. 모든 석션기초가 점차적으로 커지는 진폭의 지진동 가진에 따라 구조물이 지반으로부터 인발하는 특징을 보였다. 또한, 모든 실험이 종료한 후 지표면 침하를 확인한 결과, 아주 미소한 하향침하가 발생하였고, 따라서 수직변위 계측결과는 순수하게 구조물이 지반으로부터 인발되어 나타나는 변위로 판단된다. 또한, 이러한 현상은 선행연구인 Olalo et al.(2015)에서도 관찰된 바 있다.

Fig. 10.

(a) Cumulative residual settlement and (b) settlement ration to skirt length induced by El Centro.

지진동을 받는 석션기초의 스커트는 지진하중 방향을 따라 스커트의 전면과 후면에 압축과 인발이 번갈아가면서 작용하게 된다. 이때 지중에 관입되어 있는 스커트의 저항력은, 압축저항력이 인발저항력보다 상당히 크다. 따라서 한쪽 방향으로 수평하중이 작용하게 되면, 작용방향측 스커트의 압축관입력보다 작용방향 반대측의 스커트의 인발력이 매우 크기 때문에, 압축측이 관입되기 보다는 인발측 스커트가 인발되는 현상이 발생할 것으로 판단된다. 이후, 하중의 방향이 반대방향으로 바뀌면, 역으로 반대방향측이 인발을 받게 되고, 반대측에서 인발이 발생하여, 이러한 반복지진하중이 지속적으로 작용하면, 최종적으로 인발형태의 잔류변위가 발생하는 것으로 판단된다. 특히, 본 연구와 같이 조밀한 모래조건에서는 압축저항력이 매우 크기 때문에 이러한 현상이 심화된 것으로 판단된다.

특이하게도 석션기초 모두 일정한 한계가속도에서 인발이 발생하기 시작하였고, Model-1과 Model-2는 자유장최대가속도 0.306 g(기반암가속도 0.195 g)이상에서 인발되기 시작하였고, Model-3은 그 보다 큰 수준 자유장최대가속도 0.381 g(기반암가속도 0.254 g)에서 인발이 시작되었다. 모두 국내 일반적인 설계가속도수준을 넘는 상당한 강진에서 인발이 발생하였다. 또한, 잔류변형이 발생하기 위해서는 일정 한계가속도수준이상이 되어야 하는 것을 반증하며, 한계가속도수준은 스커트 길이의 영향을 받는 것으로 보인다.

스커트의 길이가 가장 긴 Model-3에서 누적되는 인발변위량이 매우 작게 관측된 반면, Model-1과 Model-2의 누적 인발변위량은 유사한 값을 보였다. 스커트 길이가 더 긴 Model-2가 약간 큰 인발변위량을 보이고 있다. 결론적으로 스커트의 길이가 짧아지면 인발량이 증가하나, Model-2의 길이 보다 짧아지면 인발량이 다시 감소하는 것으로 보인다. 매우 짧은 스커트의 경우, 인발에 기여할 스커트의 길이가 충분하지 못하기 때문에 인발변위량이 작아지는 것으로 판단된다. 인발변위량을 스커트의 길이로 정규화하여 나타내면 Fig. 10b와 같고, 스커트길이/석션기초직경비가 0.75이하인 Model-1과 Model-2의 단위스커트길이당 변위는 거의 유사하게 나타났다. 결과적으로 Model-3과 같이 스커트길이/석션기초직경비가 1이상의 긴 스커트 석션기초는 잔류수직변위에 유리한 것으로 나타났다.

3.3 잔류경사변위

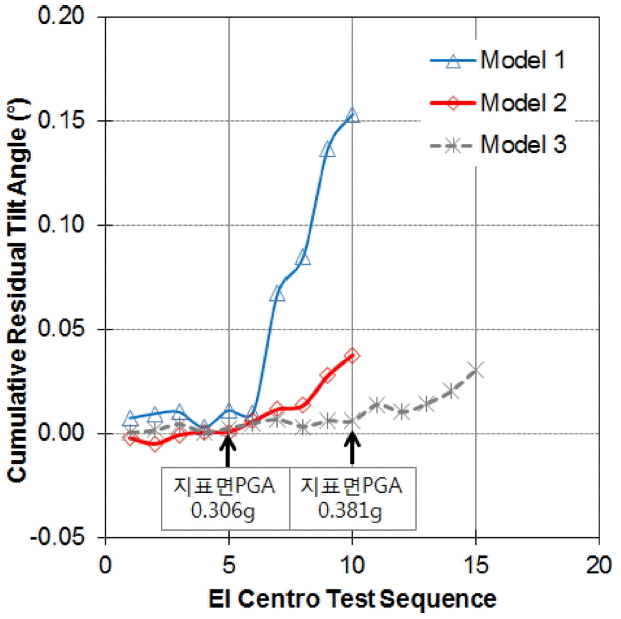
지지구조물의 양측면에서 측정된 침하량의 차이로부터 잔류경사변위를 측정하였다. Fig. 11는 지진하중 가진후 잔류경사각의 변화를 나타낸다. 지진하중 직후 발생하는 잔류경사각은 자유장최대가속도에 따라 증가한다. 스커트길이가 가장 얕은 Model-1이 가장 큰 경사각 발생하고 있고, 길이가 깊어짐에 따라 발생하는 경사가 줄어든다.

Fig. 11.

Cumulative residual tilt angle during El Entro excitations.

인발이 발생했던 동일한 가속도수준에서 잔류경사가 발생하는 것이 관측된다. 그러나 잔류경사는 뚜렷하게 스커트의 길이가 커짐에 따라 Model-1, Model-2, Model-3의 순서로 잔류경사가 작아지는 경향이 관찰되었다. 스커트길이가 길어지면 잔류경사에 대해 유리한 것으로 판단된다. 한계가속도는 Model-1과 Model-2는 자유장최대가속도 0.275 g (기반암 가속도 0.135 g)이상에서 회전경사가 잔류되기 시작하였고, S5는 그보다 큰 수준 자유장최대가속도 0.385 g(기반암가속도 0.258 g)에서 회전경사가 시작되었다. 잔류경사변위는 수직변위와 동시에 발생하였고, 한계가속도수준은 스커트 길이가 길어짐에 따라서 커지는 것으로 나타났다.