Article information

Abstract

Trans Abstract

1. 서 론

효율적인 국토의 이용과 물류수송을 위하여 도로, 항만, 플랜트 등이 해안에 건설되고 있으며, 해안의 연약지반 상에 구조물을 설치하기 위한 대규모 지반개량이 요구되고 있다. 연약지반 상에 시공되는 구조물 기초는 준설치환, 다짐말뚝, 심층혼합처리 등이 있으며, 경제적·환경적 측면을 고려하여 쇄석다짐말뚝(Gravel Compaction Pile, GCP)의 적용 및 연구가 점차 증가하는 추세이다. 쇄석다짐말뚝공법은 연약지반에 높은 다짐에너지를 이용하여 쇄석을 압입하여 지중에 조립질 재료로 구성된 말뚝을 조성함으로써 모래지반에서는 밀도증대, 액상화 방지, 수평저항력을 증가시키고, 점토지반에서는 전단강도 및 지지력 증가, 측방변위 억제, 압밀침하량 저감을 목적으로 하는 공법이다.

최근 북미지역에서 하중저항계수설계법은 지반공학분야에서 표준화된 설계법으로 자리잡고 있으며, 세계 주요 지반분야 설계기준이 허용응력설계법에서 한계상태설계법으로 전환되고 있다. 현재 지반공학 분야 중에서 깊은기초, 얕은기초 등 일부 분야에만 상세한 시방서가 준비되었을 뿐, 한계상태설계법이 이미 적용되고 있는 국가들에서 조차도 쇄석다짐말뚝과 같은 연약지반개량에 의한 기초에 대한 연구가 상당히 미흡하여 이에 대한 연구가 요구되고 있다.

하중저항계수설계법에서 신뢰성이론에 기반한 저항계수를 보정하기 위해서는 정재하시험 등에 의해 측정된 실제 저항치와 현재 설계기준 등으로 이용되고 있는 경험식 사이의 편향치에 대한 데이터베이스를 구성하고, 이에 대한 확률통계학적 분석이 필요하다. 천 등(2004a)과 Stuedlein(2008)이 쇄석다짐말뚝의 정재하시험 결과로부터 분석된 실측지지력과 현재 설계에 이용되고 있는 팽창파괴에 대한 이론식으로부터 산정된 예측지지력의 비, 즉 저항편향치가 0.64~2.99으로 비교적 넓은 범위로 분포하고 있으므로 정재하시험 데이터를 이용한 극한지지력의 평가법은 쇄석다짐말뚝의 저항계수 보정 시 매우 중요한 과정이라 할 수 있다.

쇄석다짐말뚝의 극한지지력을 평가하는데 가장 신뢰도가 높다고 알려진 정재하시험은 정 등(1992), 이 등(2000), 천 등 (2000, 2004b), 이 등(2003), 황 등(2005), 배·이(2007), 윤 등(2007), 최(2007), 김 등(2010)에 의해 수행된 바 있지만 대부분의 연구에서는 쇄석다짐말뚝의 보강효과를 확인하거나 응력분담율을 산정하는데 목적을 두었다.

정재하시험에서 하중-침하량 곡선이 침하량 축에 거의 평형상태에 도달하는 극한지지력을 구하는 것은 재하장치의 용량과 성능, 시험조건, 말뚝의 재사용 등의 제반여건으로 인하여 말뚝이 파괴에 이르는 극한하중까지 재하 되지 못하고 계획하중의 150~200%에 해당하는 하중만이 재하 되며, 파괴에 이르는 충분한 변위가 발생되지 못한 채 시험이 종료된다. 이에 대한 대안으로 구조물 기초 설계기준 해설(한국지반공학회, 2009)에서는 logP-logS, dS/d(logt), S-logt 방법 등을 이용한 도해적인 방법을 이용하여 항복하중을 산정하거나 말뚝의 침하량이 재하판 또는 말뚝직경의 10%일 때의 하중을 극한지지력으로 간주하도록 규정하고 있다. Kondner(1963), Chin (1971) 등은 도해적인 방법에서 발생되는 도면의 축척에 의한 시각적 오차와 개인오차의 영향을 배제하기 위하여 쌍곡선회귀분석을 이용한 극한지지력 평가법을 제안한 바 있으며, 류 등(1995), 원 등(1996)은 정재하시험에서 얻어진 하중-침하량 곡선의 최대곡률점을 항복하중으로 평가하는 연구를 수행하였다.

북미지역의 대표적인 한계상태설계기준인 AASHTO(2010) 시방서의 말뚝기초와 얕은기초의 저항계수 보정에 근간이 되고 있는 NCHRP Report 507(Paikowsky et al., 2004), Report 651(Paikowsky et al., 2010)에서는 실제 극한지지력을 평가하기 위한 방법으로 정재하시험 데이터를 이용하였다. 말뚝기초에서는 Davisson 판정법(Davisson, 1972), 하중-침하량곡선의 형상 판정법(Butler and Hoy, 1977), 25.4 mm 한계침하량 판정법, 0.1B 침하량 판정법(Terzaghi, 1942), 대수하중(logP)-대수침하(logS) 판정법(DeBeer, 1970) 등 5가지 판정법을 고려하였으며, 파일의 직경과 정재하시험법에 관계없이 저항편향계수가 1에 가까운 Davisson 판정법을 적용하였다. 얕은기초에서는 최소 경사 판정법(Vesic, 1963), 0.1B 침하량판정법, 대수하중(logP)-대수침하(logS) 판정법(DeBeer, 1970), 이중 경사 판정법 등이 고려되었으며, 극한지지력을 평가하기에 간편성과 다용성을 갖춘 최소 경사 판정법을 적용하였다.

쇄석다짐말뚝은 구성 재료들의 움직임이 구속되어 있는 강체상태가 아니며, 말뚝기초 및 얕은기초와는 다른 팽창파괴의 거동을 보이므로 기존의 판정법보다 쇄석다짐말뚝에 적합한 극한지지력 판정법이 필요하다.

본 연구에서는 쇄석다짐말뚝에 대한 한계상태설계법을 개발하기 위한 연구의 일환으로 정재하시험으로부터 얻어진 하중-침하량 곡선을 기반으로 비선형 회귀분석법을 이용하여 극한지지력을 예측하고, 도해법을 이용한 기존의 판정법들에 의해 예측된 극한지지력과 비교분석하였다. 또한 하중-침하량 곡선의 형상에 따른 비선형 회귀곡선의 변화와 실제 극한지지력과의 비를 검토하여 한계상태설계법을 위한 정재하시험 수행 시 극한지지력의 정확도를 확보하기 위한 시험 조건을 분석하였다.

2. 비선형 회귀분석에 의한 극한지지력 평가법

비선형 회귀분석은 관련 변수들 사이의 관계를 분석하고, 모형화 시키는 통계학적 기법으로 물리, 화학, 생물, 공학, 의학 등 자연과학 분야의 거의 모든 분야에서 응용되고 있으며, 최근에는 통계 소프트웨어(SPSS, SAS, MINITAB 등)를 활용하여 변수들 사이의 복잡한 함수관계를 추정하는데 사용되고 있는 자료분석 기법이다. 본 연구에서는 지난 수십여 년간 여러 분야에서 다양한 모형식으로 제안된 회귀모형을 쇄석다짐말뚝의 극한지지력을 판정하는데 이용하고자 하였다.

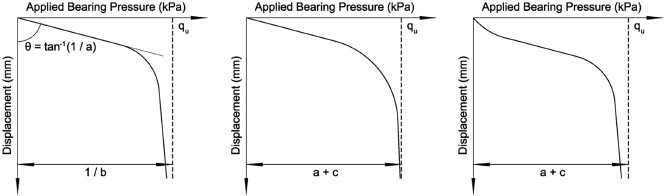
대표적인 회귀모형으로는 Fig. 1과 같이 생산-밀도 모형(yield-density model), 점근적 회귀모형(asymptotic regression model), S자 형태의 성장곡선 모형(sigmoidal growth model)이 있다. 각각의 다른 형태의 모형은 적용 분야에 따라 특성이 다르며, 같은 분야의 모형식이라도 적합도가 다르게 나타날 수 있으므로 데이터의 특성에 따라 적합도가 우수한 비선형 회귀모형을 선택하여야 한다.

Fig. 1.

Geometrical illustration of the nonlinear regression models.

생산-밀도 회귀모형 중 포물선의 성격을 가지는 쌍곡선 회귀방정식은 지반공학 분야에서 가장 많이 적용된 사례가 있다. 점토에 대한 삼축압축시험으로부터 응력-변형률의 관계를 이용한 Kondner(1963)의 연구에서 나타나며, Chin(1971)은 이 이론을 말뚝에 적용하여 쌍곡선 형태의 하중-침하량 곡선에서 하중을 종속변수, 침하량을 독립변수로 하는 식 (1)을 정의하였다.

여기서, q는 쇄석다짐말뚝에 재하된 하중(지지력)이며, Δ는 침하량, a와 b는 회귀분석에 의해 결정되는 회귀계수이다. 회귀계수 a는 하중-침하량 쌍곡선의 접선각 θ = tan⁻¹(1/a)의 계수가 되며, 회귀계수 b의 역수값(1/b)은 점근선까지의 거리로 극한지지력이 된다.

점근적 회귀모형은 q = a − b·c^Δ과 같은 기본 회귀방정식으로 화학비료실험, 어류의 나이와 길이의 관한 연구에서 주로 적용되었으며, 선형근사화에 가장 가까운 최소제곱추정치를 구하기 위하여 식 (2), 식 (3)과 같은 지수함수 형태의 회귀방정식이 자주 이용되고 있다.

S자 형태의 성장곡선 모형은 하중-침하량 곡선이 변곡점에 도달할 때까지 단조적으로 하중이 증가하고 극한하중에 점근적으로 도달하는 동안 침하량이 증가하는 S자 곡선에 대한 이론적 배경으로 제안되었으며, 식 (4)와 같은 Weibull(1951)분포로부터 유도된 Weibull 형태의 모형이 대표적이다.

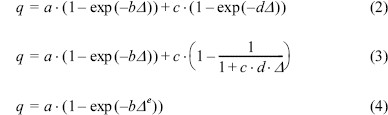
여기서, a, b, c, d, e는 비선형 회귀분석으로부터 결정되는 회귀계수로 a, c는 극한하중에 해당하는 점근선과 관련된 회귀계수로 a와 c의 합으로 극한지지력을 산정하며, b, d는 침하량 축에 대한 절편과 관련된 회귀계수이다. e는 회귀모형에서 모형이 가지는 복잡성을 의미하는 회귀계수이다.

3. 쇄석다짐말뚝의 정재하시험

3.1 개요

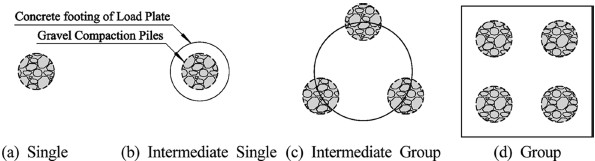
국내외에서 쇄석다짐말뚝에 대한 적용사례가 증가하면서 다양한 지반조건 및 시공조건에 부합하는 설계기법 정립과 설계지지력 확인, 단말뚝, 복합지반, 군말뚝의 거동을 평가하기위한 정재하시험이 여러 연구자들에 의해 Fig. 2와 같이 수행되었다. Fig. 2에서 (a)는 단말뚝의 지지력과 침하량을 평가하기 위한 재하시험 형태이며, (b), (c)는 주로 복합지반에서 각각 단말뚝과 군말뚝에 대한 응력분담비와 지지력, 침하량을 평가하기 위한 재하시험 형태이다. (d)는 말뚝의 배치형태에 따른 군말뚝의 지지력과 침하량을 평가하기 위한 재하시험이다.

Fig. 2.

Typical static load test setup for gravel compaction piles (Stuedlein, 2008).

정재하시험에서는 Fig. 3과 같이 말뚝 두부에 말뚝과 동일한 직경의 콘크리트 또는 철재 평판으로 된 강성기초를 설치하고, 하중재하는 반력말뚝(반력앵커) 또는 실물을 이용한다.

Fig. 3.

Sketch of static load test setup for GCP(Lillis et al., 2004; Bae and Lee, 2007).

3.2 정재하시험 데이터

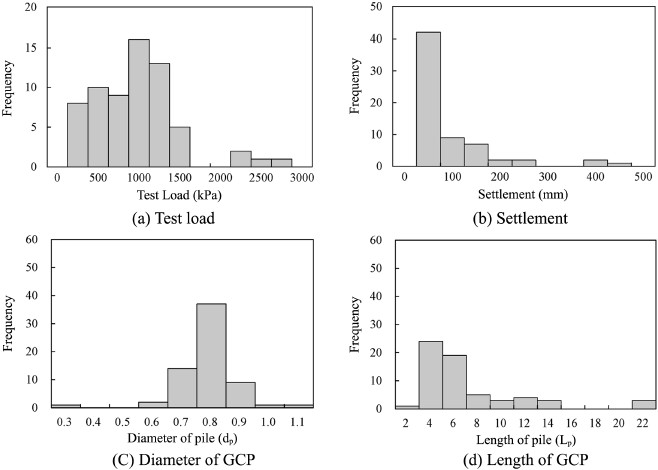
본 연구에서는 쇄석다짐말뚝의 저항편향계수에 통계학적 의미가 부여될 수 있도록 문헌 및 재하시험 보고서로부터 65개소의 정재하시험 데이터를 Table 1과 같이 수집하였으며, 정재하시험과 관련된 설계변수 데이터베이스의 분포를 Fig. 4에 나타내었다.

Table 1.

Number of test cases conducted in each country.

Fig. 4.

Frequency histograms for variables in static load test database.

정재하시험에 적용된 하중은 133~2,684 kPa 범위로 재하되었으며, 이 때 발생된 침하량은 4~436 mm로 나타났다. 정재하시험이 수행된 쇄석다짐말뚝의 직경은 대부분 0.76 m로 대부분 0.7~0.9 m 범위에 분포하였으며, 쇄석다짐말뚝은 1.5~20.7 m의 심도로 시공되었다.

비선형 회귀분석을 이용하여 쇄석다짐말뚝의 극한지지력을 예측하고, 예측된 극한지지력의 정확성을 평가하기 위하여 국내외에서 실시된 정재하시험 자료 중에서 쇄석다짐말뚝이 항복하중 및 극한하중에 도달할 때까지 재하된 검증용 정재하시험 자료를 Table 2와 같이 선정하였으며, 정재하시험으로부터 얻어진 하중-침하량 곡선을 Fig. 5에 나타내었다.

Table 2.

Summary of static load test for gravel compaction piles.

Fig. 5.

Load-displacement curve obtained from static load test result of gravel compaction piles.

정재하시험은 쇄석다짐말뚝을 시공장비 선단의 다짐기(Rammer)를 이용하여 직접 다짐하는 램머방식 3개소와 진동기(Vibrator)에 의해 발생되는 진동력으로 쇄석을 다지는 진동방식 1개소에서 수행되었으며, 단말뚝(2개소)과 군말뚝(2개소)에 대한 정재하시험이 적용되었다. 쇄석다짐말뚝의 직경은 0.61~1.0 m, 길이는 2.7~16.0 m로 구성되어 있으며, 원지반점토의 비배수전단강도는 11.0~30.0 kPa로 다양한 상태의 재하시험 데이터를 구성하고자 하였다.

3.3 비선형 회귀분석에 의한 극한지지력 예측

본 연구에서는 쇄석다짐말뚝의 정재하시험 데이터를 기반으로 여러 분야의 확률통계학적 분석에 적용되고 있는 SPSS (PASW version 18)를 이용하여 비선형 회귀분석을 수행하였으며, 최적의 회귀계수를 추정하기 위한 최소제곱추정량은 지반공학 분야에서도 적용되고 있는 Levenberg-Marquardt(Hagan et al., 1996) 알고리즘을 이용하였다.

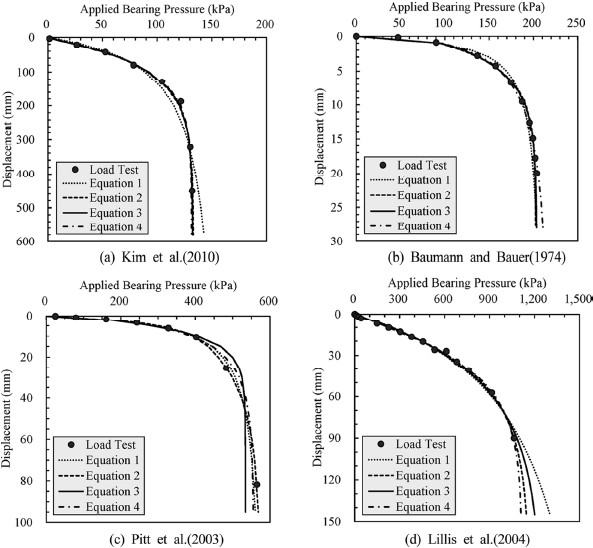
극한지지력의 예측은 극한하중(q)을 종속변수, 침하량(Δ)을 독립변수로 하는 네 가지 비선형 회귀모델(식 1~4)을 적용하였으며, 비선형 회귀분석으로부터 예측된 극한지지력을 Table 3 과 Fig. 6에 나타내었다. 비선형 회귀분석으로부터 예측된 극한지지력의 곡선적합도는 상관계수와 실제 극한지지력과의 비로 평가할 수 있으며, 정재하시험 데이터에 대한 상관계수는 R²= 0.985~1.000으로 매우 높은 상관성을 나타내었다. Kim et al.(2010) 및 Baumann and Bauer(1974)의 정재하시험으로부터 측정된 극한지지력과 회귀분석으로 예측된 극한지지력의 비를 분석한 결과, 성장-밀도 모형의 쌍곡선 회귀방정식에서는 최대 24%의 편차를 보였으며, 점근적 회귀모형과 S자 성장곡선 모형에서는 7% 편차 이내로 비교적 정확하게 예측하는 것으로 나타났다. 따라서 상관계수 및 극한지지력비를 고려한 전체적인 곡선적합도는 점근적 회귀모형이 가장우수하며, 식 (3)의 회귀방정식이 가장 극한지지력을 잘 예측하는 것으로 평가된다.

Table 3.

Nonlinear regression analysis result to estimate ultimate bearing capacity.

Fig. 6.

Yield and ultimate bearing pressure-displacement curve for load test in database.

3.4 기존 극한지지력 평가법과 비교

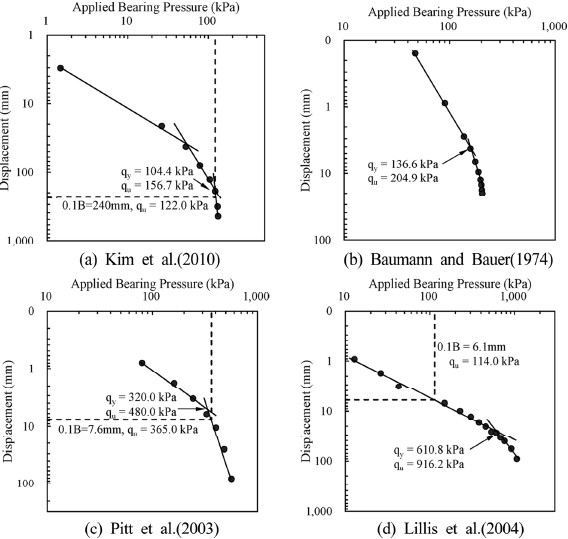
구조물 기초 설계기준 해설(한국지반공학회, 2009)에서는 극한지지력이 분명하게 규명되지 않는 경우에는 하중(P)-시간(t)-침하량(S) 거동특성에 의하여 S-log t, dS/d(log t)-P, log P-log S 분석법 등으로 항복하중을 구하고, 항복하중의 1.5배를 취하여 극한하중으로 하거나, 말뚝 직경의 10% 즉, 0.1B의 하중강도를 극한하중으로 판정하도록 규정하고 있다. 본 절에서는 현재 실무에서 적용되고 있는 대수하중-대수침하(log P-log S) 분석법과 0.1B 분석법을 적용하여 정재하시험 데이터에 대한 항복하중과 극한하중을 Fig. 7과 같이 예측하였으며, 3.3절에서 수행된 비선형 회귀분석에 의해 산정된 극한지지력과 비교하였다(Table 4).

Fig. 7.

Estimate of yield and ultimate bearing capacity based on logP-logS, 0.1B method.

Table 4.

Comparison of estimated ultimate bearing capacity by various method.

log P-log S 분석법에 의해 예측된 극한지지력은 비선형 회귀분석에 의한 극한지지력과 최대 28%의 오차를 보였으며, Bauman and Bauer(1974)의 정재하시험 데이터에서는 실제 극한지지력과 예측된 극한지지력이 거의 일치하였다. Kimet al.(2010)의 데이터에서는 2개의 변곡점이 나타나 기술자의 판단에 따라 항복하중을 다르게 판정할 수 있으며, 최대곡률점을 항복하중으로 판정하여 극한지지력을 산정하더라도 실제 극한지지력 보다 약 16% 크게 예측되었다. Pitt et al. (2003) 및 Lillis et al.(2004)의 데이터에서는 비선형 회귀분석으로 산정된 극한지지력에 비해 안전측으로 약 20~28% 오차를 보였다.

0.1B 분석법은 정재하시험에서 침하량이 0.1B 이하로 수행된 Bauman and Bauer(1974)의 데이터를 제외한 나머지 정재하시험 데이터로부터 극한지지력을 예측하였으며, Kim et al. (2010) 및 Pitt et al.(2003)의 데이터에서는 비선형 회귀분석에 의해 산정된 극한지지력과 약 8~57%의 오차를 보였다. Lillis et al.(2004)의 하중-침하량 곡선에서는 말뚝의 직경만큼 침하량이 발생될 때 항복하중이 나타나 0.1B 분석법에 의해 예측된 극한지지력은 비선형 회귀분석 및 log P-log S 분석법에서 산정된 극한지지력 보다 매우 낮은 극한지지력이 예측되었다.

기존 극한지지력 판정법을 이용하여 예측된 극한지지력은 실제 극한지지력과 거의 일치하는 경우도 있으나, 변곡점이 여러 개 나타날 경우 개인오차가 포함될 가능성이 높다. 또한 쇄석다짐말뚝은 Fig. 4(b)와 같이 원지반 연약층의 두께와 비배수 전단강도에 따라 강관말뚝이나 현장타설말뚝에 비해 상당한 침하량을 수반하는 경우가 있으므로 침하량을 기준으로 극한지지력을 판정하는 0.1B 분석법은 쇄석다짐말뚝의 극한지지력을 예측하는데 적합하지 않은 평가법으로 판단된다.

4. 극한지지력 판정법이 저항계수에 미치는 영향

한계상태설계법에서는 공간적 불확실성, 조사의 불확실성, 설계 및 해석모델의 불확실성 등 저항의 불확실성을 저항편향계수로 정량화하여 저항계수 보정이 이용하고 있으며, 저항편향계수는 현재 설계에 적용되고 있는 이론식에 의해 예측된 극한지지력과 정재하시험으로부터 얻어진 실측 극한지지력의 비를 저항편향계수로 정의한다. 저항편향계수의 평균값(λ_R)은 실제 극한지지력에 대한 극한지지력 이론식의 평균적인 내재적 보수성을 나타내는 값이며, 변동계수(COV_R)는 저항편향계수의 평균값에 대한 표준편차의 비로서 저항편향계수의 불확실성을 정량화 한 값이다.

한계상태설계법 중 북미지역에서 채택하고 있는 하중저항계수설계법(LRFD)의 저항계수(Φ)는 식 (5)와 같은 LRFD 기본식으로 보정되며, 하중과 관련된 변수들은 상부 구조물의 특성에 따라 결정되므로, 저항계수는 저항편향계수(λ_R)와 저항편향계수의 변동계수(COV_R)의 함수가 된다. 즉, 하중과 관련된 계수가 일정하다면, 정재하시험으로부터 판정된 극한지지력에 따라 저항편향계수와 변동계수가 결정되고, 쇄석다짐말뚝의 저항계수의 신뢰성은 실측된 극한지지력의 정확성에 좌우된다.

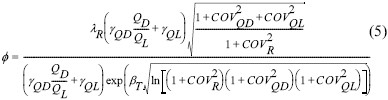
여기서, Φ는 신뢰성이론에 기반하여 보정된 저항계수, γ_QD, γ_QL은 사하중계수와 활하중계수, Q_D/Q_L은 사하중과 활하중의 비, λ_QD, λ_QL, λ_R은 사하중과 활하중, 저항의 편향계수, COV_QD,COV_QL, COV_R은 사하중과 활하중, 저항의 변동계수, β_T는 목표신뢰도지수이다.

본 연구에서 수집된 65개소의 정재하시험 데이터를 log Plog S 분석법과 비선형 회귀분석을 이용하여 극한지지력을 판정하였으며, 각 극한지지력 판정법과 팽창파괴에 대한 극한지지력 이론식에 대한 저항편향계수와 변동계수, 저항계수를 산정하여 Table 5에 나타내었다.

Table 5.

Calibrated resistance factor for different theoretical formulations using log P-log S method and nonlinear regression method.

log P-log S 판정법을 이용한 저항편향계수는 λ_R= 0.63~0.79 범위로 극한지지력이 이론식에 비해 비교적 보수적으로 평가되는 것으로 분석되었으며, 비선형 회귀분석을 이용한 저항편향계수는 λ_R = 0.86~1.09 범위로 극한지지력은 이론식과 유사한 범위로 평가되었다. 저항편향계수의 변동계수로 부터 비선형 회귀분석 판정법이 log P-log S 판정법보다 낮아 저항편향계수의 불확실성이 낮은 것으로 분석되었다.

실측 극한지지력을 비선형 회귀분석에서 보다 상대적으로 낮게 평가하고 있는 log P-log S 판정법에서는 쇄석다짐말뚝의 저항계수가 Φ = 0.199~0.264으로 보정되었으며, AASHTO(2010) 등의 시방서에서 규정하고 있는 기초 구조물의 저항계수에 비해 상당히 낮은 값에 해당한다. 비선형 회귀분석으로부터 보정된 저항계수는 Φ = 0.344~0.434의 범위로 국내외 항타말뚝에 대한 저항계수(AASHTO, 2010; Park et al., 2008)와 유사한 범위를 보였다.

5. 극한지지력 평가법의 검증과 정재하시험의 조건

최근 구조물 기초 설계기준의 한계상태설계법으로 전환이 요구됨에 따라 한계상태설계법을 구성하기 위하여 신뢰성 있는 데이터베이스의 축적이 필요하며, 정재하시험은 말뚝 분야에서 뿐만 아니라 쇄석다짐말뚝에서도 극한지지력을 예측하는 가장 신뢰도가 높은 시험으로 여겨지고 있다. 그러나 실제 극한지지력을 예측하기 위해서는 극한하중을 확인할 수 있는 충분한 하중-침하량 곡선이 얻어져야 함에도 불구하고 현행 쇄석다짐말뚝의 정재하시험(KS F 2445)에서는 설계하중의 200%를 재하 하도록 규정하고 있기 때문에 극한지지력을 정확히 추정하기에는 한계가 있다.

본 연구에서는 쇄석다짐말뚝의 저항력에 대한 데이터베이스 축적을 목적으로 정재하시험을 수행하는 경우, 비선형 회귀분석으로 평가된 극한지지력의 신뢰도를 분석하고, 정재하시험으로부터 얻어야 할 하중-침하량 데이터의 조건을 검토하고자 하였다.

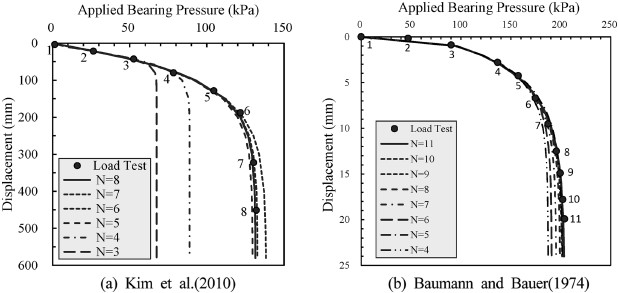
비선형 회귀분석으로 평가된 극한지지력의 신뢰도는 정재하시험이 충분히 수행되지 않았을 경우를 가정하여 본 연구에 이용된 두 현장의 정재하시험 데이터를 인위적으로 제거하면서 비선형 회귀분석을 수행하고, 실제 극한지지력과의 편차를 Table 6과 같이 나타내었다. 또한 정재하시험의 데이터수에 따른 하중-침하량 추정 곡선의 변화를 Fig. 8과 같이 검토하여 한계상태설계법을 구성하기 위한 정재하시험의 조건을 검토하였다.

Table 6.

Nonlinear regression analysis result according to load-displacement curve shape in static load test.

Fig. 8.

Load-displacement curve with change of number of data effect in static load test.

Kim et al.(2010)의 정재하시험 결과에서 하중-침하량 데이터가 5개(N = 5), 즉 항복하중(104.4 kPa)까지만 재하된 경우를 가정하면, log P-log S 분석법(Fig. 6(a))에서는 첫 번째 변곡점을 항복하중(40 kPa)으로 판단하고 실제 극한지지력의 50% 수준인 극한지지력으로 판정되는 반면, 비선형 회귀분석에서는 Table 4에서와 같이 실제 극한지지력(132.0 kPa)에 대하여 약 2% 오차 이내로 극한지지력(129.6 kPa)을 정확히 추정할 수 있는 것을 알 수 있다. Baumann and Bauer(1974)의 정재하시험에서도 항복하중 근처의 데이터만으로도 실제 극한지지력을 10% 오차범위 이내로 추정할 수 있는 것으로 나타나 비선형 회귀분석을 이용한 쇄석다짐말뚝의 극한지지력 판정법은 기존의 극한지지력 평가법에 비하여 유용성이 있으며, 실제 극한 지지력을 예측하는데 신뢰성이 높다고 평가할 수 있다.

실제 극한지지력에 대하여 10% 이내의 오차 정도로 예측할 수 있는 하중-침하량 데이터의 한계는 파괴시 침하량의 약14~28%, 극한하중의 67~79%가 재하될 경우이며, 도해적으로는 하중-침하량 곡선이 초기 직선부를 지나 최소한 한번의 변곡점이 발생되어야 하는 것으로 분석되었다. 따라서 향후한계상태설계법에서 쇄석다짐말뚝의 저항계수를 보정하기 위한 정재하시험을 별도로 수행하고, 실제 극한지지력을 정확히 예측하기 위해서는 정재하시험 시 항복하중 이상으로 재하시켜야 할 것으로 판단된다.

5. 결 론

본 연구에서는 쇄석다짐말뚝의 극한지지력을 비선형 회귀분석에 의해 판정하는 방법과 극한지지력 판정법이 한계상태설계법의 저항계수에 미치는 영향을 분석하고, 한계상태설계법의 데이터베이스 구축 시 요구되는 정재하시험 조건에 관하여 연구를 수행하였으며, 다음과 같은 결론을 얻었다.

(1) 다양한 회귀모형을 적용한 비선형 회귀분석으로 극한지지력을 예측한 바, 점근적 회귀모형인 지수함수 형태의 회귀방정식의 곡선적합도가 우수하여 실제 극한지지력과 을 예측하기에 적합한 것으로 평가되었다.

(2) 비선형 회귀분석을 이용한 극한지지력은 log P-log S 판정법을 이용한 극한지지력보다 비교적 크게 평가되는 경향을 보였으며, 0.1B 침하량 분석법에서는 큰 오차를 보이는 경우도 있었다.

(3) 쇄석다짐말뚝은 연약층의 심도, 비배수전단강도 등 원지반의 상태에 따라 큰 침하량이 발생하기도 하므로 침하량을 기준으로 극한지지력을 판정하는 0.1B 분석법은 쇄석다짐말뚝의 극한지지력을 예측하는데 적합하지 않은 평가법으로 판단된다.

(4) 비선형 회귀분석에 의해 산정된 저항편향계수는 1.0에 가까우며, 저항편향계수의 불확실성이 낮은 것으로 평가되었으며, 비선형 회귀분석으로 보정된 저항계수는 국내외 항타말뚝의 저항계수와 유사한 범위로 분석되었다.

(5) 현재 정재하시험법에서는 설계하중의 200%를 재하하중으로 규정하고 있으나, 향후 한계상태설계법을 위한 데이터베이스 구축을 목적으로 정재하시험을 수행하고 비선형 회귀분석을 수행하여 신뢰도 높은 극한지지력을 산정하기 위해서는 재하하중을 항복하중 이상으로 계획하여야 할 것으로 검토되었다.

Article information Continued