2.1 해석해

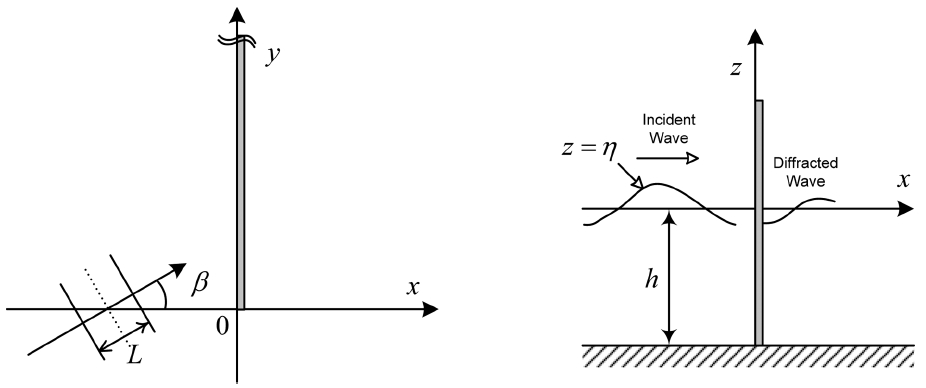
회절을 고려한 파력분포 해석을 위해 선형파 이론과 Penney and Price(1952)의 회절에 대한 해석해를 이용하여 파력식을 유도하였다. 수치해석을 위한 변수 및 구조물에 대한 설명은 Fig. 1을 참고할 수 있다. Fig. 1에서 L은 파장, β는 경사 입사각(즉, 구조물 전면에 수직인 선과 입사 파향선과의 교각)을 뜻하고, h는 평균수심, η는 자유수면변위를 뜻한다.

Fig. 1.

Definition sketch for the analysis of wave forces on a vertical breakwater.

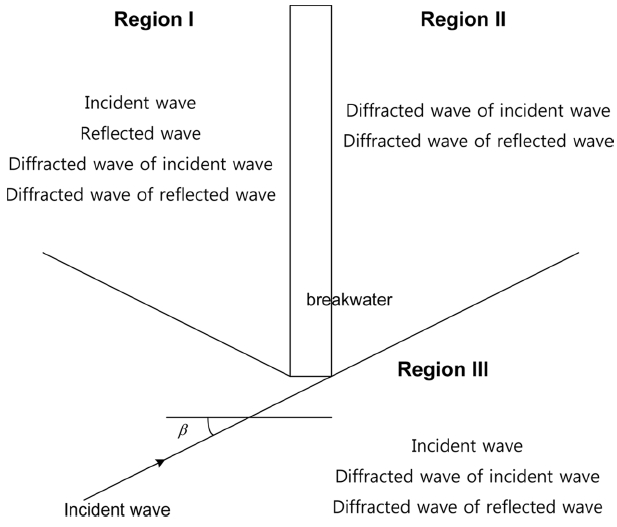
본 연구에서는 입사파, 반사파, 입사파의 회절 성분, 반사파의 회절 성분을 모두 반영하여 직립방파제에 작용하는 파력의 해석해를 제시하였다. 방파제 주위에서 각 영역별 파랑성분은 Fig. 2와 같다. 방파제의 전면(Region I)에는 입사파, 반사파, 입사파의 회절 성분 및 반사파의 회절 성분이 존재하고, 방파제의 후면(Region II)에는 입사파 및 반사파의 회절 성분이 존재한다.

Fig. 2.

Wave components in each area around the breakwater.

선형파 이론으로부터 방파제 전면에서의 입사파 및 반사파의 속도포텐셜을 다음과 같이 표현할 수 있다.

여기서, ϕ_i, ϕ_r은 각각 입사파와 반사파의 속도포텐셜이고, a_i(x,y), a_r(x,y)는 각각 입사파와 반사파의 진폭이고, ω는 각주파수, g는 중력가속도, K_r은 반사율이다. 방파제 전면에서 입사파 및 반사파 회절 성분의 속도포텐셜을 식 (4)와 같이 표현할 수 있고, 방파제 후면에서 입사파 및 반사파 회절성분의 속도포텐셜을 식 (5)와 같이 표현할 수 있다.

여기서, b_i,f(y), b_r,f(y) 는 방파제 전면에서 입사파의 진폭으로 무차원화 된 회절파의 진폭으로 각각 입사파와 반사파의 회절 성분이고, b_i,l(y), b_r,l(y)는 방파제 후면에서 입사파의 진폭으로 무차원화 된 회절파의 진폭으로 각각 입사파와 반사파의 회절 성분이다. 회절 성분들의 위상정보가 Penney and Price(1952)의 복소수로 표현된 해석해에 포함되어 있다. 각 회절 성분은 Penney and Price의 해석해를 이용하여 계산할 수 있으며, 다음과 같이 표현된다.

여기서

식 (9)와 식 (10)으로부터 다음과 같은 관계식이 성립한다.

식 (11)을 통해서 방파제 전면 및 후면에서 입사파 및 반사파의 회절 성분은 모두 동일한 값을 가짐을 알 수 있으며, 이를 통해서 방파제 후면에서 회절에 의해 생성된 에너지와 방파제 전면에서 회절에 의해 감소한 에너지가 동일함을 알 수 있다. 방파제 전면에서의 총 속도포텐셜은 다음과 같이 입사파, 반사파, 회절파의 합으로 나타낼 수 있다.

방파제 전면 및 후면에서 정수압을 제외한 파압(즉, p_f와 p_l)은 다음과 같다.

방파제 단위 폭당 파력은 파압을 바닥에서부터 평균해수면까지 적분하여 구할 수 있다. 본 연구에서 방파제 전면에서 후면으로 작용하는 파력의 방향을 + 로 두었다. 방파제 전면 및 후면에서의 단위 폭당 파력(즉, P_f와 P_l)은 다음과 같다.

방파제에서의 단위 폭당 총 파력은 방파제 전면 및 후면에서 작용하는 파력의 합으로 표현할 수 있으며 이는 다음과 같다.

회절을 무시한 지점별 총 파력은 식 (17)에서 회절 성분을 제거함으로써 구할 수 있으며 이는 다음과 같다.

회절을 고려한 경우의 지점 별 단위 폭당 총 파력과 회절을 무시한 경우의 지점 별 총 파력의 비(즉, 상대 총 파력, relative total force)는 다음과 같다.

방파제 전면에서 회절을 고려한 경우의 파력과 회절을 무시한 경우의 파력의 비(즉, 상대 전면 파력, relative front-side force)와 방파제 후면에서 회절을 고려한 경우의 파력과 회절을 무시한 경우의 파력의 비(즉, 상대 후면 파력, relative lee-side force)를 각각 다음과 같이 표현할 수 있다.

본 연구에서 유도한 회절을 고려한 파력과 회절을 무시한 경우의 파력의 비는 e^iωt항 및 e^–ikysinβ항이 약분되어 없어지므로 일정한 값을 갖는다. 따라서 본 연구에서 제안한 파력의 비는 e^iωt항 및 e^–ikysinβ항이 1인 경우에도 성립하므로 상대 파력의 최대값으로 볼 수 있다.

2.2 반무한방파제에 작용하는 파력 분포 특성

직립방파제 전면에서의 파고 및 파력은 입사파와 반사파 성분의 합으로 결정된다. 완전반사 조건에서 방파제 전면에서의 파고는 입사파고의 2배이다. 하지만 회절이 고려될 경우에는 이 값과는 다르다.

Tanimoto et al.(1976)은 일련의 수리모형실험 결과로부터 방파제 전면에 작용하는 파력으로 파랑이 경사지게 입사하는 경우 수직 입사 파력에 0.5(1 + cosβ)를 곱한 값을 제안하였다. 이후 실제 방파제 설계(Ministry of Oceans and Fisheries, 2005)에서 파랑의 경사 입사각 β가 15° 이상인 경우 방파제 전면에 작용하는 파력으로 수직입사 파력에 0.5(1 + cosβ')를 곱한 값을 사용하고 있다(Goda, 2000). 여기서는 경사 입사각 β(=β-15°)에 15° 만큼 보정한 경사 입사각이다. 본 절에서는 해석해를 이용하고 회절을 고려하여 경사 입사각에 따른 반무한방파제에서의 총 파력을 제시하고 Tanimoto et al.에 의한 보정값 0.5(1 + cosβ')와 비교하였다. 본 연구에서 직립방파제의 반사율 K_r 은 완전반사조건인 1.0으로 가정하였다.

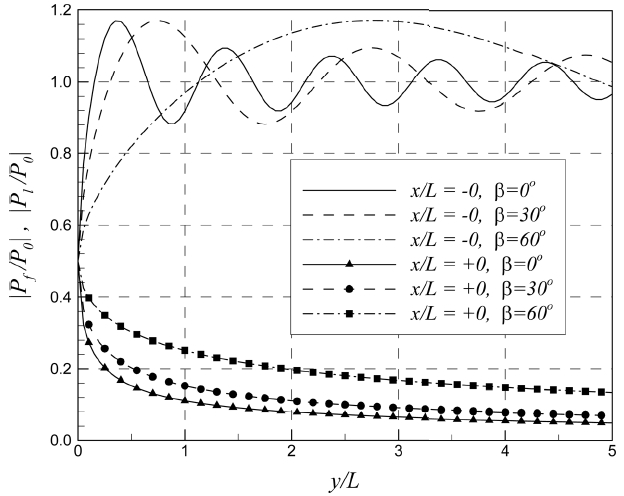
반무한방파제의 전면과 후면에 작용하는 상대 파력 분포를 Fig. 3에 도시하였다. 이 그림에서 x/L=+0은 방파제 후면을 의미하며, x/L=-0은 방파제 전면을 의미한다. 방파제 두부(y/L=0)에서 방파제 전면 및 후면에 작용하는 상대 파력은 반사가 발생하지 않기 때문에 0.5이다. 방파제 두부에서 멀어질수록 방파제 전면의 상대 파력은 위·아래로 진동하면서 1로 수렴하였다. 반면 방파제 후면에 작용하는 상대 파력은 방파제 두부에서 멀어질수록 감소하였다. 파랑의 경사입사각이 증가할수록 방파제 후면에 작용하는 회절파의 파력은 더 크게 증가하였다. 방파제 전면에서 중복파의 위상과 회절파의 위상이 일치하는 지점에서는 입사파, 반사파, 회절파이 파봉이 중첩되어 큰 파력이 발생할 것이다. 중복파의 위상과 회절파의 위상이 180^o 만큼 차이가 나는 지점에서는 중복파의 파봉과 회절파의 파곡이 중첩되어 작은 파력이 발생할 것이다. 따라서 방파제 전면에서 파력의 진동 양상이 발생하게 되는 것이다. 방파제 전면에서의 회절뿐만 아니라 후면에서의 회절까지 고려하면 파력의 진동 양상이 더 크게 발생할 것이다. 이는 전면의 회절 성분과 후면의 회절 성분이 180º 만큼 위상차가 나기 때문이다. 즉, 전면의 회절 성분이 파봉일 때 후면의 회절 성분은 항상 파곡이 되어 전·후 양면의 회절 성분에 의한 파력차가 더 크게 증폭되는 것이다. 방파제 전면에서의 회절파와 방파제 후면에서의 회절파가 180º 위상차가 난다는 사실을 Penney and Price(1952)와 Lee et al.(2005)의 연구에서 확인할 수 있겠다.

Fig. 3.

Distribution of relative front-side and lee-side wave forces on a semi-infinite breakwater.

경사 입사각이 β =0º, 30º, 60º 인 경우 반무한방파제의 전면, 후면, 전·후 양면에 작용하는 파력으로 회절을 고려한 것과 회절을 무시한 파력의 비(즉, 상대 전면 파력, 상대 후면 파력, 상대 총 파력)를 Fig. 4~6에 도시하였다. 해석해의 정확성을 검증하기 위해 Radder and Digemans(1985)가 제시한 쌍곡선형 완경사방정식을 이용한 수치해도 함께 비교하였다. 경사 입사파를 조파하기 위해 직선조파기법을 쓰면 90º 각도의 두 조파선이 만나는 지점에서 파랑에너지가 과다하게 또는 과소하게 생성되어 에너지 불연속에 의한 회절이 발생한다. 이러한 문제를 최소화하기 위하여 Lee and Yoon(2007)이 제안한 곡선조파기법을 사용하였다. 해석해와 완경사방정식에 의한 수치해가 거의 일치하여 본 연구에서 제시한 해석해가 타당함을 확인하였다. 방파제의 두부(즉, |P_t|)에서 방파제에 작용하는 총 파력(즉, y/L=0)은 방파제의 앞·뒤 폭이 0인 조건에서 전면에 작용하는 입사파의 파력과 후면에서 작용하는 회절파의 파력이 상쇄되어 0이 된다. 방파제에 작용하는 총 파력은 전면에 작용하는 파력에 비해 진동하는 진폭이 더욱 컸다. 이는 전면의 회절 성분과 후면의 회절 성분이 180° 만큼 위상차가 나서 총 파력에 고려된 전면에서의 회절성분에 후면에서의 회절 성분을 뺀 값의 크기가 전면의 파력에 고려된 전면에서의 회절 성분의 크기보다 더 크기 때문이다. 파랑의 경사 입사각이 증가할수록 방파제 전면에 작용하는 파력 진동패턴의 파장이 더 크게 증가하였다.

Fig. 4.

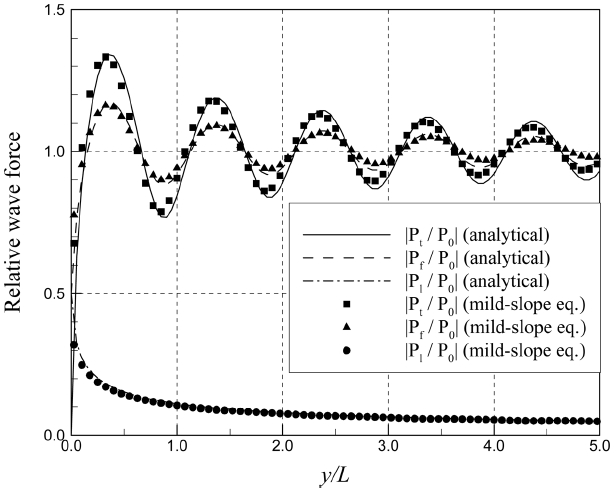
Distribution of relative front-side, lee-side, and total wave forces on a semi-infinite breakwater (β = 0°).

Fig. 5.

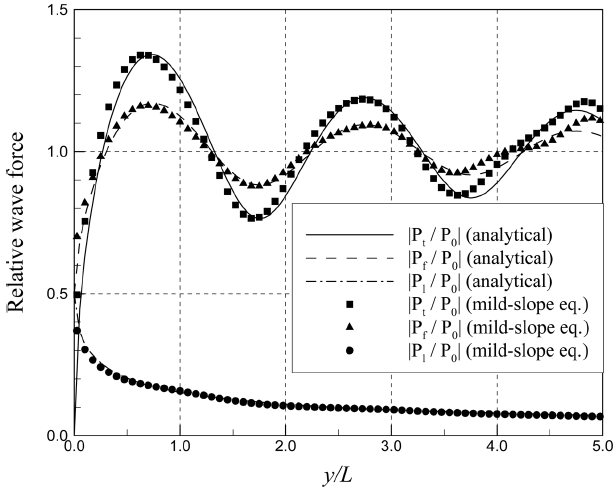
Distribution of relative front-side, lee-side, and total wave forces on a semi-infinite breakwater (β = 30°).

Fig. 6.

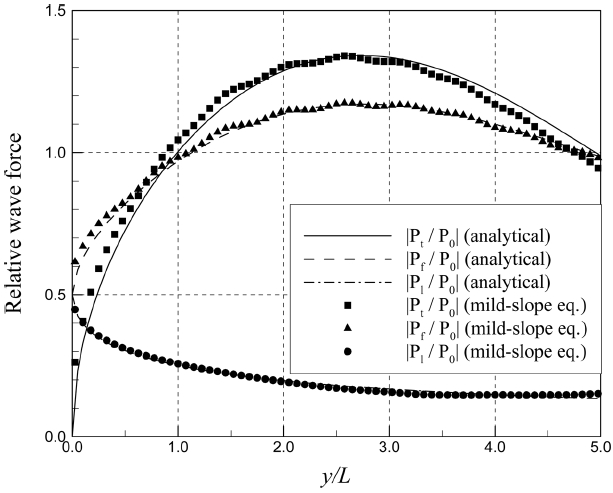
Distribution of relative front-side, lee-side, and total wave forces on a semi-infinite breakwater (β = 60°).

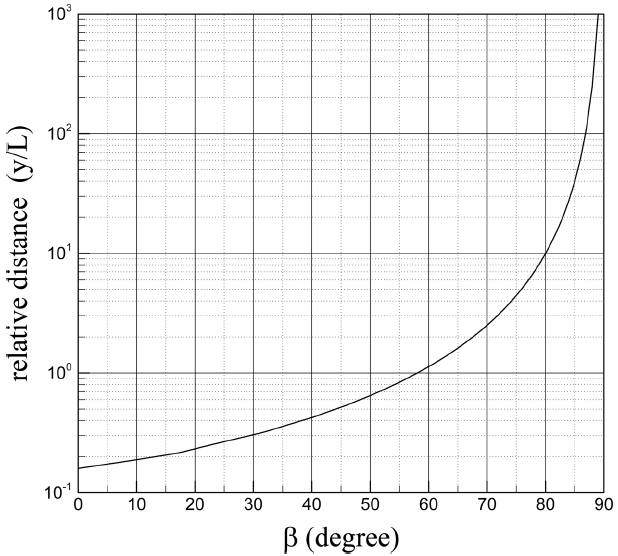
Fig. 7은 상대 전면 파력이 방파제 두부에서 시작하여 처음으로 1.0에 도달하는 지점이 두부로부터 떨어진 거리를 경사 입사각의 함수로 도시한 그림이다. 두부로부터 떨어진 거리를 파장으로 나눈 상대 거리로 표현하였다. 파랑의 경사 입사각이 증가할수록 파력의 비가 1.0에 도달하는 상대 거리가 기하급수적으로 증가함을 볼 수 있다. 경사 입사각이 60° 이상인 경우 y/L이 1.0 이상인 상대 거리의 지점에서 상대 파력이 1.0에 도달하였다. 또한 경사 입사각이 80° 이상인 경우에는 y/L이 10.0 이상의 지점에서 상대 파력이 1.0에 도달하였다. 따라서 경사 입사각이 큰 경우 회절에 의해 방파제 전면에서의 상대 파력 분포가 대부분 1.0 이하임을 알 수 있다. 방파제 두부에서 벽면 쪽으로 위치한 중복파 에너지와 벽면 반대 쪽에 위치한 입사파 에너지의 불연속선이 경사각이 클수록 두부에서 벽면 쪽으로 더 멀어지기 때문에 두부에 가까운 벽면에서 상대 파력이 작아지게 되는 것이다.

Fig. 7.

First relative distance where |PfP0|=1.0 according to incident wave angle.

파랑의 경사 입사각(β)과 방파제 두부로부터의 상대 거리(y/L)에 따른 반무한방파제 전면에 작용하는 상대 파력(즉, 상대 전면 파력)의 분포를 Fig. 8 및 Fig. 9에 나타내었다. Fig. 8에는 Tanimoto et al.(1976)이 제안한 항도 함께 비교하였다. 방파제 전면에서 회절에 의하여 파력이 아래 위로 진동하는 경향이 있는데 이를 무시하면 대체적으로 경사 입사각이 증가할수록 상대 전면 파력이 1.0에서 0.5로 감소하는 경향이 있다. 이러한 경향은 Tanimoto et al.이 제안한 0.5(1 + cosβ'와 유사하다. 하지만 엄밀히 말하면 경사 입사각이 β = 90° 인 경우 Tanimoto et al.이 제시한 상대 전면 파력은 0.5가 아니라 0.63이다. 경사 입사각이β = 0° 인 경우 상대 전면 파력은 두부에서 떨어진 상대 거리(즉,y/L)가 멀어지면서 1.0을 중심으로 아래 위로 진동하였다. 이러한 진동은 회절로 발생한 것이다.

Fig. 8.

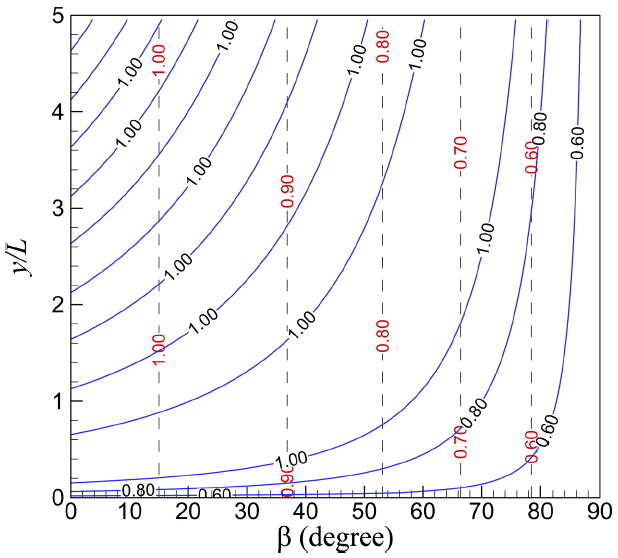
Comparison of the relative wave force distribution in front of a breakwater when considering diffraction (solid line) and from Goda’s formula 0.5(1 + cosβ′) (dashed line).

Fig. 9.

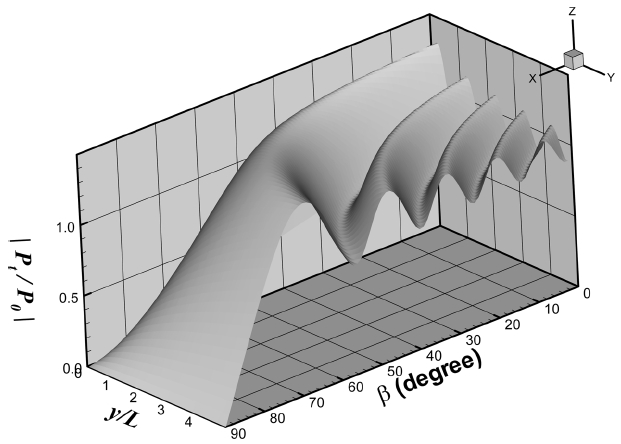
Relative wave force distribution in front of a breakwater for y-directional distances and obliquely incident wave angles.

파랑의 경사 입사각(β )과 방파제 두부로부터의 상대 거리(y/L)에 따른 반무한방파제 전·후 양면에 작용하는 상대 파력(즉, 상대 총 파력)의 분포를 Fig. 10 및 Fig. 11에 나타내었다. 과거 대부분의 연구에서는 방파제 전면에 작용하는 파력만을 고려하였다. 회절이 발생할 경우 방파제 후면에도 파력이 작용한다. 또한 방파제 후면 뿐만 아니라 전면에서도 회절이 발생한다. 만약 전면의 어느 지점에서 중복파의 파봉이 위치하고, 그 지점의 후면에 회절파의 파곡이 위치할 경우 방파제에 작용하는 상대 파력은 후면 방향으로 더 증가하게 될 것이다. 따라서, 회절이 발생하는 경우 방파제 전·후 양면에 작용하는 총 파력을 설계파로 사용하는 것이 더욱 타당할 것이다. 상대 총 파력은 방파제 두부로부터의 상대 거리가 y/L=0이거나 경사 입사각이 β = 90° 일 때 0이 된다.

Fig. 10.

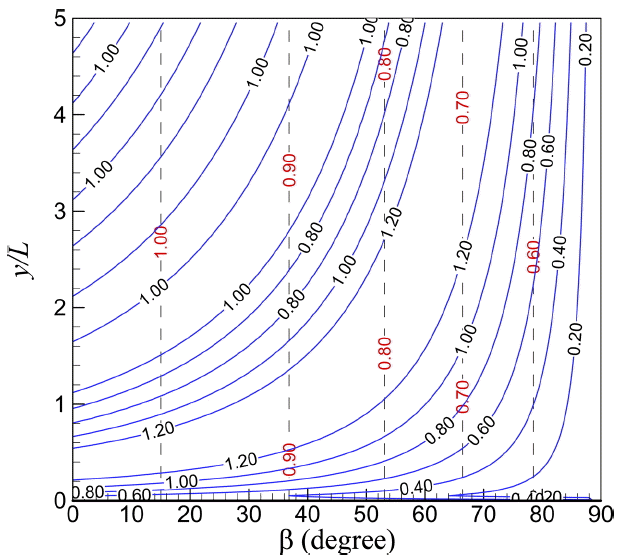
Comparison of the total relative wave force distribution on a breakwater when considering diffraction (solid line) and from Goda’s formula 0.5(1 + cosβ′) (dashed line).

Fig. 11.

Total relative wave force distribution on a breakwater for y-directional distances and obliquely incident wave angles.

3.1 다방향 불규칙파의 상대 파력 정의

회절을 고려하여 반무한방파제에 작용하는 다방향 불규칙파의 파력은 2.1절에서 제시한 규칙파의 상대 파력을 이용하여 계산할 수 있다. 즉, 불규칙파를 구성하는 에너지스펙트럼을 각각의 규칙파로 분해하여 2.1절에서 제시한 상대 파력을 계산하고 이를 재합성하는 방법을 사용하였다. 규칙파의 경우 진폭만으로 상대 파력을 결정할 수 있다. 왜냐하면 주파수 성분이 하나여서 위상 값이 규칙적으로 변하기 때문이다. 하지만 불규칙파의 경우 서로 다른 주파수 성분의 제곱은 위상 값이 서로 다르기 때문에 진폭만으로 상대 파력을 결정할 수 없다. 따라서, 불규칙파의 경우 각 성분의 제곱의 평균을 취한 후 제곱근을 취하여 상대 파력을 결정할 필요가 있다. 다방향 불규칙파의 파력 계산을 위해서 주기는 0.05 Hz에서 0.41 Hz까지 Δf=0.02 Hz 를 적용하였으며, 방향은 -180도에서 +180도까지 Δβ=1°를 적용하여 총 6,498개의 성분파로 분해하여 계산한 후 합성하였다. 방파제의 각 위치에 작용하는 다방향 불규칙파의 각 성분파의 파력은 식 (17)을 이용하여 다음과 같이 다시 쓸 수 있다.

여기서 f는 주파수를 나타내며, ν는 0에서 2π까지 변하는 난수(random number)로 불규칙파 각 성분의 위상을 나타낸다. 회절을 고려하지 않은 경우 방파제 단면에 작용하는 파력은 식 (18)을 이용하여 다음과 같이 표현할 수 있다.

방파제에 작용하는 다방향 불규칙파의 상대 파력은 회절을 고려한 경우 방파제에 작용하는 각 성분 파력의 제곱 평균의 제곱근(root mean square)과 회절을 무시한 경우 파력의 제곱 평균의 제곱근의 비로 정의할 수 있다. 이는 식 (22)와 식 (23)을 이용하여 나타낼 수 있다. 다방향 불규칙파의 상대 파력은 각 성분파의 위상정보를 고려하여야 하므로 아래 식과 같이 실수부만 취해야 한다.

위 식에서 Re[P(f, β)]란 복소수인 P(f, β)의 실수부만 취한다는 의미이다. 식 (24)을 다시 정리하면 다음과 같다.

여기서 S(f, β)는 다방향 불규칙파 스펙트럼을 뜻하며, δ(f, β)는 다음과 같이 표현된다.

다방향 불규칙파 스펙트럼 구성을 위해서 주파수 스펙트럼으로 Hasselmann et al.(1973)이 제안한 JONSWAP 스펙트럼을 사용하고, 방향스펙트럼으로 방향의 비대칭을 고려한 Lee et al.(2010)의 방향 분포 함수를 사용하였다.

3.2 다방향 불규칙파의 파력 특성

반무한방파제 형식의 직립구조물에 작용하는 불규칙파의 상대 파력을 검토하였다. 수심은 10 m로 두고 유의파고는 1m 로 두었다. 불규칙파 상대 파력의 정의는 3.1절 식 (25)와 같은데, 식 (25)에는 각 성분파의 불규칙적인 위상이 포함되어 있어 실무에서 적용하기에는 어려움이 있다. 따라서, 아래 식 (27)과 같은 파력 스펙트럼을 이용한 상대 파력과 제곱 평균 제곱근 비를 이용한 상대 파력을 함께 비교 검토하였다.

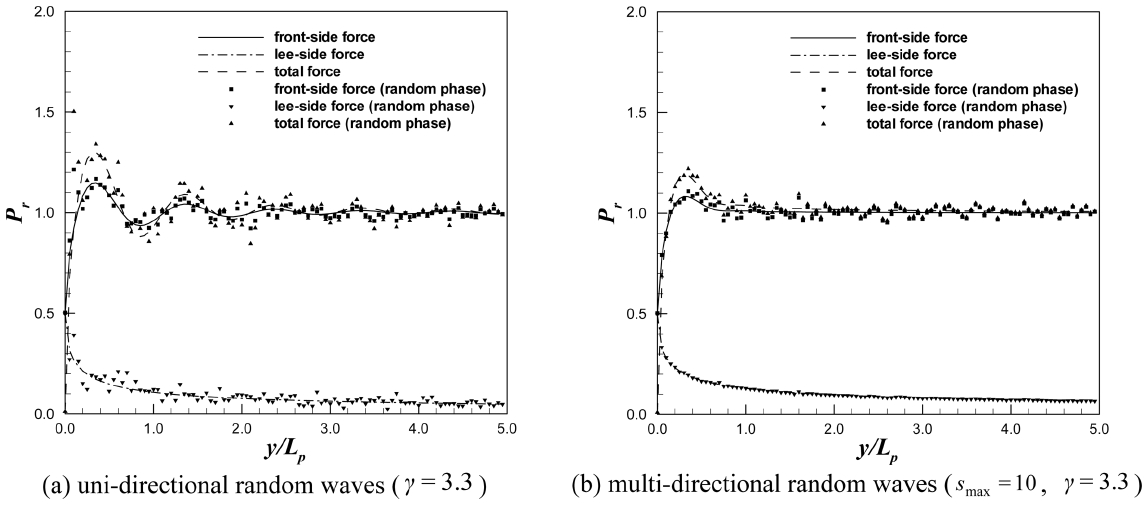
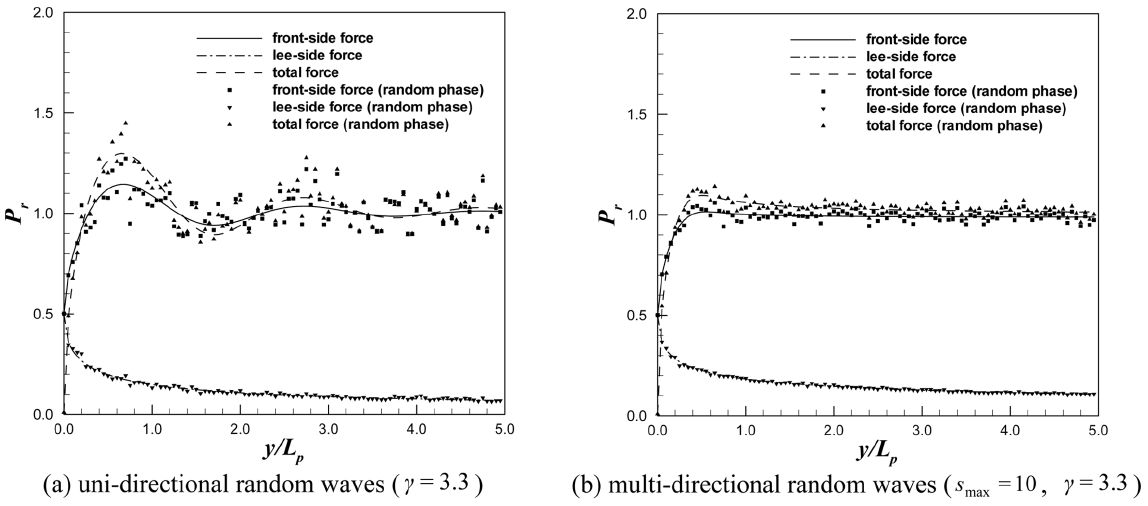
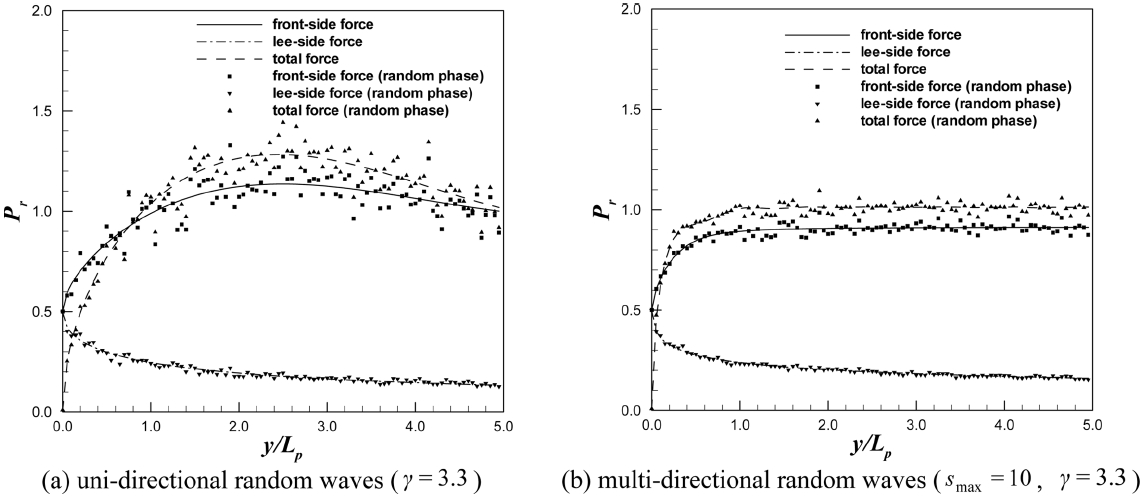
불규칙파 각 성분파의 위상을 고려한 경우(즉, 제곱 평균 제곱근 비를 이용한 상대 파력)와 고려하지 않은 경우(파력 스펙트럼을 이용한 상대 파력)를 Fig. 12-14에 도시하였다. 각 그림에서 (a)는 일방향 불규칙파를 나타내며, (b)는 다방향 불규칙파를 뜻한다. 실선은 파력 스펙트럼을 이용한 상대 파력으로 전·후 양면에 작용하는 총 파력, 파선은 전면에 작용하는 파력, 그리고 일점쇄선은 후면에 작용하는 파력을 나타낸다. 그리고, 부호로 표현된 그림은 불규칙파 각 성분파의 위상을 고려한 제곱 평균 제곱근 비를 이용한 경우이다. 다방향 불규칙파 해석을 위해 첨두신장계수(peak enhancement factor)로 3.3을 사용하고 방향 분포 계수(directional spreading parameter)로 10을 사용하였다.

Fig. 12.

Relative wave force for random waves on semi-infinite breakwater (β = 0°).

Fig. 13.

Relative wave force for random waves on semi-infinite breakwater (β = 30°).

Fig. 14.

Relative wave force for random waves on semi-infinite breakwater (β = 60°).

해석 결과 각 성분파의 재곱 평균 제곱근 비를 이용한 상대 파력과 파력 스펙트럼을 이용한 상대 파력은 거의 일치하였다. 일방향 불규칙파랑의 경우 임의의 위상을 고려한 제곱 평균 제곱근 비의 경우 좀 더 불규칙한 파력 특성을 보였는데, 이는 일방향 불규칙파의 경우 다방향 불규칙파에 비해 구성하는 파랑 성분의 숫자가 적어서 각 성분파의 위상이 미치는 영향이 좀 더 크기 때문인 것으로 판단된다. 반면 다방향 불규칙파의 경우 매우 많은 규칙파 성분이 존재하여 각 성분의 임의의 위상이 서로 상쇄되어 파력 스펙트럼을 이용한 상대 파력과 거의 일치하였다. 따라서, 회절을 고려하여 반무한 방파제 각 지점에 작용하는 불규칙파의 상대 파력은 식 (27)을 적용하여도 충분히 정확한 결과를 나타냄을 알 수 있다.

일방향 불규칙파의 경우 주파향각(β_p)이 증가할수록 방파제에 작용하는 총 파력의 최대치는 방파제 두부로부터 먼 곳에서 나타났다. 그리고, 규칙파와 같이 전반적으로 주파향각(β_p)이 증가할수록 상대 파력은 감소하는 경향을 보였다.

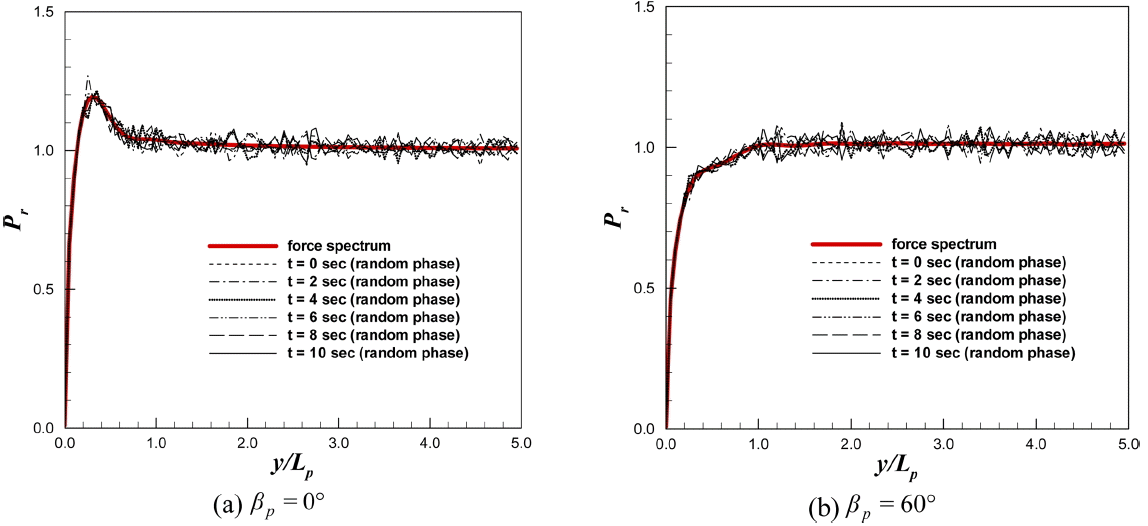
시간의 경과에 따라 달라지는 불규칙파의 상대 파력에 대해 Fig. 15에서 검토하였다. 입사파랑의 주 파향이 0°와 60° 인 경우의 상대 파력을 각각 Fig. 15(a), Fig. 15(b)에 도시하였다. 경과한 시각이 2초 간격으로 0초에서 10초까지의 상대 파력을 검토하였는데, 제곱 평균 제곱근 비를 이용한 상대 파력은 Fig. 15에서 보는 바와 같이 파력 스펙트럼을 이용한 상대 파력을 중심으로 위 아래로 진동하는 형태로 분포하였다. 이는 제곱 평균 제곱근 비를 이용할 경우 시간에 따라 바뀌는 회절파 성분의 위상 정보가 포함되어 있기 때문이다. Fig. 15를 통해 볼 때, 파력 스펙트럼을 이용한 상대 파력은 제곱 평균 제곱근비를 이용한 상대 파력의 평균값을 나타내므로 충분히 파력 검토에 활용할 수 있다. 좀 더 보수적인 파력 검토를 위해서는 제곱 평균 제곱근 비를 이용하는 것도 충분히 고려할 필요가 있을 것이다.

Fig. 15.

Relative wave force for random waves progressing time (s_max = 10, γ = 3.3).

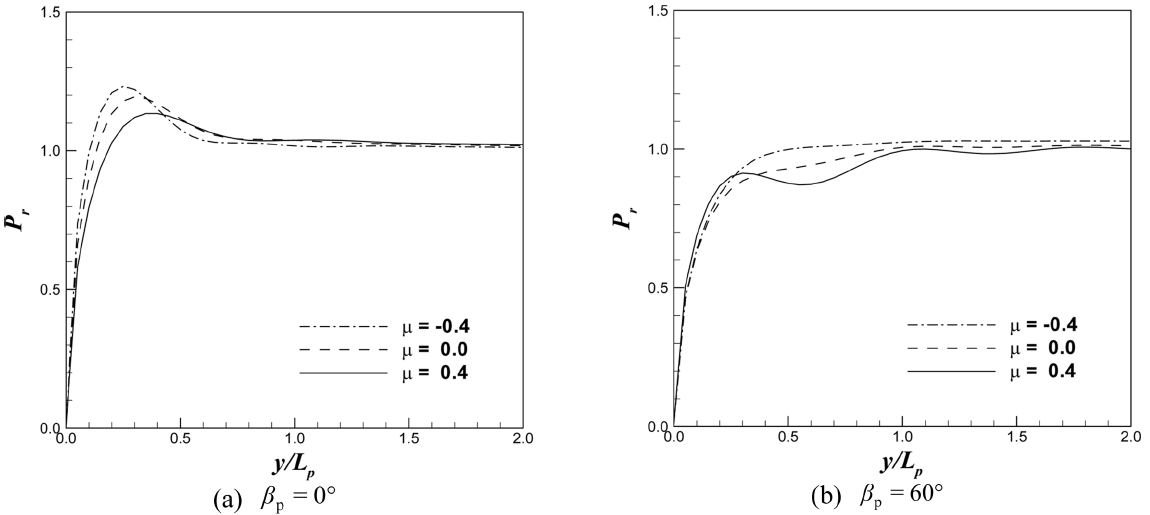
다방향 불규칙파의 방향 비대칭의 영향에 대해서도 검토하였다. 주 파향의 경사 입사각이 양수일 때 비대칭계수(μ)가 음수이면 방파제에 수직인 파향 성분이 넓게 분포하고, 비대칭계수가 양수이면 방파제에 수직인 파향 성분은 좁게 분포한다. 주파향의 입사각이 0° 인 경우는 Fig. 16(a), 입사각이 60° 인 경우는 Fig. 16 (b)에 도시하였다. 주 파향이 0° 인 경우 비대칭계수가 음수이면 입사각이 음수인 성분의 에너지가 더 크다. 따라서, Fig. 16 (a)와 같이 비대칭계수가 μ=-0.4인 경우 상대 파력이 가장 크게 계산되었다. 주 파향이 60° 인 경우 비대칭계수가 음수(즉, )이면 경사 입사각이 60° 보다 작은 성분이 더 넓게 분포하여 상대 파력의 크기가 커진다. 반면 비대칭계수가 양수(즉, μ=-0.4)인 경우에는 방파제에 수직인 성분이 좁게 분포하여 상대적으로 파력의 크기가 작아지게 된다.

Fig. 16.

Relative wave force for random waves as directional asymmetry (s_max = 10, γ = 3.3).