해운대의 겨울철 파랑 및 흐름에 대한 평면 2차원 수치모델링
Numerical Simulation of Winter Waves and Currents in the Haeundae Coast using 2DH Model
Article information
Abstract
겨울철 해운대 해역에서 발생하는 파랑 및 흐름에 대한 공간적 변화특성을 살펴보기 위하여, 평면 2차원 파랑변형 모델(SWAN)과 수심평균 2차원 해수유동 모델(Delft3D)을 사용하여 수치실험을 수행하였다. 2014년 2월 중 해운대 여러 정점에서 관측한 현장자료를 사용하여 수치모델을 검증하였다. 두 모델의 보정결과로부터 발견된 파랑 및 흐름의 특징 중 하나는, 해저면에 곳곳에 돌출되어 자리잡고 있는 암반지형의 영향으로 파고 및 파향 뿐만 아니라 유속 및 유향도 만내로 들어올수록 외해역과 다르게 크게 변형되어 나타난다는 것이다. 두 모델의 커플링을 통하여 겨울철 입사파를 고려한 연안 해수유동 모델링 결과, 해안선 인근 천해에서는 겨울철에 발생하는 동쪽(E)계열의 입사파의 영향으로 파고가 높을수록 동에서 서로 흐르는 연안류도 크게 발달하고 조석에 의한 조류의 세기는 상대적으로 약한 것으로 나타났다.
Trans Abstract
In order to investigate characteristics of waves and currents varying in space in the Haeundae coast in winter, numerical simulations by using a 2-D spectral wave model(SWAN) and 2-DH hydrodynamic model(Delft3D) were carried out in this study. The results of numerical simulations were validated with the field data collected at several different locations in the study area in February, 2014. From the numerical simulations, it was found that waves and currents were significantly influenced in terms of direction and magnitude by bottom topography characterized by straggling rock crops covered with sea grasses. The coupling of SWAN and Delft3D models also revealed that alongshore currents directing from the east to the west were developed in the nearshore, due to the influence of larger waves with the main incident direction from the east.
1. 서 론
연안에서의 지형변화 현상은 주로 파랑과 조석을 외력으로 하여 발생하는 흐름에 의해서 야기된다. 흐름에 의해서 모래가 움직이기 시작하고, 또한 흐름에 의해서 다른 지역으로 이동하게 된다. 이러한 이유로, 연안에서의 지형변화 현상에 대한 이해도를 높이기 위해서는 먼저 연안 흐름패턴의 특성에 대한 깊이 있는 연구가 요구된다.
수심이 얕은 천해에서는 쇄파대에서 파고의 쇄파응력(radiation stress)에 기인하는 연안류의 발생정도에 따라 연안의 흐름패턴이 변하게 된다. 조차가 작고 조석운동의 영향이 미미하며 파랑이 우세한 환경에서 흐름패턴의 구조는 일반적으로 파랑의 입사특성에 의해서 크게 좌우된다. 반면, 우리나라의 서해 및 남해와 같이 조석운동의 영향을 무시할 수 없는 환경에서는, 조석현상과 파랑운동을 함께 고려하여 연안의 흐름패턴을 이해해야 한다.
우리나라 연안에서 발생하는 파랑의 특성은 계절적으로 뚜렷한 차이를 보이고 있다. 여름철에는 주로 평상시에 잔잔하지만 태풍 내습시에는 파고가 매우 크고 주기가 대체로 긴 파랑이 발생한다. 겨울철에는 지속적으로 강하게 불어오는 북서풍의 영향으로 겨울내 대체로 높은 파고와 다양한 주기를 갖는 파랑이 지배적이다. 겨울철 북서풍의 영향으로 서해안에서는 북서쪽으로부터 높은 파고의 파랑이 발생하여 전파해오며, 반면 동해안에서는 고파랑이 북쪽 ~ 북동쪽 사이의 방향으로부터 전파해 들어온다. 이 때문에, 여름철 보다는 겨울철에 연안 지형변화 현상이 심각하게 발생하는 경우가 많다. 반면, 남해안은 겨울철 북서풍의 방향과는 먼 쪽으로 바다를 마주하고 있어 고파랑의 영향이 상대적으로 작다. 또한, 남해안은 서해안 보다 조차가 작지만 동해안 보다 조차가 크다. 이로 인해, 남해안에서의 겨울철 해수유동을 이해하는 데에는 파랑 및 조류의 영향을 동시에 고려하는 것이 필요하다.
해운대 해수욕장은 부산시 해운대구에 위치해 있으며, 남남동(SSE) 방향으로 남해와 접해있다. 이 해수욕장은 포켓비치 형태(pocket-shape)의 사질 해안으로, 길이가 약 1.5 km 그리고 폭은 약 100 m 정도의 크기를 가지고 있다. 해수욕장의 동·서방향으로 양 끝단에서, 서쪽의 동백섬 바위돌출부와 동쪽의 미포항 해안구조물이 모래사장의 경계가 되고 있다. 해안선의 수직방향으로 해저면의 경사도는 평균적으로 약 1:35 정도이며, 서쪽은 이 보다 약간 경사도가 낮은 반면 동쪽은 이 보다 좀 더 높은 경사도를 보인다. 이 지역에서 조석운동은 일조부등인 반일주조 형태를 띠고 있으며, 조차는 약 0.5 ~ 1.3 m 범위에서 변화를 보인다.
본 연구의 대상해역인 해운대 해수욕장에서 발생하는 파랑 및 흐름에 대한 연구는 이안류 예경보 및 연안 지형변화 현상의 이해도를 높이기 위해 많은 연구자들에 의해 수행되었다. Choi et al.(2004)과 Lee et al.(2007a)에서는 방사선 동위원소 추적자 실험을 통해 해운대 해역의 흐름 및 모래이동에 대한 연구를 수행하였으나, 그 결과를 수치모델과 직접적으로 비교 및 검증하지는 않았다. Lee et al.(2007b)과 Kim et al.(2013)에서는 해운대에 내습하는 파랑 및 해빈류에 대한 수치모의를 수행하였으나, 상대적으로 깊은 수심(20 m 이상)에서 장비를 계류하여 연안에서 발생하는 수리현상을 규명하기에는 한계가 있다. Kim et al. (2011)에서는 해운대에서 발생하는 이안류를 모의하기 위해 파랑 변형 및 해빈류에 대한 수치모의를 수행하였다. 기존의 연구와는 다르게 상대적으로 수심이 얕은 연안역에 ADCP 1기를 계류하여 자료를 수집하였으나, 수치모델과의 직접적인 비교는 수행하지 않았다. Kim et al.(2014)에서는 해운대 해역의 중앙 부분에 Aquadopp Profiler를 설치하여 해빈류에 대한 수직 연직 분포를 파악하였으나, 이를 수치모델과의 비교 및 검증에 활용하지 않았다.
본 연구에서는, 남해안의 동부 끝단에 해당하는 해운대 해역을 대상으로 조석운동의 영향과 함께 겨울철에 발생하는 파랑을 동시에 고려하여 흐름패턴의 구조를 살펴보고자 하였다. 2차원 파랑모델(SWAN)과 수심평균 2차원 해수유동 모델(Delft3D)을 사용하여 수치모의를 수행하였으며, 여러 정점에서의 파랑 및 흐름 자료를 이용하여 수치모델과의 비교하였다. 그리고 해운대 전면에 위치한 암반 지역의 마찰계수(bottom roughness)를 조절하여 수치모의 결과의 신뢰도를 크게 향상시켰으며, 이를 통해 해운대 해역에서 발생하는 파랑 및 흐름에 대한 공간적인 변화 특성을 분석하였다.
2. 현장 관측 자료
본 연구에서는 2014년 2~3월 부산 해운대의 전면 해역에서 집중 관측실험의 수행을 통하여 수집한 관측자료들(Do et al., 2015) 중 2월 13일부터 2월 27일까지 수집된 약 14일간의 관측자료를 사용하였다. 현장 관측실험 기간 중, 파랑 및 해류 등 해수동력학자료는 3개 정점에서 층별 유속 관측장비(AWAC)와 또 다른 3개 정점에서 정밀 수리 관측시스템(SPHINX 및 TISDOS)를 설치하여 측정하였다. Fig. 1은 관측장비들의 설치위치를 나타낸다. 위 3대의 AWAC 장비들은 해안선의 법선 방향으로 평균수심이 약 5 ~ 22 m의 범위이고, 해안선으로부터 거리가 약 100 ~ 1,500 m인 범위에 설치되었다. 또한, 3대의 정밀 수리 관측시스템은 해안선을 따라 해수욕장의 양 끝단과 중앙부에 평균수심의 범위가 4 ~ 9 m인 지역에 설치되었다. 특히, 해류의 연직 프로파일 자료는 AWAC 및 정밀 수리 관측시스템의 ADCP 장비로 바닥 저면에서 수직 상향으로 0.5 또는 1.0 m 간격으로 측정되었다. 바닥 저면의 경계층 유속을 측정하기 위하여, 또한 3대의 Aquadopp 장비를 해안선을 따라 연안 가까이 설치하였으나, 본 연구에서는 수심평균 2차원 수리모델을 사용하기 때문에 여기서는 그 관측자료를 사용하지 않았다.
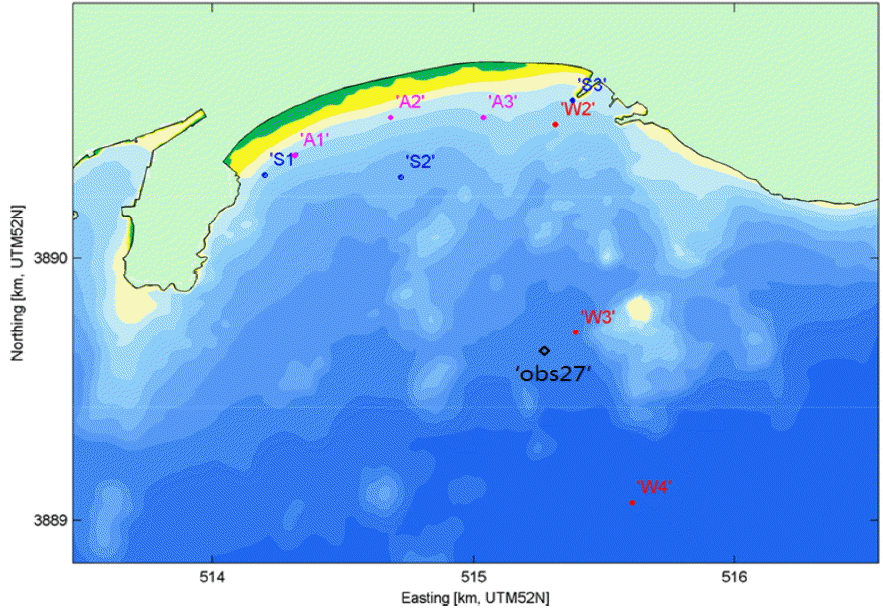
Monitoring locations in Haeundae bay during the February 2014 field campaign. W, S and A denote AWAC, ADCP and Aquadopp, respectively. The indication of ‘obs27’ is the location arbitrarily selected for consistency check of current modeling through grid nesting between the local and detailed domains, which is discussed in the section 4.
3. 연구 방법
3.1 해수유동모델
해수유동모델인 Delft3D 모델은 비압축성 유체를 가정한 연속방정식과, 3차원 운동량 방정식에서 천수(shallow water) 조건 및 Boussinesq 근사를 적용한 나비에스톡스(Navier Stokes) 방정식을 계산하여 수심평균한 2차원 또는 3차원 유속 벡터장을 산출해낸다. 또한, 이 해수유동 모델은 해수유동을 유발하는 주요 외력으로 바람, 조석 및 파랑을 고려할 수 있으며, 주로 공학적인 사용을 목적으로 수심평균한 평면 2차원 영역에 대한 수치모델링을 위하여 최적화되어 있다. Delft3D 모델에 사용되는 연속방정식은 식 (1)과 같이 수심평균한 편미분방정식으로 표현될 수 있다.
여기서, t는 시간, d는 수심, η는 해수면높이, x 및 y는 수평방향 거리, u 및 수평방향 유속을 나타낸다.
운동량 방정식에서는, 천수조건 및 Boussinesq 근사에 의한 정수압 가정에 의해서 수직방향(z방향) 성분의 운동량 방정식은 생략되고, 수평방향 성분의 운동량 방정식만이 사용된다. 수평성분인 x 및 y 방향의 운동량 방정식은 각각 식(2) 및 (3)과 같이 수심평균한 형태로 표현될 수 있다. 만약 이 해수유동 모델로부터 3차원 공간에 대한 유속장을 계산하는 3차원 모델링의 경우, 수직방향(z 방향) 유속은 3차원 연속방정식을 사용하여 계산하게 된다.
여기서, g는 중력가속도, f는 코리올리스(Coriolis) 파라미터, Fx 및 Fy 는 x방향과 y방향으로 각각 작용하는 외력(파랑, 바람 등), ρw는 물의 밀도, v는 물의 확산계수, τbx 및 τby는 x방향과 y방향으로 작용하는 해저면 전단응력이다. 본 연구에서는, 연구 대상지역의 해수유동모델링에 대해서 3차원 모델링 대신에 수심방향(z-방향)으로 흐름을 평균하여 계산하는 수심평균 2차원(2DH) 모델링을 사용하였다.
3.2 파랑모델
Delft3D-WAVE의 파랑변형 모델인 SWAN 모델에 사용되는 기본방정식은 파랑작용의 평형방정식(wave action balance equation)이다. 이 파랑모델은 파랑 작용을 파향 에너지 스펙트럼의 형태로 표현하고, 2차원 수평공간에 대해서 파랑 스펙트럼 의변화를식 (4)와 같이 에너지 평형 방정식에 의하여 계산한다.
여기서, θ는 방향, σ는 상대 각주파수, N은 작용 밀도 스펙트럼, S는 원천항을 나타낸다. 또한, cx, cy, cσ 및 cθ는 각각 x, y, σ 및 θ에 대한 파랑의 전파속도를 나타낸다. 작용 밀도 스펙트럼 N(σ, θ)은 에너지 밀도 스펙트럼 E(σ, θ)에 대해서 N(σ, θ) = E(σ, θ)/σ의 관계를 갖는다.
3.3 모델링 절차
연구대상지역인 해운대 해수욕장의 연안에서 해수유동의 특성과 파랑의 공간적 변형특성을 동시에 고려하기 위하여, Delft3D 모델과 SWAN 모델을 결합하여 모델링하였다. 해운대 연안에서 해수유동 모델링을 위해 조석운동의 경계조건은 광역 격자체계 내에 중역 및 협역 격자체계로 이어지는 3단계 네스팅(nesting) 과정을 통해 광역으로부터 끌어오는 것으로 하였다. 해운대 연안에 해당하는 협역 격자체계에서 파랑모델링을 위한 외해 경계조건은 수심 약 22 m 지점에서(Fig. 1에서 W4 정점) 측정한 파랑자료를 사용하였다. Fig. 2는 해수유동모델의 네스팅 3단계 과정과 협역 격자체계에서 수행된 해수유동 모델과 파랑변형 모델 사이의 결합이 수행되는 단계를 보여주는 모델링 절차를 보여주고 있다. Delft3D 모듈 내에서 수행되는 해수유동 모델과 파랑모델 결합은 각 시간마다 1차적으로 파랑 모의를 수행한 후, 계산 결과를 통신(Communication)파일을 생성하여 저장한다. 그 후, 해수유동 모델 계산 시 통신 파일을 통해 파랑 모델의 결과를 읽어 들여, 조석과 파랑에 의해 발생하는 흐름에 대한 수치모의를 수행한다(Lesser et al., 2004). 해수유동 모델의 계산결과는 다시 다음 단계의 파랑모델 계산을 위해 통신파일을 업데이트시킨다.
3.4 격자체계의 구성 및 매개변수의 설정
Fig. 3(a)은 해수유동모델에 사용한 3단계 모델 네스팅 격자체계를 보여준다. 광역모델의 계산영역은 대한해협 및 일본열도의 서쪽 해안선을 포함하도록 격자체계를 정방격자로 구성하였다. 이 광역모델의 격자크기는 약 2 × 2 km이고, 수심자료는 GEBCO-08의 데이터베이스로부터 추출하였다.
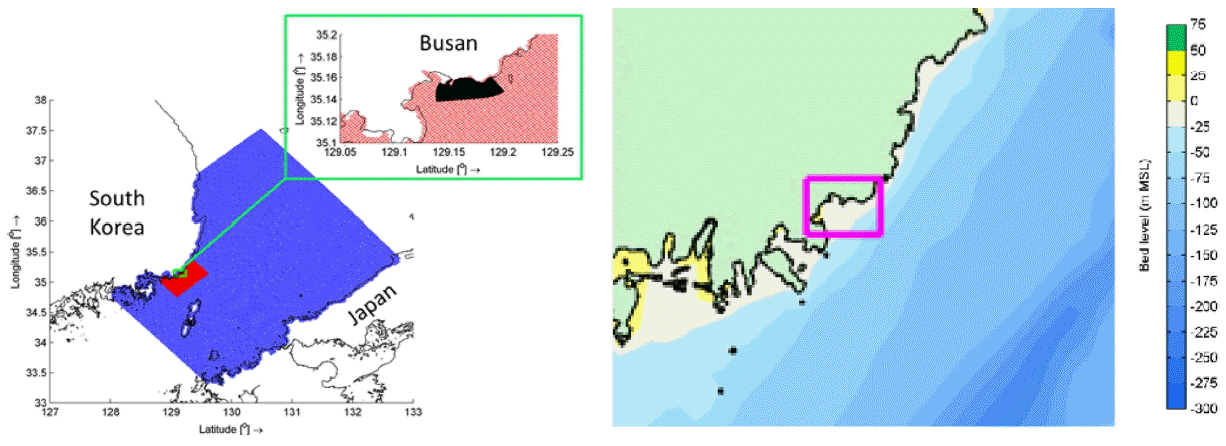
(a) Grid systems of the hydrodynamic model for three-stage nesting procedure: (blue) regional model, (red) local model and (black) Haeundae model domains. (b) wave model domain for the Haeundae coastal area within the red open box.
중역모델의 계산영역은 해운대 뿐만 아니라 부산시의 해역을 포함하도록 격자체계를 정방격자 구성하였으며, 격자크기는 약 200 × 200 m이다. 이 영역의 수심자료는 국립해양조사원의 해도자료로부터 추출한 자료이다. 상세역인 해운대모델의 계산영역은 천해로부터 심해의 수심 약 25 m 지점 정도까지를 포함하도록 격자체계를 직교곡선격자체계(curvilinear grid)로 구성하였다. 이 격자체계의 크기는 외해측에서는 약 20 × 20 m 정도이고, 내해측 천해에서는 8 × 8 m 정도로 줄어든다. 수심자료는 해운대 연안정비사업에서 2014년 3월에 수행한 수심측량조사로부터 획득한 자료를 사용하였다. Fig. 3(b)는 파랑모델에 사용한 해운대 연안의 계산영역을 보여준다. 격자크기는 약 20 × 20 m 정도이며, 수심자료는 2014년 3월에 수집한 수심측정자료를 사용하였다.
Table 1은 해수유동모델과 파랑모델을 설정하는 과정에서 사용한 매개변수의 값을 요약한 것이다. 이 중에서 해수유동 모델에 사용한 수평적 와점성계수(horizontal eddy viscosity)는 격자크기도 고려하여 결정해 주어야 하는 값으로, 여기서는 해운대 연안의 계산영역에 대한 민감도 테스트를 통하여 1.5 m/s2으로 정했다.
3단계 네스팅의 각 해수유동모델의 계산시간 간격(time step)은 조석의 전파속도를 고려한 쿨랑수(Courant number for wave propagation: CFL)가 각 계산영역에 걸쳐 10 이하가 유지되도록 식 (5)를 통하여 결정하였다.
여기서, Δt는 계산시간 간격, H는 수심, Δx 및 Δy는 각각 x방향 및 y방향의 격자크기를 나타낸다.
3.5 경계조건
해수유동모델과 파랑모델의 각 계산영역의 모서리 부분에 해당하는 경계면에 대해서 적절한 경계조건 값을 입력해 주어야 한다. 파랑모델의 경우, 해운대 연안에 해당하는 협역 계산영역만을 고려하므로, 앞의 3.3에서 설명하였듯이 외측 경계조건은 수심 약 22 m 지점에서 측정한 파랑자료를 사용하였다.
해수유동모델의 경우, 3단계 네스팅을 위한 3개의 계산영역이 설정되어 있으므로 각 계산영역에 대한 경계조건을 설정해 주어야 한다. 여기서는, 광역 계산영역에 대한 경계조건으로 토펙스 포세이돈(Topex Poseidon) 7.2 데이터베이스로부터 추출한 9개의 조화상수(M2, S2, N2, K2, K1, O1, P1, Q1, M4) 값들을 입력해 주었다. 포세이돈 7.2는 오레곤 주립대학에서 연산하여 제공하는 전 지구 조석 데이터베이스로 라플라스 조석 방정식 연산 및 위성자료와의 자료 동화를 통해 1/4도의 해상도로 13개 조화 상수에 대한 자료를 포함하고 있다(Egbert and Erofeeva, 2002). 중역 계산영역에 대해서는, 외해측 경계조건으로 광역 계산영역에서 계산된 수위결과를 경계 입력조건으로 사용하였고, 양측면의 경계선을 따라서는 광역 계산영역에서 계산된 유속결과를 경계조건으로 사용하였다. 협역 계산영역에 대해서는, 외해측 및 양측면의 모든 경계선에 대해서 리만 경계조건(Riemann invariant boundaries)을 적용하였다.
4. 연구 결과 및 토론
해운대에서 2014년 2~3월 중 수집한 관측자료를 사용하여 해운대 연안의 협역에 대한 해수유동 모델과 파랑변형 모델을 보정하기에 앞서, 해수유동 모델의 광역과 중역에서 조석운동의 수치모델링을 보정 및 검증하였다. 이후, 광역과 중역에서 검증된 해수유동 모델의 수치계산 결과를 연구대상지역인 협역의 경계조건으로 사용하여, 협역에서 Delft3D 모델과 SWAN 모델의 결합을 통하여 흐름과 파랑변형을 계산하였다. 협역에 대해서 수행된 흐름과 파랑의 수치계산은 관측자료와 비교를 통하여 보정 및 검증되었다.
4.1 광역과 중역의 해수유동 모델링 결과
광역과 중역에 대해서는, 해수유동 모델로부터 조석운동에 의한 조위와 조류를 계산하였으며, 조위의 계산결과는 부산에서 가까이에 위치한 조위관측소들의 관측자료와 비교를 통하여 보정하였다. 여기서 사용된 조위관측소들은 4개 지점으로 부산, 울산, 거제도 및 일본 대마도 북단에 위치한 오카와티이다. 이들 관측소의 위치에서 계산된 조위의 모델링 결과는 관측결과와 비교되었으며, 모델 계산결과의 오차를 최소화하기 위하여 광역격자 영역의 경계조건으로 사용한 토펙스 포세이돈 데이터베이스의 9개 조화상수들의 값들을 Table 2와 같이 조정하였다. Fig. 4는 보정된 조화상수를 경계조건으로 사용하여 부산 조위관측소의 위치에서 계산된 약 40일 간 예측결과이다. 관측결과의 비교하여 전체 평균오차가 1% 이내로 잘 일치하며, 최대 오차는 사리기간 중 저조시 약 9~10% 정도로 발생하기도 하였다.

Correction factors used to calibrate the tidal predictions by the regional model and applied to tidal constituents along the open boundaries.
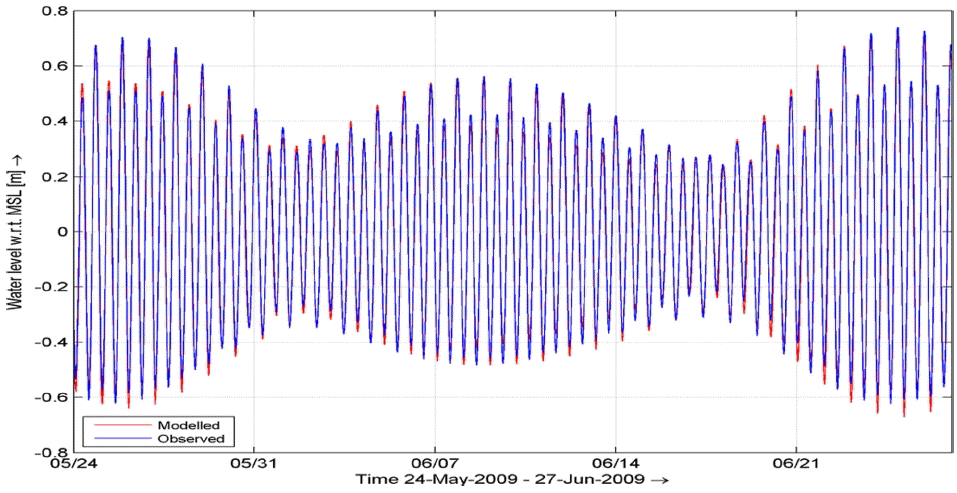
Comparison between the predicted and observed water levels in the period of May 24 ∼ June 27, 2007 for the Busan tidal station.
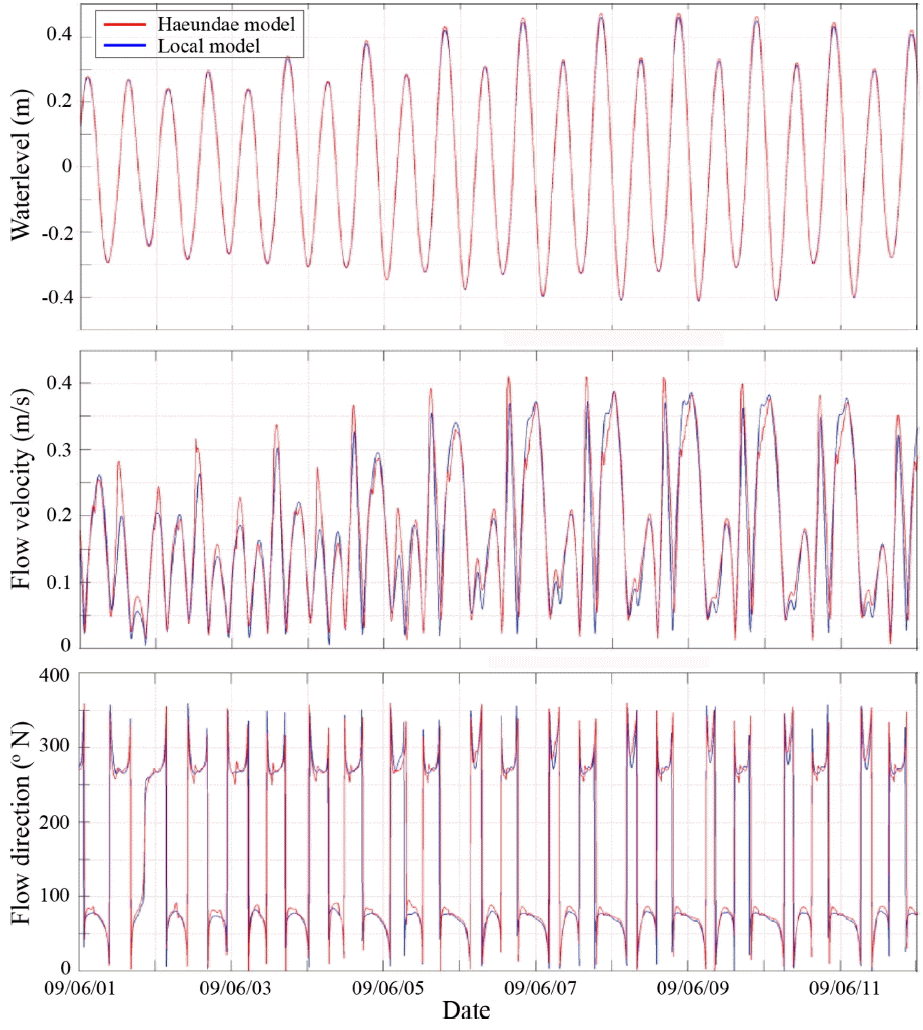
해수유동 모델의 수치계산체계가 광역-중역-협역의 3단계 네스팅 체계로 구축되어 있으므로, 네스팅을 통하여 흐름의 수치계산 과정이 일관성있게 이루어지는 지의 여부를 Fig. 5와 같이 확인하였다. Fig. 5는 광역에서 계산된 조위 및 조류의 계산결과를 중역의 경계조건으로, 또한 중역의 계산결과를 협역의 경계조건으로 입력하여 계산한 예측결과들을 비교한 것이다. 이 그림은 Fig. 1의 해운대 해역에 표시된 지점 obs27의 위치에서 중역 격자체계에서 산출된 조위, 조류 및 유향의 계산결과와 협역 격자체계에서 산출된 계산결과를 비교한 것을 보여준다. 중역과 협역에서 각각 계산된 조위 및 조류가 동일한 값을 예측하고 있으며, 이는 중역에서 협역으로의 네스팅에 따른 수치계산이 일관되게 이루어지고 있음을 보여준다.
4.2 협역에서 해수유동모델과 파랑모델의 수치모의 결과
협역에서의 해수유동 모델링은 실제 현장에서 해수유동을 일으키는 주요 두가지 외력인 조석운동과 파랑의 영향을 동시에 고려하기 위하여, 조석운동에 의한 흐름과 파랑운동 사이의 상호작용을 반영하도록 해수유동 모델과 파랑변형 모델을 결합하여 수행하였다. 이를 위하여, 해수유동모델 Delft3D와 파랑모델 SWAN을 30분 간격으로 각각 수치계산 결과를 주고 받도록 결합(coupling)하였다. 결과적으로, 협역에서 계산된 해수유동 수치모의 예측결과는 조위 및 조류 뿐만 아니라 파랑의 쇄파에 의한 야기되는 연안류도 같이 포함하고 있다. 협역에서 해수유동 모델링과 파랑변형 모델링의 정확도는 2015년 2월 중 현장 실험기간에 수집된 관측자료와 수치계산 결과의 비교를 통하여 동시에 보정되었다. 관측자료와 비교하여 수치모의 예측결과의 오차를 줄이기 위해, 모델 구성 시 사용된 물리적 인자를 조정하여 두 모델을 보정하였다.
Fig. 6~7은 협역에서 해수유동 모델과 파랑변형 모델의 모델 보정 전후 수치모의 예측결과와 관측자료를 비교한 것이다. 해수유동 모델과 파랑변형 모델을 보정하기 전에는 수심 7m 안쪽에 위치한 W2, S1 및 S3 지점에서 고파랑 발생 시 수치모의 결과와 0.3 m/s 이상 유속을 과대하게 산정하였으며, 파고의 경우에는 0.4 m 정도의 오차를 보인다. W3 지점은 수심이 약 15 m에 이르지만 동편에 높은 암초가 위치하고 있어, 파랑 및 흐름이 주변 지형의 영향을 많이 받고 있다. 이러한 지형적 영향으로 인해 고파랑 내습시 수치모의 결과가 관측치보다 0.5 m 이상 적게 재현하였다.

Comparisons between the observed and the modeled of (a) currents and (b) significant wave heights for the locations of W2, W3 and W4.
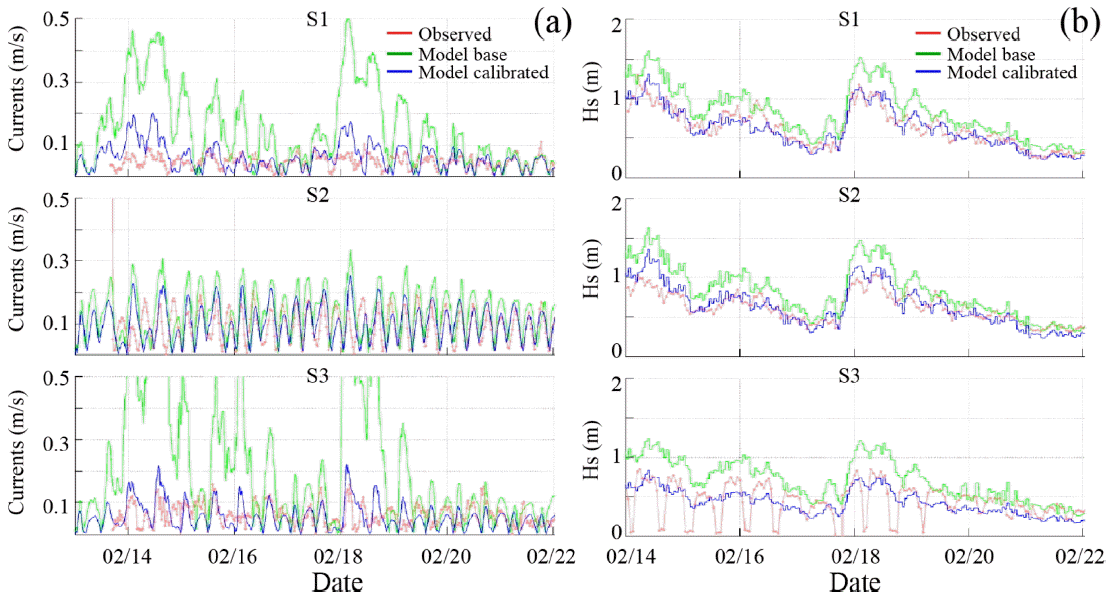
Comparisons between the observed and the modeled of (a) currents and (b) significant wave heights for the locations of S1, S2 and S3.
해수유동 모델 및 파랑변형 모델을 보정하기 위해서, 모델 설정에 사용된 물리적 인자들 중에서 해저 바닥면의 마찰계수(bottom roughness)를 조정하였다. 모델의 초기 구성시 사용한 마찰계수의 값으로 매닝계수(Manning coefficient)의 기본값인 0.02 s/m1/3을 협역의 전 영역에 대해서 동일하게 적용하였었다. 이 기본값을 사용한 모델링 결과가 해안선 인근에서 유속 및 파고가 크게 나타남에 따라 이렇게 과대로 계산된 예측결과를 효과적으로 감소시키기 위하여, 바닥면에서 마찰계수를 매닝계수 대신 마찰특성길이(roughness length)를 사용하여 공간적인 지형특성을 반영하도록 다른 값들을 적용하였다. Fig. 8(b)은 해운대 협역에 흐름모델 및 파랑모델의 보정을 위해 적용된 마찰특성길이의 분포를 보여 준다. Fig. 8(a)는 해운대 해역에 대한 위성사진이다. 이 그림에서 빨간색 타원모양으로 표시된 지역은 모래가 아닌 암반지역이며 수초가 많이 자라는 지역으로, 특히 여름철에는 수초가 바닥면에서 해수면에 이르기까지 무성하게 자란다. 이러한 지형적 특성을 고려하여 모래지역과 암반지역에 각각 바닥면의 마찰특성길이 값을 달리 적용하여, Fig. 8(b)와 같이 수초가 자라는 암반지역에는 높은 값(ks = 1.00)을 사용하여 마찰 계수를 증가 시켰으며, 그 외 모래지역은 기본값을 사용하였다.
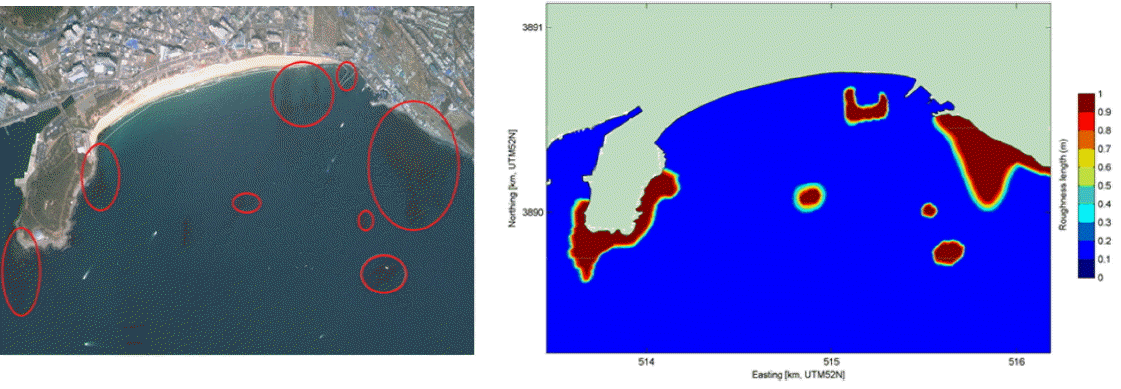
(left) Satellite image showing the Haehundae coast and (right) spatial varying bed roughness field specified in White-Colebrook Ks values.
해저 바닥면에서 마찰계수의 조정으로 해수유동모델 및 파랑모델을 보정한 이후에는 (Fig. 7), 해안선 인근의 관측지점에서 유속의 크기 및 파고가 많이 감소하였고 관측자료와 비교하여 비교적 잘 일치하였다. 반면, 수심 약 15 m 깊이의 W3 지점에서는 모델을 보정한 이후에도 파고의 예측자료가 관측자료와 비교하여 0.5m 내의 오차가 나타나고 있다(Fig. 6). 이는 동쪽에 위치하고 있는 암반지형의 영향으로 실제로는 회절현상이 많이 일어나고 있지만, SWAN 모델은 이러한 현상을 재현하는데 한계가 있는 것에 기인한 것으로 판단된다.
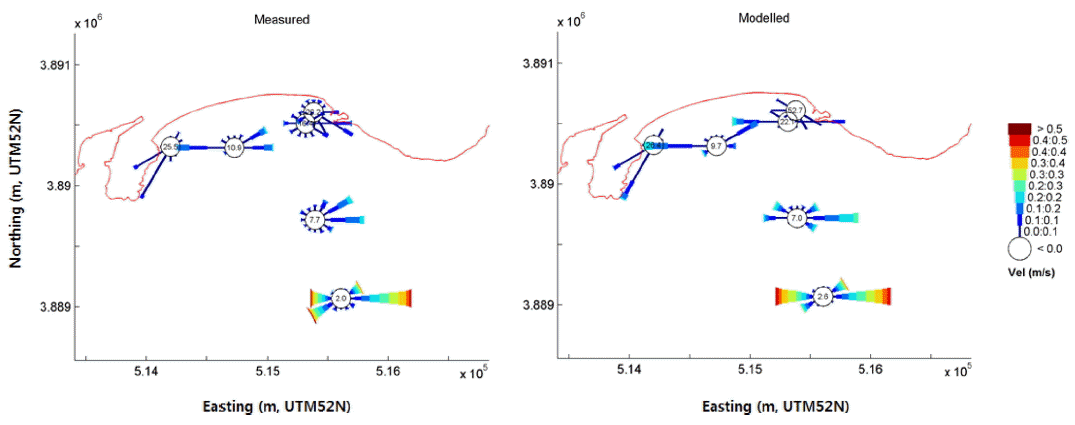
Fig. 9~10은 모델 보정 이후 각 관측지점에서 관측된 유속의 세기 및 유향, 그리고 파랑의 파고 및 파향에 대한 통계치(장미도)를 모델링 결과자료와 서로 비교한 것이다. 우선, 해수유동 모델링 결과를 보면(Fig. 9), 수심이 상대적으로 깊은 외해의 W3 및 W4 지점에서는 조석운동의 지배적인 영향으로 형성되는 유향 및 유속의 동서방향 패턴이 잘 재현되는 것을 확인할 수 있다. 수심이 얕은 해안선 인근의 천해에서는, 주변지형 및 수심의 영향으로 유속은 감소되고 유향은 해안선에 평행하게 형성되는 특징을 또한 잘 재현하고 있다.
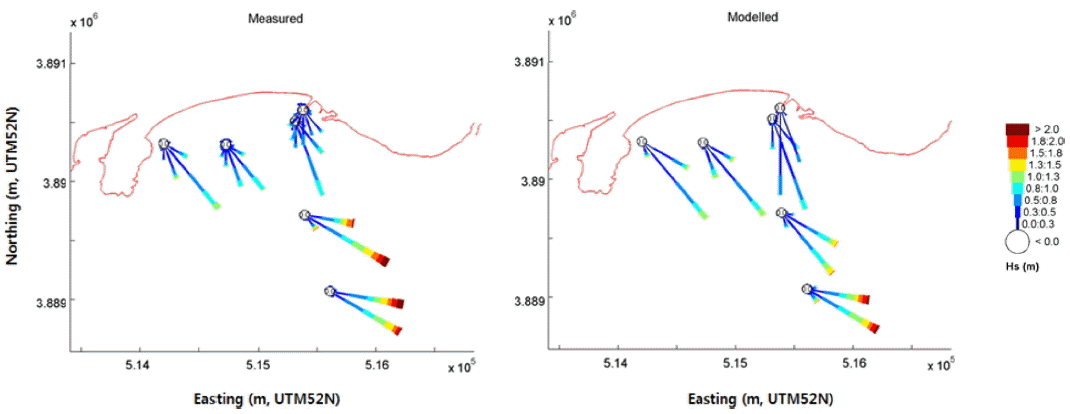
The observed (left) and the modeled (right) significant wave height roses for the validation period.
다음으로, 파랑변형 모델링 결과를 보면 (Fig. 10), 해수유동 모델링의 경우와 유사하게 외해에서 천해로 이동할수록 수심 및 주변지형의 영향을 받아 파고가 감소하는 경향을 잘 재현하고 있다. 또한, 겨울철 관측기간 중 외해에서는 동남동 계열의 입사파향이 발생하였으나, 해안선 인근까지 진행하는 동안 파향이 점차 굴절되어 해안선에 거의 수직으로 나타나는 현상을 잘 재현하고 있다.
4.3 파랑이 해수유동 패턴에 미치는 영향
앞의 서론에서 언급하였듯이 천해를 포함하는 협역에서는 파랑의 쇄파로 인하여 연안류(파랑류)가 발생한다. 일반적으로 파고가 높을수록 그리고 해안선의 법선방향에 대해서 입사각이 클수록 강한 연안류가 발생한다. 반면, 파고가 낮을수록 쇄파대가 발달하지 않아 연안류의 발생은 미미하며 조석운동에 의한 흐름만이 지배적으로 존재하게 된다. 본 연구에서도 천해에서 조류 이외에 흐름과 파랑 사이의 상호작용의 효과를 고려하도록 해수유동 모델과 파랑변형 모델을 결합하였고, 앞의 4.2에서 제시된 것과 같이 여러 지점에서의 현장 관측자료를 사용하여 이 두 모델을 보정 및 검증하였다.
해운대 해역은 겨울철에 주로 동쪽계열의 파랑이 입사하는 것으로 제시된 바 있다(Lee et al., 2007; Kim et al., 2013). 본 연구에서 사용된 관측자료도 겨울철인 2014년 2월 중에 수집된 것으로, Fig. 10(a)에서 제시된 것과 같이 동남동 계열의 입사파가 지배적인 것을 알 수 있다. Fig. 11 ~ 12는 본 연구의 관측자료 수집기간 동안 협역에 대해서 해수유동 모델과 파랑변형 모델의 결합을 통하여 계산된 시계열 유속장 결과 중 일부를 보여준다. Fig. 11의 (a)와 (b)는 조위가 만조일 경우 고파랑 및 저파랑 조건에서 각각 발생하는 유속장이다. 외해역에서 전체적인 흐름의 방향은 고파랑 및 저파랑 조건에서 모두 공통적으로 우리나라를 둘러싼 조석운동의 영향으로 서쪽에서 동쪽으로 발달하고 있는 것을 알 수 있다. 반면, 해안선 부근에서는 수심이 얕아 바닥마찰이 크고 또한 지형배치의 상대적인 복잡성 때문에 조석운동의 영향이 줄어들어, 흐름이 약하게 발생하는 것을 Fig. 11(b)에서 확인할 수 있다. 하지만, Fig. 11(a)는 해안선 부근에서 E계열의 고파랑 조건이 만조시 발생했을 경우 강한 연안류가 동에서 서쪽으로 발달하는 것을 보여준다. 이는 연안 쇄파대에서 약 2 m 이상의 입사파가 부서지면서 동쪽계열 입사파향의 영향으로 동에서 서쪽으로 강한 연안류를 발생시키기 때문이다. 이 연안류의 유향은 만조시의 조류의 유향에 반하는 것으로, 이 해역의 연안에서는 높은 파고에 의해 기인하는 연안류가 조류에 의한 유속 보다 더 강하게 영향을 미치고 있음을 나타낸다.
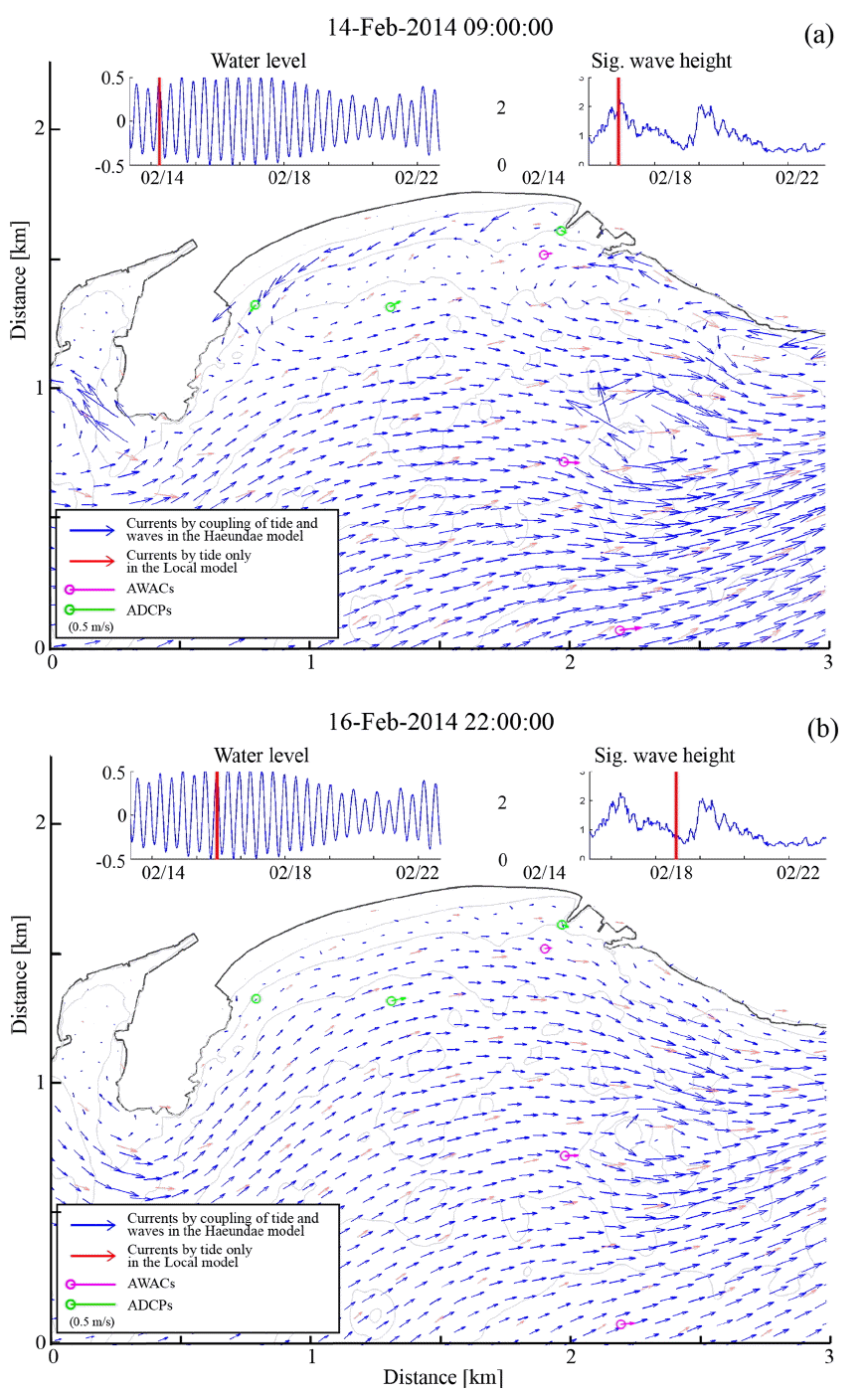
An instantaneous capture of the modeled velocity fields for the high tide with (a) a large wave case (Hm0 = 2.36 m; Tp = 7.66 sec; Dp = 111.64 degN) and (b) a small wave case (Hm0 = 0.84 m; Tp = 10.36 sec; Dp = 117.46 degN).
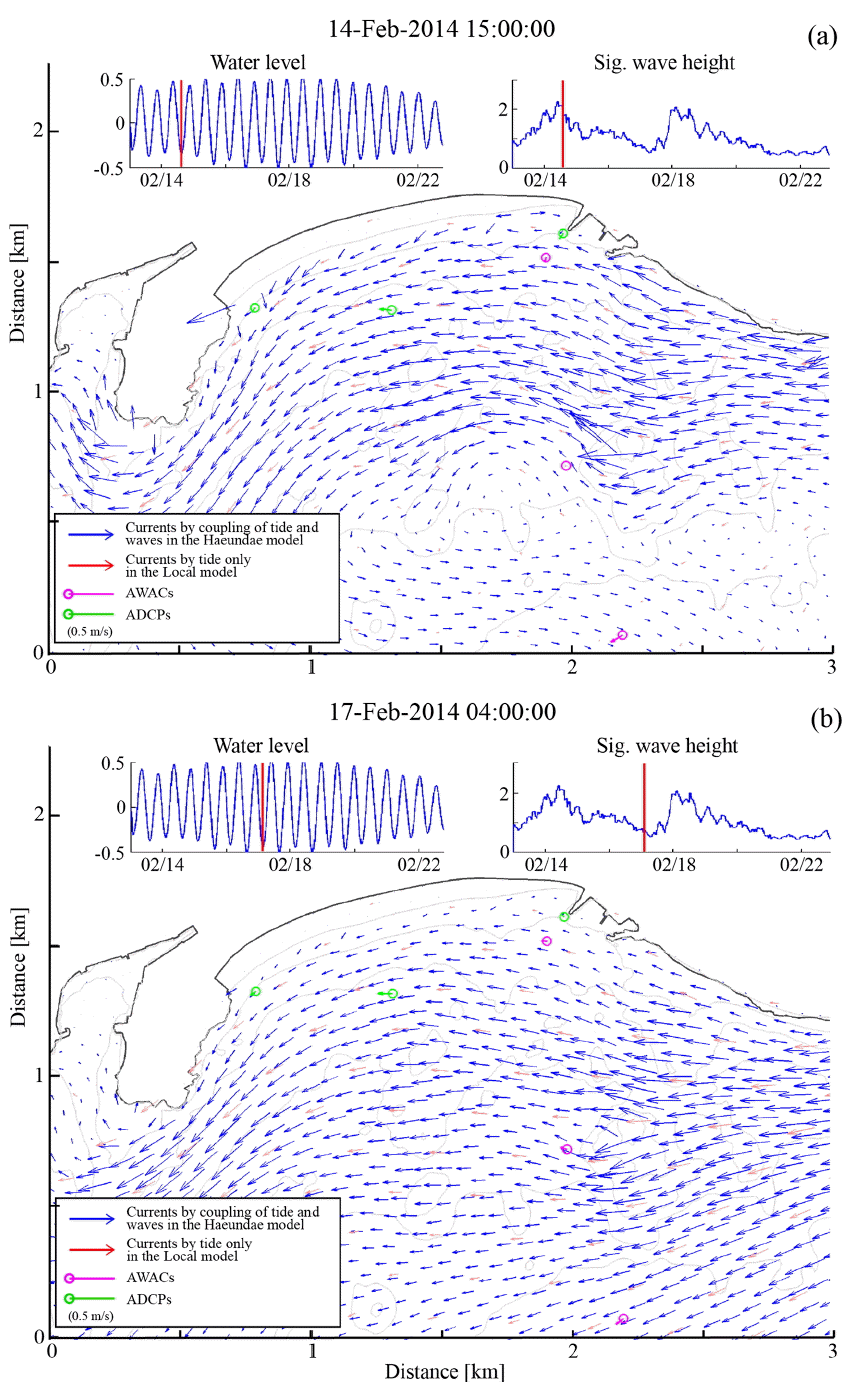
An instantaneous capture of the modeled velocity fields for the low tide with (a) a large wave case (Hm0 = 2.01 m; Tp = 8.30 sec; Dp = 108.36 degN) and (b) a small wave case (Hm0 = 0.68 m; Tp = 9.93 sec; Dp = 110.80 degN).
Fig. 12의 (a)와 (b)는 조위가 간조일 경우 고파랑 및 저파랑 조건에서 각각 발생하는 유속장이다. 외해역에서 전체적으로 큰 흐름의 방향은 고파랑 및 저파랑 조건에서 모두 만조일 경우와는 반대방향으로 즉 동쪽에서 서쪽으로 발달하고 있는 것을 알 수 있다. 해안선 부근에서는, 저파랑 조건에서 흐름이 약하게 발생하지만(Fig. 12(b)) 고파랑 조건의 경우(Fig. 12(a))는 만조시에서 처럼 동에서 서쪽으로 흐르는 비교적 강한 연안류가 발달한 것을 알 수 있다.
결론적으로, 겨울철 파고가 낮을 때는 연안류의 영향이 미비할 뿐 아니라 조류 또한 지형적인 영향으로 매우 작아 해안선 인근에서는 흐름이 매우 약하게 나타난다. 그렇지만, 파고가 높을 때는, 동쪽 계열의 입사파의 영향으로 연안류가 해안선 인근에 강하게 발달하여 조석운동에 의한 동서방향의 조류의 왕복운동과는 무관하게 동쪽에서 서쪽으로 흐르는 일관된 흐름을 유발시키는 것으로 나타났다.
5. 결 론
연안에서의 지형변화 현상은 주로 파랑과 조석을 외력으로 하여 발생하는 흐름에 의해서 야기된다. 남해안은 겨울철 북서풍과는 먼 쪽으로 남해를 마주하고 있어 고파랑의 영향이 상대적으로 작다. 또한, 남해안은 서해안 보다 조차가 작아 조류의 세기도 그 만큼 영향을 적게 받는다. 본 연구에서는, 남해안의 동부 끝단에 해당하는 해운대 해역을 대상으로 조석운동의 영향과 함께 겨울철에 발생하는 파랑을 동시에 고려하여 흐름의 구조를 살펴보았다.
해운대 해역에서 발생하는 파랑 및 흐름에 대한 공간적 변화특성을 살펴보기 위하여, 2차원 파랑모델(SWAN)과 수심 평균 2차원 해수유동 모델(Delft3D)을 사용하여 수치실험을 수행하였다. 2014년 2월 중 해운대 여러 정점에서 관측한 현장자료를 사용하여 수치모델을 보정 및 검증하였다. 수치실험 결과, 파랑 및 흐름은 해저면으로부터 곳곳에 돌출되어 있는 암반지형에 의해서 크게 영향을 받아 파향 및 유향 뿐만 아니라 파고 및 유속의 세기도 크게 변형되는 것으로 나타났다. 해운대 연안에 대한 파랑모델과 해수유동 모델의 결합을 통한 수치계산 결과는, 겨울철 파고가 낮을 때는 연안 쇄파대에서 발생하는 연안류의 영향이 미비할 뿐 아니라 조류 또한 지형적인 영향으로 매우 작아 해안선 인근에서는 흐름이 매우 약하게 나타난다. 하지만, 파고가 높을수록 겨울철 E계열의 입사파의 영향으로 동에서 서로 흐르는 연안류가 크게 발달하는 것을 보였다. 결론적으로, 본 연구는 해운대 해변의 쇄파대 지역에서 겨울철에 발생하는 흐름은 외해역과 다르게 조석으로 인한 동서 방향으로 조류의 왕복운동보다는 E 계열 외해 고파랑에 의한 입사파에 의해 발생하는 서측 흐름이 더 우세함을 밝혔다. 또한 이 결과로부터 해운대 내만에서 발생하는 이안류, 모래이동 및 지형변화는 조석운동의 영향보다는 계절별로 변하는 입사파 특성에 의해서 크게 영향을 받을 것으로 추정할 수 있다.
Acknowledgements
이 논문은 2016년 해양수산부 재원으로 한국해양과학기술진흥원의 지원을 받아 수행된 연구임(연안침식 대응기술 개발).