Article information

Abstract

Trans Abstract

1. 서 론

최근 동해안에서 너울성 파랑에 의해 인명 및 재산 피해가 잇따라 발생함에 따라 이에 대한 연구가 활발히 진행되고 있다(Chun et al., 2014; Kim et al., 2011; Oh and Jeong, 2014; Lee et al., 2010; Lee, 2013; Yuk et al., 2016). 이 중 Oh and Jeong(2014)은 동해안 너울성 파랑이 동해에 진출한 온대성 저기압에 의해 심해역에서 발생된 폭풍파랑이 연안역으로 전달된 것으로 분석하였다. 지형 특성상 동해안은 해안선이 단조로울 뿐만 아니라 대부분의 지역이 동해에 대해 열려 있어, 가을부터 이듬해 봄까지 한반도상에 형성되는 계절풍에 의해 너울성 파랑이 빈번하게 내습하는 특성이 있다. 특히, 2008년 2월의 경우처럼 현지 기상이 쾌청함에도 불구하고, 너울성 파랑이 내습하여 다수의 인명 피해가 발생하기도 한다.

이러한 이유 때문에 일부 너울성 파랑을 이상 파랑(Abnormal wave)으로 보고, 풍파 수치모의 실험을 통해 이를 정확히 재현하는 연구가 다수 수행되어 왔다(Kim et al., 2011; Lee et al., 2010; Lee, 2013; Yuk et al., 2016). 일반적으로 풍파 수치모의 실험은 WAM(Wave model) 또는 SWAN(Simulating WAve at Nearshore)과 같은 3세대 풍파 모형에 수심자료 및 바람장 정보를 입력하여 수행된다. 이 때문에 바람장의 정확도에 따라 풍파 수치모의 실험 결과의 정확도가 좌우되는 특성이 있다 (National Emergency Management Agency, 2014). 그러나 National Emergency Management Agency(2014)에 의하면, 정확한 바람장 정보를 사용하더라도, 2008년 2월 강릉항에서 발생한 이상 파랑을 정확히 재현하는 데 일정한 한계가 있었다. 이처럼 수치모의 실험을 통해 동해 이상 파랑 재현이 쉽지 않은데, Kim et al.(2011)은 Rogers et al.(2003)의 기법을 적용하여 백파(White capping)에 의한 파랑 에너지 감쇠항의 계수를 조정하여 2008년 2월의 이상 파랑을 비교적 정확하게 재현하였다. Yuk et al.(2016) 역시 이와 동일한 방법을 이용하여 2006년 10월의 이상 파랑을 성공적으로 계산하였다.

이처럼 정확한 수치모의 실험을 통해 파랑 예보의 정확도를 높이는 것이 중요하지만, 너울성 파랑에 대한 효과적인 대응책을 수립하기 위해서 이상 파랑들의 발생빈도를 파악하는 것 또한 중요하다. 하지만, 이에 대한 연구는 많지 않아, 본 연구에서는 2008년 2월 다수의 인명 피해가 발생한 바 있는 강릉항을 대상으로 이상 파랑을 포함한 극한 파랑의 발생빈도를 분석하고자 한다. 이를 위해서는 불연속적인 장기 파랑관측자료를 바탕으로 극한 파랑의 발생빈도를 분석해야 한다. 하지만, 양질의 장기 파랑관측자료를 확보하는 것이 현실적으로 많이 어려워 본 연구에서는 동해에 대해 장기간의 풍파 수치모의 실험을 실시한 다음, 이를 바탕으로 파랑 극치 분석을 실시하여 이들 파랑의 재현 주기를 산정하였다. 그리고 폭풍파랑에 의한 해난사고는 파고 자체가 높아서 발생하는 경우도 많지만, 월파 혹은 이안류의 형태로 나타나는 경우 또한 다수 있다. 이들 현상은 파고 크기 외에도 주기의 영향도 크게 받는 특성이 있기 때문에 본 연구에서는 유의파고에 대한 유의파 주기의 관계도 함께 산정하였다. 한편, 이상 파랑을 포함한 동해안 너울성 파랑은 모두 폭풍에 의해서 발생하므로, 본 논문에서는 이상 파랑 혹은 너울성 파랑이라는 용어 대신 폭풍파랑으로 이들을 기술하고자 한다.

2. 동해 풍파 수치모의 실험

2.1 파랑 모형 및 파랑 계산 조건

본 연구에서는 Chun et al.(2006)의 수정 WAM 모형을 사용하여 파랑 후측모의 실험을 수행하였다. 본 파랑 모형은 심해역 파랑 모형인 WAM을 천해역으로 확장한 것으로, 실제 수심에 의한 파랑 굴절, 천해역 파랑작용인 쇄파, 3파 상호작용 등이 포함되어 있는 데다가, 음해법(Implicit scheme)을 이용하여 파랑을 계산하여 천해역에 대해 효과적인 파랑 계산이 가능하다(Chun et al., 2006; Chun et al., 2007; Chun et al., 2008). 본 파랑 모형의 지배방정식은 천해역 파랑모형인 SWAN과 동일한 파랑 작용 평형 방정식(Wave action balance equation)으로, 이를 식 (1)에 나타내었다(WAMDI Group, 1988).

(1) ∂F∂t+∂(cλF)∂λ+1cosϕ∂(cϕcosϕF)∂ϕ+∂(cθF)∂θ=S

여기서, S는 파랑 에너지 원천항을 나타내는데, 바람에 의한 파랑 에너지 생성, 백파에 의한 파랑 에너지 감쇠, 3파 상호작용에 의한 파랑 에너지 전달, 4파 상호작용에 의한 파랑 에너지 전달 , 쇄파에 의한 파랑 에너지 감쇠 등이 포함되어 있다. 그리고 F는 파랑에너지 스펙트럼을 나타낸다. λ와 φ는 각각 경·위도를 나타내며, θ는 파랑 에너지 스펙트럼의 방향을 가리킨다. c_λ, c_φ, c_θ는 각각 λ, φ, θ 방향으로의 파랑 에너지 전달 속도를 나타낸다. 본 파랑 모형은 3차원 유동 모형과 동적결합을 통해 성공적으로 해빈류 계산을 수행했을 뿐 아니라, 천해역 및 심해역에서의 폭풍파랑을 성공적으로 재현한 바 있다 (Chun, 2012; Chun et al., 2014). 이러한 이유로 본 연구에서는 본 파랑모형을 이용하여 동해 풍파 수치모의 실험을 수행하였다. 본 파랑 후측모의 실험에서의 수심도는 미해양대기청(NOAA, National Oceanic and Atmospheric Administration)의 ETOPO5 수심자료를 이용하여 구성하였으며, 효과적인 계산을 위해 5분 간격의 격자를 사용하였는데, 본 연구 수치모의 실험의 수심도를 Fig. 1에 나타내었다.

Fig. 1.

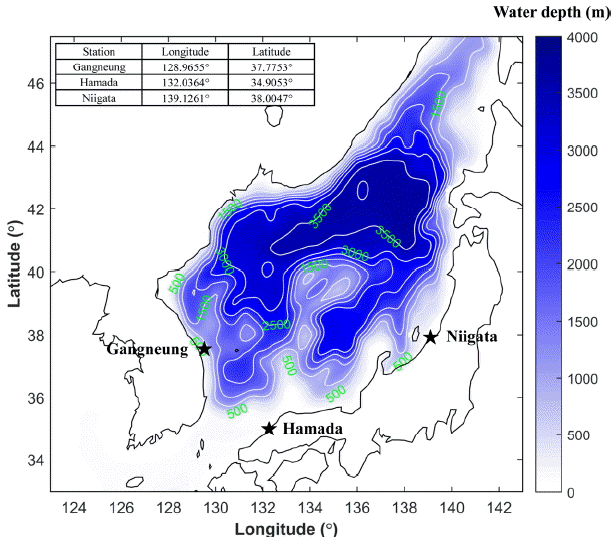
Bathymetry of the present numerical study and the locations of the wave measurements for the validation of the present numerical model.

본 연구의 파랑 후측모의 실험에서 파랑 에너지 스펙트럼은 Phadke et al.(2003)가 태풍 파랑 계산을 위해 도입한 것과 동일하게 25개의 주파수 및 48개의 파향 성분으로 나타내었다. 이 때, 주파수는 대수(Logarithmic) 스케일로 증가하는데, 이를 식 (2)에 나타내었다.

(2) fi=fr,0×1.1i−1

여기서, f_r,0는 최저 주파수를 나타내는데, 본 연구에서는 0.04 Hz를 사용하였다. 이로 인해 본 연구의 파랑 후측모의 실험은 2.5~25 s 의 주기에 대해서 파랑계산을 수행하게 된다. 그리고 효과적인 파랑계산을 위해 시간 간격으로 20분을 사용하였는데, λ, φ, θ 방향에 대한 Courant number는 식(3)과 같다.

(3) |cλΔtΔλ|max≈4.4,|cϕΔtΔϕ|max≈3.4,|cθΔtΔθ|max≈20.8

일반적으로 Courant number는 방향에 관계없이 하나의 숫자로 정의되지만, 본 파랑모형은 fractional step method를 도입하여 λ, φ, θ방향 각각에 대해서 파랑 스펙트럼을 계산하기 때문에 식 (3)처럼 3개의 Courant number로 정의된다. 이 외에 파랑계산을 위해 2차원의 시계열 바람장 자료가 필요한데, 본 연구에서는 NCEP Final Operational Global Tropospheric Analysis 바람장 자료를 사용하였다. Lee(2013)와 Swail and Cox(2000)은 본 바람장을 이용하여 한반도 동해안 및 대서양에 대해 성공적으로 파랑 후측모의 실험을 수행한 바 있다. 본 자료는 NOAA에서 구축한 기상자료로, 1^o 간격으로 구성되어 있으며, 6시간 간격으로 제공되고 있는데, 폭풍 및 태풍 바람장이 모두 포함되어 있다. 이 때문에 본 연구의 수치모의 실험이 폭풍파랑에 대한 것이지만, 태풍 파랑 또한 계산되었다. 하지만, 6시간 간격으로 바람장 자료가 제공되기 때문에 진행 속도가 빠른 일부 태풍의 경우 태풍파랑을 과소산정하는 경향이 있다.

2.2 파랑 계산 결과 검증

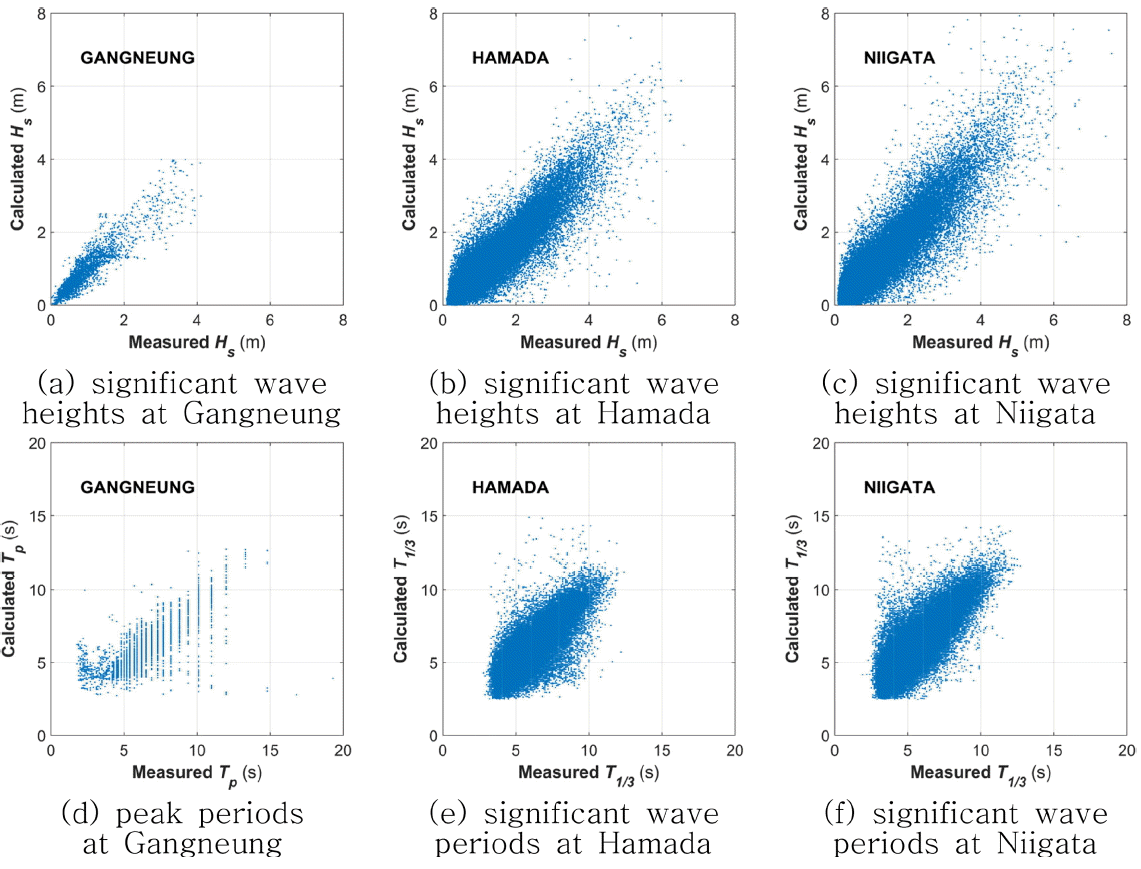
본 연구의 파랑 계산결과는 강릉항, 일본 서해안의 Hamada 및 Niigata 등에서의 파랑 관측결과와의 비교를 통해 검증되었는데, 각 관측지점에 대한 유의파고 및 파주기의 비교를 Fig. 2에 나타내었다. 이 때 각 파랑 관측 자료의 관측지점과 이들의 좌표를 Fig. 1에 표시하였다. 파랑 계산결과의 검증을 위해 먼저 파랑 계산결과로부터 유의파고 및 첨두주기를 추출하였는데, 일본 Hamada 및 Niigata에서는 첨두주기 대신 유의파 주기가 제공되어 파랑 계산결과로 얻은 파랑스펙트럼으로부터 유의파 주기 T_1/3를 산정하였다. 이 때의 변환 관계식은 Suh et al. (2010)에 제시된 식으로, T1 ⁄ 3=1.14( m0 /m2)1 ⁄ 2 와 같다. 여기서 m₀와 m₂는 각각 파랑 스펙트럼의 0 차 및 2 차 모멘트를 나타낸다. Fig. 2에 따르면, 첨두주기의 정확도가 유의파 주기에 비해서 상대적으로 낮게 나타나고 있다. 첨두주기는 파랑 스펙트럼에서 최대 에너지에 해당되는 주기를 나타내는 것으로, FFT(Fast fourier transform) 과정에서 도입된 특정 주파수들로부터 최대 에너지에 대한 주파수를 선정하여 불연속적으로 첨두주기가 분포한 탓에 계산 첨두주기의 정확도가 떨어진 것으로 추정된다. 이 외에 유의파고는 파랑 관측 자료에 관계없이 잘 일치하는 것으로 나타나고 있는데, Niigata의 경우, 유의파고가 커질수록 유의파고를 과대산정하는 경향이 있는 것으로 파악되고 있다. 한편, 강릉항 파랑관측자료의 개수가 일본 Niigata 및 Hamada 의 자료보다 적어 유의파고 분포 범위가 서로 다르게 나타나고 있었다.

Fig. 2.

Comparison of the computed significant wave heights and periods with the measurements.

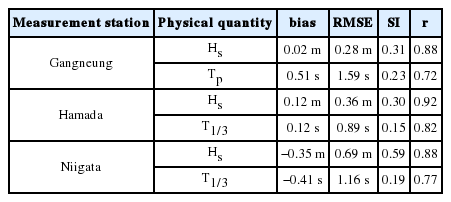
이 외에 본 연구에서는 수치모의 실험의 정확도를 bias, RMSE, SI, Pearson 상관계수 r 등의 항목으로 정량적으로 나타낸 후, 이들 결과를 Table 1에 제시하였다. Table 1에서 H_s, T_p는 각각 유의파고, 첨두주기를 각각 나타내는데, 이들 통계량의 수식들을 식 (4)~(7) 등에 나타내었다.

Table 1.

Model accuracy of the numerical results for July, 1999∼June, 2010

(4) bias=1N∑i=1Nxi−yi

(5) RMSE=1N∑i=1N(xi−yi)2

(6) SI=1N∑i=1N(xi−yi−bias)2/x¯

(7) r=∑i=1N(xi−x¯)(yi−y¯)∑i=1N(xi−x¯)2∑i=1N(yi−y¯)2

여기서, x_i 와 y_i 는 각각 관측치와 계산치를 나타내며, x 및 y는 관측치 및 계산치의 평균을 각각 나타낸다.

Table 1에 의하면, 강릉항 유의파고의 r은 0.88로 Hamada에 비해서 다소 낮은 편이나, Niigata 와는 동일하다. Pilar et al.(2008)의 파랑 계산결과에 따르면, 유의파고의 Pearson 상관계수는 0.80~0.92에 이르는데, 이로 볼 때, 본 연구의 계산 유의파고의 정확도가 낮지 않은 것으로 파악된다. 그리고 강릉항에서 유의파고는 전반적으로 2 cm 정도 과소산정되고 있는데, 오차의 크기를 나타내는 RMSE는 0.28 m로, Hamada 및 Niigata에 비해서 비교적 작아 본 연구에서 유의파고가 성공적으로 계산된 것으로 보인다. 한편, 강릉항 첨두주기는 0.51 s 정도 과대 산정되고 있는 가운데, 첨두주기의 RMSE는 1.59 s로 Hamada 및 Niigata 에서 유의파 주기의 RMSE보다 약 0.5 s 정도 큰 것으로 파악되고 있다. 강릉항 첨두주기의 Pearson 상관계수는 앞서 언급한 바와 같은 이유로 매우 낮은데, Pilar et al.(2008)의 경우 계산 평균 주기의 Pearson 상관계수가 0.69~0.86에 이르고 있어 본 연구의 계산결과 얻은 첨두주기의 정확도가 낮은 것이 아닌 것으로 판단된다. 이로 볼 때, 본 연구의 수치모의 실험이 성공적으로 수행된 것으로 보인다.

2.3 강릉항 파랑 계산

강릉항 파랑 계산결과의 시계열도를 관측결과와 함께 Fig. 3에 나타내었다. 이 중, 폭풍 파랑에 의해 다수의 인명피해가 발생한 바 있는 2008년 2월 폭풍파랑의 유의파고 및 첨두주기를 Fig. 3(e)와 Fig. 3(f)에 각각 나타내었다. Fig. 3(e)의 파랑 관측결과에 따르면, 유의파고 최대값은 2월 24일 15:00시 경에 4.09 m 으로 나타났다. 당시 유의파고 계산치는 3.89 m로, 약 20 cm 정도 과소산정되어 있다. 이는 당시 수치모의 실험에서 파랑이 상대적으로 느리게 발달한 결과로, 2월 24일에 대한 계산 유의파고의 bias는 9 cm 정도에 지나지 않는다. 그리고 당시 유의파고의 Pearson 상관계수는 0.89로 Table 1에 있는 강릉항의 수치와 비슷한 것으로 나타나, 강릉항 유의파고가 성공적으로 재현된 것으로 판단된다. 한편, 최대 유의파고 출현 시점의 첨두주기는 10 s 인 반면에, 파랑 계산 결과의 첨두주기는 13 s 로 나타나, 본 연구의 수치모의 실험 결과, 첨두주기가 3 s 정도 과대산정되었다. 그러나 2월 24일 당일의 첨두주기의 bias 는 0.36 s 인데다가, 첨두주기의 Pearson 상관계수는 0.84로, 이는 강릉항 전체에 대한 수치보다 매우 높은 것으로 나타나, 본 연구의 수치모의 실험에서 첨두주기 또한 성공적으로 재현한 것으로 파악된다.

Fig. 3.

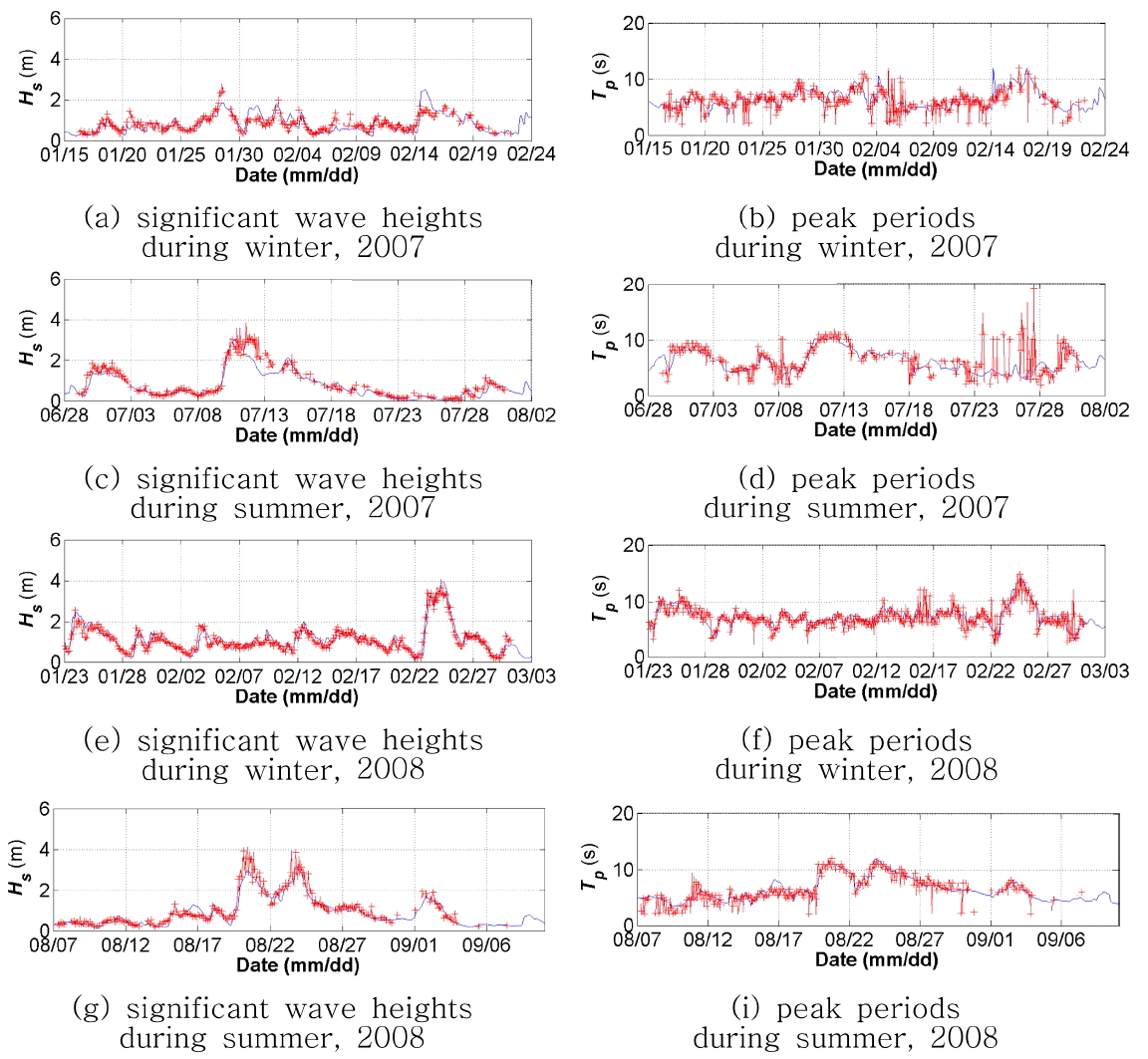
Time series plot of the calculated significant wave heights and peak periods (solid line) with the measurements (solid line with crosses) at Gangneung port.

한편, Fig. 3(c) 및 Fig. 3(g)를 보면, 하계임에도 강릉항에서 고파랑이 관측되었는데, 이는 T0704 MAN-YI 및 T0813 SINLAKU 에 의한 태풍파랑으로, 일본 태평양 연안에 상륙한 태풍에 의해 동해에서 폭풍파랑이 형성되어, 연안역으로 전달된 결과이다. Fig. 3(c)에 따르면, 파랑 계산결과의 최대 유의파고는 약 3 m 정도로 나타나, T0704 MAN-YI에 의한 고파랑을 본 연구의 수치모의 실험이 성공적으로 재현한 것으로 보인다. 하지만, 이 뒤를 이어 수치모의 실험 입력자료의 풍속이 감소함에 따라 유의파고가 급격하게 줄어들어, 당시 태풍에 대한 본 연구의 파랑계산 결과가 전반적으로 과소산정되는 경향이 있는 것으로 파악된다. 그리고, Fig. 3(g)의 고파랑은 T0813 SINLAKU 의 강도 변화가 반영되어 이중 구조 형태를 띄고 있다. 하지만, 당시 계산 유의파고는 약 3.16 m 로 70 cm 정도 전반적으로 과소산정하는 것으로 파악되고 있다. 이 역시 본 연구의 바람장이 태풍 바람장을 정밀하게 고려하지 못한 결과로 유의파고를 과소산정한 것으로 보인다.

3. 강릉항 폭풍파랑 특성

본 연구에서는 POT (Peask Over Threshold) 기법을 이용하여 강릉항 유의파고에 대해 파랑 극치 분석을 실시하였다. POT 기법을 수행하기 위해서는 기준파고 설정이 필요한데, 본 연구에서는 Chun et al. (2014)에서 수행한 것과 동일하게 첨두 유의파고의 값을 평균하였는데, 그 값은 1.5 m 와 같다. 이를 기준으로 폭풍파랑 유의파고를 추출하고, 이 때 추출된 폭풍파랑 유의파고를 GPD(Generalized Pareto Distribution)에 적용하였다. GPD 함수의 확률밀도분포 함수와 누적확률 함수를 각각 식 (8)과 식 (9)에 각각 나타내었다.

여기서, α, κ, ξ는 GPD 함수의 모수로서, 본 연구에서는 최대 엔트로피법 (maximum entropy method)을 이용하여 모수를 산정하였다. 최대 엔트로피법에 의한 모수 산정 방법은 Singh and Guo(1995)에 자세히 기술되었는데, 본 기법은 자료의 비대칭도(skewness)가 높거나 낮을 경우에도 잘 적용된다는 장점을 가지고 있다. 본 기법의 알고리즘은 Singh and Guo(1995)에 제시되어 있어, 본 논문에서 이에 대한 기술을 생략한다. 본 연구에서 강릉항 유의파고에 대해 GPD 함수의 모수를 산정한 결과, 식 (8)과 식 (9)의 모수들은 α = 0.63, κ = -0.11, ξ = 1.51과 같다. 이들 모수의 정확도는 K-S (Kolmogorov-Smirnov) 및 χ²-test 를 통해 확인하였는데, 유의수준 0.05에서 이들이 적합한 것으로 나타났다. 극치분석 결과 얻은 폭풍파랑의 확률밀도 분포함수와 이들의 재현주기를 Fig. 4(a)와 Fig. 4(b)에 각각 나타내었다. Fig. 4(a)에는 폭풍파랑의 확률밀도 분포함수 외에 폭풍파랑의 히스토그램도 함께 제시되어 있다. 한편, Fig. 4(b)에 의하면, 1년 재현 주기를 가지는 유의파고의 크기는 4.4 m 로, 2008년 2월 강릉항에서 관측된 폭풍파랑의 재현 주기는 1년보다 작은데, 당시 폭풍파랑의 재현주기는 약 8.2개월로 산정된다. 이로 볼 때, 당시 강릉항에서 발생한 해난사고는 단순히 비정상적으로 큰 고파랑이 내습해 발생한 사고라기보다는 고파랑에 다른 요인이 더해져 월파고가 크게 나타났던 것으로 파악된다.

Fig. 4.

Results of the extreme wave analysis at Gangneung port.

이 외에 1년 이상의 재현 주기를 가지는 계산 파랑의 유의파고, 첨두주기를 날짜별로 Table 2에 정리하여 나타내었다. 이에 따르면, 본 연구의 파랑 계산결과에 1년 이상의 재현주기를 가지는 파랑이 12회 발생한 것으로 파악되고 있다. 이 중 5회는 태풍 파랑에 의한 것으로, T0215 Rusa 를 제외한 나머지 태풍들은 한반도에 상륙하지 않고 동해에 진출한 태풍으로, 한반도 동해안이 태풍 진로의 좌반구에 위치해 있음에도 동해안에 큰 피해를 유발한 바 있다. 이 외 나머지는 폭풍에 의한 고파랑으로, 1년 이상의 재현주기를 가지는 폭풍파랑의 58.3 %는 폭풍에 의해 발생된 것으로 집계되어 강릉항에서는 폭풍파랑에 의한 고파랑의 발생빈도가 태풍 파랑에 비해 더 우세한 것으로 파악되고 있다. 그리고, 수치모의 실험 기간 중 최대 유의파고는 2006년 10월 23일에 나타났는데, 당시 유의파고의 크기는 9.2 m로, 이의 재현 주기는 50년에 해당된다. 그리고 본 연구의 계산기간 동안 태풍 파랑의 최대 유의파고는 T0514 Nabi에 의한 것으로 나타났는데, 이의 재현 주기는 약 7년 정도 되는 것으로 산정되었다.

Table 2.

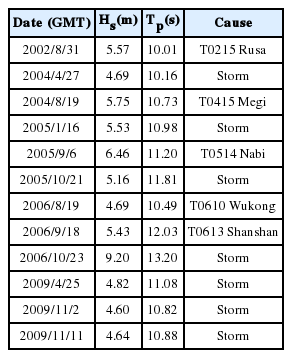
List of the computed waves with the return periods of 1 year from the numerical results for the period of July, 1999 through June, 2010

한편, 폭풍파랑은 해안지역에서 주로 월파 형태로 해난 사고를 야기하는데, 월파 크기는 입사파고 외에 입사파 주기에 대해서 비례하여 증가하는 특성이 있다 (Sorensen, 1993). 이처럼 파랑의 주기 또한 중요하여, 본 연구에서는 파랑 계산결과 얻은 유의파고 및 유의파 주기에 대해 회귀분석을 실시하여 유의파고에 따른 유의파 주기를 산정하였다. 이를 위해서 본 연구에서는 강릉항 파랑 계산결과에서 재현 주기가 1개월 이상에 해당되는 파랑 정보를 추출한 다음, 첨두주기를 유의파 주기로 변환한 후, 회귀 분석을 실시하였는데, 유의파고에 대한 유의파 주기의 관계식을 식(10)에 나타내었다.

식 (10)에 의한 유의파고 대비 유의파 주기의 관계식을 Suh et al.(2010)의 관계식과 함께 Fig. 5에 나타내었다. Suh et al.(2010) 의 관계식은 한국해양과학기술원의 파랑 후측모의 실험 결과 중, 동해안에 대한 연최대 파랑을 추출하여 구축한 식으로 본 연구의 계산 결과보다 약 2초 정도 더 큰 것으로 파악되고 있다. 한편, 본 연구의 파랑계산 결과에 의하면 2008년 2월 24일 강릉항에서의 유의파고, 유의파 주기의 평균값은 각각 3.66 m, 11.9 s 과 같은데, 식 (10)에 의하면, 당시 유의파고에 대한 유의파 주기는 9.7 s로 산정된다. 이로 볼 때, 2008년 2월 24일 강릉항에서 발생한 해난 사고는 통상적인 유의파고 크기 대비해서 유의파 주기가 상당히 커서 이에 따라 월파고가 이례적으로 크게 나타났던 것으로 추정된다.

Fig. 5.

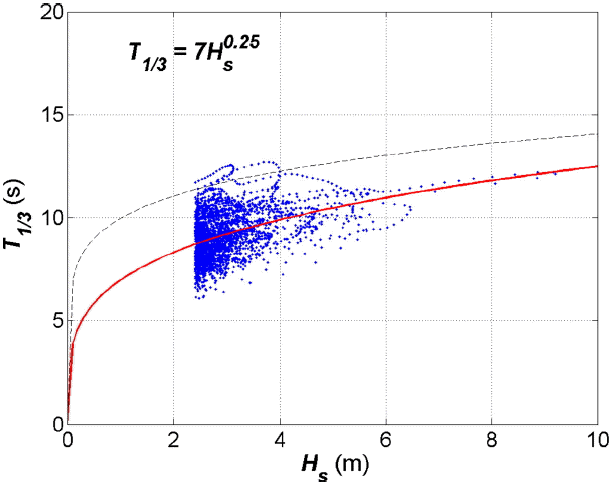
The relationship between the significant wave heights and significant wave periods from the numerical results at Gangneung port (solid line) and Suh et al.’s (2010) study (broken line).

4. 결 론

최근 한반도 동해안을 중심으로 폭풍파랑에 의한 피해가 다수 발생해 이를 정확히 재현하는 수치모의 실험 연구가 많이 진행되어 왔다. 하지만, 이들의 발생빈도에 대한 연구는 많지 않아 본 연구에서는 동해에 대해 파랑 후측모의 실험을 수행한 후, 2008년 2월 폭풍파랑에 의해 다수의 인명피해가 발생한 강릉항에 대해서 폭풍파랑 발생빈도를 조사하였다.

이에 따라 본 연구에서는 천해역으로 확장된 수정 WAM모형을 이용해 1999년 7월부터 2010년 6월까지 12년에 대해 동해역에 대해 파랑 후측모의 실험을 실시한 다음, 파랑 계산결과를 강릉항, 일본 Hamada 및 Niigata 에서의 파랑관측 자료와의 비교하여 본 연구의 파랑 계산결과를 검증하였다. 비교 결과, 유의파고 및 파주기의 Pearson 상관계수는 각각 0.88, 0.72 이상인 것으로 나타났다. 이 중 첨두주기는 이산적(discrete)으로 산정되어 정확도가 다소 떨어지는 편이었는데, 첨두주기를 포함한 본 연구의 파랑 계산결과의 정확도는 Pilar et al.(2008) 의 파랑 후측모의 실험 결과에 비해서 낮지 않아 본 연구의 파랑 후측모의 실험이 성공적으로 이뤄진 것으로 판단된다. 이 후, 강릉항 파랑 계산결과에 대해 POT 방법을 이용하여 파랑 극치 분석을 실시하였다. 극치 분석 실시 결과, 1년 재현 주기 유의파고는 4.4 m 로 나타났는데, 1년 재현 주기 이상의 폭풍파랑을 추출한 결과, 이 중 58.3 %는 폭풍에 의한 것이고, 나머지는 태풍에 의한 것으로 나타났다. 이 중 거의 대부분은 한반도에 상륙하지 않고 동해를 통과한 태풍으로, 한반도 동해안이 태풍의 좌반구에 위치해 있음에도 불구하고, 이들 태풍이 동해를 통과하면서 발생한 폭풍파랑이 강릉항으로 전달된 것으로 보인다. 이 외에 수치 모의 실험 결과상 강릉항 최대 유의파고는 2006년 10월 23일 나타났는데, 당시 유의파고 크기는 9.2 m 로, 본 연구의 극치분석 결과에 의하면 이의 재현 주기는 약 50년에 해당된다. 이 외에 1개월 이상의 재현 주기를 가지는 파랑을 추출하여, 유의파고에 대한 유의파 주기의 관계식을 산정하였는데, 본 연구 결과에 의하면, 유의파고에 대한 유의파 주기는 T1 ⁄ 3=7Hs0.25와 같이 쓸 수 있다.

한편, 본 연구의 극치 분석 결과에 따르면, 2008년 2월 폭풍파랑 내습 당시 강릉항 유의파고의 재현주기는 8.2 개월로 1년에 못 미친다. 하지만, 당시의 유의파 주기는 11.9 s로, 앞서 구한 유의파고 대비 유의파 주기인 9.7 s 보다 2.2 s 가 더 큰 것으로 파악되고 있다. 이로 볼 때, 2008년 2월의 폭풍파랑 내습은 단순히 고파랑 예측 관점에서 접근하기 보다는 통상적인 경우보다 높은 유의파 주기까지 더해진 비교적 큰 월파가 나타난 결과로 해석할 필요가 있다.

Article information Continued