2.1 실험조건

수리실험은 Fig. 1과 같이 전체 길이 40 m, 폭 30 m, 높이 1.2 m의 조파실험수조에서 수행하였다. Ranasinghe et al.(2010)에서 모의한 잠제 설치 연안을 재현하기 위해 실험수조의 단면지형은 아래의 평형단면 경험식을 사용하여 구성하였다(Dean, 1991).

Fig. 1.

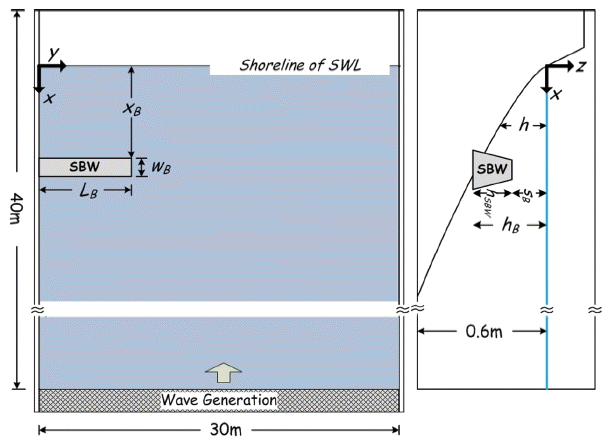
Sketch of experimental bathymetry and a submerged breakwater model where its length (L_B), its width (w_B), its height (h_SBW), the distance from the shoreline (x_B), the distance from the water surface (s_B), the water depth at the submerged breakwater (h_B).

여기서 h는 수심, x는 해안선부터 외해 쪽으로의 수평거리, 그리고 A는 평형단면 형상계수이다. 평형단면 지형의 수심을 위해 적용되는 형상계수는 표사의 침강속도에 의해 결정되며, 이는 표사의 입경(D₅₀)에 따라 추정할 수 있다(Rouse, 1937). 본 실험 지형의 규모에 적합한 형상계수를 결정하기 위해 표사입경의 침강속도에 대한 Froude 상사를 적용하였다(Kriebel et al., 1986). 임의의 원형 해안에 대하여 1/10의 축척으로 가정하고, 원형표사 D₅₀ = 0.40 mm의 침강속도에 대하여 Froude 상사를 만족하는 모형의 표사입경 D₅₀ = 0.19 mm을 가정하였다. 가정된 모형의 표사입경에 따른 침강속도(= 2 cm/s)에 해당하는 형상계수(A = 0.097)를 적용하였다. 참고로 이는 향후 연구로 계획하고 있는 이동상 실험에서 사용할 표사입경(D₅₀ = 0.19 mm)을 고려한 것임을 밝힌다. 평형단면 경험식의 적용 밖인 포말대의 지형 경사는 1:5.6로 구성하였다. 이 경사는 본 연구와 유사한 평형단면 형상계수를 사용한 Choi et al.(2016)의 이동상 실험결과로부터 평형상태 포말대의 단면 경사를 추출한 것이다. 또한 실험조건의 파랑에 대한 변형을 무시할 수 있는 수심을 60 cm로 가정하여 Fig. 1과 같이 구성하였으며 해안선 방향으로 수심변화를 최소화하여 모형을 제작하였다.

본 수리실험은 잠제를 중심으로 좌우측에서 발달하는 물리적 특성이 대칭이라고 가정하였다. 이는 예비실험으로 잠제주변 파굴절에 의한 파봉의 간섭이 발생하지 않음을 확인하였고, 수로벽에 의한 마찰 영향은 무시할 수 있다고 가정하였다. 본 논문에는 제시하지 않았으나 중심벽의 유무에 따른 수치실험을 통해서도 흐름대칭성을 확인할 수 있었다. 이는 잠제에 의한 흐름발달과 관심영역 밖 측면 수로벽의 간섭문제를 최소화하기 위한 방안이었음을 밝힌다.

본 실험연구를 위해서 상기 경험식(1)에서 사용한 파라미터들로 조합하여 총 35개의 실험 조건들을 Table 1과 같이 구성하였다. 잠제 파라미터 중에 잠제의 길이(L_B)는 10.0m, 잠제의 폭(w_B)은 0.5 m로 고정하였음을 밝힌다. 대칭가정 실험으로 실제 설치된 잠제 길이(L_B) 5.0 m는 잠제 파라미터 L_B = 10.0 m에 해당한다. 또한 잠제모형은 Ranasinghe et al.(2010)의 조건과 같이 불투수성으로 제작되었다. 다양한 실험조건을 재현하기 위해 잠제는 이동이 가능하고, 높낮이를 조절 할 수 있도록 블록 형태로 제작하였다. 앞서 언급한 바와 같이 본 연구에서는 규칙파 조건을 입사파 조건으로 사용하였고, 경험식(1) 산정을 위해서 관측결과를 유의파고(0차 모멘트 파고)로 환산하여 적용하였다. 주기 변화에 따른 흐름 패턴 조사를 위한 조건도 포함시켰으며, Ranasinghe et al.(2010)에 의해 결정되는 침퇴적 반응결과도 함께 제시하였다.

Table 1.

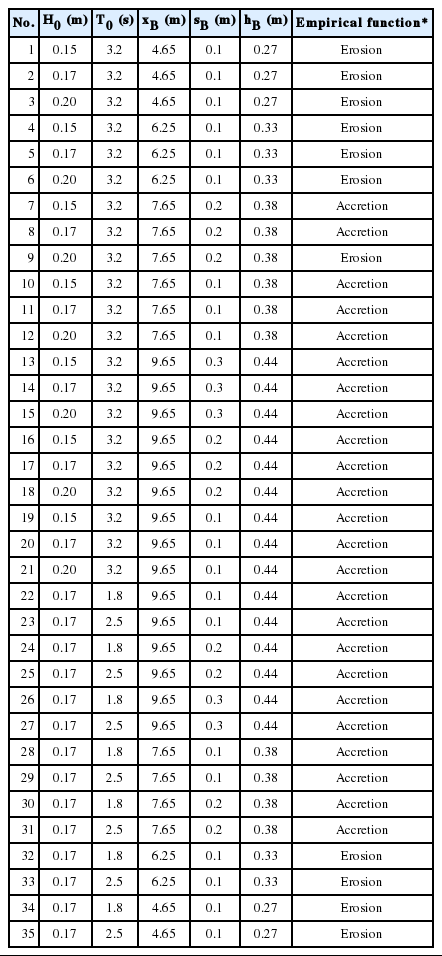
The experimental parameters of the incident waves and the submerged breakwater and the resultant shoreline response of Ranasinghe et al. (2010)

파고측정을 위해 잠제와 해안선 주변에 측점 120곳을 선정하고, Kenek사의 용량식 파고계를 사용하였다. 잠제의 후면부와 해안선 부근에 파고계를 조밀하게 설치하였으며, 특히 잠제 주변 파고계는 해안선으로부터 수직방향의 잠제 설치 거리(x_B)에 따라 위치를 이동시켜 계측하였다.

잠제 후면의 유속 측정을 위한 카메라는 정사보정 오차를 줄이기 위해 실험수조 바닥으로부터 약 8 m 높이의 실험실 천장에 카메라를 설치하였으며, 잠제 설치 연안 부근을 수직으로 촬영하도록 설정하였다. 촬영 카메라의 기종은 삼성테크윈사의 피쉬아이타입 카메라(SND-K2083R)이며, 촬영영상의 프레임 구성은 1920 × 1080 pixels, 프레임 속도는 60 fps이다. 추적입자는 지름 4 cm의 구멍이 있는 폴리프로필렌 공을 사용하였다. 수면위에서 이동하는 구멍이 없는 추적입자와 비교하여 일정 부분 수면에 잠겨 이동하기 때문에 급격한 수면변화 구간에서 발생할 수 있는 슬라이딩 현상이 최소화될 수 있고 물입자 이동에 따른 유속측정에 더 적합하다고 판단된다.

2.2 실험절차

잠제 주변의 수면변위 및 흐름패턴 관측을 위해 각 실험조건에 대하여 조파를 20분간 지속하였고, 다음과 같은 절차로 측정하고 분석하였다. 각 조건에서 조파된 첫 파가 해안선에 도달 후 약 5.0초가 경과한 t₀로부터 각 측정위치에서 계측된 5분 동안의 수면변위자료(약 90파 이상)를 추출하여 평균수면변위와 평균파고를 산정하여 그 분포를 결과에 제시하였다. 흐름유속 측정을 위하여 각 실험조건의 조파된 첫 파가 해안선에 도달한 직후에 약 2000개의 추적 입자를 해안선 위에서 동시에 방출하였고, 입자의 이동을 천장 카메라로 촬영하였다. 녹화된 영상으로부터 추출한 이미지는 카메라 렌즈에 의한 왜곡을 정사보정하고(Heckbert, 1989), 보정된 추출이미지에서 이동하는 입자를 추적하여 잠제 후면과 해안선 부근의 유속분포를 LSPIV 기법으로 산정하였다(Fujita et al., 1998; Kantoush et al., 2011). 본 연구에서 제시되는 실험결과는 조파된 첫 파가 해안선에 도달 후 약 5.0초(추적 입자가 방출되는 시간)가 경과한 t₀로부터 60초 동안의 이미지가 정사 보정되고 LSPIV 기법으로 분석된 평균유속 분포이다. 분석시간 60초는 추적 입자의 관심지역 밖 이동에 따라 입자 분포도 감소되었기 때문에 이에 따른 오차를 최소화하기 위한 것이다.

Fig. 2는 규칙파 H₀ = 17 cm, T₀ = 3.2 s, 그리고 잠제 위치는 x_B = 9.65 m, s_B = 0.2 m의 경우로 각 시간별로 촬영영상에서 추출한 이미지이다. Fig. 2(a)는 조파된 첫 번째 파봉이 해안선에 도달 후 5초가 경과한 후 추적 입자가 방출된 실험장면이다. 추적 입자가 방출된 시간을 t₀라고 하고, t₀부터 15초 간격으로 녹화된 실험장면을 Fig. 2(b)와 Fig. 2(c)에 각각 나타냈다. 그림으로부터 방출된 입자가 y=0m에 위치한 측면벽, 즉 잠제 후면 중앙부로 이동하는 것을 확인할 수 있다.

Fig. 2.

Snapshots of video images of moving particles near the shoreline for LSPIV analysis (H₀ = 17 cm, T₀ = 3.2 s, x_B = 9.65 m, s_B = 0.2 m) (a) t = t₀ (b) t = t₀ + 15 sec (c) t = t₀ + 30 sec.

3.1 잠제 후면 관측 결과

연안에서의 위상평균된 흐름 발달은 파랑잉여응력 기울기와 평균수면 기울기와의 균형에 의해 결정된다고 알려져 있다(Mei, 1989). 정상상태의 연안평균흐름의 지배방정식은 다음과 같이 나타낼 수 있다.

여기서 x_i 는 좌표계, g는 중력가속도, ρ는 밀도, h는 수심, ξ는 평균수면변위, U_i 는 수심 및 위상 평균유속, S_ij는 파랑잉여응력, 그리고 τ⏜jB는 바닥 마찰응력을 나타낸다. 즉, 식(3)에서 좌변항은 평균유속의 공간가속도항이고 우변의 첫 번째 항은 평균수면 기울기, 두 번째 항은 파랑잉여응력 기울기, 세 번째 항은 평균유속에 따른 저항항이다. 이로부터 연안의 평균흐름은 천수의 연속방정식 조건 아래에서 파랑잉여응력 기울기와 평균수면 기울기항의 균형으로 결정됨을 알 수 있다. 위 내용을 근거로 본 수리실험의 결과인 평균수면변위와 해안선에 직각 입사하는 파향에 큰 변화가 없다는 가정하에 파랑잉여응력에 가장 지배적인 요소인 파고의 분포를 제시하였다.

Fig. 3은 규칙파 H₀ = 17 cm, T₀ = 2.5 s, 그리고 잠제 위치는 x_B = 9.25 m, s_B = 0.1 m인 조건(case 23)에서의 평균수면 분포, 파고 분포, 그리고 유속 분포를 나타내고 있다. 유속 분포로부터 잠제 후면의 흐름패턴이 측면부에서 잠제 후면 중심으로 집중됨을 알 수 있다. 이 경우의 흐름은 파고 분포로부터 설명될 수 있다. 잠제 배후의 측면부에서 파고가 높고, 잠제 후면 중심부에서는 상대적으로 낮기 때문에 파랑잉여응력의 기울기에 의해 측면부에서 후면부로의 흐름이 발달하는 것으로 보인다. 비록 평균수면 분포에서도 잠제 배후 중심부가 상승되어 있으나, 다음에 제시된 흐름이 잠제 밖으로 흐르는 경우에 비해서 그 기울기가 상대적으로 작아 보인다. 이 평균수면 상승은 잠제 배후 중심부로 수렴하는 흐름에 의한 상승으로 보이며, 잠제 상단에서의 쇄파에 따른 파랑잉여응력 기울기 및 쇄파유도류에 의한 수면상승 효과는 상대적으로 긴 xB로 인해 크지 않은 것으로 판단된다. 앞서 언급한 바와 같이 이러한 경우의 흐름패턴 발달로부터 해안선의 퇴적반응을 예측할 수 있다. Fig. 4는 규칙파 H₀ = 15 cm, T₀ = 3.2 s, 그리고 잠제 위치는 x_B = 6.25 m, s_B = 0.2 m인 실험조건(case 4)의 평균수면 분포, 파고 분포, 그리고 유속 분포를 나타내고 있다. 유속 분포로부터 흐름이 잠제 후면 중심부에서 측면부로 발달하며, 해안선은 침식 반응임을 예측할 수 있다. Fig. 3의 경우와 다르게 평균수면 분포에서 잠제 후면의 평균수면의 상승이 두드러져 보인다. 이는 잠제 상단에서 발생하는 쇄파에 따른 파랑잉여응력 기울기 및 쇄파유도류에 의한 수면상승이며, 이로부터 잠제 후면 연안방향으로의 기울기가 증가하여 흐름이 발달한 것으로 판단된다. 반면에 파고분포의 잠제 후면 연안방향으로의 기울기는 상대적으로 약한 것으로 보인다.

Fig. 3.

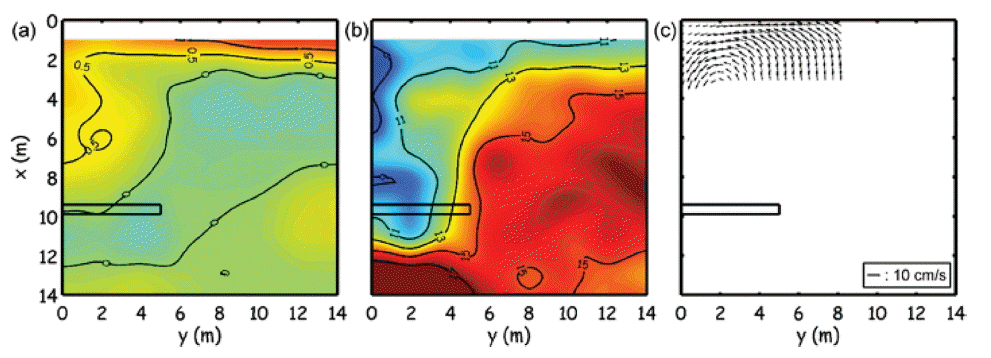
(a) Mean surface elevation (cm) (b) wave height distribution (cm) (c) Lagrangian flow velocity vector (cm/s) of case 23 presenting the erosion response (convergent flow pattern): H₀ = 17 cm, T₀ = 2.5 s, x_B = 9.65 m, s_B = 0.1 m.

Fig. 4.

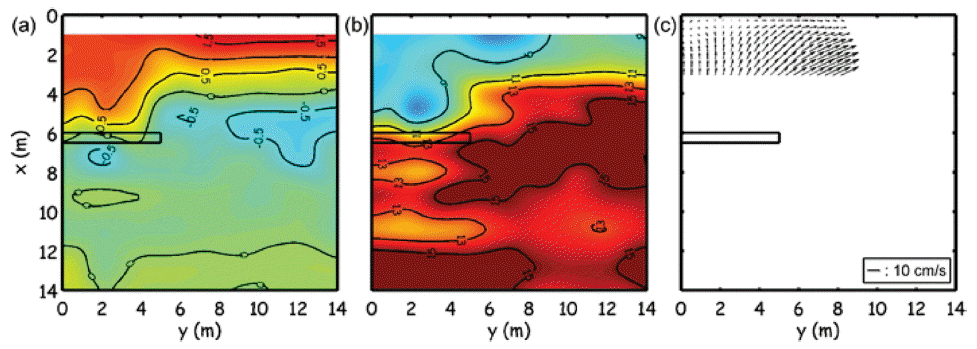
(a) Mean surface elevation (cm) (b) wave height distribution (cm) (c) Lagrangian flow velocity vector (cm/s) of case 4 presenting the accretion response (divergent flow pattern): H₀ = 15 cm, T₀ = 3.2 s, x_B = 6.25 m, s_B = 0.2 m.

Fig. 5는 규칙파 H₀ = 20 cm, T₀ = 3.2 s, 잠제 위치는 x_B = 7.65 m, s_B = 0.1 m인 실험조건(case 12)의 평균수면 분포, 파고 분포 그리고 유속 분포를 나타내고 있다. 이 경우의 유속분포는 잠제 후면 중심부로 집중되는 흐름과 측면부 밖으로 흘러 나가는 흐름이 동시에 발달하고 있음을 알 수 있다. 즉, 잠제 후면 중심부에서는 해안선의 퇴적 반응으로 구분되는 흐름패턴이 보이고, 동시에 잠제 후면 측면부에서는 해안선 침식 반응으로 구분되는 흐름패턴이 관찰되었다. 평균수면 분포 뿐만 아니라 파고 분포로부터 잠제 후면부 연안방향으로의 기울기가 상호 역방향으로 두드러져 보인다. 평균수면 분포는 해안선 침식 반응의 흐름패턴(Fig. 4)의 분포와 유사하고 파고분포는 해안선 퇴적 반응의 흐름패턴(Fig. 3)의 분포와 유사한 것을 알 수 있다.

Fig. 5.

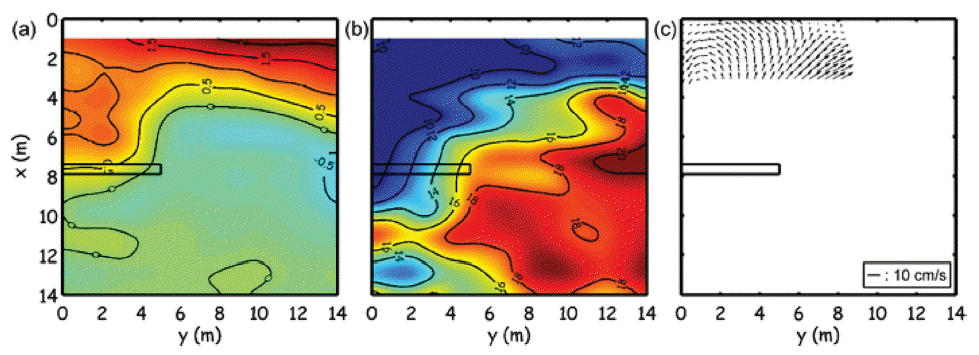
(a) Mean surface elevation (cm) (b) wave height distribution (cm) (c) Lagrangian flow velocity vector (cm/s) of case 12 presenting the transient response: H₀ = 20 cm, T₀ = 3.2 s, x_B = 7.65 m, s_B = 0.1 m.

결론적으로, 퇴적반응은 잠제 후면 중심의 낮은 파고 영역으로 연안류가 집중되어 발달하여 초기의 평행한 해안선이 전진하는 경우이며, 침식반응은 잠제 상단의 쇄파에 따른 쇄파 유도류와 상승한 평균수면 기울기에 의해 흐름이 중심부의 좌우로 발달되어 초기의 평행한 해안선이 후퇴하는 경우이다. 그러나 Fig. 5와 같은 경우의 실험결과는 해안선의 퇴적 반응과 침식 반응만으로는 구분하기 어렵다고 판단되며, 퇴적 반응과 침식 반응이 혼재된 흐름패턴으로 구분할 수 있다. 이와 같이 일부 실험조건에서는 해안선의 퇴적 또는 침식 반응 중 하나의 경우로 구분하기 어려운 혼재된 형태의 흐름패턴을 확인할 수 있었다. 또한 관측된 잠제 전면부 파고분포로부터 확인되는 파랑 반사효과는 잠제후면 파고와 그에 따른 파랑잉여응력 기울기에도 영향을 준다. 따라서 파랑 반사효과는 이를 고려하지 못하는 기존 수치모형 연구결과와 본 연구의 실험결과와의 차이를 나타내는 하나의 인자로 판단된다.

3.2 잠제 후면 관측결과에 따른 해안선 침퇴적 반응 경험식 검토

경험식에 의한 분석결과와 비교하여 수리실험의 분석결과가 전반적으로 유사하였으나, 실험조건에 따라 경험식에서는 퇴적반응이었던 경우가 실험결과에서는 침식반응으로 나타나기도 했다. 또한, 앞서 언급한 것처럼 일부 실험조건에서 잠제 후면의 침식과 퇴적반응이 혼재된 흐름패턴을 확인할 수 있었다. 수리실험의 관측 유속분포에 따른 침퇴적 반응 결과와 Ranasinghe et al.(2010)이 제시한 경험식을 적용한 결과를 비교하여 서로 일치하지 않는 경우에 대하여 Table 2에 제시하였다. 전체 35 실험케이스 가운데 7개의 경우가 불일치하였으며, 5개의 경우는 침식반응이나 퇴적반응의 한 가지로만 구분되기 어려웠다. 즉, 앞에서 언급한 것처럼 잠제 후면에서 수렴되는 흐름과 분기되는 흐름이 동시에 혼재된 경우이다. 이러한 결과를 Ranasinghe et al.(2010)의 결과와 비교하여 Fig. 6에 나타내었다.

Table 2.

The experimental cases disagreed with the resultant shoreline response of Ranasinghe et al. (2010)

Fig. 6.

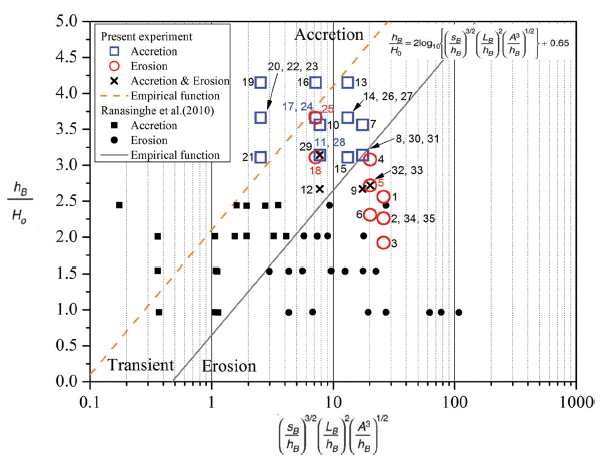
The shoreline response mode of the present experimental results with the results of Ranasinghe et al. (2010).

Fig. 6에 Ranasinghe et al.(2010) 에서 제시하고 있는 입사파 및 잠제의 조건으로 구성된 무차원 파라미터(h_B/H_o, (s_B/h_B) ^3/2(L_B/h_B) ² (A³ /h_B) ^1/2)에 따라 흐름 패턴에 따른 침퇴적 반응의 결과를 도식화한 그래프에 본 연구의 실험결과를 함께 나타내었다. 식(1)에 제시하였던 침퇴적 반응 경계를 추정한 경험식도 함께 도시하였다. 앞서 Table 2에서 제시되었던 경험식(1)과 일치하지 않는 경우들을 확인할 수 있으며, 이들은 대체로 퇴적반응으로 예측되었던 영역에 위치해 있음을 알 수 있다. 즉, 기존 경험식(1)에 따라 퇴적반응이 예측되던 잠제 조건에서 침식이 발생할 수 있음을 뜻한다. 수치모의 기반의 기존 경험식(1)과 불일치하는 수리실험 결과가운데 case 11, case 18, case 29의 무차원 파라미터 값은 서로 비슷하여 그래프상에서 거의 동일한 위치(h_B/H_o = 3.2, (s_B/h_B) ^3/2(L_B/h_B) ² (A³ /h_B) ^1/2 = 7.2)에서 겹쳐있으나 실험결과로는 세 가지 유형의 흐름패턴이 관측되었다.

Fig. 7에 위에 나타난 그래프에서 거의 동일한 파라미터 값에 위치해 있는 세 종류의 흐름패턴 결과를 제시하였다. Fig. 7(a)는 해안선 변동이 퇴적반응으로 구분되는 흐름패턴이 보이고, Fig. 7(b)는 해안선 변동이 침식 반응으로 구분되는 흐름패턴으로 보인다. 그리고 Fig. 7(c)에서는 퇴적반응과 침식 반응 흐름패턴이 동시에 나타나고 있다. 특히, Fig. 7(a)에 나타낸 case 11과 Fig. 7(c)에 나타낸 case 29는 주기를 제외하면 동일한 조건의 실험임에도 불구하고 서로 구별되는 흐름패턴을 나타내고 있다. 입사파 주기는 침퇴적 반응 흐름패턴을 결정하는데 무시할 수 있는 파라미터가 아닌 것으로 판단된다. 결과적으로 퇴적반응과 침식반응 흐름패턴 구간 사이에 천이영역이 있는 것으로 가정하여, 다음과 새로운 수정 경험식을 제시하였고, 이를 Fig. 7에 함께 도시하였다.

Fig. 7.

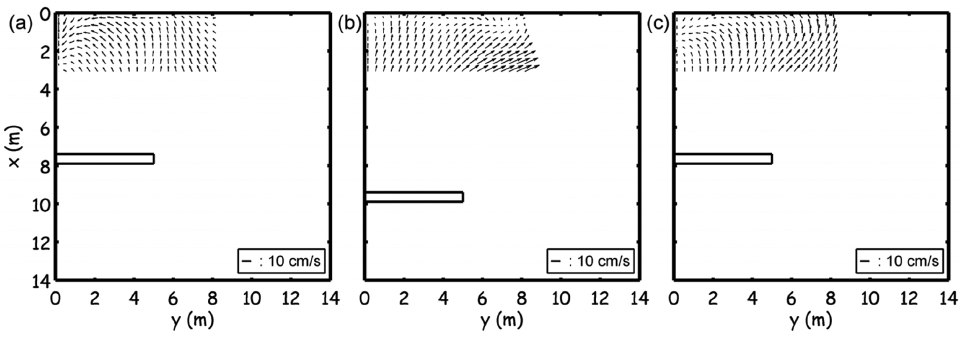
Flow patterns of the three cases with the similar values of the non-dimensional parameters of Ranasinghe et al. (2010) (h_B/H_o = 3.2, (s_B/h_B)^3/2(L_B/h_B)²(A³/h_B)^1/2 = 7.2) (a) case 11 (H₀ = 17 cm, T₀ = 3.2 s, x_B = 7.65 m, s_B = 0.1 m) presenting the accretion response flow pattern (b) case 18 (H₀ = 20 cm, T₀ = 3.2 s, x_B = 9.65 m, s_B = 0.2 m) presenting the erosion response flow pattern (c) case 29 (H₀ = 17 cm, T₀ = 2.5 s, x_B = 7.65 m, s_B = 0.1 m) presenting the accretion response flow pattern.

이 경험식을 기준으로 천이구간 밖의 퇴적구간 잠제는 해변 보전에 적절한 역할을 할 수 있다고 판단된다. 그러나 이러한 불확실성으로 부터 실제 복잡한 지형과 다양한 입사파 조건에서 상기 파라미터와 이를 바탕으로 하고 있는 경험식만으로 해안선 반응을 결정하는 것은 현실적으로 어려워 보인다.