이완법을 이용한 SWASH 모형의 파랑 조파기법 개선

Improvement of Wave Generation for SWASH Model Using Relaxation Method

Article information

J Korean Soc Coast Ocean Eng. 2017;29(4):169-179

Publication date (electronic) : 2017 August 31

doi : https://doi.org/10.9765/KSCOE.2017.29.4.169

^*Industry-University Cooperation Foundation, ERICA Campus, Hanyang University

^**Dept. of Civil, Env. and Plant Engrg., ERICA Campus, Hanyang University, 55 Hanyangdaehak-ro, Sangnok-gu, Ansan, Gyeonggi-do 15588, Korea

신충훈^*, 윤성범^,^**

^*한양대학교 ERICA 산학협력단

^**한양대학교 건설환경플랜트공학과

Corresponding author: Sung Bum Yoon, Dept. of Civil, Env. and Plant Engrg., ERICA Campus, Hanyang University, 55 Hanyangdaehak-ro, Sangnok-gu, Ansan, Gyeonggi-do 15588, Korea, Tel: +82-31-400-5144, Fax: +82-31-436-8147, sbyoon@hanyang.ac.kr

Received 2017 June 30; Revised 2017 July 18; Accepted 2017 July 26.

Abstract

본 연구에서는 선형 및 비선형파의 안정적이고 정확한 조파를 위해 이완법을 이용한 조파기법을 비정수압 수치모형인 SWASH 모형에 적용하였다. 이완법을 이용한 조파기법을 검증하기 위해 선형파와 비선형파인 경우에 대해 수치실험을 수행하였고 해석해와 비교하였다. 그 결과 Stokes 파 영역으로부터 cnoidal 파 영역에 이르는 모든 경우의 입사파랑이 성공적으로 생성되고 전파되었다. 또한 파고와 파형이 해석해와 잘 일치하는 것을 확인할 수 있었다.

Trans Abstract

In this study, we applied the wave generation method by relaxation method to the SWASH model, which is a non - hydrostatic numerical model, for stable and accurate wave generation of linear and nonlinear waves. To validate the relaxation wave generation method, we were simulated various wave, including the linear wave and nonliner wave and compared with analytical solution. As a result, the incident wave was successfully generated and propagated in all cases from Stokes waves to cnoidal wave. Also, we were confirmed that the wave height and the waveform were in good agreement with the analytical solution.

Keywords: 비선형파 조파; 이완법; 비정수압 수치모형; SWASH

Keywords: nonlinear wave generation; relaxation method; non-hydrostatic model; SWASH

1. 서 론

관심영역 내에서 파랑변형을 다루는 수치실험을 잘 재현하기 위해서는 조파경계에서 입사파랑이 정확히 조파되어 실험영역 내에서 잘 전파되어야 한다. 이를 위해 안정적이고 효과적인 파랑 조파 기법의 개발은 필수적이다. 다양한 수치모형에서 사용되는 파랑의 조파 방법은 크게 외부조파와 내부조파로 나눌 수 있다. 외부조파는 수치실험 영역의 경계조건에서 매시간 단계의 수면 변위나 유속 또는 흐름 등을 임의로 부가하는 방법이다. 외부조파 기법은 실험영역 내에 직접적으로 경계를 통해 파가 조파되기 때문에 목표파랑의 파고와 위상이 정확하게 재현된다. 그러나 외부조파 기법을 사용한 조파 방법의 경우 실험 영역 내의 구조물이나 수심의 갑작스런 변화로 생긴 반사파를 적절하게 처리하지 못해 반사파가 실험영역 내로 재반사 되는 문제가 발생한다. 구조물이나 수심의 변화로 생긴 반사파가 측면경계에서 외해로 빠져나가지 못하고 실험영역 내에 쌓이게 되면 수치오류가 발생하게 된다. 이러한 문제를 해결하기 위해 Larsen and Dancy(1983)에 의해 내부조파기법이 제안되었으며, 그 이후 많은 연구가 수행되어 왔다.

내부조파기법은 조파방법에 따라 선 조파기법(line source method)과 원천함수기법(source function method)으로 나눌 수 있다. 선 조파기법은 Larsen and Dancy(1983)가 Peregrine(1967)의 Boussinesq 방정식에 처음 적용한 이후 Lee and Suh(1998), Lee et al.(2001), Lee et al.(2006)과 Lee et al.(2007)에 의해 다양한 지배방정식을 가지는 수치모형에 적용되어 왔으며, 입사파랑을 성공적으로 내부조파 할 수 있었다. 그러나 선 조파기법을 이용해 파를 조파할 경우 특정 방정식에서 조파선 위치에 수치진동현상이 나타나는 문제가 발생되었다(Wei et al., 1999; Kim et al., 2005). 또한 이를 적절히 제어하지 않을 경우 해가 급속하게 발산하는 것이 확인되었다. 이를 해결하기 위해 Wei et al.(1999)은 원천함수기법을 이용하여 Boussinesq 방정식 수치모형을 위한 조파기법을 제안하였다. 원천함수기법은 그 이후 비선형 천수방정식과 확장형 Boussinesq 방정식, 완전비선형 Boussinesq 방정식 등을 지배방정식으로 하는 다양한 수치모형에 적용되었으며, 많은 연구가 이루어 졌다(Wei et al., 1999; Skotner and Apelt, 1999; Chawla and Kirby, 2000; Kim et al., 2004; Kim et al., 2007). 그러나 원천함수기법을 이용해 비선형성이 강한 비선형파(e.g. stokes wave, cnoidal wave)를 조파하는 경우 파의 파고와 위상을 정확하게 재현하지 못하는 것으로 나타났다.

본 연구에서는 이완법(relaxation method)을 이용한 안정적이고 효과적인 파랑 조파 기법을 소개하고자 한다. 이 기법은 수치실험 영역 내에 이완영역(relaxation zone)을 설정하고 그 영역 안에서 매시간 단계의 수면 변위나 유속 또는 흐름 등을 임의로 부과하는 방법이다. 상기 기법은 다양한 수치모형에 적용되었으며, 비선형파의 경우에도 정확하게 파를 조파하는 것으로 입증되었다(Madsen et al., 2003; Fuhrman and Madsen, 2006; Fuhrman et al., 2006; Jamois et al., 2006).

본 연구에서는 비선형파의 안정적이고 정확한 조파를 위해 이완법을 이용한 조파기법을 비정수압 수치모형인 SWASH에 적용하였다. 또한 수치실험을 통해 다양한 비선형파의 경우에 대해 그 정확성을 해석해와 비교해봄으로써 타당성을 검증하였다.

2. 수치모형

2.1 지배방정식

컴퓨터의 발달과 함께 다양한 수치모형들이 개발되어 활용되어 왔다. 대부분의 모형들은 정수압(hydrostatic) 가정에 근거하여 개발되어왔으나 최근에는 비정수압(non-hydrostatic) 가정을 이용한 수치모형들이 많이 개발되고 있다. 비정수압 가정을 이용한 수치모형들은 비선형분산파의 거동을 수치모의하기 위해 연직방향으로 많은 격자의 층을 나눠야만 했다. 그러나 최근 Delft 대학에서 개발된 비정수압 수치모형인 SWASH(Surface WAves till SHore; Zijlema et al., 2011)는 Keller-box기법을 이용해 자유수면 위치의 압력 경계조건을 손쉽게 정의해 연직방향으로 2개~4개의 층만으로도 자유수면변위를 정확하게 수치모의 하였다. 또한 층을 증가시켜 심해영역까지 분산효과의 정확성을 증대시킬 수 있다. 현재 SWASH 모형은 오픈소스 소프트웨어로 누구나 특별한 제한없이 무상으로 사용할 수 있다. 따라서 향후 파랑변형 수치모의 분야에서 그 활용도가 더욱 증가할 것으로 예상된다.

SWASH 모형은 Stelling and Zijlema(2003), Stelling and Duinmeijer(2003), Zijlema and Stelling(2005, 2008), Smit et al.(2013) 등의 연구자들에 의해 개발되었다. Navier-Stokes 방정식에서 유도한 수심 적분된 비정수압 비선형 천수 방정식을 지배방정식으로 하고 있으며 지배방정식은 다음과 같다.

(1) ∂ζ∂t+∂hu∂x+∂hv∂y=0

(2) ∂u∂t+u∂u∂x+v∂u∂y+g∂ζ∂x+1h∫−dζ∂q∂xdz+cfuu2+v2h =1h(∂hτxx∂x+∂hτxy∂y)

(3) ∂v∂t+u∂v∂x+v∂v∂y+g∂ζ∂y+1h∫−dζ∂q∂ydz+cfvu2+v2h =1h(∂hτyx∂x+∂hτyy∂y)

여기서 ζ(x, y, t)는 정수면을 기준으로 하는 자유수면변위, d(x, y)는 정수면하 수심, h(= ζ + d)는 총 수심, u(x, y, t)과 v(x, y, t)는 수심 평균된 x방향, y방향 유속, q(x, y, z, t)는 비정수압, g는 중력가속도, c_f는 바닥 거칠기, τ_xx, τ_xy, τ_yx, τ_yy는 수평 난류 응력이다. 수평난류응력은 다음과 같은 방정식으로 산정된다.

(4) τxx=2νt∂y∂x,τxy=τyx=νt(∂v∂x+∂u∂y), τxx=2νt∂v∂y

여기서, ν_t(x, y, t)는 쇄파와 난류성분에 의한 수평와점성계수이다.

식(2)와 (3)의 수심에 따른 비정수압 구배(non-hydrostatic pressure gradient)의 적분은 다음과 같이 나타낼 수 있다.

(5) 1h∫−dζ∂q∂xdz=12h∂qb∂x+12∂qb∂(ζ−d)∂x

(6) 1h∫−dζ∂q∂ydz=12h∂qb∂y+12∂qb∂(ζ−d)∂y

여기서 q_b는 바닥면에서의 비정수압이다. 이 수치모형은 그 결과들이 충분히 검증되어 많은 문헌에 소개되어 있다. 따라서 자세한 내용은 그 문헌들로 대신한다.

2.2 SWASH 모형의 조파기법

SWASH 모형은 외부조파기법을 이용해 수치실험 영역 내로 파를 조파하고 있다. 조파하고자 하는 파의 파고와 위상을 시간에 따른 유속으로 변환하여 계산 영역의 한쪽 끝에 부과하고 있으며 또한 외부조파로 인한 실험영역 내 재반사 문제를 해결하기 위해 weakly reflective 조건으로 경계조건이 구성되어 있다. 조파 경계조건은 다음과 같다.

(7) ub=±gh(2ζb−ζ)

여기서 u_b는 경계에서의 매시간 단계의 유속, ζ_b는 조파하고자하는 입사파의 매시간 단계의 수면변위이다. 또한 경계조건에서의 ± 기호는 경계조건의 위치에 따라 달라진다. 플러스(+) 기호는 좌측경계에서 파가 조파되는 경우를 나타내며 마이너스(−) 기호는 우측경계에서 파가 조파되는 경우를 나타낸다.

2.3 Relaxation 조파기법

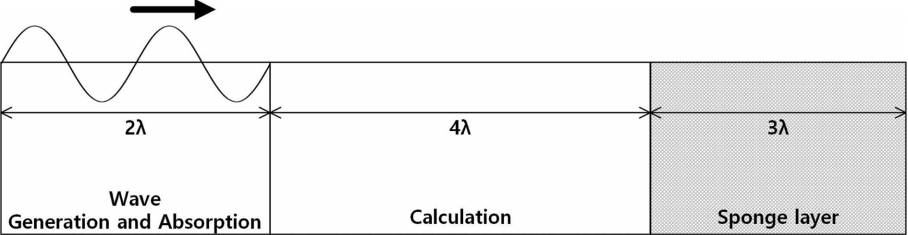
본 연구에서는 계산영역 내에 이완영역을 설정하고 그 영역 안에서 매시간 단계의 수면변위를 임의로 부과하였다. 일반적으로 이완영역은 조파하고자 하는 입사파의 1~2 파장의 길이로 구성되면 충분하다. 다음 Fig. 1은 본 연구에서 이용한 relaxation 조파기법에 대한 개념도이다.

Fig. 1.

A sketch of the relaxation zones.

1번 영역은 조파 및 흡수 경계로 이완영역 내에서 이완함수(relaxation function)와 입사파의 해석해(analytical wave solution)를 결합해 입사파를 조파하고 실험영역 내 재반사 문제를 해결하는 역할을 한다. 2번 영역에서는 이완영역이 없으며 계산된 값이 그래도 유지된다. 3번 영역은 계산영역이 끝나는 지점에서 모든 파랑 에너지를 감쇠시켜 반사파를 최소화하기 위해 스펀지 층을 두어 영역 내로 들어오는 파의 에너지를 흡수하였다. 스펀지 층을 이용한 에너지 흡수 방법은 매우 효과적이며 널리 활용되고 있다. 스펀지 층을 이용한 에너지 흡수 방법은 이미 SWASH 모형에 적용되어 있어 그 방법을 그대로 사용하였다. SWASH 모형에서는 스펀지 층의 길이를 입사파의 파장대비 3~5배의 길이로 제안하고 있다. 각 영역 내에서 매시간 단계에 부과되는 자유수면변위와 이완함수의 관계식은 다음과 같다.

1번 영역 : ζ=1-Rcζanalytical× ramf+ Rcζcomputational

2번 영역 : ζ=ζcomputational

3번 영역 : ramf=0.5*1+tanhtimeT-3, SPONc = bβ3+(1-b )β6

여기서 ζ_analytical는 조파하고자 하는 입사파의 매시간 단계 수면변위, ζ_{computational}는 매시간 단계에 계산된 수면변위, R_c는 이완함수를 통해 계산된 이완계수(relaxation coefficient), SPON_c는 스펀지 층의 계수이다. ramf는 램프함수(ramp function)이며 시작단계에서부터 파를 점진적으로 증가시키기 위해 매시간 단계에 부과되는 자유수면변위에 곱하였다. 스펀지 층의 계수는 Mayer et al.(1998)이 제안한 식으로 여기서 b는 계수의 증가율로 SWASH 모형에서는 0.5를 사용 중이며, β = |x − x_s|/|x_e − x_s|로 x_s는 스펀지 층의 시작위치, x_e는 스펀지 층이 끝나는 위치이다. 이완계수(R_c)는 이완영역이 시작되는 지점에서 0의 값을 가지며 서서히 증가해 영역이 끝나는 부분에서 1의 값을 가진다.

이완영역이 시작되는 지점에서는 이완계수가 0으로 조파하고자 하는 입사파의 매시간 단계 수면변위가 이완영역 내에서의 수면변위가 된다(ζ = ζ_analytical). 경계로부터 점점 멀어짐에 따라 이완영역 내에서의 수면변위는 조파하고자 하는 입사파의 매시간 단계 수면변위와 지배방정식에 의해 계산된 매시간 단계 수면변위 이 두 가지 값의 합으로 산정되는데 이때 각 위치에 따른 이완계수를 이용해 비중을 서로 달리하여 계산한다(ζ = (1 − R_c)ζ_analytical + R_cζ_{computational}). 마지막으로 이완영역이 끝나는 지점에서는 이완계수가 1이 되므로 지배방정식에 의해 계산된 매시간 단계 수면변위가 이완영역 내에서의 수면변위가 된다(ζ = ζ_{computational}). 즉, relaxation 조파기법은 이완영역 내에서 수면변위를 임의로 부과하는데 조파하고자 하는 입사파의 해석해의 수면변위와 지배방정식에 의해 계산된 수면변위, 이 두 가지 수면변위에 서로 다른 가중치를 주고 그 합을 이완영역 내에서 매시간 단계의 수면변위로 부과하는 기법이다. 이렇게 산정된 이완영역 내에서의 수면변위는 수치필터(numerical filter) 등을 사용하지 않고 조파영역 내에서의 수치진동현상을 근본적으로 제거할 수 있다.

본 연구에서는 파의 조파 및 흡수를 위해 Engsig-Karup(2006)이 제안한 3차 다항식의 이완함수를 사용하였다. 이완함수는 사용하는 수치기법(numerical scheme)에 따라 크게 좌우된다. 따라서 사용하는 수치기법에 따른 적절한 이완함수를 찾는 추가적인 연구가 필요하다. 본 연구에서 사용한 3차 다항식의 이완함수는 다음과 같다.

(8) Rc=−2(X2)3+3(X2)2 (0≤X≤2),X=x/λ

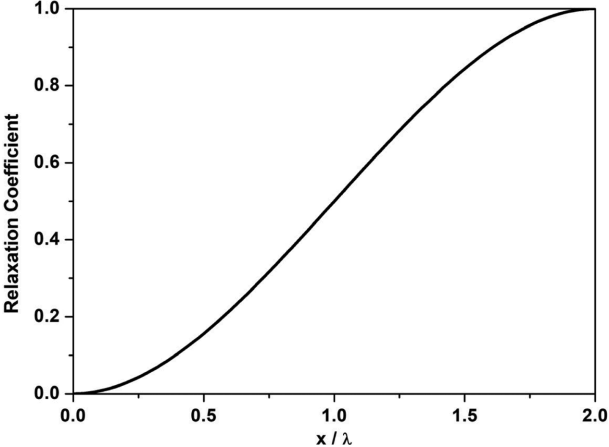
Fig. 2는 1번 영역에서 사용하는 이완계수 분포를 도시하였다. Relaxation 조파기법은 다음 시간 단계로 진행하기 전에 매시간 부과하는 수면변위를 사전처리 하여 각 시간 단계에서 간단히 구현할 수 있다. 또한 이 방법은 3차원 수치모형에도 쉽게 확장시켜 적용할 수 있다.

Fig. 2.

Relaxation coefficient for zone 1.

3. 수치실험

3.1 선형파의 조파

SWASH 모형에 적용된 weakly reflective 외부조파기법과 본 연구에서 사용한 Relaxation 조파기법의 선형파 조파 성능을 검증하였다. 수심(h)이 1 m일 때 천해(kh = 0.1π)와 심해(kh = 1.0π)인 경우에 대해 상대파고(H/h)를 0.001로 충분히 작게 하여 선형파를 조파하였다. 매시간 단계에 부과되는 자유수면변위는 Airy 파 이론을 이용해 계산하였으며 계산영역은 Fig. 3과 같이 구성하였다. 격자 구성은 Δx = λ/40으로 파형을 충분히 재현할 수 있도록 하였으며 우측 경계에는 3λ 길이의 스펀지 층을 설치하여 파랑 에너지를 감쇠시켜 경계에서 파랑의 반사를 최소화 하였다. 또한 Sommerfeld 방사조건을 이용한 개경계조건(open boundary)을 이용해 장시간 동안 수치모의를 수행하여도 수위 및 파고가 상승하지 않도록 경계조건을 구성하였다.

Fig. 3.

Schematic diagram of horizontally one-dimensional computational domain.

Fig. 4는 SWASH 모형에 사용 중인 외부조파기법을 사용하여 선형파를 조파한 결과이다. 천해의 경우 선형파의 파고와 파형이 정확하게 재현되나 심해의 경우 파고의 크기가 목표파고 대비 약 0.94배로 작게 조파되는 것을 확인할 수 있다. 따라서 SWASH 모형에 적용된 외부조파기법을 사용하여 모든 수심조건에 목표 파형을 정확하게 조파하는 것이 힘들다는 것을 알 수 있다.

Fig. 4.

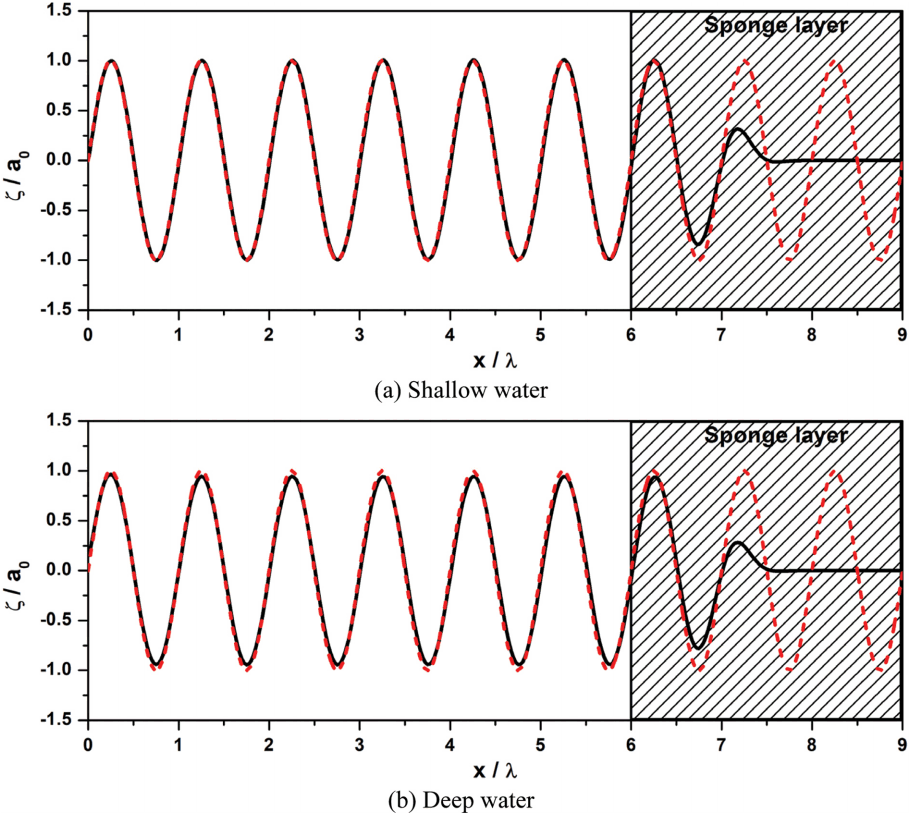
Normalized water surface elevation of linear waves using boundary wave generation method at t = 30T : (a) shallow water (kh = 0.1π), (b) deep water (kh = 1.0π); solid line : numerical, dashed line : analytical.

Fig. 5는 relaxation 조파기법을 사용하여 선형파를 조파한 결과이다. 천해와 심해 모든 경우에 대해 선형파의 파고와 파형이 모두 정확하게 재현되는 것을 확인할 수 있다. 이로부터 relaxation 조파기법은 천해역과 심해역에 관계없이 적용할 수 있다는 것을 알 수 있다.

Fig. 5.

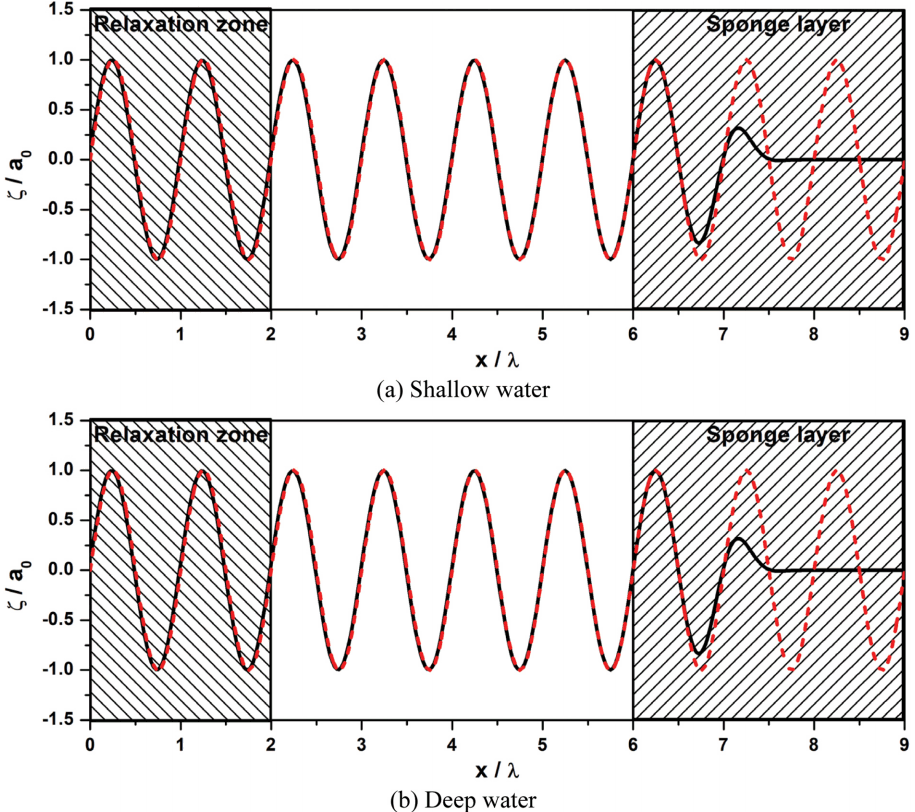
Normalized water surface elevation of linear waves using relaxation wave generation method at t = 30T : (a) shallow water (kh = 0.1π), (b) deep water (kh = 1.0π); solid line : numerical, dashed line : analytical.

조파경계에서의 재반사 문제에 대해 검증하고자 선형파 수치실험과 동일한 계산영역에 우측 경계에서 설치하였던 스펀지층을 제거하고 수치모의를 수행하였다. 계산 격자의 크기와 입사파의 재원은 앞서 수행한 심해인 경우의 선형파 수치실험 조건과 동일하다. SWASH 모형에 적용된 weakly reflective 외부조파기법과 본 연구에서 이용한 relaxation 조파기법을 비교하였다.

다음 Fig. 6은 각 시간에 따른 수면변위를 보여준다. 조파 시작 후 60T 시간 경과 후부터 (1/4)T 마다의 수면변위를 도시하였다. SWASH 모형에 적용된 weakly reflective 외부조파기법을 이용해 장시간 동안 수치실험을 수행한 경우 우측경계에서 반사된 파를 조파 경계에서 흡수하고 있으나 완벽하게 흡수처리 하지 못해 장시간 수치실험 수행 시 조파경계에서 반사파가 다시 반사되어 수치실험영역 내로 전파되는 것을 확인할 수 있다. 조파경계에서 재반사된 반사파가 합쳐져 진폭은 2배가 넘게 증폭되고, 입사파와 반사파가 완벽하게 상쇄되지 않아 수면변위가 상승되어 있는 것을 확인할 수 있다. 그러나 relaxation 조파기법을 사용한 경우 우측경계에서 반사된 파가 조파된 파와 합쳐져서 중복파를 형성하고, 조파영역에서는 반사파가 잘 흡수되어 소실되는 것을 확인할 수 있다. 또한 입사파와 반사파가 보강 간섭하여 진폭이 2배가 되는 지점과 상쇄 간섭하여 진동하지 않는 지점이 정확하게 나타난다. 이로부터 relaxation 조파기법은 계산영역내의 반사파로 인한 수치적 문제가 발생하지 않는다는 것을 확인할 수 있다.

Fig. 6.

Superposition of normalized water surface elevation of linear waves at t = 60T, 60T = 1/4T, 60T + 2/4T, 60T + 3/4T.

3.2 비선형파의 조파

3.2.1 Stokes 5^th order wave

심해의 비선형파에 대한 조파 성능을 검증하기 위해서 수심 1 m, 주기 1.0 s인 경우에 대해 파고 0.01 m, 0.1 m, 0.2 m인 파를 조파하였다. 이 때 상대수심은 이며 Ursell 수는 각각 0.024, 0.258, 0.595이다. 매시간 단계에 부과되는 자유수면변위는 Fenton(1985)의 Stokes 5^th order 파 이론식을 이용하였으며 계산영역 및 계산격자의 크기는 선형파 수치실험의 제원과 동일하다. Fig. 7은 relaxation 조파기법을 사용하여 조파한 Stokes 파를 해석해와 비교한 결과이다. 파고가 증가함에 따라 파봉이 뾰족해지는 Stokes 파의 파형을 잘 재현하는 것을 확인할 수 있다. 또한 조파영역을 벗어난 파가 전파되며 파형이 변하지 않고 목표하였던 비선형파의 수면변위와 위상을 잘 재현하는 것을 확인할 수 있다.

Fig. 7.

Normalized water surface elevation of stokes waves at t = 30T : (a) H = 0.01 m, (b) H = 0.1 m, (c) H = 0.2 m; solid line : numerical, dashed line : analytical.

3.2.2 Cnoidal wave

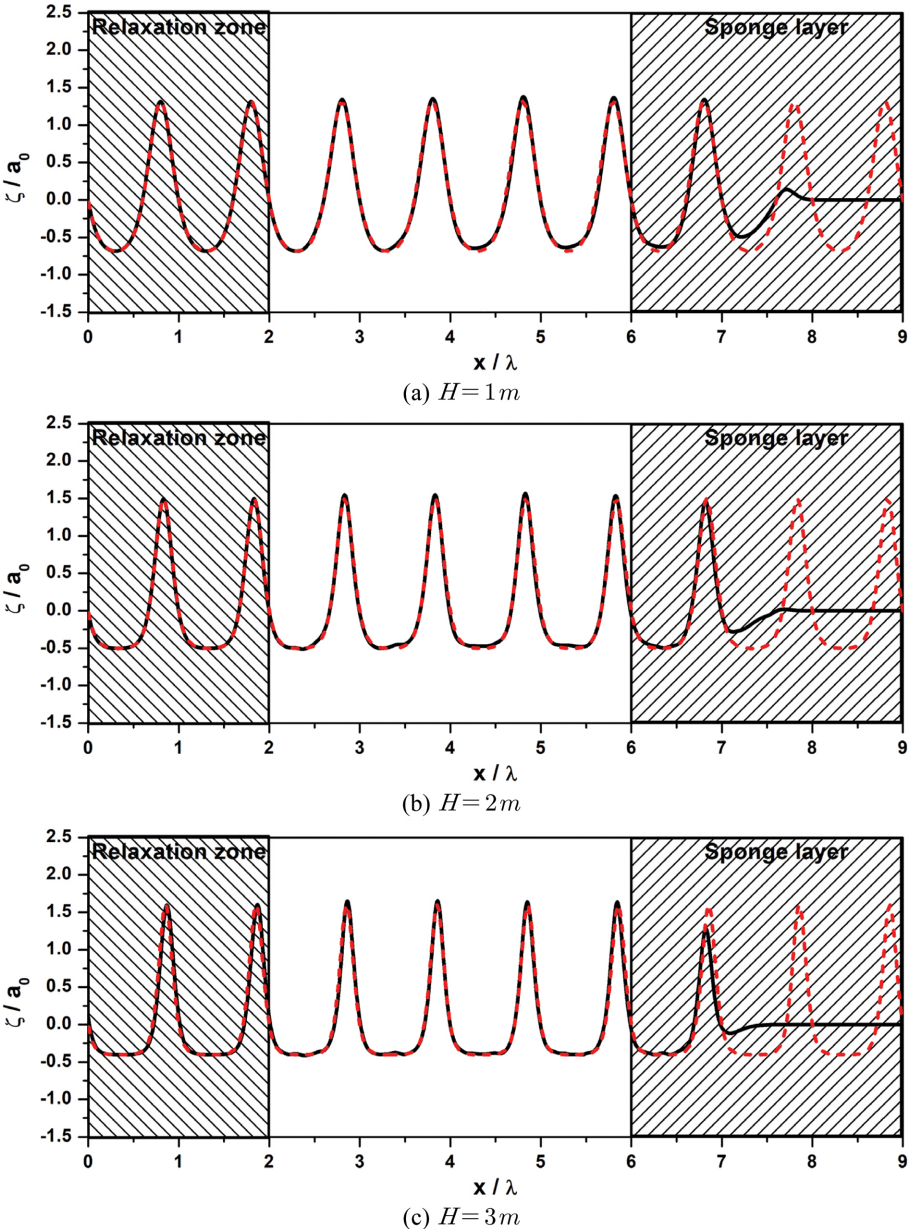
천해의 비선형파에 대한 조파 성능을 검증하기 위해서 수심 10 m, 주기 20 s인 경우에 대해 파고 1 m, 2 m, 3m인 파를 조파하였다. 매시간 단계에 부과되는 자유수면변위는 Fenton(1979)의 고차 cnoidal 파 이론을 이용해 계산하였으며, 이 때 상대수심은 kh = 0.1π이며 Ursell 수는 각각 0.48, 0.96, 1.44이다. Fig. 8은 relaxation 조파기법을 사용하여 조파한 cnoidal 파를 해석해와 비교한 결과이다. Cnoidal 파의 특징인 파봉이 뾰족하고 골이 평평한 파형을 잘 재현하는 것을 확인할 수 있다. 또한 목표하였던 비선형파의 파고와 위상이 해석해와 잘 일치하였으며 조파영역을 벗어나서도 비선형파의 전파를 정확히 재현하는 것을 확인할 수 있다.

Fig. 8.

Normalized water surface elevation of cnoidal waves at t = 30T : (a) H = 1m, (b) H = 2 m, (c) H = 3 m; solid line : numerical, dashed line : analytical.

3.3 경사지게 입사하는 파랑의 조파

파를 조파하는 조파기법들은 Fig. 9와 같이 x축 방향으로 조파영역을 설정하고 y축 방향으로 동일하게 조파영역을 분포하여 목표파랑을 조파하였다. 이러한 방식은 외부조파기법과 내부조파기법 모두 동일하기 사용되어 왔다. 따라서 조파된 파랑은 Fig. 9의 위쪽 영역으로만 전파 되어 조파영역으로부터 조파된 파랑이 전체 계산영역으로 전파되지 못하고 일부 영역은 빈 영역으로 남게 된다. 그로 인해 전파된 파의 경계선을 따라 회절현상이 발생하게 되고 수치실험영역 내에 회절의 영향을 차단하고 목표파랑을 정확하게 조파하기 위해 y축 방향으로 계산영역을 증가시켜야만 했다. 따라서 불필요한 계산 영역이 증가하게 되고 그로인해 계산시간이 증가하는 문제가 발생하게 된다. 또한 y축 방향으로 계산영역을 증가시켜 문제를 해결하는 방식은 단시간의 수치실험을 수행할 경우 큰 문제가 되지 않지만, 장시간 수행해야 하는 파랑 변형에 대한 연구에서는 오차를 발생시킬 수도 있다. 이러한 문제를 해결하기 위해 조파영역과 조파경계를 다양한 형태로 바꾸어 조파된 파랑이 빈 영역으로까지 조파될 수 있도록 하는 연구들이 수행된바 있다(Lee et al., 2006; Choi and Yoon, 2009; Lee and Yoon, 2007; Ha et al., 2012).

Fig. 9.

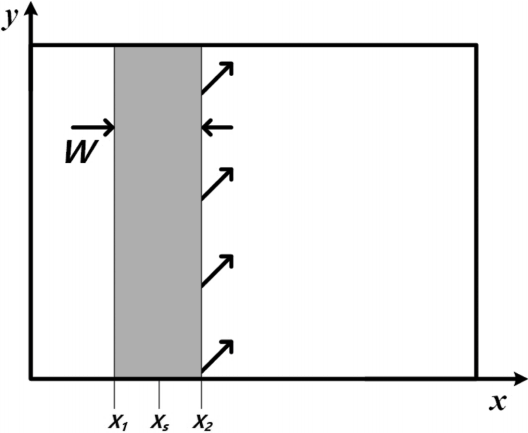
Source function definition in computational domain (Wei et al., 1999).

본 연구에서는 이러한 문제를 해결하기 위해 L자 형태의 조파영역을 구성하여 경사지게 입사하는 파랑을 조파하였다. L자 형태의 조파영역을 이용한 조파방법은 Choi and Yoon(2009), Ha et al.(2012), Ha et al.(2013), Chen and Hsiao(2016)에 의해 평가되었다. 또한 Lee et al.(2006), Lee and Yoon(2007)은 직사각형 격자체계에서 원호형 내부조파 기법(선 조파기법)을 개발하였다. 앞서 언급한 연구자들은 L자 형태의 조파기법과 원호형태의 조파기법을 이용하여 경사지게 입사하는 파랑을 조파하였고 그 결과 목표파랑을 잘 재현하는 것을 확인하였다.

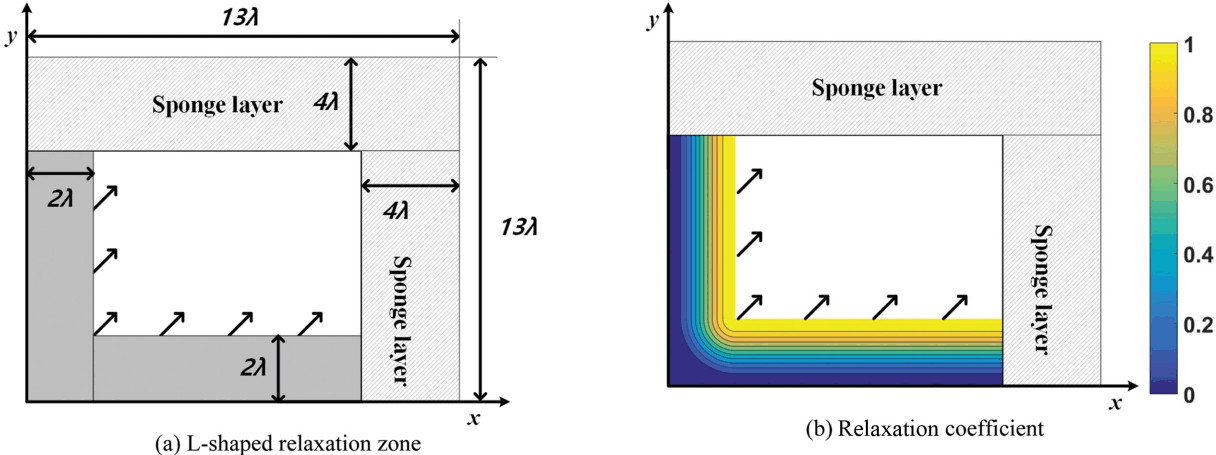
수치실험에 사용한 계산영역 및 L자 형태의 조파영역내의 이완계수분포는 Fig. 10과 같이 구성하였다. 이완계수분포는 각각 x축 방향을 따라 y = 0을 기준으로 2λ 길이로 분포하였고, y축 방향을 따라 x = 0을 기준으로 2λ 길이로 분포하였으며 L자 형태의 직각 부분은 원호형태로 처리하였다. 격자구성은 Δx = Δy = λ/40으로 파형을 충분히 재현할 수 있도록 하였으며 x축과 y축의 경계에는 4λ 길이의 스펀지 층을 설치하여 파랑 에너지를 감쇠시켰다. L자 형태의 조파영역으로부터 조파된 파랑은 추가적인 경계조건의 적용 없이 수평면에서의 임의의 방향으로 목표파랑을 전체 수치실험 영역 내에 조파할 수 있다.입사파는 앞서 수행한 심해인 경우의 선형파 수치실험 조건과 동일하다.

Fig. 10.

L-shaped relaxation zone and relaxation coefficient in computational domain.

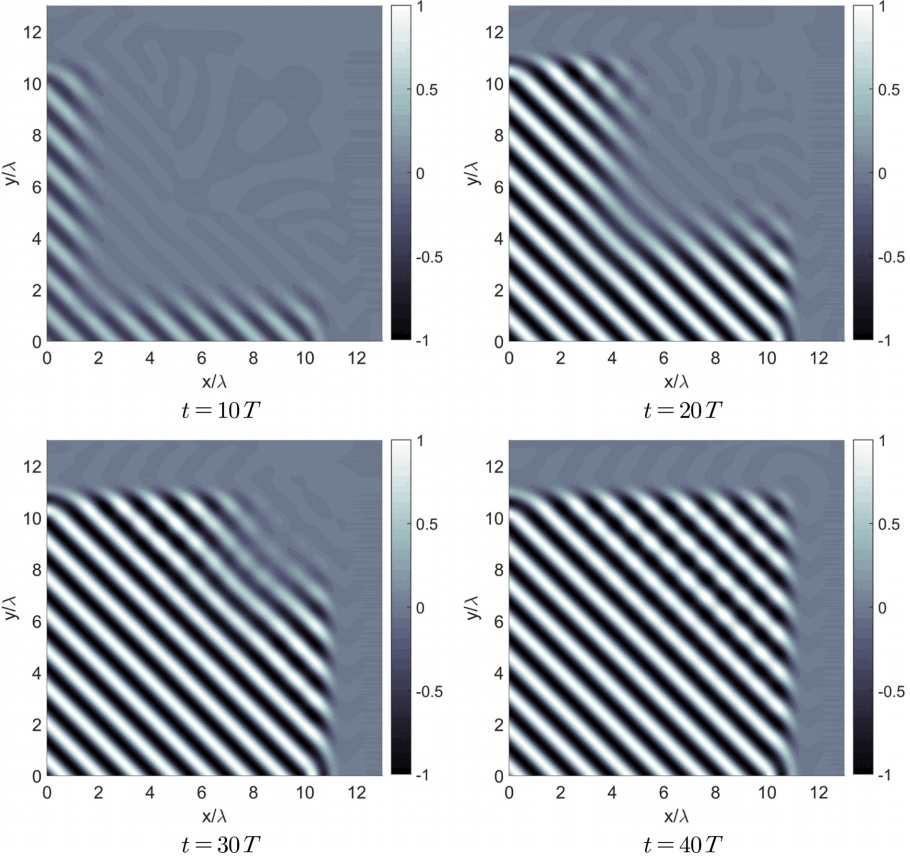
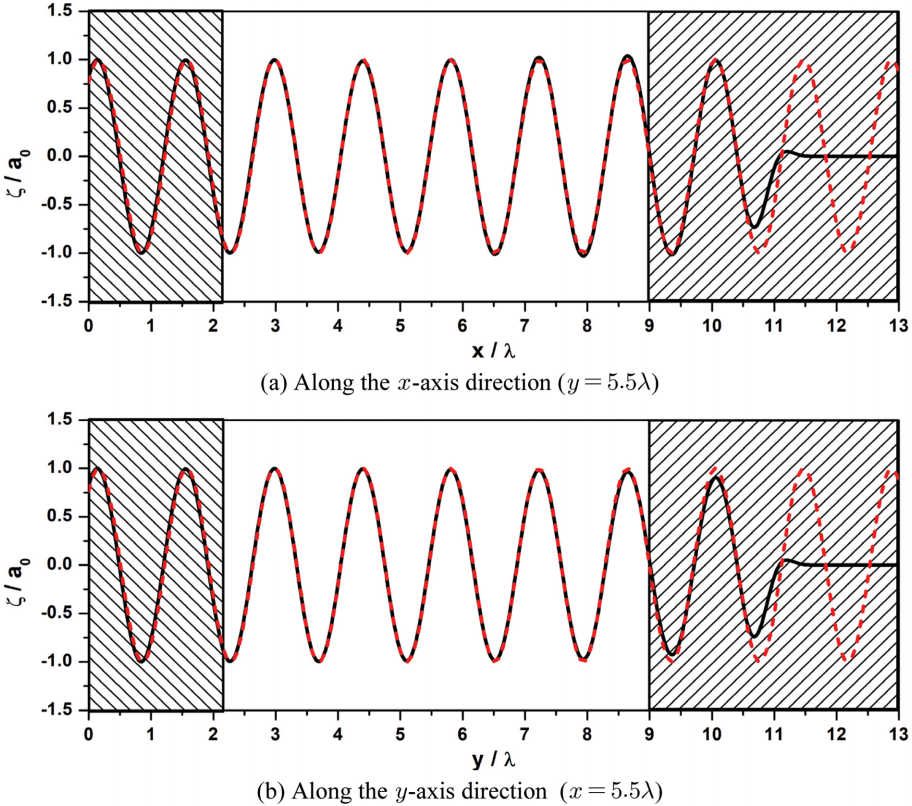
Fig. 11은 L자 형태의 조파영역으로부터 경사지게 입사하는 파랑을 조파한 결과이다. 파랑의 진형방향은 축을 기준으로 45o이며 시간에 따른 수면변위를 나타낸 결과이다. L자 형태의 조파영역의 중심으로부터 x축과 y축 양쪽방향으로 파랑이 조파되기 시작한다. 조파된 파랑은 수치실험 영역의 중심을 따라 합쳐지고, 충분한 시간이 지난 뒤에는 조파된 파랑이 전 영역에 걸쳐 나타나게 된다. Fig. 12와 Fig. 13는 수치실험 결과를 해석해와 비교한 결과이다. 파고와 위상이 해석해와 잘 일치하는 것을 확인할 수 있다.

Fig. 11.

Contour of normalized water surface elevation.

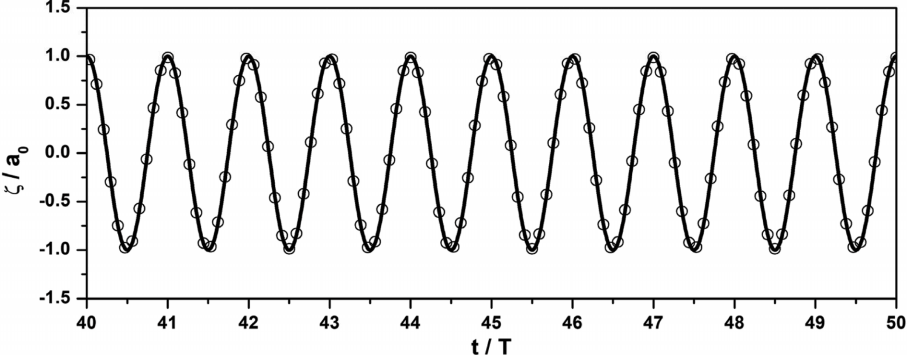
Fig. 12.

Time series of normalized water surface elevation at gauges (x = y = 5.5λ); circle : numerical, solid line : analytical.

Fig. 13.

Normalized water surface elevation of directional waves at t = 50T.

4. 결 론

기존의 SWASH 모형의 파랑 조파기법은 외부조파기법을 이용해 조파하고자 하는 파의 파고와 위상을 시간에 따른 유속으로 계산 영역의 한쪽 끝에 부과하고 있다. 그러나 외부조파기법은 실험영역 내 재반사 문제가 있어 그 활용도가 크지 않고 현재 SWASH 모형에 사용 중인 외부조파기법의 경우 심해조건에서 파고가 작게 조파되는 문제가 있다. 따라서 본 연구에서는 relaxation 조파기법을 이용해 SWASH 모형의 파랑 조파기법을 개선하였다. Relaxation 조파기법을 이용해 선형파에 대해 천해와 심해 조건에서 안정적이고 효과적으로 파랑을 조파하였다. 또한 비선형파랑인 Stokes 5^th order 파, cnoidal 파에 대해서도 파고와 파형을 성공적으로 재현하였다.

L자 형태의 조파영역을 구성하여 경사지게 입사하는 파랑을 조파하였다. 그 결과 L자 형태의 조파영역으로부터 조파된 파랑은 추가적인 경계조건의 적용 없이 목표파랑을 전 영역에 걸쳐 정확하게 잘 재현하였다. 본 연구에서 적용된 조파기법을 활용해 SWASH 모형을 이용한 파랑변형 수치실험을 실해역에 적용하기 위해서는 다양한 불규칙파의 조파에 대한 검증이 추가로 필요하다. 향후 다양한 파랑조건에서 조파기법을 개선한 SWASH 모형을 이용해 파랑변형 수치모의를 수행할 수 있을 것으로 기대된다.

Acknowledgements

이 논문은 2017년 해양수산부 재원으로 한국해양과학기술진흥원의 지원을 받아 수행된 연구임(연안 이상현상(이상고파, 이안류) 발생원인 규명 및 대응체계 구축).

References

Engsig-Karup Allan P. 2006. Unstructured nodal DG-FEM solution of high-order Boussinesq-type equations. Ph.D. Thesis. Technical University of Denmark; Lyngby, Denmark:

Chawla A, Kirby JT. 2000;A source function method for generation of waves on currents in Boussinesq models. J. Fluid Mech 22:75–83.

Chen Y, Hsiao S. 2016;Generation of 3D water waves using mass source wavemaker applied to Navier-Stokes model. Coastal Eng 109:76–95.

Choi JW, Yoon SB. 2009;Numerical simulation using momentum source wave-maker applied RANS equation model. Coastal Eng. 56(10):1043–1060.

Fenton JD. 1979;A high-order cnoidal wave theory. J. Fluid Mech. 94:129–161.

Fenton JD. 1985;A fifth-order Stokes theory for steady waves. J. Waterw. Port Coast. Ocean Eng. 111(2):216–234.

Fuhrman DR, Madsen PA. 2006;Short-crested waves in deep-water : a numerical investigation of recent laboratory experiments. J. Fluid Mech. 559:391–411.

Fuhrman DR, Madsen PA, Bingham HB. 2006;Numerical simulation of lowest-order short-crested wave instabilities. J. Fluid Mech. 563:415–441.

Ha T, Don N, Cho Y. 2012;Directional wave generation in the Navier-Stokes equations using the internal wave maker. Journal of Korea Water Resources Association 45(6):545–555. (in Korean).

Ha T, Lin PZ, Cho YS. 2013;Generation of 3D regular and irregular waves using Navier-Stokes equations model with an internal wave maker. Coastal Eng. 76:55–67.

Jamois E, Fuhrman DR, Bingham HB, Molin B. 2006;A numerical study of nonlinear wave run-up on a vertical plate. Coastal Eng. 53(11):929–945.

Kim G, Lee C, Suh KD. 2004;Internal generation of waves for time-dependent wave transformation equations - the line source method and the source function method. KSCE J. Civil Engrg. 24(6B):585–594. (in Korean).

Kim G, Lee C, Suh KD. 2005;Internal generarion of nonlinear waves for extended boussineswq equations: line source method and source function method. Journal of Korean Society of Coastal and Ocean Engineers 17(1):21–31. (in Korean).

Kim G, Lee C, Suh KD. 2007;Internal generation of waves: Delta source function method and source term addition method. Ocean Engineering 34:2251–2264.

Larsen J, Dancy H. 1983;Open boundaries in short wave simulations—A new approach. Coastal Eng. 7:285–297.

Lee C, Suh KD. 1998;Internal generation of waves for time-dependent mild-slope equations. Coastal Eng. 34:35–57.

Lee C, Cho Y-S, Yum K. 2001;Internal generation of waves for extended Boussinesq equations. Coastal Eng. 42:155–162.

Lee C, Choi HJ, Kim DG. 2006;Internal generation of waves on an Arc In A rectangular grid system. Journal of Korean Society of Coastal and Ocean Engineers 18(1):1–14. (in Korean).

Lee C, Yoon SB. 2007;Internal generation of waves on an arc in a rectangular grid system. Coastal Eng. 54:357–368.

Madsen PA, Bingham HB, Schäffer HA. 2003;Boussinesq-type formulations for fully nonlinear and extremely dispersive water waves: derivation and analysis. Proc. R. Soc. Lond. A. 459:1075–1104.

Mayer ST, Garapon A, Sørensen LS. 1998;A fractional step method for unsteady freesurface flow with applications to nonlinear wave dynamics. Int. J. Numer. Meth. Fluids 28:293–315.

Peregrine DH. 1967;Long waves on a beach. J. Fluid Mech. 27:815–827.

Skotner C, Apelt CJ. 1999;Application of a Boussinesq model for the computation of breaking waves, Part 2: Waveinduced setdown and setup on a submerged coral reef. Ocean Engineering 26(10):927–947.

Smit P, Zijlema M, Stelling G. 2013;Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coastal Engng. 76:1–16.

Stelling G, Zijlema M. 2003;An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. Int. J. Numer. Meth. Fluids 43:1–23.

Stelling GS, Duinmeijer SPA. 2003;A staggered conservative scheme for every froude number in rapidly varied shallow water flows. Int. J. Numer. Meth. Fluids 43:1329–1354.

Wei G, Kirby JT, Sinha A. 1999;Generation of waves in Boussinesq models using a source function method. Coastal Eng 36:271–299.

Zijlema M, Stelling GS. 2005;Further experiences with computing non-hydrostatic free-surface flows involving water waves. Int. J. Numer. Meth. Fluids 48:169–197.

Zijlema M, Stelling GS. 2008;Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure. Coastal Engng. 55:780–790.

Zijlema M, Stelling G, Smit P. 2011;SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coastal Engng. 58:992–1012.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.