2.1 자기회귀모델(auto-regressive model, AR 모델)

i번째 시간에서의 임의의 지점에서의 유의파고(H_{s, i})는 이전 시간에서 관측 또는 해석된 N_m개의 과거자료를 이용하여 다음과 같이 자기회귀모델(auto-regressive model, AR 모델)을 이용하여 추정할 수 있다.

여기서, a_i는 AR계수(auto-regressive coefficient)이고, H_{s, i}는 i번째 시간에서의 유의파고이다. 총 N개의 관측자료 혹은 해석된 자료를 훈련자료로 사용하는 경우, 다음과 같이 N − N_m개의 관계식을 구성할 수 있다.

위의 관계에서 좌항의 열벡터를 y, 우항의 행렬 및 열벡터를 각각 A, x라 두면, AR계수로 구성된 열벡터 x는 다음과 같이 A의 의사역행렬(pseudo inversion)을 이용하여 구할 수 있다(Sohn et al., 1999).

2.2 인공신경망 모델(artificial neural networks model, ANN 모델)

입력자료와 출력자료 사이의 관계를 다중회귀식을 이용하여 선형적으로 구성하는 AR 모델과 함께 복잡한 형상을 가진 항내 파고 예측을 위하여 다층 퍼셉트론즈(multi-perceptrons) 신경망을 적용하여 그 성능을 AR 모델의 성능과 비교하였다. 인공신경망 기법은 1990년대 중반 이후 기계, 토목, 전기전자, 회계분석 등 여러 분야에서 활발하게 응용된 바 있으며 최근 GPU 및 멀티코어 프로세서 등 하드웨어 성능의 획기적인 개선과 함께 다시 많은 관심을 받고 있는 모델이다(Haykins, 1994). 다층퍼셉트론즈 신경망은 Fig. 1과 같이 하나의 입력층(input layer), 여러 개의 은닉층(hidden layer), 그리고 하나의 출력층(output layer)으로 구성되어 있다. 입력층을 통하여 이전 시간에서 관측 또는 해석을 통하여 알고 있는 유의파고 등의 파랑자료가 입력되고, 출력층에서는 예측하고자 하는 시간에서의 파랑자료가 출력되는 구조로 되어있다. 훈련과정(training process)에서는 기존 확보되어 있는 파랑자료를 이용하여 신경망의 시냅스 강도(synaptic weight) 등을 구하는데, 이를 위하여 일반적으로 역전파학습 알고리즘(back-propagation learning algorithm)을 가장 널리 사용하고 있다.

Fig. 1.

Architecture of multi-perceptrons artificial neural networks.

2.3 파랑변형 수치실험 모델, SWAN(Simulating WAves Nearshore)

본 연구에서 사용한 범용 파랑변형 수치모형 SWAN은 파랑에너지의 천수, 굴절, 회절, 흐름, 바람에 의한 에너지 생성, 백파, 쇄파 등에 의한 에너지감쇠, 파랑간의 4차 비선형 현상, 바닥마찰 등을 모의할 수 있어 주어진 바람과 해저면 및 해류 조건으로부터 연안역, 호수 및 하구 등에서의 파랑을 모사할 수 있다(Booij, 1981; Booij et al., 1999). 한편 SWAN 모형에 사용되는 원천항(source term)에 따라 제1 세대, 제2 세대 및 제3 세대 모형으로 분류되며 이 연구에서는 제3 세대 모형을 사용하였다(The SWAN team, 2008). SWAN 모형의 기본방정식은 파동 평형방정식(wave action balance equation)이며 다음 식에 의하여 표현된다.

여기서, N은 각각 파작용 스펙트럼(wave action spectrum)을 c_x, c_y, c_θ, c_σ는 각각 x, y, θ, σ에 대한 선형파이론에 의한 전파속도를 나타난다. 위 식에서 좌변의 제1 항은 파동 밀도의 시간 변화량, 제2 항과 제3 항은 지리적 공간에서의 파동의 전파, 제4 항은 수심과 흐름의 변화에 의한 상대주파수의 천이, 그리고 제5 항은 수심과 흐름에 의한 굴절을 나타낸다. 평형방정식의 우변 S[=S(σ, θ)]는 파랑의 생성, 감쇠 및 비선형 상호작용 등에 의한 에너지 밀도를 나타내는 항을 포함한다.

여기서, S_in은 바람에 의한 에너지 유입을, S_ds는 백파와 저면마찰 및 쇄파 등에 의한 에너지 소산을 나타내며, S_nl은 성분파간의 비선형 상호작용을 나타낸다. SWAN은 천해역에서의 파랑수치실험을 위하여 많이 이용되고 있으며 보다 자세한 내용은 다른 문헌을 참조할 수 있다(The SWAN Team, 2008; Kim et al., 2007; Jeong et al., 2012; Eum et al., 2016).

3.1 대상 항만 개요 및 관측 위치

본 연구에서 대상항만으로 고려한 포항신항은 영일만 내에 위치하고 있으며, 건설 초기부터 하역중단이 빈번하게 발생하여 부진동 등의 장주기파 영향을 하역중단의 원인에 대한 연구가 진행된 바 있다. 우선 포항신항 내에서의 하역중단에 대한 기록을 간략하게 살펴보면, 겨울철을 포함한 10월에서 3월까지 총 40.1일(75.7%)의 하역중단이 발생하였고, 여름철을 포함한 4월에서 9월까지 총 12.9일(24.3%)의 하역중단이 발생하여, 하역중단은 주로 동계에 발생하는 것을 알 수 있다. 이와 같은 포항신항에서의 하역중단과 관련하여 Jeong et al.(1997)은 1994년 2월 17일부터 3월 31일까지 포항신항 내외에서 파랑을 동시관측하고, 선석별 하역중단기록(1987~1994년)을 분석하여 항만정온도 불량원인이 풍파와 너울임을 제시한 바 있으며, 또한 Jeong et al.(2011)은 2008년 9월부터 2009년 8월까지 1년 이상 파랑을 관측하고, 관측 파랑 자료와 기상청 기상자료, 선석별 하역중단기록을 분석하여 포항신항에서의 하역중단의 주요 원인이 풍파와 너울임을 재차확인한 바 있다.

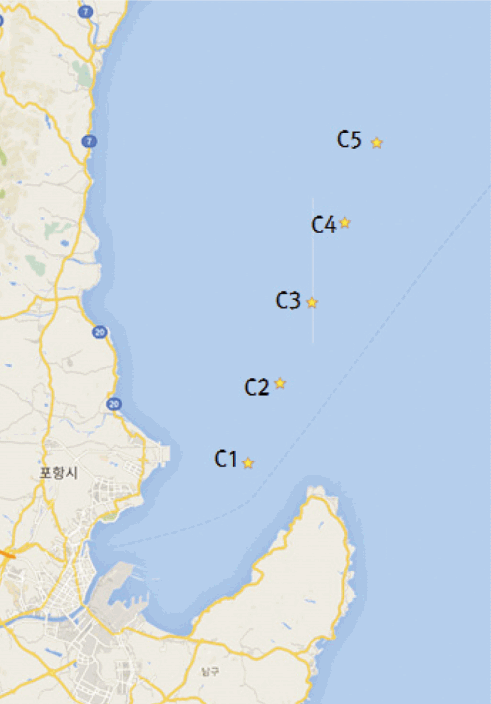
포항신항은 Fig. 2에서 제시한 바와 같이 영일만 내에 위치하며, 포켓형상의 항내는 지형이 매우 복잡하고 또한 정온도 확보를 위하여 외곽 방파제인 북방파제 외에도 항내에 제1, 제2파제제가 설치되어 있어 수치실험을 통하여 파랑을 분석하기 매우 어려운 조건에 있다. 따라서 본 연구에서는 파랑예측 모델을 구성하기 위한 항내 파랑자료로 장기 파랑관측 자료를 사용하고자 하였다. 포항신항 내 다수의 정점에서 수압식 파고계(WTG, wave and tide gauge)를 설치하여 2008년부터 현재까지 파랑 관측을 실시하고 있으며, 2013년 10월부터 2014년 12월까지 15개월의 연속 관측자료가 확보되어 있는 W03, W04, W05, W10, W11 등 총 5개 파고계 자료를 이용하여 AR 모델 및 ANN 모델에 의한 파고예측 모델을 구성하고 그 결과를 분석하였다.

Fig. 2.

Location of Pohang New Harbour and Observation Stations.

3.2 광역 수치실험

일본기상청(JMA, Japan Meteorological Agency)의 바람예보자료와 SWAN 모형을 사용하여 외해역에서의 역추산 파랑자료를 산정하고, 이를 이용하여 AR 모델 및 ANN 모델의 입력자료로 사용하였다. 바람자료의 공간 범위는 위도 22.4~47.6oN, 경도 120.0~150.0oE이며, 공간해상도는 경도와 위도에 따라 각각 1/16o, 1/20o이다. 한편, 바람자료의 시간 해상도는 6시간 간격의 자료를 사용하였다. 다방향 불규칙파 파랑 수치모형인 SWAN으로 계산한 영역은 117.0~147.0oE, 20.0~50.0oN이며, 계산영역의 공간해상도는 경도, 위도 모두 1/20°로 설정하였다. 한편 매 10분 간격으로 계산 결과를 출력하였으며, 방향 스펙트럼은 0~360o에서 72분할, 주파수는 1/25~1/2.5 Hz에서 21분할하여 적용하였다. 한편, AR 모델 및 ANN 모델을 구성하기 위하여 Fig. 3과 같은 총 5개 지점에서의 계산결과를 이용하였다.

Fig. 3.

Locations of calculation points for input data in AR and ANN models.

3.3 AR 모델을 이용한 항내 파고 예측

2.1절에서 간략하게 소개한 AR 모델의 경우 하나의 지점에서 계산된 과거 파고자료를 이용하는 것으로 실제 적용의 경우 i번째 항내 위치에 대한 t_j 시점에서의 파고예측을 위하여 항외의 여러 지점에서의 과거자료를 활용할 수 있도록 모델을 구성할 수 있다. 구체적으로 항내에 설치된 파고계 중 2013년 10월 1일부터 2014년 12월 31일까지의 15개월 동안 연속 관측자료가 확보된 W03, W04, W05, W10, W11의 다섯 개 위치에서의 파고를 AR 모델로 추정하기 위하여 수치실험 결과 중 계산 정확성을 확보할 수 있으면서 영일만 내의 파고와 연관성이 높은 C₁ 지점에서부터 C₅ 지점까지의 파고자료를 이용하여 다음의 Table 1에 제시되어 있는 조건과 같이 AR 모델을 구성하였다.

Table 1.

Input information for AR model

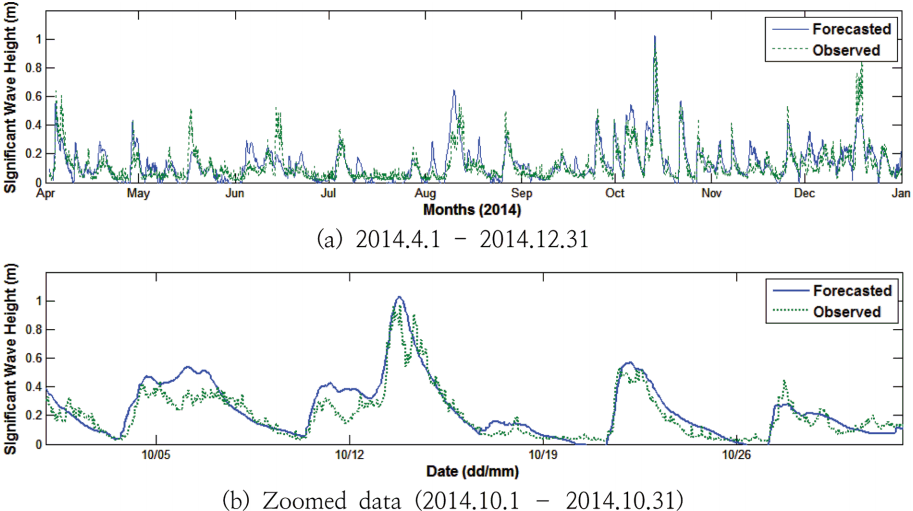
한편, 각 Case별로 사용된 과거자료의 수를 1개에서 30개까지 증가시켜가며 훈련자료를 이용하여 AR 계수를 결정하고, 시험자료를 이용하여 결과를 검증하였다. 훈련자료로는 2013년 10월 1일부터 2014년 3월 31일까지의 6개월 자료를 사용하였으며, 시험자료로는 2014년 4월 1일부터 2014년 12월 31일까지의 9개월 자료를 사용하였다. Fig. 4는 AR 모델에 의한 결과의 한 사례로, C1부터 C3 지점에서의 과거 계산자료 30개를 이용하여 W03 위치에서의 파고를 예측한 결과이다. C1부터 C3 지점에서의 과거 계산자료 30개를 사용한 W03 위치에 대한 파고 예측의 경우, 훈련자료에 대한 상관계수 및 RMS 오차는 각각 0.8581, 0.0656 m이며, 시험자료에 대한 상관계수 및 RMS 오차는 각각 0.7406, 0.0751 m이다.

Fig. 4.

Comparison between wave heights observed and forecasted by AR model at W03 station.

한편, Fig. 5는 W03, W05, W11 등 항내 파고계 3개 위치에서의 Case 1에서부터 Case 5까지 상관계수 및 RMS 오차를 과거 자료의 개수에 대하여 분석한 결과이다. 과거 계산자료의 개수가 증가할 경우 상관계수가 증가하고, RMS 오차가 감소하는 경향을 가지고 있으며, 특히 계산자료의 수가 10개까지 증가하는 경우 그 개선효과가 더욱 뚜렷함을 알 수 있다. 과거 계산자료가 30개라는 것의 의미는 30시간 이전의 파고와 현재의 파고가 어느 정도 관계가 있다는 의미로 분석할 수 있으나, 물리적으로 볼 때 30시간 이전의 파고가 현재 파고에 미치는 영향은 거의 없을 것으로 보이며, 따라서 과거 계산자료의 수가 증가할 때 예측 정확도가 높아지는 것은 일종의 통제(regulation) 효과라 판단하는 것이 바람직할 것으로 판단된다.

Fig. 5.

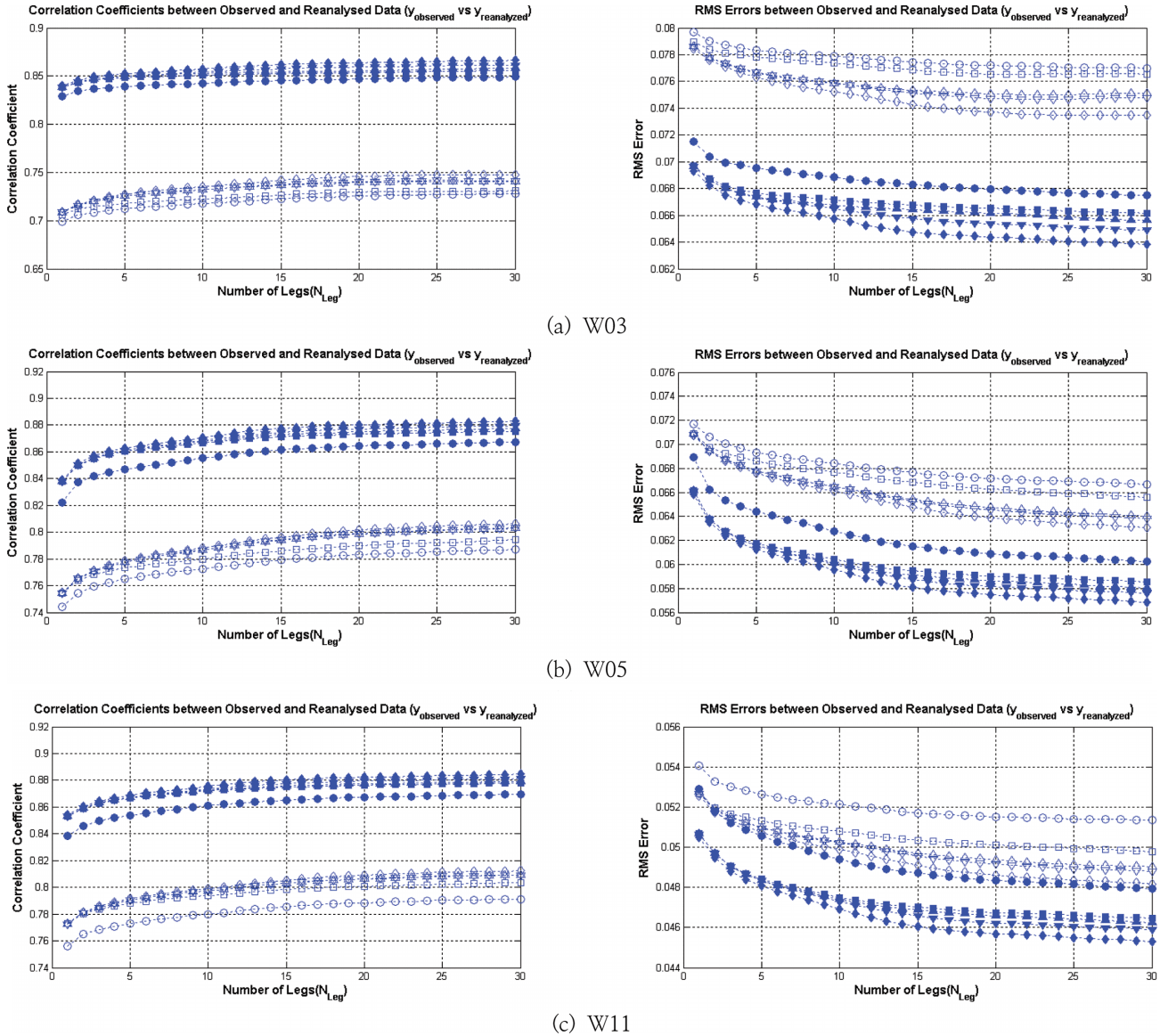
Correlation coefficients and RMS errors between observed and reanalyzed wave heights (Symbols ○, □, △, ▽ and ♢ are for the Case 1, Case 2, Case 3, Case 4, and Case 5 with training data set and symbols ●, ■, ▲, ▼ and ♦ are the same cases with testing data set).

한편 계산지점을 증가시킬 경우 상관계수 및 RMS 오차를 살펴보면, W11의 결과와 같이 Case 1에 비하여 Case 2의 결과가 크게 개선되거나 혹은 W05의 결과와 같이 Case 2에 비하여 Case 3의 결과가 크게 개선되는 경향이 있지만, Case 4와 Case 5는 Case 3에 비하여 개선되는 효과가 크지 않음을 알 수 있다. 따라서 Case 3에서와 같이 C1, C2, C3 계산지점에서의 결과를 이용하는 것이 효과적이라는 결과를 도출할 수 있다.

3.4 ANN 모델을 이용한 항내 파고 예측

ANN 모델의 경우 파고만을 사용한 AR 모델과는 달리 주기, 파향 등 다양한 입력정보를 처리할 수 있다. 그러나 과도하게 많은 정보를 입력자료로 사용할 경우 신경망의 훈련을 통하여 추정하여야 변수, 즉 시냅스 강도(synaptic weight)의 수가 과도하게 증가하여 필요한 훈련패턴의 수도 증가하게 되며, 또한 신경망의 전체적인 성능 또한 오히려 악화될 수 있다. 따라서 추정하고자하는 물리량과 관련성이 높은 정보를 이용하여 입력자료를 구성하는 것이 필요하다. AR 모델에 의하여 항내 파고를 예측한 결과 C1, C2, C3의 세 지점에서의 계산결과를 사용할 때 가장 효과적이었다는 사실을 고려하여, ANN 모델에서도 C1에서의 계산결과만 이용하는 경우, C1, C2에서의 계산결과를 이용하는 경우, 그리고 C1, C2, C3에서의 계산결과를 이용하는 경우로 구분하여 신경망을 구성하고 그 결과를 비교하였다. 또한 ANN 모델의 경우에는 파고와 함께 주기, 그리고 파향 정보를 함께 사용하였다. 파향의 경우 Lopez et al.(2015)의 연구에서와 유사하게 파향에 대한 cosine값과 sine값을 사용하였다. 그리고 AR 모델에서 시간지연효과를 고려할수록 예측결과가 향상된 사실을 고려하여 최대한 많은 과거자료를 사용하고자 하였으나, 너무 많은 과거자료를 사용할 경우 입력자료의 수가 과도하게 증가하므로, 과거 계산자료는 10개까지 사용하였다. 따라서 입력자료의 수는, C1에서의 계산자료만을 사용할 경우, 파고자료 10개, 주기자료 10개, 파향의 cosine값과 sine값 10개 등 총 40개이며, C1, C2를 사용하는 경우에는 총 80개, 그리고 C1, C2, C3에서의 계산결과를 사용하는 경우에는 총 120개가 된다. 한편 은닉층(hidden layer)의 뉴런 수도 경험적, 또는 프루닝(pruning)을 이용하여 결정할 수 있는데, 이 연구에서는 입력자료의 수와 출력자료의 수를 고려하여 경험적으로 첫 번째 은닉층과 두 번째 은닉층의 뉴런 수를 각각 10개로 고려하였다. 출력층은 AR 모델에서 고려한 것과 같이 W03, W04, W05, W10, W11 등 다섯 개 파고계 위치에서의 파고를 사용하였다.

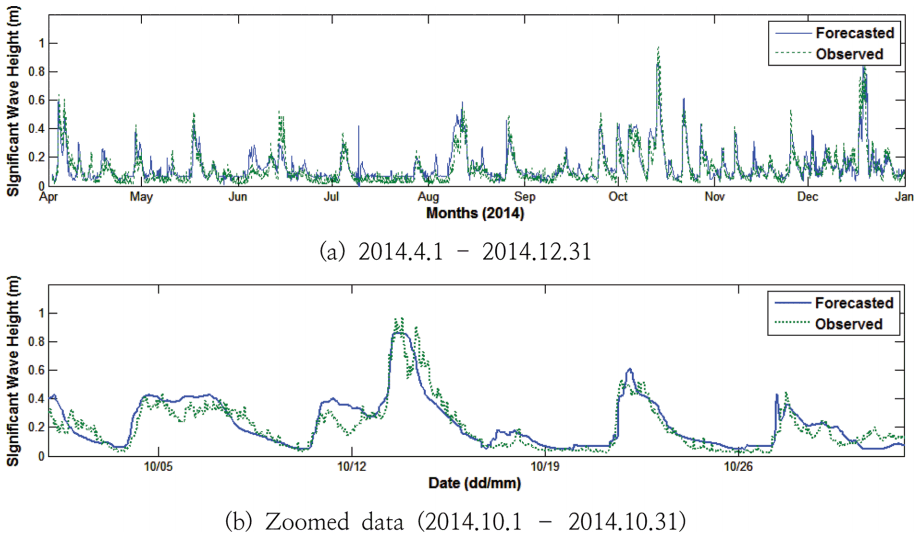
한편 아래의 Fig. 6는 C1, C2, C3에서의 계산결과를 이용하여 ANN 모델에 의하여 예측된 W03 파고계 위치에서의 파고 결과이다. 이 경우 훈련패턴에 대한 상관계수와 RMS 오차는 각각 0.9169, 0.0622 m이며, 시험패턴에 대한 상관계수와 RMS 오차는 각각 0.8493, 0.0644 m이다. 이는 30개의 과거자료를 이용한 AR 모델의 결과, 즉 훈련자료에 대한 상관계수(0.8581) 및 RMS 오차(0.0656 m) 그리고 시험패턴에 대한 상관계수(0.7406) 및 RMS 오차(0.0751 m)와 비교할 때 AR 모델의 예측결과보다는 관측자료에 더 가까운 결과를 보여줌을 알 수 있다. AR 모델과 ANN 모델을 비교할 때, AR 모델은 선형예측모델(linear estimation model)로 입력정보로 사용된 계산지점에서의 파고와 실제 관측한 지점에서의 파고 사이의 관계를 선형관계로 고려한 것인데 비하여, ANN 모델은 비선형 시그모이드 함수(nonlinear sigmoid function)를 사용함으로써 이 두 정보 사이의 관계를 비선형모델로 고려할 수 있다는 차이가 있다. 결국 ANN 모델이 AR 모델보다 예측 정확도가 높은 것은 항내에서의 복잡한 지형 및 파제제 등에 의한 비선형 파랑변형 효과를 ANN 모델이 더 잘 모사할 수 있기 때문인 것으로 판단할 수 있다.

Fig. 6.

Comparison between wave heights observed and forecasted by ANN model at W03 station.

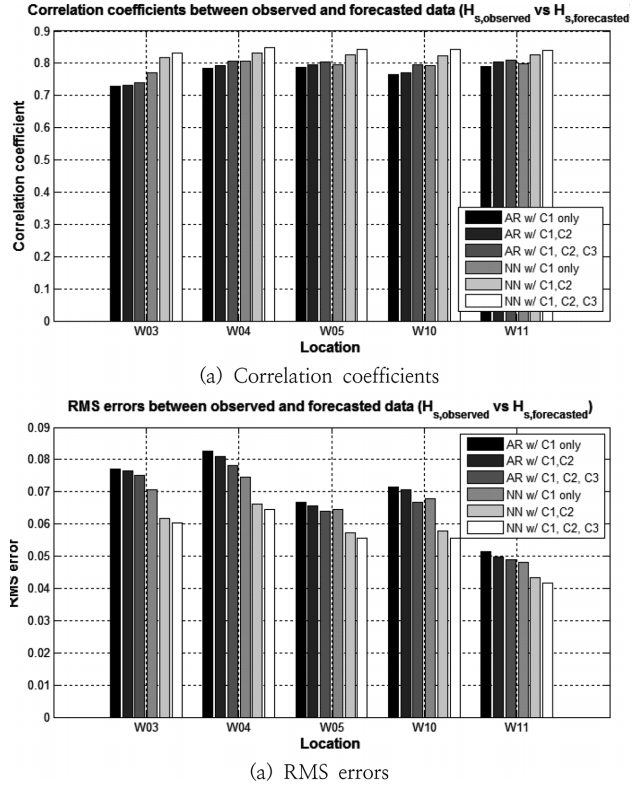
추가적인 분석을 위하여 Fig. 7에서 AR 모델과 ANN 모델을 사용할 경우 상관계수 및 RMS 오차를 비교하였다. 이 결과에서 AR 모델은 30개의 과거 계산자료를 이용한 것이며, ANN 모델은 10개의 과거 계산자료를 이용한 것이다. 또한 AR 모델은 파고자료만을 이용하고, ANN 모델은 파고와 함께 주기, 파향을 함께 고려한 자료이다. AR 모델과 ANN 모델 모두 C1에서의 계산자료를 사용한 결과보다는 C1, C2, C3에서의 계산결과를 사용할 때 상관계수가 증가하고, RMS 오차가 감소됨을 알 수 있다. 또한 ANN 모델의 경우 AR 모델보다 모든 파고계 위치에서의 예측성능이 더욱 우수함을 알 수 있다. 이는 전술한 바와 같이 복잡한 지형 및 파제제 등에 의한 비선형 파랑변형의 효과를 더 잘 모사하였기 때문인 것으로 판단된다. 한편 W03 파고계 위치에서의 상관계수가 상대적으로 작고, RMS 오차가 큰 것을 알 수 있으며, W11 파고계 위치에서의 상관계수가 상대적으로 가장 크고, RMS 오차가 가장 작은 것을 알 수 있다. 이는 W03 파고계가 안벽 내에 위치하고 있고, W11은 상대적으로 안벽 바깥에 위치하고 있어 지형적인 복잡도가 W03이 상대적으로 높은데 따른 결과라 판단된다.

Fig. 7.

Comparisons of correlation coefficients and RMS errors of the forecasted wave heights obtained from AR and ANN models.

3.5 AR 모델과 ANN 모델을 이용한 하역중단시점 예측결과

하역한계파고(limiting operational wave height)는 컨테이너선 또는 일반 화물선 등과 같이 선박 종류 및 크기에 따라 달리 제시될 수 있으나(Lopez et al., 2015), 이 연구에서는 하역중단시점을 Lopez et al.(2015)의 연구에서 컨테이너선, RO-RO 선박 등에 대하여 적용한 하역한계파고 기준인 0.5 m를 고려하였다. 하역작업은 주야간 동일한 조건으로 작업이 가능한 것으로 가정하였으며, 하역한계파고 기준으로만 하역중단시점을 분석하였다. 또한 하역중단시점을 결정하기 위한 AR 모델은 30개의 과거자료를 이용한 경우에 대해서만 분석하였고, AR 모델과 ANN 모델 모두 C1, C2, C3에서의 계산결과를 이용한 모델을 적용하였다.

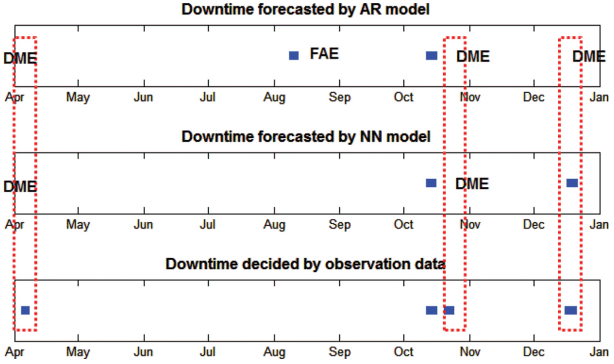
Fig. 8은 항내 설치된 W05 파고계 위치에서 관측된 파고자료로부터 안벽에서의 하역중단시점을 결정한 결과와 AR 모델 및 ANN 모델을 이용하여 하역중단시점을 예측한 결과를 비교한 것이다. 결과를 보면 2014년 10월 발생한 2번의 하역중단시점 중 첫 번째 하역중단시점의 경우 AR 모델 및 ANN 모델이 모두 정확하게 예측하였지만, 두 번째 하역중단시점은 두 모델 모두 경보하지 못하는 오류, 즉 경보누락오류(downtime event missing error, DME)가 발생하였음을 알 수 있다. 한편, 2014년 8월의 경우 하역중단이 발생하는 파고가 없었음에도 불구하고 AR 모델의 경우 오경보하는 오류(false alarming error, FAE)가 발생하였다. W05 파고계 위치에서의 경우 AR 모델은 총 3회의 경보누락 오류가 발생하고, 1회의 오경보 오류가 발생하였으며, ANN 모델의 경우 총 2회의 경보누락 오류가 발생하였음을 알 수 있다.

Fig. 8.

Comparison of downtime events forecasted by AR and ANN models in 2014.

한편, Table 2는 연구에서 사용된 5개 파고계에서의 관측 파고와 AR 및 ANN 모델을 이용하여 예측한 파고로부터 하역중단시점을 예측한 결과로, 파고가 0.5 m를 초과한 총 23개 시점에 대하여, AR 모델의 경우 13개 하역중단시점을 누락하는 오류가 발생하였고, ANN 모델의 경우 5개 하역중단시점을 누락하는 오류가 발생하였음을 알 수 있다. 한편 오경보 오류는 두 모델 모두 3개 시점으로 분석되었다. 이와 같이 오경보 및 경보누락과 같은 오류는 AR 모델, ANN 모델에 모두 발생하고 있으나, 전체적으로 볼 때 AR 모델보다는 ANN 모델이 비교적 하역중단 시점을 정확하게 예측하고 있음을 알 수 있다.

Table 2.

DME and FAE in AR and ANN models

ANN 모델과 AR 모델 모두 하역중단 시점을 예측하는데 어느 정도의 오류가 있는 것은 이 연구에서 입력정보로 사용하고 있는 파랑추산자료는 일본기상청의 바람예보자료를 바탕으로 수치실험모델인 SWAN을 이용하여 계산한 것으로, 첫째, 바람예보자료에 포함될 수 있는 오류와 둘째, 수치실험모델인 SWAN에 포함되어 있는 지형정보 및 수심정보 등에 포함되어 있는 오류 및 SWAN 모델이 고려하지 못하는 실제 물리현상 등에 의한 오류 때문인 것으로 판단된다. 따라서 보다 정확한 하역중단 시점 예측을 위해서는 이와 같은 오류를 줄이도록 하는 추가 연구가 필요하리라 판단된다.