유출유의 초기 확산예측을 위한 고해상도 결합모형 개발
Development of Highly-Resolved, Coupled Modelling System for Predicting Initial Stage of Oil Spill
Article information
Abstract
최근 빈번하게 발생하는 해상 유류사고에 대해 초기에 신속히 대응하기 위해서는 정확성 높은 수치해석 모형의 개발 및 적용이 필수적이다. 본 연구에서는 불규칙한 지형적 변화가 존재하는 근해역에서 유출유의 정확한 확산예측을 위하여 비선형성, 분산성, 난류 및 회전류 효과 등이 포함된 수심적분형 Boussinesq 모형과 유류의 이송-확산-변형모형을 통합함으로써 유출유 초기확산 예측을 위한 결합모형을 개발하였다. 개발된 모형은 지형적 복잡성 및 그에 따른 실제 흐름의 특성을 지닌 실 해역에 적용함으로써 모형의 활용성을 검토하였다. 고해상도의 해상 조건 재현이 가능한 본 개발모형은 기후변화 등에 의해 점차 강화되는 해상 기상의 극한조건에서의 유류 재해에 대비할 수 있는 방재시스템 구축에 도움이 될 것으로 기대된다.
Trans Abstract
The development and application of accurate numerical models is essential to promptly respond to early stage of oil spill incidents occurring in nearshore area. In this study, the coupled modelling system was developed by integrating the advection-diffusion-transformation model for oil slick with the Boussinesq model, which incorporates non-linear, discrete, turbulent and rotational effects of wavy flows for accurate representation of nearshore hydrodynamics. The developed model examined its applicability through the application into real coastal region with topographical complexity and characteristics of the resulting flow originated from it. The highly-resolved, coupled model developed in this study is believed to assist in establishing the disaster prevention system that can prepare effectively for oil disasters under extreme ocean climate conditions and thus minimize industrial, economical, and environmental damages.
1. 서 론
최근 기후변화에 따른 해상의 기상조건 악화와 유조선 등 대형 선박의 입출항 증가로 인해 국내 원유 등의 오염물질 유출사고가 빈번히 발생하고 있다. 2007년 서해안 태안 앞바다에서 발생한 원유 유출사고는 유조선 ‘허베이 스피리트 호(Hebei Spirit)’와 삼성중공업 해상기중기 부선 ‘삼성 1호’간의 해상 충돌로 10,900톤 가량의 유류가 유출되었고 유출유 이송-확산 과정(Advection-Diffusion Process)을 정확하게 예측한 결과가 제공되지 않았기에 적절한 초기대처가 이루어지지 못하였으며 원유가 오일펜스를 넘어가 빠르게 확산되어 많은 피해를 초래하였다. 국외 일본에서는 1997년 일본 후쿠이현 일대 페트로 파블로프스크(Pavlovsk)로 향하던 러시아 유조선 ‘나홋카호’가 침몰하면서 6,200여톤의 난방용 중유(Heavy oil)가 유출되었고 쓰시마 해류를 타고 북동쪽으로 북상하여 흐를 것이라는 예상과 달리 후쿠이현에 표착되어 남서쪽 시마네 현에서 이시카와현에 걸친 넓은 범위에 확산되었다. 이와 같이 초기 유출유의 확산 범위 예측에 실패하여 많은 피해를 입은 사례를 통해 초기 확산 범위 예측의 중요성을 알 수 있다. 더군다나 사고 현장의 지형적 여건과 기상 및 해류의 변화 그리고 유출된 유류의 성분 등에 따른 해상방제 매뉴얼의 전무로 지휘체계까지 혼란을 겪게 되면 피해의 정도는 더욱 가중된다. 이에 해양오염사고는 생태계 파괴뿐만 아니라, 인근 주민들의 생계와 직결되는 사안이며, 막대한 물적 자원 손실을 수반하기 때문에 관련 부처에서도 대응책 마련에 힘을 쏟고 있는 실정이다.
해양오염사고에 조기 대응하여 피해를 최소화 할 수 있는 방제 매뉴얼 확립의 선제조건은 오염물질 유출량과 조류 및 해상풍에 의한 정확한 확산 범위 예측이라 할 수 있다. 유류의 이송-확산-변형 범위의 예측에 대한 수치모의 연구의 예로써, Hyun et al.(2012)은 유류의 초기 거동과 확산 경향성을 파악하기 위해 공개 모델인 MOHID(MOedlo HIDrodinamico)를 이용하여 원유의 유출시간, 유출량, 유류의 특성치와 풍화작용을 반영한 유류확산모델의 수치모의를 검토한 바 있다. 수치 모의에 사용된 MOHID는 University of Lisbon in Portugal에서 개발된 연안역과 하구역에 적용할 수 있는 다기능 3차원 수치해석 모델이다. 하지만 MOHID의 경우 Lagrangian 방정식에 기반하여 유출량의 총 부피를 추적하는 계산방식을 통해 총괄형 모형을 지향하므로 유류의 유막, 입자 및 다양한 구조적 변수를 참조하여 유류의 상세한 시간적 분포결과를 제시하는 모형과는 차이점이 존재한다(Dominicis et al., 2013). 한편 Lee et al.(2000)은 PIV기법을 이용하여 3차원 디지털 화상처리 계측법을 이용한 후 유적의 3차원 퍼짐(Spreading) 현상에 대한 거동을 정량화 할 수 있는 기법을 제시하였다. Cheong(2008)은 1995년부터 2007년까지 13년간 국내 기름유출 사고 발생 건을 토대로 유출된 기름의 거동 및 풍화과정과 유출유의 방제 및 처리법에 대해 자세히 기술하였다. Yang et al.(2009)은 3차원 수치모델 EFDC(Environment Fluid Dynamics Code)와 인공위성 원격탐사 데이터를 이용하여 Hebei Spirit 유출사고를 검증하였고 이를 통해 인공위성 자료를 활용하여 초기 조건을 유추하기 위하여 다양한 시도를 하였다. 또한 Kim(2011)은 확산방정식을 이용하여 유출유의 범위와 선형파의 이론식을 이용하여 구한 확산속도에 대해 해석하였다. Kim et al.(2012)은 고해상도 해양순환 모형인 ROMS(Regional Ocean Modeling System)를 이용한 씨프린스호 유류 유출사고 수치 실험 연구를 검토한 바 있다. 1995년 씨프린스호 사고를 대상으로 바람 및 조석뿐 아니라 해류를 동시에 포함하는 3차원 고해상도 복합 해양순환 모델링을 수행하고 수치 부표추적 계산을 통해 바람, 조석 및 해류 등 각각의 성분이 유류확산 및 이동에 미치는 영향을 검토한 바 있으나 입자추적 계산시 유류의 이송과 확산 외 증발, 유화, 융해 등의 다양한 화학적 작용 및 생물학적 작용을 포함하지 않았다. Jung and Cho(2008)은 태안 지역을 대상으로 조류와 취송류에 의한 이송-확산을 입자추적법인 Randomwalk 모형으로 연구였으며, 조류를 모의하기 위해 2차원 유한요소 해수유동모형을 사용하였다. 이를 토대로 Jung(2009)은 유출유의 이송-확산에 대한 수치모형을 검토한 바가 있으나 유막의 두께나 밀도 등의 유류의 상세한 분포특성, 강한 바람에 의한 파랑, 파랑에 의한 확산 등에 대하여는 고려하지는 못하였다. Cho et al.(2012)은 천수방정식으로부터 이류 확산 작용방정식을 사용하여 비선형 조류와 조류의 흐름, 이송-확산 작용을 계산하였고 Hebei Spirit호 유출유의 위성사진과 비교하였다. 유막의 확산, 이류, 난류 확산, 증발 및 용해 과정에 대한 모의를 위해 3차원궤도 거동 모델을 개발한 Chao et al.(2001)은 질량 이송 방정식을 기반으로 하여 수층의 유류 입자 농도의 분포를 모의하였다. 이어 Chao et al.(2003)은 싱가폴 해안에 대하여 유출유의 움직임 및 거동을 예측하는 3차원 모델을 적용하였고 수면 위 유출유의 위성사진 데이터 관측으로 모델을 입증하였다. 한편, Dominicis et al.(2008, 2013)은 지중해 지역을 대상으로 하여 유류의 이송-확산 모형인 MEDSLIK 및 MEDSLIK-II를 개발하였다. MEDSLIK-II는 해류와 해상풍 정보에 의해 지배되는 유출유의 이송-확산 및 변형(Transformation)이 모의가능한 모형이다. 흐름의 비선형성을 고려함으로써 Stoke’s Drift 이동속도를 Lagrangian 좌표계상 이류속도 성분으로 표현하였다.
이와 같은 다양한 유류유출 관련연구에도 불구하고 현재까지 해역에서 중요시되는 파랑성분의 분산성, 비선형성, 조류-파랑 상호작용 등을 모두 고려한 유류의 이송-확산 및 변형관한 연구는 미비한 실정이다. 따라서 선박의 입출항이 빈번한 근해역의 복잡한 지형적 영향을 고려할 수 있는 흐름모형과 유류의 이송-확산-변형 모형간의 결합을 통하여 정확도 높은 수치모의를 실현할 수 있으며 이는 해상 방제 매뉴얼 확립에 필요하다고 판단된다. 본 연구에서는 우선 Boussinesq 모형과 MEDSLIK-II 모형간 결합을 통해 유출유의 초기 확산예측을 위한 고해상도 수치모형 개발을 실현한다. 즉 MEDSLIK-II 모형의 적용을 통해 부유물 추적 모의방법이나 단순 입자 추적법에 의한 유류 이송-확산이 아닌, 유류의 물리적 성질인 유막을 표현하여 실제 유류의 이송-확산-변형을 모두 모의하도록 하였으며 기존의 일부 모형에서는 고려되지 못한 유류의 풍화과정을 추가적으로 고려하여 유출유 확산의 물리적 과정을 총체적이며 정확하게 표현하고자 하였다. 개발된 모형을 대상으로 석유화학공단이 위치하여 대형선박의 입출항 증가로 유출사고가 빈번히 발생하고, 또한 지형적 특성 및 조류/파랑에 의해 빠르게 확산되어 많은 피해를 받고 있는 울산해역을 시범지역으로 선정해 유출유의 이송과 확산 및 변형을 고려하고 지형적 영향을 고려한 정확도 높은 수치모의를 수행하고자 한다.
2. 수치모형
2.1 동수역학 모형
연안역에서 정확한 오염물질 이송-확산-변형 모의가 가능하기 위해서는 우선적으로 정도 높은 해상 조건의 입력이 선제적으로 이루어져야 한다. 즉, 유류 등의 해상 오염물질은 특성상 흐름에 의해 지배적으로 이동, 전파 및 확산되므로 파랑 및 조류의 영향을 많이 받고 불규칙한 지형적 변화가 존재하는 천해역에서의 흐름 예측은 오염물질 이송-확산-변형 예측에 있어 매우 중요한 과정이다. 하지만 이처럼 중요한 흐름특성을 파악하기 위해 현재 광범위하게 사용되는 천수방정식 모형은 해안지역에서 수심방향의 수리학적 특성을 고려하기 어려워 부정확한 해상조건을 제공하고 있다(Dominicis et al., 2013). 즉, 수심평균한 비분산성 흐름 모형을 사용하여 파랑의 분산성이 무시되고 이로 인하여 오차를 포함하는 흐름 조건을 산출하게 되므로 이는 고스란히 오염물 이송-확산-변형 예측의 오차로 나타나게 된다. 따라서 본 연구에서는 이를 해결하기 위하여 동수역학적 특성 및 고차의 흐름특성(난류, 쇄파, 바닥마찰에 의한 회전류 흐름특성 등)을 고려할 수 있는 수리 모형을 적용하였다. 천수방정식모형에 비하면 물리적으로 더 정확히 모의할 수 있는 수심적분형 Boussinesq 모형을 적용하면 보다 정확한 해상 조건 재현이 가능하다. 또한 Boussinesq 모형은 넓은 해역의 파랑 및 조류조건을 빠르고 정도 높게 해석하여 그 결과를 활용 가능케 한다. 천수 모형 및 Boussinesq 모형 간의 결합모형을 이용하면 광대한 해역에서의 정도 높은 파랑 모의가 현실화 되므로 결합모형 사용이 필수적이라고 할 수 있다. 본 연구에서 사용하는 Boussinesq 모형의 이론적 배경은 다음과 같다. 최근 Kim et al.(2009)에 의해 개발된 수심적분된 비선형성, 분산성, 난류 및 회전류 효과를 포함한 Boussinesq 모형은 연안역에서 복잡한 특성을 보이는 장파 흐름의 거동을 비교적 정확히 모의할 수 있다. Boussinesq 모형의 지배방정식은 아래와 같이 표현된다.
위 식들에서 H는 전수심, Uα 및 Vα는 각각 일정수심에서의 x 및 y 방향 유속을 의미한다. 그 이외의 변수에 대한 자세한 설명은 Son et al.(2011)에 수록되어 있다. Boussinesq 모형은 위 지배방정식의 수치해를 구하기 위해 공간차분항은 유한체적법에 기반한 4차 정확도의 MUSCL-TVD 기법을 사용하였고, 시간차분항은 3차 정확도의 Adam-Bashforth 예측자와 4차 정확도의 Adam-Moulton 수정자 기법을 이용하여 수치분산으로 인한 오차발생을 최소화하였다. 또한 바닥마찰, 난류 및 회전류 효과 등을 추가적으로 고려함으로 근해에서 발생할 수 있는 국부적인 비선형효과를 잘 묘사하도록 하였다. 개발된 모형은 지진해일, 파랑-흐름간 상호작용, 밀도변화가 있는 유체에서의 파랑 변형 등에 적용됨으로써 그 정확성 및 안정성이 이미 검증된 바 있다.
2.2 유류 이송-확산-변형 모형
해역상에서 예측된 흐름 정보와 해상풍 정보 그리고 이론과 수치적으로 결합될 오염물질 이송확산모형은 기본적으로 Lagrangian 좌표를 기반으로 한다. 이는 유류의 특성상 이송의 메커니즘이 유류 입자의 이송으로 가정될 수 있기 때문이다. 따라서 이송-확산-변형 과정은 Lagrangian 모델과 흐름의 관한 Eulerian 순환 모델의 결합모형을 사용하여 해수 표면 유류의 변환 작용을 예측할 수 있다. Lagrangian 모형은 기존에 유럽지역에서 개발되고 폭넓게 적용된 바 있는 MEDSLIK-II를 배경으로 제안될 수 있다(Dominicis et al., 2013). MEDSLIKII는 Eulerian 좌표계 기반의 이송-확산-변형식에서 유막, 유류의 입자 등에 대한 Lagrangian 표현을 사용함으로써 유출된 유류의 이송-확산 및 풍화 상태를 예측하는데 사용될 수 있도록 설계된 프로그램이다. 따라서 본 모형에서는 앞서 소개된 부유물 추적 모의방법이나 단순 입자법에 의한 유류이송확산이 아닌, 유류의 물리적 성질인 유막을 Lagrangian 좌표의 형태로 표현하여 실제적인 유류 이송-확산-변형을 모의하도록 노력하였다. 또한 해역에서의 유류의 움직임은 통상 난류 성분에 의해 발생한 분산과 함께 대규모 유동장에 의한 이류에 종속되게 된다. 유류가 움직일 동안 물리적 및 화학적 공정으로 알려진 풍화 공정 때문에 또한 유류의 농도가 변화된다. 이러한 일련의 과정이 앞서 소개한 기존의 모형에서는 고려되지 못한 바 있으므로 본 모형에서는 유류의 풍화과정 또한 고려하도록 개발되었다. 본 논문에서는 해당 모형의 이론내용을 아래와 같이 간략하게 소개하고자 하며 상세한 내용은 Dominicis et al.(2013)을 참고하기 바란다.
유류의 추적자 농도인 C(x, y, z, t)는 단위체적당 질량의 단위를 지닌 해역상에의 유류농도이며 아래 이송-확산-변형 방정식을 따른다.
여기서 좌변의 첫 번째 항은 시간에 대한 편미분항으로써, 국부적인 유류 농도변화를 나타낸 항이고, 벡터성분인 U는 해역에서의 흐름요소을 의미하며, 각 방향별 유속성분인 (U, V, W)를 요소로 갖는다. 또한, K는 난류효과를 파라미터로 나타낸 확산계수 Tensor이고 rj(C)는 유류의 변형 정도, 즉 물리적, 화학적 변형과정에 의한 농도 수정성분을 나타낸다. 한편, 식(4)을 대상으로 Eulerian 좌표계에서 수치적으로 표현하는 방식은 해양학 등에서도 이미 잘 알려진 바 있다(Noye, 1987).
식(4)을 대상으로 효과적인 수치차분을 통해 수치해를 구하기 위하여, 능동적 추적자(Active tracer) 방정식을 두 개의 구성방정식으로 분할할 수 있으며 그 식들은 아래와 같다.
C1은 오로지 풍화 과정에 변화하는 유류의 농도성분이다. C의 시간변화율은 C1의 이송 및 확산 작용에 의해 주어지게 된다. 위 식(6)은 환경공학, 수리학, 생태학 등에서 광범위하게 사용되는 일반적인 이송-확산-변형 방정식이다. 한편, 식(5)는 전체 유막의 체적의 변형 작용에 의해 고려된 식이라고 할 수 있으며 유막의 상태변수로 정의된다. Lagrangian 입자 형식을 대상으로 한 방정식은 식(6)에 나타내며 유류의 농도 C는 표면 유류 농도 등으로 구성된 (CS, CD, CC, CB)로 나누어진다. 우선 수표면에서의 농도 CS는 아래 식으로 표현된다.
여기서 m은 유류의 중량, A는 해당 표면적이며 체적과 밀도로 표현하면 식(8)로 표현될 수 있다.
해수의 표면 아래에서는 다양한 크기의 작은 방울로 형성된 유류가 유막의 표면 또는 바닥의 침전물과 함께 다시 합쳐질 수 있다. 이 때문에 표면 아래 또는 분산된 유류의 농도 CD는 아래와 같이 유류의 체적 VD로 표현할 수 있다.
또한, 식(5)에 사용되는 CS와 CD를 각각 유류의 체적으로 표현하면 식(10)과 식(11)로 나타낼 수 있다.
표면 기름이 해안에 가까이 도착하면, 참조위치(Reference Segment)로 정의된 LC와 해안에서의 기름 흡착 농도인 CC로 정의된다.
마지막으로 바닥에서의 유류 농도는 CB로 표현된다. 한편 유막의 얇은 부분 체적은 VTN, 두터운 부분 체적은 VTK으로 표면체적을 세분화하여 식(10), (11)을 해결한다.
여기서 ATK, ATN은 각각 두껍고 얇은 부분의 유막 표면적이고, TTK, TTN는 표면두께를 나타낸다. 따라서 식(9) 등과 입자상태변수로 정의된 CS, CD, CC는 이송-확산-변형과정으로 해석된다. 한편 이송-확산-변형과정을 풀기 위해, 표면 체적 VS는 입자 체적(υ(nk, t)), 입자상태지수(σ(nk, t)) 및 입자 위치 벡터로 특징지어진 N개의 구성성분 입자로 나누어 나타낸다.
여기서 nk는 입자식별번호이다. 입자 위치 벡터 xk(nk, t)의 시간에 따른 변화는 Langevin의 방정식에 의해 주어질 수 있으며, Mackay’s의 개념화된 모델에 따르면 입자체적상태변수는 내부적으로 증발(υE(nk, t))과 비증발(υNE(nk, t))로 세분화된다(Table 1 참조).
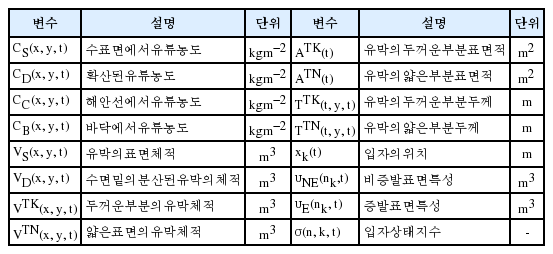
State variables in oil spill model (Dominics et al., 2013)
이러한 입자체적 υ(nk, t)는 매시간간격마다 경험식에 의해 갱신된다. 또한 식(4)에 의한 완벽한 이송-확산 및 변형 문제를 풀기 위해, 수치격자에서 입자의 개수를 매 시간 산정하게 된다. 마지막으로 본 모형은 앞서 설명한 바와 같이, 이송-확산-변형(풍화)의 과정이 두 개의 식으로 분할되어 표현되었으며(즉, 이송-확산과 변형(풍화)), 유류의 총 농도를 통해 서로 종속되어 있다. 이렇게 분할된 식은 서로 다른 좌표체계에서의 계산이 진행되는데, 변형(풍화)의 경우 연속적인 농도분포를 나타내는 체적 및 질량의 개념으로 산출되고, 이송-확산의 경우 입자를 기반으로 하여 Lagrangian 좌표계에서 계산되게 된다. 따라서 두 식이 자연스럽고 정확하게 연계되기 위해서는 Eulerian 좌표계와 Lagrangian 좌표계 간의 변환이 필수적이다. 본 모형은 이를 고려하여, 입자농도의 유한한 표현과 체적에 의한 연속적 표현을 연계하였다. 보다 자세한 내용은 Dominicis et al.(2013)에 기술되어 있으므로 참고하기 바란다. Table 1에서는 본 모형에 사용되는 상태변수를 요약하여 설명하였다.
2.3 동수역학 모형과 유류 이송-확산-변형 모형 간 결합모형 구축
본 연구에서는 Boussinesq 모형과 오염물질 이송-확산-변형 모형(MEDSLIK-II)간 외적 결합을 통하여 결합모형을 구축하고자 한다. 즉, 해역에서의 파랑 및 조류 흐름 상태를 Boussinesq 모형으로 예측하고 그 결과에 의하여 유류가 이송-확산-변형되는 양상을 모의하게 되는 것이다. 앞서 언급한 대로 MEDSLIK-II모형은 지중해 지역의 해상풍 및 해역예측망 시스템에 의한 정규화된 해역정보를 수동적으로 활용하는 모형이므로 동수역학 모형인 Boussinesq 모형과 결합을 통해서 파랑에 의한 이송확산 효과 고려, 사전 유류유출 모의 등 정확도 및 방제분야 활용성을 확대하고자 하였다. 다만, 두 모형의 기본 좌표계가 각각 Eulerian과 Lagrangian으로 다른 형태를 지니기 때문에 이들 상호간의 정보 교환시 정확한 위치에서의 정보가 공유되기 위한 면밀한 고려가 필요하며, 이를 통해서 외적 결합이 성공적으로 이루어 질 수 있을 것이다. 즉, MEDSLIK-II의 경우 이송-확산-변형의 과정이 식(4)에서 제시된 바대로 Eulerian 좌표계상에서 묘사되며 이를 활용해 Lagrangian 좌표 기반의 유막, 유류입자, 구조적 변수 등에 대한 계산이 이루어 진다. 따라서 공간적으로는 Boussinesq 모형에서 산출된 Eulerian 기반의 흐름정보가 MEDSLIK-II에 전달되어 Eulerian 기반의 정보로 입력 및 활용되고, 시간적으로는 Boussinesq모형의 흐름정보를 정규화된 시점의 정보로 추출함으로써 두 모형간 시간적 분포를 일치하도록 하였다.
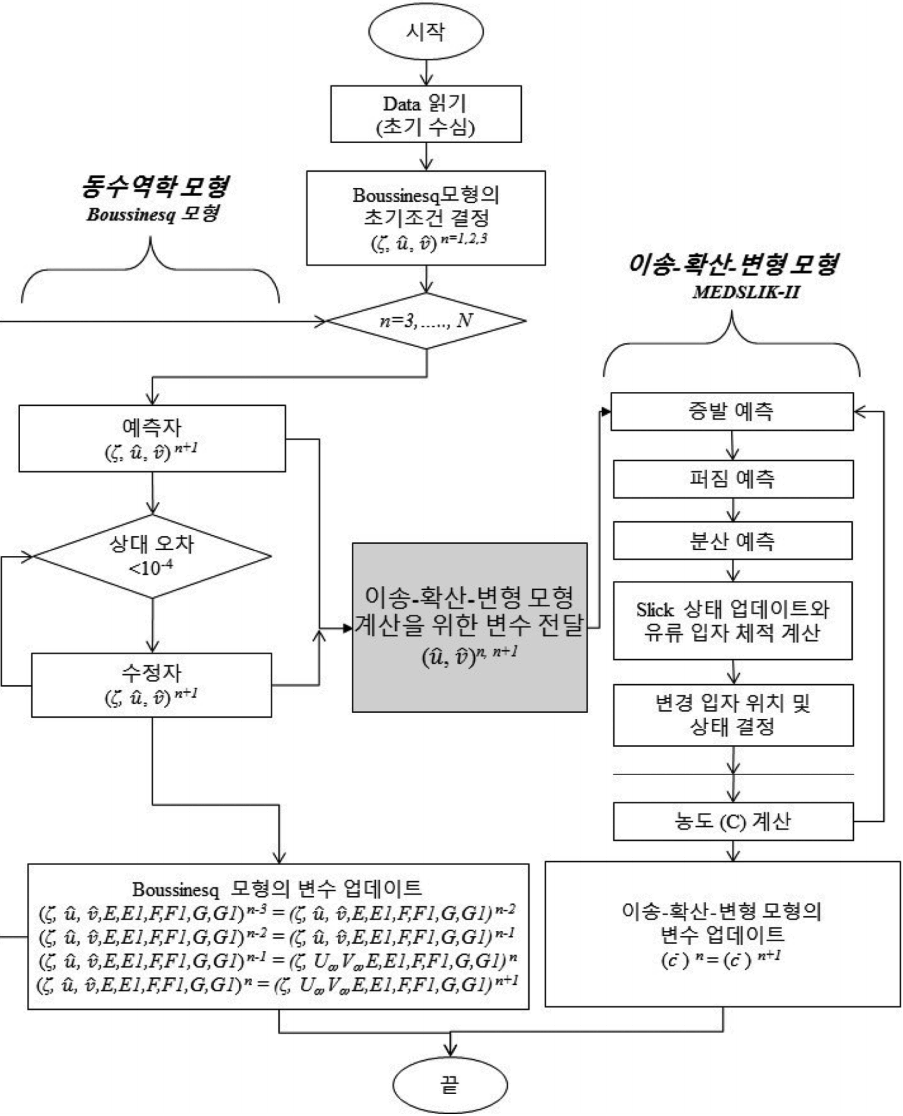
Fig. 1은 이러한 과정을 기반으로 이들 두 모형이 이론적으로 결합되는, 즉 정보를 교환하는 순서를 나타내고 있으며, 최종적으로 유류의 이송과 변형, 풍화상태 등을 모의결과로 보여줌을 알 수 있다. 이를 순서대로 설명하면, Boussinesq 모형에서 예측자-확인자 수치해석방법에 의해 유속정보가 산출되면 MEDSLIK-II 모형에 전달되고 이는 Eulerian 좌표계에서의 정보이므로 Lagrangian 좌표계로 변환되는 과정을 거친 후, 유류의 이송-확산-변형 계산에 활용된다. 이후 전달된 유속 정보 및 입력 조건에 의해 추가된 풍속 정보를 바탕으로 유류 체적에 대한 풍화 과정과 유류 입자에 대한 이송-확산-변형 과정이 순차적으로 계산된다. 마지막 단계로써, 다음 시간단계에서의 계산을 위해 흐름 정보를 통한 유류 입자의 위치 변화와 농도변화를 Update하게 된다. 이러한 일련의 과정이 초기시간부터 종료시간까지 반복적으로 이루어지면서 수치해석이 진행되게 된다.
Diagram depicting coupling process between hydrodynamic model and oil advection-diffusion-transformation model.
3. 수치해석 결과
3.1 대상지역 선정
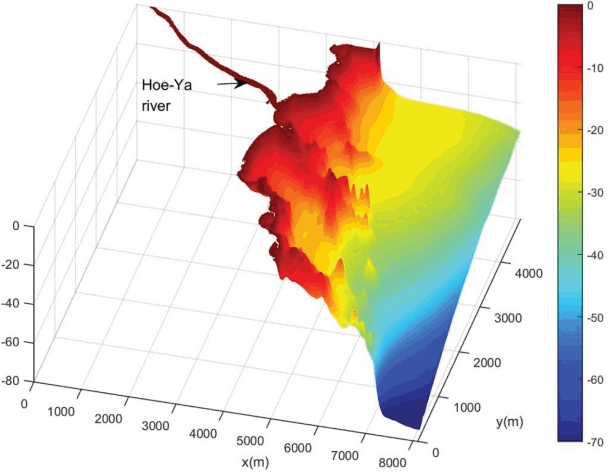
모형 적용 대상지역 선정에 있어 진하해역은 회야강 하구역과 작은 도서지역(명선도) 등을 포함하고 있어 흐름의 양상이 다른 지역과 달리 복잡할 것으로 예상되는 바, 개발 모형을 보다 복잡한 해역조건에 적용하기 위해서 해당해역을 대상지역으로 선정하였다. 한편, 진하해역의 수치지형 구성을 위해 해양조사원에서 발행하는 전자해도를 활용하였으며, 이는 수치격자 작성을 위한 입력자료를 전달되었다. Fig. 2는 수치화된 진하해역 일원의 지형을 나타내고 있다.
Bathymetry of Jinha beach connected to Hoe-Ya river.
3.2 실해역 유류 이송-확산-변형 모의결과
선정된 해역에 대해 동수역학적 모형인 Boussinesq 모형을 적용하였고, 그 과정에서 시범지역에 해당되는 진하해수욕장 해역의 수치 해석이 행해졌다. 외해의 경계조건으로는 해양조사원에서 운영하는 울산 조위관측소 자료를 참조하여 대표기간(2014년 6월 4일, Fig. 3 참조)의 관측 수위자료를 직접 입력하였다. 해당 자료는 Fig. 3에서 알 수 있듯이 장주기의 조석성분과 단주기의 파랑성분의 합성으로 구성되어있어 파랑과 조석의 상호작용을 고려하도록 선택되었다. Boussinesq 모형의 모의격자는 약 13.7 m 간격으로 하여 601개 × 367개의 고해상도 격자로 구성하였으며 모의 시간은 만조시와 간조시를 각각 포함할 수 있도록 13시간으로 설정하였다. 이를 바탕으로 수치해석을 실행하여 우선 조석-파랑 흐름상태에 대한 결과가 도출되고, 각 시간에서의 유속 성분은 유류의 이송-확산-변형 모형으로 전달되어 해상풍 정보와 함께 유류의 확산 및 농도변화 수치계산에 활용되었다. 이 때, 해상풍 정보 역시 해당시점의 울산 조위관측소 자료를 참고하였다.
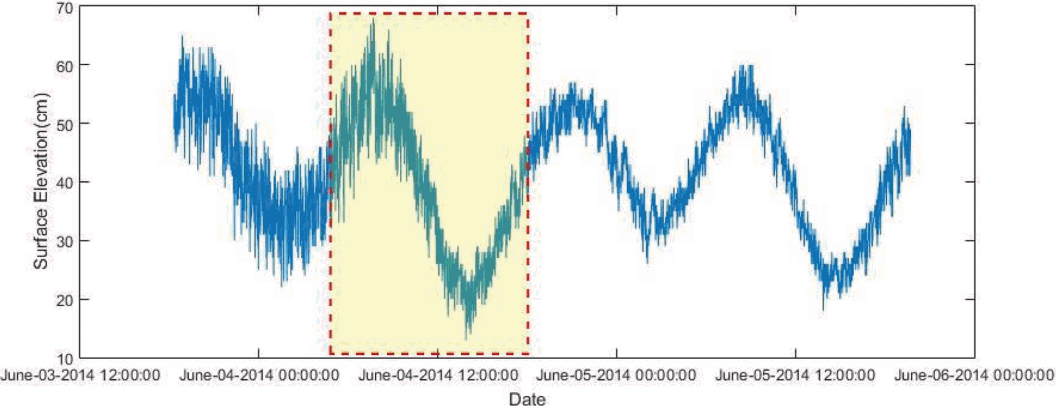
Surface elevation record at the offshore boundary (Yellow window defines the time span applied for the simulation).
이러한 과정을 통해 진하해역 및 인근지역에 발생할 수 있는 기름유출사고를 사전 모의해보고 이 결과는 방제대책 수립에 활용 가능할 것으로 기대할 수 있다. 각각 다른 조석-파랑 위상에서 산출된 흐름상태를 Fig. 4에 예시적으로 나타냈으며 이 결과는 유류 이송-확산-변형의 최종 결과 산출을 위해 MEDSLIK-II에 입력조건으로 전달되었다.
Instantaneous hydrodynamics at phases corresponding to t = 1.5 hrs (left) and t = 4 hrs (right). Vectors indicate current speed and color contours represent water levels.
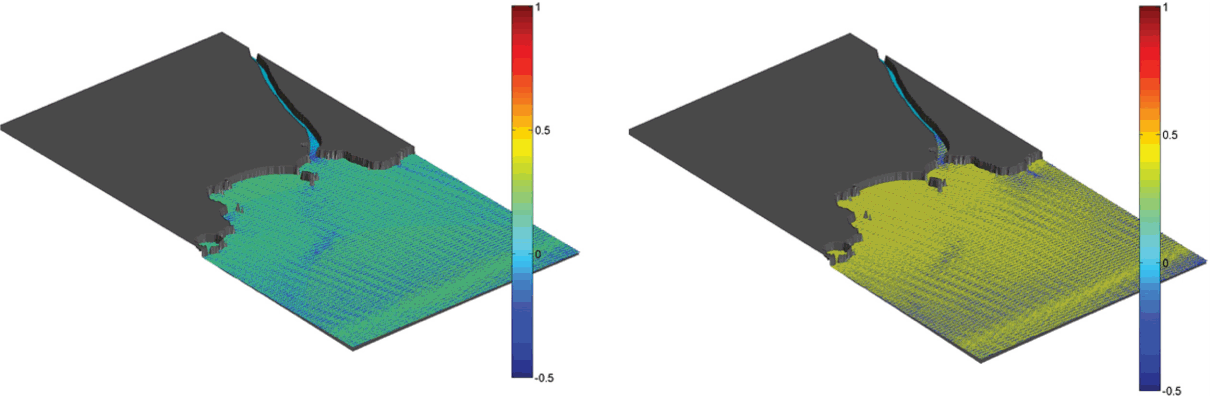
이로써 동수역학모형에서 계산된 유속정보를 기초로 하여 대상지역인 진하해역의 유출유의 이송-확산-변형을 모의할 수 있었다. 이 때 유류의 유출은 순간유출과 지속유출의 2가지 경우를 가정하였다. 즉 해상선박의 추돌 등에 따른 제한된 양의 유류유출사고와 해저유류수송 파이프라인의 파손 등과 같은 지속적인 유류유출사고를 모의하고자 하였다. 순간유출의 경우 유출량을 684.42톤으로 설정하고 지속유출의 경우 시간당 68.44톤으로 설정하였으며 각각의 모의 결과는 Fig. 5와 Fig. 6에 도시하였다. Fig. 5는 다양한 위상에서 순간 유출한 유류의 이송-확산-변형을 나타내고 있으며 Fig.6은 연속 유출하는 유류의 이송-확산-변형을 보여주고 있다.
Simulation results of instantaneous oil spill off the Jinha coast. Time elapses from upper left to lower right direction for entire tidal period and color contour represents concentration of oil slick.
Simulation results of continuous oil spill off the Jinha coast. Time elapses from upper left to lower right direction for entire tidal period and color contour represents concentration of oil slick
4. 결론 및 토의
본 연구에서는 최근 발생빈도가 잦아지고 있는 유류사고에 대비하여 정확도 및 적용성을 높인 수치해석모형을 개발하였다. 기존에 개발 및 활용되었던 모형들은 여러 가지 한계점(유류의 물리적, 화학적 변형 미고려, 저해상도 해석, 파랑의 분산성 및 난류효과 미고려 등)을 드러내고 있으며, 이러한 이유로 현재까지 유류유출에 대한 정도 높은 해석이 이루어지지 못하고 있는 실정이다. 본 연구에서 사용된 모형은 유류의 풍화작용 뿐 아니라 해상풍의 영향, 고해상도의 격자사용, 흐름(파랑)의 분산성 및 근해역에서의 난류효과 등을 포괄적으로 고려함으로써 해석결과의 신뢰도 향상 가능성을 제시하고자 하였다. 개발된 모형은 대표적 해상조건(2014년 6월 3일 울산 진하해역)에의 적용을 통해 파랑과 조석이 혼재한 흐름상태에서의 유류 이송-확산-변형의 유형을 시범적으로 파악하였고, 지형적 복잡성 및 그에 의한 실제 흐름의 성질을 나타낼 수 있는 지역에 예시적으로 적용함으로써 결합모형의 활용성을 검토하였다. Boussinesq 모형의 경우 수심방향의 유속 또는 압력의 분포를 수학적 기법을 통해 간략화하여 고려하고 있으므로 3차원 모형에 비해 간편하면서도 비교적 정도 높게 광역의 흐름모의 해석이 가능하다는 장점을 지니고 있지만, 3차원 모형과의 분명한 정확성 차이를 고려한다면 추후 3차원모형으로의 확장을 통해 결합모형의 정확성을 향상시키기 위한 노력이 요구된다. 마지막으로 유출사고 초기에 적절한 예측이 이루어지지 않은 태안 기름유출 사고의 사례에서 보듯이, 현재까지 재난안전 관련부처 등에서는 기름유출 양상에 관한 신속하고 정확한 데이터 및 방제활동에 필요한 적절한 유출예측시스템을 갖추지 못하고 있다고 판단되기에 본 연구결과는 추후 해양 기상의 극한조건에서 유류유출 재해에 대비할 수 있는 방재시스템 구축에 도움이 될 수 있을 것으로 판단되며 나아가 유류 유출사고에 대한 산업적, 환경적, 경제적 피해를 최소화시킬 것으로 기대된다. 다만, 본 논문의 연구결과는 결합모형의 예시적 모의를 통해 순간/지속유출 상황에의 적용가능성만을 제시하므로, 후속연구를 바탕으로 실제 유출상황 및 다양한 조건에서의 모의를 진행하여 결합모형의 신뢰성을 폭넓게 검증할 계획이다.
Acknowledgements
첫 번째 및 두 번째 저자는 국민안전처 재난관리지원기술개발사업에 의해 연구비 지원(2017-MPSS31-001)을 받아 연구를 수행하였으며 네 번째 저자는 2016년도 한밭대학교 교내학술연구비의 지원을 받아 연구를 수행하였습니다.